Метод половинного деления (метод дихотомии или метод бисекции)
Теорема 2. Итерационный процесс половинного деления сходится к искомому корню ξ с любой наперед заданной точностью ε.
Доказательство: Рассмотрим последовательность чисел ξi являющихся приближением корня на i -ом шаге.
ξi=½(bi+ai), i=0,1.
где a0=a; b0=b; ai;bi – границы подынтервалов, в которых f(ai)f(bi) 0 мы ни задали, всегда можно найти такое n , что  ч.т.д.
ч.т.д.
Графически метод дихотомии выглядит следующим образом

|f(c)|≤δ f(a)f(c) 10 = 1024 ≈ 10 3 раз. За 20 итераций (n=2) уменьшается в 2 20 ≈ 10 6 раз.
Пример №1 . Найти экстремум функции: y=5x 2 -4x+1 методом дихотомии, если ε=0.1, а исходный интервал [0,10].
- Решение
- Видео решение
Пример №3 . Методом бисекции найти решение нелинейного уравнения на отрезке [a,b] с точностью ε = 10 -2 . Выбрав полученное решение в качестве начального приближения, найти решение уравнения методом простой итерации с точностью ε = 10 -4 . Для метода простой итерации обосновать сходимость и оценить достаточное для достижения заданной точности число итераций.
sqrt(t)+x 2 = 10, a = 2.6, b = 3
Найдем корни уравнения: 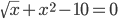
Используем для этого Метод половинного деления (метод дихотомии)..
Считаем, что отделение корней произведено и на интервале [a,b] расположен один корень, который необходимо уточнить с погрешностью ε.
Итак, имеем f(a)f(b) 1 /2(a+b) и вычисляем f(c). Проверяем следующие условия:
1. Если |f(c)| 1 /2 n (b-a)
В качестве корня ξ. возьмем 1 /2(an+bn). Тогда погрешность определения корня будет равна (bn – an)/2. Если выполняется условие:
(bn – an)/2 1 /2(an+bn).
Решение.
Поскольку F(2.6)*F(3) 0, то a=2.8
Итерация 2.
Находим середину отрезка: c = (2.8 + 3)/2 = 2.9
F(x) = 0.113
F(c) = -0.487
Поскольку F(c)•F(x) 0, то a=2.825
Остальные расчеты сведем в таблицу.
| N | c | a | b | f(c) | f(x) |
| 1 | 2.6 | 3 | 2.8 | -1.6275 | -0.4867 |
| 2 | 2.8 | 3 | 2.9 | -0.4867 | 0.1129 |
| 3 | 2.8 | 2.9 | 2.85 | 0.1129 | -0.1893 |
| 4 | 2.8 | 2.85 | 2.825 | -0.1893 | -0.3386 |
| 5 | 2.825 | 2.85 | 2.8375 | -0.3386 | -0.2641 |
| 6 | 2.8375 | 2.85 | 2.8438 | -0.2641 | -0.2267 |
Ответ: x = 2.8438; F(x) = -0.2267
Решение было получено и оформлено с помощью сервиса Метод Ньютона онлайн
Пример №2 . Локализовать корень нелинейного уравнения f(x) = 0 и найти его методом бисекции с точностью ε1 = 0,01. Выбрав полученное решение в качестве начального приближения, найти решение уравнения методом простой итерации с точностью ε2 = 0,0001. Для метода простой итерации обосновать сходимость и оценить достаточное для достижения заданной точности ε2 число итераций.
Метод половинного деления
Домашняя лабораторная работа по теме «Приближенное решение уравнений с одной переменной»
Задание. Найти один из корней уравнения методом деления отрезка пополам (методом Фибоначчи, «золотого сечения», рандомизации) с точностью до : 1) отделить корень на отрезке , проверить его единственность; 2) реализовать один из методов деления отрезка в заданном отношении (использовать ЭВМ или калькулятор); 3) сделать проверку точности найденного решения подстановкой его в исходное уравнение.
Порядок выполнения работы
1) Графическое отделение корня в случае достаточно сложного выражения y=f(х) можно производить следующим образом. Допустим, что уравнение можно представить в виде f1(x) = f2(x). В этом случае строим графики функций у=f1(x) и y=f2(x); абсциссы точек пересечения кривых будут действительными корнями уравнения. Найдем, например, приближенно корни уравнения x-sin x-1 = 0, записав это уравнение в виде x-1 = sin x. Построим графики функций y = sin x и у = х-1 (рис.2). Точка пересечения этих линий имеет абсциссу х ≈ 1,9, что можно считать грубым приближением значения корня.
Интервал [а;b] является интервалом изоляции корня, если его можно считать настолько малым, что на нем лежит точно один корень исходного уравнения. Выбор этого интервала производится на основании свойства непрерывных функций: если функция у=f(x) непрерывна на отрезке [а;b] и на концах отрезка принимает значения разных знаков (f(a)f(b) 3 +x 2 -1=0. Для этого представим уравнение в виде: х 3 =1-x 2 , т. е. f(x)=x 3 и g(x)=1-x 2 . Построим приближенно графики функций y=f(x) и y=g(x) (рис 4). Точка пересечения графиков двух функций, а значит, и корень уравнения находится на отрезке [0;1]. Проверим аналитические условия: f(0)=0 3 +0 2 -1=-1 3 +1 2 -1=1>0, и f'(х)=3х²+2x>0 на отрезке [0;1]. Таким образом, мы определили интервал изоляции корня, для нахождения которого достаточно применить любой из аналитических методов численного решения уравнений.
Задача отыскания корней уравнений может считаться практически решенной, если удалось определить корни с нужной степенью точности и указать пределы возможной погрешности.
Метод половинного деления
Рассмотрим один из самых простых численных методов решения уравнений – метод половинного деления. Пусть для уравнения найден интервал изоляции корня – отрезок [а;b]. Для уточнения искомого корня отрезок [а;b] делим пополам и из двух, полученных в результате этого деления отрезков выбираем тот, для которого выполняются условия существования и единственности корня (на концах отрезка функция принимает значения разных знаков). Середину отрезка находим по формуле хi=(a+b)/2, i=1,2,3…, и продолжаем данный процесс пока не достигнем необходимой точности (рис.5).
Рассмотрим применение метода половинного деления на примере решения уравнения х 3 +x 2 -1 = 0 на отрезке [0;1]. Разделим интервал изоляции пополам – это точка х=0,5. Получим два подотрезка – [0;0,5] и [0,5;1]. Вычислим значения функции на концах отрезков, f(0)=-1 3 +0,5 2 -1=0,125+0,25-1=-0,625 3 +1 2 -1=1+1–1=1>0, т. е. на концах отрезка [0,5;1] функция имеет значения разных знаков, следовательно, корень уравнения принадлежит отрезку [0,5;1]. Выбираем этот отрезок для дальнейшего рассмотрения.
Повторяем метод половинного деления уже для нового отрезка. Середина отрезка x=(0,5+1)/2=0,75, и из двух полученных отрезков выбираем правый отрезок [0,75;1], т.к. f(0,75) = -0,015625 0. Процесс продолжается до получения корня с заданной степенью точности.
Если делить отрезок [a;b] сразу на десять частей, то на следующем шаге можно получить отрезок в десять раз меньший, чем [a;b].
2. Метод Фибоначчи
Рассмотрим одну из разновидностей метода половинного деления – метод Фибоначчи.
Пусть дано уравнение , где функция у= непрерывна на и . Для уточнения корня данного уравнения введем последовательность чисел Фибоначчи: , , , это будут числа 1,1,2,3,5,8,13,21 и т.д. Согласно данному методу, на каждом ом этапе отрезок делят в отношении , где и соответственно е и е число из последовательности Фибоначчи. Так на первом шаге отрезок делят в отношении (пополам) и выбирают тот из них, на концах которого функция имеет разные знаки. На втором этапе выбранный суженный отрезок делят в отношении , следующие в отношениях , , В результате получаем на некотором этапе точный корень уравнения, или же бесконечную последовательность отрезков таких, что (n=1,2,…). Формула для вычисления имеет вид: В качестве корня можем принять .
Метод половинного деления. Алгоритм
Решение алгебраического уравнения. Для численного решения алгебраических уравнений существует множество способов. Среди самых известных можно назвать метод Ньютона, метод Хорд, и «всепобеждающий» метод Половинного Деления. Сразу оговоримся, что любой метод является приближенным, и по сути дела лишь уточняющим значение корня. Однако уточняющим до любой точности, заданной Нами.
Метод половинного деления или дихотомии (дихотомия – сопоставленность или противопоставленность двух частей целого) при нахождении корня уравнения f(x)=0 состоит в делении пополам отрезка [a; b], где находится корень. Затем анализируется изменение знака функции на половинных отрезках, и одна из границ отрезка [a; b] переносится в его середину. Переносится та граница, со стороны которой функция на половине отрезка знака не меняет. Далее процесс повторяется. Итерации прекращаются при выполнении одного из условий: либо длина интервала [a; b] становится меньше заданной погрешности нахождения корня ?, либо функция попадает в полосу шума ?1 – значение функции сравнимо с погрешностью расчетов.
Сначала поставим задачу. Дана монотонная, непрерывная функция f(x), которая содержит корень на отрезке [a,b], где b>a. Определить корень с точностью ?, если известно, что f(a)*f(b) Дано уравнение вида:
необходимо найти удовлетворяющие ему значения x.
Итак, приступим к решению. Первым делом, определимся, что значит f(x)=0. Посмотрите на рис.1. На нем изображен график некоей функции. В некоторых точках этот график пересекает ось абсцисс. Координаты x этих точек нам и нужно найти. Если вид уравнения простой или стандартный, например, квадратное уравнение или линейное, то применять численный метод здесь совершенно ни к чему. Но если уравнение у нас такое:
то ни в каком учебнике вы не найдете метода аналитического решения этого кошмара. Здесь и приходит на помощь непобедимый численный метод. Метод половинного деления. Из самого названия метода можно предположить, что нам понадобится что-то делить пополам.
Ученикам метод половинного деления можно преподнести в виде решения задачи.
Идет осада неприятельской крепости. На некотором расстоянии от нее установили новую пушку. Под каким углом к горизонту надо стрелять из этой пушки, чтобы попасть в заданный участок крепостной стены.
Над моделью этой задачи физики изрядно поработали. Оно и понятно: ведь многие научные задачи, как и эта, возникали прежде всего в военном деле. И решение этих задач почти всегда считалось приоритетным.
Какие же факторы принять за существенные в этой задаче? Поскольку речь идет о средневековье, то скорость снаряда и дальность полета невелики. Значит можно считать несущественным, что Земля круглая (помните обсуждение в параграфе 27), и пренебречь сопротивлением воздуха. Остается единственный фактор – сила земного притяжения.
Математик тут бы сказал, что надо решить уравнение. Мы тоже будем решать, только приближенно и очень похоже на то, как делают настоящие артиллеристы. Они же поступают следующим образом: производят несколько выстрелов, беря цель «в вилку», т.е. одно попадание выше цели, а другое ниже. Затем делят пополам угол между этими выстрелами, и при стрельбе под таким углом снаряд ложится к цели намного ближе. Но если все же не попали, то новую «вилку» снова делят пополам и т.д.
Мы заранее можем указать «вилку» для угла: 0 и ?/4 (мы надеемся, что вы помните какой угол имеет радианную меру ?/4 и чему приближенно равно ?). А дальше будем делить пополам эту «вилку» и смотреть, куда попадает снаряд, пока не добьемся нужного результата.
Как же долго нам придется вести «пристрелку», чтобы получить угол ?, с нужной точностью? Чтобы ответить на этот вопрос, отвлечемся от нашей задачи и сформулируем на чисто математическом языке, что и как мы находили.
Нам даны некоторая функция f(x) и отрезок [a;b], причем на концах этого отрезка эта функция принимает значения противоположных знаков. Если функция непрерывна, т.е. ее график – непрерывная линия, то ясно, что график функции пересекает ось абцисс в некоторой точке с отрезка [a;b], как показано на рисунке 1. Иными словами, f(c)=0, т.е. с – корень уравнения f(x)=0.
Как же предлагается находить этот корень? А вот так. Делим отрезок [a;b] пополам, т.е. берем середину отрезка а+b/2. В этой точке вычисляем значение функции f(x) (рис. 2). Если это значение 0, то корень найден; если нет, то оно имеет тот же знак, что и значение на одном из концов отрезка [a;b]. Тогда этот конец заменям точкой а+b/2. Новый отрезок тоже содержит корень уравнения f(x)=0, поскольку на его концах функция f(x) снова имеет разные знаки. Однако этот отрезок в 2 раза короче предыдущего. И самое главное – с ним можно поступить точно так же. со следующим отрезком еще раз проделать то же самое и т.д. поскольку длина отрезка каждый раз уменьшается вдвое, мы можем получить отрезок сколь угодно малой длины, внутри которого содержится корень уравнения f(x)=0. Например, если исходный отрезок был [3;4], т.е. имел длину 1, то через десять шагов мы получим отрезок длиной. Это означает, что концы отрезка дают нам приближенное значение корня с точностью, равной длине отрезка: левый конец отрезка – приближенное значение корня с недостатком, правый конец – приближенное значение корня с избытком.
Фактически мы сейчас сформулировали метод приближенного решения уравнения f(x)=0. Его можно было бы назвать методом артиллерийской пристрелки. Но математики называют его методом половинного деления.
Далее ученикам предлагается записать алгоритм и блок-схему нахождения корня уравнения с помощью метода половинного деления.
1) Найдем середину отрезка [a; b]: c=(a+b)/2;
2) Вычислим значения функции в точках a и c и найдем произведение полученных значений: d=f(c)?f(a);
3) Если d>0, то теперь точкой a станет c: a=c; Если d ?, то идем в пункт 1) если нет, то корень с нужной нам точностью найден, и он равен: x=(a+b)/2;
[spoiler title=”источники:”]
http://megaobuchalka.ru/3/14610.html
http://www.apxu.ru/article/geoforma/obey/metod_polovinnogo_delenia_algoritm.htm
[/spoiler]
Метод
основан на делении текущего отрезка
[а,
b],
где
содержится искомый экстремум, на две
равные части с последующим выбором
одной из половин, в которой локализуется
минимум (максимум) в качестве следующего
текущего отрезка. Экстремум локализуется
путем сравнения двух значений критерия
оптимальности в точках, отстоящих от
середины отрезка на ε/2,
где ε
–погрешность решения задачи оптимизации.
Если
R(x
+ ε/2)
> R(x
–
ε/2),
то максимум располагается на правой
половине текущего отрезка [а,
b],
в
противном случае – на левой.
Процесс
поиска завершается при достижении
отрезком [а,
b]
величины
заданной погрешности е
ε.
К
недостаткам метода относится его
работоспособность только для
одноэкстремальных функций R(x)
(т.е. таких, которые содержат один
экстремум того типа, который мы ищем в
задаче), так как в других случаях при
сравнении двух критериев в соседних
точках невозможно правильно выбрать
следующий интервал, где находится
минимум (максимум).
На
рис. 2 приведены три этапа метода
половинного деления. Сплошными
вертикальными линиями отмечены середины
отрезков, а пунктирными – вычисляемые
значения критерия оптимальности слева
и справа на ε/2
от середин.

Рис.
2. Иллюстрация
метода половинного деления: 1 – интервал,
включающий в себя искомый максимум
функции после первого этапа (первого
деления пополам); 2, 3 – то же соответственно
после второго и третьего этапов
Существует
и другой вариант алгоритма, заключающийся
в следующем. После нахождения середины
отрезка (например, точка с1)
в одной из половинок (допустим, в левой)
находят среднюю точку (точка с2
и,
сравнивая значения функции в этих
точках, определяют, в какой из половинок
находится экстремум. Если R(с1)<
R(с2),
то в качестве следующего отрезка выбираем
отрезок [а, с1],
если же R(с1)>
R(с2),
то
берут новую точку в середине правой
половины (точка с3)
и в ней вычисляют функцию. В зависимости
от сравнения значений функции в
точках с3
и с1
выбирают новый отрезок [с1,
b]
или
[с2,
с3]
и т.д.
Второй
вариант метода не имеет с точки зрения
эффективности принципиального отличия
от первого, так как эффективность принято
оценивать по наихудшему варианту (т.е.
по двум вычислениям R(x)
на
каждом шаге). В первом варианте метода
есть одна особенность, которая его
делает очень эффективным при
экспериментальном отыскании экстремума
(например, при автоматической настройке
технических систем или при практическом
поиске наилучших условий деятельности
экономического объекта). Малые отклонения
от текущей точки обеспечивают в процессе
поиска отсутствие “шараханий”,
сопровождающихся резкими отклонениями
состояния системы.
Алгоритм метода дихотомии для минимизации функции.
Начальный
этап. Выбрать
константу различимости 2ε > 0 и допустимую
конечную длину интервала неопределённости
l
> 0. Пусть [а1,
b1]
– начальный интервал неопределённости.
Положить k
= 1 и перейти к основному этапу.
Основной этап.
Шаг
1. Если bk
– ak
< l,
то остановиться; точка минимума
принадлежит интервалу [аk,
bk].
В противном случае вычислить
![]() и
и![]()
и перейти к шагу 2.
Шаг
2.
Если R(pk)
< R(qk),
положить
ak+1
= ak
и bk+1
= qk.
В противном случае положить ak+1
= pk
и bk+1
= bk.
Заменить k
на k
+
1 и перейти к шагу 1.
Пример.
Дана
функция R(x)
= D
sin(АхB
+ С), где
коэффициенты имеют следующие значения:
А
=1,0,
В = 1,0,
С
= 1,0,
D
= 1,0.
Найти максимум на интервале: [-1, 2]. Ошибка
задается по х:
ε
=0,05.
Результаты
расчетов. Середина отрезка x0
= 0,5000, значение критерия R0
=
0,9975, значение R(0,5
– ε/2)
=
R(0,475)
= 0,97922273, значение R
(0,5 + ε/2)
= R
(0,525) = 0,9989513. Следовательно, искомый
максимум лежит в правой половине отрезка,
т.е. теперь отрезком является [0,5, 2].
Далее приводятся
только координаты середин отрезков с
номером итерации, значения критерия
в них и указывается новый отрезок (правый
или левый).
x1
= 1,25000000 R1
= 0,77807320 левый
х2
= 0,87500000 R2
=
0,95408578 левый
x3
= 0,68750000 R3
= 0,99319785 левый
x4
=
0,59375000 R4
= 0,99973658 левый
x5
=
0,54687500 R5
= 0,99971390
|х4
– x5|
< ε,
поэтому в качестве решения можно принять
любое из этих значений или середину
между ними.
Всего
восемь раз (4·2 = 8) вычислялся критерий
оптимальности (не считая вычислений
непосредственно в середине отрезка,
которые не используются в алгоритме
метода).
Соседние файлы в папке Системный анализ и принятие решений
- #
- #
27.02.2016389.68 Кб50Тугаринов.xmcd
Материал из MachineLearning.
Перейти к: навигация, поиск
Содержание
- 1 Введение
- 2 Метод половинного деления
- 2.1 Метод половинного деления как метод поиска корней функции
- 2.1.1 Изложение метода
- 2.1.2 Реализация метода на С++ и числовой пример
- 2.2 Метод половинного деления как метод оптимизации
- 2.1 Метод половинного деления как метод поиска корней функции
- 3 Метод хорд
- 3.1 Изложение метода
- 4 Комбинация метода хорд и метода половинного деления
- 5 Список литературы
- 6 См. также
Введение
Существует довольно очевидная теорема: “Если непрерывная функция на концах некоторого интервала имеет значения разных знаков, то внутри этого интервала у нее есть корень (как минимум, один, но м.б. и несколько)”. На базе этой теоремы построено численное нахождение приближенного значения корня функции. Обобщенно этот метод называется дихотомией, т.е. делением отрезка на две части. Обобщенный алгоритм выглядит так:
- Задать начальный интервал
;
- Убедиться, что на концах функция имеет разный знак;
- Повторять
- пока не будет достигнута нужная точность.
Варианты метода дихотомии различаются выбором точки деления. Рассмотрим варианты дихотомии: метод половинного деления и метод хорд.
Метод половинного деления
Метод половинного деления известен также как метод бисекции. В данном методе интервал делится ровно пополам.
Такой подход обеспечивает гарантированную сходимость метода независимо от сложности функции – и это весьма важное свойство. Недостатком метода является то же самое – метод никогда не сойдется быстрее, т.е. сходимость метода всегда равна сходимости в наихудшем случае.
Метод половинного деления:
- Один из простых способов поиска корней функции одного аргумента.
- Применяется для нахождения значений действительно-значной функции, определяемому по какому-либо критерию (это может быть сравнение на минимум, максимум или конкретное число).
Метод половинного деления как метод поиска корней функции
Изложение метода
Перед применением метода для поиска корней функции необходимо отделить корни одним из известных способов, например, графическим методом. Отделение корней необходимо в случае, если неизвестно на каком отрезке нужно искать корень.
Будем считать, что корень функции
отделён на отрезке
. Задача заключается в том, чтобы найти и уточнить этот корень методом половинного деления. Другими словами, требуется найти приближённое значение корня с заданной точностью
.
Пусть функция непрерывна на отрезке
,
-
и
– единственный корень уравнения
.
(Мы не рассматриваем случай, когда корней на отрезке несколько, то есть более одного. В качестве
можно взять и другое достаточно малое положительное число, например,
.)
Поделим отрезок пополам. Получим точку
и два отрезка
.
- Новый отрезок
делим пополам. Получаем середину этого отрезка
и так далее.
Для того, чтобы найти приближённое значение корня с точностью до , необходимо остановить процесс половинного деления на таком шаге
, на котором
и вычислить
. Тогда можно взять
.
Реализация метода на С++ и числовой пример
Решим уравнение методом половинного деления. Графическим методом находим отрезок
, которому принадлежит искомый корень. Так как
, то принимаем
.
Ниже приведен пример программы на Си++, которая решает поставленную задачу.
Программа 1. Корень уравнения
#include <iostream> #include <cmath> using namespace std; const double epsilon = 1e-2; double f(double x) { return 4- exp(x) - 2*x^2; } int main() { double a, b, c; a = 0; b = 2; while (b - a > epsilon){ c = (a + b) / 2; if(f(b) * f(c) < 0) a = c; else b = c; } cout << (a + b) / 2 << endl; return 0; }
Искомый корень . Вычисления проводились с точностью
.
Промежуточные вычисления представлены в таблице ниже.
| n | an | bn | cn | bn-cn |
|---|---|---|---|---|
| 1 | 0 | 1 | 0.5 | 0.5 |
| 2 | 0.5 | 1 | 0.75 | 0.25 |
| 3 | 0.75 | 1 | 0.875 | 0.125 |
| 4 | 0.875 | 1 | 0.9375 | 0.0625 |
| 5 | 0.875 | 0.9375 | 0.90625 | 0.03125 |
| 6 | 0.875 | 0.90625 | 0.890625 | 0.015625 |
| 7 | 0.875 | 0.890625 | 0.8828125 | 0.0078125 |
Метод половинного деления как метод оптимизации
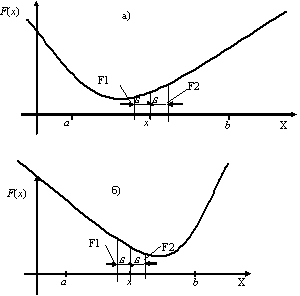
Рис. 1. Поиск экстремума функции методом половинного деления
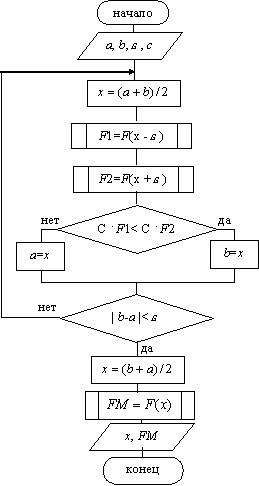
Рис. 2. Схема алгоритма метода половинного деления
Однопараметрическая оптимизация (поиск экстремумов функций одной переменной) является самостоятельной и часто встречаемой задачей. Кроме того, к ней сводится гораздо более сложная задача – поиск экстремума функции многих переменных.
Рассмотрим метод половинного деления как простейший однопараметрический метод безусловной оптимизации. Данный метод является методом прямого поиска. В нем при поиске экстремума целевой функции используются только вычисленные значения целевой функции.
Дана функция . Необходимо найти
, доставляющий минимум (или максимум) функции
на интервале
с заданной точностью
, т.е. найти
-
.
Запишем словесный алгоритм метода.
- На каждом шаге процесса поиска делим отрезок
пополам,
– координата середины отрезка
.
- Вычисляем значение функции
в окрестности
вычисленной точки
, т.е.
.
- Сравниваем
и
и отбрасываем одну из половинок отрезка
(рис. 1).
- При поиске минимума:
- При поиске максимума:
- Деление отрезка
продолжается, пока его длина не станет меньше заданной точности
, т.е.
.
Схема алгоритма метода представлена на рис 2.
На рис 2:
-
– константа,
При выводе – координата точки, в которой функция
имеет минимум (или максимум),
– значение функции
в этой точке.
Метод хорд
Недостаток деления отрезка строго пополам проистекает от того, что он использует лишь знак функции, игноририруя отклонение (абсолютную величину). Но очевидно, что чем меньше (по абсолютной величине) значение функции, тем ближе мы находимся к корню. Метод хорд предлагает делить отрезок в точке, отстоящей от краев отрезка пропорционально абсолютному значению функции на краях. (Название “метод хорд” происходит от того, что точка деления является пересечением отрезка – хорды – с осью абцисс.)
Изложение метода
Метод основан на замене функции на каждом шаге поиска хордой, пересечение которой с осью
дает приближение корня.
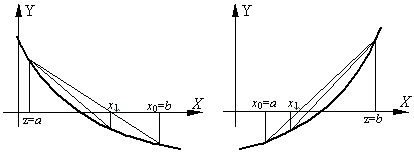
Рис. 3. Метод хорд
При этом в процессе поиска семейство хорд может строиться:
- при фиксированном левом конце хорд, т.е.
, тогда начальная точка
(рис. 3а);
- при фиксированном правом конце хорд, т.е.
, тогда начальная точка
(рис. 3б);
В результате итерационный процесс схождения к корню реализуется рекуррентной формулой:
- для случая а):
- для случая б):
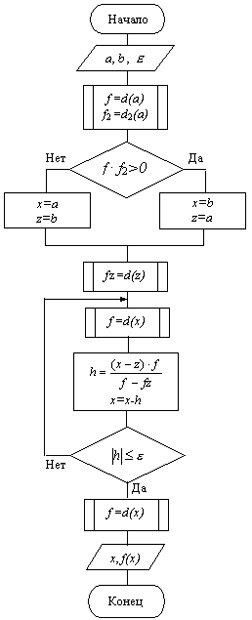
Рис. 4. Схема алгоритма уточнения корня методом хорд
Процесс поиска продолжается до тех пор, пока не выполнится условие
или
.
Метод обеспечивает быструю сходимость, если , т.е. хорды фиксируются в том конце интервала
, где знаки функции
и ее кривизны
совпадают.
Схема алгоритма уточнения корня методом хорд представлена на рис. 4.
Комбинация метода хорд и метода половинного деления
Метод хорд можно применить в качестве “последнего штриха” после того, как метод половинного деления гарантирует требуемую точность – это не улучшит существенно гарантируемой точности, но, скорее всего, на несколько порядков повысит точность решения.
Если применять аналогичное уточнение к интервалу, полученному методом хорд, то эффект будет значительно слабее. Это ещё раз иллюстрирует тот факт, что метод хорд очень хорошо работает в условиях малого интервала (близости обеих границ интервала к корню), но неспособен сам создать себе эти условия (приблизить обе границы к корню).
На вопрос о том, стоит ли использовать попеременное применение метода половинного деления и метода хорд, ответ отрицателен. После того, как метод хорд приближает одну из границ почти вплотную к корню, методу половинного деления придётся долго работать, чтобы гарантировать заданную точность, т.к. метод хорд ее гарантировать не может.
Поэтому лучше использовать в качестве точки деления что-то среднее: если метод половинного деления предлагает использовать , а метод хорд –
, то возьмем
. Коэффициент
.
Чему должен быть равен коэффициент ? Его следует не задавать, а вычислять по ходу работы: если при очередной операции интервал уменьшился более чем в два раза (это то, что гарантирует метод половинного деления), то значит, нужно больше доверять методу хорд (уменьшить
), и наоборот.
Может показаться, что при большом доверии к методу хорд этот комбинированный метод работает так же, как метод хорд. На самом деле, это не так: метод хорд передвигает по направлению к корню только одну границу, а комбинированный метод даже при высоком доверии к методу хорд передвигает и вторую границу, обеспечивая лучшие условия для работы метода хорд, а значит – для ещё большего доверия к нему.
Список литературы
- http://dmitrykarpov.nm.ru/misc/dihotomy.htm
- http://mathfunc.narod.ru/met_dih.html
- http://www.intuit.ru/department/mathematics/mathprog/9/
- http://www.intuit.ru/department/calculate/intromathmodel/4/3.html
- http://calc-x.com/chm/dich.php
- http://elib.ispu.ru/library/math/sem1/kiselev1/node84.html
См. также
- Практикум ММП ВМК, 4й курс, осень 2008
Решение алгебраического уравнения. Для численного решения алгебраических уравнений существует множество способов. Среди самых известных можно назвать метод Ньютона, метод Хорд, и «всепобеждающий» метод Половинного Деления. Сразу оговоримся, что любой метод является приближенным, и по сути дела лишь уточняющим значение корня. Однако уточняющим до любой точности, заданной Нами.
Метод половинного деления или дихотомии (дихотомия – сопоставленность или противопоставленность двух частей целого) при нахождении корня уравнения f(x)=0 состоит в делении пополам отрезка [a; b], где находится корень. Затем анализируется изменение знака функции на половинных отрезках, и одна из границ отрезка [a; b] переносится в его середину. Переносится та граница, со стороны которой функция на половине отрезка знака не меняет. Далее процесс повторяется. Итерации прекращаются при выполнении одного из условий: либо длина интервала [a; b] становится меньше заданной погрешности нахождения корня ?, либо функция попадает в полосу шума ?1 – значение функции сравнимо с погрешностью расчетов.
Сначала поставим задачу. Дана монотонная, непрерывная функция f(x), которая содержит корень на отрезке [a,b], где b>a. Определить корень с точностью ?, если известно, что f(a)*f(b)<0
Дано уравнение вида:
f(x)=0; (1)
необходимо найти удовлетворяющие ему значения x.
Итак, приступим к решению. Первым делом, определимся, что значит f(x)=0. Посмотрите на рис.1. На нем изображен график некоей функции. В некоторых точках этот график пересекает ось абсцисс. Координаты x этих точек нам и нужно найти. Если вид уравнения простой или стандартный, например, квадратное уравнение или линейное, то применять численный метод здесь совершенно ни к чему. Но если уравнение у нас такое:
f(x)=x3-14×2+x+ex; (2)
то ни в каком учебнике вы не найдете метода аналитического решения этого кошмара. Здесь и приходит на помощь непобедимый численный метод. Метод половинного деления. Из самого названия метода можно предположить, что нам понадобится что-то делить пополам.
Ученикам метод половинного деления можно преподнести в виде решения задачи.
Задача
Идет осада неприятельской крепости. На некотором расстоянии от нее установили новую пушку. Под каким углом к горизонту надо стрелять из этой пушки, чтобы попасть в заданный участок крепостной стены.
Над моделью этой задачи физики изрядно поработали. Оно и понятно: ведь многие научные задачи, как и эта, возникали прежде всего в военном деле. И решение этих задач почти всегда считалось приоритетным.
Какие же факторы принять за существенные в этой задаче? Поскольку речь идет о средневековье, то скорость снаряда и дальность полета невелики. Значит можно считать несущественным, что Земля круглая (помните обсуждение в параграфе 27), и пренебречь сопротивлением воздуха. Остается единственный фактор – сила земного притяжения.
Математик тут бы сказал, что надо решить уравнение. Мы тоже будем решать, только приближенно и очень похоже на то, как делают настоящие артиллеристы. Они же поступают следующим образом: производят несколько выстрелов, беря цель «в вилку», т.е. одно попадание выше цели, а другое ниже. Затем делят пополам угол между этими выстрелами, и при стрельбе под таким углом снаряд ложится к цели намного ближе. Но если все же не попали, то новую «вилку» снова делят пополам и т.д.
Мы заранее можем указать «вилку» для угла: 0 и ?/4 (мы надеемся, что вы помните какой угол имеет радианную меру ?/4 и чему приближенно равно ?). А дальше будем делить пополам эту «вилку» и смотреть, куда попадает снаряд, пока не добьемся нужного результата.
Как же долго нам придется вести «пристрелку», чтобы получить угол ?, с нужной точностью? Чтобы ответить на этот вопрос, отвлечемся от нашей задачи и сформулируем на чисто математическом языке, что и как мы находили.
Нам даны некоторая функция f(x) и отрезок [a;b], причем на концах этого отрезка эта функция принимает значения противоположных знаков. Если функция непрерывна, т.е. ее график – непрерывная линия, то ясно, что график функции пересекает ось абцисс в некоторой точке с отрезка [a;b], как показано на рисунке 1. Иными словами, f(c)=0, т.е. с – корень уравнения f(x)=0.
Как же предлагается находить этот корень? А вот так. Делим отрезок [a;b] пополам, т.е. берем середину отрезка а+b/2. В этой точке вычисляем значение функции f(x) (рис. 2). Если это значение 0, то корень найден; если нет, то оно имеет тот же знак, что и значение на одном из концов отрезка [a;b]. Тогда этот конец заменям точкой а+b/2. Новый отрезок тоже содержит корень уравнения f(x)=0, поскольку на его концах функция f(x) снова имеет разные знаки. Однако этот отрезок в 2 раза короче предыдущего. И самое главное – с ним можно поступить точно так же. со следующим отрезком еще раз проделать то же самое и т.д. поскольку длина отрезка каждый раз уменьшается вдвое, мы можем получить отрезок сколь угодно малой длины, внутри которого содержится корень уравнения f(x)=0. Например, если исходный отрезок был [3;4], т.е. имел длину 1, то через десять шагов мы получим отрезок длиной. Это означает, что концы отрезка дают нам приближенное значение корня с точностью, равной длине отрезка: левый конец отрезка – приближенное значение корня с недостатком, правый конец – приближенное значение корня с избытком.
Фактически мы сейчас сформулировали метод приближенного решения уравнения f(x)=0. Его можно было бы назвать методом артиллерийской пристрелки. Но математики называют его методом половинного деления.
Далее ученикам предлагается записать алгоритм и блок-схему нахождения корня уравнения с помощью метода половинного деления.
Алгоритм
1) Найдем середину отрезка [a; b]: c=(a+b)/2;
2) Вычислим значения функции в точках a и c и найдем произведение полученных значений: d=f(c)?f(a);
3) Если d>0, то теперь точкой a станет c: a=c; Если d<0, то точкой b станет c: b=c;
4) Вычислим разность a и b, сравним ее с точностью ?: если |a-b|> ?, то идем в пункт 1) если нет, то корень с нужной нам точностью найден, и он равен: x=(a+b)/2;
Метод половинного деления (метод также известен как метод Больцано или метод дихотомии) один из методов решения нелинейных уравнений и основан на последовательном сужении интервала, содержащего единственный корень уравнения ![]() . Итерационный процесс выполняется до того момента, пока не будет достигнута заданная точность
. Итерационный процесс выполняется до того момента, пока не будет достигнута заданная точность ![]() .
.
Пусть дано уравнение ![]() и определен отрезок
и определен отрезок ![]() такой, что данный отрезок содержит один единственный корень уравнения
такой, что данный отрезок содержит один единственный корень уравнения ![]() . Тогда по концам заданного отрезка функция имеет значения, противоположные по знаку:
. Тогда по концам заданного отрезка функция имеет значения, противоположные по знаку: ![]() . Противоположность знаков значений функции на концах отрезка можно определить множеством способов. Один из множества этих способов — умножение значений функции на концах отрезка и определение знака произведения путём сравнения результата умножения с нулём:
. Противоположность знаков значений функции на концах отрезка можно определить множеством способов. Один из множества этих способов — умножение значений функции на концах отрезка и определение знака произведения путём сравнения результата умножения с нулём:
![]() .
.
Отрезок ![]() называется начальным интервалом неопределенности, потому что известно, что корень ему принадлежит, но его местоположение с требуемой точностью не определено.
называется начальным интервалом неопределенности, потому что известно, что корень ему принадлежит, но его местоположение с требуемой точностью не определено.
Процедура уточнения положения корня заключается в построении последовательности вложенных друг в друга отрезков, каждый из которых содержит корень уравнения. Для этого находится середина текущего интервала неопределенности ![]() ,
, ![]() , и в качестве следующего интервала неопределенности из двух возможных выбирается тот, на концах которого функция
, и в качестве следующего интервала неопределенности из двух возможных выбирается тот, на концах которого функция ![]() имеет разные знаки.
имеет разные знаки.
Процесс завершается, когда длина текущего интервала неопределенности становится меньше заданной величины ![]() , задающей точность нахождения корня. В качестве приближенного значения корня берется середина последнего интервала неопределенности.
, задающей точность нахождения корня. В качестве приближенного значения корня берется середина последнего интервала неопределенности.
› Рассмотрим алгоритм метода половинного деления.
1. Найти начальный интервал неопределенности ![]() одним из методов отделения корней, задать малое положительное число
одним из методов отделения корней, задать малое положительное число ![]() . Положить
. Положить ![]() .
.
2. Найти середину текущего интервала неопределенности:
![]() .
.
3. Необходимо найти значение функции ![]() в точках
в точках ![]() ,
, ![]() и
и ![]() . Далее необходимо проверить два условия:
. Далее необходимо проверить два условия:
– если выполняется условие ![]() , то искомый корень находится внутри левого отрезка положить
, то искомый корень находится внутри левого отрезка положить![]() ,
, ![]() ;
;
– если выполняется условие ![]() , то искомый корень находится внутри правого отрезка принять
, то искомый корень находится внутри правого отрезка принять ![]() ,
, ![]() .
.
В результате находится новый интервал неопределенности, на котором находится искомых корень уравнения:
![]() .
.
4. Проверяем новый отрезок на предмет заданной точности, в случае:
– если длина нового отрезка меньше заданной точности ![]() , то итерационный процесс заканчивается. Приближенное значение корня определяется по формуле:
, то итерационный процесс заканчивается. Приближенное значение корня определяется по формуле:
![]() .
.
– если длина нового отрезка не достигает необходимой точности ![]() , то необходимо продолжить итерационный процесс
, то необходимо продолжить итерационный процесс ![]() и перейти к п.2 рассматриваемого алгоритма.
и перейти к п.2 рассматриваемого алгоритма.
Метод имеет линейную, но безусловную сходимость, и его погрешность за каждую итерацию уменьшается в два раза:
![]()
Из данного соотношения можно оценить число итераций k для достижения заданной точности ![]() :
:
![]()
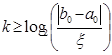
Из полученной формулы можно сделать вывод, что для достижения точности ![]() от длины первоначального промежутка
от длины первоначального промежутка ![]() необходимо выполнить примерно десять итераций.
необходимо выполнить примерно десять итераций.
К достоинствам метода также следует отнести то, что он позволяет найти простой корень уравнения ![]() любых непрерывных функций
любых непрерывных функций ![]() при любых значениях
при любых значениях ![]() таких, что
таких, что ![]() .
.
Недостатки метода — он не обобщается на системы нелинейных уравнений и не может использоваться для нахождения корней четной кратности.
В качестве примера, рассмотрим решение нелинейного уравнения ![]() методом половинного деления. Корень необходимо найти в рассматриваемом диапазоне
методом половинного деления. Корень необходимо найти в рассматриваемом диапазоне ![]() с точностью
с точностью ![]() .
.
Вариант решения нелинейного уравнения в программном комплексе MathCAD.

Результаты расчетов, а именно динамика изменения приближенного значения корня, а также погрешности расчета от шага расчета представлены графической форме (см. рис.1).
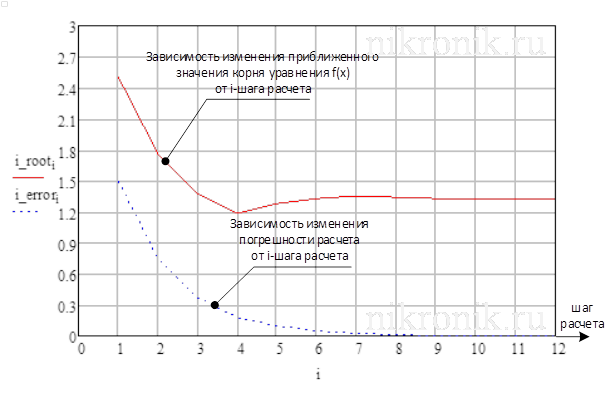
Рис.1. Результаты расчета по методу половинного деления
Для обеспечения заданной точности ![]() при поиске уравнения в диапазоне
при поиске уравнения в диапазоне ![]() необходимо выполнить 12 итераций. На последнем шаге итерации приближенное значение корня нелинейного уравнения будет определяться значением:
необходимо выполнить 12 итераций. На последнем шаге итерации приближенное значение корня нелинейного уравнения будет определяться значением: ![]() .
.
