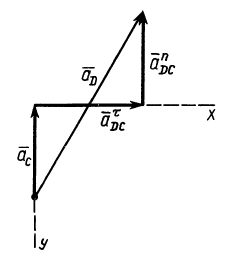
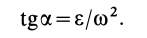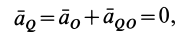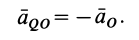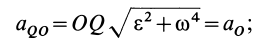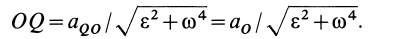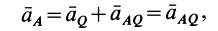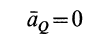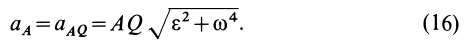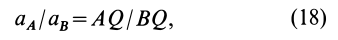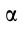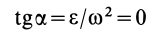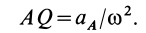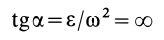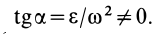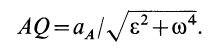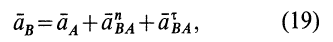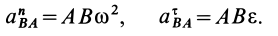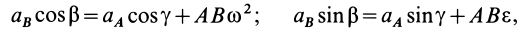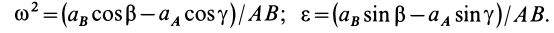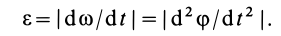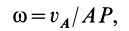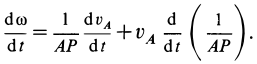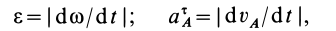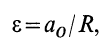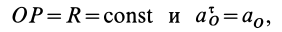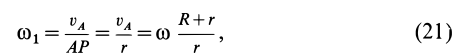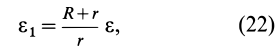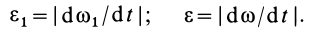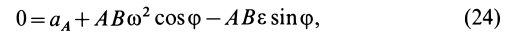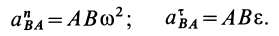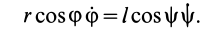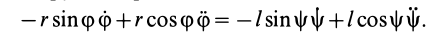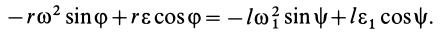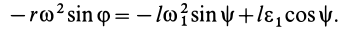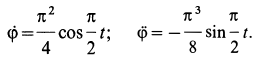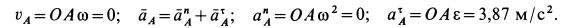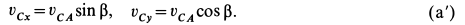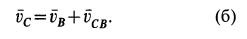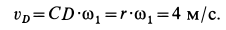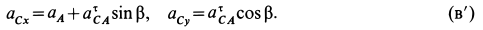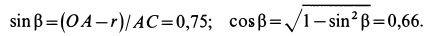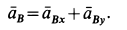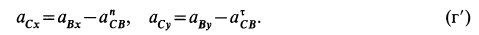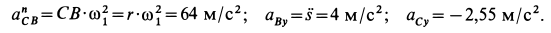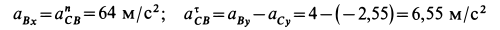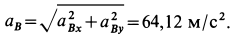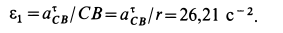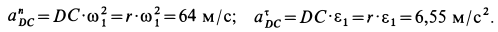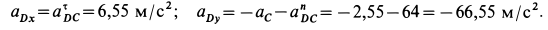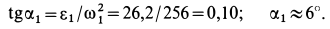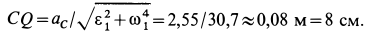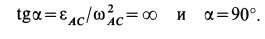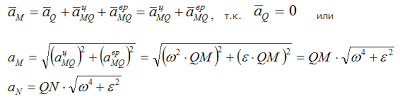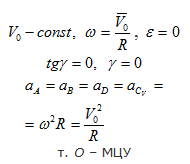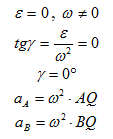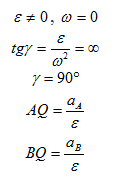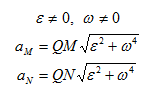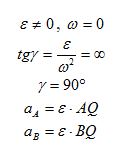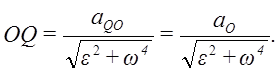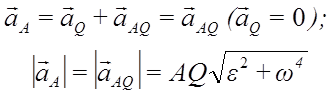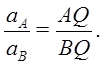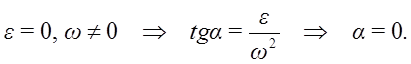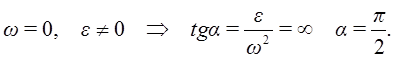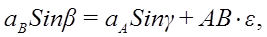Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 14 июля 2014 года; проверки требуют 4 правки.
Мгнове́нный центр ускоре́ний — при плоскопараллельном движении абсолютно твёрдого тела точка, связанная с этим телом и находящаяся в плоскости движения тела, ускорение которой в данный момент времени равно нулю.
Положение мгновенного центра ускорений в общем случае не совпадает с положением мгновенного центра скоростей. Однако в некоторых случаях, например, при чисто вращательном движении, положение этих двух точек может совпадать.
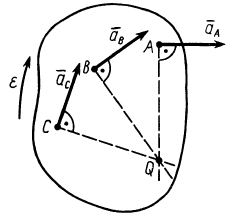
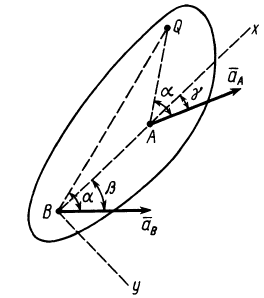
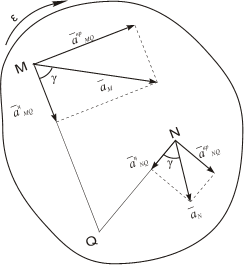
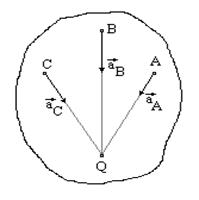
Для того, чтобы определить положение мгновенного центра ускорений, необходимо к векторам ускорений двух различных точек тела провести прямые под равными углами 

где
— угловое ускорение тела;
— угловая скорость тела.
Величина ускорения точки пропорциональна её расстоянию до мгновенного центра ускорений
Литература[править | править код]
- Тарг С. М. Краткий курс теоретической механики. Учеб. для втузов.— 10-е изд., перераб. и доп. — М.: Высш. шк., 1986.— 416 с, ил.
- Основной курс теоретической механики (часть первая) Н. Н. Бухгольц, изд-во «Наука», Главная редакция физико-математической литературы, Москва, 1972, 468 стр.
- Жуковский Н.Е. Теоретическая механика
Содержание:
Мгновенный центр ускорений:
В каждый момент движения плоской фигуры в своей плоскости, если 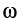
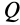
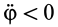
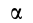
Рис. 56
При этом угол 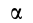
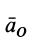
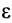
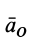
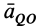
и тогда
Но
следовательно,
Из приведенного доказательства следует, что мгновенный центр ускорений является единственной точкой плоской фигуры, ускорение которой в рассматриваемый момент времени равно нулю. В другой момент времени мгновенный центр ускорений находится в общем случае в другой точке плоской фигуры.
Если мгновенный центр ускорений известен, то, выбрав его за полюс, для ускорения точки 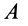
так как
и, следовательно,
Ускорение 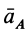
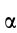
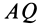
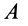
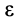
Для точки 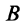
и ускорение 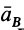
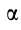
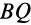
Рис. 57
Из формул (16) и (17) имеем
т. е. ускорения точек плоской фигуры при плоском движении пропорциональны расстояниям от этих точек до мгновенного центра ускорений.
Итак, суммируя результаты, получаем, что ускорения точек плоской фигуры при плоском движении можно определить так же, как и при вращательном движении плоской фигуры вокруг мгновенного центра ускорений с угловой скоростью 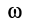
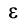
Для вычисления скоростей точек плоской фигуры при плоском движении принимают, что плоская фигура вращается вокруг мгновенного центра скоростей, а для вычисления ускорения следует считать, что она вращается вокруг мгновенного центра ускорений.
При качении без скольжения колеса по прямой (см. пример в § 7) получается, что ускорение мгновенного центра скоростей не равно нулю; следовательно, в общем случае мгновенные центры скоростей и ускорений являются различными точками плоской фигуры.
Ускорения точек плоской фигуры при плоском движении, подобно скоростям точек, можно определять двумя способами: по формуле (10), выражающей зависимость ускорений двух точек плоской фигуры, и по формуле (16), используя мгновенный центр ускорений. Обычно мгновенный центр ускорений, кроме частных случаев, когда угловая скорость или угловое ускорение равны нулю, располагается на плоской фигуре так, что трудно определить расстояние от него до рассматриваемых точек фигуры. Поэтому определение ускорения точек рекомендуется вычислять по формуле (10).
Рассмотрим способы нахождения мгновенного центра ускорений как в частных, так и в общем случаях.
1. Пусть известно, что угловое ускорение 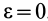
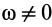
и, следовательно, угол 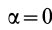
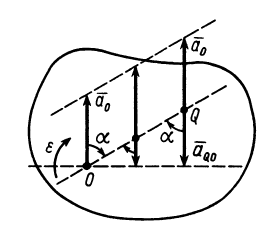
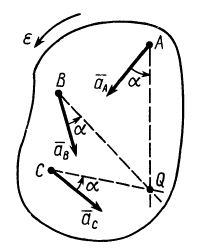
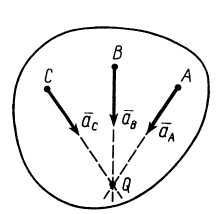
Мгновенный центр ускорений лежит на прямой линии, по которой направлено ускорение какой-либо точки плоской фигуры (рис. 58). Так как это справедливо для любой точки фигуры, то, следовательно, мгновенный центр ускорений лежит в точке пересечения прямых линий, по которым направлены ускорения точек плоской фигуры. Ускорения точек плоской фигуры в этом случае направлены к мгновенному центру ускорений, так как они состоят только из одной относительной нормальной составляющей от вращения вокруг мгновенного центра ускорений.
Рис. 58
Если известно ускорение, например точки 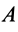
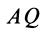
Эта формула получается из (16) в том случае, когда угловое ускорение равно нулю.
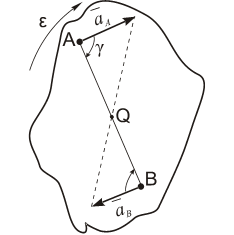
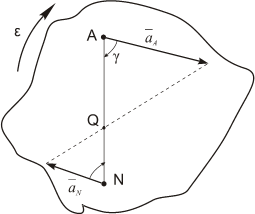
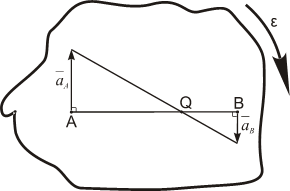
2. Пусть угловая скорость 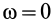
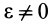
Тогда
и, следовательно, угол 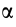
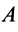
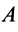
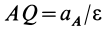
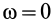
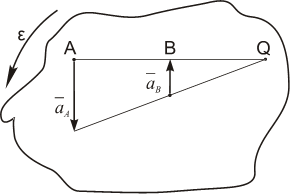
3. В общем случае, когда угловая скорость 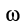
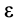
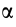
Мгновенный центр ускорений лежит на пересечении прямых линий, проведенных к ускорениям точек фигуры под одним и тем же углом 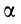
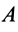
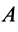
Рис. 59
4. Пусть в данный момент времени известны ускорения двух точек плоской фигуры: 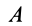
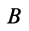
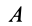
где
Проецируя левую и правую части векторной формулы (19) на две взаимно перпендикулярные оси 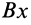
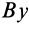
где 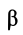
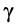
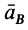
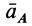
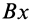
При принятом направлении оси 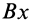
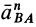
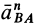
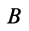
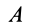
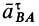
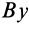
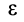
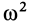
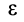
Естественно, что в реальных случаях величина 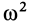
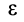
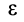
После того как найдены 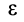
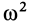
Рис. 60
Основные способы вычисления углового ускорения при плоском движении
При вычислении ускорений точек фигуры при плоском движении необходимо знать угловое ускорение. Рассмотрим некоторые приемы его определения.
1. Если известен угол поворота или угловая скорость в зависимости от времени, то угловое ускорение е определяем путем дифференцирования их по времени, т. е.
2. Обычно требуется определить угловое ускорение в какой-либо момент времени по другим величинам, известным в этот же момент времени. В этом случае угловое ускорение тоже можно получить путем дифференцирования угловой скорости по времени, считая ее для вывода формулы известной функцией времени. Угловую скорость можно найти по формуле (7):
где 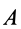
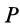
Дифференцируя 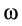
В тех случаях, когда 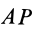
так как
где 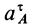
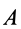
Так, например, при качении колеса без скольжения по неподвижной прямой линии (см. рис. 55), если за точку 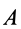
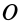
так как в этом случае
где 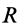
При качении без скольжения одного колеса по неподвижному другому колесу сначала установим зависимость между угловой скоростью 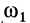
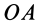
где 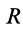
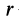
Дифференцируя по времени (21), имеем
так как
Рис. 61
Из сравнения (21) и (22) видно, что связь между угловыми скоростями и угловыми ускорениями колес полностью аналогична. Это справедливо и для углов поворота колес, если нулевые их значения выбрать в один и тот же момент времени.
При внешнем зацеплении дуговые стрелки угловой скорости и углового ускорения подвижного колеса совпадают с дуговыми стрелками соответственно угловой скорости и углового ускорения кривошипа 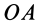
Рис. 62
При внутреннем зацеплении колес дуговые стрелки 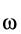
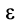
3. Иногда угловое ускорение 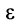
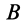
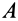
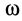
Так, если ускорение точки
то, проецируя обе части (23) на ось 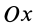
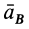
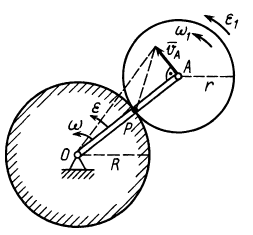
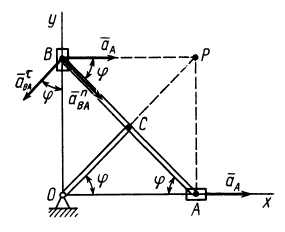
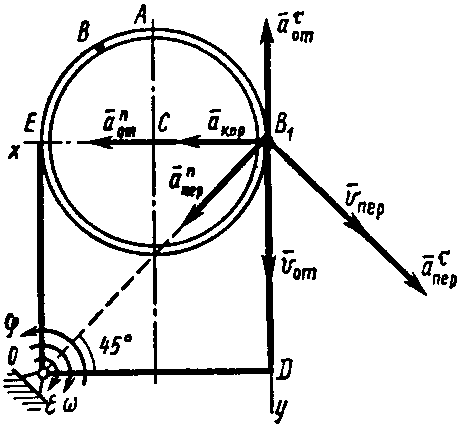
Определим этим способом угловое ускорение линейки эллипсографа 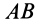
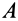
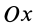
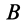
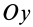
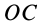
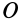
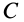
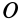
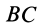
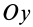
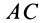
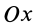
В эллипсографе, когда ускорения точек 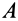
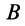
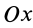
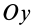
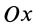
так как
Соотношение (24) и служит для определения углового ускорения линейки эллипсографа 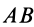
Описанным выше приемом удобно определять угловое ускорение шатунов в различных кривошипно-шатунных механизмах, когда у шатуна есть точка, движущаяся прямолинейно.
Если известны ускорения двух точек 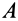
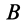
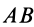
Наоборот, по угловой скорости и угловому ускорению из этих уравнений можно найти числовые значения ускорений точек 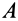
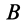
4. В задачах (см. § 6, рис. 53), где зависимость между угловыми скоростями различных тел можно установить путем дифференцирования по времени тождественных соотношений между углами поворота, зависимость между угловыми ускорениями часто можно получить путем двукратного дифференцирования по времени этих тождеств. Так, после первого дифференцирования в рассматриваемом случае
Дифференцируя вторично, имеем
Так как 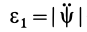
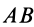

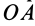
Если дополнительно известно, что угловая скорость 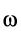
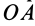
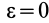
Отсюда можно определить угловое ускорение шатуна в зависимости от углов 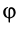
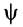
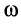
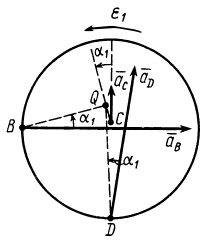
Пример:
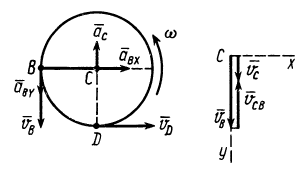
Диск радиусом 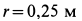
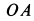
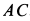
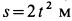
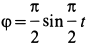
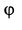
Определить угловые скорость и ускорение диска и шатуна, а также скорости и ускорения точек 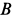
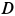
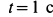
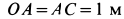
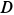
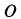
Рис. 63
Рис. 64
Рис. 65
Решение. Положение кривошипа в момент времени 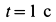
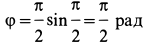
Для алгебраических угловой скорости и углового ускорения кривошипа имеем
При 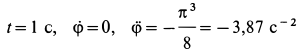
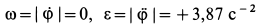
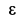
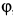
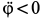
Для скорости и ускорения точки 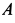
Ускорение 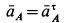
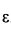
У точки 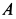
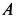
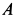
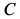
Но 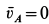
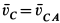
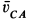
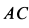
Траекторией точки 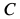
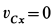
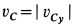
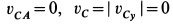
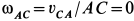
Вычисляем скорость и ускорение точки 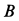
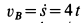
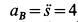
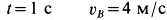
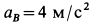
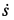
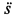
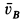
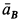
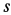
При отсутствии скольжения у точки 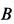
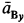
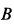
Приняв за полюс точку 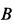
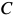
Рис. 66
Предположив, что диск вращается против часовой стрелки, строим треугольник скоростей для точки 
В проекциях на оси координат из (б) имеем 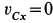
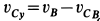
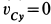
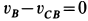
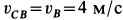
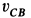
Мгновенным центром скоростей диска является его точка 
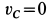
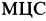
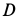
Перейдем к определению ускорений точек и углового ускорения диска 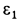
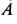

где 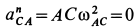
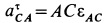
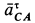
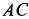

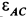
В проекциях на оси координат из (в) (см. рис. 65 и 67, а) имеем
Ускорение точки 
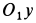
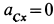
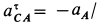
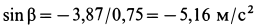
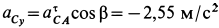
Так как 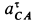
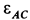
Угловое ускорение шатуна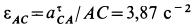
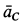
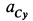
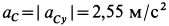
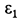

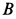
где
В соответствии с (г) строим многоугольник ускорений для точки 
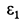
В проекциях на выбранные оси координат из (г) с учетом рис. 67, б получаем
Но
С учетом полученных значений из (г’) имеем:
и
Ускорение 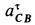
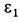
Рис. 68
Рис. 69
Приняв за полюс точку 
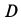
где
На рис. 68 приведен многоугольник ускорений для точки 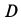
Определим ускорение точки 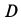
Для определения мгновенного центра ускорений 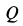
Угол 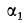
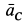
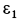

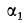
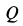

Точка 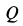

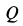
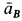
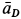
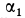
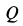
Мгновенный центр ускорений шатуна 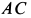
- Заказать решение задач по теоретической механике
Теорема о конечном перемещении плоской фигуры
Понятие мгновенного центра скоростей плоской фигуры при плоском движении можно ввести используя теорему о конечном перемещении плоской фигуры. Фигуру в ее плоскости из заданного положения I в любое другое положение II (рис. 70) можно перевести одним поворотом в этой плоскости вокруг точки 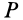
Пусть в положении I плоская фигура характеризуется отрезком 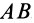
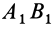
Рис. 70
Рассмотрим случай, когда 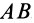
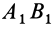
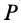
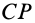
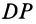
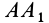
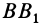
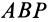
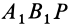
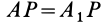
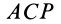
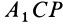
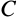
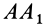
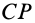
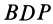
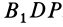
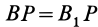
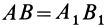
Для перевода плоской фигуры из положения I в положение II достаточно совместить между собой равные треугольники 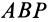
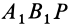
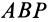
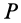
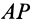
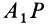
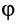
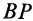
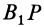
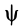
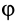
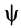
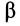
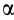
Итак, если отрезок 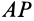
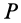
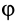
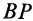
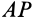
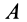
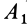
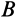
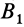
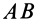
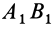
В том случае, когда отрезок 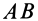
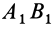
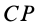
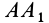
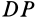
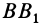
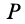
- Мгновенный центр вращения
- Вращение твердого тела вокруг неподвижной точки
- Сложное движение точки
- Сложение движение твердого тела
- Центр тяжести
- Кинематика точки
- Плоское движение твердого тела
- Мгновенный центр скоростей
Мгновенным центром ускорений (сокр. — МЦУ) при движении фигуры в плоскости называют точку плоской фигуры, ускорение которой в этот момент равно нулю.
Такая точка существует в каждый момент времени.
В наших рассуждениях будем обозначать ее буквой Q. Взяв эту точку за полюс, получим формулу для определения ускорения произвольной точки:
Рис. 1.12
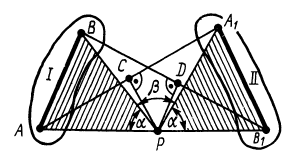
Угол, который составляет вектор ускорения точки М с линией MQ определится из соотношения:
Т.е. у всех точек плоской фигуры этот угол одинаков. Из рис. 1.12 видно, что мгновенный центр ускорений лежит в точке пересечения линий, составляющих угол
γ с соответствующими ускорениями точек.
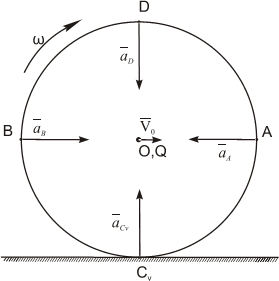
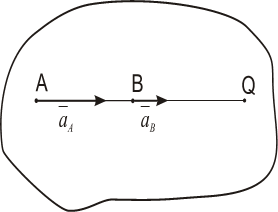
На рис. 1.13-1.15 приведены частные случаи определения положения мгновенного центра ускорений.
Рис. 1.13а
Рис. 1.13б
Рис. 1.14а
Рис. 1.14б
Рис. 1.15а
Рис. 1.15б
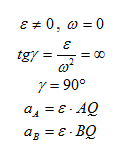
Примеры решения задач >
Сложное движение точки >
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее
Решение задач и лекции по технической механике, теормеху и сопромату
В
каждый момент движения плоской фигуры
в своей плоскости, если
и
не равны нулю одновременно, имеется
единственная точка этой фигуры, ускорение
которой равно нулю. Эту точку называют
мгновенным центром ускорений.
Обозначим ее через
.
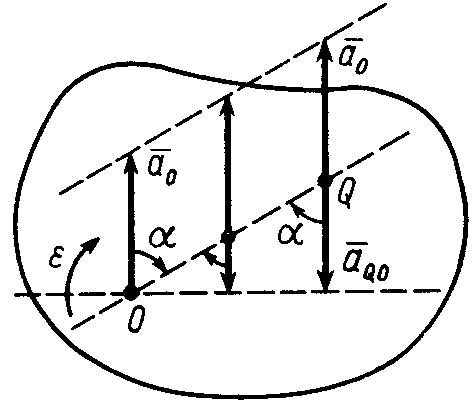
Пусть(рис. 39). Мгновенный центр ускорений
лежит на линии, проведенной под угломк ускорению точки, тангенс которого
вычисляем по формуле:
П
Рис. 39
ри этом уголнадо отложить от ускорения
в направлении дуговой стрелки углового
ускорения,
т.е. в рассматриваемом случае по часовой
стрелке. Только в точках этой прямой
ускорениеи ускорение от вращения
могут иметь противоположные направления
и одинаковые значения, т.е.:
,
и тогда
.
Но
,
следовательно,
.
Мгновенный
центр ускорений является единственной
точкой плоской фигуры, ускорение которой
в рассматриваемый момент времени равно
нулю. В другой момент времени мгновенный
центр ускорений находится в общем случае
в другой точке плоской фигуры.
Если
мгновенный центр ускорений известен,
то, выбрав его за полюс, для ускорения
точки
плоской фигуры по формуле (93) получаем
,
т.к.
.
Следовательно:
.
(99)
У
направлено под углом
к отрезку
,
соединяющему точкус мгновенным центром ускорений в сторону
дуговой стрелки углового ускорения(рис. 40).
Для
точки
аналогично
(100)
и
ускорение
также направлено под углом
к отрезку
И
Рис. 40
з формул (99) и (100) имеем
, (101)
т.е. ускорения
точек плоской фигуры при плоском движении
пропорциональны расстояниям от этих
точек до мгновенного центра ускорений.
Итак,
суммируя результаты, получаем, что
ускорения
точек плоской фигуры при плоском движении
можно определить так же, как и при
вращательном движении плоской фигуры
вокруг мгновенного центра ускорений с
угловой скоростью
и угловым ускорением
.
Для вычисления
скоростей точек плоской фигуры при
плоском движении принимают, что плоская
фигура вращается вокруг мгновенного
центра скоростей, а для вычисления
ускорения следует считать, что она
вращается вокруг мгновенного центра
ускорений.
2.5. Решение задач кинематики
Пример 3.
Даны
уравнения движения точки в плоскости
:
,
(,
– в сантиметрах,
– в секундах).
Определить:
уравнение траектории точки; для момента
времени
с найти скорость и ускорение точки, а
также ее касательное и нормальное
ускорения и радиус кривизны в
соответствующей точке траектории.
Решение:
1. Для
определения уравнения траектории точки
исключим из заданных уравнений движения
время
.
Поскольку
входит в аргументы тригонометрических
функций, где один аргумент вдвое больше
другого, используем формулу
:
. (102)
Из уравнений
движения находим выражения соответствующих
функций и подставляем в равенство (102).
Получим

,
следовательно,
.
О
Рис. 41
тсюда окончательно находим следующее
уравнение траектории точки (параболы,
рис. 41):
. (103)
2. Скорость точки
найдем по ее проекциям на координатные
оси:
,
,
.
Для
момента времени
с:
,
,
. (104)
3. Аналогично найдем
ускорение точки:
,
,
.
Для
момента времени
с:
,
,
. (105)
4. Касательное
ускорение найдем, дифференцируя по
времени равенство:
Получим
,
откуда
. (106)
Числовые
значения всех величин, входящих в правую
часть (106), определены и даются в (104) и
(105). Подставив в (106) эти числа, найдем
сразу, что при
с:
.
5.
Нормальное ускорение точки
.
Подставляя сюда найденные при
с числовые значения
и
,
получим, что
.
6.
Радиус кривизны траектории
.
Подставляя
сюда числовые значения
и
при
с, найдем, что
см.
Ответ:
,
,
,
,
см.
П
Рис. 42
ример 4.Т
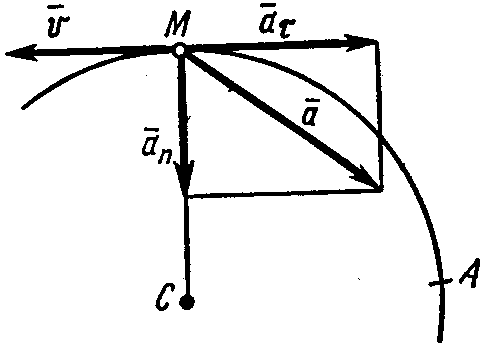
движется по дуге окружности радиусам по закону
,
(– в метрах,
– в секундах), где
(рис. 42).
Определить:
скорость и ускорение точки в момент
времени
с.
Решение:
Определяем скорость
точки:
.
При
с получим
.
Ускорение находим
по его касательной и нормальной
составляющим:
,
,
.
При
с получим
,
,
.
Изобразим
на рис. 42 векторы
и
,
учитывая знаки и считая положительным
направление от
к
.
Ответ:
,
.
П
5.Механизм
(рис. 43) состоит из стержней 1, 2, 3, 4 и
ползуна
,
соединенных друг с другом и с неподвижными
опорамии
шарнирами.
Д
Рис. К2,а.
Рис. 43
ано:
,
,
,
,
,
,
м,
м,
м,
с-1,
с-2
(направления
и
– против хода часовой стрелки).
О
,
,
,
,
.
Решение:
1. Строим положение
механизма в соответствии с заданными
углами и выбранным масштабом длин (рис.
44; на этом рисунке изображаем все векторы
скоростей).
2
Рис. 44
. Определяем.
Точкапринадлежит стержню
.
Чтобы найти,
надо знать скорость какой-нибудь другой
точки этого стержня и направление.
По данным задачи, учитывая направление,
можем определить.
Численно:
м/с,
. (107)
Направление
найдем, учтя, что точка
принадлежит одновременно ползуну,
движущемуся вдоль направляющих
поступательно. Теперь, знаяи направление
,
воспользуемся теоремой о проекциях
скоростей двух точек тела (стержня)
на прямую, соединяющую эти точки (прямая).
Сначала по этой теореме устанавливаем,
в какую сторону направлен вектор(проекции скоростей должны иметь
одинаковые знаки). Затем, вычисляя эти
проекции, находим
,
м/с. (108)
3.
Определяем
.
Точка
принадлежит стержню
.
Следовательно, по аналогии с предыдущим,
чтобы определить
,
надо сначала найти скорость точки
,
принадлежащей одновременно стержню
.
Для этого, зная
и
,
строим мгновенный центр скоростей (МЦС)
стержня
.
Это точка
,
лежащая на пересечении перпендикуляров
к
и
,
восставленных из точек
и
(к
перпендикулярен стержень 1). По направлению
вектора
определяем направление поворота стержня
вокруг МЦС
.
Вектор
перпендикулярен отрезку
,
соединяющему точки
и
,
и направлен в сторону поворота. Величину
найдем из пропорции:
. (109)
Чтобы
вычислить
и
,
заметим, что
– прямоугольный, так как острые углы в
нем равны 30° и 60°, и что
.
Тогда
является равносторонним и
.
В результате равенство (3) дает
м/с,
. (110)
Так
как точка
принадлежит одновременно стержню
,
вращающемуся вокруг
,
то
.
Тогда, восставляя из точек
и
перпендикуляры к скоростям
и
,
построим МЦС
стержня
.
По направлению вектора
определяем направление поворота стержня
вокруг центра
.
Вектор
направлен в сторону поворота этого
стержня. Из рис. 44 видно, что
,
откуда
.
Составив теперь пропорцию, найдем, что
,
м/с. (110)
4.
Определяем
.
Так как МЦС стержня 2 известен (точка
)
и
м, то
с–1. (111)
5
Рис. 45
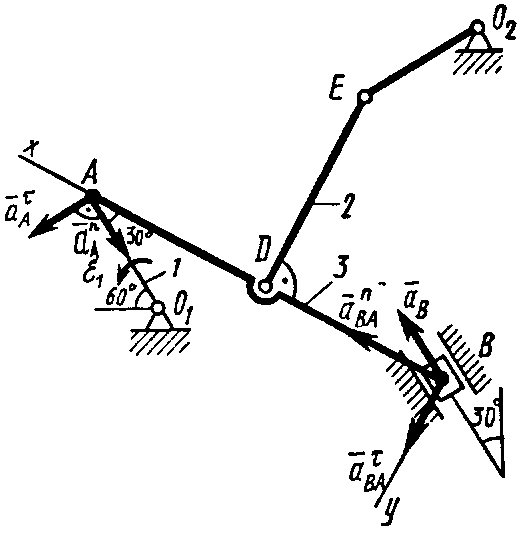
Определяем(рис. 45, на котором изображаем все векторы
ускорений). Точкапринадлежит стержню
.
Чтобы найти,
надо знать ускорение какой-нибудь другой
точки стержняи траекторию точки
.
По данным задачи можем определить,
где численно
м/с2,
м/с2. (112)
Вектор
направлен вдоль
,
а– перпендикулярно
.
Изображаем эти векторы на чертеже (см.
рис. 45). Так как точкаодновременно принадлежит ползуну, то
векторпараллелен направляющим ползуна.
Изображаем векторна чертеже, полагая, что он направлен в
ту же сторону, что и
.
Для
определения
воспользуемся равенством
. (113)
Изображаем
на чертеже векторы
(вдоль
от
к
)
и(в любую сторону перпендикулярно
).
ЧисленноНайдя
с помощью построенного МЦС
стержня 3, получим
с–1,
м/с2. (114)
Таким
образом, у величин, входящих в равенство
(113), неизвестны только числовые значения
и
.
Их можно найти, спроектировав обе части
равенства (113) на какие-нибудь две оси.
Чтобы
определить
,
спроектируем обе части равенства (113)
на направление(ось
).
Тогда получим
. (115)
Подставив в
равенство (10) числовые значения всех
величин из (112) и (114), найдем, что
м/с2. (116)
Так
как получилось
,
то, следовательно, векторнаправлен как показано на рис. 45.
6.
Определяем
.
Чтобы найти
,
сначала определим
.
Для этого обе части равенства (113)
спроектируем на направление,
перпендикулярное
(ось
).
Тогда получим:
. (117)
Подставив
в равенство (12) числовые значения всех
величин из (116) и (112), найдем, что
м/с2.
Знак минус указывает, что направление
противоположно показанному на рис. 45.
Теперь
из равенства
получим:
с–2.
Ответ:
м/с,
м/с,
с–1,
м/с2,
с–2.
П
Рис. 46
ример 6.Пластина
(,
рис. 46) вращается вокруг оси, проходящей
через точку
перпендикулярно плоскости пластины,
по закону
(положительное направление отсчета
угла
показано на рис. 46 дуговой стрелкой). По
дуге окружности радиуса
движется точка
по закону
(положительное направление отсчета
– от
к
).
Дано:
м,
,
(
– в радианах,
– в метрах,
– в секундах).
Определить:
и
в момент времени
с.
Решение:
Рассмотрим
движение точки
как сложное, считая ее движение по дуге
окружности относительным, а вращение
пластины – переносным движением. Тогда
абсолютная скорость
и абсолютное ускорение
точки найдутся по формулам:
,
, (118)
где, в свою очередь,
,
.
Определим все,
входящие в равенства (118) величины.
1. Относительное
движение. Это движение происходит по
закону
. (119)
Сначала
установим, где будет находиться точка
на дуге окружности в момент времени
.
Полагая в уравнении (119)
с, получим
.
Тогда
.
Знак
минус свидетельствует о том, что точка
в момент
с находится справа от точки
.
Изображаем ее на рис. 46 в этом положении
(точка)).
Теперь
находим числовые значения
,
и
:
,
,
,
где
– радиус кривизны относительной
траектории, равный радиусу окружности.
Для момента
с, учитывая, что
м, получим
м/с,
м/с2,
м/с2.
Знаки
показывают, что вектор
направлен в сторону положительного
отсчета расстояния,
а вектор— в противоположную сторону; вектор
,
направлен к центруокружности. Изображаем все эти векторы
на рис. 46.
2.
Переносное движение. Это движение
(вращение) происходит по закону
.
Найдем сначала угловую скорость
и угловое ускорение
переносного вращения:
,
и при
с
с–1
,
с–2. (120)
Знаки
указывают, что в момент
с направления
и
противоположны направлению положительного
отсчета угла;
отметим это на рис. 46.
Для
определения
и
находим сначала расстояние
точки
от оси вращения
.
Из рисунка видно, чтом. Тогда в момент времени
с, учитывая равенства (4), получим
м/с,
м/с2,
м/с2. (121)
Изображаем
на рис. 46 векторы
и
с учетом направлений
и
и вектор
(направлен к оси вращения).
3. Кориолисово
ускорение. Модуль кориолисова ускорения
определяем по формуле
,
где
– угол между вектором
и осью вращения (вектором
).
В нашем случае этот угол равен 90°, так
как ось вращения перпендикулярна
плоскости пластины, в которой расположен
вектор.
Численно в момент времени
с, так как в этот момент
м/с,
с–1,
получим
м/с2. (122)
Направление
найдем по правилу Н.Е. Жуковского: так
как векторлежит в плоскости, перпендикулярной
оси вращения, то повернем его на 90° в
направлении,
т.е. по ходу часовой стрелки. Изображаемна рис. 46. (Иначе направление
можно найти, учтя, что
.)
Таким
образом, значения всех входящих в правые
части равенств (118) векторов найдены и
для определения
и
остается только сложить эти векторы.
Произведем это сложение аналитически.
4.
Абсолютная скорость. Проведем координатные
оси
(см. рис. 46) и спроектируем почленно обе
части равенствана эти оси. Получим для момента времени
с:
м/с,
м/с.
После этого находим
м/с.
Учитывая,
что в данном случае угол между
и
равен 45°, значение
можно еще определить по формуле
м/с.
5. Абсолютное
ускорение. По теореме о сложении ускорений
. (123)
Для
определения
спроектируем обе части равенства (7) на
проведенные оси
.
Получим для момента времени
с:
м/с2,
м/с2,
После этого находим
м/с2.
Ответ:
м/с,
м/с2.
Рис. 31
Мгновенный центр ускорений лежит на прямой, проведенной под углом α ( tgα=ε/ω2) к ускорению точки О.
При этом α надо отложить от ускорения aO в направлении дуговой стрелки углового ускорения ε.
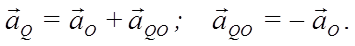
Но 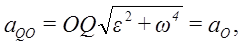
Мгновенный центр ускорений является единственной точкой фигуры, ускорение которой в рассматриваемый момент времени равно нулю. В другой момент времени мгновенный центр ускорений находится в общем случае в другой точке плоской фигуры.
Если положение мгновенного центра ускорений известно, то выбрав его за полюс, для ускорения произвольной точки А, имеем:
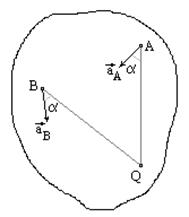
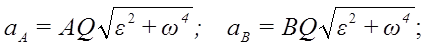
Рис. 32
Следовательно, ускорения точек плоской фигуры при плоском движении можно определить так же, как и при вращательном движении плоской фигуры вокруг мгновенного центра ускорений с угловой скоростью ω и угловым ускорением ε.
Для вычисления скоростей принимают, что фигура вращается вокруг мгновенного центра скоростей, для вычисления ускорений принимают, что фигура вращается вокруг мгновенного центра ускорений. В общем случае эти центры являются разными точками плоской фигуры.
Ускорения точек плоской фигуры при плоском движении подобно скоростям точек можно вычислить двумя способами: по формуле 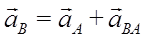
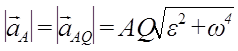
Способы нахождения мгновенного центра ускорений.
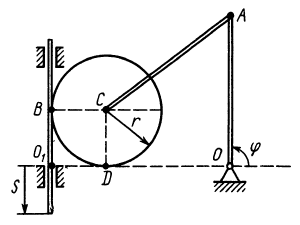
1.
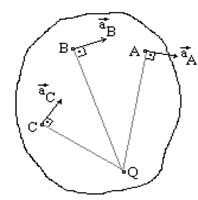
Ускорения всех точек направлены к мгновенному центру ускорений (Рис. 33), так как они состоят только из одной нормальной составляющей от вращения вокруг мгновенного центра ус
Рис. 33 корений.
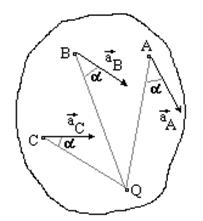
2.
мгновенное поступательное движение (Рис. 34). Мгновенный центр ускорений лежит на пересечении перпендикуляров к ускорениям точек.
Рис. 34
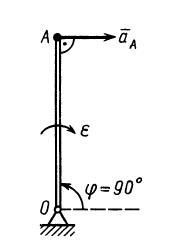
3.
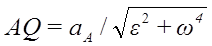
Если известно aA, то
Рис. 35
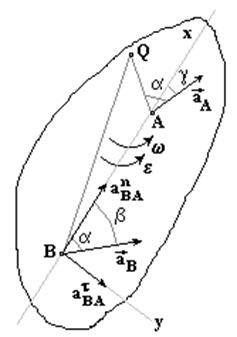
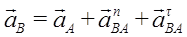
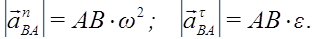
Проецируя левую и правую части векторной формулы (*) на оси Bx и By получаем:
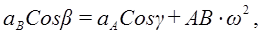
Рис. 36
где β и γ в принципе известные углы.
Проекцию anBA на ось Вх берем со знаком (+), так как она всегда направлена к оси вращения (к полюсу). Проекцию aτBA, берем со знаком (+) предполагая, что стрелка ε направлена против часовой стрелки.
Из уравнений проекций находим
знак ε определяется после подстановки данных в формулу.
После того, как найдены ε и ω, задача нахождения мгновенного центра ускорений сводится к случаю 3.
Вопросы для самопроверки:
1. Как задается скорость и ускорение в декартовой системе координат?
2. Какие системы координат Вы знаете?
3. Какое движение называется абсолютным, относительным, переносным?
4. Какое движение называется поступательным?
5. Какое движение называется вращательным?
6. Как определить мгновенный центр скоростей?
7. Как определить мгновенный центр ускорений?
3. ДИНАМИКА
3.1. Основные понятия
Динамикой называется раздел механики, в котором изучается движение материальных тел под действием сил.
В динамике, в отличие от кинетики, при изучении движения тел принимают во внимание как действующие на них силы, так и инертность самих материальных тел.
Инертность тела проявляется в том, что оно сохраняет свое движение при отсутствии действующих сил, а когда на него начинает действовать сила, то скорость точек тела изменяются не мгновенно, а постепенно и тем медленнее, чем больше инертность этого тела. Количественной мерой инертности материального тела является физическая величина, называемая массой тела. В классической механике масса m рассматривается как величина скалярная, положительная и постоянная для каждого данного тела.
Кроме суммарной массы движение тела зависит еще в общем случае от формы тела, точнее от взаимного расположения образующих его частиц, т. е. от распределения масс в теле.
Чтобы при первоначальном изучении динамики отвлечься от учета тела (распределения масс), вводят абстрактное понятие о материальной точке, как о точке, обладающей массой, и начинают изучение динамики с динамики материальной точки.
3.2. Классификация сил. Динамика материальной точки
Сила тяжести – постоянная сила, действующая на тело, находящееся вблизи земной поверхности. P= mg,
где m – масса тела, g – ускорение свободного падения.
Сила упругости – P = cλ,
где c – коэффициент жесткости, λ – перемещение тела.
Сила трения – P = fN,
где f – коэффициент трения, N – нормальная реакция.
Сила тяготения – сила с которой притягиваются к друг к другу два материальных тела P = fm1m2/r2,
где f – гравитационная постоянная, m1 и m2 – массы двух тел, r – расстояние между центрами этих тел.
Сила вязкого сопротивления – P = μv ,
где μ – коэффициент сопротивления среды, v – скорость тела.
Движение материальных точек и тел следует рассматривать относительно определённой системы отсчёта. В классической механике в основу, которой положены законы И. Ньютона, такая система называется инерционной системой отсчёта. Пространство считается трёхмерным эвклидовым пространством, свойства которого не зависят от движущихся в нём материальных объектов.