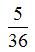поделиться знаниями или
запомнить страничку
- Все категории
-
экономические
43,655 -
гуманитарные
33,653 -
юридические
17,917 -
школьный раздел
611,939 -
разное
16,901
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
2018-08-02
Минимальная частота линии спектральной серии Бальмера для атома водорода $2,5 cdot 10^{15} Гц$. Чему равны частоты двух ближайших линий этой серии?
Решение:
При переходе в атоме водорода электрона с $n$-й орбиты на $k$-ю будет излучаться фотон, энергия которого равна
$h nu = frac{q_{e}^{4}m }{8 epsilon_{0}^{2}h^{2} } left ( frac{1}{k^{2} } – frac{1}{n^{2} } right )$.
Минимальная частота линии в серии Бальмера ($k = 2$) соответствует переходу с уровня $n = 3$ на уровень $k = 2$, разность $left ( frac{1}{k^{2} } – frac{1}{n^{2} } right )$ принимает при этом минимальное значение. Ближайшие линии спектра будут соответствовать переходам с четвертой и пятой боровских орбит на вторую боровскую орбиту,
$h nu_{1} = frac{q_{e}^{4}m }{8 epsilon_{0}^{2}h^{2} } left ( frac{1}{2^{2} } – frac{1}{4^{2} } right )$. (1)
$h nu_{2} = frac{q_{e}^{4}m }{8 epsilon_{0}^{2}h^{2} } left ( frac{1}{2^{2} } – frac{1}{5^{2} } right )$. (2)
$h nu_{мин} = frac{q_{e}^{4}m }{8 epsilon_{0}^{2}h^{2} } left ( frac{1}{2^{2} } – frac{1}{3^{2} } right )$. (3)
Поделив почленно выражения (3) и (1) и (3) и (2), находим
$nu_{1} = nu_{мин} frac{27}{20}, nu_{1} = 3,38 cdot 10^{15} Гц$,
$nu_{2} = nu_{мин} frac{189}{125}, nu_{2} = 3,76 cdot 10^{15} Гц$.

6. Квантовая физика и физика атома
25. Спектр атома водорода. Правило отбора.
|
На рисунке изображена схема энергетических |
Для орбитального квантового числа l имеется пра- |
||
|
уровней атома водорода. Показаны состояния с |
вило отбора |
. Это означает, что возмож- |
|
|
различными значениями орбитального кванто- |
|||
|
ны только такие переходы, в которых l изменяется |
|||
|
вого числа |
на единицу. |
Поэтому запрещены |
перехо- |
|
ды: |
, где |
орбитальное квантовое чис- |
|
|
ло l не изменяется, и |
, где |
. |
Запрещенными правилом отбора для орбитального квантового числа являются переходы
Ответ: 
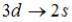
4. 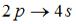
|
Установить соответствие квантовых чисел, |
Главное квантовое число (n) – целое число, обо- |
||||
|
определяющих волновую функцию электрона в |
значающее номер энергетического уровня. Харак- |
||||
|
атоме водорода, их физическому смыслу |
теризует энергию электронов, занимающих дан- |
||||
|
1. n |
А. определяет ориентации электронно- |
ный энергетический уровень. С возрастающим |
|||
|
го облака в пространстве |
главным квантовым числом возрастают радиус |
||||
|
2. l |
Б. определяет форму электронного об- |
орбиты и энергия электрона. |
|||
|
лака |
Орбитальное квантовое число (l) – определяет |
||||
|
3. m |
В. Определяет размеры электронного |
форму электронного облака и определяет энерге- |
|||
|
облака |
тический |
подуровень |
данного |
энергетического |
|
|
Г. Собственный механический момент |
уровня. Орбитальное квантовое число связано с |
||||
|
1: 1-В, 2-Б, 3-А* |
главным |
квантовым |
числом |
соотношением: |

|
2: 1-Г, 2-Б, 3-А |
l 0, 1, 2, 3, …, n 1. |
|||||
|
3: 1-В, 2-А, 3-Г |
Магнитное квантовое число (m) – характеризует |
|||||
|
4: 1-А, 2-Б, 3-В |
ориентацию в пространстве орбитального момента |
|||||
|
количества движения электрона или простран- |
||||||
|
ственное расположение электронной орбитали. |
||||||
|
Магнитное квантовое число принимает целые зна- |
||||||
|
чения m |
0, 1, 2, 3, …, l . |
Каждое из |
2l 1 воз- |
|||
|
можных значений магнитного квантового числа |
||||||
|
определяет проекцию вектора орбитального мо- |
||||||
|
мента на данное направление (обычно ось Z). Про- |
||||||
|
екция орбитального момента импульса на ось Z |
||||||
|
равна LZ |
m . |
|||||
|
Спин – собственный момент импульса (или маг- |
||||||
|
нитный момент) элементарных частиц, имеющий |
||||||
|
квантовую природу и не связанный с перемещени- |
||||||
|
ем частицы как целого. Спином называют также |
||||||
|
собственный момент импульса атомного ядра или |
||||||
|
атома. |
||||||
|
Ответ: 1 |
||||||
|
Главное квантовое число n определяет … |
Собственные функции электрона в атоме водорода |
|||||
|
содержат три целочисленных па- |
||||||
|
раметра: n, l и m. Параметр n называется главным |
||||||
|
квантовым числом, параметры l и m – орбиталь- |
||||||
|
ным (азимутальным) и магнитным квантовыми |
||||||
|
числами соответственно. Главное квантовое число |
||||||
|
n определяет энергию стационарного состояния |
||||||
|
электрона в атоме. |
||||||
|
1* |
проекцию орбитального момента и |
|||||
|
электрона на заданное направление |
||||||
|
2 |
орбитальный механический момент |
|||||
|
электрона в атоме |
||||||
|
3 |
собственный механический момент |
|||||
|
электрона в атоме |
||||||
|
4 |
энергию стационарного состояния |
|||||
|
электрона в атоме |
||||||
|
Спиновое квантовое число s определяет … |
Собственные функции электрона в атоме водорода |
|||||
|
содержат три целочисленных па- |
||||||
|
раметра: n, l и m. Параметр n называется главным |
||||||
|
квантовым числом, параметры l и m – орбиталь- |
||||||
|
ным (азимутальным) и магнитным квантовыми |
||||||
|
числами |
соответственно. |
Четвертое |
квантовое |
|
число s называется спином и определяет собствен- |
|||||||||||||||||
|
ный механический момент электрона в атоме. |
|||||||||||||||||
|
В атоме водорода уровню энергии номера n |
Для каждого n существует n орбитальных кванто- |
||||||||||||||||
|
отвечает (без учѐта спина) … |
вых чисел, и соответственно электронных облаков. |
||||||||||||||||
|
1: 2n2 различных квантовых состояний |
Для каждого l-облака существует 2l+1 простран- |
||||||||||||||||
|
2: (n – 1)2 различных квантовых состояний |
ственных расположение электронных орбиталей. |
||||||||||||||||
|
3: n 2 различных квантовых состояний* |
Т.о. |
для |
каждого |
n |
существует |
||||||||||||
|
4: n – 1 различных квантовых состояний |
n 1 |
n 1 |
n n |
1 |
|||||||||||||
|
2l |
1 2 l |
n |
2 |
n n2 . |
|||||||||||||
|
5. n + 1 различных квантовых состояний |
l 0 |
l 0 |
2 |
||||||||||||||
|
Ответ: 3 |
|||||||||||||||||
|
1* |
5 |
||||||||||||||||
|
2 |
4 |
||||||||||||||||
|
3 |
3 |
||||||||||||||||
|
4 |
2 |
||||||||||||||||
|
5 |
1 |
||||||||||||||||
|
На рисунке представлена диаграмма энергети- |
|||||||||||||||||
|
ческих |
уровней |
атома |
водорода: |
||||||||||||||
|
Излучение фотона с наименьшей длиной вол- |
|||||||||||||||||
|
ны происходит при переходе, обозначенном |
|||||||||||||||||
|
стрелкой под номером … |
|||||||||||||||||
|
1* |
5s→3d |
||||||||||||||||
|
2 |
5d→3p |
||||||||||||||||
|
3 |
4p→3s |
||||||||||||||||
|
4 |
4d→3p |
||||||||||||||||
|
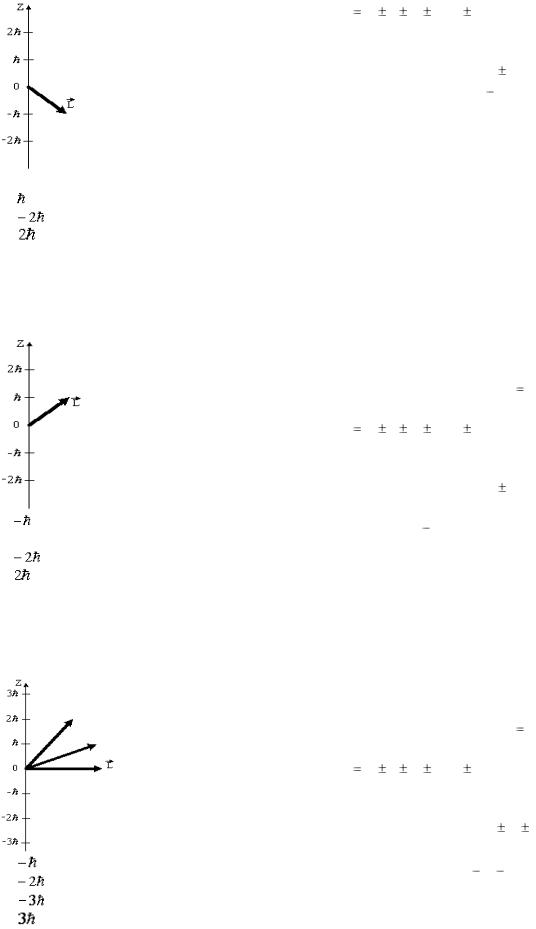
На рисунке приведена одна из возможных ори- |
p-состоянию соответствует орбитальное квантовое |
||||||||||||||||
|
ентаций момента импульса электрона в p- |
число l=1. |
||||||||||||||||
|
состоянии. Какие еще значения может прини- |
Существует |
пространственное |
квантование: век- |
||||||||||||||
|
мать проекция момента импульса на направле- |
тор момента импульса электрона может иметь |
||||||||||||||||
|
ние Z внешнего магнитного поля? |
лишь такие ориентации в пространстве, при кото- |
||||||||||||||||
|
рых |
проекция LZ |
вектора |
на направление z |
||||||||||||||
|
L |
|||||||||||||||||
|
внешнего магнитного поля принимает квантовые |
|||||||||||||||||
|
значения; кратные : LZ |
m , |
где m – магнитное |
|||||||||||||||
|
квантовое |
число, |
принимающее |
значения: |
|
m |
0; 1; |
2; |
3; …; |
, где |
– орбитальное кванто- |
||||
|
вое число. |
|||||||||
|
Значит, p-уровню соответствуют следующие зна- |
|||||||||
|
чения проекции LZ : 0; |
, |
а на рисунке представ- |
|||||||
|
лен только значение . Поэтому ещѐ могут быть |
|||||||||
|
проекции 0, . |
|||||||||
|
Ответ: 1, 2 |
|||||||||
|
1: 0* |
|||||||||
|
2: |
* |
||||||||
|
3: |
|||||||||
|
4: |
|||||||||
|
На рисунке приведена одна из возможных ори- |
p-состоянию соответствует орбитальное квантовое |
||||||||
|
ентаций момента импульса электрона в p- |
число l=1. |
||||||||
|
состоянии. Какие еще значения может прини- |
Существует пространственное квантование: век- |
||||||||
|
мать проекция момента импульса на направле- |
тор момента импульса электрона может иметь |
||||||||
|
ние Z внешнего магнитного поля? |
лишь такие ориентации в пространстве, при кото- |
||||||||
|
рых проекция LZ |
вектора |
L на направление z |
|||||||
|
внешнего магнитного поля принимает квантовые |
|||||||||
|
значения; кратные : LZ |
m , где m – магнитное |
||||||||
|
квантовое |
число, |
принимающее |
значения: |
||||||
|
m |
0; 1; |
2; |
3; …; |
, где |
– орбитальное кванто- |
||||
|
вое число. |
|||||||||
|
Значит, p-уровню соответствуют следующие зна- |
|||||||||
|
чения проекции LZ : 0; |
, |
а на рисунке представ- |
|||||||
|
1: |
* |
лен только значение . Поэтому ещѐ могут быть |
|||||||
|
проекции 0, |
. |
||||||||
|
2:0* |
|||||||||
|
Ответ: 1, 2 |
|||||||||
|
3: |
|||||||||
|
4: |
|||||||||
|
На рисунке приведены некоторые из возмож- |
d-состоянию соответствует орбитальное квантовое |
||||||||
|
ных ориентаций момента импульса для элек- |
число l=2. |
||||||||
|
тронов в d-состоянии. Какие еще значения мо- |
Существует пространственное квантование: век- |
||||||||
|
жет принимать проекция момента импульса на |
тор момента импульса электрона может иметь |
||||||||
|
направление Z внешнего магнитного поля? |
лишь такие ориентации в пространстве, при кото- |
||||||||
|
рых проекция LZ |
вектора |
L на направление z |
|||||||
|
внешнего магнитного поля принимает квантовые |
|||||||||
|
значения; кратные : LZ |
m , где m – магнитное |
||||||||
|
квантовое |
число, |
принимающее |
значения: |
||||||
|
m |
0; 1; |
2; |
3; …; |
, где |
– орбитальное кванто- |
||||
|
вое число. |
|||||||||
|
Значит, p-уровню соответствуют следующие зна- |
|||||||||
|
чения проекции LZ : 0; |
; |
2 , а на рисунке пред- |
|||||||
|
ставленs только значения 0, , 2 . Поэтому ещѐ мо- |
|||||||||
|
1: |
* |
гут быть проекции |
, |
2 . |
|||||
|
2: |
* |
||||||||
|
Ответ: 1, 2 |
|||||||||
|
3: |
|||||||||
|
4: |
|||||||||
|
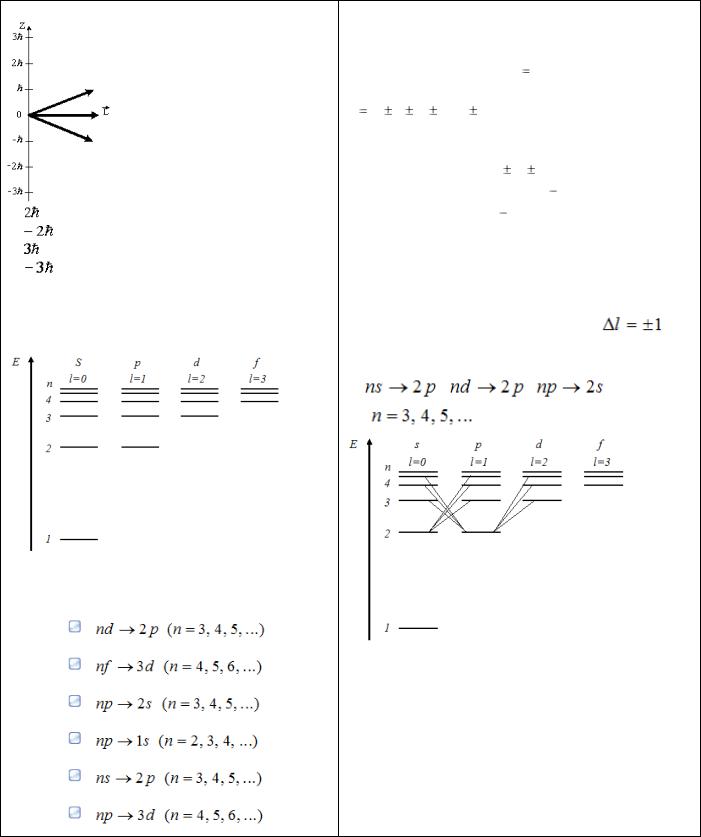
На рисунке приведены некоторые из возмож- |
d-состоянию соответствует орбитальное квантовое |
||||||||
|
ных ориентаций момента импульса для элек- |
число l=2. |
||||||||
|
тронов в d-состоянии. Какие еще значения мо- |
Существует пространственное квантование: век- |
||||||||
|
жет принимать проекция момента импульса на |
тор |
момента |
импульса электрона может иметь |
|
направление Z внешнего магнитного поля? |
лишь такие ориентации в пространстве, при кото- |
|||||
|
рых проекция LZ вектора |
L на направление z |
|||||
|
внешнего магнитного поля принимает квантовые |
||||||
|
значения; кратные : LZ |
m , где m – магнитное |
|||||
|
квантовое |
число, |
принимающее значения: |
||||
|
m 0; 1; 2; |
3; …; , где |
– орбитальное кванто- |
||||
|
вое число. |
||||||
|
Значит, p-уровню соответствуют следующие зна- |
||||||
|
чения проекции LZ : 0; |
; |
2 , а на рисунке пред- |
||||
|
ставленs только значения 0, , . Поэтому ещѐ мо- |
||||||
|
1: |
* |
гут быть проекции 2 , |
2 . |
|||
|
2: |
* |
Ответ: 1, 2 |
||||
|
3: |
||||||
|
4: |
||||||
|
На рисунке изображена схема энергетических |
Серию Бальмера дают переходы на второй энерге- |
|||||
|
уровней атома водорода. Показаны состояния с тический уровень (n=2). Учитывая правило отбора |
||||||
|
различными значениями орбитального кванто- |
по орбитальному квантовому числу |
, пе- |
||||
|
вого числа. |
реходы, приводящие к возникновению серии |
|||||
|
Бальмера, |
можно |
представить |
в |
|||
|
де |
, |
, |
, |
|||
|
где |
Серию Бальмера дают переходы …
Ответ: 

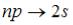
Варианты ответа:
Ответ: 3 Варианты ответа:
|
На рисунке дана схема энергетических уровней |
829 |
|
|
атома водорода. |
122 |
|
|
661 |
||
|
368 |
||
|
Серию Пашена дают переходы в состояние с n = 3. |
||
|
Учитывая связь длины волны и частоты |
||
|
и правило частот Бора |
, можно |
|
|
сделать вывод о том, что линии с наименьшей |
||
|
длиной волны (то есть с наибольшей частотой) в |
||
|
серии Пашена соответствует переход с |
||
|
энергетического уровня Е = 0. |
Тогда |
|
Наименьшая длина волны спектральной линии |
||
|
(в нм) серии Пашена равна __829 нм___ . |
||
|
(h = 6,63·10-34 Дж·с) |
||
|
На рисунке дана схема энергетических уровней |
Серию Лаймана дают переходы в состояние с n = |
|
|
атома водорода. |
1. Учитывая связь длины волны и частоты |
|
|
и правило частот Бора |
, |
|
|
можно сделать вывод о том, что линии с |
||
|
наибольшей длиной волны (то есть с наименьшей |
||
|
частотой) в серии Лаймана соответствует переход |
||
|
со второго энергетического уровня. Тогда |

Наибольшая длина волны спектральной линии
(в нм) серии Лаймана равна 122 нм
(h = 6,63·10-34 Дж·с)
|
На рисунке дана схема энергетических уровней |
Серию Лаймана дают переходы на первый энерге- |
|
|
атома водорода, а также условно изображены |
тический уровень, серию Бальмера – на второй |
|
|
переходы электрона с одного уровня на |
уровень. Максимальная частота линии в серии |
|
|
другой, сопровождающиеся излучением кванта |
||
|
энергии. В ультрафиолетовой области спектра |
||
|
эти переходы дают серию Лаймана, в видимой |
Лаймана |
. Минималь- |
|
области – серию Бальмера, в инфракрасной |
ная частота линии в серии Бальмера |
|
|
области – серию Пашена и т.д. |
||
|
. |
||
|
Тогда |
. |
Отношение минимальной частоты линии в серии Бальмера 
спектра атома водорода равно …
На рисунке дана схема энергетических уровней Серию Пашена дают переходы на третий энерге-
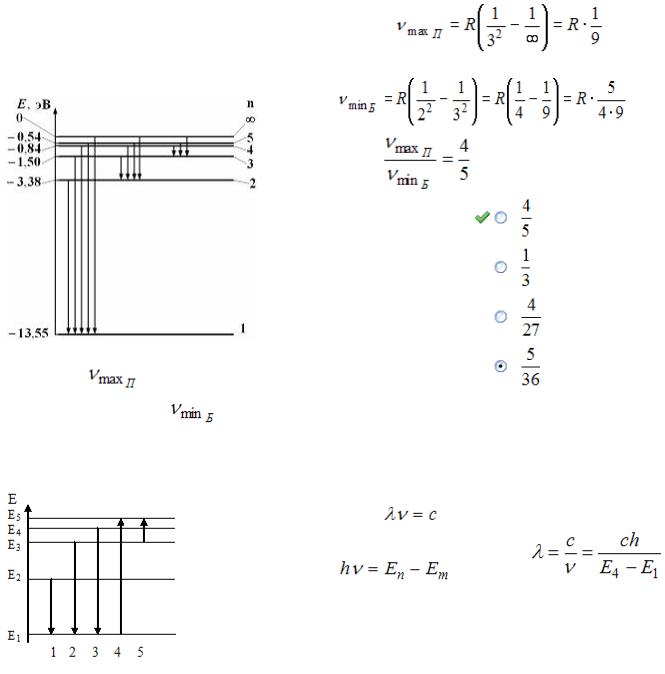
|
атома водорода, а также условно изображены |
тический уровень, серию Бальмера – на второй |
||||
|
переходы электрона с одного уровня на дру- |
уровень. Максимальная частота линии в серии |
||||
|
гой, сопровождающиеся излучением кванта |
|||||
|
энергии. В ультрафиолетовой области спектра |
|||||
|
эти переходы дают серию Лаймана, в видимой |
Пашена |
. Мини- |
|||
|
области – серию Бальмера, в инфракрасной об- |
мальная частота линии в серии Бальмера |
||||
|
ласти – серию Пашена и т.д. |
|||||
|
. |
|||||
|
Тогда |
|||||
|
Отношение максимальной частоты линии в се- |
|||||
|
рии Пашена |
к минимальной частоте |
. |
|||
|
линии в серии Бальмера |
равно … |
||||
|
На рисунке представлена диаграмма |
Излучение фотона происходит при переходе элек- |
||||
|
энергетических уровней атома водорода: |
трона с более высокого энергетического уровня на |
||||
|
более низкий. Учитывая связь длины волны и ча- |
|||||
|
стоты |
и правило частот Бора |
||||
|
, получаем |
. |
||||
|
Отсюда можно сделать вывод о том, что излучение |
|||||
|
фотона с наименьшей длиной волны (то есть с |
|||||
|
наибольшей частотой) происходит при переходе |
|||||
|
электрона с энергетического уровня Е4 |
на уровень |
||||
|
Излучение фотона с наименьшей длиной |
Е1, что соответствует переходу, обозначенному |
||||
|
стрелкой под номером 3. |
|||||
|
волны происходит при переходе, обозначенном |
|||||
|
стрелкой под номером …3 |
|
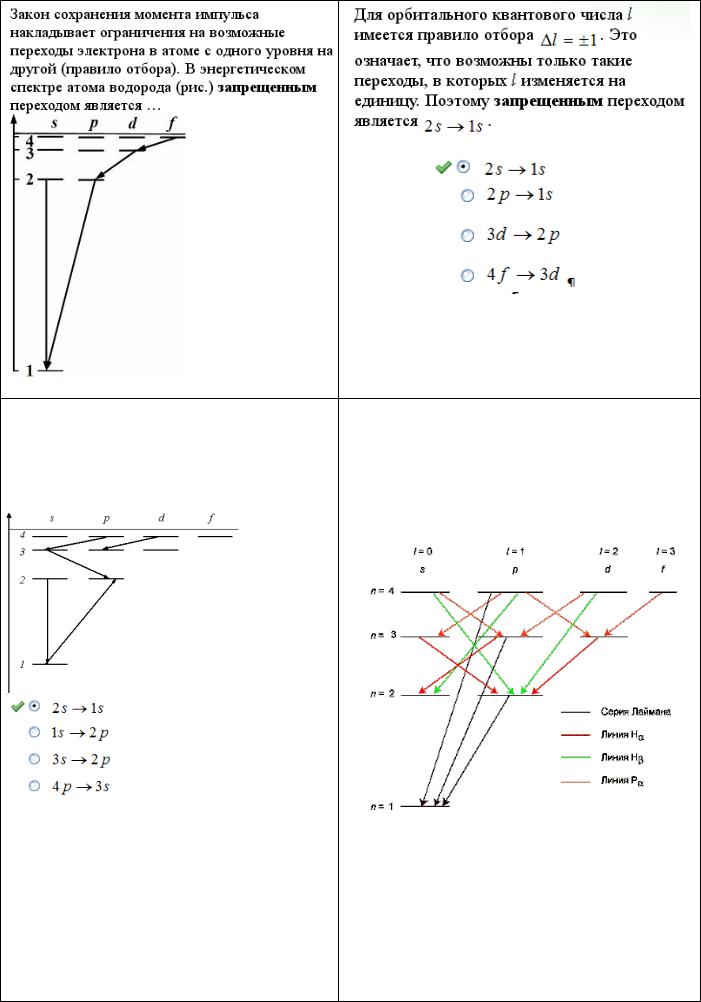
Закон сохранения момента импульса |
Правило отбора гласит, что возможны только |
|
накладывает ограничения на возможные |
такие переходы, при которых орбитальное |
|
переходы электрона в атоме с одного уровня на |
квантовое число l меняется на единицу: Δl = ±1. |
|
другой (правило отбора). В энергетическом |
Это правило является следствием закона |
|
спектре атома водорода (см. рис.) |
сохранения момента количества движения. |
|
запрещенным является переход … |
Изменение главного квантового числа n может |
|
быть любое. Возможные переходы показаны на |
|
|
схеме уровней. |
|
Ответ: 3s-2s |
|
|
Закон сохранения момента импульса наклады- |
Правило отбора гласит, что возможны только |
|
вает ограничения на возможные переходы |
такие переходы, при которых орбитальное |
|
электрона в атоме с одного уровня на другой |
квантовое число l меняется на единицу: Δl = ±1. |
|
(правило отбора). В энергетическом спектре |
Это правило является следствием закона |
|
атома водорода (рис.) запрещѐнным переходом |
сохранения момента количества движения. |
|
является … |
Изменение главного квантового числа n может |
|
быть любое. Возможные переходы показаны на |
|
|
схеме уровней. |

так как в этом случае
Закон сохранения момента импульса накладыДля орбитального квантового числа l существует
вает ограничения на возможные переходы правило отбора . Это означает, что воз- электрона в атоме с одного уровня на другой можны только такие переходы, в которых l изме- (правило отбора). В энергетическом спектре няется на единицу. Поэтому запрещенным являетатома водорода (рис.) запрещенным перехо-
дом является …
.
ся переход
1:3p – 2s
2:3s – 2s*
3:4f – 3d
|
Закон сохранения момента импульса наклады- |
1* |
4f-2p |
|
вает ограничения на возможные переходы |
2 |
2p-1s |
|
электрона в атоме с одного уровня на другой |
3 |
3s-2p |
|
(правило отбора). В энергетическом спектре |
4 |
4p-3d |
|
атома водорода (рис.) запрещѐнным переходом |
||
|
является … |
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Частоты всех
спектральных линий атома водорода можно представить одной формулой, которая
была получена экспериментально и называется обобщенной формулой Бальмера:
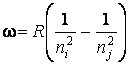
где –
циклическая (круговая) частота;
– постоянная Ридберга. Она равна
с-1;
– целые числа, которые для различных
серий и различных линий спектра принимают следующие значения:
– – для серии Лаймана;
– – для серии Бальмера;
– – для серии Пашена и т.д.
Таким образом, частоты
спектральных линий в серии Бальмера опишутся формулой:
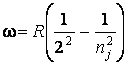
где ….
В спектроскопе
принято характеризовать спектральные линии не частотой, а обратной длине волны
величиной:
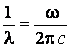
Формула Бальмера в этом случае имеет вид:
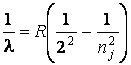
Постоянная Ридберга в формуле (1.4) имеет значение
и измеряется в м-1.
В таблице 1.1 приведены
значения длин волн серии Бальмера,
рассчитанные по формуле (1.4).
При возрастании длина волны
стремится
к предельному значению , которое называется
границей серии. Для серии Бальмера () граница серии
обозначается символом .
Таблица 1.1
|
Название линии |
Цвет |
|
Длина волны в м |
|
|
Красная |
3 |
6,5628×10-7 |
|
|
Голубая |
4 |
4,8813×10-7 |
|
|
Фиолетовая |
5 |
4,3405×10-7 |
|
|
Фиолетовая |
6 |
4,1017×10-7 |
|
|
Ультрафиолетовая |
¥ |
2,7434×10-8 |
Спектральные серии атома
#21097
2015-02-16 17:15 GMT
Возможно, пишу не туда, куда надо, простите. Вопрос вот в чем. Имеют ли ограничения серии Лаймана, Бальмера, Пашена и тд? В школе говорят, что n стремится к бесконечности и нужно подаставлять бесконечность в формулы. Репетитор говорит, что берутся до 11 включительно уровня серии, без бесконечностей. Кому верить не знаю, в интернете схожих задач нашел только одну. ( Задача типа найти отношение максимальной частоты в серии Пашена к минимальной в серии Бальмера)
#21103
2015-02-16 21:46 GMT
Почитай на http://alexandr4784.narod.ru/Detlaf_3.html Глава XIII. Строение и линейчатые спектры водородоподобных систем по Бору § 13.3. Линейчатый спектр атома водорода и увидишь, что правы все.
Бальмер нашел в 1885 г. формулу для известных в то время девяти линий спектра, поэтому n=3, 4, …, 11.
#21104
2015-02-16 22:41 GMT
Прочитал, но, что подставлять-то в формулы. Результат разный получается. На егэ это одна из вероятных задач. Например, если в задаче фигурирует отношение … к максимальной частоте в серии Бальмера, представлять 11 или бесконечность?
#21105
2015-02-17 00:40 GMT
Граница серии Бальмера:
( nu = Rc( frac {1} {2^2} – frac {1} {n^2})) при ( n to infty )