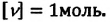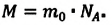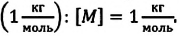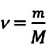| Концентрация | |
|---|---|
 |
|
| Размерность | L−3 |
| Единицы измерения | |
| СИ | м−3 |
| СГС | см−3 |
Концентра́ция части́ц — физическая величина, равная отношению числа частиц N к объёму V, в котором они находятся:
Размерность в СИ [n] = 1/м3, в системе СГС — [n] = 1/см3.
Если концентрация является функцией координаты 
Таким образом,
Однако такое представление является в некоторой степени условным, поскольку концентрация (как, например, и температура) относится к макропараметрам и при переходе к бесконечно малому объёму, по большому счёту, теряет смысл. Бесконечно малый объём в данном случае должен определяться как объём, число частиц в котором велико, однако изменение макропараметров в пределах объёма мало́.
Концентрация имеет следующую связь с плотностью и насыщенностью:
Формулы, в которых присутствует концентрация[править | править код]
[1] — давление идеального газа (см. уравнение Клапейрона).
— средняя длина свободного пробега молекулы газа (здесь D — эффективный диаметр молекулы).
— число ударов молекул газа о единицу поверхности стенки за единицу времени (здесь
— средняя скорость молекул).
— плотность тока (здесь q — заряд носителя,
— средняя скорость носителей заряда в данной точке).
См. также[править | править код]
- Концентрация смеси
Примечания[править | править код]
- ↑ Клапейрона уравнение // Физическая энциклопедия : [в 5 т.] / Гл. ред. А. М. Прохоров. — М.: Советская энциклопедия, 1990. — Т. 2: Добротность — Магнитооптика. — С. 371. — 704 с. — 100 000 экз. — ISBN 5-85270-061-4.
Концентрация
частиц (молекул, атомов и т. п.) однородной
системы
n=N/V,
где
V
— объем
системы.
Основное уравнение
кинетической теории газов
p=2/зn<п>,
где р
— давление
газа; <п>—
средняя кинетическая энергия*
поступательного
движения молекулы.
Средняя
кинетическая энергия:
приходящаяся на
одну степень свободы молекулы
<1>=½kT;
-
Здесь и далее
кинетическая энергия молекул и других
частиц обозначается .
приходящаяся на
все степени свободы молекулы (полная
энергия молекулы)
![]() ;
;
поступательного
движения молекулы
![]() ,
,
где
k
—
постоянная Больцмана; Т
—
термодинамическая температура;
i — число
степеней свободы молекулы;
вращательного
движения молекулы
![]()
Зависимость
давления газа от концентрации молекул
и температуры
p=nkT.
Скорость
молекул:
средняя квадратичная
![]() ,
,
или
![]() ;
;
средняя арифметическая
![]() ,
,
или
![]() ;
;
наиболее вероятная
![]() ,
,
или
![]() ,
,
где
m1
—
масса одной
молекулы.
Примеры решения задач
Пример
1. В
баллоне вместимостью
V=6,9 л
находится азот массой m=2,3
г. При нагревании часть молекул
диссоциировали на атомы. Коэффициент
диссоциации*
=0,2.
Определить:
1) общее
число
N1
молекул и концентрацию
n1
молекул азота до нагревания;
2) концентрацию
n2
молекул и n3
атомов азота после нагревания.
Решение.
По определению, концентрация частиц
газа есть отношение числа частиц к
вместимости сосуда, занимаемого газом:
n=N/V.
(1)
1.
Число
N1
молекул газа до нагревания найдем из
соотношения
![]() .
.
(2)
где
v
— количество
вещества азота;
na
—
постоянная Авогадро;
М
— молярная
масса азота;
Mr
—
относительная молекулярная масса азота;
k=10-3
кг/моль (см. пример
1 на с.
114). Подставив
значения величин в
(2), получим
![]() .
.
*
См. примечание к задаче
8.15.
Концентрацию
n1
найдем, подставив значения величин в
(1):
![]() .
.
2.
Концентрацию после нагревания найдем
из соотношения
![]() , (3)
, (3)
где
N
— число
молекул, не распавшихся на атомы.
После подстановки
значений величин в
(3) получим
![]() .
.
Концентрация
атомов после нагревания азота
![]() . (4)
. (4)
Число
2 в формуле
(4) выражает
тот факт, что каждая молекула после
распада дает два атома.
Подставим в
(4) значения
величин и произведем вычисления:
![]() .
.
Пример
2. В колбе
вместимостью V=0,5
л находится кислород при нормальных
условиях. Определить среднюю энергию
![]() поступательного движения всех молекул,
поступательного движения всех молекул,
содержащихся в колбе.
Решение.
Средняя энергия
![]() поступательного
поступательного
движения всех молекул может быть
выражена соотношением
![]() ,
,
(1)
где <п>—
средняя энергия поступательного движения
одной молекулы;
N
— число
всех молекул, содержащихся в колбе.
Как известно,
![]() ,
,
(2)
где
k
—
постоянная Больцмана; Т
—
термодинамическая температура.
Число молекул,
содержащихся в колбе, найдем по формуле
N=vNA,
(3)
где
v
— количество
вещества кислорода; NA
— постоянная
Авогадро.
Количество
вещества v найдем из таких соображений:
известно, что при нормальных условиях
молярный объем Vm равен 22,410-3
м3/моль. Так как, по условию задачи,
кислород в колбе находится при нормальных
условиях, то количество вещества
кислорода в колбе выражается
соотношением
v=V/Vm.
(4)
Подставив выражение
v
по
(4) в
(3), получим
N=VNA/Vm.
(5)
С учетом
(2) и
(5) выражение
(1) энергии
поступательного движения молекул
примет вид
![]()
Проверим, дает ли
правая часть расчетной формулы единицу
энергии (джоуль). Для этого вместо
символов величин подставим единицы, в
которых эти величины выражаются:
![]() .
.
Подставив значения
величин в
(6) и произведя
вычисления, найдем
![]()
Пример
3. Найти
среднюю кинетическую энергию одной
молекулы аммиака
NH3
при температуре
t=27 °С и
среднюю энергию вращательного движения
этой молекулы при той же температуре.
Решение.
Средняя полная энергия молекулы
определяется по
формуле
![]()
(1)
где
i
— число
степеней свободы молекулы;
k
—
постоянная Больцмана; Т—термодинамическая
температура газа: T=t+Т0,
где Т0=273
К.
Число степеней
свободы
i
четырехатомной молекулы, какой является
молекула аммиака, равно
6.
Подставим значения
величин в
(l):
![]() .
.
Средняя энергия
вращательного движения молекулы
определяется по формуле
![]() ,
,
(2)
где число
3 означает
число степеней свободы поступательного
движения.
Подставим в
(2) значения
величин и вычислим:
![]() .
.
Заметим, что энергию
вращательного движения молекул аммиака
можно было получить иначе, разделив
полную энергию ()
на две равные части. Дело в том, что у
трех (и более) атомных молекул число
степеней свободы, приходящихся на
поступательное и вращательное
движение, одинаково (по
3), поэтому
энергии поступательного и вращательного
движений одинаковы. В данном случае
![]()
Идеальный газ — газ, удовлетворяющий трем условиям:
- Молекулы — материальные точки.
- Потенциальная энергия взаимодействия молекул пренебрежительно мала.
- Столкновения между молекулами являются абсолютно упругими.
Реальный газ с малой плотностью можно считать идеальным газом.
Измерение температуры
Температуру можно измерять по шкале Цельсия и шкале Кельвина. По шкале Цельсия за нуль принимается температура, при которой происходит плавление льда. По шкале Кельвина за нуль принимается абсолютный нуль — температура, при котором давление идеального газа равно нулю, и его объем тоже равен нулю.
Обозначение температуры
- По шкале Цельсия — t. Единица измерения — 1 градус Цельсия (1 oC).
- По шкале Кельвина — T. Единица измерения — 1 Кельвин (1 К).
Цена деления обеих шкал составляет 1 градус. Поэтому изменение температуры в градусах Цельсия равно изменению температуры в Кельвинах:
∆t = ∆T
При решении задач в МКТ используют значения температуры по шкале Кельвина. Если в условиях задачи температура задается в градусах Цельсия, нужно их перевести в Кельвины. Это можно сделать по формуле:
T = t + 273
Если особо важна точность, следует использовать более точную формулу:
T = t + 273,15
Пример №1. Температура воды равна oC. Определить температуру воды в Кельвинах.
T = t + 273 = 2 + 273 = 275 (К)
Основное уравнение МКТ идеального газа
Давление идеального газа обусловлено беспорядочным движением молекул, которые сталкиваются друг с другом и со стенками сосуда. Основное уравнение МКТ идеального газа связывает давление и другие макропараметры (объем, температуру и массу) с микропараметрами (массой молекул, скоростью молекул и кинетической энергией).
Основное уравнение МКТ
Давление идеального газа пропорционально произведению концентрации молекул на среднюю кинетическую энергию поступательного движения молекулы.
p=23n−Ek
p — давление идеального газа, n — концентрация молекул газа, −Ek — средняя кинетическая энергия поступательного движения молекул.
Выражая физические величины друг через друга, можно получить следующие способы записи основного уравнения МКТ идеального газа:
|
p=13m0n−v2 |
m0— масса одной молекулы газа; n — концентрация молекул газа; −v2 — среднее значение квадрата скорости молекул газа. Среднее значение квадрата скорости не следует путать со среднеквадратичной скоростью v, которая равна корню из среднего значения квадрата скорости: v=√−v2 |
|
p=13ρ−v2 |
ρ — плотность газа |
|
p=nkT |
k — постоянная Больцмана (k = 1,38∙10–3 Дж/кг) T — температура газа по шкале Кельвина |
Пример №2. Во сколько раз уменьшится давление идеального одноатомного газа, если среднюю кинетическую энергию теплового движения молекул и концентрацию уменьшить в 2 раза?
Согласно основному уравнению МКТ идеального газа, давление прямо пропорционально произведению средней кинетической энергии теплового движения молекул и концентрации его молекул. Следовательно, если каждая из этих величин уменьшится в 2 раза, то давление уменьшится в 4 раза:
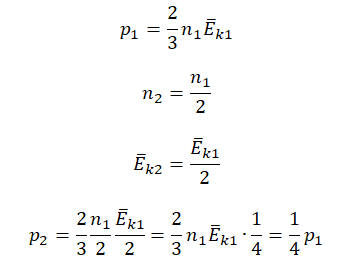
Следствия из основного уравнения МКТ идеального газа
Через основное уравнение МКТ идеального газа можно выразить скорость движения молекул (частиц газа):
v=√3kTm0=√3RTM
R — универсальная газовая постоянная, равная произведения постоянной Авогадро на постоянную Больцмана:
R=NAk=8,31 Дж/К·моль
Температура — мера кинетической энергии молекул идеального газа:
−Ek=32kT
T=2−Ek3k
Полная энергия поступательного движения молекул газа определяется формулой:
E=N−Ek
Пример №3. При уменьшении абсолютной температуры на 600 К средняя кинетическая энергия теплового движения молекул неона уменьшилась в 4 раза. Какова начальная температура газа?
Запишем формулу, связывающую температуру со средней кинетической энергией теплового движения молекул, для обоих случаев, с учетом что:
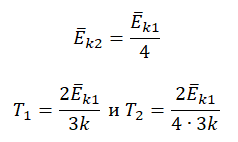
Следовательно:
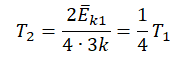
Составим систему уравнений:
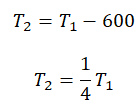
Отсюда:
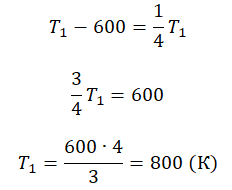
Задание EF19012
 На графике представлена зависимость объёма постоянного количества молей одноатомного идеального газа от средней кинетической энергии теплового движения молекул газа. Опишите, как изменяются температура и давление газа в процессах 1−2 и 2−3. Укажите, какие закономерности Вы использовали для объяснения.
На графике представлена зависимость объёма постоянного количества молей одноатомного идеального газа от средней кинетической энергии теплового движения молекул газа. Опишите, как изменяются температура и давление газа в процессах 1−2 и 2−3. Укажите, какие закономерности Вы использовали для объяснения.
Алгоритм решения
1.Указать, в каких координатах построен график.
2.На основании основного уравнения МКТ идеального газа и уравнения Менделеева — Клапейрона выяснить, как меняются указанные физические величины во время процессов 1–2 и 2–3.
Решение
График построен в координатах (V;Ek). Процесс 1–2 представляет собой прямую линию, исходящую из начала координат. Это значит, что при увеличении объема растет средняя кинетическая энергия молекул. Но из основного уравнения МКТ идеального газа следует, что мерой кинетической энергии молекул является температура:
T=2−Ek3
Следовательно, когда кинетическая энергия молекул растет, температура тоже растет.
Запишем уравнение Менделеева — Клапейрона:
pV=νRT
Так как количество вещества одинаковое для обоих состояния 1 и 2, запишем:
νR=p1V1T1=p2V2T2
Мы уже выяснили, что объем и температура увеличиваются пропорционально. Следовательно, давление в состояниях 1 и 2 равны. Поэтому процесс 1–2 является изобарным, давление во время него не меняется.
Процесс 2–3 имеет график в виде прямой линии, перпендикулярной кинетической энергии. Так как температуры прямо пропорциональна кинетической энергии, она остается постоянной вместе с этой энергией. Следовательно, процесс 2–3 является изотермическим, температура во время него не меняется. Мы видим, что объем при этом процессе уменьшается. Но так как объем и давление — обратно пропорциональные величины, то давление на участке 2–3 увеличивается.
Ответ:
• Участок 1–2 — изобарный процесс. Температура увеличивается, давление постоянно.
• Участок 2–3 — изотермический процесс. Температура постоянно, давление увеличивается.
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17560
Первоначальное давление газа в сосуде равнялось р1. Увеличив объём сосуда, концентрацию молекул газа уменьшили в 3 раза, и одновременно в 2 раза увеличили среднюю энергию хаотичного движения молекул газа. В результате этого давление р2 газа в сосуде стало равным
Ответ:
а) 13p1
б) 2p1
в) 23p1
г) 43p1
Алгоритм решения
1.Записать исходные данные.
2.Записать основное уравнение МКТ идеального газа.
3.Составить уравнения для состояний 1 и 2.
4.Выразить искомую величину.
Решение
Исходные данные:
• Начальное давление: p0.
• Начальная концентрация молекул: n1 = 3n.
• Конечная концентрация молекул: n2 = n.
• Начальная средняя энергия хаотичного движения молекул: Ek1 = Ek.
• Конечная средняя энергия хаотичного движения молекул: Ek2 = 2Ek.
Основное уравнение МКТ:
p=23n−Ek
Составим уравнения для начального и конечного состояний:
p1=23n1−Ek1=233n−Ek=2n−Ek
p2=23n2−Ek2=23n2−Ek=43n−Ek
Отсюда:
n−Ek=p12=3p24
p2=4p16=23p1
Ответ: в
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18416
Цилиндрический сосуд разделён неподвижной теплоизолирующей перегородкой. В одной части сосуда находится кислород, в другой – водород, концентрации газов одинаковы. Давление кислорода в 2 раза больше давления водорода. Чему равно отношение средней кинетической энергии молекул кислорода к средней кинетической энергии молекул водорода?
Алгоритм решения
1.Записать исходные данные.
2.Записать основное уравнение МКТ идеального газа.
3.Составить уравнения для обоих газов.
4.Найти отношение средней кинетической энергии молекул кислорода к средней кинетической энергии молекул водорода.
Решение
Анализируя условия задачи, можно выделить следующие данные:
• Концентрации кислорода и водорода в сосуде равны. Следовательно, n1 = n2 = n.
• Давление кислорода вдвое выше давления водорода. Следовательно, p1 = 2p, а p2 = p.
Запишем основное уравнение идеального газа:
p=23n−Ek
Применим его для обоих газов и получим:
p1=23n1−Ek1 или 2p=23n−Ek1
p2=23n2−Ek2 или p=23n−Ek2
Выразим среднюю кинетическую энергию молекул газа из каждого уравнения:
−Ek1=3pn
−Ek2=3p2n
Поделим уравнения друг на друга и получим:
−Ek1−Ek2=3pn·2n3p=2
Ответ: 2
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18824
В одном сосуде находится аргон, а в другом – неон. Средние кинетические энергии теплового движения молекул газов одинаковы. Давление аргона в 2 раза больше давления неона. Чему равно отношение концентрации молекул аргона к концентрации молекул неона?
Алгоритм решения
1.Записать исходные данные.
2.Записать основное уравнение МКТ идеального газа.
3.Составить уравнения для обоих газов.
4.Найти отношение концентрации молекул аргона к концентрации молекул неона.
Решение
Анализируя условия задачи, можно выделить следующие данные:
• Средние кинетические энергии теплового движения молекул газов одинаковы. Следовательно, −Ek1=−Ek2=−Ek.
• Давление аргона в 2 раза больше давления неона. Следовательно, p1 = 2p, а p2 = p.
Запишем основное уравнение идеального газа:
p=23n−Ek
Применим его для обоих газов и получим:
p1=23n1−Ek1 или 2p=23n1−Ek
p2=23n2−Ek2 или p=23n2−Ek
Выразим концентрации молекул газа из каждого уравнения:
n1=3p−Ek
n2=3p2−Ek
Поделим уравнения друг на друга и получим:
n1n2=3p−Ek·2−Ek3p=2
Ответ: 2
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 10.6k
Смесь кислорода и азота
при температуре T = 290 K и давлении p = 5,8 кПа имеет плотность ρ = 0,40 кг/м3 .
Определите концентрацию молекул кислорода в смеси.
Решение.
Давление смеси газов,
согласно закону Дальтона, равно сумме парциальных давлений.
Эти давления найдем из
уравнения Клапейрона-Менделеева.
Где ρ1 и ρ2
– парциальные плотности кислорода и азота, т.е. плотности, которые имели бы
газы, если бы каждый из них отдельности занимал весь этот объем.
Так как из основного
уравления молекулярно-кинетической теории следует, что p
= nkT, уравнения (1) можно записать в следующем виде.
Подставим их в
равенство (2).
Концентрация молекул
смеси газов равна сумме концентрация компонентов.
Решая совместо
уравнения уравнения (3) и (4), находим концентрацию молекул кислорода.
Ответ: n1 =
5,9•1025 м-3 .
Источник: Физика. Полный курс подготовки к ЦТ. Под общей редакцией проф. В.А. Яковенко.
Содержание:
Молекулярная физика:
«Если бы все накопленные научные знания были уничтожены и к грядущим поколениям перешла только одна фраза, то какое утверждение принесло бы наибольшую информацию? Я считаю, что это атомная гипотеза: все тела состоят из атомов, маленьких телец, которые находятся в непрерывном движении, притягиваются на небольших расстояниях, но отталкиваются, если одно из них плотнее прижать к другому». Это слова Ричарда Фейнмана, лауреата Нобелевской премии по физике 1965 г., и они практически дословно повторяют идеи Демокрита, высказанные более 25 веков назад.
Основные положения молекулярно-кинетической теории
Молекулярно-кинетическая теория (МКТ) — теория, рассматривающая строение вещества с точки зрения трех основных положений.
- Все вещества состоят из частиц — атомов, молекул, ионов, то есть имеют дискретное строение; между частицами есть промежутки (рис. 26.1).
- Частицы вещества пребывают в непрерывном беспорядочном (хаотическом) движении; такое движение называют тепловым.
- Частицы взаимодействуют друг с другом (притягиваются и отталкиваются).
Вспомним определения основных структурных единиц вещества.
Атом — наименьшая частица, являющаяся носителем свойств химического элемента. Каждому химическому элементу соответствует атом, обозначаемый символом элемента (атом Гидрогена Н, атом Карбона С, атом Урана U). Атом имеет сложную структуру и представляет собой ядро, окруженное облаком электронов. Число электронов в атоме равно числу протонов в его ядре. Заряд электрона по модулю равен заряду протона, поэтому атом электрически нейтрален. Объединяясь, атомы образуют молекулы.
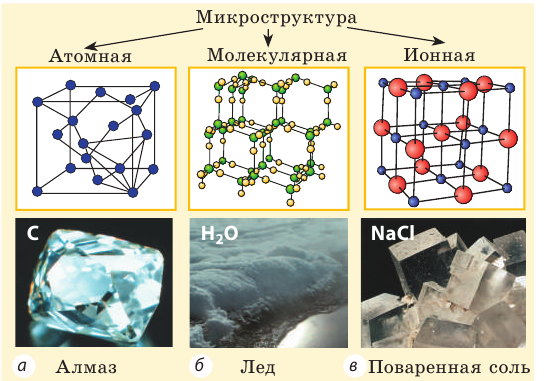
Рис. 26.1. Микроструктура некоторых веществ в кристаллическом Алмаз состоянии
Молекула — наименьшая частица вещества, обладающая химическими свойствами этого вещества и состоящая из атомов. Молекулы разных веществ имеют разный атомный состав. Все огромное разнообразие веществ обусловлено различными сочетаниями атомов в молекулах.
Если атом (молекула) теряет один или несколько электронов, образуется положительный ион; если же к атому (молекуле) присоединились один или несколько электронов, образуется отрицательный ион.
Какие факты доказывают существование атомов и молекул
Мы не можем увидеть частицы вещества из-за их микроскопических размеров, однако еще философы древности приводили немало косвенных доказательств их существования.
Со временем появились доказательства существования частиц вещества, основанные на строгих количественных расчетах. Так, в конце XVIII в. был установлен закон кратных отношений: если два элемента, вступая в реакцию друг с другом, образуют несколько соединений, то разные массы одного элемента, соединяясь с неизменной массой второго элемента, соотносятся как небольшие целые числа.
Например, азот и кислород дают три соединения: 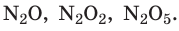
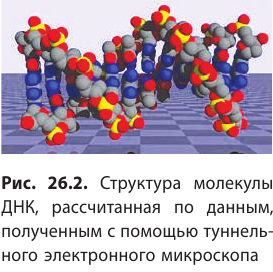
Сейчас физики создали ряд приборов (ионные проекторы, электронные и туннельные микроскопы), позволяющих исследовать не только состав молекул (рис. 26.2), но и внутреннее строение атома (рис. 26.3).

Насколько мала молекула
Достаточно точно установлено: размеры большинства молекул и диаметры всех атомов составляют порядка 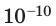 м. Разумеется, что массы атомов и молекул тоже малы (порядка
м. Разумеется, что массы атомов и молекул тоже малы (порядка 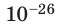 кг). Измерять их в таких единицах, как килограмм, очень неудобно, поэтому была принята внесистемная единица — атомная единица массы, равная 1/12 массы атома Карбона
кг). Измерять их в таких единицах, как килограмм, очень неудобно, поэтому была принята внесистемная единица — атомная единица массы, равная 1/12 массы атома Карбона 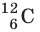 :
:
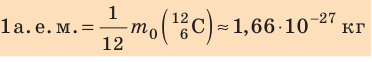
Массу молекулы, представленную в атомных единицах массы, называют относительной молекулярной массой 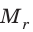 :
:
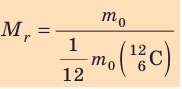
Относительная молекулярная масса показывает, во сколько раз масса 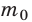 молекулы больше, чем 1/12 массы атома Карбона
молекулы больше, чем 1/12 массы атома Карбона 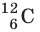 .
.
В каких единицах считают молекулы
Макроскопические тела состоят из огромного количества частиц. Выясним, например, количество молекул в стакане воды (m= 0,2 кг). Масса молекулы воды 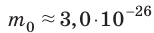 кг. Следовательно, в стакане воды содержится:
кг. Следовательно, в стакане воды содержится: 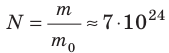 молекул! Считают такое огромное количество микрочастиц определенными «порциями» — молями. 1 моль любого вещества содержит одинаковое число частиц, — столько, сколько атомов Карбона содержится в углероде массой 12 г. Это число называют постоянной Авогадро:
молекул! Считают такое огромное количество микрочастиц определенными «порциями» — молями. 1 моль любого вещества содержит одинаковое число частиц, — столько, сколько атомов Карбона содержится в углероде массой 12 г. Это число называют постоянной Авогадро: 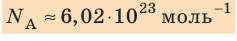 .
.
Физическая величина, равная количеству молей частиц вещества, называется количеством вещества ν: 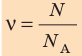 , где N — число частиц вещества.
, где N — число частиц вещества.
Единица количества вещества в СИ — моль: [ν] = 1 моль (mol)
Размеры молекул
Размеры молекул настолько малы, что это трудно представить. Если молекулу воды (d≈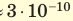 м) увеличить в миллион раз, то она будет иметь размер точки (≈ 0,3 мм). В результате такого же увеличения толщина волоса (0,1 мм) окажется равной 100 м, диаметр вишни (1 см) — 10 км, а средний рост человека (170 см) — 1700 км.
м) увеличить в миллион раз, то она будет иметь размер точки (≈ 0,3 мм). В результате такого же увеличения толщина волоса (0,1 мм) окажется равной 100 м, диаметр вишни (1 см) — 10 км, а средний рост человека (170 см) — 1700 км.
Чтобы продемонстрировать огромное количество молекул, английский физик Уильям Томсон (лорд Кельвин) предложил мысленный эксперимент: «Допустим, мы взяли стакан «меченых» молекул воды, вылили эту воду в Мировой океан и тщательно перемешали его. Затем зачерпнули стакан воды из океана на другом краю Земли и посчитали в ней все «меченые» молекулы. В стакане их окажется около тысячи!»
Массу данного вещества, взятого в количестве 1 моль (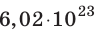 молекул), называют молярной массой M вещества:
молекул), называют молярной массой M вещества:
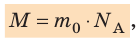
где 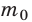 — масса молекулы (атома) вещества.
— масса молекулы (атома) вещества.
Единица молярной массы в СИ — килограмм на моль: 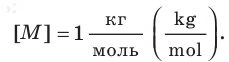
- Молярная масса равна относительной молекулярной массе, представленной в граммах:
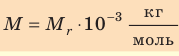
- Количество вещества массой m и молярной массой M можно определить по формуле:
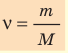
- Число N молекул вещества равно:
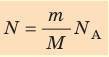
Пример №1
Сколько свободных электронов находится в алюминиевом бруске размерами 1 × 4 × 5 см? Считайте, что каждый атом Алюминия дает один свободный электрон.
Анализ физической проблемы. По условию задачи количество электронов равно числу атомов Алюминия в бруске объемом 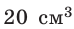 (1 × 4 × 5 см). Молярную массу алюминия найдем, воспользовавшись Периодической системой химических элементов:
(1 × 4 × 5 см). Молярную массу алюминия найдем, воспользовавшись Периодической системой химических элементов: 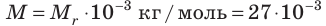 кг /моль. Плотность алюминия найдем в таблице плотностей.
кг /моль. Плотность алюминия найдем в таблице плотностей.
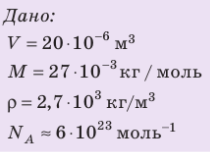
Решение:
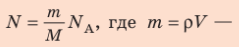 масса Алюминия
масса Алюминия
Окончательно получим: 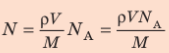
Проверим единицу найдём значение искомой величины:
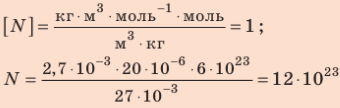
Ответ: 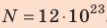
Выводы:
Карта основ молекулярно-кинетической теории:
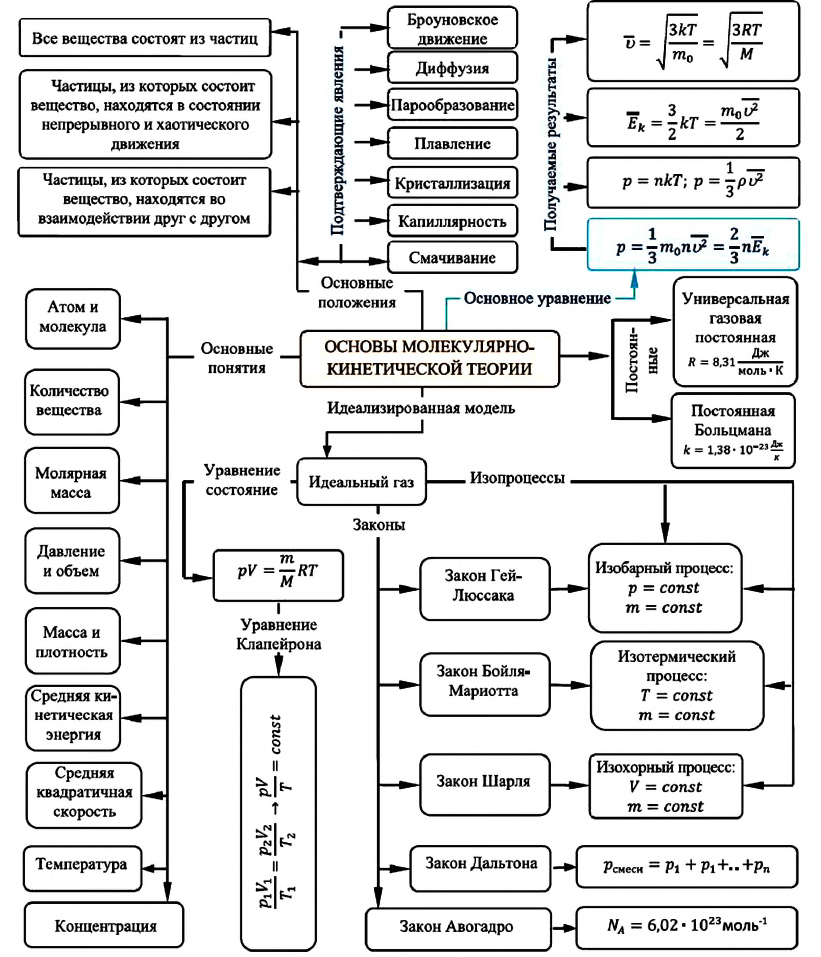
Молекулярно-кинетическая теория и ее основные положения
Вы, наверно, не раз наблюдали движение взвешенных в воздухе пылинок в солнечных лучах, проникающих в комнату через окно.
Известно, что вдыхаемый нами воздух состоит из газов разной плотности – азота 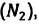 кислорода
кислорода 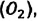 углекислого газа
углекислого газа  и других. Эти газы должны были бы расположиться слоями последовательно друг над другом, в соответствии с их плотностями и силе тяжести, действующей на них: сначала, как самый плотный, у поверхности Земли углекислый газ
и других. Эти газы должны были бы расположиться слоями последовательно друг над другом, в соответствии с их плотностями и силе тяжести, действующей на них: сначала, как самый плотный, у поверхности Земли углекислый газ  над ним кислород –
над ним кислород –  и выше азот –
и выше азот – Однако этого не происходит – нас окружает однородный газ.
Однако этого не происходит – нас окружает однородный газ.
Молекулярно-кинетическая теория (MKT). Мы сами и окружающий нас мир являемся системой макроскопических тел.
Макроскопическое тело – это тело, состоящее из большого числа атомов и молекул.
Примером макроскопических тел могут быть песчинка, вода в сосуде, газ в баллоне, железный стержень, Луна, Солнце и другие. В механике макроскопическое тело рассматривается как объект, обладающий определенной массой, пространственными размерами, энергией, изучается положение этого тела в пространстве и взаимодействие его с другими телами. Однако механика не может объяснить внутреннее строение макроскопических тел, взаимодействие между атомами и молекулами, из которых они состоят, и ряд свойств вещества (тепловое расширение, нагревание, охлаждение, парообразование, конденсацию, плавление, затвердевание, диффузию, конвекцию и др.). В физике выделен раздел – молекулярная физика, в котором собраны результаты изучения внутреннего строения вещества.
Молекулярная физика — это раздел физики, в котором изучаются внутреннее строение макроскопических тел, их свойства и основные закономерности теплового движения материи.
Молекулярно-кинетическая теория (MKT) – теория, объясняющая свойства макроскопических тел и тепловые процессы в этих телах на основе представлений о веществе как о системе атомов и молекул, беспрерывно и хаотически движущихся и взаимодействующих друг с другом.
Основные положения молекулярно-кинетической теории. В основе MKT лежат три положения:
I положение: все вещества состоят из частичек — атомов и молекул. Существование атомов и молекул было предсказано еще древними философами. Однако ясную количественную теорию этого факта впервые предложил английский ученый-химик Джон Далтон (1766-1844). Составив таблицу относительных атомных масс ряда элементов, он заложил основу теории атомного строения вещества. В наше время, используя способность электронного микроскопа увеличивать в миллионы раз размеры объекта, можно увидеть и сфотографировать достаточно большие молекулы.
II положение: частицы, из которых состоит вещество, находятся в непрерывного и беспорядочного (хаотического) движения.
Верность этого положения была установлена на основе открытия, сделанного в 1827 году английским ботаником Робертом Броуном, наблюдавшим в микроскоп за движением цветочной пыльцы в воде. Он обнаружил, что пыльца совершает хаотическое движение и изменяет свое положение по сложной траектории (с).
Беспорядочное движение частиц, называемое “броуновским движением”, теоретически было объяснено А.Эйнштейном в 1905 году, а опытным путем было подтверждено в 1909-1911 годах французским физиком Яном Батистом Перреном (1870— 1942). Он подтвердил предположение Эйнштейна, что причиной хаотического движения частичек краски в воде является тепловое движение молекул воды. Перрен определил, что интенсивность броуновского движения частиц зависит не от их химической природы, а от температуры: с увеличением температуры интенсивность броуновского движения также увеличивается. Таким образом:
Броуновским движением называется беспорядочное движение частиц, взвешенных в жидкости (или газе).
Другим явлением, подтверждающим второе положение MKT, является диффузия.
Диффузией называется процесс самопроизвольного взаимного проникновения атомов или молекул одного вещества в межатомные или межмолекулярные промежутки другого вещества.
Первое количественнное описание процесса диффузии дал в 1855 году немецкий физик и физиолог Адольф Фик (1829-1901) в законе, названном “законом диффузии Фика “.
III положение: частицы вещества взаимодействуют друг с другом, то есть между ними существуют силы взаимного притяжения и отталкивания.
Подтверждением этого положения является возникновение силы упругости во время деформации тела. Эти силы имеют характер близкодействия, электромагнитную природу и в значительной степени зависят от расстояния между частицами. Например, было определено, что силы притяжения между молекулами уменьшаются по закону 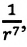 а силы отталкивания между ними уменьшаются по закону
а силы отталкивания между ними уменьшаются по закону 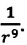 Равнодействующая этих сил на расстояниях, в 2-3 раза больших диаметра молекулы
Равнодействующая этих сил на расстояниях, в 2-3 раза больших диаметра молекулы 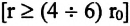 и на расстоянии, равном диаметру молекулы
и на расстоянии, равном диаметру молекулы 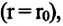 можно сказать, равна нулю (d).
можно сказать, равна нулю (d).
Характеристика атомов и молекул
Вам известны характеристики атомов и молекул: их линейные размеры, относительная масса, их число в единице объема, количество вещества и другие количественные характеристики (см.: таблица 6.1).
Таблица 6. 1
| Характеристика частицы | Выражается |
| Атомная единица массы (а.е.м) |
Атомная единица массы (а.е.м.) – это единица измерения массы в атомной и ядерной физике, равна 1/12 массы изотопа
|
| Относительная молекулярная масса вещества |
Относительной молекулярной (атомной) массой вещества называется отношение массы молекулы (атома) вещества
|
| Число Авогадро | Число Авогадро – это постоянная величина, равная числу молекул ( или атомов) в одном моле любого вещества:  |
| Количество вещества |
Количество вещества 1 моль — это количество вещества, в котором содержится столько же молекул или атомов, сколько их в 0,012 кг углерода. |
| Молярная масса |
Молярной массой называется масса одного моля вещества:
Единицей молярной массы в СИ является килограмм на моль
Следовательно, количество вещества равно отношению массы вещества его молярной массе: |
| Число молекул в веществе | Число молекул в любом веществе массой  и молярной массой и молярной массой  определяется формулой: определяется формулой: 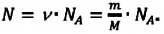 |
Молекулярная физика — раздел физики, в котором изучают свойства тел и происходящие в них процессы, связанные с огромным числом частиц, содержащихся в этих телах.
В основе молекулярной физики лежит молекулярно-кинетическая теория, объясняющая свойства тел в зависимости от их строения, сил взаимодействия между частицами, из которых состоят тела, характера движения этих частиц. Термодинамика изучает способы и формы передачи энергии от одного тела к другому, закономерности превращения одних видов энергии в другие.

Применяя законы молекулярной физики и термодинамики, конструируют тепловые двигатели, холодильные аппараты, установки для сжижения газов (рис. 1) и другие технические устройства, создают новые материалы (различные сплавы, керамики, пластмассы, сорта резины, стекла, бетона, всевозможные полупроводниковые материалы и др.) с заданными физическими (механическими, электрическими, магнитными, оптическими) свойствами. Новейшие открытия в молекулярной физике и термодинамике оказывают влияние на развитие химии и биологии. Например, возникшая на стыке наук молекулярная биология объясняет явления, происходящие в живых организмах.
В 9-м классе, изучая механику, вы рассматривали механическую форму движения материи, т. е. перемещение тел относительно друг друга и их взаимодействие. При этом внутреннее строение того или иного тела не имело значения.
В молекулярной физике и термодинамике рассматривают явления, происходящие с макроскопическими телами и обусловленные тепловой формой движения материи. Макроскопическими телами (системами) в физике называют тела (системы), состоящие из огромного числа частиц. Капля воды, газ в воздушном шаре, деревянная доска, серебряная ложка, наша планета (рис. 2) — всё это макроскопические тела.
Для описания тепловых явлений, происходящих с макроскопическими телами (системами), необходимы подходы и методы, отличные от тех, которые применяют в механике. Движение одной молекулы, происходящее в пространстве, может быть описано с использованием законов динамики одним векторным уравнением или его проекциями на координатные оси. Однако применить законы Ньютона ко всем молекулам, число которых в любом макроскопическом теле огромно, не реально. Пользуясь законами динамики для нахождения характеристик макроскопического тела, например воздуха в объёме 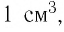 понадобилось бы решить приблизительно
понадобилось бы решить приблизительно 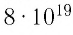 уравнений движения частиц.
уравнений движения частиц.

Для описания макроскопической системы, например газа в сосуде, можно использовать любой из двух методов — молекулярно-кинетический (статистический) или термодинамический. Эти методы качественно различны, но взаимно дополняют друг друга. Первый лежит в основе молекулярной физики, второй — термодинамики.
При молекулярно-кинетическом описании используют средние значения физических величин, характеризующих поведение частиц, образующих систему. Например, среднюю кинетическую энергию и среднюю квадратичную скорость теплового (беспорядочного) движения частиц.
При термодинамическом описании используют физические величины, характеризующие систему в целом. Например, давление, объём, температуру системы.
Основы молекулярно-кинетической теории
Что представляет собой внутреннее строение любого вещества? Сплошное оно или имеет дискретную структуру? Почему свойства различных веществ отличаются друг от друга? От чего зависят те или иные свойства вещества?
Представление о том, что все тела состоят из мельчайших частиц — атомов, возникло ещё в глубокой древности, и его достаточно отчётливо сформулировали древнегреческие философы Левкипп (приблизительно 500—440 до н. э.) и Демокрит (460—371 до н. э.). Однако в дальнейшем атомистические воззрения были забыты. Только во второй половине XVII в. английский учёный Р. Бойль в книге «Химик-скептик» придал понятию «химический элемент» новый смысл, близкий к современному. Затем в XVIII—XIX вв. М. В. Ломоносов, Д. Дальтон, А. Крёниг, Л. Больцман, Д. Максвелл и другие учёные разрабатывали и совершенствовали атомистические воззрения в качестве научной теории, получившей название классической молекулярно-кинетической теории.
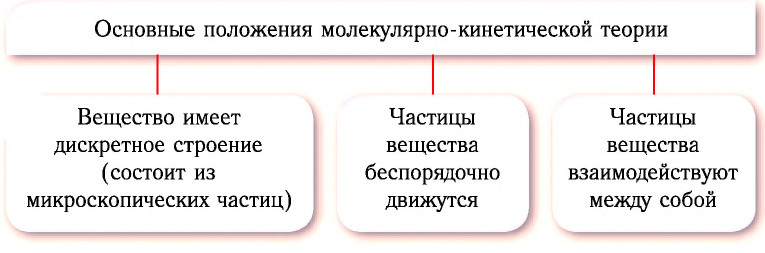
В основе молекулярно-кинетической теории лежат три положения:
- Вещество имеет дискретное строение, т. е. состоит из микроскопических частиц.
- Частицы вещества беспорядочно движутся.
- Частицы вещества взаимодействуют между собой.

Дискретное строение вещества
Как вы уже знаете, реальность существования молекул подтверждают экспериментальные факты. Например, растворение веществ в воде и в других растворителях, механическое дробление вещества (рис. 3), сжатие и расширение всех тел и особенно газов, диффузия, броуновское движение и многое другое.
Вещество имеет дискретное строение, т. е. состоит из отдельных частиц (молекул, атомов, ионов). Глаз может различить две точки, если расстояние между ними не менее 0,1 мм. Благодаря современным оптическим микроскопам можно различать структуры с расстоянием между элементами порядка 200 нм и более. Они позволяют наблюдать и фотографировать очень большие молекулы, состоящие из сотен и даже тысяч атомов (молекулы некоторых витаминов, гормонов и белков). На рисунке 4 представлена фотография молекулы нуклеиновой кислоты нитевидной формы, общая длина которой 34 мкм.

Использование электронных микроскопов позволяет наблюдать и фотографировать атомарные структуры.
От теории к практике:
Расстояние между центрами соседних атомов золота 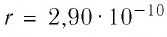 м. Какое число атомов определяет толщину листочка золота, числовое значение которой
м. Какое число атомов определяет толщину листочка золота, числовое значение которой 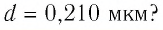
Из истории физики:
4 марта 1981 г. немецкий учёный Герд Бинниг и швейцарский учёный Генрих Рорер впервые в мире наблюдали отдельные атомы на поверхности кремния с помощью туннельного микроскопа (рис. 5). За разработку и создание электронного микроскопа (рис. б, а) немецкому учёному Эрнсту Руске и за изобретение сканирующего туннельного микроскопа (рис. 6, б) Г. Биннигу и Г. Рореру присуждена Нобелевская премия по физике за 1986 г.

Тепловое движение частиц вещества
Молекулы, атомы п другие частицы, образующие вещество, находятся в непрерывном тепловом движении.
Тепловое движение — беспорядочное движение частиц вещества, интенсивность которого зависит от температуры тела.
В 1827 г. английский ботаник Роберт Броун (1773—1858), наблюдая в микроскоп взвесь цветочной пыльцы в воде, обнаружил, что частицы взвеси непрерывно двигались, описывая весьма причудливые траектории. Это движение частиц, признанное экспериментальным подтверждением теплового движения частиц вещества, назвали броуновским движением.
Броуновское движение — беспорядочное движение взвешенных* в жидкости или газе мельчайших нерастворимых твёрдых частиц размерами порядка 1 мкм и меньше.
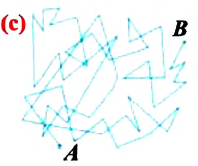
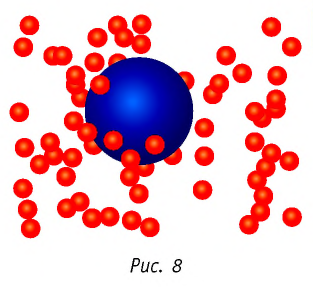
Броуновские частицы движутся непрерывно и беспорядочно, а траектории их движений очень сложны. На рисунке 7 изображена упрощённая траектория движения броуновской частицы. Точками отмечены положения частицы через одинаковые промежутки времени. Траектория движения в течение каждого промежутка времени заменена отрезком прямой, который представляет собой модуль результирующего перемещения частицы.
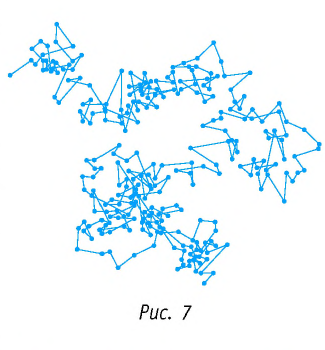
Броуновское движение обусловлено свойствами жидкости или газа. Оно не зависит от природы вещества броуновской частицы и внешних воздействий (кроме температуры). Причиной броуновского движения является тепловое движение частиц среды, окружающих броуновскую частицу, и отсутствие точной компенсации ударов, испытываемых частицей со стороны окружающих её молекул (атомов или ионов) (рис. 8).
Чем меньше размеры и масса броуновской частицы, тем заметнее становятся изменения её импульса под воздействием ударов.
* Взвешенные частицы — это частицы с плотностью вещества, сравнимой с плотностью среды (жидкости или газа), в которой они находятся, распределившиеся определённым образом по всему объёму этой среды.
Интенсивность движения броуновских частиц растёт с повышением температуры и уменьшением вязкости среды. Броуновское движение едва удаётся подметить в глицерине, а в газах оно, напротив, чрезвычайно интенсивно.
Из истории физики:
Первую количественную теорию броуновского движения предложил в 1905 г. Альберт Эйнштейн (1879-1955). Польский физик Мариан Смолуховский (1872-1917) в 1906 г. также разработал количественную теорию броуновского движения. Экспериментальное подтверждение предложенной учёными теории явилось заслугой французского физика Жана Перрена (1870-1942). «За доказательство существования молекул» Ж. Перрену присуждена Нобелевская премия по физике за 1926 г.
Ещё одним подтверждением теплового движения частиц (молекул, атомов или ионов) вещества является диффузия (лат. diffusio — распространение, растекание, рассеивание).
Диффузия — процесс взаимного проникновения частиц соприкасающихся веществ между частицами другого вещества вследствие их теплового движения.
Если частицы соприкасающихся веществ распределены в пространстве неоднородно, то данный процесс приводит к самопроизвольному выравниванию их концентраций.
Концентрация частиц — физическая величина, численно равная числу частиц, содержащихся в единичном объёме:
Если в разных частях одного и того же тела концентрации частиц не совпадают, то вследствие их теплового движения при постоянной температуре и отсутствии внешних сил происходит упорядоченное перемещение. Оно приводит к выравниванию концентраций (рис. 11).
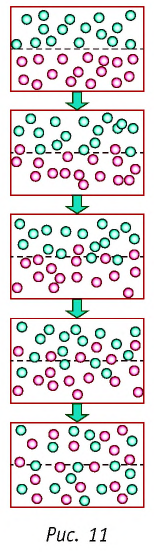
Скорость диффузии зависит от характера движения частиц вещества, который определяется температурой и особенно агрегатным состоянием. В газах диффузия происходит быстрее, чем в жидкостях, а тем более в твёрдых телах.
Диффузия играет важную роль в природе и технике. Благодаря диффузии осуществляется питание растений необходимыми веществами из почвы, в живых организмах происходит всасывание питательных веществ через стенки сосудов пищеварительного тракта. Для увеличения твёрдости стальных деталей их поверхностный слой подвергают диффузионному насыщению углеродом. Диффузию используют в ядерных технологиях как один из способов обогащения урана.
Интересно знать:
Впервые воочию убедиться, что диффузия происходит не только в газах и жидкостях, но и в твёрдых телах, удалось в 1896 г. английскому металлургу Робертсу-Аустену. Он прижал друг к другу золотой диск и свинцовый цилиндр и поместил их на 10 суток в печь, в которой поддерживалась температура 200 °С. Когда печь открыли и извлекли из неё диск и цилиндр, оказалось, что их невозможно разъединить. Диффузия привела к тому, что золото и свинец буквально «проросли» друг в друга. В настоящее время такая технология соединения деталей хорошо изучена и получила название диффузионной сварки.
Взаимодействие частиц вещества
Факт существования твёрдых и жидких тел подтверждает, что между частицами веществ, образующих эти тела, действуют силы взаимного притяжения. Именно этими силами частицы (молекулы, атомы или ионы) в телах удерживаются вместе.
Из повседневного опыта известно, что силы взаимного притяжения нагляднее всего проявляются в твёрдых телах. Тонкий стальной трос диаметром 2 мм достаточно прочен, чтобы удержать на весу гирю, масса которой 150 кг.
То, что газы занимают весь предоставленный им объём, указывает на весьма незначительное проявление сил взаимного притяжения между их молекулами*. Причина в том, что усреднённое расстояние между молекулами газов существенно превышает размеры самих молекул, а также расстояния между центрами соседних частиц жидкости и твёрдых тел.
Относительно малая сжимаемость жидкостей и твёрдых тел указывает на то, что между молекулами вещества существуют и силы взаимного отталкивания. Силы притяжения и силы отталкивания действуют одновременно. В противном случае устойчивых состояний больших совокупностей молекул не могло бы существовать: составляющие их частицы стягивались бы в одном месте пли разлетались в разные стороны.
* Несмотря на то что не все газы и жидкости состоят из молекул (они могут состоять и из атомов, и из ионов), в дальнейшем, говоря о газах и жидкостях, мы будем использовать термин «молекула».
1. В одном из учебников, изданном в 1885 г., можно прочитать: «Твёрдый атом… живёт в виде невероятной, но всё ещё неопровергнутой гипотезы… Однако несравненно правдоподобнее теория, по которой материя… непрерывна, то есть не состоит из частиц с промежутками». Какие аргументы вы можете привести автору этих строк, чтобы доказать существование мельчайших частиц вещества?
2. Представьте себе, что ваш друг скептически относится к атомам и молекулам и полагает, что броуновское движение не является доказательством их существования. Он считает, что движение взвешенных в жидкости или газе частиц может быть также хорошо объяснено движением потоков воздуха или жидкости, их окружающих. Какие аргументы вы можете привести против такой интерпретации экспериментальных наблюдений (рис. 12)?
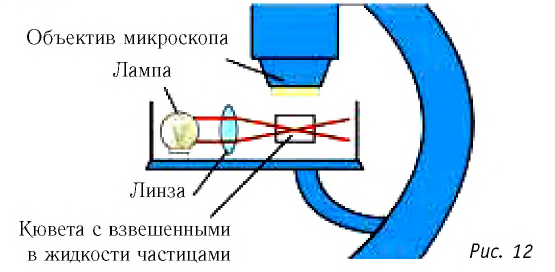
3. Почему броуновское движение заметно лишь у частиц с малыми размерами 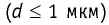 и массой?
и массой?
4. Почему стеклянную хорошо притёртую пробку трудно вынуть из горлышка стеклянного флакона?
5. Дополните схему в кратких выводах, добавив опытные обоснования основных положений молекулярно-кинетической теории.
Масса и размеры молекул и количество вещества
В 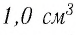 любого газа, находящегося при нормальных условиях (температура
любого газа, находящегося при нормальных условиях (температура 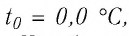 давление
давление 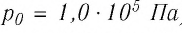 ), содержится
), содержится 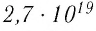 молекул. Чтобы представить, насколько велико это число, предположим, что из отверстия в ампуле вместимостью
молекул. Чтобы представить, насколько велико это число, предположим, что из отверстия в ампуле вместимостью 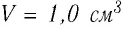 ежесекундно вылетает 100 молекул. Тогда, для того чтобы все молекулы вылетели из ампулы, потребуется 8,6 млрд лет, т. е. промежуток времени, сравнимый с возрастом Вселенной (12—15 млрд лет). Такое огромное число молекул в веществе свидетельствует о том, что их размеры очень малы. Каковы же размеры и масса частиц вещества? Как определить число атомов в любом макроскопическом теле?
ежесекундно вылетает 100 молекул. Тогда, для того чтобы все молекулы вылетели из ампулы, потребуется 8,6 млрд лет, т. е. промежуток времени, сравнимый с возрастом Вселенной (12—15 млрд лет). Такое огромное число молекул в веществе свидетельствует о том, что их размеры очень малы. Каковы же размеры и масса частиц вещества? Как определить число атомов в любом макроскопическом теле?
Молекулярно-кинетическая теория предоставляет возможность оценить массу и размеры частиц, образующих макроскопические тела. Молекулы, как и атомы, не имеют чётких границ. Если представить молекулу в виде шарика, то её радиус имеет значение от 0,1 нм у простейших до 100 нм у сложных
молекул, состоящих из нескольких тысяч атомов. Например, оценочный диаметр молекулы водорода составляет 0,2 нм, а диаметр молекулы воды — 0,3 нм. При таких размерах число частиц в веществе очень велико. Например, в одном грамме воды содержится 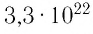 молекул.
молекул.
Размеры и масса молекулы возрастают с увеличением числа атомов, которые входят в её состав. Атомы и молекулы (кроме многоатомных молекул органических веществ) имеют массу порядка 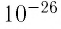 кг. Из-за малых значении выражать массы атомов и молекул в килограммах (кг) неудобно. Поэтому для измерения масс атомов и молекул в химии и физике используют атомную единицу массы (а. е. м.). Атомную единицу массы выражают через массу изотопа углерода
кг. Из-за малых значении выражать массы атомов и молекул в килограммах (кг) неудобно. Поэтому для измерения масс атомов и молекул в химии и физике используют атомную единицу массы (а. е. м.). Атомную единицу массы выражают через массу изотопа углерода 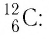
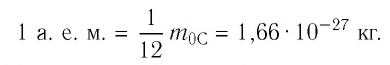
Массу молекулы (или атома), выраженную в атомных единицах массы, называют относительной молекулярной массой 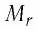 (или относительной атомной массой
(или относительной атомной массой 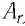 ). Относительная молекулярная (или атомная) масса
). Относительная молекулярная (или атомная) масса 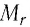 показывает, во сколько раз масса
показывает, во сколько раз масса 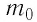 молекулы (пли атома) больше атомной единицы массы:
молекулы (пли атома) больше атомной единицы массы:
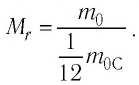
В периодической системе химических элементов Д. И. Менделеева (см. форзац 2) возле символов элементов указаны и их относительные атомные массы. В большинстве случаев при проведении расчётов значение относительной атомной массы округляют до целого числа, используя правила приближённых вычислений. Так, например, относительная атомная масса водорода равна 1, кислорода — 16, азота — 14.
Количество вещества, содержащегося в макроскопическом теле, определяют числом частиц в нём. Приведённые выше примеры показывают, насколько велико это число. Поэтому при расчётах принято использовать не абсолютное число частиц вещества, а относительное:
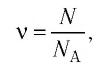
т. е. количество вещества 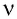 определяют отношением числа частиц N этого вещества к постоянной Авогадро
определяют отношением числа частиц N этого вещества к постоянной Авогадро 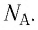
Основной единицей количества вещества в СИ является 1 моль (моль). 1 моль равен количеству вещества, содержащему столько же частиц, сколько атомов содержится в 0,012 кг изотопа углерода 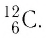 Значит, в одном моле любого вещества находится одинаковое число атомов или молекул. Это число частиц обозначили
Значит, в одном моле любого вещества находится одинаковое число атомов или молекул. Это число частиц обозначили 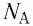 и назвали постоянной Авогадро в честь итальянского учёного Амедео Авогадро (1776—1856). Постоянная Авогадро является одной из фундаментальных физических постоянных, её значение
и назвали постоянной Авогадро в честь итальянского учёного Амедео Авогадро (1776—1856). Постоянная Авогадро является одной из фундаментальных физических постоянных, её значение
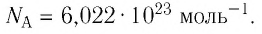
В молекулярно-кинетической теории наряду с относительной молекулярной (или атомной) массой используют молярную массу М — массу вещества, взятого в количестве 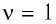 моль. Молярную массу М определяют отношением массы т вещества к его количеству
моль. Молярную массу М определяют отношением массы т вещества к его количеству 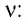
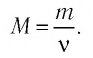
Основной единицей молярной массы в СИ является килограмм на моль 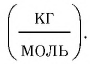 Молярная масса вещества связана с его относительной молекулярной массой следующим соотношением:
Молярная масса вещества связана с его относительной молекулярной массой следующим соотношением:
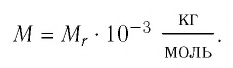
Молярную массу вещества также можно вычислить по формуле
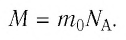
С учётом того, что 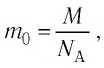 получим формулу для расчёта числа молекул в данном веществе:
получим формулу для расчёта числа молекул в данном веществе:
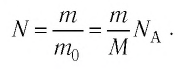
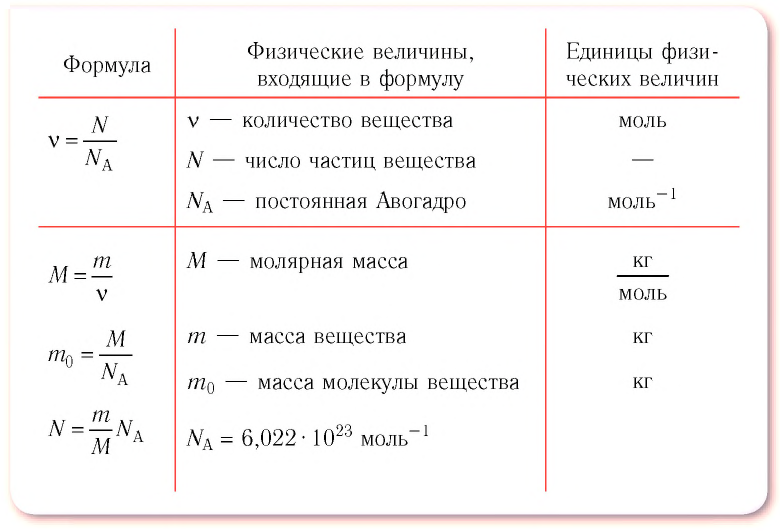
Пример №2
Определите молярную массу и массу одной молекулы сульфата меди(II) 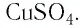
Решение. Чтобы вычислить молярную массу М любого вещества, необходимо по химической формуле найти относительную молекулярную массу 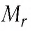 этого вещества и полученное значение умножить на
этого вещества и полученное значение умножить на 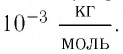 Поскольку химическая формула сульфата меди(II) имеет вид
Поскольку химическая формула сульфата меди(II) имеет вид 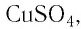 то
то
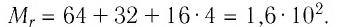
Тогда молярная масса 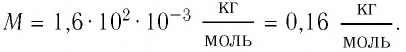
Для определения массы молекулы 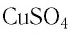 воспользуемся формулой
воспользуемся формулой 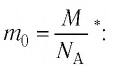
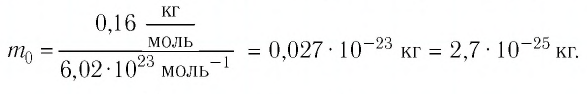
Ответ: 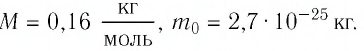
Пример №3
Определите количество вещества и число атомов, содержащихся в железном бруске объёмом 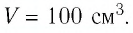 Плотность железа
Плотность железа 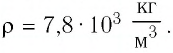
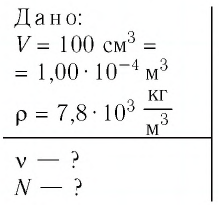
Решение. Количество вещества можно определить, воспользовавшись формулой 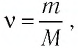 где
где 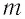 — масса железного бруска, а
— масса железного бруска, а 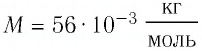 — молярная масса железа. Поскольку
— молярная масса железа. Поскольку 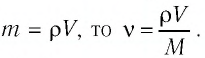

Число атомов в данном железном бруске 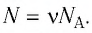 .
.
Ответ: 
* При решении задач постоянную Авогадро принять равной 
Молекулярно-кинетическая теория
Что представляет собой внутреннее строение любого вещества? Сплошное оно или имеет дискретную структуру? Почему свойства различных веществ отличаются друг от друга? От чего зависят те или иные свойства вещества?
В основе молекулярно-кинетической теории лежат три положения:
- Вещество имеет дискретное строение, т. е. состоит из микроскопических частиц.
- Частицы вещества хаотически движутся.
- Частицы вещества взаимодействуют между собой.
Дискретное строение вещества
Согласно первому положению молекулярно-кинетической теории вещество имеет дискретное строение, т. е. состоит из отдельных частиц (молекул, атомов, ионов). При изучении физики в 6 и 8 классах вы узнали, что реальное существование молекул подтверждают экспериментальные факты. Такими фактами, в частности, являются растворение веществ в воде и в других растворителях, сжатие и расширение любых тел и особенно газов, механическое дробление вещества, диффузия, броуновское движение и многое другое.
Глаз может различить две точки, если расстояние между ними не менее 0,1 мм. Современные оптические микроскопы позволяют различать структуры с расстоянием между элементами порядка двухсот нанометров и более ( 200 нм), что обеспечивает возможность наблюдать и фотографировать очень большие молекулы, состоящие из сотен и даже тысяч атомов (молекулы некоторых витаминов, гормонов и белков). На рисунке 2 приведена
200 нм), что обеспечивает возможность наблюдать и фотографировать очень большие молекулы, состоящие из сотен и даже тысяч атомов (молекулы некоторых витаминов, гормонов и белков). На рисунке 2 приведена

фотография молекулы нуклеиновой кислоты нитевидной формы, общая длина которой 34 мкм.
Переход от световых волн в оптических микроскопах к ускоренным пучкам электронов, управляемым электрическими и магнитными полями, в электронных микроскопах улучшил пределы разрешения до десятых долей нанометра. Использование электронных микроскопов позволило наблюдать и фотографировать атомарные структуры.
4 марта 1981 г. немецкий учёный Герд Бинниг и швейцарский учёный Генрих Рорер впервые в мире наблюдали отдельные атомы на поверхности кремния (рис. 3). На рисунке 4, а, б изображены электронный и туннельный микроскопы. За создание первого электронного микроскопа немецкому учёному Эрнсту Руске и за изобретение сканирующего туннельного микроскопа Г. Биннигу и Г. Рореру была присуждена Нобелевская премия по физике за 1986 год.

Тепловое движение частиц вещества
Согласно второму положению молекулярно-кинетической теории частицы, составляющие вещество, находятся в непрерывном хаотическом движении, которое называют тепловым.
Наиболее ярким экспериментальным подтверждением теплового движения частиц вещества (молекул, атомов и ионов) является броуновское движение, т. е. движение «взвешенных» в жидкости или газе мельчайших нерастворимых твёрдых частиц размерами примерно 1 мкм и меньше. «Взвешенные» частицы — это частицы, плотность вещества которых близка к плотности окружающей их среды (жидкости или газа). Они распределяются по всему объёму среды, не оседая на дно сосуда и не поднимаясь на её поверхность (рис. 5).

Первым обратил внимание на указанное явление в 1827 г. английский ботаник Роберт Броун (1773—1858). Броуновские частицы движутся непрерывно и хаотично, а траектории их движений очень сложны. На рисунке 6 изображена упрощённая траектория движения броуновской частицы. Точками отмечены положения частицы через одинаковые промежутки времени. Траектория движения в течение каждого промежутка времени заменена отрезком прямой, который представляет собой модуль результирующего перемещения частицы.
Броуновское движение обусловлено свойствами жидкости или газа, не зависит от природы вещества броуновской частицы и внешних воздействий (кроме температуры). Причиной броуновского движения является тепловое движение частиц среды, окружающей броуновскую частицу, и отсутствие точной компенсации ударов, испытываемых частицей со стороны окружающих её молекул (атомов или ионов) (рис. 7). Чем меньше размеры и масса броуновской частицы, тем заметнее становятся изменения её импульса под воздействием ударов. Интенсивность движения броуновских частиц растёт с повышением температуры и уменьшением вязкости среды, т. е. внутреннего трения, оказываемого ею. Броуновское движение едва удаётся подметить в глицерине, а в газах оно, напротив, чрезвычайно интенсивно.
Первую количественную теорию броуновского движения предложил в 1905 г. Альберт Эйнштейн (1879—1955). Польский физик Мариан Смолуховский (1872—1917) в 1906 г. также разработал количественную теорию броуновского движения. Экспериментальное подтверждение предложенной теории явилось заслугой французского физика Жана Перрена (1870—1942). «За доказательство существования молекул» Ж. Перрену присуждена Нобелевская премия по физике за 1926 г. Броуновское движение свидетельствует, что молекулы действительно существуют и что они непрерывно и хаотически движутся.
Подтверждением теплового движения частиц вещества является также диффузия — процесс выравнивания концентраций неоднородно распределённых в пространстве атомов, молекул или ионов вещества. Концентрация — величина, равная отношению числа частиц N к занимаемому ими N объёму V: 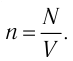
Если в разных частях одного и того же тела в объёмах 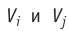 концентрации
концентрации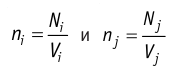 частиц не совпадают, то вследствие их теплового движения происходит упорядоченное перемещение, приводящее к выравниванию концентрации при постоянной температуре и отсутствии внешних сил. Если температура не постоянна или на систему действуют внешние силы, то в результате диффузии устанавливается пространственно неоднородное равновесное распределение концентраций частиц.
частиц не совпадают, то вследствие их теплового движения происходит упорядоченное перемещение, приводящее к выравниванию концентрации при постоянной температуре и отсутствии внешних сил. Если температура не постоянна или на систему действуют внешние силы, то в результате диффузии устанавливается пространственно неоднородное равновесное распределение концентраций частиц.
Скорость диффузии зависит от характера движения частиц вещества, который определяется температурой и особенно агрегатным состоянием. В газах диффузия происходит быстрее, чем в жидкостях, а тем более в твёрдых телах. Диффузия играет важную роль в природе и технике. Благодаря диффузии осуществляется питание растений необходимыми веществами из почвы, в живых организмах происходит всасывание питательных веществ через стенки сосудов пищеварительного тракта. Для увеличения твёрдости стальных деталей их поверхностный слой подвергают диффузному насыщению углеродом. Диффузия используется в ядерных технологиях как один из способов обогащения урана.
Взаимодействие частиц вещества
Сам факт существования твёрдых и жидких тел свидетельствует, что между частицами веществ, образующих эти тела, действуют силы взаимного притяжения. Частицы (атомы или молекулы) в этих телах удерживаются вместе именно силами взаимного притяжения. Из повседневного опыта известно, что эти силы нагляднее всего проявляются в твёрдых телах. Тонкий стальной трос диаметром 2 мм достаточно прочен, чтобы удержать на весу гирю массой 100 кг. То, что газы занимают весь предоставленный им объём, указывает на весьма незначительное проявление сил взаимного притяжения между их молекулами*. Усреднённое расстояние между молекулами газов существенно превышает размеры самих молекул,
* Несмотря на то что не все газы и жидкости состоят из молекул (они могут состоять и из атомов, и из ионов), в дальнейшем, говоря о газах и жидкостях, мы будем использовать термин «молекула».
а также расстояния между частицами, из которых состоят жидкости и твердые тела. Такое различие в проявлении сил взаимного притяжения между частицами твёрдых тел и жидкостей, с одной стороны, и частицами газов — с другой возможно в том случае, когда модуль сил взаимного притяжения между частицами быстро убывает с возрастанием расстояния между их центрами. При этом кинетическая энергия 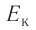 теплового движения молекул газов намного превышает модуль потенциальной энергии
теплового движения молекул газов намного превышает модуль потенциальной энергии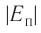 их взаимодействия:
их взаимодействия: 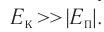
Относительно малая сжимаемость жидкостей и твёрдых тел указывает на то, что между молекулами вещества существуют и силы взаимного отталкивания. Силы притяжения и силы отталкивания действуют одновременно. В противном случае устойчивых состояний больших совокупностей молекул не могло бы существовать: составляющие их частицы стягивались бы в одном месте или разлетались в разные стороны. Зависимость модулей сил взаимного притяжения и взаимного отталкивания от расстояния между центрами частиц должна быть различной. Кроме того, должно существовать некоторое расстояние 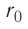 между центрами частиц, при котором силы притяжения уравновешиваются силами отталкивания — их равнодействующая равна нулю (рис. 8, а). Расстояние
между центрами частиц, при котором силы притяжения уравновешиваются силами отталкивания — их равнодействующая равна нулю (рис. 8, а). Расстояние 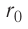 называют равновесным.
называют равновесным.
Рассмотрим взаимодействие электрически нейтральных частиц — атомов и молекул. В 8 классе вы узнали, что перераспределение заряда в теле, вызываемое воздействием другого заряженного тела, называют электризацией через влияние. Если расстояние между центрами молекул превышает их размеры (рис. 8, б), то происходит своеобразная «электризация» этих молекул через влияние. Чтобы уяснить, почему это происходит, надо учесть следующее. Во-первых, протоны и электроны, имеющие заряды противоположных знаков, внутри частицы не находятсяв одной точке, поэтому вблизи всякого атома или молекулы существует электрическое поле.
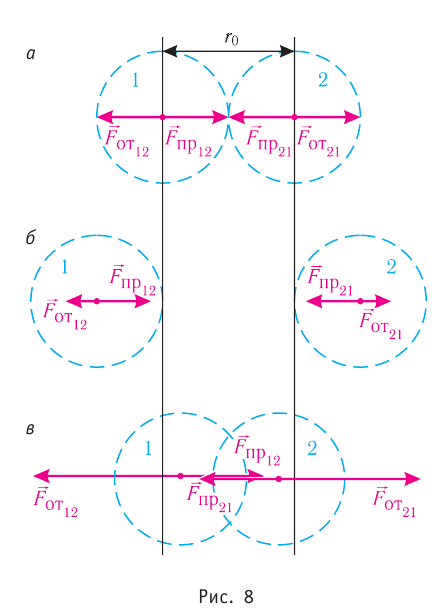
Во-вторых, под воздействием этого поля положение и движение заряженных частиц внутри соседних молекул слегка изменяется таким образом, что ядра, содержащие протоны, смещаются в направлении внешнего электрического поля, а электроны — в противоположную сторону. Это явление получило название электрической поляризации. Электрическое поле, созданное поляризационными зарядами молекулы 2, в свою очередь, вызывает перераспределение ядер, содержащих протоны, и электронов в молекуле 1. В результате молекулы будут обращены друг к другу противоположно заряженными частями, что и обеспечивает их взаимное притяжение.
Согласно теоретическим и экспериментальным исследованиям на близких расстояниях, когда электронные оболочки взаимодействующих молекул перекрываются (рис. 8, в), силы молекулярного отталкивания преобладают над силами притяжения. Модуль сил отталкивания очень велик при малых расстояниях между центрами взаимодействующих молекул, но быстро убывает с увеличением расстояния. Взаимному перекрытию электронных оболочек препятствует взаимное отталкивание электронов.
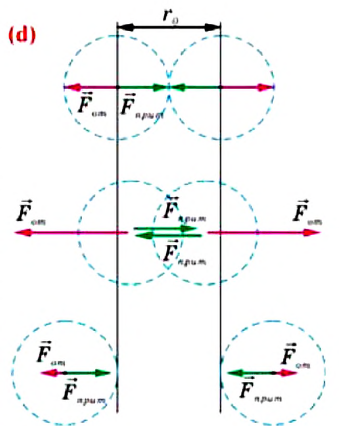
Модуль сил межмолекулярного взаимодействия обратно пропорционален n-й степени расстояния между центрами молекул 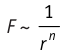 , где для сил притяжения n = 1, а для сил отталкивания n= 13.
, где для сил притяжения n = 1, а для сил отталкивания n= 13.
Зависимость проекции равнодействующей 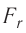 сил притяжения и отталкивания двух соседних молекул от расстояния r между их центрами можно изобразить графически. Направим ось Or от молекулы 1, центр которой совпадает с началом координат, к находящемуся от него на изменяющемся расстоянии r центру молекулы 2 (рис. 9). Будем считать молекулу 1 условно неподвижной, а молекулу 2 изменяющей своё положение относительно молекулы 1.
сил притяжения и отталкивания двух соседних молекул от расстояния r между их центрами можно изобразить графически. Направим ось Or от молекулы 1, центр которой совпадает с началом координат, к находящемуся от него на изменяющемся расстоянии r центру молекулы 2 (рис. 9). Будем считать молекулу 1 условно неподвижной, а молекулу 2 изменяющей своё положение относительно молекулы 1.
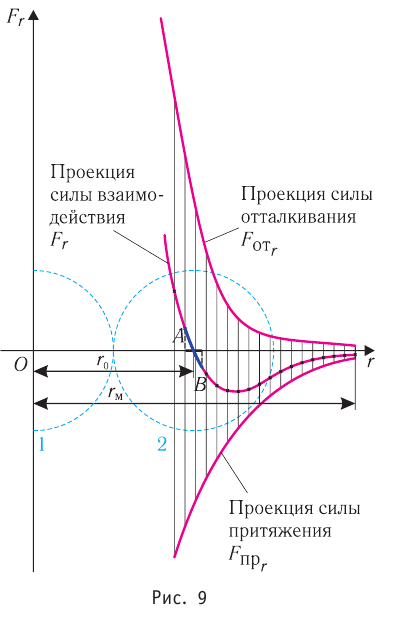
Тогда проекция силы отталкивания молекулы 2 от молекулы 1 на ось Or будет положительной, а проекция силы притяжения молекулы 2 к молекуле 1 — отрицательной.
На малых расстояниях  модуль силы отталкивания (см. рис. 9) больше модуля силы притяжения, но с увеличением расстояния r он убывает быстрее, чем модуль силы притяжения. Начиная с некоторого расстояния
модуль силы отталкивания (см. рис. 9) больше модуля силы притяжения, но с увеличением расстояния r он убывает быстрее, чем модуль силы притяжения. Начиная с некоторого расстояния  взаимодействием молекул можно пренебречь. Наибольшее расстояние
взаимодействием молекул можно пренебречь. Наибольшее расстояние  , на котором ещё учитывают взаимодействие молекул, называют радиусом молекулярного действия. Расстояние
, на котором ещё учитывают взаимодействие молекул, называют радиусом молекулярного действия. Расстояние 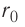 соответствует устойчивому (равновесному) взаимному положению молекул. Тонкие «вертикальные» (параллельные
соответствует устойчивому (равновесному) взаимному положению молекул. Тонкие «вертикальные» (параллельные  ) линии проведены при выполнении сложения проекций сил.
) линии проведены при выполнении сложения проекций сил.
График зависимости проекции равнодействующей 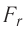 сил притяжения и отталкивания двух соседних молекул от расстояния г между их центрами (кривая проекции силы взаимодействия
сил притяжения и отталкивания двух соседних молекул от расстояния г между их центрами (кривая проекции силы взаимодействия  на рисунке 9) позволяет объяснить молекулярный механизм возникновения сил упругости в твёрдых телах. При действии на тело растягивающих внешних сил расстояние r между центрами частиц вещества становится больше равновесного расстояния
на рисунке 9) позволяет объяснить молекулярный механизм возникновения сил упругости в твёрдых телах. При действии на тело растягивающих внешних сил расстояние r между центрами частиц вещества становится больше равновесного расстояния 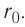 . Модуль силы притяжения на расстояниях
. Модуль силы притяжения на расстояниях 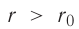 превышает модуль силы отталкивания (см. рис. 9). Действие сил притяжения между частицами возвращает их в первоначальные положения после прекращения внешнего воздействия. При сжатии твёрдого тела его частицы сближаются на расстояния
превышает модуль силы отталкивания (см. рис. 9). Действие сил притяжения между частицами возвращает их в первоначальные положения после прекращения внешнего воздействия. При сжатии твёрдого тела его частицы сближаются на расстояния 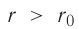 . Теперь силы отталкивания становятся преобладающими и препятствуют дальнейшему сжатию. При малых смещениях частиц из первоначальных положений устойчивого равновесия, вызванных деформацией твёрдого тела, зависимость проекции результирующей силы
. Теперь силы отталкивания становятся преобладающими и препятствуют дальнейшему сжатию. При малых смещениях частиц из первоначальных положений устойчивого равновесия, вызванных деформацией твёрдого тела, зависимость проекции результирующей силы 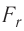 от расстояния r практически линейна (участок АВ кривой
от расстояния r практически линейна (участок АВ кривой 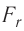 графика на рисунке 9 можно считать отрезком прямой).
графика на рисунке 9 можно считать отрезком прямой).
1. В основе молекулярно-кинетической теории лежат три положения:
- 1) Вещество имеет дискретное строение, т. е. состоит из микроскопических частиц.
- 2) Частицы вещества хаотически движутся.
- 3) Частицы вещества взаимодействуют между собой.
2. Силы взаимодействия между частицами вещества имеют электромагнитную природу и очень быстро убывают с увеличением расстояния между частицами.
Масса и размеры молекул
Количество вещества:
1,0 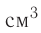 любого газа, находящегося при нормальных условиях (температура
любого газа, находящегося при нормальных условиях (температура 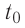 = 0,0°С, давление
= 0,0°С, давление 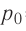 = 1,0
= 1,0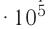 Па), содержит
Па), содержит 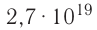 молекул. Насколько велико это число, показывает следующий пример. Предположим, что из отверстия в ампуле вместимостью К=1,0
молекул. Насколько велико это число, показывает следующий пример. Предположим, что из отверстия в ампуле вместимостью К=1,0 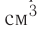 ежесекундно вылетает сто молекул. Тогда для того, чтобы все молекулы вылетели из ампулы, потребуется 8,6 миллиардов лет, т. е. промежуток времени, сравнимый с возрастом Вселенной (12—15 млрд лет). Такое огромное число молекул в веществе свидетельствует о том, что их размеры очень малы. Каковы же размеры и масса частиц вещества? Как их можно определить?
ежесекундно вылетает сто молекул. Тогда для того, чтобы все молекулы вылетели из ампулы, потребуется 8,6 миллиардов лет, т. е. промежуток времени, сравнимый с возрастом Вселенной (12—15 млрд лет). Такое огромное число молекул в веществе свидетельствует о том, что их размеры очень малы. Каковы же размеры и масса частиц вещества? Как их можно определить?
Молекулярно-кинетическая теория дала возможность оценить массу и размеры частиц, образующих макроскопические тела. Молекулы, как и атомы, не имеют чётких границ. Если представить молекулу в виде шарика, то её радиус имеет значение от 0,1 нм у простейших до 100 нм у сложных молекул, состоящих из нескольких тысяч атомов. Например, оценочный диаметр молекулы водорода составляет 0,2 нм, а молекулы воды — 0,3 нм. При таких размерах число частиц в веществе очень велико. Например, в одном грамме воды содержится 3,3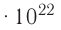 молекул.
молекул.
Размеры и масса молекулы возрастают с увеличением числа атомов, которые входят в её состав. Атомы и молекулы (кроме многоатомных молекул органических веществ) имеют массу порядка 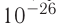 кг. Из-за малых значений выражать массы атомов и молекул в килограммах (кг) неудобно. Поэтому для измерения масс молекул в химии и физике используют атомную единицу массы (а. е. м.).
кг. Из-за малых значений выражать массы атомов и молекул в килограммах (кг) неудобно. Поэтому для измерения масс молекул в химии и физике используют атомную единицу массы (а. е. м.).
Атомную единицу массы выражают через массу изотопа углерода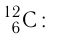
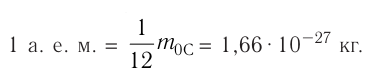
Массу молекулы (атома), выраженную в атомных единицах массы, называют относительной молекулярной (атомной) массой и обозначают символом 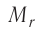 Относительная молекулярная (атомная) масса
Относительная молекулярная (атомная) масса 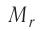 показывает, во сколько раз масса молекулы (атома) больше атомной единицы массы:
показывает, во сколько раз масса молекулы (атома) больше атомной единицы массы:
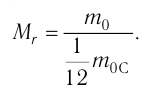
Количество вещества v определяют отношением числа частиц этого вещества N к постоянной Авогадро 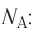
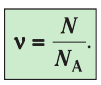
Основной единицей количества вещества в СИ является моль (моль). / моль равен количеству вещества, содержащему столько же частиц, сколько атомов содержится в 0,012 кг изотопа углерода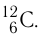 В одном моле любого вещества находится одинаковое число атомов или молекул, которое в честь итальянского учёного Амедео Авогадро (1776—1856) получило название постоянная Авогадро
В одном моле любого вещества находится одинаковое число атомов или молекул, которое в честь итальянского учёного Амедео Авогадро (1776—1856) получило название постоянная Авогадро 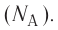 Эта величина является одной из фундаментальных физических постоянных, её значение
Эта величина является одной из фундаментальных физических постоянных, её значение
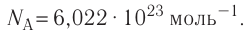
В молекулярно-кинетической теории наряду с относительной молекулярной (атомной) массой 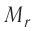 используют молярную массу M.
используют молярную массу M.
Молярная масса — масса вещества, взятого в количестве v=l моль. Молярную массу М определяют отношением массы m вещества к его количеству v:
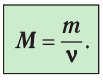
Основной единицей молярной массы в СИ является килограмм на
моль Молярная масса вещества связана с его относительной молекулярной (атомной) массой следующим соотношением:
Молярная масса вещества связана с его относительной молекулярной (атомной) массой следующим соотношением:
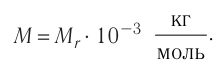
При решении задач относительную атомную массу определяют, пользуясь периодической системой химических элементов. В большинстве случаев значение относительной атомной массы округляют до целого числа. Так, например, относительная атомная масса водорода равна 1, кислорода — 16, азота — 14.
Молярную массу М вещества можно вычислить, умножив массу одной молекулы  на число молекул в одном моле (постоянная Авогадро
на число молекул в одном моле (постоянная Авогадро 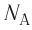 ):
):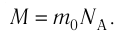
С учётом того, что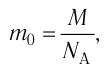 , получим формулу для расчёта числа А моле-
, получим формулу для расчёта числа А моле-
кул в данном веществе:
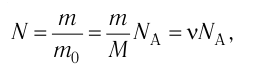
где m — масса вещества, v — количество вещества (число молей). Используя данную формулу, можно рассчитать число молекул в одном грамме воды. Сделайте это самостоятельно и убедитесь в справедливости приведённого в начале параграфа значения. *
- Один моль — количество вещества, в котором содержится столько же частиц (атомов, молекул или ионов), сколько атомов находится в 0,012 кг изотопа углерода
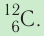
- Постоянная Авогадро — фундаментальная физическая постоянная, равная числу частиц в одном моле любого вещества:

- Количество вещества (число молей) определяют отношением числа частиц этого вещества к постоянной Авогадро:
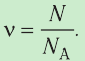
- Молярную массу определяют отношением массы вещества к количеству вещества:
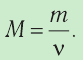
- Массу молекулы вещества можно вычислить по формуле
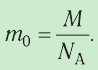
Пример №4
Определите молярную массу и массу одной молекулы сульфата меди(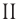 )
) 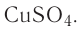
Решение. Чтобы вычислить молярную массу M любого вещества, необходимо по химической формуле найти относительную молекулярную массу 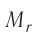 . этого вещества и полученное значение умножить на
. этого вещества и полученное значение умножить на 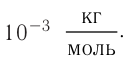
Поскольку химическая формула сульфата меди(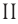 ) имеет вид
) имеет вид 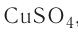 , то
, то 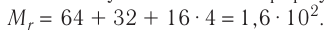
Тогда молярная масса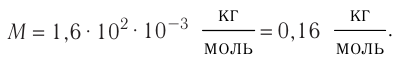
Для определения массы молекулы  воспользуемся формулой
воспользуемся формулой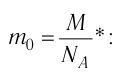
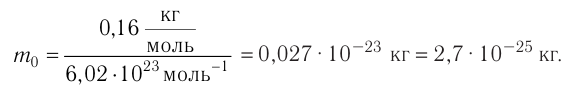
Ответ: 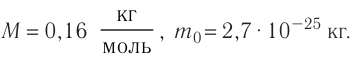
*При решении задач постоянную Авогадро можно принять 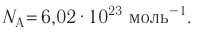
Пример №5
Определите количество вещества, содержащегося в железном бруске, объём которого 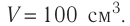 Чему равно число атомов железа в бруске? Плотность железа
Чему равно число атомов железа в бруске? Плотность железа 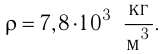
Дано:
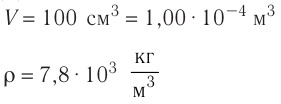
v — ?
N — ?
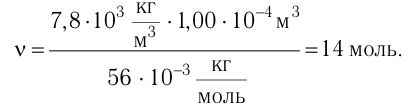
Решение. Количество определить по формуле 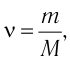 где m —масса железного бруска, а
где m —масса железного бруска, а 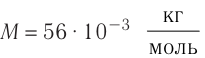 —молярная масса железа. Поскольку
—молярная масса железа. Поскольку 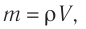 то
то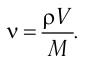
Число атомов в железном бруске 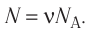
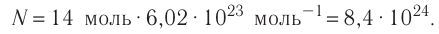
Ответ: v = 14 моль, 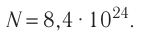
Основное уравнение молекулярно-кинетической теории идеального газа
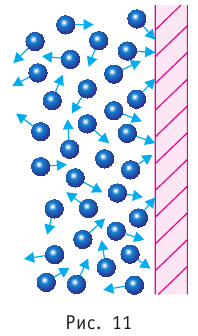
Наиболее простым из всех агрегатных состояний вещества является газообразное. Поэтому изучение свойств веществ начинают с газов. Газ (греч. chaos — хаос) — такое агрегатное состояние вещества, когда составляющие его частицы почти свободно и хаотически движутся между соударениями, во время которых происходит резкое изменение их скорости. Термин «газ» предложил в начале XVII в. нидерландский химик Ян Батист ван Бельмонт (1579—1644). Из физики 7 класса вы знаете, что давление газа на стенки сосуда, в котором он находится, как и на любое тело, помещённое внутрь сосуда, создаётся в результате ударов частиц, образующих газ (рис. II). Вследствие хаотичности их движения усреднённое по времени давление газа во всех точках сосуда одинаково. В общем случае давление — физическая скалярная величина, равная отношению модуля силы давления, действующей на плоскую поверхность, к площади этой поверхности: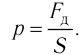 основной единицей давления является паскаль (Па).
основной единицей давления является паскаль (Па).
Макро- и микропараметры
При изучении механики вы познакомились с понятием «состояние механической системы тел» и параметрами этого состояния — координатами, скоростями и импульсами. В тепловых процессах основными физическими величинами, характеризующими некоторое количество газа как макроскопическую систему, являются давление р, объём V и температура Т. Эти физические величины называют макроскопическими параметрами состояния газа. К микроскопическим параметрам состояния газа относят индивидуальные характеристики молекул: массу отдельной молекулы 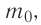 , а также скорость
, а также скорость 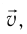 , импульс
, импульс 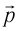 и кинетическую энергию
и кинетическую энергию 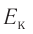 её теплового движения. Заметим, что речь идёт о средних значениях как макро-, так и микроскопических параметров.
её теплового движения. Заметим, что речь идёт о средних значениях как макро-, так и микроскопических параметров.
Одна из важнейших задач молекулярно-кинетической теории состоит в установлении связи между макроскопическими и микроскопическими параметрами.
Идеальный газ
Для теоретического объяснения свойств газов используют их упрощённую модель. Идеальный газ — модель газа, удовлетворяющая следующим условиям: 1) молекулы газа можно считать материальными точками, которые хаотически движутся; 2) силы взаимодействия между молекулами идеального газа практически отсутствуют (потенциальная энергия взаимодействия равна нулю); они действуют только при столкновениях молекул, причём это силы отталкивания. Поведение молекул идеального газа можно описать,
пользуясь законами Ньютона. Между соударениями молекулы движутся практически равномерно и прямолинейно.
Для реальных газов модель идеального газа можно использовать в ограниченном как снизу, так и сверху диапазоне температур и при достаточно малых давлениях. Так, например, свойства водорода и гелия при нормальном атмосферном давлении и комнатной температуре близки к свойствам идеального газа.
Конечно, ни одна модель, в том числе и модель идеального газа, не в состоянии описать все свойства системы. Однако использование модели идеального газа существенно упрощает задачу нахождения количественных соотношений между макроскопическими и микроскопическими параметрами газа.
Давление газа в молекулярно-кинетической теории
С точки зрения молекулярно-кинетической теории давление газа возникает в результате ударов молекул, образующих газ, по телу, соприкасающемуся с ним. При ударе
импульс молекулы газа изменяется: 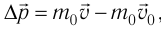 , где
, где 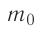 — её масса, a
— её масса, a 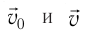 — скорости до и после удара. Если
— скорости до и после удара. Если 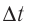 — промежуток времени между двумя последовательными ударами о тело одной и той же молекулы, то
— промежуток времени между двумя последовательными ударами о тело одной и той же молекулы, то
средней силе 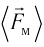 с которой тело действует на молекулу во время удара
с которой тело действует на молекулу во время удара
продолжительностью 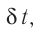 соответствует средняя сила
соответствует средняя сила 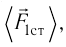 с которой одна молекула действует на тело (например, стенку сосуда) на протяжении промежутка времени
с которой одна молекула действует на тело (например, стенку сосуда) на протяжении промежутка времени  . Используя второй закон Ньютона для описания удара молекулы
. Используя второй закон Ньютона для описания удара молекулы 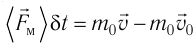 и третий закон Ньютона для мгновенных значений сил взаимодействия молекулы и тела
и третий закон Ньютона для мгновенных значений сил взаимодействия молекулы и тела 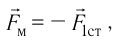 получим:
получим:
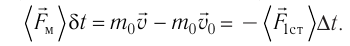 (3.1)
(3.1)
При нормальных условиях и макроскопических размерах сосуда число ударов молекул газа о плоскую поверхность площадью 1  составляет порядка
составляет порядка  в секунду. Очень слабые силы ударов отдельных молекул
в секунду. Очень слабые силы ударов отдельных молекул 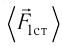 складываются для громадного количества молекул в значительную по величине и почти постоянную силу, действующую на тело. Усреднённое по времени значение этой силы, отнесенное к единичной площадке, и есть давление газа.
складываются для громадного количества молекул в значительную по величине и почти постоянную силу, действующую на тело. Усреднённое по времени значение этой силы, отнесенное к единичной площадке, и есть давление газа.
Пусть в сосуде, имеющем форму куба с ребром длиной l (рис. 12), находится идеальный газ, состоящий из одинаковых молекул массой 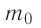 каждая. Будем считать, что молекулы упруго ударяются только о стенки сосуда, не сталкиваясь друг с другом. Так как молекулы, образующие стенки сосуда, совершают тепловые колебания, то скорости движения молекул газа при соударениях с ними изменяются случайным образом. Однако если газ и сосуд находятся в тепловом равновесии, то средняя кинетическая энергия молекул не изменяется со временем. Это позволяет реальное хаотическое движение молекул газа со всевозможными направлениями и модулями скоростей упрощённо рассматривать как движение, при котором модули проекций скорости на каждую из координатных осей одинаковые, т. е.
каждая. Будем считать, что молекулы упруго ударяются только о стенки сосуда, не сталкиваясь друг с другом. Так как молекулы, образующие стенки сосуда, совершают тепловые колебания, то скорости движения молекул газа при соударениях с ними изменяются случайным образом. Однако если газ и сосуд находятся в тепловом равновесии, то средняя кинетическая энергия молекул не изменяется со временем. Это позволяет реальное хаотическое движение молекул газа со всевозможными направлениями и модулями скоростей упрощённо рассматривать как движение, при котором модули проекций скорости на каждую из координатных осей одинаковые, т. е.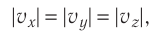 и остаются неизменными, а при соударениях изменяется знак только у одной из трёх проекций скорости на координатные оси.
и остаются неизменными, а при соударениях изменяется знак только у одной из трёх проекций скорости на координатные оси.
Для описания удара молекулы газа о стенку ABCD (см. рис. 12) запишем соотношение (3.1) в проекциях на координатные оси: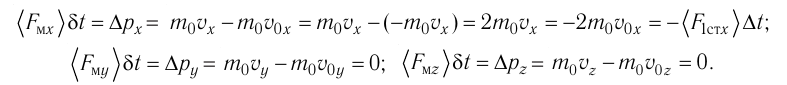
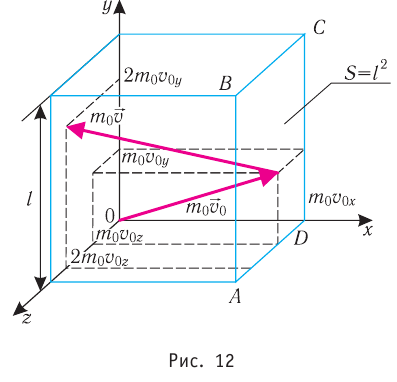
Так как промежуток времени между двумя последовательными соударениями молекулы со стенкой ABCD 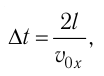 то
то
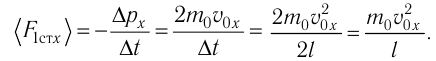
Проекция полной средней силы, с которой все N молекул, находящиеся в сосуде, действуют на стенку ABCD 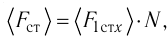 так как
так как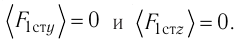
Следовательно,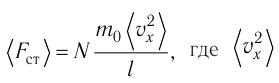 — усреднённый но всем N частицам квадрат проекций их скоростей на ось Ох.
— усреднённый но всем N частицам квадрат проекций их скоростей на ось Ох.
Разделив обе части соотношения для  на площадь стенки
на площадь стенки  получим формулу для давления, оказываемого молекулами газа на стенку ABCD:
получим формулу для давления, оказываемого молекулами газа на стенку ABCD:
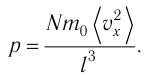
Так как 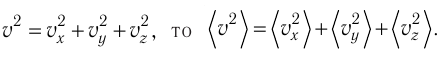 Поскольку молекулы газа совершенно одинаково отражаются от трёх пар противоположно расположенных граней куба, то
Поскольку молекулы газа совершенно одинаково отражаются от трёх пар противоположно расположенных граней куба, то 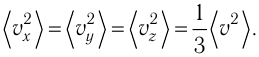 С учётом того, что занимаемый газом объём
С учётом того, что занимаемый газом объём 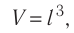 а концентрация молекул газа
а концентрация молекул газа 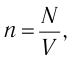 получим:
получим:
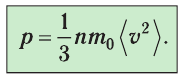 (3.2)
(3.2)
Уравнение (3.2) называют основным уравнением молекулярно-кинетической теории идеального газа. Это уравнение позволяет рассчитать макроскопический параметр давление р газа через концентрацию п молекул, массу т0 молекулы и среднюю квадратичную скорость её теплового движения, определяемую по формуле 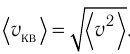 Иначе говоря, формула (3.2) связывает между собой макро- и микроскопические параметры системы «идеальный газ».
Иначе говоря, формула (3.2) связывает между собой макро- и микроскопические параметры системы «идеальный газ».
Зависимость давления газа от среднего квадрата скорости движения его молекул объясняется тем, что с увеличением скорости, во-первых, возрастает импульс молекулы, а следовательно, и сила удара о стенку. Во-вторых, возрастает число ударов, так как молекулы чаще соударяются со стенками.
Обозначим через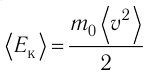 среднюю кинетическую энергию поступательного движения молекул. Тогда основное уравнение молекулярно-кинетической теории примет следующий вид:
среднюю кинетическую энергию поступательного движения молекул. Тогда основное уравнение молекулярно-кинетической теории примет следующий вид:
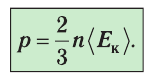 (3.3)
(3.3)
Из выражения (3.3) видно, что давление идеального газа зависит от средней кинетической энергии поступательного движения его молекул и их концентрации.
Проиллюстрировать зависимость давления от скорости движения молекул газа можно, используя механическую модель. Соберём установку, изображённую на рисунке 13. Закрепим пластину П таким образом, чтобы она могла поворачиваться вокруг горизонтальной оси. Насыплем в воронку с узким горлышком мелкую дробь. Используя наклонный жёлоб, направим на пластину струйку дроби (дробинки играют роль молекул). В результате многочисленных ударов дробинок пластина отклонится на некоторый угол под действием силы давления дробинок. Увеличив высоту, с которой скатываются дробинки, а следовательно, и их скорость в момент удара о пластину, можно заметить, что пластина отклонилась на больший угол. Отсюда можно сделать вывод: чем больше скорость движения дробинок, тем больше производимое на пластину давление.
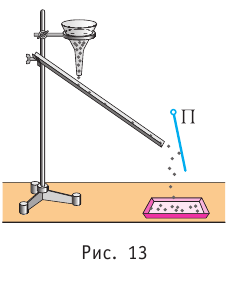
1. Идеальный газ — модель газа, удовлетворяющая следующим условиям: 1 ) молекулы газа можно считать материальными точками, которые хаотически движутся; 2) силы взаимодействия между молекулами идеального газа практически отсутствуют (потенциальная энергия взаимодействия равна нулю); они действуют только при столкновениях молекул, причём это силы отталкивания.
2. Уравнение, связывающее микронараметры состояния идеального газа (массу молекулы и её среднюю квадратичную скорость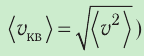 с его макропараметром (давлением, характеризующим газ как целое), непосредственно измеряемым на опыте, называют основным уравнением молекулярно-кинетической теории идеального газа:
с его макропараметром (давлением, характеризующим газ как целое), непосредственно измеряемым на опыте, называют основным уравнением молекулярно-кинетической теории идеального газа:
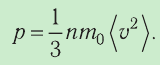
3. Давление идеального газа зависит от средней кинетической энергии поступательного движения его молекул и их концентрации:
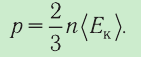
Пример №6
Электрическая лампа наполнена газом, плотность которого кг
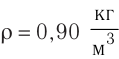 После включения лампы давление газа в ней увеличилось от
После включения лампы давление газа в ней увеличилось от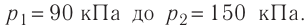 Определите, на сколько при этом увеличился средний квадрат скорости теплового движения молекул газа.
Определите, на сколько при этом увеличился средний квадрат скорости теплового движения молекул газа.
Дано
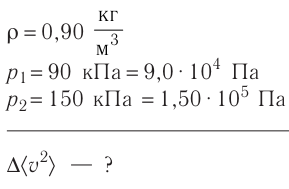
Решение.
Пример №7
В сосуде вместимостью V= 10 л находится одноатомный газ, количество вещества которого v = 2,0 моль и давление 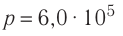 Па. Определите среднюю кинетическую энергию теплового движения атомов этого газа.
Па. Определите среднюю кинетическую энергию теплового движения атомов этого газа.
Дано
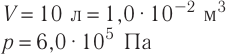
v = 2,0 моль
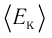 – ?
– ?
Решение. Из основного уравнения молекулярно-кинетической теории, записанного в виде 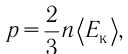 следует, что
следует, что 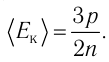 Так как концентрация атомов
Так как концентрация атомов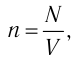 а число атомов газа
а число атомов газа 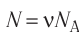 , то
, то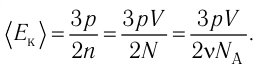
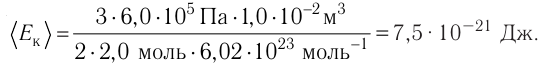
Ответ: 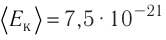 Дж.
Дж.
Тепловое равновесие
Температура — мера средней кинетической энергии теплового движения частиц вещества.
В повседневной жизни под температурой мы понимаем степень нагретости тела (холодное, тёплое, горячее). Такой подход является довольно субъективным, он зависит не только от состояния рассматриваемого тела, но и от наших ощущений. Чтобы избежать субъективной неопределенности, необходимо установить способ измерения температуры.
Тепловое равновесие
Если привести в соприкосновение два тела, то молекулы этих тел будут взаимодействовать между собой. При этом происходит передача энергии от молекул с большей кинетической энергией к молекулам с меньшей кинетической энергией. В результате средняя энергия поступательного движения молекул одного тела увеличивается, а другого — уменьшается. Отдающее энергию тело называют более нагретым, а тело, к которому энергия переходит, — менее нагретым. Как показывает опыт, такой переход энергии продолжается до тех пор, пока не установится некоторое состояние, в котором тела могут находиться сколь угодно долго. В этом состоянии степень нагретости тел становится и остаётся одинаковой, а следовательно, тела имеют одинаковую температуру. Это учитывают при измерении температуры тела. Термометр приводят в соприкосновение с телом, но отсчёт его показаний производят не сразу, а через некоторый промежуток времени. Это необходимо для того, чтобы между термометром и телом установилось тепловое равновесие.
Тепловым равновесием называют такое состояние, при котором все макроскопические параметры изолированной системы остаются неизменными в течение неограниченно большого промежутка времени. Под изолированной, или замкнутой, системой понимают систему тел, которая не обменивается энергией с окружающими телами.
Отметим, что у тел, входящих в физическую систему, находящуюся в состоянии теплового равновесия, могут быть различные значения плотности, концентрации, давления и объёма. Однако температура всех тел, входящих в такие системы, всегда одинакова.
Температура и средняя кинетическая энергия поступательного движения молекул газа
Определение температуры должно основываться на такой физической величине, которая характеризует состояние тел и является одинаковой для любых тел, находящихся в состоянии теплового равновесия. Необходимым свойством обладает средняя кинетическая энергия теплового движения частиц вещества. Эту энергию легче всего определять для идеального одноатомного газа, атомы которого совершают только поступательное движение.
Возьмём несколько сосудов разной вместимости, снабжённых манометрами для измерения давления (рис. 14). Заполнив их различными газами, например, аргоном, неоном и гелием, поместим сначала в сосуд с тающим льдом ( =0 °С), а затем будем изменять температуру содержимого сосудов, пока она не станет равной температуре кипения воды (t = 100 °С). Давления газов в сосудах могут отличаться. Массы газов можно определить взвешиванием откачанных и заполненных сосудов. Зная массу m и молярную массу М газа, по
=0 °С), а затем будем изменять температуру содержимого сосудов, пока она не станет равной температуре кипения воды (t = 100 °С). Давления газов в сосудах могут отличаться. Массы газов можно определить взвешиванием откачанных и заполненных сосудов. Зная массу m и молярную массу М газа, по
формуле 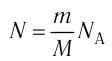 можно вычислить число частиц и, следовательно, определить их концентрацию
можно вычислить число частиц и, следовательно, определить их концентрацию 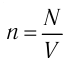 в каждом из сосудов.
в каждом из сосудов.
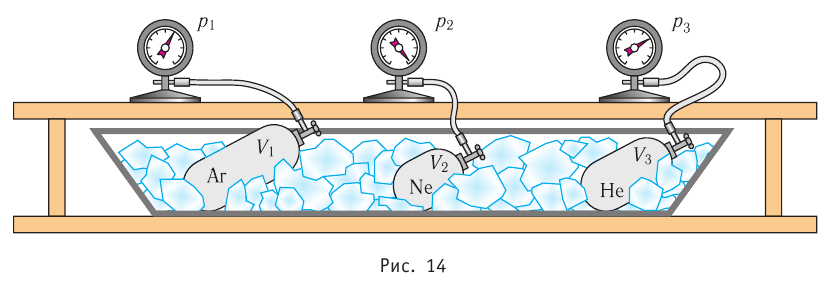
Опытным путём было установлено, что в состоянии теплового равновесия, несмотря на различные значения давления р и концентрации n частиц, отношение 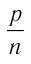 давления к концентрации во всех сосудах оказалось практически п
давления к концентрации во всех сосудах оказалось практически п
одинаковым: 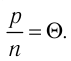 Это отношение для разреженных газов (удовлетворяющих требованиям модели «идеальный газ») зависит только от температуры, и эта зависимость является линейной, т. е.
Это отношение для разреженных газов (удовлетворяющих требованиям модели «идеальный газ») зависит только от температуры, и эта зависимость является линейной, т. е.
Здесь 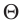 характеризует температуру газов в энергетических единицах (в СИ измеряют в джоулях), k — коэффициент пропорциональности, зависящий от выбора температурной шкалы. Коэффициент k носит название постоянной Больцмана в честь австрийского физика Людвига Больцмана (1844 — 1906), одного из основателей молекулярно-кинетической теории газов:
характеризует температуру газов в энергетических единицах (в СИ измеряют в джоулях), k — коэффициент пропорциональности, зависящий от выбора температурной шкалы. Коэффициент k носит название постоянной Больцмана в честь австрийского физика Людвига Больцмана (1844 — 1906), одного из основателей молекулярно-кинетической теории газов:
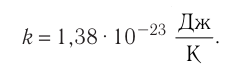
Если для измерения температуры использовать шкалу Кельвина, то при определении числового значения температуры по этой шкале полагают
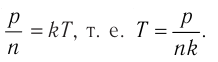 (4.1)
(4.1)
Соотношение (4.1) позволяет создать температурную шкалу, не зависящую от рода вещества (газа). Такую шкалу, называемую абсолютной (термодинамической) шкалой температур, предложил в 1848 г. выдающийся английский физик Уильям Томсон (1824—1907), удостоенный за работы в области физики в 1892 г. титула лорда Кельвина. Поэтому эту шкалу обычно называют шкалой Кельвина.
Нулевая точка по шкале Кельвина соответствует самой низкой теоретически возможной температуре (абсолютный нуль температуры). Температура тающего льда по этой шкале 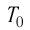 =273,15 К. Связь между температурами по шкале Цельсия (t) и по шкале Кельвина (Т) имеет вид Т = t + 273,15.
=273,15 К. Связь между температурами по шкале Цельсия (t) и по шкале Кельвина (Т) имеет вид Т = t + 273,15.
Единица температуры по абсолютной шкале один кельвин (1К) является основной единицей температуры в СИ и совпадает с одним градусом (1 °С) по шкале Цельсия. Поэтому разность температур по шкале Кельвина и по шкале Цельсия одинакова, т. е. 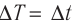 (рис. 15).
(рис. 15).

Из основного уравнения молекулярно-кинетической теории идеального газа (3.2) следует:
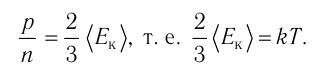
Средняя кинетическая энергия поступательного движения молекул газов, находящихся при одинаковой температуре, одинакова для разных газов, причём её значение пропорционально температуре и не зависит от массы молекулы газа:
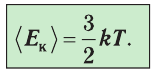 (4.2)
(4.2)
Данное соотношение устанавливает связь между макроскопическим параметром состояния идеального газа — температурой Т и микроскопическим — средней кинетической энергией 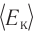 поступательного движения его частиц. Таким образом, из формулы (4.2) следует, что средняя кинетическая энергия поступательного движения частиц идеального газа пропорциональна его абсолютной температуре.
поступательного движения его частиц. Таким образом, из формулы (4.2) следует, что средняя кинетическая энергия поступательного движения частиц идеального газа пропорциональна его абсолютной температуре.
Этот вывод, основанный на экспериментах с разреженными газами, справедлив для жидкостей и твёрдых тел.
Уравнение (4.2) можно записать следующим образом: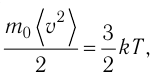
откуда
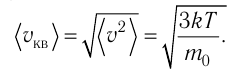
С учётом формулы (4.2) основное уравнение молекулярно-кинетической теории идеального газа может быть записано в виде
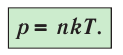 (4.3)
(4.3)
Из уравнения (4.3) видно, что при одинаковых значениях температуры Т и концентрации n частиц давление любых газов одинаково независимо от того, из каких частиц они состоят.
Закон Дальтона
Рассмотрим смесь химически не реагирующих разреженных газов, находящихся в сосуде вместимостью V. Тепловое движение частиц каждого газа равномерно распределяет их по всему объёму сосуда. В результате столкновений частиц друг с другом в смеси устанавливается тепловое равновесие. Докажем, что давление каждого газа, входящего в состав смеси, не зависит от наличия остальных разреженных газов и результирующее давление определяется суммарным давлением всех компонентов смеси газов.
Общее число частиц газов в сосуде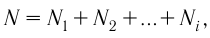 где
где 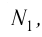
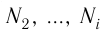 — число частиц каждого газа.
— число частиц каждого газа.
Обозначим через 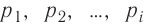 – парциальные давления каждого газа. Парциальное давление — давление газа, входящего в состав газовой смеси, если бы он один занимал весь объём, предоставленный смеси, при той же температуре. Тогда, учитывая соотношение (4.3), запишем:
– парциальные давления каждого газа. Парциальное давление — давление газа, входящего в состав газовой смеси, если бы он один занимал весь объём, предоставленный смеси, при той же температуре. Тогда, учитывая соотношение (4.3), запишем:
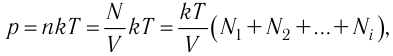 следовательно,
следовательно,
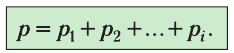 (4.4)
(4.4)
Формула (4.4) является математическим выражением закона, экспериментально установленного в 1801 г. английским учёным Джоном Дальтоном (1766—1844) и называемого законом Дальтона. Согласно этому закону давление смеси химически не реагирующих между собой газов равно сумме парциальных давлений каждого из газов.
- Тепловым равновесием называют такое состояние изолированной физической системы, при котором все её макроскопические параметры остаются неизменными с течением времени. В состоянии теплового равновесия температура различных частей физической системы одинакова.
- Средняя кинетическая энергия поступательного движения молекул газа пропорциональна абсолютной температуре:
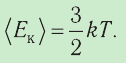
- Средняя квадратичная скорость молекул газа
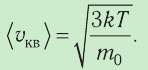
- Давление идеального газа прямо пропорционально концентрации его молекул и абсолютной температуре газа: p = nkT.
- Температурную шкалу, не зависящую от рода вещества, называют абсолютной (термодинамической) шкалой температур (шкалой Кельвина). Температура по шкале Кельвина (Т) приближённо связана с температурой по шкале Цельсия (t) соотношением Т = t + 273.
- Давление смеси химически не реагирующих между собой разреженных газов равно сумме парциальных давлений каждого из газов (закон Дальтона):
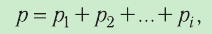 где парциальное давление — давление газа, входящего в состав газовой смеси, если бы он один занимал весь объём, предоставленный смеси, при той же температуре.
где парциальное давление — давление газа, входящего в состав газовой смеси, если бы он один занимал весь объём, предоставленный смеси, при той же температуре.
Пример №8
Сравните средние квадратичные скорости атомов гелия и молекул кислорода, если оба газа находятся в состоянии теплового равновесия.
Дано:
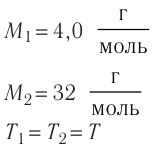
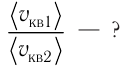
Решение. Из основного уравнения молекулярно-кинетической теории 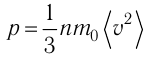 и уравнения
и уравнения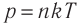 следует, что
следует, что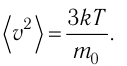
Поскольку 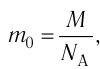 то
то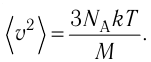 Так как газы находятся в состоянии теплового равновесия, т. е.
Так как газы находятся в состоянии теплового равновесия, т. е. 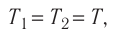 то средние квадраты скоростей атомов гелия
то средние квадраты скоростей атомов гелия 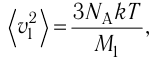 молекул кислорода —
молекул кислорода —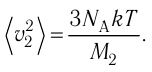
Отсюда 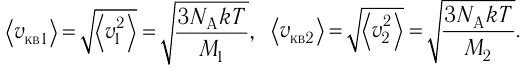
Тогда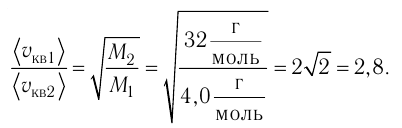
Ответ: в состоянии теплового равновесия средняя квадратичная скорость атомов гелия в 2,8 раза больше средней квадратичной скорости молекул кислорода.
Пример №9
В баллоне вместимостью V= 14 л находится газ, температура которого 7=290 К. Расходуя газ, из баллона выпустили N= 1,0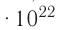 молекул. Определите, на сколько уменьшилось давление газа в баллоне, если через некоторый промежуток времени его температура увеличилась до первоначального значения.
молекул. Определите, на сколько уменьшилось давление газа в баллоне, если через некоторый промежуток времени его температура увеличилась до первоначального значения.
Дано:
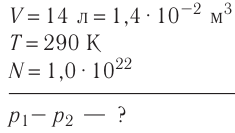
Решение. Начальное давление газа 
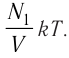 Когда израсходовали часть газа, его давление после того, как температура увеличилась до первоначального значения T, стало
Когда израсходовали часть газа, его давление после того, как температура увеличилась до первоначального значения T, стало 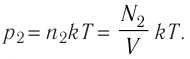 Тогда убыль давления газа
Тогда убыль давления газа 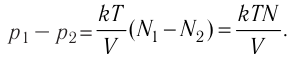
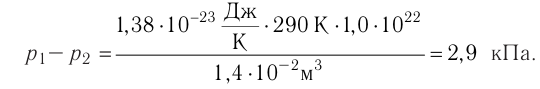
Ответ: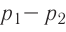 =2,9 кПа.
=2,9 кПа.
Изотермический, изобарный и изохорный процессы
Мы рассмотрели идеальный газ с позиций молекулярно-кинетической теории. Выяснили зависимость давления идеального газа от концентрации его молекул и температуры. Но как связаны между собой давление идеального газа, его масса, объём и температура?
Уравнение состояния идеального газа
Состояние макроскопической системы полностью определено, если известны её макроскопические параметры — давление р, температура Т и объём V. Уравнение, которое связывает параметры данного состояния, называют уравнением состояния системы. Изменение двух и более параметров состояния системы с течением времени называют процессом.
Если при переходе идеального газа из одного состояния в другое число его т
молекул 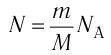 остаётся постоянным, т. е. масса и молярная масса газа не изменяются, то из уравнении
остаётся постоянным, т. е. масса и молярная масса газа не изменяются, то из уравнении 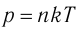 и
и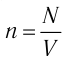 следует:
следует:
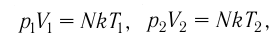 (5.1)
(5.1)
где k — постоянная Больцмана,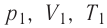 — параметры начального состояния газа, а
— параметры начального состояния газа, а 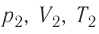 — конечного. Из соотношений (5.1) следует, что
— конечного. Из соотношений (5.1) следует, что
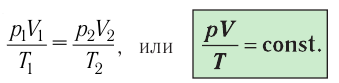 (5.2)
(5.2)
Уравнение состояния в виде (5.2) впервые вывел в 1834 г. французский физик Бенуа Клапейрон (1799—1864), поэтому его называют уравнением Клапейрона.
Таким образом, при неизменных массе и молярной массе идеального газа отношение произведения его давления и объёма к абсолютной температуре является величиной постоянной. Уравнение (5.2) связывает два состояния идеального газа независимо от того, каким образом газ перешёл из одного состояния в другое.
В справедливости уравнения состояния можно убедиться, используя установку, изображённую на рисунке 16. Манометром 1, соединённым с герметичным гофрированным сосудом, регистрируют давление газа внутри сосуда. Объём газа в сосуде можно измерить, используя линейку 2. Температура газа в сосуде равна температуре окружающей среды и может быть измерена термометром.
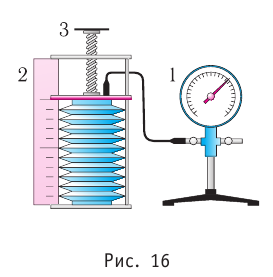
Измерив параметры газа 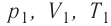 в начальном состоянии, вычисляют отношение
в начальном состоянии, вычисляют отношение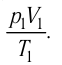 После этого помещают сосуд в горячую воду, тем самым изменяя температуру газа и его давление. Вращая винт 3, изменяют вместимость сосуда. Измерив снова
После этого помещают сосуд в горячую воду, тем самым изменяя температуру газа и его давление. Вращая винт 3, изменяют вместимость сосуда. Измерив снова
давление газа 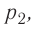 , его объём
, его объём 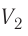 и температуру
и температуру 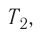 , вычисляют отношение
, вычисляют отношение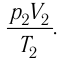
Как показывают расчёты, уравнение состояния (5.2) выполняется в пределах погрешности эксперимента.
Реальные газы удовлетворяют уравнению состояния идеального газа при не очень больших давлениях (пока собственный объём всех молекул газа пренебрежимо мал по сравнению с вместимостью сосуда, в котором находится газ) и при не слишком низких или же высоких температурах (пока абсолютное значение потенциальной энергии межмолекулярного взаимодействия пренебрежимо мало по сравнению с кинетической энергией теплового движения молекул).
Поскольку число частиц 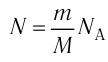 , где m — масса газа, М — его молярная масса,
, где m — масса газа, М — его молярная масса, 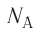 — число Авогадро, то из (5.1) следует:
— число Авогадро, то из (5.1) следует:
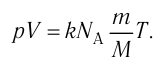
Введём новую постоянную R, равную произведению постоянных Больцмана и Авогадро: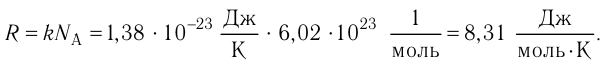
Постоянную R называют универсальной газовой постоянной. Тогда

или с учетом того, что количество вещества 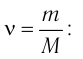
pV = vRT.
Уравнение состояния в виде (5.3) впервые получено русским учёным Д. И. Менделеевым (1834—1907) в 1874 г., поэтому его называют уравнением Клапейрона — Менделеева.
Отметим, что уравнение Клапейрона—Менделеева связывает между собой параметры конкретного состояния идеального газа. Используя уравнение Клапейрона — Менделеева, можно описать различные процессы, происходящие в идеальном газе.
Процессы в газах часто происходят так, что изменяются только два параметра из пяти (р, V, Т, m, М). Если один из макропараметров (р, V, Т), входящих в уравнение состояния идеального газа, не изменяется, то такие процессы называют изопроцессами.
Изотермический процесс
Процесс изменения состояния газа при постоянной температуре (Т = const) называют изотермическим. Если масса идеального газа и его молярная масса не изменяются, то из уравнения Клапейрона— Менделеева следует: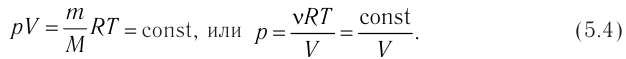
Следовательно, давление данной массы газа при постоянных молярной массе и температуре обратно пропорционально его объёму. Это утверждение называют законом Бойля — Мариотта. Закон Бойля—Мариотта описывает изотермический процесс в идеальном газе, масса и молярная масса которого при переходе из начального состояния в конечное не изменяются.
Справедливость закона Бойля—Мариотта можно проверить экспериментально, используя установку, изображённую на рисунке 16. Если поддерживать постоянной температуру газа, то уменьшение его объёма при вращении винта 3 повлечёт за собой увеличение давления, и наоборот, увеличение объёма приведёт к уменьшению давления. Однако произведение pV остаётся постоянным: pV = const.
График такого процесса в координатах (р, V) представляет собой гиперболу (рис. 17). В физике эту кривую называют изотермой. Разным значениям температуры соответствуют разные изотермы.
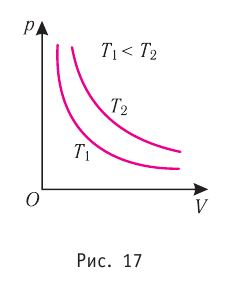
Согласно уравнению состояния 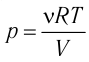 для одного и того же объёма газа, чем больше давление, тем больше его температура (см. рис. 17).
для одного и того же объёма газа, чем больше давление, тем больше его температура (см. рис. 17).
Опыты показали, что реальные газы подчиняются закону Бойля — Мари-отта тем точнее, чем меньше их плотность. При значительном увеличении давления этот закон перестаёт выполняться.
Изотермический процесс можно изобразить и в координатах (р, Т) и (V, Т). Сделайте это самостоятельно.
Изобарный процесс
Процесс изменения состояния газа при постоянном давлении (р = const) называют изобарным. Впервые он был рассмотрен в 1802 г. французским учёным Жозефом Гей-Люссаком (1778—1850). Если при переходе из начального состояния в конечное масса и молярная масса газа не изменяются, то объём газа, как следует из уравнения Клапейрона—Менделеева (5.3):
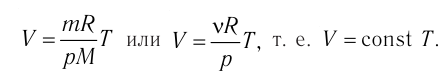 (5.5)
(5.5)
Таким образом, изобарный процесс в идеальном газе описывает закон, согласно которому объём данной массы газа при постоянных молярной массе и давлении прямо пропорционален абсолютной температуре. Справедливость закона Гей-Люссака можно проверить экспериментально, используя установку, изображённую на рисунке 18. Жидкость в сосуде находится в тепловом равновесии с тонкой трубкой, заполненной воздухом, запертым столбиком масла. При увеличении температуры жидкости объём воздуха, находящегося в трубке под столбиком масла, возрастает, а при уменьшении температуры — уменьшается.
Поскольку V~ Т, то в координатах (V, Т) график изобарного процесса для идеального газа представляет собой прямую линию, продолжение которой проходит через начало координат (рис. 19). Эту линию называют изобарой. Изобара реального газа не может быть продлена до нулевого значения температуры (на графике пунктирная линия), потому что при низких температурах все газы начинают существенно отличаться от модели «идеальный газ» и при дальнейшем уменьшении температуры превращаются в жидкости. В одних и тех же координатах (V, Т) можно построить несколько изобар, которые будут соответствовать разным давлениям данной массы идеального газа при неизменной молярной массы.
Анализ графиков (см. рис. 19) и соотношения 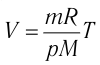 позволяет сделать вывод, что большему давлению р соответствует меньший наклон изобары к оси температур Т.
позволяет сделать вывод, что большему давлению р соответствует меньший наклон изобары к оси температур Т.
Изобарный процесс можно изобразить и в координатах (р, V) и (р, Т). Сделайте это самостоятельно.
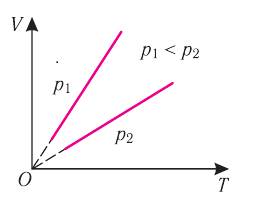
Рис. 19
Уравнение (5.5) изобарного процесса можно записать в другом виде. Пусть данная масса идеального газа при давлении р и температуре 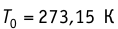 занимает некоторый объём
занимает некоторый объём  Уравнение состояния газа для этого случая имеет вид
Уравнение состояния газа для этого случая имеет вид 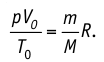
Будем считать, что газ изобарно нагрели до температуры 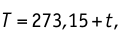 где t — температура по шкале Цельсия. Для этого состояния можно записать
где t — температура по шкале Цельсия. Для этого состояния можно записать 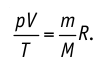
После сопоставления двух равенств приходим к выводу, что 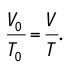 Тогда
Тогда
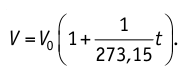
Отношение 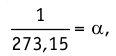 , являющееся постоянной величиной для всех разреженных газов, называют температурным (термическим) коэффициентом объёмного расширения газа при постоянном давлении, который характеризует относительное увеличение объёма газа при изменении его температуры на один градус Коэффициент
, являющееся постоянной величиной для всех разреженных газов, называют температурным (термическим) коэффициентом объёмного расширения газа при постоянном давлении, который характеризует относительное увеличение объёма газа при изменении его температуры на один градус Коэффициент  измеряют в
измеряют в  С учётом этого уравнение для изобарного процесса будет иметь вид
С учётом этого уравнение для изобарного процесса будет иметь вид 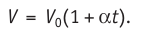
Как видно из последнего соотношения, объём данной массы газа при постоянном давлении линейно возрастает с ростом температуры.
Изохорный процесс
Процесс изменения состояния газа при постоянном объёме (V = const) называют изохорным. Впервые он был рассмотрен в 1787 г. французским учёным Жаком Шарлем (1746—1823). Если при переходе из начального состояния в конечное масса и молярная масса газа не изменяются,
то давление газа, как следует из уравнения Клапейрона — Менделеева (5.3):
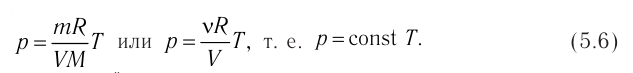
Таким образом, изохорный процесс в идеальном газе описывает закон, согласно которому давление данной массы газа при постоянных молярной массе и объёме прямо пропорционально абсолютной температуре. Справедливость закона Шарля можно проверить экспериментально, используя установку, изображённую на рисунке 20. Колба с воздухом, соединённая с манометром, находится в тепловом равновесии с жидкостью в сосуде. При увеличении температуры жидкости давление воздуха в колбе возрастает, а при уменьшении температуры давление воздуха уменьшается.
В координатах (р, Т) график изохорного процесса для идеального газа, масса и молярная масса которого постоянны, представляет собой прямую линию, продолжение которой проходит через начало координат (рис. 21). Эту линию называют изохорой.
Как и в случае изобарного процесса, изохора реального газа не может быть продлена до нулевого значения температуры. Изохору можно изобразить и в координатах (р, V) и (V, Т). Сделайте это самостоятельно.
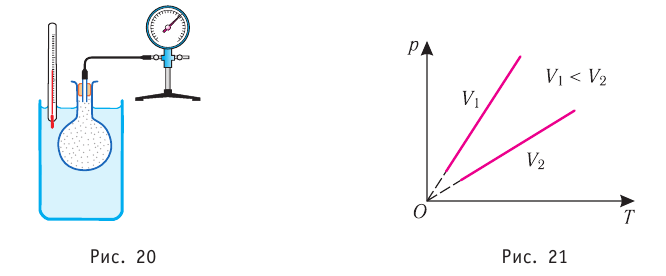
В одних и тех же координатах (р, Т) можно построить несколько изохор, соответствующих разным объёмам данной массы газа при неизменной молярной массе. Анализ соотношений (5.6) показывает, что большему объёму V соответствует меньший наклон изохор к оси температур Т (см. рис. 21).
Если температуру t измерять по шкале Цельсия, то 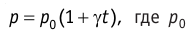 — давление газа при температуре
— давление газа при температуре 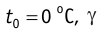 — температурный коэффициент давления, который для всех разреженных газов
— температурный коэффициент давления, который для всех разреженных газов 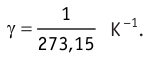
1. При постоянных массе и молярной массе идеального газа отношение произведения давления газа и его объёма к абсолютной температуре является величиной постоянной (уравнение состояния идеального газа):
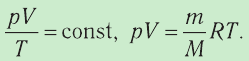
2. Давление данной массы идеального газа при постоянных молярной массе и температуре обратно пропорционально объёму газа (изотермический процесс):
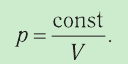
3. Объём данной массы идеального газа при постоянных молярной массе и давлении прямо пропорционален абсолютной температуре (изобарный процесс):

4. Давление данной массы идеального газа при постоянных молярной массе и объёме прямо пропорционально абсолютной температуре (изо-хорный процесс):

Пример №10
В двух сосудах вместимостью 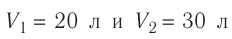 находятся химически не реагирующие идеальные газы, давления которых
находятся химически не реагирующие идеальные газы, давления которых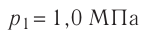 и
и 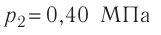 соответственно. Определите давление в сосудах, после того как их соединили тонкой короткой трубкой. Температура газов до и после соединения сосудов одинаковая.
соответственно. Определите давление в сосудах, после того как их соединили тонкой короткой трубкой. Температура газов до и после соединения сосудов одинаковая.
Дано:
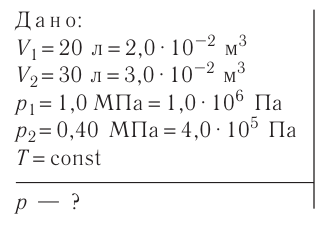
Решение. Давление смеси газов равно сумме парциальных давлений (закон Дальтона): 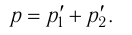
Найдём парциальные давления газов после соединения сосудов. Так как температура и массы газов не изменяются, то начальное и конечное состояния каждого из газов связаны законом Бойля — Мариотта, т. е. 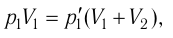
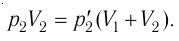 Отсюда парциальные давления газов после соединения сосудов соответственно
Отсюда парциальные давления газов после соединения сосудов соответственно
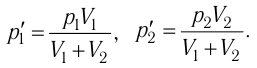
Следовательно,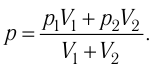
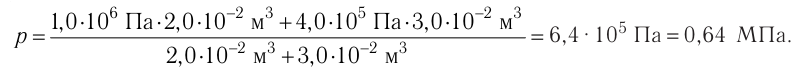 Ответ: р = 0,64 МПа.
Ответ: р = 0,64 МПа.
Пример №11
Баллон с газом, давление которого 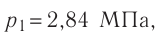 находился в неотапливаемом помещении, где температура воздуха
находился в неотапливаемом помещении, где температура воздуха 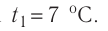 После того как некоторое количество газа было израсходовано, баллон внесли в помещение, где температура воздуха
После того как некоторое количество газа было израсходовано, баллон внесли в помещение, где температура воздуха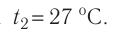 Определите, какая часть газа была израсходована, если после длительного пребывания баллона в помещении давление газа в нём стало
Определите, какая часть газа была израсходована, если после длительного пребывания баллона в помещении давление газа в нём стало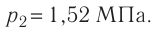
Дано:
Решение. Если пренебречь тепловым расширением баллона, то его вместимость не изменяется. Запишем уравнения Клапейрона— Менделеева для начального и конечного состояний газа, считая его идеальным:
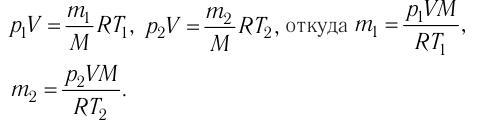
Тогда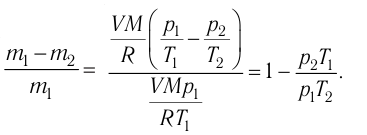
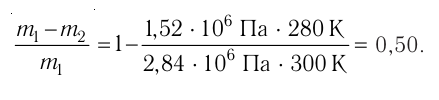
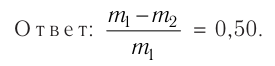
Пример №12
На рисунке 22 изображён график процесса изменения состояния некоторой массы идеального газа. Как изменялись параметры газа на участках  Изобразите этот процесс в координатах
Изобразите этот процесс в координатах 
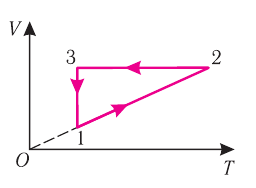 рис.22
рис.22
Решение. На участке объём газа прямо пропорционален температуре, следовательно, процесс перехода газа из состояния 1 в состояние 2 является изобарным. Из графика видно, что в состоянии 2 температура и объём газа больше, чем в состоянии 1. Следовательно, в процессе изобарного расширения некоторой массы газа из состояния 1 в состояние 2 температура и объём газа увеличились. Это можно записать таким образом: переход
объём газа прямо пропорционален температуре, следовательно, процесс перехода газа из состояния 1 в состояние 2 является изобарным. Из графика видно, что в состоянии 2 температура и объём газа больше, чем в состоянии 1. Следовательно, в процессе изобарного расширения некоторой массы газа из состояния 1 в состояние 2 температура и объём газа увеличились. Это можно записать таким образом: переход  происходит изобарное нагревание газа.
происходит изобарное нагревание газа.
В процессе перехода газа из состояния 2 в состояние 3 остаётся постоянным объём (процесс изохорный), а температура газа уменьшается. Непосредственно из графика не видно, что будет происходить с давлением газа, но из соотношения (5.6) следует, что при изохорном охлаждении давление газа уменьшается пропорционально его температуре. Поэтому можно записать: переход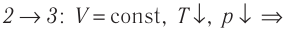 происходит изохорное охлаждение газа.
происходит изохорное охлаждение газа.
Процесс перехода газа из состояния 3 в состояние 1 — изотермический. При этом объём газа уменьшается, что влечёт за собой, согласно закону Бой-ля— Мариотта, увеличение давления газа:
переход 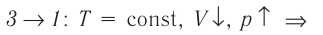 происходит изотермическое сжатие газа.
происходит изотермическое сжатие газа.
Опираясь на сделанные выводы, изобразим все три процесса в координатах 
Строение и свойства твёрдых тел
В повседневной жизни мы считаем твёрдым любое тело, сохраняющее форму и объём в отсутствие внешних воздействий. Например, мы считаем твёрдыми тела, изготовленные из металлов, пластмассы, льда, стекла. Твёрдые тела делят на две группы, различающиеся по своим свойствам: кристаллические и аморфные. К кристаллическим телам относят минералы, например поваренную соль, медный купорос, кварц, квасцы, горный хрусталь, и металлы в твёрдом состоянии; к аморфным телам — опал, обсидиан, эбонит, сургуч, стекло, различные пластмассы, смолы (вар, канифоль, янтарь) и др. В чём отличие между кристаллическими и аморфными твёрдыми телами?
Кристаллы
Кристаллами называют такие твёрдые тела, атомы, ионы или молекулы которых совершают тепловые колебания около определённых, упорядоченных в пространстве положений равновесия. Упорядоченное размещение частиц твёрдого кристаллического тела обусловливает его правильную геометрическую форму, вследствие чего поверхность кристалла образована плоскими гранями (рис. 25).

Рис. 25
Частицы кристалла удерживаются на определённом усреднённом расстоянии друг от друга (-0,1 нм) силами межатомного и межмолекулярного взаимодействия. Несмотря на тепловые колебания, они образуют упорядоченную пространственную структуру, геометрическим образом которой является кристаллическая решётка. Узлы кристаллической решётки — это положения устойчивого равновесия колеблющихся частиц (ионов, атомов или молекул), из которых состоит кристалл. Основой строения кристалла служит так называемая элементарная кристаллическая ячейка — многогранник наименьших размеров, последовательным переносом которого вместе с частицами, находящимися внутри этого многогранника, можно построить весь кристалл. На рисунке 26 показаны самые простые элементарные ячейки: кубические (а — примитивная, б — объёмно-центрированная, в — гранецентрированная) и гексагональная призма (г).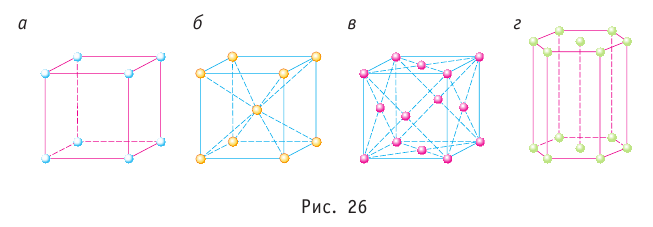
В кристаллических телах упорядоченное размещение частиц повторяется во всём объёме кристалла, поэтому говорят, что в кристалле существует дальний порядок в расположении частиц.
В зависимости от вида частиц, из которых состоит кристалл, и от характера сил взаимодействия между ними, различают четыре основных типа кристаллов: ионные, атомные, металлические и молекулярные. В узлах ионной кристаллической решётки размещены положительно и отрицательно заряженные ионы, «связанные» между собой электростатическими силами. Типичным примером ионного кристалла является кристалл хлорида натрия NaCl (рис.27). Кристаллы с ионной решёткой тугоплавки и обладают высокой твёрдостью.
В узлах атомной кристаллической решётки находятся нейтральные атомы. Связь между атомами осуществляется электронными парами — по одному валентному электрону от каждого атома. Примером атомных кристаллов могут служить алмаз и графит. Эти кристаллы тождественны по химической природе (они состоят из атомов углерода), но отличаются по своему строению (рис. 28). Это существенно сказывается на их свойствах: алмаз — твёрдый минерал (рис. 28, а), графит — наоборот, мягкий и крохкий (рис. 28, б).
В узлах кристаллической решётки металлов находятся положительные ионы, например, полония Ро (рис. 26, а), железа Fe (рис. 26, б), серебра Ag (рис. 26, в), магния Mg (рис. 26, г). Между колеблющимися ионами непрерывно движутся свободные электроны.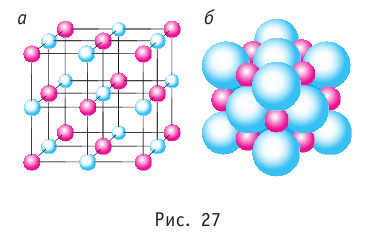
В узлах молекулярных кристаллических решёток находятся молекулы. Большинство простых веществ неметаллов в твёрдом состоянии, например под  водород
водород  и их соединений друг с другом, например лёд
и их соединений друг с другом, например лёд  (рис. 29, б), а также практически все твёрдые органические вещества образуют молекулярные кристаллы.
(рис. 29, б), а также практически все твёрдые органические вещества образуют молекулярные кристаллы.
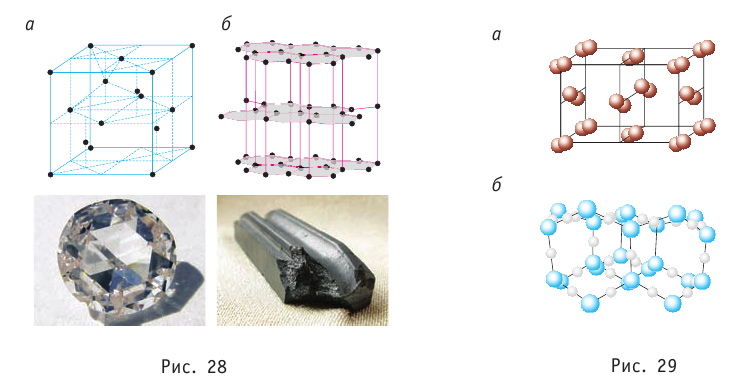
Твёрдые тела, имеющие во всём объёме единую кристаллическую решётку, называют монокристаллами. Это одиночные кристаллы, которые могут иметь довольно большие размеры (встречаются кристаллы горного хрусталя, размеры которых соизмеримы с ростом человека). Многие твёрдые тела состоят из большого числа сросшихся между собой маленьких кристаллов. Такие твёрдые тела называют поликристаллами. Вы сами можете в домашних условиях вырастить монокристаллы (рис. 30, а) и поликристаллы (рис. 30, б) медного купороса
Характерной особенностью монокристаллов является их анизотропия, т. е. зависимость физических свойств (механических, тепловых, электрических, оптических) от направления. Анизотропия монокристаллов обусловлена взаимодействием частиц и их упорядоченным расположением. На рисунке 31 показано, что расстояния между атомными плоскостями в кристалле неодинаковы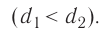 Поэтому, в частности, отличаться будут и модули сил, необходимых для его разрыва
Поэтому, в частности, отличаться будут и модули сил, необходимых для его разрыва

В отличие от монокристаллов поликристаллы изотропны, т. е. их свойства одинаковы по всем направлениям. Это следствие того, что поликристалл состоит из большого количества хаотически ориентированных маленьких монокристаллов.
Аморфные тела
Аморфное состояние (от греч. amorphous — бесформенный) — твёрдое некристаллическое состояние вещества, характеризующееся изотропией свойств и отсутствием определённой температуры плавления.
При повышении температуры аморфное вещество размягчается и постепенно переходит в жидкое состояние. В аморфном состоянии вещество не имеет строгого порядка в расположении атомов и молекул. На рисунке 32 схематически изображено строение кристаллического кварца (рис. 32, а) и аморфного кварца (рис. 32, б). Аморфное состояние — бесформенное состояние со слабо выраженной текучестью. Аморфные тела называют переохлаждёнными жидкостями, так как у них, как и у жидкостей, существует только ближний порядок расположения частиц.
Аморфные тела при определённых условиях могут кристаллизоваться. Сахар-песок является кристаллическим телом. Если его расплавить, то, застывая, он превращается в прозрачный стеклообразный леденец, который является аморфным телом. Через некоторый промежуток времени леденец «засахаривается», т. е. опять становится кристаллическим.
При скоростях охлаждения, превышающих миллион градусов в секунду, удалось получить аморфные металлические сплавы — стеклообразные металлы. Аморфный металл чрезвычайно твёрд и прочен. Его используют как режущий инструмент. Он обладает высокими магнитными свойствами, поэтому незаменим при изготовлении магнитных головок для звуко- и видеозаписи. Кроме того, аморфные металлы обладают высокой антикоррозийной стойкостью.
- Твёрдые тела делят на две группы, различающиеся по своим свойствам: кристаллические и аморфные.
- Атомы, ионы или молекулы в твёрдых кристаллических телах совершают тепловые колебания около определённых, упорядоченных в пространстве положений равновесия.
- Монокристаллическим телам присуща анизотропия, т. е. зависимость физических свойств от направления. Поликристаллические тела изотропны, т. е. их физические свойства одинаковы по всем направлениям.
- Аморфное состояние — твёрдое некристаллическое состояние вещества, характеризующееся изотропией свойств и отсутствием определённой температуры плавления.
Строение и свойства жидкостей и поверхностное натяжение
Среднее расстояние между молекулами вещества в жидком состоянии меньше (рис. 33, а), чем среднее расстояние между молекулами этого же вещества в газообразном состоянии (рис. 33, б). Оно равно приблизительно одному-двум диаметрам молекулы. Это приводит к тому, что плотность жидкости приблизительно в 103 раз превышает плотность пара, находящегося в динамическом равновесии с жидкостью (насыщенного пара). Например, плотность воды при температуре  раз больше плотности насыщенного водяного пара. Свойства жидкостей зависят как от особенностей движения молекул, так и от взаимодействия между ними.
раз больше плотности насыщенного водяного пара. Свойства жидкостей зависят как от особенностей движения молекул, так и от взаимодействия между ними.

Строение и свойства жидкостей:
В опытах по рассеянию рентгеновских лучей в жидкостях обнаружен ближний порядок в расположении частиц (см. рис. 33, а). В отличие от твёрдых тел (рис. 33, в) в жидкостях упорядоченность в расположении молекул сохраняется лишь среди ближайших соседей (на расстояниях, равных нескольким диаметрам молекул), сочетаясь с непрерывными и беспорядочными колебаниями около положений равновесия. Средняя кинетическая энергия колебаний молекул определяет температуру жидкости. Молекулы, получившие дополнительную энергию в результате столкновений с другими молекулами, могут «перепрыгнуть» в новое положение равновесия. Таким образом, ближний порядок в жидкости постоянно разрушается в результате теплового движения молекул и вновь создаётся силами молекулярного действия.
Расстояния между молекулами, соизмеримые с их собственными размерами, и возможность молекул относительно свободно перемещаться определяют свойства жидкостей. Жидкости, как и твёрдые тела, практически несжимаемы, но они текучи, поэтому их форма определяется формой предоставленного им сосуда. На форму жидкости оказывают влияние внешние силы (например, сила тяжести совместно с силами реакции дна и стенок сосуда, в котором находится жидкость) и силы поверхностного натяжения.
Поверхностное натяжение:
Рассмотрим явления, происходящие на границе раздела жидкости с воздухом или с её паром. Своим возникновением эти явления обязаны особым физическим условиям, в которых находятся молекулы поверхностного слоя жидкости.
В поверхностном слое жидкости проявляется нескомпенсированность молекулярных сил притяжения. В самом деле, любая молекула внутри жидкости со всех сторон окружена соседними (одинаковыми) молекулами, действие которых взаимно компенсируется (рис. 34). Поэтому здесь молекулярные силы притяжения уравновешиваются и равнодействующая этих сил равна нулю. Так как концентрация молекул в воздухе (паре) значительно меньше, чем в жидкости, то равнодействующая сил притяжения каждой молекулы поверхностного слоя к молекулам газа меньше равнодействующей сил её притяжения к молекулам жидкости. Таким образом, равнодействующие сил притяжения, действующих на молекулы поверхностного слоя, направлены внутрь жидкости. Под действием этих сил молекулы поверхностного слоя втягиваются внутрь, число молекул на поверхности уменьшается и площадь поверхности жидкости сокращается до определённой величины. 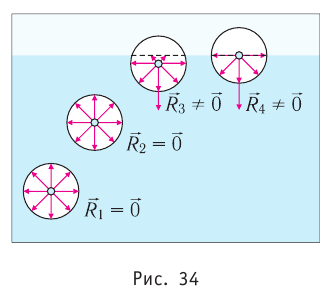
Толщина поверхностного слоя, в котором проявляется нескомпенсирован-ность сил молекулярного притяжения, равна приблизительно радиусу сферы молекулярного действия (-1 нм). Под действием сил притяжения и вследствие текучести жидкости на её поверхности остаётся такое количество молекул, при котором площадь поверхности минимальна для данного объёма жидкости. Процесс сокращения площади поверхности на этом прекращается, жидкость переходит в состояние равновесия. В этом состоянии силы притяжения молекул поверхностного слоя, направленные внутрь жидкости, уравновешиваются силами отталкивания, возникшими при сближении молекул поверхностного слоя с молекулами внутри жидкости, вызванном её сжатием.
Чтобы переместить молекулу, расположенную внутри жидкости, на поверхность (увеличить площадь поверхности жидкости), необходимо совершить работу против сил взаимодействия этой молекулы с молекулами поверхностного слоя жидкости. Следовательно, молекулы, образующие поверхностный слой жидкости, обладают избыточной потенциальной энергией по сравнению с молекулами, находящимися внутри жидкости. Эту энергию называют поверхностной энергией.
Так как потенциальная энергия тела (системы тел) в состоянии устойчивого равновесия минимальна, то наличие поверхностной энергии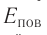 у жидкости обусловливает её стремление к сокращению площади S своей поверхности. Работу внешних сил по увеличению площади поверхности жидкости на единицу площади при сохранении объёма и температуры жидкости неизменными называют коэффициентом поверхностного натяжения
у жидкости обусловливает её стремление к сокращению площади S своей поверхности. Работу внешних сил по увеличению площади поверхности жидкости на единицу площади при сохранении объёма и температуры жидкости неизменными называют коэффициентом поверхностного натяжения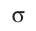 или, кратко, поверхностным натяжением. Эту физическую скалярную величину можно определить по формуле
или, кратко, поверхностным натяжением. Эту физическую скалярную величину можно определить по формуле
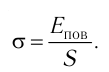
Минимальную площадь поверхности при данном объёме имеют шарообразные тела. Например, капли жидкости при соприкосновении сливаются в одну, форма которой отличается от сферической только из-за действия силы тяжести и силы реакции опоры. Чем меньше радиус капли, тем большую роль играет поверхностная энергия по сравнению с потенциальной энергией капли в гравитационном поле Земли и тем ближе форма капель жидкости на опоре к сферической. Поэтому маленькие капельки росы на листьях растений принимают форму, близкую к шарообразной (рис. 35).
Рассмотрим следующий опыт. Опустим проволочное кольцо с привязанной к нему нитью в мыльный раствор. Контур кольца, извлечённого из раствора, затянут мыльной плёнкой, а нить в ней размещается случайным образом (рис. 36, а). Если проколоть плёнку с одной стороны нити, то оставшаяся часть плёнки сократится так, что площадь её поверхности станет минимальной (рис. 36, б). Нить удерживается в натянутом состоянии силами, получившими название сил поверхностного натяжения. Они направлены по касательным к свободным поверхностям плёнки перпендикулярно к линии, ограничивающей эти поверхности.
Рассмотрим ещё один опыт. Прямоугольную рамку с подвижной перекладиной длиной 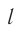 опустим в мыльный раствор. После извлечения рамки из раствора видим, что перекладина перемещается, так как мыльная плёнка стремится сократить площадь своей поверхности. Чтобы перекладину удержать в
опустим в мыльный раствор. После извлечения рамки из раствора видим, что перекладина перемещается, так как мыльная плёнка стремится сократить площадь своей поверхности. Чтобы перекладину удержать в
равновесии, к ней следует приложить силу 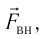 которая уравновесит действующие на каждой из двух поверхностей плёнки силы поверхностного натяжения:
которая уравновесит действующие на каждой из двух поверхностей плёнки силы поверхностного натяжения: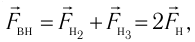 так как
так как 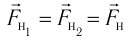 (рис.37). Если проводить опыты с рамками разных размеров, можно установить, что отношение
(рис.37). Если проводить опыты с рамками разных размеров, можно установить, что отношение 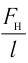 для пленки данной жидкости при фиксированной температуре всегда одинаковое.
для пленки данной жидкости при фиксированной температуре всегда одинаковое.
Значит, это отношение можно взять в качестве характеристики поверхностного слоя жидкости:
Поверхностное натяжение численно равно отношению модуля силы поверхностного натяжения
численно равно отношению модуля силы поверхностного натяжения 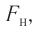 действующей на прямолинейный участок границы поверхностного слоя жидкости, к длине
действующей на прямолинейный участок границы поверхностного слоя жидкости, к длине 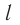 этого участка.
этого участка.
Силовое определение поверхностного натяжения дополняет энергетическое. Единицей поверхностного натяжения в СИ является джоуль на метр в квадрате 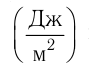
или ньютон на метр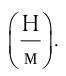 Покажите самостоятельно, что
Покажите самостоятельно, что
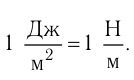
Поверхностное натяжение зависит от рода жидкости и той среды, с которой она граничит, наличия растворённых в жидкости других веществ и от её температуры. Повышение температуры жидкости, добавление в неё так называемых поверхностно-активных веществ (мыло, жирные кислоты) приводит к уменьшению поверхностного натяжения. Чрезвычайно разнообразны проявления сил поверхностного натяжения жидкости в природе и технике. Поверхностное натяжение приводит к тому, что вода собирается в капли (рис. 38), образуются мыльные пузыри (рис. 39), жук-водомерка передвигается по поверхности воды (рис. 40), а в состоянии невесомости любой объём жидкости принимает сферическую форму.

Смачивание
На границе соприкосновения твёрдых тел, жидкостей и газов наблюдается явление смачивания или несмачивания, являющееся результатом взаимодействия между молекулами жидкости, твёрдого тела и газа, которое приводит к искривлению поверхности жидкости около поверхности твёрдого тела на границе с газом. При контакте жидкости с твёрдым телом возможны случаи, когда жидкость смачивает (частично или полностью) или не смачивает (частично или полностью) его. Так, ртуть хорошо смачивает чистые поверхности металлов и не смачивает чистое стекло. Вода хорошо смачивает чистое стекло и не смачивает жирные поверхности.
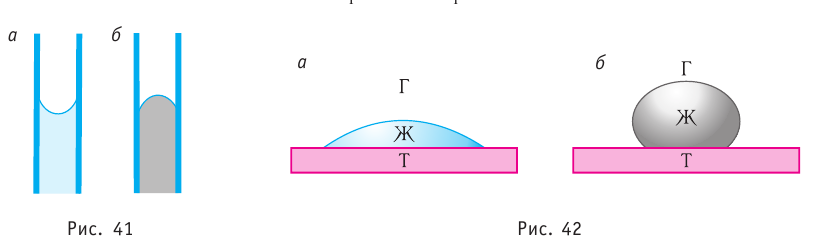
Свободная поверхность жидкости на границе с твёрдым телом искривляется, образуя мениск. Если жидкость смачивает поверхность тела, образуется вогнутый мениск (рис. 41, а), если не смачивает — выпуклый мениск (рис. 41, б). На границе соприкосновения трёх сред — твёрдой, жидкой и газообразной — жидкость принимает такую форму, при которой сумма потенциальной энергии жидкости в гравитационном поле Земли и поверхностной энергии всех тел минимальна (твёрдые тела также обладают поверхностной энергией). Поверхностное натяжение на границе твёрдого тела и жидкости обозначают 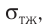 на границе твёрдого тела и газа —
на границе твёрдого тела и газа — 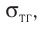 на границе жидкости и газа —
на границе жидкости и газа —  Если
Если  то жидкость полностью смачивает поверхность твёрдого тела, покрывая его тонкой плёнкой. Если
то жидкость полностью смачивает поверхность твёрдого тела, покрывая его тонкой плёнкой. Если  то жидкость полностью не смачивает поверхность твёрдого тела, стягиваясь в каплю, несколько сплюснутую действием силы тяжести и силы реакции опоры. В большинстве случаев имеет место частичное смачивание (рис. 42, а) или частичное несмачивание (рис. 42, б).
то жидкость полностью не смачивает поверхность твёрдого тела, стягиваясь в каплю, несколько сплюснутую действием силы тяжести и силы реакции опоры. В большинстве случаев имеет место частичное смачивание (рис. 42, а) или частичное несмачивание (рис. 42, б).
Явление смачивания используют в промышленности и в быту. Хорошее смачивание необходимо при окраске и мытье разных тканей, нанесении лакокрасочных покрытий и т. д. На явлении смачивания основано склеивание различных изделий. Покрытие металлических изделий масляной плёнкой для их защиты от коррозии основано на несмачивании водой жирных поверхностей.
Непромокаемую одежду изготавливают из тканей, которые не смачиваются водой. Со свойством смачивания связана пайка металлов. Чтобы расплавленный припой хорошо растекался по поверхности металлических изделий и прилипал к ним, нужно эти поверхности очистить от жира, пыли и оксидной плёнки.
Капиллярные явления
Под капиллярными явлениями понимают явление подъёма или опускания жидкости в узких трубках, называемых капиллярами. Если жидкость смачивает стенки капилляра, то при его опускании в сосуд с этой жидкостью уровень жидкости в капилляре будет выше, чем в сосуде (рис. 43, а). При несмачивании уровень жидкости в капилляре устанавливается ниже уровня жидкости в сосуде (рис. 43, б). Такое явление наблюдается, например, при опускании стеклянного капилляра в сосуд с ртутью.
Высота подъёма (опускания) жидкости в капилляре зависит от свойств жидкости и радиуса капилляра (рис. 44). Если жидкость полностью смачивает капилляр, то высоту подъёма жидкости в капилляре определяют по формуле
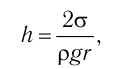
где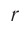 — внутренний радиус капилляра,
— внутренний радиус капилляра, 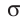 — поверхностное натяжение жидкости,
— поверхностное натяжение жидкости, 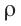 — плотность жидкости. Если жидкость полностью не смачивает капилляр, то
— плотность жидкости. Если жидкость полностью не смачивает капилляр, то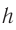 — глубина, на которую опускается жидкость в капилляре.
— глубина, на которую опускается жидкость в капилляре.
Капиллярные явления играют значительную роль в природе и технике. Так, ствол, ветви, стебель и листва растений пронизаны множеством капиллярных каналов, по которым поступают питательные вещества. По капиллярам в почве грунтовые воды поднимаются к корневой системе растений. Мелкие кровеносные сосуды человека и животных можно также рассматривать как капилляры. Капиллярные явления довольно часто встречаются и в быту. Полотенца хорошо впитывают в себя воду при вытирании, в авторучке чернила поступают к перу по капилляру. Чтобы избежать поглощения воды кожаной обувью, её насыщают жирным гуталином. Капиллярные явления лежат в оенове множеетва технических процессов: при смазке деталей машин и механизмов применяют фитильный способ; при окраске кожи и тканей краска заполняет капилляры изделия; при строительстве домов фундамент отделяют от стен рубероидом или битумом, чтобы избежать капиллярного подъёма воды из почвы.
1. Расстояния между молекулами, соизмеримые с их собственными размерами, и подвижность молекул определяют свойства жидкостей: малую зависимость объёма жидкости от давления и её текучесть.
2. Работу внешних сил по увеличению площади поверхности жидкости на единицу площади при сохранении объёма и температуры жидкости неизменными называют коэффициентом поверхностного натяжения (поверхностным натяжением):
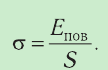
3. Силы поверхностного натяжения направлены по касательной к свободной поверхности жидкости и стремятся сократить эту поверхность до минимума.
4. Поверхностное натяжение численно равно отношению модуля силы поверхностного натяжения, действующей на прямолинейный участок границы поверхностного слоя жидкости, к длине этого участка:
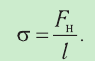
5. Высота подъёма (опускания) жидкости в капилляре зависит от поверхностного натяжения жидкости, плотности жидкости и внутреннего радиуса капилляра:
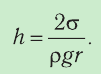
Пример №13
Тонкостенное кольцо массой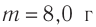 и радиусом
и радиусом 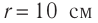 соприкасается с мыльным раствором (рис. 45, а). Кольцо изготовлено из материала, хорошо смачиваемого мыльным раствором. Определите модуль силы, с которой надо подействовать на кольцо, чтобы оторвать его от поверхности раствора (рис. 45, б). Поверхностное натяжение мыльного раствора
соприкасается с мыльным раствором (рис. 45, а). Кольцо изготовлено из материала, хорошо смачиваемого мыльным раствором. Определите модуль силы, с которой надо подействовать на кольцо, чтобы оторвать его от поверхности раствора (рис. 45, б). Поверхностное натяжение мыльного раствора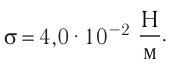
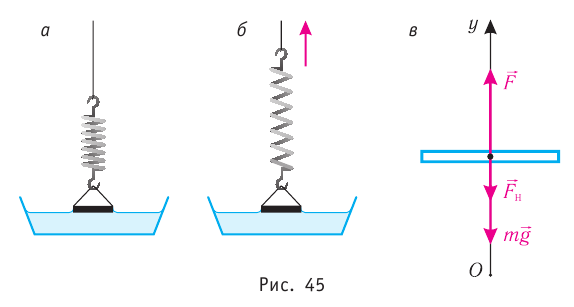
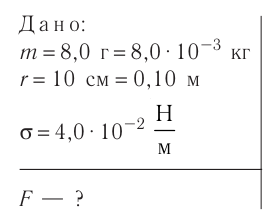
Решение. В момент отрыва от поверхности раствора на кольцо действуют искомая сила  сила тяжести
сила тяжести и сила поверхностного натяжения
и сила поверхностного натяжения  (рис. 45, в). «Разрежем» поверхность жидкой плёнки, тянущейся от раствора к кольцу, воображаемой горизонтальной поверхностью. Нижняя часть плёнки граничит с верхней по кольцу, ограниченному двумя окружностями — внутренней и внешней, общая длина которых близка к
(рис. 45, в). «Разрежем» поверхность жидкой плёнки, тянущейся от раствора к кольцу, воображаемой горизонтальной поверхностью. Нижняя часть плёнки граничит с верхней по кольцу, ограниченному двумя окружностями — внутренней и внешней, общая длина которых близка к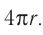 Модуль силы поверхностного натяжения определим по формуле
Модуль силы поверхностного натяжения определим по формуле
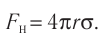
Условие равновесия кольца в проекции на ось в момент его отрыва от раствора, как видно из рисунка 45, в, имеет вид
в момент его отрыва от раствора, как видно из рисунка 45, в, имеет вид
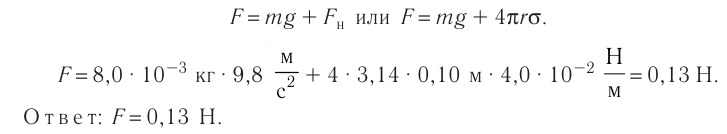
Испарение и конденсация
Из повседневного опыта мы знаем, что жидкости, например вода, находясь в открытых сосудах, с течением времени переходят в газообразное состояние — испаряются. Причём скорость испарения зависит от рода жидкости, её температуры, площади свободной поверхности и от притока воздуха. Вследствие испарения воды с поверхности водяной оболочки Земли — гидросферы, с поверхности почвы и растительного покрова в воздухе всегда находятся водяные пары, которые могут конденсироваться, образовывать облака, выпадать в виде осадков. Процессы испарения и конденсации распространены в природе и технике, и изучение их особенностей имеет большое практическое значение.
Рассмотрим сосуд, который частично заполнили водой и плотно закрыли. В сосуде одновременно протекают два противоположно направленных процесса — переход воды в газообразное состояние (испарение) и переход водяного пара в жидкость (конденсация) (рис. 47). 
В течение некоторого промежутка времени после герметизации сосуда испарение жидкости преобладает над конденсацией её пара. Если энергия к системе жидкость—пар не поступает из окружающей среды, то при испарении жидкость охлаждается. Это происходит вследствие того, что поверхностный слой жидкости покидают молекулы, обладающие наибольшей скоростью и, соответственно, кинетической энергией теплового движения, что позволяет им преодолеть силы притяжения, действующие в жидкости. Скорость вылетающих из жидкости молекул уменьшается, а скорость молекул, влетающих в жидкость, наоборот, увеличивается. Такие изменения скорости, а значит, и кинетической энергии молекул, пересекающих поверхность жидкости, позволяют системе достичь состояния теплового равновесия, при котором температуры жидкости и её пара одинаковы.
Концентрация молекул пара возрастает до тех пор, пока число молекул, покидающих жидкость, не станет равным числу молекул, возвращающихся в неё, за тот же промежуток времени. В этом случае говорят, что между жидкостью и паром устанавливается состояние динамического равновесия. Оно будет существовать до тех пор, пока не изменится температура или объём системы.
Воздушная оболочка Земли — атмосфера — представляет собой смесь газов. Атмосферный воздух всегда содержит водяной пар, концентрация молекул которого у поверхности Земли колеблется от 3% в тропиках до 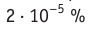 в Антарктиде. Из океанов, морей и рек, а также суши за год испаряется свыше
в Антарктиде. Из океанов, морей и рек, а также суши за год испаряется свыше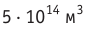 воды, что приблизительно равно объёму воды в Чёрном море. На испарение затрачивается около половины всей поглощённой поверхностью Земли энергии солнечного излучения. При конденсации пара количество теплоты, ранее потребовавшееся для испарения жидкости выделяется в атмосферу. Это приводит к нагреванию атмосферы и предотвращает резкие колебания температуры. При перемещении водяных паров в атмосфере на большие расстояния происходит их конденсация в областях с более низкой температурой. Таким образом, в одних областях поверхности и атмосферы Земли преобладают процессы испарения воды, а в других — процессы конденсации водяного пара.
воды, что приблизительно равно объёму воды в Чёрном море. На испарение затрачивается около половины всей поглощённой поверхностью Земли энергии солнечного излучения. При конденсации пара количество теплоты, ранее потребовавшееся для испарения жидкости выделяется в атмосферу. Это приводит к нагреванию атмосферы и предотвращает резкие колебания температуры. При перемещении водяных паров в атмосфере на большие расстояния происходит их конденсация в областях с более низкой температурой. Таким образом, в одних областях поверхности и атмосферы Земли преобладают процессы испарения воды, а в других — процессы конденсации водяного пара.
Насыщенный пар
Пар, находящийся в состоянии динамического равновесия с жидкостью, называют насыщенным. Насыщенный пар обладает свойствами, отличающимися от свойств идеального газа. Во-первых, давление насыщенного пара не зависит от его объёма при постоянной температуре. Количество молекул, переходящих из жидкости в пар через единичную площадку за единичный промежуток времени, зависит только от температуры и является постоянной величиной. Количество молекул, переходящих из пара в жидкость, зависит от концентрации пара, а значит, от его давления. Поэтому сразу при уменьшении объёма пара его давление увеличивается, что тут же приводит к возрастанию количества молекул, переходящих в жидкость. В результате количество молекул пара уменьшается и спустя некоторый промежуток времени устанавливается прежнее давление. При увеличении объёма пара его давление, наоборот, уменьшается. Вместе с этим уменьшается и количество молекул, переходящих из пара в жидкость. В результате количество молекул, которые покидают поверхность жидкости (оно не изменяется при Т= const), превышает количество молекул, возвращающихся в жидкость. Равновесие опять восстанавливается при достижении первоначального значения давления.
Второе отличительное свойство насыщенного пара связано с зависимостью его давления от температуры. Давление 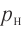 насыщенного пара возрастает значительно быстрее, чем давление
насыщенного пара возрастает значительно быстрее, чем давление 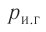 идеального газа при увеличении температуры. В случае идеального газа рост давления обусловлен только увеличением его температуры
идеального газа при увеличении температуры. В случае идеального газа рост давления обусловлен только увеличением его температуры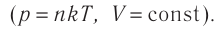 В случае же насыщенного пара рост температуры приводит к увеличению числа молекул, переходящих из жидкости в пар, т. е. к росту концентрации молекул пара. В соответствии с формулой
В случае же насыщенного пара рост температуры приводит к увеличению числа молекул, переходящих из жидкости в пар, т. е. к росту концентрации молекул пара. В соответствии с формулой 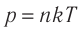 давление пара увеличивается не только в результате непосредственного повышения температуры, но и в результате увеличения концентрации молекул пара, вызванного всё тем же повышением температуры.
давление пара увеличивается не только в результате непосредственного повышения температуры, но и в результате увеличения концентрации молекул пара, вызванного всё тем же повышением температуры.
При переходе из одного состояния в другое масса насыщенного пара изменяется. Поэтому законы идеального газа для изопроцессов можно применять к пару только в том случае, если он далёк от насыщения и его масса остаётся неизменной. Однако уравнение Клапейрона—Менделеева 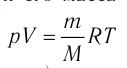 можно использовать для нахождения любых параметров
можно использовать для нахождения любых параметров  насыщенного пара.
насыщенного пара.
Давление (плотность) насыщенного пара при данной температуре — мак-симальное давление (плотность), которое может иметь пар, находящийея в состоянии динамического равновесия с жидкостью при этой температуре. Пар, давление (плотность) которого меньше давления (плотности) насыщенного пара при той же температуре, называют ненасыщенным паром.
Влажность воздуха
Воздух, содержащий водяной пар, называют влажным воздухом. Основными количественными характеристиками такого воздуха являются его абсолютная и относительная влажности.
Абсолютной влажностью 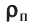 воздуха называют физическую величину, равную плотности водяного пара, находящегося в воздухе при данных условиях. Обычно абсолютную влажность выражают в граммах на кубический метр
воздуха называют физическую величину, равную плотности водяного пара, находящегося в воздухе при данных условиях. Обычно абсолютную влажность выражают в граммах на кубический метр 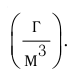 Используя уравнение Клапейрона — Менделеева, плотность пара можно определить через его парциальное давление
Используя уравнение Клапейрона — Менделеева, плотность пара можно определить через его парциальное давление 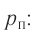
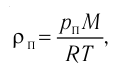
где 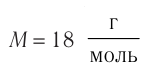 — молярная масса воды, Т — температура воздуха.
— молярная масса воды, Т — температура воздуха.
Зная только плотность 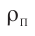 или парциальное давление
или парциальное давление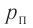 пара, нельзя судить о том, в каком состоянии находится пар в данных условиях и насколько он далёк от насыщения. Вот почему вводят вторую характеристику влажности воздуха — относительную влажность
пара, нельзя судить о том, в каком состоянии находится пар в данных условиях и насколько он далёк от насыщения. Вот почему вводят вторую характеристику влажности воздуха — относительную влажность Относительная влажность показывает, насколько водяной пар при данной температуре далёк от насыщения.
Относительная влажность показывает, насколько водяной пар при данной температуре далёк от насыщения.
Относительной влажностью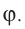 воздуха называют физическую величину, равную отношению абсолютной влажности
воздуха называют физическую величину, равную отношению абсолютной влажности 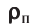 к плотности
к плотности 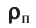 насыщенного водяного пара при данной температуре. Обычно относительную влажность выражают в процентах:
насыщенного водяного пара при данной температуре. Обычно относительную влажность выражают в процентах:
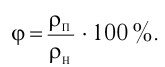
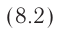
Поскольку плотность пара и его парциальное давление связаны соотношением (8.1), то относительную влажность можно определить как отношение парциального давления 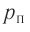 водяного пара, находящегося в воздухе при данной температуре, к давлению
водяного пара, находящегося в воздухе при данной температуре, к давлению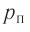 насыщенного пара при той же температуре:
насыщенного пара при той же температуре:

Таким образом, относительная влажность определяется не только абсолютной влажностью, но и температурой воздуха. Значения давления 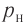 и плотности
и плотности 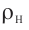 насыщенного водяного пара при различных температурах приведены в таблице 1.
насыщенного водяного пара при различных температурах приведены в таблице 1.
Таблица 1 — Давление и плотность насыщенного водяного пара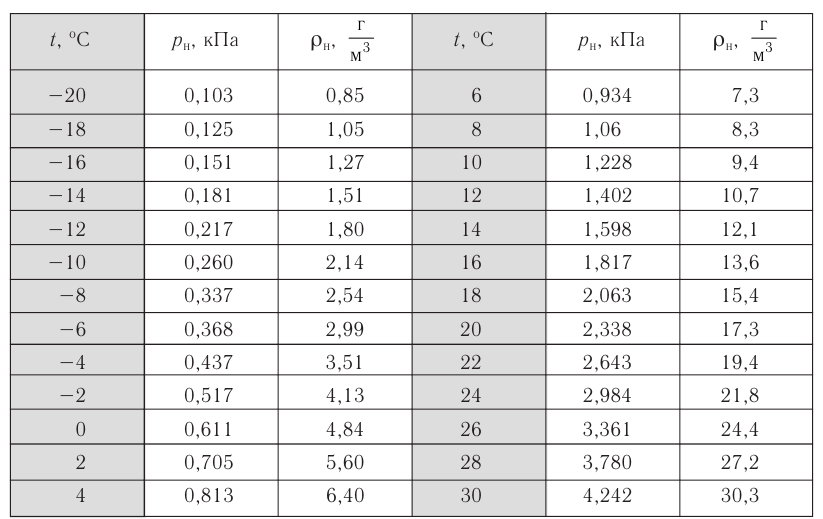
Когда парциальное давление водяного пара в воздухе равно давлению насыщенного пара при той же температуре, говорят, что воздух насыщен водяными парами. Если же плотность водяного пара превышает плотность насыщенного пара, то пар в воздухе считают пересыщенным. Такое состояние является неустойчивым и заканчивается конденсацией.
Температуру, при которой водяной пар в результате изобарного охлаждения становится насыщенным, называют точкой росы. При понижении температуры ниже точки росы происходит конденсация водяного пара. Например, днём температура воздуха была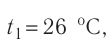 а плотность водяного пара
а плотность водяного пара 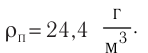
Ночью температура понизилась до 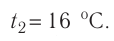 При этой температуре плотность насыщенного водяного пара
При этой температуре плотность насыщенного водяного пара 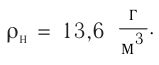 Значит, избыток пара сконденсируется и выпадет в виде росы. Этот процесс является причиной образования тумана, облаков и дождя. В технике конденсация обычно осуществляется на охлаждаемых поверхностях.
Значит, избыток пара сконденсируется и выпадет в виде росы. Этот процесс является причиной образования тумана, облаков и дождя. В технике конденсация обычно осуществляется на охлаждаемых поверхностях.
Если относительная влажность меньше 100 %, то температура, соответствующая точке росы, всегда ниже температуры воздуха, и тем ниже, чем меньше относительная влажность.

Приборы для измерения влажности
Относительную влажность воздуха обычно измеряют психрометром (рис. 48). Психрометр состоит из двух термометров — сухого и влажного. Сухой термометр показывает температуру воздуха. Резервуар влажного термометра обёрнут полоской ткани, конец которой опущен в воду. Вода с ткани испаряется, в результате чего термометр охлаждается. Чем меньше относительная влажность воздуха, тем более интенсивно идёт процесс испарения воды из ткани и тем сильнее охлаждается влажный термометр. И наоборот — при большой относительной влажности влажный термометр охлаждается незначительно. Если относительная влажность  , вода и её пар находятся в динамическом равновесии, и показания обоих термометров совпадают. Зная показания сухого и влажного термометров, относительную влажность воздуха определяют, используя специальную таблицу, называемую психрометрической (таблица 2).
, вода и её пар находятся в динамическом равновесии, и показания обоих термометров совпадают. Зная показания сухого и влажного термометров, относительную влажность воздуха определяют, используя специальную таблицу, называемую психрометрической (таблица 2).
Живые организмы и растения весьма восприимчивы к относительной влажности воздуха. При температуре 20 — 25 °С наиболее благоприятная для человека относительная влажность составляет 40—60 %. При высокой влажности, особенно в жаркий день, испарение влаги с поверхности кожи затрудняется, что приводит к нарушению важнейших биологических механизмов регулирования температуры тела. При низкой влажности происходит интенсивное испарение с поверхности тела и высыхание слизистой оболочки носа, гортани, лёгких, что приводит к ухудшению самочувствия. При низкой влажности в воздухе дольше сохраняются патогенные микроорганизмы, что также небезопасно для человека. В случае низкой влажности воздуха интенсивность испарения с листьев увеличивается, и при малом запасе влаги в почве они быстро вянут и засыхают. Влажность воздуха нужно учитывать и в различных технологических процессах, таких, например, как сушка и хранение готовых изделий. Стальные изделия при высокой влажности быстро ржавеют. Сохранение произведений искусства и книг также требует поддержания влажности воздуха на необходимом уровне.
Большое значение имеет влажность в метеорологии для предсказания погоды. Если воздух у поверхности Земли охлаждается ниже точки росы, то могут образовываться туман, облака, роса или иней.
Таблица 2 — Психрометрическая таблица
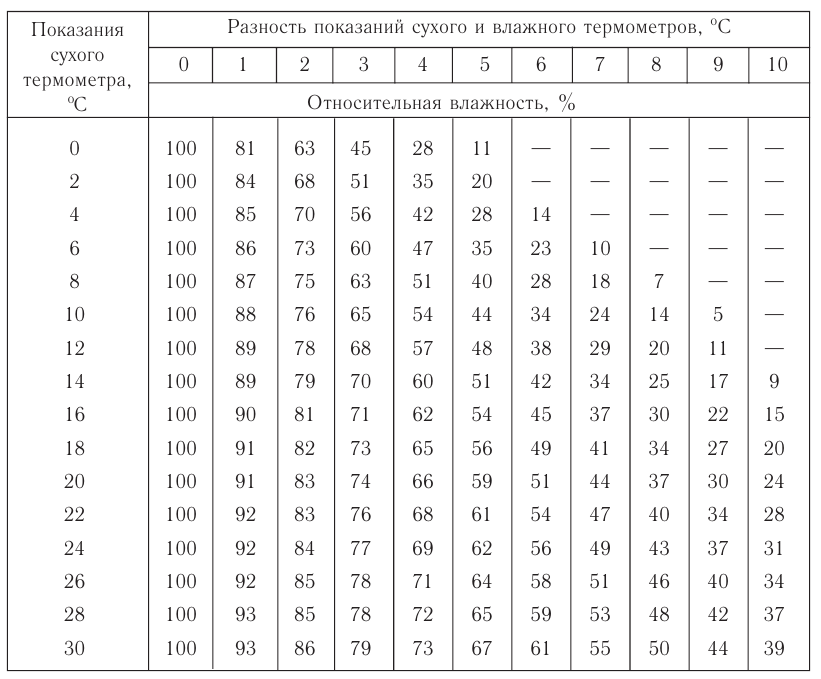
1. Давление насыщенного пара при постоянной температуре не зави-
сит от его объёма.
2. Давление насыщенного пара зависит от температуры пара и концентрации его молекул:
р = nkT.
3. Абсолютной влажностью воздуха называют физическую величину, равную плотности водяного пара, находящегося в воздухе при данных условиях.
4. Относительной влажностью воздуха называют физическую величину, равную отношению абсолютной влажности к плотности насыщенного водяного пара при данной температуре:
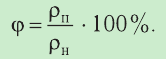
Пример №14
Вечером при температуре = 20 °С относительная влажность воздуха
= 20 °С относительная влажность воздуха  = 60%. Выпадет ли роса, если ночью температура понизится до
= 60%. Выпадет ли роса, если ночью температура понизится до 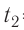 = 12 °С?
= 12 °С?
Дано
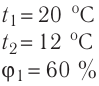
Выпадает ли?
Решение. Для того чтобы узнать, выпадет ли роса при понижении температуры воздуха до 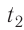 = 12 °С, необходимо сравнить плотность (давление) насыщенного пара при этой температуре с плотностью (парциальным давлением) пара при температуре
= 12 °С, необходимо сравнить плотность (давление) насыщенного пара при этой температуре с плотностью (парциальным давлением) пара при температуре 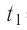 = 20 °С. При температуре
= 20 °С. При температуре 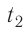 = 12 °С плотность насыщенного водяного пара
= 12 °С плотность насыщенного водяного пара 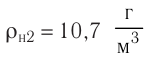 (см. таблицу 1 § 8).
(см. таблицу 1 § 8).
Плотность водяного пара, содержащегося в воздухе при температуре 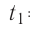 = 20 °С,
= 20 °С,
можно найти из формулы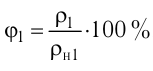 , где
, где 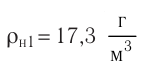 (см. таблицу 1 § 8):
(см. таблицу 1 § 8):
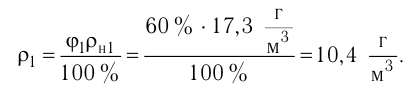
Поскольку 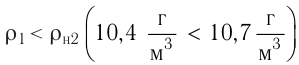 , то имеющегося в воздухе количества водяного пара недостаточно для насыщения, роса не выпадет.
, то имеющегося в воздухе количества водяного пара недостаточно для насыщения, роса не выпадет.
Ответ: роса не выпадет.
Пример №15
В помещении вместимостью V=1,0103 м3 при температуре = 10 °С относительная влажность воздуха
= 10 °С относительная влажность воздуха 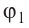 = 40%. Определите массу воды, которую надо испарить в помещении, чтобы при температуре
= 40%. Определите массу воды, которую надо испарить в помещении, чтобы при температуре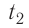 =18 °С относительная влажность воздуха повысилась до
=18 °С относительная влажность воздуха повысилась до 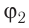 = 60%.
= 60%.
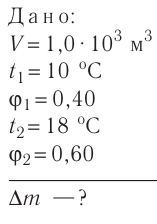
Решение. При температуре 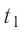 = 10 °С в воздухе помещения содержится водяной пар массой
= 10 °С в воздухе помещения содержится водяной пар массой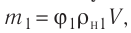 где
где 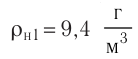 (см. таблицу 1 § 8). Масса водяного пара в данном объёме воздуха при температуре
(см. таблицу 1 § 8). Масса водяного пара в данном объёме воздуха при температуре 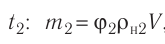 где
где 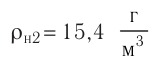 (см. таблицу 1 § 8). Тогда
(см. таблицу 1 § 8). Тогда 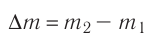 или
или 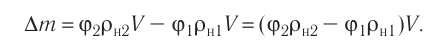
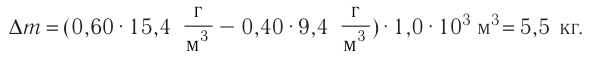
Ответ:  = 5,5 кг.
= 5,5 кг.
- Работа в термодинамике
- Первый закон термодинамики
- Второй закон термодинамики
- Тепловые двигатели и их КПД
- Теория относительности Эйнштейна
- Термодинамика – основные понятия, формулы и определения
- Необратимость тепловых процессов
- Адиабатический процесс




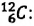
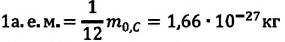
 – масса атома углерода.
– масса атома углерода.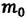 к 1/12 массы атома углерода:
к 1/12 массы атома углерода: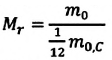
 — относительная молекулярная масса,
— относительная молекулярная масса,  — масса молекулы (атома) вещества,
— масса молекулы (атома) вещества, 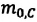 — масса атома углерода. Относительная молекулярная масса не имеет размерности.
— масса атома углерода. Относительная молекулярная масса не имеет размерности. — это отношение числа молекул или атомов данного вещества, к числу Авогадро
— это отношение числа молекул или атомов данного вещества, к числу Авогадро 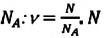 — число молекул в данном веществе. Единица количества вещества является основной единицей в СИ:
— число молекул в данном веществе. Единица количества вещества является основной единицей в СИ: