Нахождение мнимых корней квадратного уравнения
Алгебраическое уравнение 2-й степени иначе называется квадратным. Наиболее общий вид квадратного уравнения с одним неизвестным есть
где a, b, c – данные числа или буквенные выражения, содержащие известные величины (причем коэффициент а не может быть равен нулю, иначе уравнение будет не квадратным, а 1-й степени).. Разделив обе его части на a, мы получим уравнение вида
(p = b/a; q = c/a).
Квадратное уравнение такого вида называется приведенным; уравнение ах 2 + bx + c = 0 (где а ≠ 0), называется неприведенным. Если одна из величин b, с или обе вместе равны нулю, то квадратное уравнение называется неполным; если и b и с не равны нулю, квадратное уравнение называется полным.
Примеры
3x 2 + 8x -5 = 0 – полное неприведенное квадратное уравнение;
3x 2 – 5 = 0 – неполное неприведенное квадратное уравнение;
x 2 – ax = 0 – неполное приведенное квадратное уравнение;
x 2 – 12x +7 = 0 – полное приведенное квадратное уравнение.
Неполное квадратное уравнение вида
x 2 = m (m – известная величина)
является самым простым типом квадратного уравнения и вместе с тем очерь важным, так как к нему приводится решение всякого квадратного уравнения. Решение этого уравнения имеет вид
Возможны три случая:
1) Если m = 0, то и x = 0.
2) Если m – положительное число, то его квадратный корень может иметь два значения: одно положительное, другое отрицательное. Абсолютные величины этих значений одинаковы. Например, уравнение x 2 = 9 удовлетворяется значением х = + 3 и х = – 3. Другими словами, x имеет два значения: +3 и – 3. Часто это выражают тем, что перед радикалом ставят два знака – плюс и минус.
При таком написании подразумевается, что выражение обозначает общую абсолютную величину-двух значений корня; в нашем примере – число 3. Величина может быть иррациональным чиcлом. Заметим, что и само m может быть иррациональным числом. Например, пусть требуется решить уравнение
(геометрически это означает найти длину стороны квадрата равного по площади кругу с радиусом 1). Его корень x = √π.
3) Если m – отрицательное число, то уравнение х 2 = m (например, х 2 = – 9) не может иметь никакого положительного и никакого отрицательного корня: ведь и положительное и отрицательное число по возведении в квадрат дает положительное число. Таким образом, можно сказать, что уравнение х 2 = – 9 не имеет решений, т.е. число не существует.
Но с таким же основанием до введения отрицательных чисел можно было говорить, что и уравнение 2x + 6 = 4 не имеет решений. Однако после введения отрицательных чисел это уравнение стало разрешимым. Точно так же уравнение х 2 = – 9, не имеющее решений среди положительных и отрицательных чисел, становится разрешимым после введения новых величин – квадратных корней из отрицательных чисел. Эти величины были впервые введены итальянским математиком Кардано в середине 16 века в связи с решением кубического уравнения. Кардано назвал эти числа «софистическими» (т. е. «мудреными»). Декарт в 30-х годах 17 века ввел наименование «мнимые числа», которое, к сожалению, удерживается до сих пор. В противоположность мнимым числам прежде известные числа (положительные и отрицательные, в том числе иррациональные) стали называть действительными или вещественными. Сумма действительного и мнимого числа называется комплексным числом*.Часто и комплексные числа называют мнимыми.
Введя в рассмотрение мнимые числа, можно сказать, что неполное квадратное уравнение x 2 = m всегда имеет два корня. Если m > 0, эти корни действительны, они имеют одинаковую абсолютную величину и различны по знаку. Если m = 0, оба они равны нулю; если m *Этот термин введен Гауссом в 1831 г. Слово «комплексный» означает в переводе «совокупный».
Числа. Извлечение корней из комплексных чисел. Квадратное уравнение с комплексными корнями.
Рассматривать будем на таком примере:
Если говорить о действительных числах, то, вы знаете, что корень из отрицательного числа нельзя извлекать. Однако в комплексных числах можно. Если конкретнее, 2 корня:
Выполним проверку того, что эти корни и права оказываются решением уравнения:
Что и требовалось доказать.
Зачастую используют сокращенную запись, корни записывают в одну строчку в таком виде: 
.
Такие корни являются сопряженными комплексными корнями.
Теперь вы знаете как можно извлечь квадратный корень из отрицательного числа. Приведем еще несколько примеров:
, 
,
,
,
В каждом случае получаем 2 сопряженных комплексных корня.
Решим квадратное уравнение .
Первым шагом определим дискриминант уравнения:
В нашем случае дискриминант оказался отрицательным, и в случае с действительными числами у уравнения нет решений, но у нас вариант с комплексными числами, поэтому можем продолжать решение:
Как известно из формул дискриминанта у нас образуется 2 корня:
– сопряженные комплексные корни
Т.о., у уравнения есть 2 сопряженных комплексных корня:
,
Теперь можно решить любое квадратное уравнение!
У любого уравнения с многочленом n-ой степени есть ровно n корней, некоторые из них могут быть комплексными.
Как извлечь корень из произвольного комплексного числа?
Рассмотрим уравнение z n = w, либо, записав в другом виде: . Здесь n может принимать всякое натуральное значение, которое больше 1-цы.
В частности, при n = 2 получаем квадратный корень .
У уравнения типа есть ровно n корней z0, z1, z2, … zn-1, которые можно вычислить с помощью формулы:
,
где – это модуль комплексного числа w,
φ – его аргумент,
а параметр k принимает значения: .
Найдем корни уравнения: .
Перепишем уравнение как: .
В этом примере , , поэтому у уравнения будет 2 корня: z0 и z1. Детализируем общую формулу:
, .
Далее найдем модуль и аргумент комплексного числа :
Число w находится в 1-ой четверти, значит:
Помним, что определяя тригонометрическую форму комплексного числа лучше делать чертеж.
Детализируем еще немного общую формулу:
, .
Так подобно расписывать не обязательно. Здесь мы это сделали, что бы было ясно откуда что образовалось.
Подставляем в формулу значение k = 0 и получаем 1-й корень:
.
Подставляем в формулу значение k = 1 и получаем 2-й корень:
.
Ответ: ,
Если необходимо, корни, которые мы получили можно перевести обратно в алгебраическую форму.
Часто вычисленные корни нужно изобразить геометрически:
Как выполнить чертеж?
Для начала на калькуляторе вычисляем, чему равен модуль корней и чертим с помощью циркуля окружность этого радиуса. Все корни будем откладывать на данной окружности.
Далее берем аргумент 1-го корня и вычисляем, чему равен угол в градусах:
.
Отмеряем транспортиром 45° и ставим на чертеже точку z0.
Берем аргумент 2-го корня и переводим его тоже в градусы: . Отмеряем транспортиром 165° и ставим на чертеже точку z1.
По этому же алгоритму ставим точку z2.
Видно, что корни располагаются геометрически правильно с интервалом между радиус-векторами. Чертеж обязательно делать при помощи транспортира.
Решение квадратного уравнения
Решает квадратное уравнение, в том числе и с мнимыми корнями.
Для решения общего вида квадратного уравнения с одним неизвестным
используется следующая формула
При этом могут представиться следующие три случая
0″ />
тогда два корня уравнения действительны и различны между собой
тогда два корня уравнения действительны и равны между собой
тогда оба корня уравнения мнимы.
Выражение , величина которого позволяет различать эти три случая, называется дискриминантом.
С корнями квадратного уравнения связано интересное свойство — квадратный трехчлен можно разложить на множители первой степени следующим образом
Калькулятор, находящий корни квадратного уравнения:
[spoiler title=”источники:”]
http://www.calc.ru/Chisla-Izvlecheniye-Korney-Iz-Kompleksnykh-Chisel-Kvadratnoy.html
http://planetcalc.ru/168/
[/spoiler]
Сергей Евгеньевич Грамотинский
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Рассмотрим решение уравнений с комплексными корнями и коэффициентами.
Определение 1
Двучленным называется уравнение вида $x^{n} =A$.
Рассмотрим три случая:
- В случае если $A$ – это положительное действительное число, то корни уравнения находятся по формуле
- В случае если $A$ – это отрицательное действительное число, то корни уравнения находятся по формуле
- В случае если $A$ – это комплексное число, то корни уравнения находятся по формуле
[x_{k} =sqrt[{n}]{A} cdot left(cos frac{2kpi }{n} +icdot sin frac{2kpi }{n} right),, , , k=0,..,n-1.]
[x_{k} =sqrt[{n}]{|A|} cdot left(cos frac{pi +2kpi }{n} +icdot sin frac{pi +2kpi }{n} right),, , , k=0,..,n-1.]
[x_{k} =sqrt[{n}]{r} cdot (cos frac{varphi +2pi k}{n} +isin frac{varphi +2pi k}{n} ),, , , k=0..n-1.]
Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
Пример 1
Решить уравнение: $x^{3} =8$.
Решение:
Так как $A>0$, то $x_{k} =sqrt[{3}]{8} cdot left(cos frac{2kpi }{3} +icdot sin frac{2kpi }{3} right),, , , k=0,..,2$.
При $k=0$ получаем $x_{0} =sqrt[{3}]{8} cdot left(cos 0+icdot sin 0right)=sqrt[{3}]{8} =2$.
При $k=1$ получаем
[x_{1} =sqrt[{3}]{8} cdot left(cos frac{2pi }{3} +icdot sin frac{2pi }{3} right)=sqrt[{3}]{8} cdot (-frac{1}{2} +frac{sqrt{3} }{2} cdot i)=2cdot (-frac{1}{2} +frac{sqrt{3} }{2} cdot i)=-1+sqrt{3} cdot i.]
При $k=2$ получаем
[x_{2} =sqrt[{3}]{8} cdot left(cos frac{4pi }{3} +icdot sin frac{4pi }{3} right)=sqrt[{3}]{8} cdot (-frac{1}{2} -frac{sqrt{3} }{2} cdot i)=2cdot (-frac{1}{2} -frac{sqrt{3} }{2} cdot i)=-1-sqrt{3} cdot i.]
Пример 2
Решить уравнение: $x^{3} =1+i$.
«Квадратное уравнение с комплексными корнями» 👇
Решение:
Так как $A$ – комплексное число, то
[x_{k} =sqrt[{n}]{r} cdot (cos frac{varphi +2pi k}{n} +isin frac{varphi +2pi k}{n} ),, , , k=0..n-1,, , , k=0,..,2.]
Тригонометрическая форма записи некоторого комплексного числа имеет вид $z=r(cos varphi +icdot sin varphi )$.
По условию $a=1,b=1$.
Вычислим модуль исходного комплексного числа:
[r=sqrt{1^{2} +1^{2} } =sqrt{1+1} =sqrt{2} ]
Вычислим аргумент исходного комплексного числа:
[varphi =arg z=arctgfrac{1}{1} =arctg1=frac{pi }{4} ]
Подставим полученные значения и получим:
[A=sqrt{2} cdot (cos frac{pi }{4} +isin frac{pi }{4} )]
Уравнение перепишем в виде:
[x^{3} =sqrt{2} cdot (cos frac{pi }{4} +isin frac{pi }{4} )]
При $k=0$ получаем $x_{0} =sqrt[{3}]{sqrt{2} } cdot left(cos frac{pi /4}{3} +icdot sin frac{pi /4}{3} right)=sqrt[{3}]{sqrt{2} } cdot left(cos frac{pi }{12} +icdot sin frac{pi }{12} right)=sqrt[{6}]{2} cdot left(cos frac{pi }{12} +icdot sin frac{pi }{12} right)$.
При $k=1$ получаем
[begin{array}{l} {x_{1} =sqrt[{3}]{sqrt{2} } cdot left(cos frac{pi /4+2pi }{3} +icdot sin frac{pi /4+2pi }{3} right)=sqrt[{3}]{sqrt{2} } cdot left(cos frac{3pi }{4} +icdot sin frac{3pi }{4} right)=} \ {=sqrt[{6}]{2} cdot left(cos frac{3pi }{4} +icdot sin frac{3pi }{4} right)} end{array}]
При $k=2$ получаем
[begin{array}{l} {x_{2} =sqrt[{3}]{sqrt{2} } cdot left(cos frac{pi /4+4pi }{3} +icdot sin frac{pi /4+4pi }{3} right)=sqrt[{3}]{sqrt{2} } cdot left(cos frac{17pi }{12} +icdot sin frac{17pi }{12} right)=} \ {=sqrt[{6}]{2} cdot left(cos frac{17pi }{12} +icdot sin frac{17pi }{12} right)} end{array}]
Определение 2
Квадратным называется уравнение вида $ax^{2} +bx+c=0$, где коэффициенты $a,b,c$ в общем случае являются некоторыми комплексными числами.
Решение квадратного уравнения находится с помощью дискриминанта $D=b^{2} -4ac$, при этом
[x_{1,2} =frac{-bpm sqrt{D} }{2a} .]
Примечание 1
В случае, когда дискриминант является отрицательным числом, корни данного уравнения являются комплексными числами.
Пример 3
Решить уравнение $x^{2} +2x+5=0$ и изобразить корни на плоскости.
Решение:
Вычислим дискриминант:
[D=2^{2} -4cdot 1cdot 5=4-20=-16.]
Так как $D
[x_{1,2} =frac{-2pm sqrt{-16} }{2} =frac{-2pm icdot sqrt{16} }{2} =frac{-2pm icdot 4}{2} =-1pm 2i.]
Изображение корней уравнения на комплексной плоскости (так как корни комплексные) приведено на рис. 1.
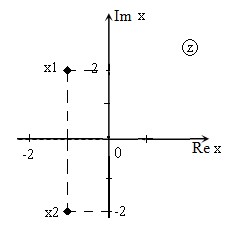
Рис. 1
Примечание 2
В случае, когда уравнение имеет комплексные корни, они являются комплексно-сопряженными числами.
Определение 3
Комплексное число вида $overline{z}=a-bi$ называется числом комплексно-сопряженным для $z=a+bi$.
Примечание 3
Известно, что если $x_{1,2} $ являются корнями квадратного уравнения $ax^{2} +bx+c=0$, то данное уравнение можно переписать в виде $(x-x_{1} )(x-x_{2} )=0$. В общем случае $x_{1,2} $ являются комплексными корнями.
Пример 4
Зная корни уравнения $x_{1,2} =1pm 2i$, записать исходное уравнение.
Решение:
Запишем уравнение следующим образом:
[(x-(1-2i))cdot (x-(1+2i))=0.]
Выполним умножение комплексных чисел
[x^{2} -(1-2i)cdot x-xcdot (1+2i)+(1-2i)cdot (1+2i)=0][x^{2} -x+2icdot x-x-2icdot x+1-4i^{2} =0] [x^{2} -2x+1+4=0] [x^{2} -2x+5=0]
Следовательно, $x^{2} -2x+5=0$ – искомое уравнение.
Рассмотрим квадратное уравнение с комплексными коэффициентами.
Пример 5
Решить уравнение: $z^{2} +(1-2i)cdot z-(1+i)=0$ и изобразить корни на плоскости.
Решение:
Вычислим дискриминант:
[D=(1-2i)^{2} +4cdot 1cdot (1+i)=1-4i+4i^{2} +4+4i=1-4+4=1.]
Так как $D>0$, уравнение имеет два корня:
[x_{1} =frac{-(1-2i))-sqrt{1} }{2} =frac{-1+2i-1}{2} =frac{-2+2i}{2} =-1+i.] [x_{2} =frac{-(1-2i))+sqrt{1} }{2} =frac{-1+2i+1}{2} =frac{2i}{2} =i.]
Изображение корней уравнения на комплексной плоскости (так как корни комплексные) приведено на рис. 2.
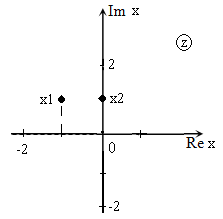
Рис. 2
Примечание 4
В случае, когда уравнение имеет комплексные коэффициенты, его корни не обязательно являются комплексно-сопряженными числами.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Числа. Извлечение корней из комплексных чисел. Квадратное уравнение с комплексными корнями.
Рассматривать будем на таком примере:
Если говорить о действительных числах, то, вы знаете, что корень из отрицательного числа нельзя извлекать. Однако в комплексных числах можно. Если конкретнее, 2 корня:
Выполним проверку того, что эти корни и права оказываются решением уравнения:
Что и требовалось доказать.
Зачастую используют сокращенную запись, корни записывают в одну строчку в таком виде: .
Такие корни являются сопряженными комплексными корнями.
Теперь вы знаете как можно извлечь квадратный корень из отрицательного числа. Приведем еще несколько примеров:
, ,
,
,
В каждом случае получаем 2 сопряженных комплексных корня.
Решим квадратное уравнение 
.
Первым шагом определим дискриминант уравнения:
В нашем случае дискриминант оказался отрицательным, и в случае с действительными числами у уравнения нет решений, но у нас вариант с комплексными числами, поэтому можем продолжать решение:
Как известно из формул дискриминанта у нас образуется 2 корня:
– сопряженные комплексные корни
Т.о., у уравнения есть 2 сопряженных комплексных корня:
,
Теперь можно решить любое квадратное уравнение!
У любого уравнения с многочленом n-ой степени 
есть ровно n корней, некоторые из них могут быть комплексными.
Как извлечь корень из произвольного комплексного числа?
Рассмотрим уравнение z n = w, либо, записав в другом виде: 
. Здесь n может принимать всякое натуральное значение, которое больше 1-цы.
В частности, при n = 2 получаем квадратный корень 
.
У уравнения типа есть ровно n корней z0, z1, z2, … zn-1, которые можно вычислить с помощью формулы:
,
где 
– это модуль комплексного числа w,
φ – его аргумент,
а параметр k принимает значения: 
.
Найдем корни уравнения: 
.
Перепишем уравнение как: 
.
В этом примере 
, 
, поэтому у уравнения будет 2 корня: z0 и z1. Детализируем общую формулу:
, 
.
Далее найдем модуль и аргумент комплексного числа :
Число w находится в 1-ой четверти, значит:
Помним, что определяя тригонометрическую форму комплексного числа лучше делать чертеж.
Детализируем еще немного общую формулу:
, .
Так подобно расписывать не обязательно. Здесь мы это сделали, что бы было ясно откуда что образовалось.
Подставляем в формулу значение k = 0 и получаем 1-й корень:
.
Подставляем в формулу значение k = 1 и получаем 2-й корень:
.
Ответ: 
, 
Если необходимо, корни, которые мы получили можно перевести обратно в алгебраическую форму.
Часто вычисленные корни нужно изобразить геометрически:
Как выполнить чертеж?
Для начала на калькуляторе вычисляем, чему равен модуль корней 
и чертим с помощью циркуля окружность этого радиуса. Все корни будем откладывать на данной окружности.
Далее берем аргумент 1-го корня 
и вычисляем, чему равен угол в градусах:
.
Отмеряем транспортиром 45° и ставим на чертеже точку z0.
Берем аргумент 2-го корня 
и переводим его тоже в градусы: 
. Отмеряем транспортиром 165° и ставим на чертеже точку z1.
По этому же алгоритму ставим точку z2.
Видно, что корни располагаются геометрически правильно с интервалом 
между радиус-векторами. Чертеж обязательно делать при помощи транспортира.
Квадратное уравнение с комплексными корнями
Вы будете перенаправлены на Автор24
Рассмотрим решение уравнений с комплексными корнями и коэффициентами.
Двучленным называется уравнение вида $x^ =A$.
Рассмотрим три случая:
Решить уравнение: $x^ <3>=8$.
Так как $A>0$, то $x_ =sqrt[<3>] <8>cdot left(cos frac<2kpi > <3>+icdot sin frac<2kpi > <3>right),, , , k=0. 2$.
При $k=0$ получаем $x_ <0>=sqrt[<3>] <8>cdot left(cos 0+icdot sin 0right)=sqrt[<3>] <8>=2$.
При $k=1$ получаем
[x_ <1>=sqrt[<3>] <8>cdot left(cos frac<2pi > <3>+icdot sin frac<2pi > <3>right)=sqrt[<3>] <8>cdot (-frac<1> <2>+frac <sqrt<3>> <2>cdot i)=2cdot (-frac<1> <2>+frac <sqrt<3>> <2>cdot i)=-1+sqrt <3>cdot i.]
При $k=2$ получаем
[x_ <2>=sqrt[<3>] <8>cdot left(cos frac<4pi > <3>+icdot sin frac<4pi > <3>right)=sqrt[<3>] <8>cdot (-frac<1> <2>-frac <sqrt<3>> <2>cdot i)=2cdot (-frac<1> <2>-frac <sqrt<3>> <2>cdot i)=-1-sqrt <3>cdot i.]
Решить уравнение: $x^ <3>=1+i$.
Готовые работы на аналогичную тему
Так как $A$ — комплексное число, то
Тригонометрическая форма записи некоторого комплексного числа имеет вид $z=r(cos varphi +icdot sin varphi )$.
По условию $a=1,b=1$.
Вычислим модуль исходного комплексного числа:
Вычислим аргумент исходного комплексного числа:
[varphi =arg z=arctgfrac<1> <1>=arctg1=frac<pi > <4>]
Подставим полученные значения и получим:
Уравнение перепишем в виде:
При $k=0$ получаем $x_ <0>=sqrt[<3>] <sqrt<2>> cdot left(cos frac<pi /4> <3>+icdot sin frac<pi /4> <3>right)=sqrt[<3>] <sqrt<2>> cdot left(cos frac<pi > <12>+icdot sin frac<pi > <12>right)=sqrt[<6>] <2>cdot left(cos frac<pi > <12>+icdot sin frac<pi > <12>right)$.
При $k=1$ получаем
При $k=2$ получаем
Квадратным называется уравнение вида $ax^ <2>+bx+c=0$, где коэффициенты $a,b,c$ в общем случае являются некоторыми комплексными числами.
Решение квадратного уравнения находится с помощью дискриминанта $D=b^ <2>-4ac$, при этом
В случае, когда дискриминант является отрицательным числом, корни данного уравнения являются комплексными числами.
Решить уравнение $x^ <2>+2x+5=0$ и изобразить корни на плоскости.
[D=2^ <2>-4cdot 1cdot 5=4-20=-16.]
Изображение корней уравнения на комплексной плоскости (так как корни комплексные) приведено на рис. 1.
В случае, когда уравнение имеет комплексные корни, они являются комплексно-сопряженными числами.
Комплексное число вида $overline=a-bi$ называется числом комплексно-сопряженным для $z=a+bi$.
Известно, что если $x_ <1,2>$ являются корнями квадратного уравнения $ax^ <2>+bx+c=0$, то данное уравнение можно переписать в виде $(x-x_ <1>)(x-x_ <2>)=0$. В общем случае $x_ <1,2>$ являются комплексными корнями.
Зная корни уравнения $x_ <1,2>=1pm 2i$, записать исходное уравнение.
Запишем уравнение следующим образом:
[x^ <2>-(1-2i)cdot x-xcdot (1+2i)+(1-2i)cdot (1+2i)=0] [x^ <2>-x+2icdot x-x-2icdot x+1-4i^ <2>=0] [x^ <2>-2x+1+4=0] [x^ <2>-2x+5=0]
Следовательно, $x^ <2>-2x+5=0$ — искомое уравнение.
Рассмотрим квадратное уравнение с комплексными коэффициентами.
Решить уравнение: $z^ <2>+(1-2i)cdot z-(1+i)=0$ и изобразить корни на плоскости.
Так как $D>0$, уравнение имеет два корня:
Изображение корней уравнения на комплексной плоскости (так как корни комплексные) приведено на рис. 2.
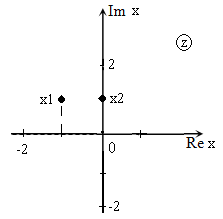
В случае, когда уравнение имеет комплексные коэффициенты, его корни не обязательно являются комплексно-сопряженными числами.
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 13 11 2021
Сергей Евгеньевич Грамотинский
Эксперт по предмету «Математика»
Работаем по будням с 10:00 до 20:00 по Мск
. и многие другие.
Успешной учебы! Будем рады вам помочь!
Как найти мнимые корни, используя фундаментальную теорему алгебры — манекены 2022 — No dummy
Table of Contents:
Основная теорема алгебры может помочь вам найти мнимые корни. Воображаемые корни появляются в квадратичном уравнении, когда дискриминант квадратного уравнения — часть под знаком квадратного корня ( b 2 — 4 ac ) — отрицательно. Если это значение отрицательное, вы не можете взять квадратный корень, и ответы не являются реальными. Другими словами, нет реального решения; поэтому граф не пересекает ось x- .
Использование квадратичной формулы всегда дает вам два решения, потому что знак плюса / минуса означает, что вы добавляете и вычитаете и получаете два совершенно разных ответа. Когда число под квадратным знаком в квадратичной формуле отрицательно, ответы называются комплексными сопряженными. Один r + si , а другой r — si. Эти числа имеют как реальные ( r ), так и мнимые ( si ).
Комплексная система чисел состоит из всех чисел
r + si , где r и s являются действительными числами. Заметим, что когда s = 0 , вы просто имеете действительные числа. Поэтому вещественные числа являются подмножеством комплексной числовой системы. Основная теорема алгебры гласит, что каждая полиномиальная функция имеет по крайней мере один корень в комплексной системе чисел. Наивысшая степень полинома дает вам максимально возможное количество различных
корней для многочлена. Между этим фактом и правилом знаков Декарта вы можете получить представление о том, сколько мнимых корней имеет многочлен.
Вот как правило знаков Декарта может дать вам число возможных реальных корней, как положительных, так и отрицательных:
Положительные истинные корни.
Для числа положительных действительных корней посмотрите на многочлен, записанный в порядке убывания, и подсчитайте, сколько раз знак меняется с термина на термин. Это значение представляет максимальное число положительных корней в многочлене. Например, в полиноме f ( x ) = 2 x 4 — 9 x 3 — 21 x 2 + 88 x + 48, вы видите две изменения в знаке (не забудьте включить знак первого слагаемого!) — от первого слагаемого ( + 2x 4 ) ко второму (- 9x 3 ) и от третьего члена (- 21x 2 ) до четвертый член ( 88x ). Это означает, что это уравнение может иметь до двух положительных решений. Правило знаков Декарта говорит, что число положительных корней равно изменениям знака
f ( x ) или меньше, чем четное число (так что вы держите вычитая 2, пока не получите 1 или 0).Следовательно, предыдущий f ( x ) может иметь 2 или 0 положительных корней. Отрицательные вещественные корни.
Для числа отрицательных действительных корней найдите f (- x ) и пересчитайте снова. Поскольку отрицательные числа, поднятые до четных степеней, являются положительными, а отрицательные числа, поднятые до нечетных степеней, отрицательны, это изменение влияет только на члены с нечетными степенями. Этот шаг будет таким же, как изменение каждого члена с нечетной степенью на противоположный знак и повторный учет знака, что даст вам максимальное количество отрицательных корней. Примерное уравнение становится f (- x ) = 2 x 4 + 9 x 3 — 21 2 — 88 x + 48, который дважды меняет знаки. Могут быть, самое большее, два отрицательных корня. Однако, подобно правилу для положительных корней, число отрицательных корней равно изменениям знака для f (- x ) или должно быть меньше, чем четное номер. Следовательно, этот пример может иметь 2 или 0 отрицательных корней. Соединить все возможные числа положительных действительных корней с каждым возможным числом отрицательных вещественных корней; оставшееся количество корней для каждой ситуации представляет собой число мнимых корней. Например, многочлен
( x ) = 2 x 4 — 9 x 3 — 21 x 2 + 88 x + 48 имеет степень 4 с двумя или нулевыми положительными вещественными корнями и двумя или нулевыми отрицательными вещественными корнями. С помощью этой информации вы можете сопоставить возможные ситуации: Два положительных и два отрицательных вещественных корня с нулевыми воображаемыми корнями Два положительных и нулевых отрицательных вещественных корня с двумя мнимыми корнями
Нулевой положительный и два отрицательных действительные корни с двумя мнимыми корнями
Нулевые положительные и нулевые отрицательные вещественные корни с четырьмя воображаемыми корнями
Следующая диаграмма облегчает представление информации:
Положительные вещественные корни
Отрицательные вещественные корни
| Воображаемые корни | 2 | 2 |
|---|---|---|
| 0 | 2 | 0 |
| 2 | 0 | 2 |
| 2 | 0 | 0 |
| 4 | Сложные числа записываются в виде | r |
+ si и имеют как действительную, так и мнимую часть, поэтому каждый многочлен имеет по крайней мере один корень в комплексной числовой системе , Реальные и мнимые числа включены в комплексную систему чисел. Реальные числа не имеют мнимой части, а чистые мнимые числа не имеют реальной части. Например, если x = 7 является одним корнем многочлена, этот корень считается как реальным, так и сложным, потому что его можно переписать как x = 7 + 0 i
источники:
http://spravochnick.ru/matematika/kompleksnye_chisla_i_mnogochleny/kvadratnoe_uravnenie_s_kompleksnymi_kornyami/
http://ru.no-dummy.com/how-to-find-imaginary-roots-using-fundamental-theorem-of-algebra
Пусть задано квадратное уравнение $ax^2+bx+c=0$, где коэффициенты
$a$,
$b$ и
$c$ – в общем случае являются комплексными.
Его решение находим с помощью дискриминанта
$$D=b^{2}-4 a c$$
тогда
$$x_{1,2}=frac{-b pm sqrt{D}}{2 a}$$
В общем случае и дискриминант, и корни уравнения являются
комплексными числами.
Пример
Задание. Составить квадратное уравнение, которое имеет корни
$z_{1}=1-i$ и
$z_{2}=4-5i$. Решить его.
Решение. Известно, что если
$z_1$, $z_2$ – корни квадратного уравнения
$z^2+bz+c=0$, то указанное уравнение можно записать в виде
$(z-z_1)(z-z_2)=0$. А тогда, учитывая этот факт, имеем, что
искомое уравнение можно записать следующим образом:
$$(z-(1-i))(z-(4-5 i))=0$$
Раскрываем скобки и выполняем операции над комплексными числами:
$$z^{2}-(4-5 i) z-(1-i) z+(1-i)(4-5 i)=0$$
$$z^{2}+z(-4+5 i-1+i)+4-5 i-4 i+5 i^{2}=0$$
$z^{2}+(-5+6 i) z-(1+9 i)=0$ – искомое квадратное уравнение.
Решим полученное уравнение. Найдем дискриминант:
$$D=(-5+6 i)^{2}-4 cdot 1 cdot(-(1+9 i))=-11-60 i+4+36 i=$$
$$=-7-24 i$$
Так как при извлечении корня из комплексного числа в
результате получится комплексное число, то корень из
дискриминанта будем искать в виде $sqrt{D}=a+b i$. То есть
$$sqrt{-7-24 i}=a+b i Rightarrow-7-24 i=(a+b i)^{2} Rightarrow$$
$$Rightarrow-7-24 i=a^{2}+2 a b i-b^{2}$$
Используя тот факт, что два комплексных числа будут равными, если равны их действительные и мнимые части соответственно,
получим систему для нахождения неизвестных значений $a$ и
$b$:
$$left{begin{array}{l}a^{2}-b^{2}=-7 \ 2 a b=-24end{array}right.$$
решив которую, имеем, что $a_1=3$,
$b_1=-4$ или $a_2=-3$, $b_2=4$. Рассматривая любую из
полученных пар, например, первую, получаем, что
$sqrt{D}=3-4 i$, а тогда
$$z_{1}=frac{-(-5+6 i)+(3-4 i)}{2 cdot 1}=4-5 i$$
$$z_{2}=frac{-(-5+6 i)-(3-4 i)}{2 cdot 1}=1-i$$
Ответ. $z^{2}+(-5+6 i) z-(1+9 i)=0$
Читать дальше: элементарные функции комплексного аргумента.
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Продолжаем знакомиться с комплексными числами, сегодня уже будут квадратные уравнения, но не простые, а с отрицательными числами под корнем. Да-да, вы не ошиблись, именно с отрицательными. Будем развеивать школьные мифы о том, что, если под корнем число отрицательное, то уравнение решений не имеет. Ещё как имеет, только не в области вещественных чисел. Пожалуй стоит приступать.
Начнём с простенького примерчика, выступит он у нас в качестве ознакомительного.
Посмотрим на решение.
Рассмотрим теперь полноценное квадратное уравнение.
Решим ещё один примерчик для закрепления.
На сегодня всё, было довольно необычно разбирать такие простые задания, зато посмотрели как решаются квадратные уравнения с комплексными числами, заметили что они не на много интереснее стандартных. Оставляйте в комментариях какие темы нужно ещё разобрать в дальнейшем. Спасибо за внимание.
Другие разделы:
