Метод множителей Лагранжа, применяемый для решения задач математического программирования (в частности, линейного программирования) — метод нахождения условного экстремума функции 





Описание метода[править | править код]
- где
.
Обоснование[править | править код]
Нижеприведенное обоснование метода множителей Лагранжа не является его строгим доказательством. Оно содержит эвристические рассуждения, помогающие понять геометрический смысл метода.
Двумерный случай[править | править код]
Пусть требуется найти экстремум функции 

Будем считать, что
- 1) функция
непрерывно дифференцируема,
- 2) функция
непрерывно дифференцируема, с частными производными, не равными нулю одновременно, то есть уравнение
задаёт гладкую кривую
из обыкновенных точек на плоскости
.
- 3) кривая
не проходит через точки, в которых градиент
обращается в
.
Нарисуем на плоскости 












Тем самым, необходимым условием экстремума в рассматриваемом случае будет совпадение касательных. Чтобы записать его в аналитической форме, заметим, что оно эквивалентно параллельности градиентов функций 

где 
Рассмотрим теперь функцию Лагранжа , зависящую от 

Необходимым условием её экстремума является равенство нулю градиента 
В полученной системе первые два уравнения эквивалентны необходимому условию локального экстремума (1), а третье — уравнению 




Замечание. Найденные таким способом точки 

Вышеприведённые рассуждения о нахождении условного экстремума с помощью вспомогательной функции 
основу метода множителей Лагранжа и обобщаются на случай произвольного числа переменных и уравнений, задающих условия.
На основе метода множителей Лагранжа можно получить достаточные условия условного экстремума, требующие анализа (в простейшем случае) вторых производных функции Лагранжа 
Применение[править | править код]
- Метод множителей Лагранжа применяется при решении задач нелинейного программирования, возникающих во многих областях (например, в экономике).
- Основной метод решения задачи об оптимизации качества кодирования аудио и видео информации при заданном среднем битрейте (см. Оптимизация искажений (англ.) (рус.).
См. также[править | править код]
- Математическое программирование
- Линейное программирование
- Условия Каруша — Куна — Таккера
Литература[править | править код]
- Акулич И.Л. Глава 3. Задачи нелинейного программирования // Математическое программирование в примерах и задачах. — М.: Высшая школа, 1986. — 319 с. — ISBN 5-06-002663-9..
- Зорич В. А. Математический анализ. Часть 1. — изд. 2-е, испр. и доп. — М.: ФАЗИС, 1997.
- Протасов В. Ю. Максимумы и минимумы в геометрии. — М.: МЦНМО. — 56 с. — (Библиотека «Математическое просвещение», выпуск 31).
Приветствую Вас, уважаемые Читатели! В школе каждый из Вас сталкивался с экстремальными задачами на поиск минимумов и максимумов. Все, так или иначе, научились находить производные, приравнивать их к нулю и анализировать полученные точки.
Но что, если мы имеем, например, функцию двух переменных, да еще и с ограничениями, заданными неявно. Например, требуется исследовать на экстремумы следующую конструкцию:
Конечно, можно пытаться выразить одну переменную через другую, но тогда получится не совсем красивая функция, с которой лень возиться. К счастью, у нас есть возможность использовать замечательный метод множителей Лагранжа. Давайте рассмотрим его, так сказать, на пальцах. Для начала запишем следующую вспомогательную функцию:
Теперь необходимо найти частные производные и решить систему уравнений:
Теперь при полученных значениях множителя находим точки, которые будем исследовать дополнительно:
Точки, найденные нами называются стационарными, а дальнейшие изыскания связаны с вычислением знака второй производной функции F в этих точках. Простейшая запись этих условий сводится к вычислению определителя:
Подставляем и вычисляем определитель в общем виде, что значительно удобнее:
Теперь, если определитель больше нуля, мы получим точку максимума, в обратном случае – минимум:
Вычисляем значения функции в найденных экстремальных точках:
Теперь посмотрим на геометрическую интерпретацию:
Как видно из рисунка, нужно найти наибольшее и наименьшее значение аппликаты плоскости z=x+2y для точек ее пересечения с цилиндром. Спасибо за внимание!
- TELEGRAM и Вконтакте– там я публикую не только интересные статьи, но и математический юмор и многое другое!
Функция Лагранжа и метод множителей Лагранжа
Краткая теория
Метод множителей Лагранжа является классическим методом
решения задач математического программирования (в частности выпуклого). К
сожалению, при практическом применении метода могут встретиться значительные
вычислительные трудности, сужающие область его использования. Мы рассматриваем
здесь метод Лагранжа главным образом потому, что он является аппаратом, активно
используемым для обоснования различных современных численных методов, широко
применяемых на практике. Что же касается функции Лагранжа и множителей
Лагранжа, то они играют самостоятельную и исключительно важную роль в теории и
приложениях не только математического программирования.
Рассмотрим классическую задачу оптимизации:
Среди ограничений этой задачи нет
неравенств, нет условий неотрицательности переменных,
их дискретности,
и функции
и
непрерывны и имеют частные производные
по крайней мере второго порядка.
Классический подход к решению задачи дает систему уравнений
(необходимые условия), которым должна удовлетворять точка
,
доставляющая функции
локальный экстремум на множестве точек, удовлетворяющих
ограничениям (для задачи выпуклого программирования найденная точка
будет одновременно и точкой глобального
экстремума).
Предположим, что в точке
функция (1) имеет локальный условный экстремум
и ранг матрицы
равен
.
Тогда необходимые условия запишутся в виде:
где
есть функция Лагранжа;
–
множители Лагранжа.
Существуют также и достаточные условия, при выполнении
которых решение системы уравнений (3) определяет точку экстремума функции
.
Этот вопрос решается на основании исследования знака второго дифференциала
функции Лагранжа. Однако достаточные условия представляют главным образом
теоретический интерес.
Можно указать следующий порядок решения задачи (1), (2)
методом множителей Лагранжа:
1) составить функцию Лагранжа (4);
2) найти частные производные функции Лагранжа по всем
переменным
и приравнять их
нулю. Тем самым будет получена система (3,
состоящая из
уравнений. Решить полученную
систему (если это окажется возможным!) и найти таким
образом все стационарные точки функции Лагранжа;
3) из стационарных точек, взятых без координат
выбрать точки, в которых функция
имеет условные локальные экстремумы при
наличии ограничений (2). Этот выбор осуществляется, например, с применением
достаточных условий локального экстремума. Часто исследование упрощается, если использовать конкретные условия задачи.
Пример решения задачи
Задача
Фирма
реализует автомобили двумя способами: через магазин и через торговых агентов.
При реализации
автомобилей через магазин расходы на
реализацию составляют
у.е., а при продаже
автомобилей через торговых агентов расходы
составляют
у.е. Найти оптимальный способ реализации
автомобилей, минимизирующий суммарные расходы, если общее число предназначенных
для продажи автомобилей составляет 200 штук.
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Составим
математическую модель задачи.
Пусть
и
– число автомобилей, реализуемых первым и
вторым способом.
Целевая
функция
(суммарные
издержки минимизируются).
Ограничения
задачи:
Математическая
модель задачи имеет вид:
Для
решения задачи применим метод множителей Лагранжа.
Функция
Лагранжа имеет вид:
Найдем
частные производные по
и
и приравняем их к нулю. Получим следующую
систему уравнений:
Решая
систему, найдем:
Составим
определитель из частных производных 2-го порядка для функции
по
и
:
Следовательно,
в силу достаточного условия существования условного экстремума, функция
в точке
имеет экстремум.
Так как
, то в полученной точке
функция
имеет условный минимум.
Итак,
оптимальное решение:
Экстремальное значение целевой функции:
Ответ: Нужно продать 99 автомобилей через магазин и 101
автомобиль через торговых агентов, при этом расходы минимизируются и составляют
20398 у.е.
Условный экстремум. Метод множителей Лагранжа. Первая часть.
Для начала рассмотрим случай функции двух переменных. Условным экстремумом функции $z=f(x,y)$ в точке $M_0(x_0;y_0)$ называется экстремум этой функции, достигнутый при условии, что переменные $x$ и $y$ в окрестности данной точки удовлетворяют уравнению связи $varphi (x,y)=0$.
Название «условный» экстремум связано с тем, что на переменные наложено дополнительное условие $varphi(x,y)=0$. Если из уравнения связи можно выразить одну переменную через другую, то задача определения условного экстремума сводится к задаче на обычный экстремум функции одной переменной. Например, если из уравнения связи следует $y=psi(x)$, то подставив $y=psi(x)$ в $z=f(x,y)$, получим функцию одной переменной $z=fleft(x,psi(x)right)$. В общем случае, однако, такой метод малопригоден, поэтому требуется введение нового алгоритма.
Метод множителей Лагранжа для функций двух переменных.
Метод множителей Лагранжа состоит в том, что для отыскания условного экстремума составляют функцию Лагранжа: $F(x,y)=f(x,y)+lambdavarphi(x,y)$ (параметр $lambda$ называют множителем Лагранжа). Необходимые условия экстремума задаются системой уравнений, из которой определяются стационарные точки:
$$
left { begin{aligned}
& frac{partial F}{partial x}=0;\
& frac{partial F}{partial y}=0;\
& varphi (x,y)=0.
end{aligned} right.
$$
Достаточным условием, из которого можно выяснить характер экстремума, служит знак $d^2 F=F_{xx}^{”}dx^2+2F_{xy}^{”}dxdy+F_{yy}^{”}dy^2$. Если в стационарной точке $d^2F > 0$, то функция $z=f(x,y)$ имеет в данной точке условный минимум, если же $d^2F < 0$, то условный максимум.
Есть и другой способ для определения характера экстремума. Из уравнения связи получаем: $varphi_{x}^{‘}dx+varphi_{y}^{‘}dy=0$, $dy=-frac{varphi_{x}^{‘}}{varphi_{y}^{‘}}dx$, поэтому в любой стационарной точке имеем:
$$d^2 F=F_{xx}^{”}dx^2+2F_{xy}^{”}dxdy+F_{yy}^{”}dy^2=F_{xx}^{”}dx^2+2F_{xy}^{”}dxleft( -frac{varphi_{x}^{‘}}{varphi_{y}^{‘}}dxright)+F_{yy}^{”}left( -frac{varphi_{x}^{‘}}{varphi_{y}^{‘}}dxright)^2=\
=-frac{dx^2}{left(varphi_{y}^{‘} right)^2}cdotleft( -(varphi_{y}^{‘})^2 F_{xx}^{”}+2varphi_{x}^{‘}varphi_{y}^{‘}F_{xy}^{”}-(varphi_{x}^{‘})^2 F_{yy}^{”} right)$$
Второй сомножитель (расположенный в скобке) можно представить в такой форме:
$$
H=left| begin{array} {ccc}
0 & varphi_{x}^{‘} & varphi_{y}^{‘}\
varphi_{x}^{‘} & normred{F_{xx}^{”}} & normred{F_{xy}^{”}} \
varphi_{y}^{‘} & normred{F_{xy}^{”}} & normred{F_{yy}^{”}} end{array} right|
$$
Красным цветом выделены элементы определителя $left| begin{array} {cc} F_{xx}^{”} & F_{xy}^{”} \ F_{xy}^{”} & F_{yy}^{”} end{array} right|$, который является гессианом функции Лагранжа. Если $H > 0$, то $d^2F < 0$, что указывает на условный максимум. Аналогично, при $H < 0$ имеем $d^2F > 0$, т.е. имеем условный минимум функции $z=f(x,y)$.
Примечание относительно формы записи определителя $H$. показатьскрыть
Алгоритм исследования функции двух переменных на условный экстремум
- Составить функцию Лагранжа $F(x,y)=f(x,y)+lambdavarphi(x,y)$
- Решить систему $
left { begin{aligned}
& frac{partial F}{partial x}=0;\
& frac{partial F}{partial y}=0;\
& varphi (x,y)=0.
end{aligned} right.$ - Определить характер экстремума в каждой из найденных в предыдущем пункте стационарных точек. Для этого применить любой из указанных способов:
- Составить определитель $H$ и выяснить его знак
- С учетом уравнения связи вычислить знак $d^2F$
Метод множителей Лагранжа для функций n переменных
Допустим, мы имеем функцию $n$ переменных $z=f(x_1,x_2,ldots,x_n)$ и $m$ уравнений связи ($n > m$):
$$varphi_1(x_1,x_2,ldots,x_n)=0; ; varphi_2(x_1,x_2,ldots,x_n)=0,ldots,varphi_m(x_1,x_2,ldots,x_n)=0.$$
Обозначив множители Лагранжа как $lambda_1,lambda_2,ldots,lambda_m$, составим функцию Лагранжа:
$$F(x_1,x_2,ldots,x_n,lambda_1,lambda_2,ldots,lambda_m)=f+lambda_1varphi_1+lambda_2varphi_2+ldots+lambda_mvarphi_m$$
Необходимые условия наличия условного экстремума задаются системой уравнений, из которой находятся координаты стационарных точек и значения множителей Лагранжа:
$$left{begin{aligned}
& frac{partial F}{partial x_i}=0; (i=overline{1,n})\
& varphi_j=0; (j=overline{1,m})
end{aligned} right.$$
Выяснить, условный минимум или условный максимум имеет функция в найденной точке, можно, как и ранее, посредством знака $d^2F$. Если в найденной точке $d^2F > 0$, то функция имеет условный минимум, если же $d^2F < 0$, – то условный максимум. Можно пойти иным путем, рассмотрев следующую матрицу:
Определитель матрицы
$$left| begin{array} {ccccc} frac{partial^2F}{partial x_{1}^{2}} & frac{partial^2F}{partial x_{1}partial x_{2}} & frac{partial^2F}{partial x_{1}partial x_{3}} &ldots & frac{partial^2F}{partial x_{1}partial x_{n}}\
frac{partial^2F}{partial x_{2}partial x_1} & frac{partial^2F}{partial x_{2}^{2}} & frac{partial^2F}{partial x_{2}partial x_{3}} &ldots & frac{partial^2F}{partial x_{2}partial x_{n}}\
frac{partial^2F}{partial x_{3} partial x_{1}} & frac{partial^2F}{partial x_{3}partial x_{2}} & frac{partial^2F}{partial x_{3}^{2}} &ldots & frac{partial^2F}{partial x_{3}partial x_{n}}\
ldots & ldots & ldots &ldots & ldots\
frac{partial^2F}{partial x_{n}partial x_{1}} & frac{partial^2F}{partial x_{n}partial x_{2}} & frac{partial^2F}{partial x_{n}partial x_{3}} &ldots & frac{partial^2F}{partial x_{n}^{2}}\
end{array} right|,$$
выделенной в матрице $L$ красным цветом, есть гессиан функции Лагранжа. Используем следующее правило:
- Если знаки угловых миноров $H_{2m+1},; H_{2m+2},ldots,H_{m+n}$ матрицы $L$ совпадают с знаком $(-1)^m$, то исследуемая стационарная точка является точкой условного минимума функции $z=f(x_1,x_2,x_3,ldots,x_n)$.
- Если знаки угловых миноров $H_{2m+1},; H_{2m+2},ldots,H_{m+n}$ чередуются, причём знак минора $H_{2m+1}$ совпадает с знаком числа $(-1)^{m+1}$, то исследуемая стационарная точка является точкой условного максимума функции $z=f(x_1,x_2,x_3,ldots,x_n)$.
Пример №1
Найти условный экстремум функции $z(x,y)=x+3y$ при условии $x^2+y^2=10$.
Решение
Геометрическая интерпретация данной задачи такова: требуется найти наибольшее и наименьшее значение аппликаты плоскости $z=x+3y$ для точек ее пересечения с цилиндром $x^2+y^2=10$.
Выразить одну переменную через другую из уравнения связи и подставить ее в функцию $z(x,y)=x+3y$ несколько затруднительно, поэтому будем использовать метод Лагранжа.
Обозначив $varphi(x,y)=x^2+y^2-10$, составим функцию Лагранжа:
$$
F(x,y)=z(x,y)+lambda varphi(x,y)=x+3y+lambda(x^2+y^2-10);\
frac{partial F}{partial x}=1+2lambda x; frac{partial F}{partial y}=3+2lambda y.
$$
Запишем систему уравнений для определения стационарных точек функции Лагранжа:
$$
left { begin{aligned}
& 1+2lambda x=0;\
& 3+2lambda y=0;\
& x^2+y^2-10=0.
end{aligned} right.
$$
Если предположить $lambda=0$, то первое уравнение станет таким: $1=0$. Полученное противоречие говорит о том, что $lambdaneq 0$. При условии $lambdaneq 0$ из первого и второго уравнений имеем: $x=-frac{1}{2lambda}$, $y=-frac{3}{2lambda}$. Подставляя полученные значения в третье уравнение, получим:
$$
left( -frac{1}{2lambda} right)^2+left( -frac{3}{2lambda} right)^2-10=0;\
frac{1}{4lambda^2}+frac{9}{4lambda^2}=10; lambda^2=frac{1}{4}; left[ begin{aligned} & lambda_1=-frac{1}{2};\ & lambda_2=frac{1}{2}. end{aligned} right.\
begin{aligned}
& lambda_1=-frac{1}{2}; ; x_1=-frac{1}{2lambda_1}=1; ; y_1=-frac{3}{2lambda_1}=3;\
& lambda_2=frac{1}{2}; ; x_2=-frac{1}{2lambda_2}=-1; ; y_2=-frac{3}{2lambda_2}=-3.end{aligned}
$$
Итак, система имеет два решения: $x_1=1;; y_1=3;; lambda_1=-frac{1}{2}$ и $x_2=-1;; y_2=-3;; lambda_2=frac{1}{2}$. Выясним характер экстремума в каждой стационарной точке: $M_1(1;3)$ и $M_2(-1;-3)$. Для этого вычислим определитель $H$ в каждой из точек.
$$
varphi_{x}^{‘}=2x;; varphi_{y}^{‘}=2y;; F_{xx}^{”}=2lambda;; F_{xy}^{”}=0;; F_{yy}^{”}=2lambda.\
H=left| begin{array} {ccc} 0 & varphi_{x}^{‘} & varphi_{y}^{‘}\ varphi_{x}^{‘} & F_{xx}^{”} & F_{xy}^{”} \ varphi_{y}^{‘} & F_{xy}^{”} & F_{yy}^{”} end{array} right|=
left| begin{array} {ccc} 0 & 2x & 2y\ 2x & 2lambda & 0 \ 2y & 0 & 2lambda end{array} right|=
8cdotleft| begin{array} {ccc} 0 & x & y\ x & lambda & 0 \ y & 0 & lambda end{array} right|
$$
В точке $M_1(1;3)$ получим:
$$H=8cdotleft| begin{array} {ccc} 0 & x & y\ x & lambda & 0 \ y & 0 & lambda end{array} right|=
8cdotleft| begin{array} {ccc} 0 & 1 & 3\ 1 & -1/2 & 0 \ 3 & 0 & -1/2 end{array} right|=40 > 0.$$
Следовательно, в точке $M_1(1;3)$ функция $z(x,y)=x+3y$ имеет условный максимум, $z_{max}=z(1;3)=10$.
Аналогично, в точке $M_2(-1;-3)$ найдем:
$$H=8cdotleft| begin{array} {ccc} 0 & x & y\ x & lambda & 0 \ y & 0 & lambda end{array} right|=
8cdotleft| begin{array} {ccc} 0 & -1 & -3\ -1 & 1/2 & 0 \ -3 & 0 & 1/2 end{array} right|=-40$$
Так как $H < 0$, то в точке $M_2(-1;-3)$ имеем условный минимум функции $z(x,y)=x+3y$, а именно: $z_{min}=z(-1;-3)=-10$.
Отмечу, что вместо вычисления значения определителя $H$ в каждой точке, гораздо удобнее раскрыть его в общем виде. Дабы не загромождать текст подробностями, этот способ скрою под примечание.
Запись определителя $H$ в общем виде. показатьскрыть
Вопрос о характере экстремума в стационарных точках $M_1(1;3)$ и $M_2(-1;-3)$ можно решить и без использования определителя $H$. Найдем знак $d^2F$ в каждой стационарной точке:
$$
d^2 F=F_{xx}^{”}dx^2+2F_{xy}^{”}dxdy+F_{yy}^{”}dy^2=2lambda left( dx^2+dy^2right)
$$
Отмечу, что запись $dx^2$ означает именно $dx$, возведённый в вторую степень, т.е. $left( dx right)^2$. Отсюда имеем: $dx^2+dy^2>0$, посему при $lambda_1=-frac{1}{2}$ получим $d^2F < 0$. Следовательно, функция имеет в точке $M_1(1;3)$ условный максимум. Аналогично, в точке $M_2(-1;-3)$ получим условный минимум функции $z(x,y)=x+3y$. Отметим, что для определения знака $d^2F$ не пришлось учитывать связь между $dx$ и $dy$, ибо знак $d^2F$ очевиден без дополнительных преобразований. В следующем примере для определения знака $d^2F$ уже будет необходимо учесть связь между $dx$ и $dy$.
Ответ: в точке $(-1;-3)$ функция имеет условный минимум, $z_{min}=-10$. В точке $(1;3)$ функция имеет условный максимум, $z_{max}=10$.
Пример №2
Найти условный экстремум функции $z(x,y)=3y^3+4x^2-xy$ при условии $x+y=0$.
Решение
Первый способ (метод множителей Лагранжа)
Обозначив $varphi(x,y)=x+y$ составим функцию Лагранжа:
$$F(x,y)=z(x,y)+lambda varphi(x,y)=3y^3+4x^2-xy+lambda(x+y).$$
$$
frac{partial F}{partial x}=8x-y+lambda; ; frac{partial F}{partial y}=9y^2-x+lambda.\
left { begin{aligned} & 8x-y+lambda=0;\ & 9y^2-x+lambda=0; \ & x+y=0. end{aligned} right.
$$
Решив систему, получим: $x_1=0$, $y_1=0$, $lambda_1=0$ и $x_2=frac{10}{9}$, $y_2=-frac{10}{9}$, $lambda_2=-10$. Имеем две стационарные точки: $M_1(0;0)$ и $M_2 left(frac{10}{9};-frac{10}{9} right)$. Выясним характер экстремума в каждой стационарной точке с использованием определителя $H$.
$$
H=left| begin{array} {ccc} 0 & varphi_{x}^{‘} & varphi_{y}^{‘}\ varphi_{x}^{‘} & F_{xx}^{”} & F_{xy}^{”} \ varphi_{y}^{‘} & F_{xy}^{”} & F_{yy}^{”} end{array} right|=
left| begin{array} {ccc} 0 & 1 & 1\ 1 & 8 & -1 \ 1 & -1 & 18y end{array} right|=-10-18y
$$
В точке $M_1(0;0)$ $H=-10-18cdot 0=-10 < 0$, поэтому $M_1(0;0)$ есть точка условного минимума функции $z(x,y)=3y^3+4x^2-xy$, $z_{min}=0$. В точке $M_2left(frac{10}{9};-frac{10}{9}right)$ $H=10 > 0$, посему в данной точке функция имеет условный максимум, $z_{max}=frac{500}{243}$.
Исследуем характер экстремума в каждой из точек иным методом, основываясь на знаке $d^2F$:
$$
d^2 F=F_{xx}^{”}dx^2+2F_{xy}^{”}dxdy+F_{yy}^{”}dy^2=8dx^2-2dxdy+18ydy^2
$$
Из уравнения связи $x+y=0$ имеем: $d(x+y)=0$, $dx+dy=0$, $dy=-dx$.
$$
d^2 F=8dx^2-2dxdy+18ydy^2=8dx^2-2dx(-dx)+18y(-dx)^2=(10+18y)dx^2
$$
Так как $ d^2F Bigr|_{M_1}=10 dx^2 > 0$, то $M_1(0;0)$ является точкой условного минимума функции $z(x,y)=3y^3+4x^2-xy$. Аналогично, $d^2F Bigr|_{M_2}=-10 dx^2 < 0$, т.е. $M_2left(frac{10}{9}; -frac{10}{9} right)$ – точка условного максимума.
Второй способ
Из уравнения связи $x+y=0$ получим: $y=-x$. Подставив $y=-x$ в функцию $z(x,y)=3y^3+4x^2-xy$, получим некоторую функцию переменной $x$. Обозначим эту функцию как $u(x)$:
$$
u(x)=z(x,-x)=3cdot(-x)^3+4x^2-xcdot(-x)=-3x^3+5x^2.
$$
Таким образом задачу о нахождении условного экстремума функции двух переменных мы свели к задаче определения экстремума функции одной переменной.
$$
u_{x}^{‘}=-9x^2+10x;\
-9x^2+10x=0; ; xcdot(-9x+10)=0;\
x_1=0; ; y_1=-x_1=0;\
x_2=frac{10}{9}; ; y_2=-x_2=-frac{10}{9}.
$$
Получили точки $M_1(0;0)$ и $M_2left(frac{10}{9}; -frac{10}{9}right)$. Дальнейшее исследование известно из курса дифференциального исчисления функций одной переменой. Исследуя знак $u_{xx}^{”}$ в каждой стационарной точке или проверяя смену знака $u_{x}^{‘}$ в найденных точках, получим те же выводы, что и при решении первым способом. Например, проверим знак $u_{xx}^{”}$:
$$u_{xx}^{”}=-18x+10;\
u_{xx}^{”}(M_1)=10;;u_{xx}^{”}(M_2)=-10.$$
Так как $u_{xx}^{”}(M_1)>0$, то $M_1$ – точка минимума функции $u(x)$, при этом $u_{min}=u(0)=0$. Так как $u_{xx}^{”}(M_2)<0$, то $M_2$ – точка максимума функции $u(x)$, причём $u_{max}=uleft(frac{10}{9}right)=frac{500}{243}$.
Значения функции $u(x)$ при заданном условии связи совпадают с значениями функции $z(x,y)$, т.е. найденные экстремумы функции $u(x)$ и есть искомые условные экстремумы функции $z(x,y)$.
Ответ: в точке $(0;0)$ функция имеет условный минимум, $z_{min}=0$. В точке $left(frac{10}{9}; -frac{10}{9} right)$ функция имеет условный максимум, $z_{max}=frac{500}{243}$.
Рассмотрим еще один пример, в котором характер экстремума выясним посредством определения знака $d^2F$.
Пример №3
Найти наибольшее и наименьшее значения функции $z=5xy-4$, если переменные $x$ и $y$ положительны и удовлетворяют уравнению связи $frac{x^2}{8}+frac{y^2}{2}-1=0$.
Решение
Составим функцию Лагранжа: $F=5xy-4+lambda left( frac{x^2}{8}+frac{y^2}{2}-1 right)$. Найдем стационарные точки функции Лагранжа:
$$
F_{x}^{‘}=5y+frac{lambda x}{4}; ; F_{y}^{‘}=5x+lambda y.\
left { begin{aligned}
& 5y+frac{lambda x}{4}=0;\
& 5x+lambda y=0;\
& frac{x^2}{8}+frac{y^2}{2}-1=0;\
& x > 0; ; y > 0.
end{aligned} right.
$$
Все дальнейшие преобразования осуществляются с учетом $x > 0; ; y > 0$ (это оговорено в условии задачи). Из второго уравнения выразим $lambda=-frac{5x}{y}$ и подставим найденное значение в первое уравнение: $5y-frac{5x}{y}cdot frac{x}{4}=0$, $4y^2-x^2=0$, $x=2y$. Подставляя $x=2y$ в третье уравнение, получим: $frac{4y^2}{8}+frac{y^2}{2}-1=0$, $y^2=1$, $y=1$.
Так как $y=1$, то $x=2$, $lambda=-10$. Характер экстремума в точке $(2;1)$ определим, исходя из знака $d^2F$.
$$
F_{xx}^{”}=frac{lambda}{4}; ; F_{xy}^{”}=5; ; F_{yy}^{”}=lambda.
$$
Так как $frac{x^2}{8}+frac{y^2}{2}-1=0$, то:
$$
dleft( frac{x^2}{8}+frac{y^2}{2}-1right)=0; ; dleft( frac{x^2}{8} right)+dleft( frac{y^2}{2} right)=0; ; frac{x}{4}dx+ydy=0; ; dy=-frac{xdx}{4y}.
$$
В принципе, здесь можно сразу подставить координаты стационарной точки $x=2$, $y=1$ и параметра $lambda=-10$, получив при этом:
$$
F_{xx}^{”}=frac{-5}{2}; ; F_{xy}^{”}=-10; ; dy=-frac{dx}{2}.\
d^2 F=F_{xx}^{”}dx^2+2F_{xy}^{”}dxdy+F_{yy}^{”}dy^2=-frac{5}{2}dx^2+10dxcdot left(-frac{dx}{2} right)-10cdot left(-frac{dx}{2} right)^2=\
=-frac{5}{2}dx^2-5dx^2-frac{5}{2}dx^2=-10dx^2.
$$
Однако в других задачах на условный экстремум стационарных точек может быть несколько. В таких случаях лучше $d^2F$ представить в общем виде, а потом подставлять в полученное выражение координаты каждой из найденных стационарных точек:
$$
d^2 F=F_{xx}^{”}dx^2+2F_{xy}^{”}dxdy+F_{yy}^{”}dy^2=frac{lambda}{4}dx^2+10cdot dxcdot frac{-xdx}{4y} +lambdacdot left(-frac{xdx}{4y} right)^2=\
=frac{lambda}{4}dx^2-frac{5x}{2y}dx^2+lambda cdot frac{x^2dx^2}{16y^2}=left( frac{lambda}{4}-frac{5x}{2y}+frac{lambda cdot x^2}{16y^2} right)cdot dx^2
$$
Подставляя $x=2$, $y=1$, $lambda=-10$, получим:
$$
d^2 F=left( frac{-10}{4}-frac{10}{2}-frac{10 cdot 4}{16} right)cdot dx^2=-10dx^2.
$$
Так как $d^2F=-10cdot dx^2 < 0$, то точка $(2;1)$ есть точкой условного максимума функции $z=5xy-4$, причём $z_{max}=10-4=6$.
Ответ: в точке $(2;1)$ функция имеет условный максимум, $z_{max}=6$.
В следующей части рассмотрим применение метода Лагранжа для функций большего количества переменных.
In mathematical optimization, the method of Lagrange multipliers is a strategy for finding the local maxima and minima of a function subject to equality constraints (i.e., subject to the condition that one or more equations have to be satisfied exactly by the chosen values of the variables).[1] It is named after the mathematician Joseph-Louis Lagrange. The basic idea is to convert a constrained problem into a form such that the derivative test of an unconstrained problem can still be applied. The relationship between the gradient of the function and gradients of the constraints rather naturally leads to a reformulation of the original problem, known as the Lagrangian function.[2]
The method can be summarized as follows: In order to find the maximum or minimum of a function 

and find the stationary points of 



and
or equivalently
and
The solution corresponding to the original constrained optimization is always a saddle point of the Lagrangian function,[4][5] which can be identified among the stationary points from the definiteness of the bordered Hessian matrix.[6]
The great advantage of this method is that it allows the optimization to be solved without explicit parameterization in terms of the constraints. As a result, the method of Lagrange multipliers is widely used to solve challenging constrained optimization problems. Further, the method of Lagrange multipliers is generalized by the Karush–Kuhn–Tucker conditions, which can also take into account inequality constraints of the form 

Statement[edit]
The following is known as the Lagrange multiplier theorem.[7]
Let 





![{displaystyle {Bigl [}operatorname {D} g(x_{star }){Bigr ]}_{j,k}=left[{frac { partial g_{j} }{partial x_{k}}}right]{bigg )} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/d4e656034f8dab7e4b30098c730df1eb74bf3e04)
Then there exists a unique Lagrange multiplier 

The Lagrange multiplier theorem states that at any local maximum (or minimum) of the function evaluated under the equality constraints, if constraint qualification applies (explained below), then the gradient of the function (at that point) can be expressed as a linear combination of the gradients of the constraints (at that point), with the Lagrange multipliers acting as coefficients.[8] This is equivalent to saying that any direction perpendicular to all gradients of the constraints is also perpendicular to the gradient of the function. Or still, saying that the directional derivative of the function is 0 in every feasible direction.
Single constraint[edit]
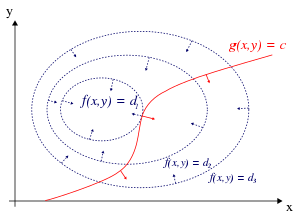
Figure 1: The red curve shows the constraint g(x, y) = c. The blue curves are contours of f(x, y). The point where the red constraint tangentially touches a blue contour is the maximum of f(x, y) along the constraint, since d1 > d2 .
For the case of only one constraint and only two choice variables (as exemplified in Figure 1), consider the optimization problem
(Sometimes an additive constant is shown separately rather than being included in 




where the 







The method of Lagrange multipliers relies on the intuition that at a maximum, f(x, y) cannot be increasing in the direction of any such neighboring point that also has g = 0. If it were, we could walk along g = 0 to get higher, meaning that the starting point wasn’t actually the maximum. Viewed in this way, it is an exact analogue to testing if the derivative of an unconstrained function is 0, that is, we are verifying that the directional derivative is 0 in any relevant (viable) direction.
We can visualize contours of f given by f(x, y) = d for various values of d, and the contour of g given by g(x, y) = c.
Suppose we walk along the contour line with g = c . We are interested in finding points where f almost does not change as we walk, since these points might be maxima.
There are two ways this could happen:
- We could touch a contour line of f, since by definition f does not change as we walk along its contour lines. This would mean that the tangents to the contour lines of f and g are parallel here.
- We have reached a “level” part of f, meaning that f does not change in any direction.
To check the first possibility (we touch a contour line of f), notice that since the gradient of a function is perpendicular to the contour lines, the tangents to the contour lines of f and g are parallel if and only if the gradients of f and g are parallel. Thus we want points (x, y) where g(x, y) = c and
for some 
where
are the respective gradients. The constant 

Notice that this method also solves the second possibility, that f is level: if f is level, then its gradient is zero, and setting 

To incorporate these conditions into one equation, we introduce an auxiliary function
and solve
Note that this amounts to solving three equations in three unknowns. This is the method of Lagrange multipliers.
Note that 





To summarize
The method generalizes readily to functions on 
which amounts to solving n + 1 equations in n + 1 unknowns.
The constrained extrema of f are critical points of the Lagrangian 

One may reformulate the Lagrangian as a Hamiltonian, in which case the solutions are local minima for the Hamiltonian. This is done in optimal control theory, in the form of Pontryagin’s minimum principle.
The fact that solutions of the Lagrangian are not necessarily extrema also poses difficulties for numerical optimization. This can be addressed by computing the magnitude of the gradient, as the zeros of the magnitude are necessarily local minima, as illustrated in the numerical optimization example.
Multiple constraints[edit]
Figure 2: A paraboloid constrained along two intersecting lines.
Figure 3: Contour map of Figure 2.
The method of Lagrange multipliers can be extended to solve problems with multiple constraints using a similar argument. Consider a paraboloid subject to two line constraints that intersect at a single point. As the only feasible solution, this point is obviously a constrained extremum. However, the level set of 

Concretely, suppose we have 








We are still interested in finding points where 






These scalars are the Lagrange multipliers. We now have 
As before, we introduce an auxiliary function
and solve
which amounts to solving 

The constraint qualification assumption when there are multiple constraints is that the constraint gradients at the relevant point are linearly independent.
Modern formulation via differentiable manifolds[edit]
The problem of finding the local maxima and minima subject to constraints can be generalized to finding local maxima and minima on a differentiable manifold 



Single constraint[edit]
Let 






Let 











where 




In this formulation, it is not necessary to explicitly find the Lagrange multiplier, a number 

Multiple constraints[edit]
Let 































Once again, in this formulation it is not necessary to explicitly find the Lagrange multipliers, the numbers 
Interpretation of the Lagrange multipliers[edit]
In this section, we modify the constraint equations from the form 



Often the Lagrange multipliers have an interpretation as some quantity of interest. For example, by parametrising the constraint’s contour line, that is, if the Lagrangian expression is
then
So, λk is the rate of change of the quantity being optimized as a function of the constraint parameter.
As examples, in Lagrangian mechanics the equations of motion are derived by finding stationary points of the action, the time integral of the difference between kinetic and potential energy. Thus, the force on a particle due to a scalar potential, F = −∇V, can be interpreted as a Lagrange multiplier determining the change in action (transfer of potential to kinetic energy) following a variation in the particle’s constrained trajectory.
In control theory this is formulated instead as costate equations.
Moreover, by the envelope theorem the optimal value of a Lagrange multiplier has an interpretation as the marginal effect of the corresponding constraint constant upon the optimal attainable value of the original objective function: If we denote values at the optimum with a star (
For example, in economics the optimal profit to a player is calculated subject to a constrained space of actions, where a Lagrange multiplier is the change in the optimal value of the objective function (profit) due to the relaxation of a given constraint (e.g. through a change in income); in such a context 
Sufficient conditions[edit]
Sufficient conditions for a constrained local maximum or minimum can be stated in terms of a sequence of principal minors (determinants of upper-left-justified sub-matrices) of the bordered Hessian matrix of second derivatives of the Lagrangian expression.[6][16]
Examples[edit]
Example 1[edit]
Illustration of the constrained optimization problem 1
Suppose we wish to maximize 



For the method of Lagrange multipliers, the constraint is
hence the Lagrangian function,
is a function that is equivalent to 

Now we can calculate the gradient:
and therefore:
Notice that the last equation is the original constraint.
The first two equations yield
By substituting into the last equation we have:
so
which implies that the stationary points of 
Evaluating the objective function f at these points yields
Thus the constrained maximum is 

Example 2[edit]
Illustration of the constrained optimization problem 2
Now we modify the objective function of Example 1 so that we minimize 






On the other hand, the minima occur on the level set for 







Example 3[edit]
Illustration of constrained optimization problem 3.
This example deals with more strenuous calculations, but it is still a single constraint problem.
Suppose one wants to find the maximum values of
with the condition that the 


As there is just a single constraint, there is a single multiplier, say 
The constraint 




Applying the ordinary Lagrange multiplier method yields
from which the gradient can be calculated:
And therefore:
(iii) is just the original constraint. (i) implies 









Evaluating the objective at these points, one finds that
Therefore, the objective function attains the global maximum (subject to the constraints) at 






Note that while 


Given any neighbourhood of 







Example 4[edit]
- Entropy
Suppose we wish to find the discrete probability distribution on the points 

For this to be a probability distribution the sum of the probabilities 

We use Lagrange multipliers to find the point of maximum entropy, 


which gives a system of n equations, 
Carrying out the differentiation of these n equations, we get
This shows that all 
we find
Hence, the uniform distribution is the distribution with the greatest entropy, among distributions on n points.
Example 5[edit]
- Numerical optimization
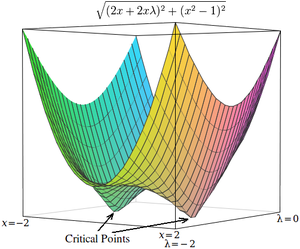
Lagrange multipliers cause the critical points to occur at saddle points (Example 5).
The magnitude of the gradient can be used to force the critical points to occur at local minima (Example 5).
The critical points of Lagrangians occur at saddle points, rather than at local maxima (or minima).[4][17] Unfortunately, many numerical optimization techniques, such as hill climbing, gradient descent, some of the quasi-Newton methods, among others, are designed to find local maxima (or minima) and not saddle points. For this reason, one must either modify the formulation to ensure that it’s a minimization problem (for example, by extremizing the square of the gradient of the Lagrangian as below), or else use an optimization technique that finds stationary points (such as Newton’s method without an extremum seeking line search) and not necessarily extrema.
As a simple example, consider the problem of finding the value of x that minimizes 

Using Lagrange multipliers, this problem can be converted into an unconstrained optimization problem:
The two critical points occur at saddle points where x = 1 and x = −1.
In order to solve this problem with a numerical optimization technique, we must first transform this problem such that the critical points occur at local minima. This is done by computing the magnitude of the gradient of the unconstrained optimization problem.
First, we compute the partial derivative of the unconstrained problem with respect to each variable:
If the target function is not easily differentiable, the differential with respect to each variable can be approximated as
where 
Next, we compute the magnitude of the gradient, which is the square root of the sum of the squares of the partial derivatives:
(Since magnitude is always non-negative, optimizing over the squared-magnitude is equivalent to optimizing over the magnitude. Thus, the “square root” may be omitted from these equations with no expected difference in the results of optimization.)
The critical points of h occur at x = 1 and x = −1, just as in 

Applications[edit]
Control theory[edit]
In optimal control theory, the Lagrange multipliers are interpreted as costate variables, and Lagrange multipliers are reformulated as the minimization of the Hamiltonian, in Pontryagin’s minimum principle.
Nonlinear programming[edit]
The Lagrange multiplier method has several generalizations. In nonlinear programming there are several multiplier rules, e.g. the Carathéodory–John Multiplier Rule and the Convex Multiplier Rule, for inequality constraints.[18]
Power systems[edit]
Methods based on Lagrange multipliers have applications in power systems, e.g. in distributed-energy-resources (DER) placement and load shedding.[19]
See also[edit]
- Adjustment of observations
- Duality
- Gittins index
- Karush–Kuhn–Tucker conditions: generalization of the method of Lagrange multipliers
- Lagrange multipliers on Banach spaces: another generalization of the method of Lagrange multipliers
- Lagrange multiplier test in maximum likelihood estimation
- Lagrangian relaxation
References[edit]
- ^ Hoffmann, Laurence D.; Bradley, Gerald L. (2004). Calculus for Business, Economics, and the Social and Life Sciences (8th ed.). pp. 575–588. ISBN 0-07-242432-X.
- ^ Beavis, Brian; Dobbs, Ian M. (1990). “Static Optimization”. Optimization and Stability Theory for Economic Analysis. New York: Cambridge University Press. p. 40. ISBN 0-521-33605-8.
- ^ Protter, Murray H.; Morrey, Charles B., Jr. (1985). Intermediate Calculus (2nd ed.). New York, NY: Springer. p. 267. ISBN 0-387-96058-9.
- ^ a b c Walsh, G.R. (1975). “Saddle-point Property of Lagrangian Function”. Methods of Optimization. New York, NY: John Wiley & Sons. pp. 39–44. ISBN 0-471-91922-5.
- ^ Kalman, Dan (2009). “Leveling with Lagrange: An alternate view of constrained optimization”. Mathematics Magazine. 82 (3): 186–196. doi:10.1080/0025570X.2009.11953617. JSTOR 27765899. S2CID 121070192.
- ^ a b Silberberg, Eugene; Suen, Wing (2001). The Structure of Economics : A Mathematical Analysis (Third ed.). Boston: Irwin McGraw-Hill. pp. 134–141. ISBN 0-07-234352-4.
- ^ de la Fuente, Angel (2000). Mathematical Methods and Models for Economists. Cambridge: Cambridge University Press. p. 285. doi:10.1017/CBO9780511810756. ISBN 9780521585125.
- ^ Luenberger, David G. (1969). Optimization by Vector Space Methods. New York: John Wiley & Sons. pp. 188–189.
- ^ Bertsekas, Dimitri P. (1999). Nonlinear Programming (Second ed.). Cambridge, MA: Athena Scientific. ISBN 1-886529-00-0.
- ^ Vapnyarskii, I.B. (2001) [1994], “Lagrange multipliers”, Encyclopedia of Mathematics, EMS Press.
- ^ Lasdon, Leon S. (2002) [1970]. Optimization Theory for Large Systems (reprint ed.). Mineola, New York, NY: Dover. ISBN 0-486-41999-1. MR 1888251.
- ^ Hiriart-Urruty, Jean-Baptiste; Lemaréchal, Claude (1993). “Chapter XII: Abstract duality for practitioners”. Convex analysis and minimization algorithms. Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences]. Vol. 306. Berlin, DE: Springer-Verlag. pp. 136–193 (and Bibliographical comments pp. 334–335). ISBN 3-540-56852-2. MR 1295240. Volume II: Advanced theory and bundle methods.
- ^ Lemaréchal, Claude (15–19 May 2000). “Lagrangian relaxation”. In Jünger, Michael; Naddef, Denis (eds.). Computational combinatorial optimization: Papers from the Spring School held in Schloß Dagstuhl. Spring School held in Schloß Dagstuhl, May 15–19, 2000. Lecture Notes in Computer Science. Vol. 2241. Berlin, DE: Springer-Verlag (published 2001). pp. 112–156. doi:10.1007/3-540-45586-8_4. ISBN 3-540-42877-1. MR 1900016. S2CID 9048698.
- ^ Lafontaine, Jacques (2015). An Introduction to Differential Manifolds. Springer. p. 70. ISBN 9783319207353.
- ^ Dixit, Avinash K. (1990). “Shadow Prices”. Optimization in Economic Theory (2nd ed.). New York: Oxford University Press. pp. 40–54. ISBN 0-19-877210-6.
- ^ Chiang, Alpha C. (1984). Fundamental Methods of Mathematical Economics (Third ed.). McGraw-Hill. p. 386. ISBN 0-07-010813-7.
- ^ Heath, Michael T. (2005). Scientific Computing: An introductory survey. McGraw-Hill. p. 203. ISBN 978-0-07-124489-3.
- ^ Pourciau, Bruce H. (1980). “Modern multiplier rules”. American Mathematical Monthly. 87 (6): 433–452. doi:10.2307/2320250. JSTOR 2320250.
- ^
Gautam, Mukesh; Bhusal, Narayan; Benidris, Mohammed (2020). A sensitivity-based approach to adaptive under-frequency load shedding. 2020 IEEE Texas Power and Energy Conference (TPEC). Institute of Electronic and Electrical Engineers. pp. 1–5. doi:10.1109/TPEC48276.2020.9042569.
Further reading[edit]
- Beavis, Brian; Dobbs, Ian M. (1990). “Static Optimization”. Optimization and Stability Theory for Economic Analysis. New York, NY: Cambridge University Press. pp. 32–72. ISBN 0-521-33605-8.
- Bertsekas, Dimitri P. (1982). Constrained optimization and Lagrange multiplier methods. New York, NY: Academic Press. ISBN 0-12-093480-9.
- Beveridge, Gordon S.G.; Schechter, Robert S. (1970). “Lagrangian multipliers”. Optimization: Theory and Practice. New York, NY: McGraw-Hill. pp. 244–259. ISBN 0-07-005128-3.
- Binger, Brian R.; Hoffman, Elizabeth (1998). “Constrained optimization”. Microeconomics with Calculus (2nd ed.). Reading: Addison-Wesley. pp. 56–91. ISBN 0-321-01225-9.
- Carter, Michael (2001). “Equality constraints”. Foundations of Mathematical Economics. Cambridge, MA: MIT Press. pp. 516–549. ISBN 0-262-53192-5.
- Hestenes, Magnus R. (1966). “Minima of functions subject to equality constraints”. Calculus of Variations and Optimal Control Theory. New York, NY: Wiley. pp. 29–34.
- Wylie, C. Ray; Barrett, Louis C. (1995). “The extrema of integrals under constraint”. Advanced Engineering Mathematics (Sixth ed.). New York, NY: McGraw-Hill. pp. 1096–1103. ISBN 0-07-072206-4.
External links[edit]
- Exposition
- Kipid. “Method of Lagrange multipliers” (blog).
- Steuard. “Conceptual introduction”. slimy.com. — plus a brief discussion of Lagrange multipliers in the calculus of variations as used in physics.
- Carpenter, Kenneth H. “Lagrange multipliers for quadratic forms with linear constraints” (PDF). Kansas State University.
- Additional text and interactive applets
- Resnik. “Simple explanation with an example of governments using taxes as Lagrange multipliers”. umiacs.umd.edu. University of Maryland.
- Klein, Dan. “Lagrange multipliers without permanent scarring] Explanation with focus on the intuition” (PDF). nlp.cs.berkeley.edu. University of California, Berkeley.
- Sathyanarayana, Shashi. “Geometric representation of method of Lagrange multipliers”. wolfram.com (Mathematica demonstration). Wolfram Research.
Needs Internet Explorer / Firefox / Safari.
— Provides compelling insight in 2 dimensions that at a minimizing point, the direction of steepest descent must be perpendicular to the tangent of the constraint curve at that point. - “Lagrange multipliers – two variables”. MIT Open Courseware (ocw.mit.edu) (Applet). Massachusetts Institute of Technology.
- “Lagrange multipliers”. MIT Open Courseware (ocw.mit.edu) (video lecture). Mathematics 18-02: Multivariable calculus. Massachusetts Institute of Technology. Fall 2007.
- Bertsekas. “Details on Lagrange multipliers” (PDF). athenasc.com (slides / course lecture). Non-Linear Programming. — Course slides accompanying text on nonlinear optimization
- Wyatt, John (7 April 2004) [19 November 2002]. “Legrange multipliers, constrained optimization, and the maximum entropy principle” (PDF). www-mtl.mit.edu. Elec E & C S / Mech E 6.050 – Information, entropy, and computation. — Geometric idea behind Lagrange multipliers
- “Using Lagrange multipliers in optimization”. matlab.cheme.cmu.edu (MATLAB example). Pittsburgh, PA: Carnegie Mellon University. 24 December 2011.































![{displaystyle {begin{aligned}&{mathcal {L}}(x_{1},x_{2},ldots ;lambda _{1},lambda _{2},ldots ;c_{1},c_{2},ldots )\[4pt]={}&f(x_{1},x_{2},ldots )+lambda _{1}(c_{1}-g_{1}(x_{1},x_{2},ldots ))+lambda _{2}(c_{2}-g_{2}(x_{1},x_{2},dots ))+cdots end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1867ddf9118c757c322a3d5c0c94965c64a65d0a)




![{displaystyle {begin{aligned}{mathcal {L}}(x,y,lambda )&=f(x,y)+lambda cdot g(x,y)\[4pt]&=x+y+lambda (x^{2}+y^{2}-1) ,end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/69623e2b0ffebabe351b9e7ed58a76751601bf66)
![{displaystyle {begin{aligned}nabla _{x,y,lambda }{mathcal {L}}(x,y,lambda )&=left({frac {partial {mathcal {L}}}{partial x}},{frac {partial {mathcal {L}}}{partial y}},{frac {partial {mathcal {L}}}{partial lambda }}right)\[4pt]&=left(1+2lambda x,1+2lambda y,x^{2}+y^{2}-1right) color {gray}{,}end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cdf9c05227cba7a2024d2ef806cf55712c1a3073)

























![{displaystyle {begin{aligned}&{frac {partial {mathcal {L}}}{partial x}}=2x+2xlambda \[5pt]&{frac {partial {mathcal {L}}}{partial lambda }}=x^{2}-1~.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/498e5f0200a9e684456385a4d6b121c2274c2737)
![{displaystyle {begin{aligned}{frac { partial {mathcal {L}} }{partial x}}approx {frac {{mathcal {L}}(x+varepsilon ,lambda )-{mathcal {L}}(x,lambda )}{varepsilon }},\[5pt]{frac { partial {mathcal {L}} }{partial lambda }}approx {frac {{mathcal {L}}(x,lambda +varepsilon )-{mathcal {L}}(x,lambda )}{varepsilon }},end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0de4bda576fdb293b9e0b1f0ebe3f93d57c84f06)
![{displaystyle {begin{aligned}h(x,lambda )&={sqrt {(2x+2xlambda )^{2}+(x^{2}-1)^{2} }}\[4pt]&approx {sqrt {left({frac { {mathcal {L}}(x+varepsilon ,lambda )-{mathcal {L}}(x,lambda ) }{varepsilon }}right)^{2}+left({frac { {mathcal {L}}(x,lambda +varepsilon )-{mathcal {L}}(x,lambda ) }{varepsilon }}right)^{2} }}~.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a19179451d91b7f354ff6326de2c76749c3e9f0f)
