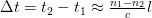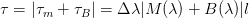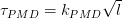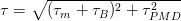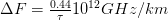Модовая дисперсия как найти

5.1. Определение и виды дисперсии

5.2. Модовая дисперсия

5.3. Хроматическая (частотная) дисперсия

5.3.1. Материальная дисперсия

5.3.2. Волноводная (внутримодовая) дисперсия

5.3.3. Профильная дисперсия

5.4. Поляризационная модовая дисперсия

5.5. Полоса пропускания оптического волокна

5.6. Измерение полосы пропускания и дисперсии оптических волокон

5.1. Определение и виды дисперсии

Наряду с коэффициентом затухания ОВ важнейшим параметром является дисперсия, которая определяет его пропускную способность для передачи информации.

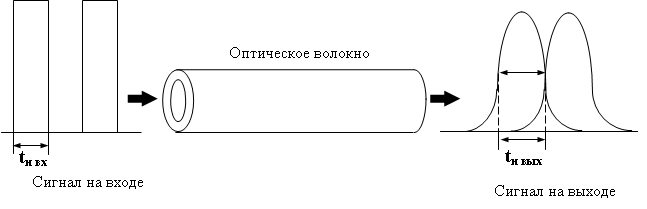
Дисперсия – это рассеяние во времени спектральных или модовых составляющих оптического  сигнала, которое приводит к увеличению длительности импульса оптического излучения при распространении его по ОВ, рисунок 5.1.

Рисунок 5.1 – Искажение формы импульсов вследствие дисперсии

Дисперсия определяется разностью квадратов длительностей импульсов на выходе и входе ОВ

                                      ,                                               (5.1.1)

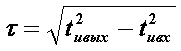
где значения t_ивых и t_ивх  определяются на уровне половины амплитуды импульсов.

Дисперсия не только ограничивает частотный диапазон ОВ, но существенно снижает дальность передачи сигналов, так как чем длиннее линия, тем больше увеличение длительности импульсов.  Она в общем случае определяется тремя основными факторами: различием скоростей распространения направляемых мод, направляющими свойствами оптического волокна и параметрами материала, из которого оно изготовлено. В связи с этим основными причинами возникновения дисперсии являются, с одной стороны, большое число мод в ОВ (модовая или межмодовая дисперсия), а с другой стороны – некогерентность источников излучения, реально работающих в спектре длин волн (Δλ) (хроматическая дисперсия). Модовая дисперсия преобладает в многомодовых ОВ и обусловлена отличием времени прохождения мод по ОВ от его входа до выхода. Механизм появления хроматической дисперсии удобно описать с помощью преобразований Фурье.

Отсутствие искажений при распространении импульсов в одномодовом световоде имеет место, если постоянная распространения b основной моды типа НЕ₁₁ является линейной функцией частоты. Это можно показать следующим образом. Обозначим импульсный сигнал на входе световода g_i(t), его преобразование Фурье G_i(t). Тогда импульс после распространения по световоду на расстояние z будет иметь вид:

                   g₀(t)=  G_i(w) exp [j(wt – b(w)z)]dw .          (5.1.2)

После распространения в световоде длины z каждая спектральная компонента получит фазовое приращение b(w)z. Если допустить (как это имеет место на практике), что спектральная ширина сигнала мала по сравнению с частотой оптической несущей w/2π, то функцию b(w) можно разложить в ряд Тейлора в окрестности центральной частоты спектра импульса w_c:

  b(w)=b(w_c)+½w=w_c (w – w_c) + ½w=w_c (w – w_c)²/ 2 + …   (5.1.3)

Если предположить, что постоянная распространения b(w) есть линейная функция частоты, то ряд Тейлора содержит только два члена и

         g₀(t)=  G_i(w) exp[jw (t – z)]dw = g_i(t – z) .        (5.1.4)

Из (5.1.4) следует, что при линейной зависимости b(w) от частоты сигнал на выходе световода является неискаженным откликом на входной сигнал (имеется лишь задержка сигнала). Постоянные члены опущены, так как они не влияют на форму импульса.

Нелинейности в постоянной распространения, которые ответственны за этот тип искажений, определяются двумя факторами. Первый из них обусловлен тем, что коэффициенты преломления материала сердечника и оболочки являются функциями частоты (материальная дисперсия). Второй фактор проявляется даже тогда, когда материалы сердечника и оболочки имеют коэффициенты преломления, не зависящие от частоты. В данном случае b сохраняет нелинейную зависимость от частоты вследствие волноводного эффекта (волноводная дисперсия). Иногда ее называют геометрической дисперсией, тем самым подчеркивая его зависимость от геометрии световода как направляющей структуры.

В реальных оптических волокнах, которые могут быть регулярными (например, с регулярной, геликоидальной структурой), нерегулярными (например, нерегулярное изменение границы раздела электрических сред) и неоднородными (например, наличие инородных частиц). Помимо перечисленных выше материальной и волновой составляющих дисперсии присутствует также профильная составляющая. К примерам ее возникновения относятся поперечные и продольные малые отклонения (флуктуации) геометрических размеров и формы волокна, например: небольшие эллиптичности  поперечного сечения волокна; изменения границ профиля показателя преломления (ППП); осевые и внеосевые провалы ППП, вызванные особенностями технологии изготовления ОВ [11].

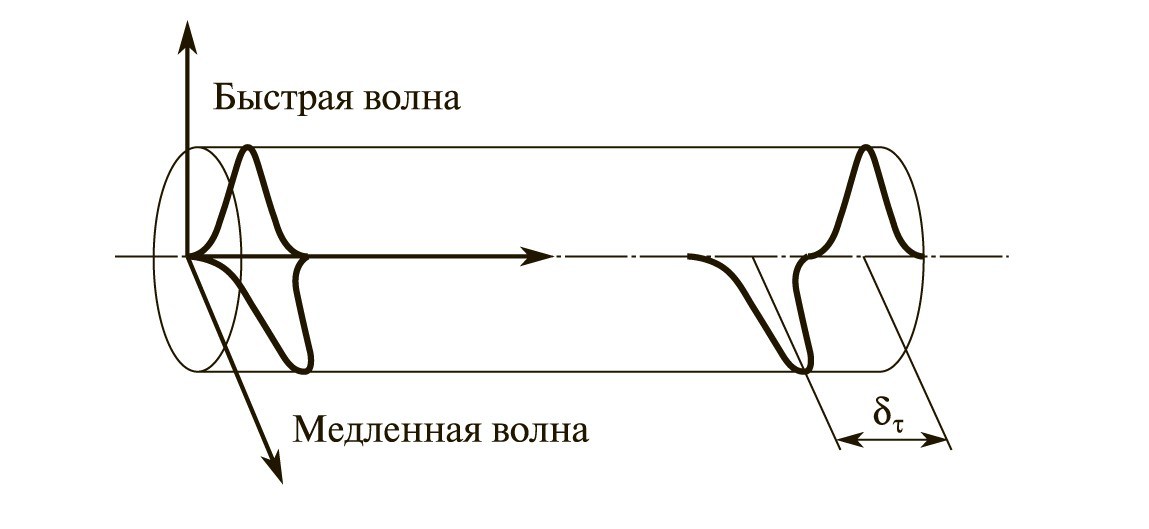
При распространении поляризованной световой волны вдоль оптического волокна при некоторых условиях может наблюдаться ее полная деполяризация. Явление деполяризации усиливается при дифференциальной задержке световых волн, распространяющихся вдоль быстрой и медленной осей волокна. Для оценки дисперсии, возникающей вследствие задержки распространения ортогонально поляризованных световых волн, используется понятие поляризационной модовой дисперсии.

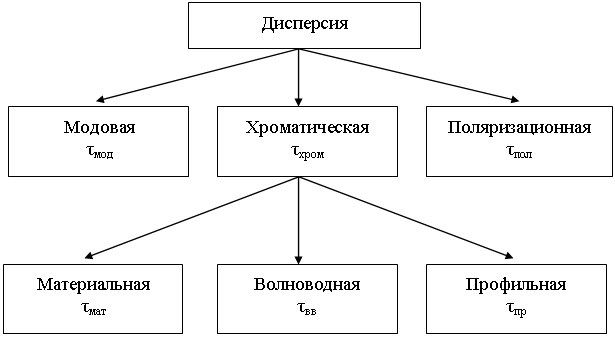
Полная классификация составляющих дисперсии оптического волокна представлена на рисунке 5.2.

Рисунок 5.2 – Классификация составляющих дисперсии оптического волокна

5.2. Модовая дисперсия

Модовая дисперсия свойственна только многомодовым волокнам и обусловлена отличием времени прохождения мод по ОВ от его входа до выхода. Следует раздельно рассматривать процесс возникновения модовой дисперсии в ступенчатых и градиентных волокнах. В ОВ со ступенчатым профилем показателя преломления скорость распространения электромагнитных волн с длиной волны l одинакова и равна:

, (5.2.1)

где с₀ – скорость света в вакууме.

В этом случае все лучи, падающие на торец ОВ под углами к его оси в пределах апертурного угла q_А (Рисунок 2.7), распространяются в сердцевине волокна по своим зигзагообразным линиям и при одинаковой скорости распространения достигают приемного конца в разное время, что естественно, приводит к увеличению длительности принимаемого импульса.

Увеличение длительности импульса из-за модовой дисперсии характеризуется временем нарастания сигнала и определяется как разность между самым большим и самым малым временем прихода лучей в сечение световода на расстоянии L от начала.

Согласно законам геометрической оптики время распространения луча в ступенчатом многомодовом ОВ зависит от угла падения q_п и, как было показано в [10], определяется выражением:

, (5.2.2)

где:

L – длина световода;

n₁ – показатель преломления сердцевины ОВ;

с₀ – скорость света в вакууме.

Так как минимальное время распространения оптического луча имеет место при q_п=0, а максимальное при q_п=q_кр, соответствующие им значения времени распространения можно записать

и , (5.2.3)

откуда значение межмодовой дисперсии равно

. (5.2.4)

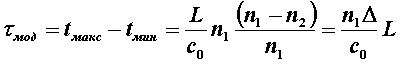
Из последнего выражения следует, что модовая дисперсия возрастает с увеличением длины волокна. Однако это справедливо только для идеального волокна, в котором взаимодействие между модами отсутствует. В реальных условиях наличие неоднородностей, кручение и изгиб волокна приводят к постоянным переходам энергии из одних мод в другие то есть к взаимодействию мод, в связи с чем дисперсия становится пропорциональной . Это влияние проявляется не сразу, а после определенного расстояния прохождения световой волны, которое носит название длины установившейся связи мод и принимается равным L_с=(5¸7) км. Оно установлено эмпирическим путем.

Модовая дисперсия градиентных ОВ, как правило, на порядок и более ниже, чем у ступенчатых волокон. Это обусловлено тем, что за счет уменьшения показателя преломления от оси ОВ к оболочке скорость распространения лучей вдоль их траекторий изменяется. Так, на траекториях, близких к оси, она меньше, а удаленных – естественно, больше. Следовательно, лучи, распространяющиеся кратчайшими траекториями (ближе к оси), обладают меньшей скоростью, а лучи, распространяющиеся по более протяженным траекториям, имеют большую скорость. В результате время распространения лучей выравнивается и увеличение длительности импульса становится меньше. При этом время распространения оптических лучей определяется законом изменения показателя преломления и при определенных условиях выравнивается, что, естественно, влечет к уменьшению дисперсии. Так, при параболическом профиле показателя преломления, когда показатель степени в выражении (2.4.2) принимает значение u=2, модовая дисперсия будет определяться выражением

. (5.2.5)

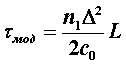
При анализе выражений (5.2.4) и (5.2.5) становится очевидным, что модовая дисперсия градиентного ОВ в 2/D раз меньше, чем у ступенчатого при одинаковых значениях D. А так как обычно D»1%, то модовые дисперсии указанных ОВ могут отличаться на два порядка.

В инженерных расчетах при определении модовой дисперсии следует иметь ввиду, что до определенной длины линии L_с, называемой длиной связи мод, нет межмодовой связи, а затем при L>L_с происходит процесс взаимного преобразования мод и наступает установившийся режим. Поэтому при L<L_с дисперсия увеличивается по линейному закону, а затем, при L>L_с, – по квадратичному закону. Следовательно, вышеприведенные формулы расчета модовой дисперсии справедливы лишь для длины линии L<L_с.

При длинах линии L>L_с следует пользоваться следующими формулами:

где L – длина линии; L_с – длина связи мод (установившегося режима), равная 5-7 км для ступенчатого волокна и 10-15 км – для градиентного. Они устанавливаются эмпирическим путем.

Дисперсионные свойства различных типов ОВ, выпускаемых по рекомендациям ITU-TG.651 и G.652, приведены в таблице 5.1. В ступенчатых световодах при многомодовой передаче доминирует модовая дисперсия и она достигает больших значений (20-50нс/км) [10].

Таблица 5.1 – Дисперсионные свойства различных ОВ

Модовая дисперсия может быть уменьшена следующими тремя способами:

– использованием ОВ с меньшим диаметром сердцевины, поддерживающей меньшее количество мод. Например, сердцевина диаметром 50 мкм поддерживает меньшее число мод, чем сердцевина в 100 мкм;

– использованием волокна со сглаженным ППП, чтобы световые лучи, распространяющиеся по более длинным траекториям, имели большую скорость и достигали противоположного конца волокна в тот же момент времени, что и лучи, распространяющиеся по коротким траекториям;

– использованием одномодового волокна, позволяющего избежать модовой дисперсии.

5.3. Хроматическая (частотная) дисперсия

Данная дисперсия вызвана наличием спектра частот у источника излучения, характером диаграммы направленности и его некогерентностью. Хроматическая дисперсия, в свою очередь, делится на материальную, волноводную и профильную (для реальных волокон).

5.3.1. Материальная дисперсия

Материальная дисперсия, или дисперсия материала, зависит (для прозрачного материала) от частоты w (или длины волны l) и материала ОВ, в качестве которого, как правило, используется кварцевое стекло. Дисперсия определяется электромагнитным взаимодействием волны со связанными электронами материала среды, которое носит, как правило, нелинейный (резонансный) характер и только вдали от резонансов может быть описано с приемлемой точностью, например, уравнением Селлмейера [5]

, (5.3.1)

где w_j – резонансные частоты, R_j – величина j-го резонанса, а суммирование по j для объемного кварцевого стекла ведется по первым трем резонансам.

Возникновение дисперсии в материале световода даже для одномодовых волокон обусловлено тем, что оптический источник, возбуждающий вход (светоизлучающий диод – СИД или лазерный диод -ЛД), формирует световые импульсы, имеющие непрерывный волновой спектр определенной ширины (например, для СИД это примерно 35-60 нм, для многомодовых ЛД (ММЛД) – 2-5 нм, для одномодовых ЛД (ОМЛД) – 0,01-0,02 нм). Различные спектральные компоненты импульса распространяются с разными скоростями и приходят в определенную точку (фазу формирования огибающей импульса) в разное время, приводя к уширению импульса на выходе и, при определенных условиях, к искажению его формы.

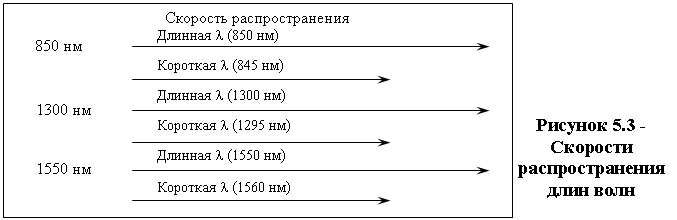
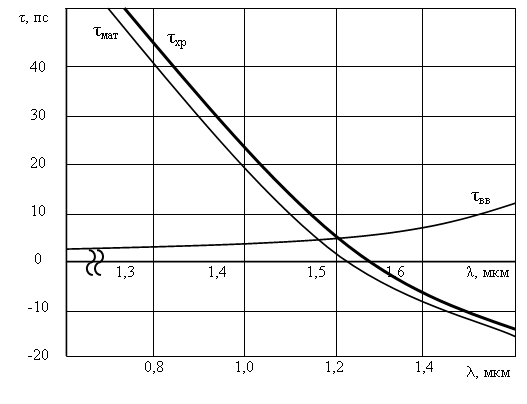
Как видно из уравнения (5.3.1) показатель преломления изменяется от длины волны. При этом уровень дисперсии зависит от диапазона длин волн света, инжектируемого в волокно (как правило, источник излучает несколько длин волн), а также от центральной рабочей длины волны источника. В области 850 нм более длинные волны (более красные) движутся быстрее по сравнению с более короткими (более голубыми) длинами волн. Волны длиной 860 нм распространяются быстрее по стеклянному волокну, чем волны длиной 850 нм. В области 1550 нм ситуация меняется: более короткие волны движутся быстрее по сравнению с более длинными; волна 1560 нм движется медленнее, чем волна 1540 нм, (рисунок 5.3).

Длина стрелок соответствует скорости длин волн, следовательно, более длинная стрелка соответствует более быстрому движению.

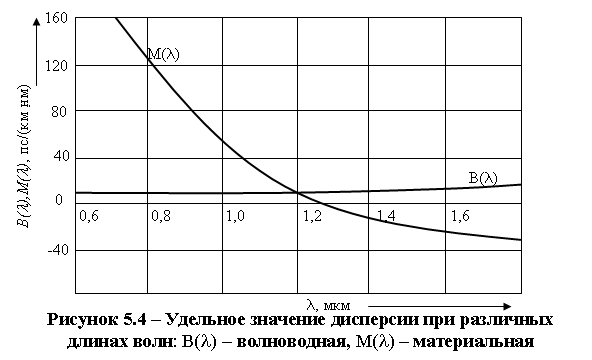
В некоторой точке спектра происходит совпадение, при этом более голубые и более красные длины волн движутся с одной и той же скоростью. Это совпадение скоростей происходит на длине волны примерно 1270 нм, называемой длиной волны с нулевой дисперсией, для объемной среды, рисунок 5.4.

Для оптоволокна эта длина волны сдвигается до порядка 1312 нм, чем и объясняется использование источников излучения 1310 нм для одномодового ОВ. Для одномодового кварцевого волокна дисперсия положительна для λ<1312 нм и отрицательна для λ>1312 нм, а в окрестности λ=1312 нм она нулевая.

Материальную дисперсию можно определить через удельную дисперсию по выражению:

. (5.3.2)

Величина М(λ) определяется экспериментальным путем. При разных составах легирующих примесей в ОВ М(λ) имеет разные значения в зависимости от λ. В таблице 5.2 представлены типичные значения удельной материальной дисперсии.

Таблица 5.2 – Типичные значения удельной материальной дисперсии

При инженерных расчетах для определения можно использовать выражение [10]:

. (5.3.3)

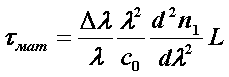
Для определения можно воспользоваться формулой Селмейера для ПП кварцевого стекла с использованием метода конечных разностей, откуда вычисляют величины n(λ-Δλ), n(λ) и n(λ+Δλ), после чего находят [10]:

, (5.3.4)

, (5.3.5)

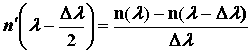
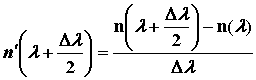
а затем

. (5.3.6)

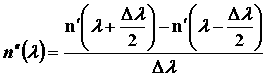
5.3.2. Волноводная (внутримодовая) дисперсия

Волноводная (внутримодовая) дисперсия обусловлена процессами внутри моды. Она характеризуется направляющими свойствами сердцевины ОВ, а именно: зависимостью групповой скорости моды от длины волны оптического излучения, что приводит к различию скоростей распространения частотных составляющих излучаемого спектра. Поэтому внутримодовая дисперсия, в первую очередь, определяется профилем показателя преломления ОВ и пропорциональна ширине спектра излучения источника Δλ, то есть

, (5.3.7)

где В(λ) – удельная внутримодовая дисперсия, значения которой представлены в таблице 5.3.

Таблица 5.3 – Значения удельной волноводной дисперсии.

При отсутствии значений В(λ) оценка характеризуется выражением

, (5.3.8)

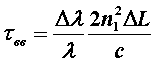
где Δλ – ширина спектральной линии источника излучения, равная 1-3 нм для лазера и 20-40 нм для светоизлучающего диода; L – длина линии, км; с – скорость света, км/с.

Проанализированные выше составляющие хроматической дисперсии суммируются арифметически. В качестве примера на рисунке 5.5 представлены зависимости материальной, волноводной и результирующей дисперсии от длины волны.

Рисунок 5.5 – Зависимость материальной, волноводной и результирующей дисперсии от длины волны

В нормальных условиях рассмотренные составляющие дисперсии могут иметь противоположный знак и различаться характером зависимости от длины волны. В ряде случаев это позволяет оптимизировать профиль показателя преломления волокна путем минимизации суммарной дисперсии на определенной длине волны за счет взаимной компенсации материальной и волноводной дисперсии. Известно, что для кварцевых ОВ минимум затухания соответствует длине волны 1,55 мкм и при больших скоростях передачи дальность связи на этой длине волны может ограничиваться дисперсией, поэтому для ее снижения осуществляется выбор соответствующего профиля показателя преломления ОВ.

Как следует из рисунка 5.5, обычное одномодовое волокно не обеспечивает минимум дисперсии для λ=1,55 мкм, поэтому были разработаны ОВ со смещенной (Dispersion Shifted) или сглаженной (Dispersion Flatterned) дисперсией, которые отличаются конфигурацией профиля показателя преломления. В результате исследований волокон со смещенной дисперсией было показано, что наилучшие показатели обеспечивают волокна с треугольным профилем, так как они обладают самофокусирующими свойствами и удерживают распространяющиеся лучи в небольшом объеме, прилегающем к оси ОВ.

Так как оптические волокна со смещенной дисперсией обеспечивают минимальную дисперсию только на одной длине волны, это затрудняет применение мультиплексирования для работы на нескольких оптических несущих в окне прозрачности ОВ. Поэтому с целью минимизации дисперсии во всем окне прозрачности используют волокна со сглаженной дисперсией, которые также выполняются с различными показателями преломления.

5.3.3. Профильная дисперсия

Данный вид дисперсии проявляется в реальных оптических волокнах, которые могут быть регулярными (например, с регулярной, геликоидальной структурой), нерегулярными (например, нерегулярное изменение границы раздела ППП), неоднородными (например, наличие инородных частиц) [11].

К основным причинам возникновения профильной дисперсии относятся поперечные и продольные малые отклонения (флуктуация) геометрических размеров и формы волокна, например: небольшой эллиптичности поперечного сечения волокна; изменение границы профиля показателя преломления (ППП); осевые и внеосевые провалы ППП, вызванные особенностями технологии изготовления ОВ.

Продольные флуктуации могут возникать в процессе изготовления ОВ и ОК, строительства и эксплуатации ВОЛС. В ряде случаев профильная дисперсия может оказать существенное влияние на общую дисперсию. Профильная дисперсия может появляться как в многомодовых, так и в одномодовых ОВ.

Величина уширения из-за профильной дисперсии может быть оценена по формуле [11]

,

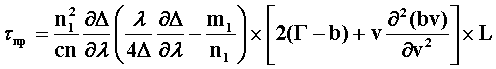
где

n – эффективный показатель преломления [];

b – нормированная постоянная распространения;

m₁ – групповой показатель преломления сердцевины;

Г – коэффициент локализации по мощности;

v – нормированная частота;

с₀ – скорость света;

;

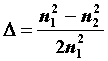
n₁ и n₂ – показатели преломления сердцевины и оболочки;

λ – длина передаваемой волны;

L – длина линии.

Это выражение справедливо для одномодовых волокон при реальной флуктуации границы раздела ППП. При наличии других внешних влияющих факторов ее величина может значительно увеличиваться.

Для инженерных расчетов можно использовать упрощенную формулу

t_пр= П(l) (Dl) L, (5.3.9)

где П(l) – удельная профильная дисперсия (табл. 5.4);

Dl – ширина спектра излучения источника;

L – длина линии.

Удельная профильная дисперсия, выражается в пикосекундах на километр длины световода и на нанометр ширины спектра.

Таблица 5.4. Значения удельной профильной дисперсии

Сравнивая дисперсионные характеристики различных световодов, можно отметить, что лучшими с этой точки зрения являются одномодовые световоды, где присутствует лишь хроматическая дисперсия, величина которой не превышает нескольких пикосекунд в определенном диапазоне длин волн (l=1,2…1,6 мкм).

Из многомодовых световодов лучшие данные по дисперсии у градиентных световодов с плавным параболическим законом изменения показателя преломления, в которых происходит выравнивание времени распространения различных мод и определяющей является материальная дисперсия.

Наиболее сильно дисперсия проявляется у ступенчатых многомодовых световодов, что приводит к уменьшению их использования на цифровых высокоскоростных линиях связи.

Результирующее значение уширения импульсов за счет модовой, материальной, волноводной и профильной дисперсий определяется выражением

. (5.3.10)

5.4. Поляризационная модовая дисперсия

В протяженных ВОЛС, в которых достигается компенсация хроматической дисперсии волокна, основное линейное искажение передаваемого сигнала связано с поляризационной модовой дисперсией (PMD). Она обусловлена дифференциальной групповой задержкой между лучами с основными состояниями поляризации. Более того, распределение энергии сигнала по различным состояниям поляризации медленно изменяется со временем, например, вследствие изменений температуры окружающей среды, что в свою очередь вызывает изменение во времени и требует запаса мощности из-за PMD. Помимо волокна, PMD может возникнуть и в других компонентах, используемых в сети.

В одномодовом волокне распространяется не одна мода, как принято считать, а две перпендикулярные поляризации (моды) исходного сигнала. В идеальном волокне эти две моды распространялись бы с одинаковой скоростью. Однако на практике волокна имеют не идеальную геометрию. Главной причиной поляризационной модовой дисперсии t_пмд является нециркулярность профиля сердцевины одномодового волокна, возникающая в процессе изготовления и эксплуатации волокна. В результате две перпендикулярные поляризационные составляющие имеют разные скорости распространения, что приводит к дисперсии оптического сигнала.

Коэффициент удельной поляризационной модовой дисперсии Т нормируется в расчете на 1 км и имеет размерность (пс/Öкм). Величина поляризационной модовой дисперсии t_пмд рассчитывается по формуле

                                             t_пмд =Т×.                                          (5.4.1)

В системах с N количеством индивидуальных источников PMD общее значение PMD может быть оценено по среднеквадратическому значению:

                               .                      (5.4.2)

В одномодовом волокне поляризационная модовая дисперсия может быть соизмерима с хроматической дисперсией.

Результирующая величина дисперсии в общем случае имеет вид:

     .      (5.4.3)

PMD на любой длине волны сигнала ОМ ОВ не является стабильной, что, естественно, требует проведения статистической оценки и не позволяет осуществить пассивную компенсацию ее влияния. Таким образом, PMD является фундаментальной характеристикой одномодовых волоконно-оптических компонентов, в которых энергия одной длины волны делится на две ортогонально поляризованные моды, распространяющиеся с различной скоростью. Как показали исследования,PMD оказывает весьма существенное влияние на высокоскоростные системы передачи, в связи с чем становится актуальным вопрос ее коррекции на линиях связи.

PMD типового волокна, как правило, составляет от 0,5 до 0,2 пс/.

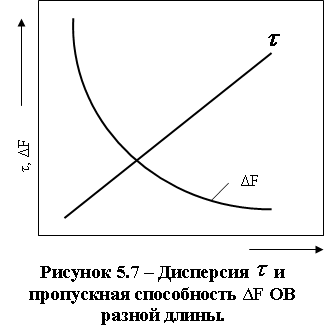
Многие производители волокна и оптического кабеля не используют в спецификации дисперсию в многомодовых изделиях. Вместо этого они указывают произведение ширины полосы пропускания на длину, или просто полосу пропускания, выраженную в мегагерцах на километр. Полоса пропускания в 400 МГц^.км означает возможность передачи сигнала в полосе 400 МГц на расстояние 1 км. Это также означает, что произведение максимальной частоты сигнала на длину передачи может быть меньше или равно 400. Другими словами, можно передавать сигнал более низкой частоты на большее расстояние или более высокой частоты на меньшее расстояние, как показано на рисунке 5.6.

Рабочая полоса частот (полоса пропускания) ОК определяет число передаваемых по нему каналов связи и лимитируется дисперсией ОВ.

На рисунке 5.7 показан характер изменения дисперсии и пропускной способности ΔF ОВ в зависимости от длины линии. Снижение из-за дисперсии величины ΔF до допустимого значения лимитирует дальность передачи по ОК.

Полоса частот ΔF и дальность передачи L взаимосвязаны. Соотношение между ними выражается формулами (для коротких линий в пределах устанавливающегося модового режима) и (для длинных линий). В этих соотношениях параметры с индексом искомые, а без индекса – заданные; L_с – длина связи мод. В реальных условиях обычно нормируется полоса пропускания на один километр ΔF и определяется полоса пропускания на всю линию по формулам [10]:

(5.5.1)

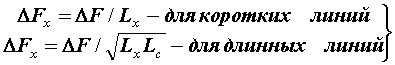
Полоса пропускания ΔF зависит от расширения импульсов и определяется соотношением

5.6. Измерение полосы пропускания и дисперсии оптических волокон

Полоса пропускания (дисперсия) относится к основным параметрам оптических кабелей, определяющим информационно-пропускную способность кабеля. Для измерения полосы пропускания многомодовых кабелей могут быть использованы импульсные и частотные методы.

Импульсный метод. Метод основан на последовательной регистрации импульсов оптического излучения на выходе волокна измеряемого кабеля и на выходе его короткого отрезка, образованного за счет обрыва в начале волокна. Для измерения отбирают отрезки кабеля с известной длиной, прошедшие испытание на оптическую целостность методом обратного рассеяния. Минимальная длина кабеля указывается в стандартах или ТУ на конкретный оптический кабель. Торцовые поверхности оптических волокон измеряемого кабеля должны быть перпендикулярны оси волокна и не иметь сколов и повреждений, препятствующих прохождению оптического излучения.

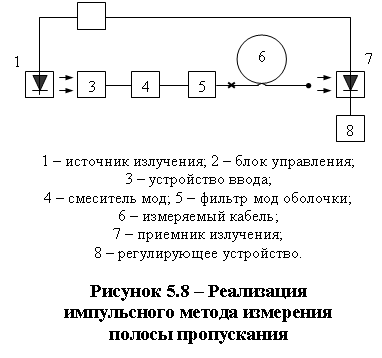
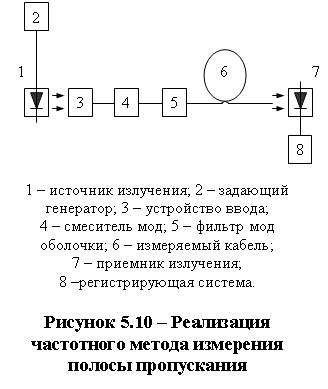
Измерение передаточных характеристик импульсным методом проводят на установке, схема которой указана на рисунке 5.8.

В качестве источника излучения применяют оптические источники типа полупроводникового лазера, светодиода и т.п., позволяющие получить импульсное оптическое излучение с длительностью импульса, обеспечивающей измерение передаточных характеристик конкретного оптического ка-беля. Длина волны и спек-тральная ширина источника излучения должна соответствовать требованиям, установленных в стандартах или ТУ на оптический кабель.

Блок управления должен обеспечивать генерацию электрических импульсов требуемой длительности и мощностью, согласованной с источником излучения, а также вырабатывать импульсы синхронизации с регулируемой задержкой.

Приемник излучения должен обеспечивать регистрацию всего конуса излучения, выходящего из оптического волокна и иметь полосу пропускания, обеспечивающую требуемое временное разрешение импульса источника излучения. Преобразовательная характеристика приемника должна быть линейной. Регистрирующее устройство должно обеспечивать регистрацию сигналов с приемника излучения в соответствующем диапазоне длительностей.

С помощью устройства ввода проводят юстировку входного торца измеряемого волокна по максимуму сигнала на выходе приемника излучения, регистрируют форму импульса на выходе волокна измеряемого кабеля.

Не изменяя положения волокна в устройстве ввода, обламывают отрезок волокна длиной (10,2) м после фильтра мод оболочки.

Подготовленный выходной торец волокна устанавливают относительно приемной площадки так, чтобы на неё попадало всё излучение с выходного торца. Вновь регистрируют форму импульса на выходе короткого отрезка волокна. Зарегистрированную форму импульса принимают за форму импульса на выходе волокна измеряемого кабеля.

Передаточную характеристику в частотном представлении К(jw) определяют по формуле

, (5.6.1)

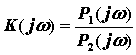
где: Р₁(jw) и Р₂(jw) – спектральная плотность мощности импульса на входе и выходе волокна измеряемого кабеля.

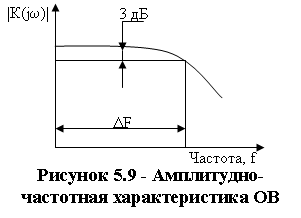
Модуль комплексной функции K(jw) есть амплитудно-частотная модуляционная характеристика измеряемого кабеля.

При этом значение спектральной плотности мощности входного (выходного) импульсов определяют по формуле

(5.6.2)

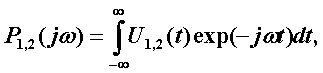
где U_1,2(t) – зарегистрированный импульс на входе (выходе) волокна измеряемого кабеля.

Значение ширины полосы пропускания принимают равной частоте, на которой амплитудно-частотная характеристика изменилась (уменьшилась) на 3 дБ, рисунок 5.9.

Если импульсы на входе и выходе измеряемого кабеля имеют гауссовскую форму, то полосу пропускания определяют на основании измерения длительности импульсов. В этом случае DF_L, МГц, вычисляют по формуле

DF_L=,

где t_ивх, t_ивых – определяемые по уровню 0,5 длительности импульсов на входе и выходе кабеля соответственно, нс.

Поскольку величина t = есть оценка дисперсии кабеля, то импульсный метод и является методом измерения дисперсии.

При необходимости проводят расчет импульсного отклика по формуле

(5.6.3)

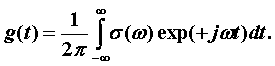
Частотный метод основан на сравнении зависимостей изменения сигнала на выходе волокна измеряемого кабеля и на выходе короткого его отрезка от частоты модуляции оптического сигнала.

Измерение передаточных характеристик частотным методом проводят на установке, схема которой указанна на рисунок 5.10.

В качестве источников излучения применяют оптические источники (светодиоды, полупроводниковые или другие лазеры), обеспечивающие модуляцию оптического излучения в полосе частот, превышающей ширину полосы пропускания измеряемого оптического кабеля. Длина волны и спектральная ширина источника излучения должны соответствовать требованиям, установленным в стандартах или технических условиях на измеряемый оптический кабель.

Задающий генератор должен иметь полосу частот перестройки, превышающую ширину полосы пропускания измеряемого оптичес-кого кабеля.

Приемник излучения должен обеспечивать регистрацию всего конуса, выходящего из оптического волокна излучения, и иметь полосу пропускания, превышающую полосу пропускания измеряемого кабеля. Преобразовательная характеристика приемника должна быть линейной.

Регистрирующее устройство должно обеспечивать регистрацию сигналов с приемника излучения в соответствующем диапазоне частот модуляции источника излучения.

С помощью задающего генератора устанавливают частоту модуляции оптического сигнала. Изменяя частоту модуляции, регистрируются зависимости переменной составляющей сигнала от частоты модуляции. Не изменяя положения волокна в устройстве ввода, обламывают волокно после фильтра мод оболочки, оставляя отрезок волокна длиной (10,2) м. Выходной торец короткого отрезка волокна подготавливают так же, как и в импульсном методе. Подготовленный выходной торец волокна устанавливают относительно приемной площади так, чтобы на нее попадало все излучение с выходного торца. Вновь регистрируют зависимость переменной составляющей сигнала на выходе короткого отрезка волокна от частоты модуляции.

Стоят график отношения значений сигналов переменной составляющей на выходе короткого отрезка и всего кабеля от частоты модуляции, то есть амплитудно-частотную характеристику измеряемого оптического кабеля. Значение ширины полосы пропускания оптического кабеля принимают равной частоте, на которой амплитуда сигнала амплитудно-частотной характеристики уменьшилась на 3 дБ.

Коэффициент широкополосности (К) оптического волокна измеряемого кабеля определяют по формуле

К=, (5.6.4)

где – ширина полосы пропускания измеряемого оптического кабеля, МГц;

L – длина измеряемого кабеля, км;

m – эмпирический параметр, установленный в стандартах или технических условиях на конкретный оптический кабель.

Для одномодовых кабелей нормируется хроматическая дисперсия. В паспортных данных указывается коэффициент хроматической дисперсии, который определяется как уширение оптического импульса на 1,0 км ОВ, отнесенное к полосе длин волн источника излучения.

Для измерения хроматической дисперсии одномодовых кабелей используются метод временной задержки и фазовый метод. Оба метода удовлетворяют требованиям точности и воспроизводимости результатов и одобрены МККТТ. Однако метод временной задержки реализовать сложнее, поскольку из-за того, что значения коэффициента хроматической дисперсии кабелей связи менее 1,5 пс/(нм×км), он требует применения чрезвычайно быстродействующих устройств.

Фазовый метод более прост в реализации, поэтому чаще применяется на практике. Метод основан на измерении фазового сдвига сигнала, модулированного по интенсивности излучения, которым зондируются ОВ кабеля на различных длинах волн. Частота модуляции интенсивности обычно фиксирована и лежит в пределах 30 … 100 МГц. Измерение зависимости фазового сдвига между сигналами от длины волны позволяет найти зависимость временной задержки сигнала от и ее производную – хроматическую дисперсию [23]

. (5.6.5)

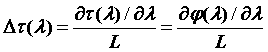
Обычно измерения производят по точкам, а затем полученную зависимость аппроксимируют многочленом. Как правило, все вычисления и сам процесс измерения выполняются автоматически с помощью микропроцессорных устройств, встроенных в средства измерения, или внешней персональной ЭВМ. Точность данного метода порядка 1,0 пс/(нм*км). Переход на лазерное излучение и более высокую частоту модуляции позволяет повысить точность измерения.

Контрольные вопросы 1. Каковы причины возникновения модовой и хроматической дисперсии? 2. Что такое «длина установившейся связи между модами» и какова ее связь с дисперсией? 3. Чем обусловлено уширение импульсных сигналов: а) в многомодовых ВС; б) в градиентных ВС; в) в одномодовых ВС? 4. Дайте определение полосы пропускания и коэффициента широкополосности ВС. 5. Сравните ширину полосы пропускания ВС различных типов. 6. Какое влияние на передачу световых сигналов оказывают значения параметров профиля оптического волокна? 7. Какие способы измерения дисперсии наиболее удобны для строительных длин ОВ? 8. Что из ниже перечисленного является наиболее важным следствием широкой полосы пропускания оптического волокна:

– высокая скорость и информационная емкость линии;

– секретность передачи;

– меньшее число повторителей;

– невосприимчивость по отношению к электромагнитным наводкам;

9. Назовите виды дисперсии. 10. Какие виды дисперсии не существуют в одномодовом волокне? 11. Какие причины уширения оптических импульсов в ОВ? 12. Расчет уширения импульсов с точки зрения геометрической оптики. 13. Какие причины ограничения ширины полосы пропускания оптического волокна?

Дисперсия
– рассеивание во времени спектральных
или модовых составляющих оптического
сигнала. В системах дальней связи в
настоящее время применяется только
одномодовое волокно. В большинстве
городских сетей связи также используется
одномодовое волокно.

Хотя
в одномодовом волокне распространяется
только одна пространственная мода, в
нем все же остаются два источника
расширения световых импульсов:
хроматическая дисперсия и поляризационная
модовая дисперсия (ПМД).

Физическая
природа хроматической дисперсии
коренится в различии групповых скоростей
распространения разных спектральных
компонент светового сигнала. Хроматическая
дисперсия зависит от спектральной
ширины Δλ входного светового импульса

,
(6.10)

где
D
– коэффициент хроматической дисперсии
волокна.

Следовательно,
для уменьшения величины хроматической
дисперсии необходимо использовать
узкополосные источники излучения.

В
свою очередь хроматическая дисперсия
состоит из материальной, волноводной
и профильной дисперсии.

Материальная
дисперсия обусловлена тем, что показатель
преломления сердцевины изменяется с
длиной волны.

_мат=М(),
пс/км , (6.11)

где:
М()
– удельная дисперсия материала,;

 –
ширина спектра источника излучения,
нм (для выбранной СП).

волноводная
дисперсия обусловлена процессами внутри
моды и характеризуется зависимостью
коэффициента распространения моды от
длины волны:

_вол=В(),
пс/км , (6.12)

где:
В()
– волноводная дисперсия,
.

профильная
дисперсия проявляется в реальных ОК и
обусловлена отклонением продольных и
поперечных геометрических размеров и
форм реального ОВ от номинала.

_пр=П(),
пс/км, (6.13)

где:
П()
– удельная профильная дисперсия,
.

для
определения М(),В(),П()
воспользуемся таблицей 6.2.

Таблица
6.2 -Значения М(),В(),П()

Длина волны ,мкм	0,6	0,8	1,0	1,2	1,3	1,4	1,55	1,6	1,8
М(), пс/(кмнм)	400	125	40	10	-5	-5	-18	-20	-25
В(), пс/(кмнм)	5	5	6	7	8	8	12	14	16
П(), пс/(кмнм)	0	1,5	5	2,5	4	5	5,5	6,5	7,5

Результирующая
хроматическая дисперсия:

,
пс/км. (6.14)

В
одномодовых ОВ имеет место только
хроматическая дисперсия, обусловленная
некогерентностью источника излучения.
В многомодовых волокнах
_мод>>_хр.

Модовую дисперсию для градиентного ов можно найти по формуле:

,
нс/км, (6.15)

где:
NA
– числовая апертура ОВ;

n₁
– показатель преломления сердцевины
ОВ;

с
– скорость света, км/с.

Соседние файлы в папке для ргз

• #
• #
• #
• #
• #

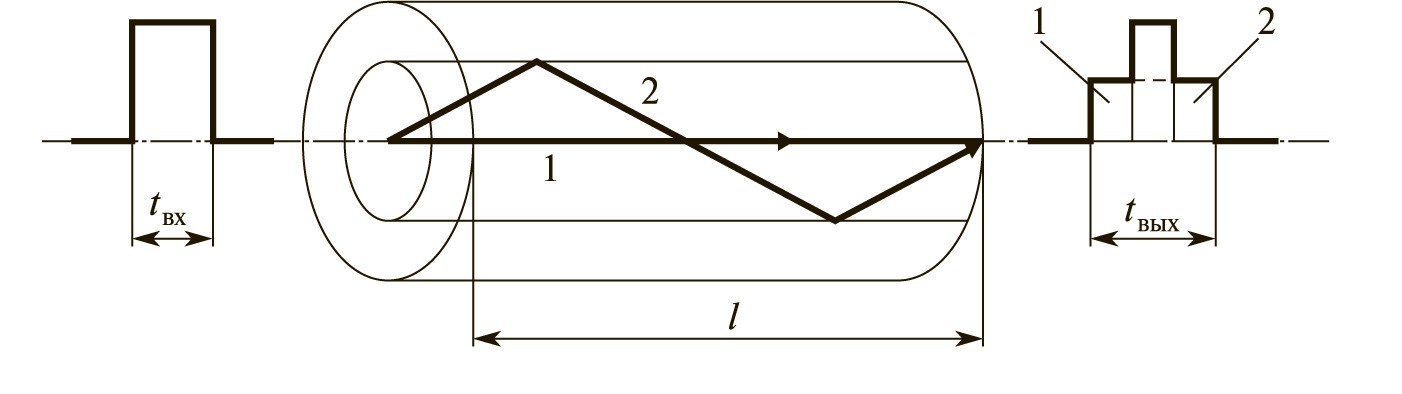
Межмодовая дисперсия – уширение светового импульса при распространении в волокне, связанное с различием времени распространения его компонент (см. рис.1). Межмодовая дисперсия обычно происходит в многомодовом оптоволокне. Когда короткий световой импульс вводится в волокно в пределах числовой апертуры, вся энергия не достигает конца оптоволокна одновременно. Разные моды переносят энергию по разным длинам. Например, многомодовое волокно с сердечником в 50 мкм имеет несколько сотен мод. Это импульс, распространяясь по разным длинам светового пути вызывает межмодовую дисперсию, или более просто, многомодовую дисперсию.

Рис.1 – Ход лучей в оптическом волокне для различных мод

Межмодовая дисперсия преобладает в многомодовых ОВ и обусловлена отличием времени прохождения мод по ОВ от его входа до выхода. Расчетные соотношения для указанной дисперсии наглядно и про­сто получаются при лучевом подходе. Следует раздельно рассматривать процесс возникновения модовой дисперсии в ступенчатых и градиентных волокнах. Уширение импульса, передаваемого по ОВ, за счет модовой дисперсии в этом случае определяется как разность длин пути лучей, распространяющихся по наи­кратчайшей и наидлиннейшей траекториям. Лучи света, введенные в ОВ со ступенчатым профилем под углом к оси (рисунок 1), из-за многократных внутренних отражений на границе сердцевина-оболоч­ка проходят более длинный путь по сравнению с лучами, распространяющимися вдоль оси ОВ.

Отсюда уширение импульса:

где

– максимальное время прохождения лучом, распространяющимся под максимальным к оси волокна углом, расстояния L в волокне,

– минимальное время прохождения лучом, распространяющимся под минимальным углом, расстояния L в волокне,

– показатель преломления сердцевины,

– показатель преломления оболочки волокна,

с – скорость света в вакууме.

Как видно из выражения (1), уширение импульсов тем меньше, чем меньше относительная разность Δ коэффициентов преломления сердцевины и оболочки ОВ. Из этой же формулы следует, что модовая дисперсия возрастает с увеличением длины волокна. Однако последнее справедливо только при отсутствии взаимодействия между модами. В реальных световодах при значительных длинах линии такое предположение ведет к большим погрешностям расчета модовой дисперсии. Связь между модами в реальном ОВ, вызванная неоднородностями показателя преломления, нерегулярностями геометрических размеров, напряжениями изгиба и растяжения, микротрещинами, разъемными и не­разъемными соединениями отрезков ОВ, всегда имеет место и проявляется обменом энергии между модами. При лучевом подходе это эквивалентно изменению углов наклона лучей к оси световода при их распространении вдоль него.

У входного торца световода наблюдается довольно интенсивное излучение мод, и соответственно стабилизируется модовая структура в сердечнике световода. При этом лишь на некотором расстоянии от входного торца световода, называемом длиной установившейся связи между модами (L_у), наступает относительно постоянное (равновесное) распределение мод, не зависящее от условий ввода излучения в световод.

Модовая дисперсия градиентных ОВ, как правило, на порядок и более ниже, чем у ступенчатых волокон. Это обусловлено тем, что за счет уменьшения показателя преломления от оси ОВ к оболочке скорость распространения лучей вдоль их траекторий изменяется. Так, на траекториях, близких к оси, она меньше, а удаленных – естественно, больше. Следовательно, лучи, распространяющиеся кратчайшими траекториями (ближе к оси), обладают меньшей скоростью, а лучи, распространяющиеся по более протяженным траекториям, имеют большую скорость. В результате время распространения лучей выравнивается и увеличение длительности импульса становится меньше. При этом время распространения оптических лучей определяется законом изменения показателя преломления и при определенных условиях выравнивается, что, естественно, влечет к уменьшению дисперсии.

В ступенчатых световодах при многомодовой передаче доминирует модовая дисперсия и она достигает больших значений (20-50нс/км).

Вывод:

Модовая дисперсия может быть уменьшена следующими тремя способами:

– использованием ОВ с меньшим диаметром сердцевины, поддерживающей меньшее количество мод. Например, сердцевина диаметром 50 мкм поддерживает меньшее число мод, чем сердцевина в 100 мкм;

– использованием волокна со сглаженным ППП, чтобы световые лучи, распространяющиеся по более длинным траекториям, имели большую скорость и достигали противоположного конца волокна в тот же момент времени, что и лучи, распространяющиеся по коротким траекториям;

– использованием одномодового волокна, позволяющего избежать модовой дисперсии.

Литература

Технологии и кабельные измерения линий связи. [Электронный реcурc]. – Режим доcтупa: http://izmer-ls.ru – зaгл. c экрaнa (дaтa обрaщения: 20.03.2018).

Лазерный Портал – коллекция научных материалов о лазерах, оптике, спектроскопии и лазерной технике. [Электронный реcурc]. – Режим доcтупa: www.laserportal.ru – зaгл. c экрaнa (дaтa обрaщения: 20.03.2018).

Различают модовую дисперсию, которая обусловлена большим количеством мод в оптических

волокнах

, а также хроматическую дисперсию, связанную с некогерентностью источников излучения, реально работающих в определенном спектре длин волн.

Рассмотрим распространение многомодового светового луча вдоль световода. В данном случае имеется две моды, два луча. Первый распространяется вдоль продольной оси световода, тогда как второй отражается от границ раздела сред. Таким образом путь прохождения второго светового луча будет больше, чем первого. В итоге когда эти два луча, переносящие электромагнитную энергию, складываются вместе, наклонный луч по сравнению с аксиальным лучом имеет временное запаздывание, которое рассчитывается по следующей формуле:

c

– скорость распространения света


l

– длина оптического волокна


n

₁

,

n

₂

– коэффициенты преломления сердечника и оболочки

---

Модовая дисперсия градиентных оптических волокон, как правило, на два порядка ниже, чем у волоконных световодов со ступенчатым профилем показателя преломления. За счет плавного изменения показателя преломления сердечника волоконного световода уменьшается путь прохождения второго луча вдоль волокна. Вследствие чего уменьшается время запаздывания второго луча относительно первого.

В одномодовых оптических волокнах модовая дисперсия отсутствует и увеличение длительности импульса определяется хроматической дисперсией, которая, в свою очередь, подразделяется на материальную и волноводную.

Материальной дисперсией называют явление зависимости абсолютного показателя преломления вещества

n

от длины волны света (

n =ϕ λ()

). Волноводная дисперсия определяется зависимостью коэффициента фазы

β

от частоты (

β=ϕ ω()

).

Уширение импульса за счет хроматической дисперсии рассчитывается по формуле:

τ

_m

– уширение импульса за счет материальной дисперсии, пс;


τ

_B

– уширение импульса за счет волноводной дисперсии, пс;


∆λ

– ширина спектра источника излучения, нм;


М(λ)

– коэффициент удельной материальной дисперсии, пс/нм·км;


В(λ)

– коэффициент удельной волноводной дисперсии, пс/нм·км.

Рассмотрим действие материальной и волноводной дисперсий в одномодовом волокне. Как видно из графика, при увеличении длины волны материальная дисперсия уменьшается, а на длине волны 1,31 мкм становится равна нули. Длина волны в таком случае считается длиной волны нулевой дисперсии. При этом свыше 1,31 мкм дисперсия становится отрицательной. Волноводная дисперсия несмещенных волокон представляет собой относительно небольшую величину и находится в области положительных чисел. При разработке оптических волокон со смещенной дисперсией, в основе которой находится волноводная компонента, пытаются компенсировать материальную дисперсию в длинноволновую область, т.е. к третьему окну прозрачности (λ = 1,55 мкм). Данный сдвиг осуществляется уменьшением диаметра сердцевины, увеличением ∆ и использованием треугольной формы профиля показателя преломления сердцевины.

При распространении поляризованной световой волны вдоль оптического волокна возникает поляризационная дисперсия. Световая волна с точки зрения волновой теории представляет собой постоянно изменяющиеся магнитное и электрическое поля, вектор которых расположен перпендикулярно распространению электромагнитной (световой) волны. Примером световой волны может служить естественный свет, у которого направление электрического вектора изменяется случайным образом. Если излучение монохроматическое и векторы колеблются с некоторой постоянной частотой, то их можно представить в виде суммы двух взаимно перпендикулярных составляющих х и у. Идеальное оптоволокно является изотропной средой, в которой электромагнитные свойства являются одинаковыми во всех направлениях, например показатели преломления. Среда с различными показателями преломления в двух ортогональных осях x и y называется двулучепреломляющей. При этом волокно в данном случае по прежнему остается одномодовым, поскольку две ортогонально поляризованных моды имеют одну и ту же постоянную распространения. Но это справедливо лишь для идеального оптического волокна.

В реальном оптическом волокне две ортогонально поляризованные моды имеют неидентичные постоянные распространения, вследствие чего появляется временная задержка и происходит уширение оптического импульса.

Уширение импульса за счет поляризационной модовой дисперсии (PMD) рассчитывается по формуле:

Таким образом, поляризационная модовая дисперсия проявляется исключительно в одномодовых оптических волокнах с нециркулярной (эллиптической) сердцевиной и при определенных условиях становится соизмеримой с хроматической. Поэтому результирующая дисперсия одномодового оптического волокна определяется следующей формулой:

Дисперсия существенно ограничивает пропускную способность волоконных световодов. Максимальная ширина полосы пропускания на 1 км оптической линии приближенно рассчитывается по формуле:

τ

— уширение импульса, пс/км.

Макеты страниц