движущих
сил
![]()
Так
как работа сил сопротивления 
, то график
![]()
можно построить путем либо численного,
либо графического интегрирования
зависимости
.
Используем численное
интегрирование по методу трапеций,
согласно которому
![]()
где
![]()
— шаг
интегрирования:![]()
=
0,5236 рад
Формула применяется
последовательно от интервала к интервалу:
![]()
![]()
Дж
![]()
![]()
Дж
![]()
![]()
Дж
![]()
![]()
Дж
![]()
![]()
![]()
![]()
![]()
Дж
![]()
![]()
Дж
![]()
![]()
![]()
![]()
Дж
![]()
![]()
![]()
![]()
Дж
![]()
![]()
Дж
Таким образом,
работа сил сопротивления за цикл
![]()
Дж
Принимаем
масштабный коэффициент
![]()
Дж / мм, вычисляем и откладываем ординаты
графика
![]()
![]()
,
Строим
график
.
Результаты вычислений заносим в таблицу
3.2.
Таблица
3.2 — Определение работы сил
сопротивления
|
№ пол. |
|
|
|
0 |
0 |
0 |
|
1 |
16,3 |
0,54 |
|
2 |
282,6 |
9,4 |
|
3 |
825,9 |
27,5 |
|
4 |
1412,2 |
47,1 |
|
5 |
1964,3 |
65,5 |
|
6 |
2241,8 |
74,7 |
|
7 |
2265,7 |
75,5 |
|
8 |
2290,6 |
76,4 |
|
9 |
2360,2 |
78,7 |
|
10 |
2466,2 |
82,2 |
|
11 |
2547 |
84,9 |
|
12 |
2571,9 |
85,7 |
Примечание:
Метод графического дифференцирования
подробно изложен в источниках [1], [8],
[9].
3.3.4 Определение
Так
как работа движущих сил за цикл
![]()
,
то приведенный момент движущих сил
равен:
![]()
Н
∙м
Ордината
графика
= const равна
![]()
мм
3.4 Определение переменной составляющей приведенного момента инерции
Величина
определяется
из равенства кинетической энергии
звена
приведения с моментом
инерции
и
суммы
кинетических
энергий
звеньев с переменными передаточными
функциями. Такими звеньями являются
звенья 3,4 и 5 исполнительного рычажного
механизма. Тогда имеем равенство:
![]()
![]()
где
![]()
;![]()
;
![]()
![]()
.
Здесь
![]()
— момент
инерции звена 3 относительно оси вращения
О2.
![]()
![]()
Масштабный
коэффициент
![]()
![]()
Вычисляем ординаты
графика
![]()
;
Для положения 3
имеем
![]()
![]()
Результаты
определения
![]()
приведены
в табл. 3.3, на основании их построен
график
![]()
.
Таблица
3.3 — Определение переменной
составляющей приведённого момента
инерции
|
№ пол. |
|
b, |
|
|
|
|
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
1 |
0,11516 |
0,00074 |
0,04581 |
0,47386 |
0,63558 |
6,4 |
|
2 |
0,2671 |
0,00082 |
0,11399 |
1,24804 |
1,62995 |
16,3 |
|
3 |
0,35435 |
0,00019 |
0,15567 |
1,72519 |
2,2354 |
22,4 |
|
4 |
0,36619 |
5,9E-05 |
0,15876 |
1,72859 |
2,2536 |
22,5 |
|
5 |
0,30028 |
0,00065 |
0,1267 |
1,3601 |
1,78774 |
17,9 |
|
6 |
0,16407 |
0,0009 |
0,06864 |
0,751 |
0,98462 |
9,8 |
|
7 |
0,0148 |
0,00012 |
0,00626 |
0,0701 |
0,09128 |
0,9 |
|
7’ |
0 |
0 |
0 |
0 |
0 |
0 |
|
8 |
0,14514 |
0,00102 |
0,0611 |
0,67682 |
0,88408 |
8,8 |
|
9 |
1,04805 |
0,00198 |
0,44342 |
4,76397 |
6,25742 |
62,5 |
|
10 |
1,33221 |
0,00082 |
0,58571 |
6,49307 |
8,41181 |
84,1 |
|
11 |
0,32686 |
0,00188 |
0,13231 |
1,39649 |
1,85755 |
18,6 |
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Задача по физике с сопротивлением воздуха
Ученик
(96),
закрыт
12 лет назад
Дополнен 12 лет назад
Мы всегда принебригали сопротивлением воздуха и не обращали на него внимания и я понятия не имел с чем его связать
Дивергент
Высший разум
(1537210)
12 лет назад
А закон сохранения энергии слабо применить? “Не решали” они, видите ли.. .
Eпот=Eкин+Aтр
Атяж=Екин=m*v^2/2=5*15^2/2=562,5 Дж
Eпот=m*g*h=5*9,8*20=980 Дж
Атр=980-562,5=417,5 Дж
Ответ: Атяж=562,5 Дж, Атр=417,5 Дж
Вадим
Высший разум
(465432)
12 лет назад
Потенциальная энергия mgh переходит в кинетическую 1/2mV². Часть энергии расходуется на преодоление сопротивления воздуха. Разница между потенциальной и кинетической и есть работа против силы сопротивления.
jemand
Мастер
(1698)
12 лет назад
Работа силы сопротивления воздуха равна разности энергий мяча в начальной и конечной точке (мяч отдал часть энергии на преодоление силы сопротивления) . В начальной точке мяч имел только пот. энергию, в конечной – только кинет. То есть A тр = m*g*h – m/2*v^2 = 5*9,8*20 – 5/2*15^2 = 417,5 Дж
Работа силы тяжести равна потен. энергии мяча в начальной точке плюс работа сил трения, т. к. силе тяжести нужно преодолевать сопротивление силы трения. А тяж = m*g*h + A тр = 5*9,8*20 + 417,5 = 1357,5 Дж
Это самая обычная задача на закон сохранения энергий. Если ты пишешь “мы такие не решали”, значит ты не умеешь применять закон сохранения энергий и вообще нихрена не шаришь в этой теме
Физика, 10 класс
Урок 13. Работа. Мощность. Энергия. Закон сохранения механической энергии
Перечень вопросов, рассматриваемых на уроке:
1. Работа
2. Мощность
3. Механическая энергия
4. Закон сохранения механической энергии.
Глоссарий по теме
Работа постоянной силы равна произведению модулей силы и перемещения точки приложения силы и косинуса угла между ними.
Мощность – отношение работы к интервалу времени, за который эта работа совершена.
Кинетическая энергия– энергия, которой обладает движущееся тело.
Кинетическая энергия материальной точки – величина равная половине произведения массы материальной точки на квадрат её скорости.
Теорема об изменении кинетической энергии: изменение кинетической энергии материальной точки при её перемещении равно работе, совершённой силой, действующей на точку при этом перемещении.
Если на точку действуют несколько сил, то изменение её кинетической энергии равно алгебраической сумме работ всех сил, действующих на неё.
Работа силы тяжести зависит только от положений начальной и конечной точек траектории и не зависит от формы траектории. При движении тела по замкнутой траектории работа силы тяжести равна нулю.
Консервативными силами называют силы, работа которых не зависит от формы траектории точки приложения силы и по замкнутой траектории равна нулю.
Работа силы упругости при растяжении пружины, т.е. когда направление силы противоположно перемещению тела, меньше нуля. Если начальное и конечное состояния пружины совпадают, то суммарная работа силы упругости при деформации пружины равна нулю.
Потенциальной энергией тела в поле силы тяжести называют величину, равную произведению массы тела на ускорение свободного падения и на высоту тела над поверхностью Земли.
Потенциальной энергией упругодеформированного тела называют величину, равную половине произведения коэффициента упругости тела на квадрат удлинения или сжатия.
Потенциальная энергия – энергия взаимодействия тел, обусловленная их взаимным расположением или взаимным расположением частей тела.
Полная механическая энергия равна сумме кинетической и потенциальной энергий тел, входящих в систему.
Закон сохранения энергии – энергия не создаётся и не уничтожается, а только превращается из одной формы в другую.
Основная и дополнительная литература по теме урока
Мякишев Г.Я., Буховцев Б.Б, Сотский Н.Н. Физика. 10 класс. Учебник для общеобразовательных организаций М.: Просвещение, 2017. С. 131-147.
Рымкевич А.П. Сборник задач по физике. 10-11 класс.-М.:Дрофа,2009. С.49-56.
ЕГЭ 2017. Физика. 1000 задач с ответами и решениями. Демидова М.Ю., Грибов В.А., Гиголо А.И. М.: Экзамен, 2017.
Теоретический материал для самостоятельного изучения
Влияние на тело сил, приводящее к изменению модуля их скорости, характеризуется величиной, которая зависит как от сил, так и от перемещения тел. Эта величина в механике называется работой силы, определяется по формуле:

Эта формула справедлива в случае, когда проекция силы на смещение постоянна.
Если есть угол между силой и смещением, то проекция силы равна произведению силы на косинус этого угла.

В этом случае работа постоянной силы равна произведению модулей силы и смещения точки приложения силы и косинуса угла между ними.
Работа по сравнению с силой и смещением – это не вектор, а скалярная величина. Она может быть, отрицательной равной нулю или положительной. Таким образом, знак работы определяется знаком косинуса угла между силой и перемещением.
Если сила F перпендикулярна перемещению тела, то работа, этой силой равна нулю. Это тот случай, когда действует сила, но тело не двигается.
Если на тело действует несколько сил, проекция результирующей силы на перемещение равна сумме проекций отдельных сил.
Fr = F1r+F2r+…
Поэтому суммарная работа, (алгебраическая сумма работ всех сил), равна работе результирующей силы.
В жизни важно те только совершение работы, но и время, за которое выполняется работа. Работу мы можем делать быстро и медленно. Отношение работы к временному интервалу, за который выполняется эта работа называется мощностью.

Как вы думаете, что необходимо для движения тела? Да, энергия необходима. Энергия характеризует способность тела (или системы тел) совершать работу. Кинетическая энергия – энергия, которой обладает движущееся тело
И энергия может быть кинетической и потенциальной.
Кинетическая энергия материальной точки равна половине массы материальной точки на квадрат её скорости:

Теорема об изменении кинетической энергии: изменение кинетической энергии материальной точки при её перемещении равно работе силы, действующей на точку во время этого перемещении.
Работа силы тяжести не зависит от формы траектории, а зависит только от положений начальной и конечной точек траектории
А = mgh1 – mgh2.
При движении тела по замкнутой траектории работа силы тяжести равна нулю.
Силы, работа которых не зависит от формы траектории точки приложения силы и на замкнутой траектории равна нулю, называют консервативными силами.
Работа при растяжении пружины силы упругости, когда направление силы совпадает с направлением движения тела, принимает положительные значения и определяется по формуле: 
В случае при увеличении деформации пружины, когда сила упругости, действующая на тело со стороны пружины, направлена противоположно деформации, работа силы упругости отрицательна:

Согласно теореме, об изменении кинетической энергии ΔЕк = Ек2 – Ек1 работа силы, действующей на тело, равна изменению его кинетической энергии:

Если силы взаимодействия между телами консервативны, то работу сил можно представить, как разность двух значений некоторой величины, зависящей от взаимного расположения тел или частей одного тела: А = mgh1 – mgh2, работы силы тяжести

и работы силы упругости.
Величина, равная произведению массы m тела на ускорение свободного падения g и высоту h тела над поверхностью Земли, называется потенциальной энергией тела в поле силы тяжести.
Закон сохранения механической энергии:
В изолированной системе, в которой действуют консервативные силы, механическая энергия сохраняется.
Е = Ек + Еп = const

Закон сохранения механической энергии является частным случаем общего закона сохранения энергии: энергия не создаётся и не разрушается, а преобразуется из одной формы в другую.
Примеры и разбор решения заданий
1.

Тело движется вдоль оси ОХ под действием силы F = 2 Н, направленной вдоль этой оси. На рисунке приведён график зависимости проекции скорости vх тела на эту ось от времени t. Какую мощность развивает эта сила в момент времени t = 3 с?
Решение: по графику проекция скорости в момент времени 3с, равна 5 м/с. Мощность, развиваемая силой F для тела, движущегося со скоростью можно найти по формуле

Ответ: 10 Вт
2. Троллейбус массой 15 т трогается с места с ускорением 1,4 м/с2. Найти работу силы тяги и работу силы сопротивления на первых 10 м пути, если коэффициент сопротивления равен 0,05. Каково изменение кинетической энергии автобуса?
Дано:
m = 15т = 15 ·103кг
S = 10м
а = 1,4 м/с2
µ = 0,05
Найти: Ат; Ас; Ек
Запишем уравнение второго закона Ньютона:

в проекции на ось ОХ:
ma = Fт – Fтр
Fтр = µmg → Fт = ma + µmg = m(a+ µg);
По определению работы:

Ат = Fт S = m(a+ µg)S ;
Aт = 15 ·103 кг (1,4 м/с2+0,05 ·10 м/с2) ·10 м = 285 кДж
Работа силы сопротивления: Ас = -FтрS = – µmgS
Ас = -0,05·15·103 кг·10 м/с2·10м = -75 кДж
Кинетическая энергия определяется по формуле:
Ек = mv2/2. Скорость определим по формуле:

Ек = 15·103 кг·14 м/с2 = 210 кДж
Ответ: Ат = 285 кДж; Ас = -75 кДж; Ек = 210 кДж.

Работа силы на конечном пути
Для определения работы силы 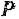 па каком-либо конечном перемещении
па каком-либо конечном перемещении 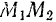 (рис. 208) ее точки приложения разобьем это перемещение на
(рис. 208) ее точки приложения разобьем это перемещение на 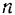 перемещений, каждое из которых в пределе (при
перемещений, каждое из которых в пределе (при 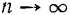 ) переходит в элементарное. Тогда работа
) переходит в элементарное. Тогда работа 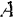 силы
силы 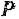 на конечном перемещении
на конечном перемещении 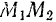 будет равна пределу суммы ее элементарных работ на всех бесконечно малых участках данного перемещения, и пользуясь формулами (187) и (189), получаем для нее следующие выражения:
будет равна пределу суммы ее элементарных работ на всех бесконечно малых участках данного перемещения, и пользуясь формулами (187) и (189), получаем для нее следующие выражения:
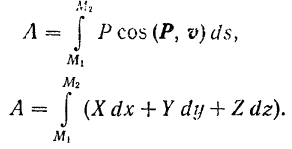
Работа любой силы на любом конечном перемещении ее точки приложения равна взятому вдоль этого перемещения интегралу от элементарной работы.
Пределами интегралов в формулах (190) и (191) являются значения соответствующих переменных интегрирования в точках 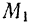 и
и 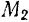 .
.
Если точка 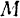 приложения силы перемещается по криволинейной траектории, то интегралы берутся вдоль соответствующей дуги
приложения силы перемещается по криволинейной траектории, то интегралы берутся вдоль соответствующей дуги 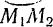 этой траектории, т. е. являются криволинейными интегралами.
этой траектории, т. е. являются криволинейными интегралами.
Если модуль касательной составляющей 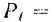
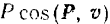 силы есть величина постоянная, то из формулы (190) будем иметь:
силы есть величина постоянная, то из формулы (190) будем иметь:
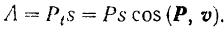
В частности, это всегда имеет место при прямолинейном движении точки под действием постоянной по модулю и направлению силы.
Работа постоянной силы при прямолинейном перемещении ее точки приложения равна произведению модуля силы на длину пути, пройденного ее точкой приложения, и на косинус угла между направлениями силы и перемещения ее точки приложения.
Если направление постоянной силы совпадает с па-правлением перемещения точки ее приложения или прямо противоположно направлению движения последней, то
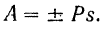
Формула (193) применима не только в случае прямолинейного перемещения точки приложения постоянной силы, но и в случае ее криволинейного движения, если только эта сила все время направлена по касательной к траектории ее точки приложения.
Работа силы имеет, очевидно, следующую размерность:
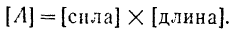
Так как в технической системе единиц сила измеряется в килограммах, а длина — в метрах, то работа в технической системе единиц измеряется в килограммометрах (кГм).
В системе СИ сила измеряется в ньютонах и длина в метрах, поэтому в этой системе за единицу работы принимается работа силы в н на пути, совпадающем с направлением силы, в 1 м. Эта единица работы называется джоулем (дж).
Найдем зависимость между килограммометром и джоулем. Ранее (стр. 242) было найдено, что сила в
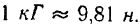
Следовательно,
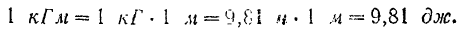
Один килограммометр равен 9,81 джоуля.
Пример задачи:
Тело совершает поступательное прямолинейное движение по закону 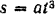 , где
, где 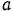 — некоторый постоянный коэффициент. Модуль силы сопротивления среды
— некоторый постоянный коэффициент. Модуль силы сопротивления среды 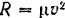 , где
, где 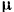 — коэффициент сопротивления среды и
— коэффициент сопротивления среды и 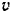 —скорость тела. Какую работу надо затратить на преодоление сопротивления среды при перемещении тела из состояния покоя на расстояние
—скорость тела. Какую работу надо затратить на преодоление сопротивления среды при перемещении тела из состояния покоя на расстояние 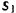 ?
?
Решение:
Тело принимаем за материальную точку 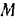 . Прямую, по которой движется эта точка (центр тяжести тела), принимаем за ось
. Прямую, по которой движется эта точка (центр тяжести тела), принимаем за ось 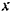 , направив ее в сторону движения топки (рис. 209).
, направив ее в сторону движения топки (рис. 209).
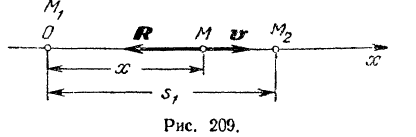
Начало координат будет совпадать с начальным положением 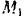 , точки (как видно из закона ее движения: при
, точки (как видно из закона ее движения: при 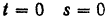 ).
).
Найдем работу силы 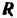 сопротивления среды, воспользовавшись для этого формулой (191):
сопротивления среды, воспользовавшись для этого формулой (191):
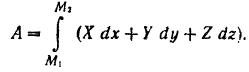
Так как сила 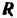 сопротивления среды всегда направлена в сторону, противоположную движению тела, то ее проекциями на координатные оси будут:
сопротивления среды всегда направлена в сторону, противоположную движению тела, то ее проекциями на координатные оси будут:
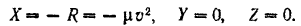
При выбранном направлении оси 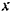 абсцисса точки
абсцисса точки
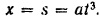
Элементарное приращение этой координаты
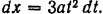
Скорость точки
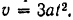
Подставляя найденные выражения в формулу (191), получим
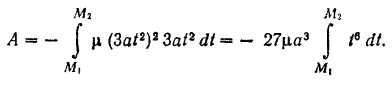
Так как подынтегральное выражение является функцией времени, то пределы интегрирования должны соответствовать значению этой переменной в точках 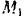 и
и 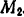 . Положению
. Положению 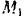 точки соответствует время
точки соответствует время 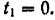 Момент
Момент 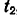 , соответствующий положению
, соответствующий положению 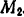 точки, находим из закона ее движения:
точки, находим из закона ее движения:
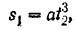
откуда
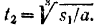
Таким образом, работа силы 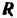 сопротивления среды на данном перемещении тела будет равна
сопротивления среды на данном перемещении тела будет равна
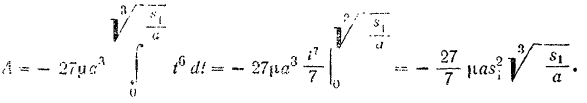
Сила сопротивления среди направлена прогни движения тела потому се работа получилась отрицательной. Чтобы преодолеть эту силу на заданном перемещении тела, надо затратить такую же по величине, но положительную работу.
Эта теория взята с полного курса лекций на странице решения задач с подробными примерами по предмету теоретическая механика:
Теоретическая механика — задачи с решением и примерами
Возможно вам будут полезны эти дополнительные темы:

Парашютист массой 80 килограмм спрыгнул с неподвижно висящего вертолета и, пройдя до раскрытия парашюта путь 200 метров, приобрел скорость 50 метров в секунду.
Найти работу силы сопротивления воздуха на этом пути.
Оцените сложность задачи:
0 голосов, средняя сложность: 0.0000
Решения задачи
Данные задачи: парашютист пролетел не раскрывая парашюта
| Масса парашютиста | m | 80 | кг |
|---|---|---|---|
| Путь парашютиста | S=h | 200 | м |
| скорость парашютиста | $v_{200}$ | 50 | м |
| Работа силы сопротивления воздуха на этом пути. | $W_{сопр}$ | ? |
Составляем уравнение силы тяжести и силы сопротивления воздух
$W=FS=maS=m(g-b)h$
откуда результируещее ускорение от силы тяжести и от силы сопр.воздуха
$a=g-b$
в то же время
$S=(g-b)t^2=200 м$
и
$v_{200}=(g-b)t=50 м/с$
время падения
$t=frac{S}{v_{200}}=frac{200}{50}=4 с$
Ускорение от силы сопротивления воздуха
$b=frac{v_{200}-gt}{t}=frac{50-9,81×4}{4}=2,69frac{м}{с^2}$
Работа силы сопротивления воздуха
$W_сопр=mbS=4×2,69×200=2152 Дж$
Ответ:
$ Работа силы сопр. воздуха равна 2152 Дж. $
Чтобы предложить решение пожалуйста войдите или зарегистрируйтесь
