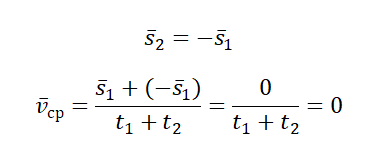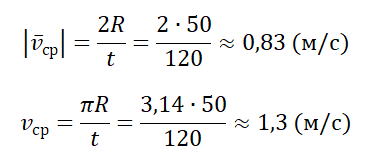Неравномерное прямолинейное движение. Средняя скорость
- График скорости при неравномерном прямолинейном движении
- Как найти путь и перемещение по графику скорости?
- Средняя скорость и средняя путевая скорость
- Задачи
- Лабораторная работа №3. Определение средней скорости движения тела
п.1. График скорости при неравномерном прямолинейном движении
Прямолинейное и равномерное движение возможно лишь на участке пути.
Любое тело со временем меняет свою скорость, как по величине, так и по направлению.
Движение с переменной скоростью называют неравномерным.
Для описания неравномерного движения его можно разбить на участки, на которых скорость постоянна, и свести задачу к уже известному нам равномерному прямолинейному движению.
Например, пусть велосипедист добрался из города A в город B за 1 час. Первые полчаса он ехал со скоростью 9 км/ч, а потом проколол шину, и вторые полчаса шел пешком со скоростью 3 км/ч.
Направим ось ОХ также от A к B и получим значения проекций скоростей: $$ v_{x1}=9 text{км/ч}, v_{x2}=3 text{км/ч} $$ Построим график скорости для этого случая:
Графиком скорости (v_x=v_x(t)) при неравномерном прямолинейном движении, которое можно разбить на участки с постоянной скоростью, является ломаная линия.
п.2. Как найти путь и перемещение по графику скорости?
Мы уже знаем, что путь равен площади прямоугольника, который образуется между отрезком графика скорости и отрезком (triangle t) на оси (t) (см. §8 данного справочника).
В таком случае, путь велосипедиста в нашем примере: begin{gather*} s=v_{x1}cdot triangle t_1+v_{x2}cdot triangle t_2\ s=9cdot 0,5+3cdot 0,5=4,5+1,5=6 text{(км)} end{gather*} Сначала велосипедист проехал 4,5 км, а затем прошел 1,5 км.
begin{gather*} s=v_{x1}cdot triangle t_1+v_{x2}cdot triangle t_2\ s=9cdot 0,5+3cdot 0,5=4,5+1,5=6 text{(км)} end{gather*} Сначала велосипедист проехал 4,5 км, а затем прошел 1,5 км.
Общий путь велосипедиста равен 6 км. Расстояние между городами 6 км. 
Если принять город A за начало отсчета с (x_0=0), то координата велосипедиста в конце пути: $$ x_{к}=x_0+s=0+6=6 text{(км)} $$ Перемещение по оси ОХ: (triangle x=x_{к}-x_0=6 text{(км)}).
Теперь рассмотрим другую ситуацию. Пусть велосипедист выехал из A в B и двигался со скоростью 9 км/ч в течение получаса. Но, после того как проколол шину, он развернулся и пошел пешком назад в A. Где будет находиться велосипедист через полчаса после разворота?
Снова направим ось ОХ от A к B и получим значения проекций скоростей: $$ v_{x1}=9 text{км/ч}, v_{x2}=-3 text{км/ч} $$ Построим график скорости для этого случая:
Путь велосипедиста по-прежнему будет равен сумме площадей прямоугольников, которые образует ломаная (v_x(t)) с осью (t): begin{gather*} x=v_{x1}cdot triangle t_1+|v_{x2}|cdottriangle t_2\ s=9cdot 0,5+3cdot 0,5=4,5+1,5=6 text{(км)} end{gather*} 
Если мы учтем знак (v_{x2}) и уберем модуль, то получим величину перемещения по оси ОХ: begin{gather*} triangle x=v_{x1}cdot triangle t_1+v_{x2}cdot triangle t_2\ triangle x=9cdot 0,5-3cdot 0,5=4,5-1,5=3 text{(км)} end{gather*} Сначала велосипедист проехал 4,5 км, а затем прошел 1,5 км в обратном направлении.
Конечная координата: $$ x_{к}=x_0+triangle x=0+3=3 text{(км)} $$ 
Ответ на вопрос задачи найден. Через полчаса после разворота велосипедист будет находиться в точке D в 3 км от города A.
Пусть неравномерное прямолинейное движение разбито на (n) участков с постоянными скоростями. Каждому такому участку соответствует промежуток времени (triangle t_i) и постоянная скорость (v_{xi}, i=overline{1,n}).
Тогда:
Весь пройденный путь равен сумме площадей прямоугольников на графике скорости: $$ s=|v_{x1}|cdottriangle t_1+|v_{x2}|cdottriangle t_2+…+|v_{xn}|cdottriangle t_n $$ Величина перемещения по оси ОХ равна сумме площадей прямоугольников с учетом знака: $$ triangle x=v_{x1}cdottriangle t_1+v_{x2}cdottriangle t_2+…+v_{xn}cdottriangle t_n $$ Конечная координата равна: (x_{к}=x_0+triangle x).
п.3. Средняя скорость и средняя путевая скорость
Средняя скорость на нескольких участках движения равна отношению общего перемещения к общему времени, затраченному на это перемещение: $$ overrightarrow{v_{cp}}=frac{overrightarrow{r_1}+overrightarrow{r_2}+…+overrightarrow{r_n}}{t_1+t_2+…+t_n}=frac{overrightarrow{r}}{t} $$
Средняя путевая скорость на нескольких участках движения равна отношению общего пути к общему времени, затраченному на этот путь: $$ v_{cp.п}=frac{s_1+s_2+…+s_n}{t_1+t_2+…+t_n}=frac{s}{t} $$
Если тело все время движется в одном направлении, величина средней скорости равна средней путевой скорости, т.к. на каждом участке путь совпадает с модулем перемещения.
Если тело меняет направление движения, величина средней скорости меньше средней путевой скорости.
В нашем примере с велосипедистом, который все время двигался в одну сторону и дошел до города B, получаем: begin{gather*} |overrightarrow{v_{cp}}|=frac{|overrightarrow{r}|}{t}=frac{triangle x}{t}=frac 61=6 text{(км/ч)}\ v_{cp.п}=frac st=frac 61=6 text{(км/ч)} end{gather*} Величина средней скорости равна средней путевой скорости.
А вот для случая, когда велосипедист развернулся и пошел обратно: begin{gather*} |overrightarrow{v_{cp}}|=frac{|overrightarrow{r}|}{t}=frac{triangle x}{t}=frac 31=3 text{(км/ч)}\ v_{cp.п}=frac st=frac 61=6 text{(км/ч)} end{gather*} Величина средней скорости меньше средней путевой скорости.
п.4. Задачи
Задача 1. По графику скоростей найдите среднюю скорость и среднюю путевую скорость движения.
a)
Все движение можно разделить на три участка с постоянной скоростью:
begin{gather*} triangle t_1=3-0=3 c, v_{x1}=5 text{м/с}\ triangle t_2=5-3=2 c, v_{x2}=1 text{м/с}\ triangle t_3=7-5=2 c, v_{x3}=2 text{м/с}\ end{gather*} Общий путь: begin{gather*} s=|v_{x1}|cdot triangle t_1+|v_{x2}|cdot triangle t_2+|v_{x3}|cdot triangle t_3\ s=5cdot 3+1cdot 2+2cdot 2=21 text{(м)} end{gather*} Все проекции скоростей положительны, тело двигалось в одном направлении, общее перемещение равно общему пути: (triangle x=s=21) (м)
Общее время: (t=triangle t_1+triangle t_2+triangle t_3=3+2+2=7) (с)
Величина средней скорости равна средней путевой скорости: $$ |overrightarrow{v_{cp}}|=v_{cp.п}=frac st=frac{21}{7}=3 text{(м/с)} $$ Ответ: (|overrightarrow{v_{cp}}|=v_{cp.п}=3 text{(м/с)})
б) 
Все движение можно разделить на три участка с постоянной скоростью:
begin{gather*} triangle t_1=3-0=3 c, v_{x1}=5 text{м/с}\ triangle t_2=5-3=2 c, v_{x2}=-2 text{м/с}\ triangle t_3=7-5=2 c, v_{x3}=1 text{м/с}\ end{gather*} Общий путь: begin{gather*} s=|v_{x1}|cdot triangle t_1+|v_{x2}|cdot triangle t_2+|v_{x3}|cdot triangle t_3\ s=5cdot 3+2cdot 2+1cdot 2=21 text{(м)} end{gather*} Проекции скоростей имеют разные знаки, тело двигалось вперед и назад.
Общее перемещение будет меньше общего пути: begin{gather*} triangle x=v_{x1}cdot triangle t_1+v_{x2}cdot triangle t_2+v_{x3}cdot triangle t_3\ triangle x=5cdot 3-2cdot 2+1cdot 2=13 text{(м)} end{gather*} Общее время: (t=triangle t_1+triangle t_2+triangle t_3=3+2+2=7) (c)
Величина средней скорости: $$ |overrightarrow{v_{cp}}|=frac{triangle x}{t}=frac{13}{7}approx 1,86 text{(м/с)} $$ Средняя путевая скорость: $$ v_{cp.п}=frac st=frac{21}{7}=3 text{(м/с)} $$ Ответ: (|overrightarrow{v_{cp}}|approx 1,86 text{(м/с)}; v_{cp.п}=3 text{(м/с)})
Задача 2. Мотоциклист проехал расстояние между двумя пунктами со скоростью 40 км/ч. Потом увеличил скорость до 80 км/ч и проехал расстояние в два раза меньше. Найдите среднюю скорость мотоциклиста за все время движения.
Мотоциклист двигался все время в одном направлении, величина средней скорости равна средней путевой скорости: (v_{cp}=frac st), где (s) – весь путь, (t) – все время.
Заполним таблицу:
| Скорость, км/ч | Время, ч | Расстояние, км | |
| 1й участок | 40 | (frac{2d}{40}=frac{d}{20}) | (2d) |
| 2й участок | 80 | (frac{d}{80}) | (d) |
| Сумма | – | (t=frac{d}{20}+frac{d}{80}) | (s=2d+d=3d) |
Упростим сумму дробей: $$ t=frac{d}{20}+frac{d}{80}=frac{4d+d}{80}=frac{5d}{80}=frac{d}{16} $$ Получаем: $$ v_{cp}=frac st=frac{3d}{d/16}=3cdot 16=48 text{(км/ч)} $$
Ответ: 48 км/ч
Задача 3. Автомобиль проехал первую половину пути по шоссе со скоростью 90 км/ч, а вторую половину – по грунтовой дороге со скоростью 30 км/ч. Найдите среднюю скорость автомобиля.
Величина средней скорости равна средней путевой скорости:
(v_{cp}=frac st), где (s) – весь путь, (t) – все время.
Заполним таблицу:
| Скорость, км/ч | Время, ч | Расстояние, км | |
| 1й участок | 90 | (frac{s}{2cdot 90}=frac{s}{180}) | (frac s2) |
| 2й участок | 30 | (frac{s}{2cdot 30}=frac{s}{60}) | (frac s2) |
| Сумма | – | (t=frac{s}{180}+frac{s}{60}) | (s) |
Упростим сумму дробей: $$ t=frac{s}{180}+frac{s}{60}=frac{s+3s}{180}=frac{4s}{180}=frac{s}{45} $$ Получаем: $$ v_{cp}=frac st=frac{s}{s/45}=45 text{(км/ч)} $$
Ответ: 45 км/ч
Задача 4*. Туристы прошли по маршруту со средней скоростью 32 км/ч. Маршрут был разделен на три участка, первый участок преодолевался пешком, второй – на автобусе, третий – на катере. Найдите скорость на каждом участке, если длины этих участков относятся как 1:4:45, а соответствующие интервалы времени как 4:1:20.
Величина средней скорости равна средней путевой скорости:
(v_{cp}=frac st), где (s) – весь путь, (t) – все время.
Заполним таблицу:
| Скорость, км/ч | Время, ч | Расстояние, км | |
| 1й участок | (frac{d}{4t}) | (4t) | (d) |
| 2й участок | (frac{4d}{t}) | (t) | (4d) |
| 3й участок | (frac{45d}{20t}) | (20t) | (45d) |
| Сумма | – | (25t) | (50d) |
По условию средняя скорость: $$ v_{cp}=frac st=frac{50d}{25t}=2cdot frac dt=32Rightarrow frac dt=16 $$ Получаем: begin{gather*} v_1=frac{d}{4t}=frac{16}{4}=4 text{(км/ч)}\ v_2=frac{4d}{t}=4cdot 16=64 text{(км/ч)}\ v_3=frac{9d}{4t}=frac{9}{4}cdot 16=36 text{(км/ч)} end{gather*}
Ответ: 4 км/ч, 64 км/ч и 36 км/ч
Задача 5*. Первую половину маршрута турист проехал на попутном автомобиле в 10 раз быстрее по сравнению с ходьбой пешком, а вторую половину – на попутном возу в 2 раза медленней. Сэкономил ли турист время на всем маршруте по сравнению с ходьбой пешком?
Пусть (v) – скорость туриста при ходьбе пешком.
Найдем среднюю путевую скорость (v_{cp}) и сравним ее со скоростью (v).
Если (v_{cp}gt v), то турист выиграл время.
Заполним таблицу:
| Скорость, км/ч | Время, ч | Расстояние, км | |
| 1й участок | (10v) | (frac{s}{2cdot 10v}=frac{s}{20v}) | (frac s2) |
| 2й участок | (frac{v}{2}) | (frac{s}{2cdot v/2}=frac sv) | (frac s2) |
| Сумма | – | (t=frac{s}{20v}+frac sv) | (s) |
Упростим сумму дробей: $$ t=frac{s}{20v}+frac sv=frac svleft(frac{1}{20}+1right)=frac{21}{20}cdot frac sv $$ Средняя скорость: $$ v_{cp}=frac{s}{frac{21}{20}cdotfrac sv}=frac{20}{21}vgt v $$Средняя скорость поездки оказалась меньше пешей скорости туриста.
Значит, он не выиграл по времени.
Ответ: нет
п.5. Лабораторная работа №3. Определение средней скорости движения тела
Цель работы
Научиться определять среднюю скорость движения тела по данным измерений на разных участках. Научиться вычислять абсолютные и относительные погрешности при подстановке данных измерений в формулы.
Теоретические сведения
В лабораторной работе изучается движение тела (шарика) по двум участкам (желобам) с различной скоростью.
Величина средней скорости при движении на двух участках определяется как средняя путевая скорость: $$ v_{cp}=frac{s_1+s_2}{t_1+t_2} $$ где (s_1) и (s_2) – длина первого и второго участка; (t_1) и (t_2) – время движения по каждому из участков.
Длина участков измеряется с помощью мерной ленты с ценой деления (triangle=1) см,
инструментальная погрешность равна: (d=frac{triangle}{2}=0,5) см
Абсолютная погрешность измерений при работе с мерной лентой равна инструментальной погрешности, поэтому: (triangle s_1=triangle s_2=d=0,5) см
Погрешность суммы двух длин: (triangle(s_1+s_2)= triangle s_1+triangle s_2=2d=1) см
Измерение времени на каждом участке проводится в сериях их 5 измерений по методике, описанной в Лабораторной работе №2 (см. §4 данного справочника).
Погрешность суммы двух измерений: (triangle(t_1+t_2)=triangle t_1+triangle t_2)
Относительная погрешность частного равна сумме относительных погрешностей делимого и делителя: $$ delta_{v_{cp}}=delta_{s_1+s_2}+delta_{t_1+t_2} $$ Абсолютная погрешность определения средней скорости: $$ triangle v_{cp}=v_{cp}cdot delta_{v_{cp}} $$
Приборы и материалы
Два желоба (не менее 1 м каждый), шарик, мерная лента, секундомер.
Ход работы
1. Ознакомьтесь с теоретической частью работы, выпишите необходимые формулы.
2. Соберите установку, как показано на рисунке. Установите один желоб под углом, другой – горизонтально, закрепите, поставьте в конце горизонтального участка упор. Подберите длину желобов и наклон так, чтобы движение по каждому участку было не менее 1 с. 
3. Измерьте фактическую длину каждого участка движения в готовой установке с помощью мерной ленты.
4. Найдите относительную погрешность суммы двух длин (delta_{s_1+s_2}=frac{triangle(s_1+s_2)}{s_1+s_2})
5. Проведите серии по 5 экспериментов для определения (t_1) и (t_2) с помощью секундомера.
6. Найдите (triangle t_1, triangle t_2, triangle(t_1+t_2), delta_{t_1+t_2})
7. По результатам измерений и вычислений найдите (v_{cp}, delta_{v_{cp}}) и (triangle v_{cp}).
8. Сделайте выводы о проделанной работе.
Результаты измерений и вычислений
1) Измерение длин
Цена деления мерной ленты (triangle =1) см
Инструментальная погрешность мерной ленты (d=frac{triangle}{2}=0,5) см
Результаты измерений:
(s_1=112) cм
(s_2=208) cм
Сумма длин участков: (s_1+s_2=112+208=320) (см)
Абсолютная погрешность суммы: (triangle (s_1+s_2)=triangle s_1+triangle s_2=2d=1) см
Относительная погрешность суммы: $$ delta_{s_1+s_2}=frac{triangle (s_1+s_2)}{s_1+s_2}=frac{1}{320}=0,3125% $$
2) Измерение времени
Цена деления секундомера (triangle =0,2) с
Инструментальная погрешность секундомера (d=frac{triangle}{2}=0,1) с
Время движения по наклонному желобу
| № опыта | 1 | 2 | 3 | 4 | 5 | Сумма |
| (t_1) c | 1,5 | 1,6 | 1,5 | 1,4 | 1,4 | 7,4 |
| (triangle) c | 0,02 | 0,12 | 0,02 | 0,08 | 0,08 | 0,32 |
Найдем среднее время спуска с наклонного желоба: $$ t_1=frac{1,5+1,6+1,5+1,4+1,4}{5}=frac{7,4}{5}=1,48 (c) $$ Принимаем среднее время за истинное значение измеряемой величины.
Найдем абсолютные отклонения каждого измерения от (t_1): $$ triangle_1=|1,5-1,48|=0,02; triangle_2=|1,6-1,48|=1,02 text{и т.д.} $$ Среднее абсолютное отклонение: $$ triangle_{cp}=frac{0,02+0,12+0,02+0,08+0,08}{5}=frac{0,32}{5}=0,064 text{c} $$ Среднее абсолютное отклонение меньше инструментальной погрешности, поэтому абсолютная погрешность измерений: $$ triangle t_1=maxleft{d;triangle_{cp}right}=maxleft{0,1;0,064right}=0,1 text{c} $$ Округляем полученное значение времени до десятых. begin{gather*} t_1=(1,5pm 0,1) text{c}\ delta_{t_1}=frac{0,1}{1,5}=frac{1}{15}approx 6,7text{%} end{gather*} Время движения по горизонтальному желобу
| № опыта | 1 | 2 | 3 | 4 | 5 | Сумма |
| (t_2) c | 2,3 | 2,4 | 2,2 | 2,2 | 2,4 | 11,5 |
| (triangle) c | 0 | 0,1 | 0,1 | 0,1 | 0,1 | 0,4 |
Найдем среднее время движения по горизонтали: $$ t_2=frac{2,3+2,4+2,2+2,2+2,4}{5}=frac{11,5}{5}=2,3 (c) $$ Принимаем среднее время за истинное значение измеряемой величины.
Найдем абсолютные отклонения каждого измерения от (t_2): $$ triangle_1=|2,3-2,3|=0; triangle_2=|2,4-2,3|=0,1 text{и т.д.} $$ Среднее абсолютное отклонение: $$ triangle_{cp}=frac{0+0,1+0,1+0,1+0,1}{5}=frac{0,4}{5}=0,08 text{c} $$ Среднее абсолютное отклонение меньше инструментальной погрешности, поэтому абсолютная погрешность измерений: $$ triangle t_2=maxleft{d;triangle_{cp}right}=maxleft{0,1;0,08right}=0,1 text{c} $$ Получаем: begin{gather*} t_2=(2,3pm 0,1) text{c}\ delta_{t_2}=frac{0,1}{2,3}=frac{1}{23}approx 4,4text{%} end{gather*}
3) Расчет погрешности суммы интервалов времени
Сумма интервалов времени: $$ t_1+t_2=1,5+2,3=3,8 text{(c)} $$ Абсолютная погрешность суммы: $$ triangle(t_1+t_2)=triangle t_1+triangle t_2=0,1+0,1=0,2 text{(c)} $$ Относительная погрешность суммы: $$ delta_{t_1+t_2}=frac{triangle (t_1+t_2)}{t_1+t_2}=frac{0,2}{3,8}=frac{1}{19}approx 5,3text{%} $$
4) Расчет средней скорости $$ v_{cp}=frac{s_1+s_2}{t_1+t_2}=frac{320}{3,8}approx 84,2 left(frac{text{см}}{text{c}}right) $$ Относительная ошибка частного: $$ delta_{v_{cp}}=delta_{s_1+s_2}+delta_{t_1+t_2}=frac{1}{320}+frac{1}{19}approx 0,003125+0,0526approx 0,0557approx 0,056=5,6text{%} $$ (оставляем две значащие цифры).
Абсолютная ошибка: $$ v_{cp}=v_{cp}cdotdelta_{v_{cp}}=84,2cdot 0,056approx 4,7 left(frac{text{см}}{text{c}}right) $$ Получаем: begin{gather*} v_{cp}=(84,2pm 4,7) text{см/с}\ delta_{v_{cp}}=5,6text{%} end{gather*}
Выводы
На основании проделанной работы можно сделать следующие выводы.
Измерения длин проводились с помощью мерной ленты. Ошибка измерений равна инструментальной ошибке 0,5 см.
Измерения времени проводились с помощью секундомера. По результатам серий экспериментов ошибка была принята равной инструментальной 0,1 с.
Получена величина средней скорости: begin{gather*} v_{cp}=(84,2pm 4,7) text{см/с}\ delta_{v_{cp}}=5,6text{%} end{gather*}
Физическое понятие «скорость» является неоднозначным термином: зависимость от расстояния и времени позволяет ввести два понятия скорости, так как в физике используются векторные (перемещение) и скалярные (модуль перемещения, пройденный путь, время) величины.
1. Отношение вектора перемещения (vec{S}) к интервалу времени (Delta{t}) определяет среднюю (по времени) скорость:
(vec{v}_{ср}=frac{vec{S}}{Delta{t}}) ((1)).
-
Направление вектора средней (по времени) скорости определяется согласно математической формуле ((1)) определения данной физической величины (сравни математическое выражение (vec{a}) (=) (frac{vec{b}}{2}) и формулу ((1))):
Длина вектора (vec{v}_{ср}) не связана с длиной вектора (vec{S}), так как данные физические величины имеют разные размерности (единицы измерения).
-
Числовое значение данной физической величины в случае равномерного прямолинейного движения является постоянным (рис. (1)):
υx=const
.
Примечание: «const» — «постоянный» (сокращение от латинского).
Рис. (1). Изменение координаты точки при равномерном движении
2. При движении тела с постоянной скоростью и его возврате в исходное положение с той же скоростью значение средней (по времени) скорости будет равно нулю.
Отношение пути (l) (длины траектории) к интервалу времени (Delta{t}) определяет средний модуль скорости (среднюю путевую скорость):
(overline{v}=frac{l}{Delta{t}}) ((2)).
Обозначение: черта над символом ((overline{v})) обозначает среднее значение этой величины.
Именно физическое понятие «средняя путевая скорость» используется при описании движения в ситуациях следующего типа: «спортсмен/турист… пробежал/прошёл… дистанцию/расстояние… со средней скоростью <…> м/с».
Источники:
Рис. 1. Изменение координаты точки при равномерном движении. © ЯКласс.
-
Радиус-вектор, путь перемещения материальной точки
Радиус-вектор
![]()
точки
Μ
— направленный отрезок прямой, соединяющий
начало отсчета О
с точкой Μ
(рис.
2).

Путь
s
— скалярная физическая величина,
определяемая длиной траектории, описанной
телом за некоторый промежуток времени.
Путь всегда положителен: s
> 0.
Перемещение
![]()
тела
за определенный промежуток времени —
направленный отрезок прямой, соединяющий
начальное (точка M0)
и конечное (точка М)
положение тела (см. рис. 2):
![]()
где
и
![]()
—
радиусы-векторы тела в эти моменты
времени.
Проекция
перемещения на ось Ox:
![]()
,
где x0
и x
— координаты тела в начальный и конечный
моменты времени.
Модуль
перемещения не может быть больше пути:
![]()
.
Знак
равенства относится к случаю прямолинейного
движения, если направление движения не
изменяется.
Зная
перемещение и начальное положение тела,
можно найти его положение в момент
времени t:
![]()
![]()
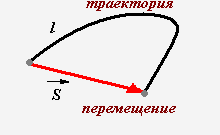
Траектория
– линия, вдоль которой движется тело.
Путь
– длина траектории.
Перемещение
– вектор, соединяющий начальное и конечное
положения тела.
Положение
тела в пространстве задается радиус
– вектором
или тремя его проекциями
на оси
координат.

![]()
Следовательно
закон движения – это зависимость
радиус-вектора от времени или зависимость
координат во времени.
где
![]()
-радиус-вектор,
x,
y,
z
–
координаты тела.
6. Средняя путевая и средняя скорость перемещения. Мгновенная линейная скорость.
Средняя
(путевая) скорость —
это отношение длины пути,
пройденного телом, ко времени,
за которое этот путь был пройден:
![]()
Средняя
путевая скорость, в отличие от мгновенной
скорости
не является векторной величиной.
Средняя
скорость равна среднему
арифметическому
от скоростей тела во время движения
только в том случае, когда тело двигалось
с этими скоростями одинаковые промежутки
времени.
В
то же время если, например, половину
пути автомобиль двигался со скоростью
180 км/ч, а вторую половину со скоростью
20 км/ч, то средняя скорость будет 36 км/ч.
В примерах, подобных этому, средняя
скорость равна среднему
гармоническому
всех скоростей на отдельных, равных
между собой, участках пути.
Средняя
скорость по перемещению
Можно
также ввести среднюю
скорость по перемещению,
которая будет вектором,
равным отношению перемещения
ко времени, за которое оно совершено:
![]()
Средняя
скорость, определённая таким образом,
может равняться нулю даже в том случае,
если точка (тело) реально двигалась (но
в конце промежутка времени вернулась
в исходное положение).
Если
перемещение происходило по прямой
(причём в одном направлении), то средняя
путевая скорость равна модулю средней
скорости по перемещению.
Мгновенная
скорость
– предел средней скорости за бесконечно
малый промежуток времени. Мгновенная
скорость направлена по касательной к
траектории движения в данной точке
траектории.
Средняя
скорость
перемещения
равна отношению полного перемещения к
промежутку времени, за которое это
перемещение совершено.
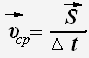
где![]()
ср
-средняя
скорость перемещения,
![]()
–
перемещение, ∆
t
– интервал
времени.
Средняя
путевая скорость
равна отношению полного пути к промежутку
времени, за который этот путь пройден.

где
υср
– средняя путевая скорость ,
l
–
путь.
Мгновенная
скорость
– скорость в заданный момент времени.
![]()
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Неравномерное движение — движение с переменной скоростью, которая может менять как направление, так и модуль.
Неравномерное движение можно охарактеризовать средней скоростью. Различают среднюю векторную и среднюю скалярную скорости.
Средняя векторная скорость
Определение и формулы
Средняя векторная скорость — это скорость, равная отношению перемещения тела ко времени, в течение которого это перемещение было совершено.
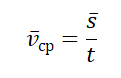
vср — средняя векторная скорость, s — перемещение тела, совершенное за время t
Направление вектора средней скорости всегда совпадает с направлением вектора перемещения.
Чтобы вычислить среднюю векторную скорость, нужно поделить сумму всех перемещений на сумму всех временных промежутков, в течение которых эти перемещения были совершены:
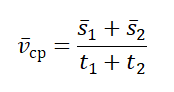
Пример №1. Миша пробежал стометровку за 16 секунд. Через 1 минуту он вернулся на старт. Найти среднюю векторную скорость мальчика.
Миша совершил одинаковые по модулю, но разные по направлению перемещения. При сложении этих векторов получается 0. Поэтому средняя векторная скорость также равна нулю:
Средняя скалярная скорость
Определение и формулы
Средняя скалярная (путевая) скорость — это скорость, равная отношению пути, пройденного телом, ко времени, в течение которого этот путь был пройден.
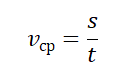
vср — средняя путевая скорость, s — путь, пройденный телом за время t
Чтобы вычислить среднюю путевую скорость, нужно поделить сумму всех путей на сумму всех временных промежутков, в течение которых эти пути были преодолены:
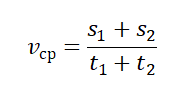
Пример №2. Мальчик пробежал по периметру квадратного поля сто стороной 100 м. На первые две стороны мальчик потратил по 15 секунд, а на последние две — по 20 секунд. Найти среднюю путевую скорость мальчика.
У квадрата 4 стороны, поэтому путь мальчика составляют 4 дистанции по 100 м каждая. Поэтому средняя путевая скорость равна:
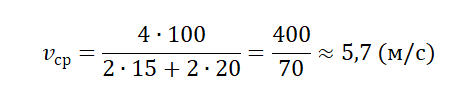
Средняя скалярная скорость всегда больше или равна модулю средней векторной скорости:
- vср=vср, если путь равен модулю перемещения. Так бывает в случае равномерного прямолинейного движения.
- vср>vср, если путь больше модуля перемещения. Так бывает в случае неравномерного прямолинейного или любого криволинейного движения.
Пример №3. Рыболов остановился на берегу круглого пруда и увидел на противоположном берегу удобное для рыбалки место. Он к нему шел в течение 2 минут. Вычислите среднюю путевую и среднюю векторную скорости рыболова после того, как он придет на новое место, если радиус пруда равен 50 м.
Две противоположные точки окружности соединяются отрезком, проходящим через его центр — диаметром. Поэтому модуль вектора перемещения равен двум радиусам пруда:
![]()
Чтобы дойти до диаметрально противоположной точки окружности, нужно пройти путь, равный половине окружности:
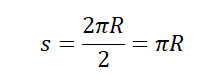
Переведя 2 минуты в СИ, получим 120 с. Модуль средней векторно скорости равен:
Полезные советы и формулы
- Если известны значения отдельных участков пути и скорости на этих участках, средняя скорость равна:
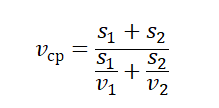
- Если известны скорости на первой и второй половине пути (s1=s2), средняя скорость равна:
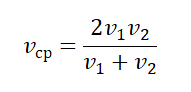
- Если известно время прохождения отдельных участков пути и скорости движения на этих участках, средняя скорость равна:
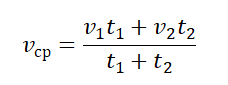
- Если тело движется прямолинейно и равноускорено, его средняя скорость равна половине суммы начальной и конечной скорости:
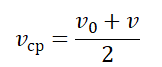
- Если известны скорости тела за равные промежутки времени, его средняя скорость равна:
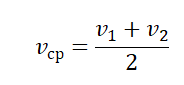
Пример №4. Первые полчаса автомобиль двигался со скоростью 90 км/ч, а потом 1 час он двигался со скоростью 60 км/ч. Найти среднюю скорость автомобиля.
Нам известны скорости на каждом из участков пути и время, в течение которого каждый из этих участков был преодолен. Поэтому:
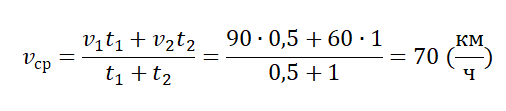
Алиса Никитина | Просмотров: 5.6k
Содержание:
- Определение и формула средней скорости
- Вектор средней скорости
- Единицы измерения
- Примеры решения задач
Определение и формула средней скорости
Определение
Средней путевой скоростью материальной точки на отрезке времени
$Delta t$называется скалярная физическая величина, равная отношению
длины пути, пройденного точкой к промежутку времени, в течение которого данный путь пройден. Среднюю скорость обозначают:
$$langle vrangle, bar{v}, v_{s r}$$
Математически определение средней скорости можно записать в следующем виде:
$$langle vrangle(t+Delta t)=frac{Delta s}{Delta t}=frac{s(t+Delta t)-s(t)}{Delta t}(1)$$
где $Delta s=s(t+Delta t)-s(t)$ – длина пути, которую прошла точка за время
$Delta t$.
Если перейти к пределу при $Delta t rightarrow 0$ , получим:
$$lim _{Delta t rightarrow 0}langle vrangle=lim _{Delta t rightarrow 0} frac{Delta s}{Delta t}=frac{d s}{d t}=v(t)(2)$$
средняя путевая скорость в пределе совпадает с величиной (модулем) мгновенной скорости точки в момент времени t.
При равномерном движении:
$$langle vrangle=v(3)$$
Вектор средней скорости
Определение
Вектором средней скорости $langlevec{v}rangle$ материальной точки на
отрезке времени $Delta t$называют величину, равную приращению радиус-вектора,
который определяет положение данной точки к промежутку времени $Delta t$:
$$langlebar{v}rangle(t+Delta t)=frac{Delta bar{r}}{Delta t}=frac{bar{r}(t+Delta t)-bar{r}(t)}{Delta t}(4)$$
где $Delta bar{r}$ – приращение радиус-вектора материальной точки.
Вектор средней скорости в пределе при $Delta t rightarrow 0$ совпадает с вектором скорости в момент времени t:
$$lim _{Delta t rightarrow 0}langlebar{v}rangle=lim _{Delta t rightarrow 0} frac{Delta bar{r}}{Delta t}=frac{d bar{r}}{d t}=bar{v}(t)(5)$$
где $bar{v}(t)$ – вектор мгновенной скорости токи.
Если точка совершает равномерное и прямолинейное движение, то выполняется равенство:
$$langlebar{v}rangle=bar{v}(6)$$
Средняя путевая скорость и модуль вектора средней скорости равны
$(langle vrangle=|langlebar{v}rangle|)$ только при прямолинейном движении.
При всех остальных видах движения выполняется неравенство:
$$langle vrangle>|langlebar{v}rangle|(7)$$
Единицы измерения
Основной единицей измерения средней скорости в системе СИ является: м/с
В СГС: см/с
Примеры решения задач
Пример
Задание. Какова средняя скорость материальной точки за время ее движения, если точка прошла первую половину
пути имея скорость v1, остальную часть пути данная точка 1/2 времени двигалась со скоростью v2, последний
участок пути точка двигалась со скоростью v3.
Решение. В качестве основы для решения задачи формулу:
$$langle vrangle=frac{s}{Delta t}(1.1)$$
где время потраченное на путь ($Delta t$) делится на три части:
$$Delta t=t_{1}+t_{2}+t_{3}(1.2)$$
При этом имеют место следующие соотношения между отрезками пути, скоростью их преодоления и временем:
$$left{begin{array}{c}frac{1}{2} s=v_{1} t_{1} rightarrow t_{1}=frac{s}{2 v_{1}} \ frac{1}{2} s=v_{2} t_{2}+v_{3} t_{3} rightarrow t_{3}=frac{s}{2left(v_{2}+v_{3}right)}(1.3) \ t_{2}=t_{3}=frac{1}{2} tend{array}right.$$
$$langle vrangle=frac{2 v_{1}left(v_{2}+v_{3}right)}{v_{2}+v_{3}+2 v_{1}}$$
Ответ. $langle vrangle=frac{2 v_{1}left(v_{2}+v_{3}right)}{v_{2}+v_{3}+2 v_{1}}$

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Какова средняя скорость частицы, движущейся по оси Xза время в течение которого, она пройдет первые
s метров пути, если функция скорости задана уравнением: $v=A sqrt{x}$,
где A=const>0. Считать, что x=0 при t=0.
Решение. Сделаем рисунок.
В качестве основы для решения задачи используем формулу для средней путевой скорости, так как движение прямолинейное,
то средняя путевая скорость равна модулю вектора средней скорости. По условию задачи точка движется по оси X, тогда:
$$langle vrangle(t+Delta t)=frac{Delta x}{Delta t}(2.1)$$
По условиям x(t=0)=0, среднюю скорость ищем, когда тело находится в точкеx=sследовательно, выражение (2.1) преобразуем к виду:
$$langle vrangle=frac{s}{t}(2.2)$$
Найдем зависимость скорости от времени, исходя из определения мгновенной скоростидля движения точки по оси X:
$$v=frac{d x}{d t}=A sqrt{x}(2.3)$$
Выразим из (2.2) x:
$$frac{d x}{sqrt{x}}=A d t rightarrow x=frac{A^{2} t^{2}}{4}(2.4)$$
Так как движение происходит по оси X, то $x=s=frac{A^{2} t^{2}}{4}$ . Выразим время, которое точка затратила на путьs :
$$t=frac{2 sqrt{s}}{A}(2.5)$$
Подставим время из (2.4) в формулу (2.2):
$$langle vrangle=frac{A}{2} sqrt{s}$$
Ответ. $langle vrangle=frac{A}{2} sqrt{s}$
Читать дальше: Формула угловой скорости.