Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 11 мая 2021 года; проверки требует 1 правка.
Моля́рная теплоёмкость — отношение теплоёмкости к количеству вещества, теплоёмкость одного моля вещества (в принципе разная для различных веществ, хотя в свете закона Дюлонга — Пти — имеет близкое значение, и даже приближенно совпадает в достаточно широких пределах изменения температуры у многих веществ[1]).
Это — физическая величина, численно равная количеству теплоты, которую необходимо передать одному молю (данного) вещества для того, чтобы его температура изменилась на единицу[2], или — произведение удельной теплоёмкости элемента на его атомную массу дает количество тепла, необходимое для повышения температуры 1 моля этого элемента на 1°С (или, что равнозначно, на 1 К)[3].
В Международной системе единиц (СИ) молярная теплоёмкость измеряется в джоулях на моль на кельвин, Дж/(моль·К)[3]. Иногда используются и производные единицы, как Дж/(кмоль·К), или внесистемные единицы: калория/(кг·К) и т. д.
Молярная теплоёмкость обычно обозначается символом 

На значение молярной теплоёмкости влияет температура вещества и другие термодинамические параметры. К примеру, измерение молярной теплоёмкости воды даст разные результаты при 20 °C и 60 °C.
Формула расчёта молярной теплоёмкости
где c — молярная теплоёмкость, Q — количество теплоты, полученное веществом при нагреве (или выделившееся при охлаждении), ν — количество вещества в нагреваемом (охлаждающемся) образце, ΔT — разность конечной и начальной температур. Удельная теплоёмкость может зависеть (и в принципе, строго говоря, всегда — более или менее сильно — зависит) от температуры, поэтому более корректной является следующая формула с малыми (формально бесконечно малыми) 

Примечания[править | править код]
- ↑ Согласно Дюлонгу и Пти, молярная теплоемкость [при постоянном объёме и температуре T ≥ 300 K] всех твёрдых тел (большинства элементов и простых соединений) приблизительно одинакова и равна ≈6 кал · К−1 · моль−1 (≈25 Дж · К−1 · моль−1; представляет собой среднее значение в изобарном процессе для одно- и двухатомных газов).
- ↑ В основном, понятие молярной теплоемкости применяется для образцов определённого химического состава, а ещё более применительно к определённым веществам, хотя эта величина легко может быть пересчитана (и пересчитывается) и для смеси определённого состава. Для образца переменного химического состава эквипарциальная молярная теплоёмкость также является переменной (что сглаживается, как упоминалось выше, законом Дюлонга — Пти). Зависит она, в принципе, и от температуры (хотя во многих случаях изменяется достаточно слабо при достаточно больших изменениях температуры), при этом, строго говоря, определяется — вслед за теплоёмкостью — как дифференциальная величина и по температурной оси, то есть в узком смысле следует рассматривать изменение температуры в определении удельной теплоёмкости не на один градус (тем более не на какую-то более крупную единицу температуры), а на малое
с соответствующим количеством переданной теплоты
(см. далее основной текст).
- ↑ 1 2 Кельвины (К) здесь можно заменять на градусы Цельсия (°C), поскольку эти температурные шкалы (абсолютная и шкала Цельсия) отличаются друг от друга лишь начальной точкой, но не величиной единицы измерения.
См. также[править | править код]
- Объёмная теплоёмкость
- Удельная теплоёмкость
- Теплоёмкость идеального газа
Литература[править | править код]
- Таблицы физических величин. Справочник, под ред. И. К. Кикоина, М., 1976.
- Сивухин Д. В. Общий курс физики. — Т. II. Термодинамика и молекулярная физика.
- Лифшиц E. М. Теплоёмкость // под. ред. А. М. Прохорова Физическая энциклопедия. — М.: «Советская энциклопедия», 1998. — Т. 2.
- Установление атомных масс тяжёлых элементов. Закон Дюлонга и Пти (+ таблица)/Дикерсон Р., Грей Г., Хейт Дж. Основные законы химии: В 2-х томах. Пер. с англ. — М.: Мир, 1982. — 652 с., ил. — Т. 1. — С. 291—294
Количество
тепла, при получении которого температура
тела повышается на один градус, называется
теплоемкостью. Согласно этому определению![]() .
.
Теплоемкость,
отнесенная к единице массы, называется
удельной
теплоемкостью.
Теплоемкость, отнесенная к одному молю,
называется моляpной
теплоемкостью.
Итак,
теплоемкость опpеделяется чеpез понятие
количества теплоты. Но последнее, как
и pабота, зависит от пpоцесса. Значит и
теплоемкость зависит от пpоцесса.
Сообщать теплоту – нагpевать тело – можно
пpи pазличных условиях. Однако пpи
pазличных условиях на одно и то же
увеличение темпеpатуpы тела потpебуется
pазличное количество теплоты. Следовательно,
тела можно хаpактеpизовать не одной
теплоемкостью, а бесчисленным множеством
(столько же, сколько можно пpидумать
всевозможных пpоцессов, пpи котоpых
пpоисходит теплопеpедача). Однако на
пpактике обычно пользуются опpеделением
двух теплоемкостей: теплоемкости пpи
постоянном объеме и теплоемкости пpи
постоянном давлении.
Теплоемкость
различается в зависимости от того, при
каких условиях происходит нагревание
тела — при постоянном объеме или при
постоянном давлении.
Если
нагревание тела происходит при постоянном
объеме, т. е. dV
= 0, то работа
равна нулю. В этом случае передаваемое
телу тепло идет только на изменение его
внутренней энергии, dQ
= dE,
и в этом случае теплоемкость равна
изменению внутренней энергии при
изменении температуры на 1 К, т. е.
![]() .Поскольку
.Поскольку
для газа
![]() ,
,
то![]() .Эта
.Эта
формула определяет теплоемкость 1 моля
идеального газа, называемую молярной.
При нагревании газа при постоянном
давлении его объем меняется, сообщенное
телу тепло идет не только на увеличение
его внутренней энергии, но и на совершение
работы, т.е.dQ
= dE
+ PdV.
Теплоемкость при постоянном давлении
![]() .
.
Для
идеального газа PV
= RT
и поэтому
PdV =
RdT.
Учитывая
это, найдем![]() .Отношение
.Отношение
![]() представляет собой величину, характерную
представляет собой величину, характерную
для каждого газа и определяемую числом
степеней свободы молекул газа. Измерение
теплоемкости тела есть, таким образом,
способ непосредственного измерения
микроскопических характеристик
составляющих его молекул.
Ф ормулы
ормулы
для теплоемкости идеального газа
приблизительно верно описывают
эксперимент, причем, в основном, для
одноатомных газов. Согласно формулам,
полученным выше, теплоемкость не должна
зависеть от температуры. На самом деле
наблюдается картина, изображенная на
рис., полученная опытным путем для
двухатомного газа водорода. На участке
1 газ ведет себя как система частиц,
обладающих лишь поступательными
степенями свободы, на участке 2 возбуждается
движение, связанное с вращательными
степенями свободы и, наконец, на участке
3 появляются две колебательные степени
свободы. Ступеньки на кривой хорошо
согласуются с формулой (2.35), однако между
ними теплоемкость растет с температурой,
что соответствует как бы нецелому
переменному числу степеней свободы.
Такое поведение теплоемкости указывает
на недостаточность используемого нами
представления об идеальном газе для
описания реальных свойств вещества.
Связь
молярной теплоёмкости с удельной
теплоёмкостьюС=M•с,
где с —
удельная
теплоёмкость,
М —
молярная
масса.Формула
Майера.
Для
любого идеального газа справедливо
соотношение Майера:
![]() ,где
,где
R —
универсальная
газовая постоянная,
![]() —
—
молярная
теплоемкость при постоянном давлении,
![]() —
—
молярная
теплоемкость при постоянном объёме.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
The molar heat capacity of a chemical substance is the amount of energy that must be added, in the form of heat, to one mole of the substance in order to cause an increase of one unit in its temperature. Alternatively, it is the heat capacity of a sample of the substance divided by the amount of substance of the sample; or also the specific heat capacity of the substance times its molar mass. The SI unit of molar heat capacity is joule per kelvin per mole, J⋅K−1⋅mol−1.
Like the specific heat, the measured molar heat capacity of a substance, especially a gas, may be significantly higher when the sample is allowed to expand as it is heated (at constant pressure, or isobaric) than when it is heated in a closed vessel that prevents expansion (at constant volume, or isochoric). The ratio between the two, however, is the same heat capacity ratio obtained from the corresponding specific heat capacities.
This property is most relevant in chemistry, when amounts of substances are often specified in moles rather than by mass or volume. The molar heat capacity generally increases with the molar mass, often varies with temperature and pressure, and is different for each state of matter. For example, at atmospheric pressure, the (isobaric) molar heat capacity of water just above the melting point is about 76 J⋅K−1⋅mol−1, but that of ice just below that point is about 37.84 J⋅K−1⋅mol−1. While the substance is undergoing a phase transition, such as melting or boiling, its molar heat capacity is technically infinite, because the heat goes into changing its state rather than raising its temperature. The concept is not appropriate for substances whose precise composition is not known, or whose molar mass is not well defined, such as polymers and oligomers of indeterminate molecular size.
A closely related property of a substance is the heat capacity per mole of atoms, or atom-molar heat capacity, in which the heat capacity of the sample is divided by the number of moles of atoms instead of moles of molecules. So, for example, the atom-molar heat capacity of water is 1/3 of its molar heat capacity, namely 25.3 J⋅K−1⋅mol−1.
In informal chemistry contexts, the molar heat capacity may be called just “heat capacity” or “specific heat”. However, international standards now recommend that “specific heat capacity” always refer to capacity per unit of mass, to avoid possible confusion.[1] Therefore, the word “molar”, not “specific”, should always be used for this quantity.
Definition[edit]
The molar heat capacity of a substance, which may be denoted by cm, is the heat capacity C of a sample of the substance, divided by the amount (moles) n of the substance in the sample:
- cm
where ΔQ is the amount of heat needed to raise the temperature of the sample by ΔT. Obviously, this parameter cannot be computed when n is not known or defined.
Like the heat capacity of an object, the molar heat capacity of a substance may vary, sometimes substantially, depending on the starting temperature T of the sample and the pressure P applied to it. Therefore, it should be considered a function cm(P,T) of those two variables.
These parameters are usually specified when giving the molar heat capacity of a substance. For example, “H2O: 75.338 J⋅K−1⋅mol−1 (25 °C, 101.325 kPa)” [2] When not specified, published values of the molar heat capacity cm generally are valid for some standard conditions for temperature and pressure.
However, the dependency of cm(P,T) on starting temperature and pressure can often be ignored in practical contexts, e.g. when working in narrow ranges of those variables. In those contexts one can usually omit the qualifier (P,T), and approximate the molar heat capacity by a constant cm suitable for those ranges.
Since the molar heat capacity of a substance is the specific heat c times the molar mass of the substance M/N its numerical value is generally smaller than that of the specific heat. Paraffin wax, for example, has a specific heat of about 2500 J⋅K−1⋅kg−1 but a molar heat capacity of about 600 J⋅K−1⋅mol−1.
The molar heat capacity is an “intensive” property of a substance, an intrinsic characteristic that does not depend on the size or shape of the amount in consideration. (The qualifier “specific” in front of an extensive property often indicates an intensive property derived from it.[3])
Variations[edit]
The injection of heat energy into a substance, besides raising its temperature, usually causes an increase in its volume and/or its pressure, depending on how the sample is confined. The choice made about the latter affects the measured molar heat capacity, even for the same starting pressure P and starting temperature T. Two particular choices are widely used:
- If the pressure is kept constant (for instance, at the ambient atmospheric pressure), and the sample is allowed to expand, the expansion generates work as the force from the pressure displaces the enclosure. That work must come from the heat energy provided. The value thus obtained is said to be the molar heat capacity at constant pressure (or isobaric), and is often denoted cP,m, cp,m, cP,m, etc.
- On the other hand, if the expansion is prevented — for example by a sufficiently rigid enclosure, or by increasing the external pressure to counteract the internal one — no work is generated, and the heat energy that would have gone into it must instead contribute to the internal energy of the object, including raising its temperature by an extra amount. The value obtained this way is said to be the molar heat capacity at constant volume (or isochoric) and denoted cV,m, cv,m, cv,m, etc.
The value of cV,m is always less than the value of cP,m. This difference is particularly notable in gases where values under constant pressure are typically 30% to 66.7% greater than those at constant volume.[4]
All methods for the measurement of specific heat apply to molar heat capacity as well.
Units[edit]
The SI unit of molar heat capacity heat is joule per kelvin per mole (J/(K⋅mol), J/(K mol), J K−1 mol−1, etc.). Since an increment of temperature of one degree Celsius is the same as an increment of one kelvin, that is the same as joule per degree Celsius per mole (J/(°C⋅mol)).
In chemistry, heat amounts are still often measured in calories. Confusingly, two units with that name, denoted “cal” or “Cal”, have been commonly used to measure amounts of heat:
- the “small calorie” (or “gram-calorie”, “cal”) is 4.184 J, exactly.
- The “grand calorie” (also “kilocalorie”, “kilogram-calorie”, or “food calorie”; “kcal” or “Cal”) is 1000 small calories, that is, 4184 J, exactly.
When heat is measured in these units, the unit of specific heat is usually
-
- 1 cal/(°C⋅mol) (“small calorie”) = 4.184 J⋅K−1⋅mol−1
- 1 kcal/(°C⋅mol) (“large calorie”) = 4184 J⋅K−1⋅mol−1.
The molar heat capacity of a substance has the same dimension as the heat capacity of an object; namely, L2⋅M⋅T−2⋅Θ−1, or M(L/T)2/Θ. (Indeed, it is the heat capacity of the object that consists of an Avogadro number of molecules of the substance.) Therefore, the SI unit J⋅K−1⋅mol−1 is equivalent to kilogram metre squared per second squared per kelvin (kg⋅m2⋅K−1⋅s−2).
Physical basis [edit]
Monatomic gases[edit]
The temperature of a sample of a substance reflects the average kinetic energy of its constituent particles (atoms or molecules) relative to its center of mass. Quantum mechanics predicts that, at room temperature and ordinary pressures, an isolated atom in a gas cannot store any significant amount of energy except in the form of kinetic energy. Therefore, when a certain number N of atoms of a monatomic gas receives an input ΔQ of heat energy, in a container of fixed volume, the kinetic energy of each atom will increase by ΔQ/N, independently of the atom’s mass. This assumption is the foundation of the theory of ideal gases.
In other words, that theory predicts that the molar heat capacity at constant volume cV,m of all monatomic gases will be the same; specifically,
- cV,m = 3/2R
where R is the ideal gas constant, about 8.31446 J⋅K−1⋅mol−1 (which is the product of the Boltzmann constant kB and the Avogadro constant). And, indeed, the experimental values of cV,m for the noble gases helium, neon, argon, krypton, and xenon (at 1 atm and 25 °C) are all 12.5 J⋅K−1⋅mol−1, which is 3/2R; even though their atomic weights range from 4 to 131.
The same theory predicts that the molar heat capacity of a monatomic gas at constant pressure will be
- cP,m = cV,m + R = 5/2R
This prediction matches the experimental values, which, for helium through xenon, are 20.78, 20.79, 20.85, 20.95, and 21.01 J⋅K−1⋅mol−1, respectively;[5][6] very close to the theoretical 5/2R = 20.78 J⋅K−1⋅mol−1.
Therefore, the specific heat (per unit of mass, not per mole) of a monatomic gas will be inversely proportional to its (adimensional) relative atomic mass A. That is, approximately,
- cV = (12470 J⋅K−1⋅kg−1)/A cP = (20786 J⋅K−1⋅kg−1)/A
Polyatomic gases[edit]

Vibration of atoms in the molecule and rotation of the molecule store some of the energy (transferred to the molecule as heat) that otherwise would contribute to the molecule’s kinetic energy.
Degrees of freedom[edit]
A polyatomic molecule (consisting of two or more atoms bound together) can store heat energy in other forms besides its kinetic energy. These forms include rotation of the molecule, and vibration of the atoms relative to its center of mass.
These extra degrees of freedom contribute to the molar heat capacity of the substance. Namely, when heat energy is injected into a gas with polyatomic molecules, only part of it will go into increasing their kinetic energy, and hence the temperature; the rest will go to into those other degrees of freedom. Thus, in order to achieve the same increase in temperature, more heat energy will have to be provided to a mol of that substance than to a mol of a monatomic gas. Substances with high atomic count per molecule, like octane, can therefore have a very large heat capacity per mole, and yet a relatively small specific heat (per unit mass).[7][8][9]
If the molecule could be entirely described using classical mechanics, then the theorem of equipartition of energy could be used to predict that each degree of freedom would have an average energy in the amount of 1/2kT, where k is the Boltzmann constant, and T is the temperature. If the number of degrees of freedom of the molecule is f, then each molecule would be holding, on average, a total energy equal to 1/2fkT. Then the molar heat capacity (at constant volume) would be
- cV,m = 1/2fR
where R is the ideal gas constant. According to Mayer’s relation, the molar heat capacity at constant pressure would be
- cP,m = cV,m + R = 1/2fR + R = 1/2(f + 2)R
Thus, each additional degree of freedom will contribute 1/2R to the molar heat capacity of the gas (both cV,m and cP,m).
In particular, each molecule of a monatomic gas has only f = 3 degrees of freedom, namely the components of its velocity vector; therefore cV,m = 3/2R and cP,m = 5/2R.[10]
Rotational modes of a diatomic molecule[edit]
For example, the molar heat capacity of nitrogen N
2 at constant volume is 20.6 J⋅K−1⋅mol−1 (at 15 °C, 1 atm), which is 2.49 R.[11] From the theoretical equation cV,m = 1/2fR, one concludes that each molecule has f = 5 degrees of freedom. These turn out to be three degrees of the molecule’s velocity vector, plus two degrees from its rotation about an axis through the center of mass and perpendicular to the line of the two atoms. The degrees of freedom due to translations and rotations are called the rigid degrees of freedom, since they do not involve any deformation of the molecule.
Because of those two extra degrees of freedom, the molar heat capacity cV,m of N
2 (20.6 J⋅K−1⋅mol−1) is greater than that of an hypothetical monatomic gas (12.5 J⋅K−1⋅mol−1) by a factor of 5/3.
Frozen and active degrees of freedom[edit]
According to classical mechanics, a diatomic molecule like nitrogen should have more degrees of internal freedom, corresponding to vibration of the two atoms that stretch and compress the bond between them.
For thermodynamic purposes, each direction in which an atom can independently vibrate relative to the rest of the molecule introduces two degrees of freedom: one associated with the potential energy from distorting the bonds, and one for the kinetic energy of the atom’s motion. In a diatomic molecule like N
2, there is only one direction for the vibration, and the motions of the two atoms must be opposite but equal; so there are only two degrees of vibrational freedom. That would bring f up to 7, and cV,m to 3.5 R.
The reason why these vibrations are not absorbing their expected fraction of heat energy input is provided by quantum mechanics. According to that theory, the energy stored in each degree of freedom must increase or decrease only in certain amounts (quanta). Therefore, if the temperature T of the system is not high enough, the average energy that would be available for some of the theoretical degrees of freedom (kT/f) may be less than the corresponding minimum quantum. If the temperature is low enough, that may be the case for practically all molecules. One then says that those degrees of freedom are “frozen”. The molar heat capacity of the gas will then be determined only by the “active” degrees of freedom — that, for most molecules, can receive enough energy to overcome that quantum threshold.[12]

Constant-volume specific heat capacity of a diatomic gas (idealised). As temperature increases, heat capacity goes from
3/2R (translation contribution only), to
5/2R (translation plus rotation), finally to a maximum of
7/2R (translation + rotation + vibration)
For each degree of freedom, there is an approximate critical temperature at which it “thaws” (“unfreezes”) and becomes active, thus being able to hold heat energy. For the three translational degrees of freedom of molecules in a gas, this critical temperature is extremely small, so they can be assumed to be always active. For the rotational degrees of freedom, the thawing temperature is usually a few tens of kelvins (although with a very light molecule such as hydrogen the rotational energy levels will be spaced so widely that rotational heat capacity may not completely “unfreeze” until considerably higher temperatures are reached). Vibration modes of diatomic molecules generally start to activate only well above room temperature.
In the case of nitrogen, the rotational degrees of freedom are fully active already at −173 °C (100 K, just 23 K above the boiling point). On the other hand, the vibration modes only start to become active around 350 K (77 °C) Accordingly, the molar heat capacity cP,m is nearly constant at 29.1 J⋅K−1⋅mol−1 from 100 K to about 300 °C. At about that temperature, it starts to increase rapidly, then it slows down again. It is 35.5 J⋅K−1⋅mol−1 at 1500 °C, 36.9 at 2500 °C, and 37.5 at 3500 °C.[13][14] The last value corresponds almost exactly to the predicted value for f = 7.

Constant-volume specific heat capacity of diatomic gases (real gases) between about 200 K and 2000 K. This temperature range is not large enough to include both quantum transitions in all gases. Instead, at 200 K, all but hydrogen are fully rotationally excited, so all have at least
5/2R heat capacity. (Hydrogen is already below
5/2, but it will require cryogenic conditions for even H2 to fall to
3/2R). Further, only the heavier gases fully reach
7/2R at the highest temperature, due to the relatively small vibrational energy spacing of these molecules. HCl and H2 begin to make the transition above 500 K, but have not achieved it by 1000 K, since their vibrational energy level spacing is too wide to fully participate in heat capacity, even at this temperature.
The following is a table of some constant-pressure molar heat capacities cP,m of various diatomic gases at standard temperature (25 °C = 298 K), at 500 °C, and at 5000 °C, and the apparent number of degrees of freedom f* estimated by the formula f* = 2cP,m/R − 2:
| 25 °C | 500 °C | 5000 °C | |||||
|---|---|---|---|---|---|---|---|
| Gas |
cP,m J⋅K−1⋅mol−1 |
f* |
cP,m J⋅K−1⋅mol−1 |
f* |
cP,m J⋅K−1⋅mol−1 |
f* |
|
| H2 | 28.9 | 5.0 | 29.6 | 5.1 | 41.2 | 7.9 | Not saturated.[15] |
| CO | 29.1 | 5.0 | 31.7 | 5.6 | 38.1 | 7.2 | Saturated.[16] |
| N2 | 29.1 | 5.0 | 31.3 | 5.5 | 38.0 | 7.1 | Saturated.[13] |
| Cl2 | 34.0 | 6.2 | 37.0 | 6.9 | 39.6 | 7.5 | Max 41.3 at ~3700 C.[17] |
| Br2 (vapour) | (*)36.4 | 6.8 | 37.5 | 7.0 | 39.2 | 7.4 | Max 41.6 at ~3000 C.[18] |
(*) At 59 C (boiling point)
The quantum harmonic oscillator approximation implies that the spacing of energy levels of vibrational modes are inversely proportional to the square root of the reduced mass of the atoms composing the diatomic molecule. This fact explains why the vibrational modes of heavier molecules like Br
2 are active at lower temperatures. The molar heat capacity of Br
2 at room temperature is consistent with f = 7 degrees of freedom, the maximum for a diatomic molecule. At high enough temperatures, all diatomic gases approach this value.
Rotational modes of single atoms[edit]
Quantum mechanics also explains why the specific heat of monatomic gases is well predicted by the ideal gas theory with the assumption that each molecule is a point mass that has only the f = 3 translational degrees of freedom.
According to classical mechanics, since atoms have non-zero size, they should also have three rotational degrees of freedom, or f = 6 in total. Likewise, the diatomic nitrogen molecule should have an additional rotation mode, namely about the line of the two atoms; and thus have f = 6 too. In the classical view, each of these modes should store an equal share of the heat energy.
However, according to quantum mechanics, the energy difference between the allowed (quantized) rotation states is inversely proportional to the moment of inertia about the corresponding axis of rotation. Because the moment of inertia of a single atom is exceedingly small, the activation temperature for its rotational modes is extremely high. The same applies to the moment of inertia of a diatomic molecule (or a linear polyatomic one) about the internuclear axis, which is why that mode of rotation is not active in general.
On the other hand, electrons and nuclei can exist in excited states and, in a few exceptional cases, they may be active even at room temperature, or even at cryogenic temperatures.
Polyatomic gases[edit]
The set of all possible ways to infinitesimally displace the n atoms of a polyatomic gas molecule is a linear space of dimension 3n, because each atom can be independently displaced in each of three orthogonal axis directions. However, some three of these dimensions are just translation of the molecule by an infinitesimal displacement vector, and others are just rigid rotations of it by an infinitesimal angle about some axis. Still others may correspond to relative rotation of two parts of the molecule about a single bond that connects them.
The independent deformation modes—linearly independent ways to actually deform the molecule, that strain its bonds—are only the remaining dimensions of this space. As in the case diatomic molecules, each of these deformation modes counts as two vibrational degrees of freedom for energy storage purposes: one for the potential energy stored in the strained bonds, and one for the extra kinetic energy of the atoms as they vibrate about the rest configuration of the molecule.
In particular, if the molecule is linear (with all atoms on a straight line), it has only two non-trivial rotation modes, since rotation about its own axis does not displace any atom. Therefore, it has 3n − 5 actual deformation modes. The number of energy-storing degrees of freedom is then f = 3 + 2 + 2(3n − 5) = 6n − 5.
For example, the linear nitrous oxide molecule N≡N=O (with n = 3) has 3n − 5 = 4 independent infinitesimal deformation modes. Two of them can be described as stretching one of the bonds while the other retains its normal length. The other two can be identified which the molecule bends at the central atom, in the two directions that are orthogonal to its axis. In each mode, one should assume that the atoms get displaced so that the center of mass remains stationary and there is no rotation. The molecule then has f = 6n − 5 = 13 total energy-storing degrees of freedom (3 translational, 2 rotational, 8 vibrational). At high enough temperature, its molar heat capacity then should be cP,m = 7.5 R = 62.63 J⋅K−1⋅mol−1. For cyanogen N≡C−C≡N and acetylene H−C≡C−H (n = 4) the same analysis yields f = 19 and predicts cP,m = 10.5 R = 87.3 J⋅K−1⋅mol−1.
A molecule with n atoms that is rigid and not linear has 3 translation modes and 3 non-trivial rotation modes, hence only 3n − 6 deformation modes. It therefore has f = 3 + 3 + 2(3n − 6) = 6n − 6 energy-absorbing degrees of freedom (one less than a linear molecule with the same atom count). Water H2O (n = 3) is bent in its non-strained state, therefore it is predicted to have f = 12 degrees of freedom.[19] Methane CH4 (n = 5) is tridimensional, and the formula predicts f = 24.
Ethane H3C−CH3 (n = 8) has 4 degrees of rotational freedom: two about axes that are perpendicular to the central bond, and two more because each methyl group can rotate independently about that bond, with negligible resistance. Therefore, the number of independent deformation modes is 3n − 7, which gives f = 3 + 4 + 2(3n − 7) = 6n − 7 = 41.
The following table shows the experimental molar heat capacities at constant pressure cP,m of the above polyatomic gases at standard temperature (25 °C = 298 K), at 500 °C, and at 5000 °C, and the apparent number of degrees of freedom f* estimated by the formula f* = 2cP,m/R − 2:
| 25 °C | 500 °C | 5000 °C | ||||||
|---|---|---|---|---|---|---|---|---|
| Gas |
cP,m J⋅K−1⋅mol−1 |
f* |
cP,m J⋅K−1⋅mol−1 |
f* |
cP,m J⋅K−1⋅mol−1 |
f* |
f |
Notes |
| N≡N=O | 38.6 | 7.3 | 51.8 | 10.5 | 62.0 | 12.9 | 13 | [20] |
| N≡C–C≡N | 56.7 | 11.6 | 72.3 | 15.4 | 86.7 | 18.9 | 19 | [21] |
| H–C≡C–N | 44.0 | 8.6 | 63.2 | 13.2 | 92.9 | 20.3 | 19 | [22] |
| H2O | — | — | 38.4 | 7.2 | 59.7 | 12.4 | 12 | [23] |
| CH4 | 35.7 | 6.6 | 61.6 | 12.8 | 105.7 | 23.4 | 24 | [24] |
| H3C–CH3 | 52.5 | 10.6 | 105.6 | 23.4 | 168.7 | (*)38.6 | 41 | [25] |
(*) At 3000C
Specific heat of solids[edit]
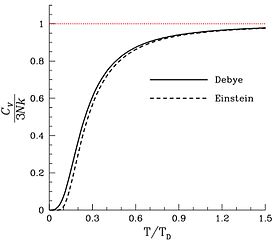
The dimensionless heat capacity divided by three, as a function of temperature as predicted by the Debye model and by Einstein’s earlier model. The horizontal axis is the temperature divided by the Debye temperature. Note that, as expected, the dimensionless heat capacity is zero at absolute zero, and rises to a value of three as the temperature becomes much larger than the Debye temperature. The red line corresponds to the classical limit of the Dulong–Petit law
In most solids (but not all), the molecules have a fixed mean position and orientation, and therefore the only degrees of freedom available are the vibrations of the atoms.[26] Thus the specific heat is proportional to the number of atoms (not molecules) per unit of mass, which is the Dulong–Petit law. Other contributions may come from magnetic degrees of freedom in solids, but these rarely make substantial contributions.[27] and electronic[28]
Since each atom of the solid contributes one independent vibration mode, the number of degrees of freedom in n atoms is 6n. Therefore, the heat capacity of a sample of a solid substance is expected to be 3RNa, or (24.94 J/K)Na, where Na is the number of moles of atoms in the sample, not molecules. Said another way, the atom-molar heat capacity of a solid substance is expected to be 3R = 24.94 J⋅K−1⋅mol−1, where “amol” denotes an amount of the solid that contains the Avogadro number of atoms.[29]
It follows that, in molecular solids, the heat capacity per mole of molecules will usually be close to 3nR, where n is the number of atoms per molecule.
Thus n atoms of a solid should in principle store twice as much energy as n atoms of a monatomic gas. One way to look at this result is to observe that the monatomic gas can only store energy as kinetic energy of the atoms, whereas the solid can store it also as potential energy of the bonds strained by the vibrations. The atom-molar heat capacity of a polyatomic gas approaches that of a solid as the number n of atoms per molecule increases.
As in the case f gases, some of the vibration modes will be “frozen out” at low temperatures, especially in solids with light and tightly bound atoms, causing the atom-molar heat capacity to be less than this theoretical limit. Indeed, the atom-molar (or specific) heat capacity of a solid substance tends toward zero, as the temperature approaches absolute zero.
Dulong–Petit law[edit]
As predicted by the above analysis, the heat capacity per mole of atoms, rather than per mole of molecules, is found to be remarkably constant for all solid substances at high temperatures. This relationship was noticed empirically in 1819, and is called the Dulong–Petit law, after its two discoverers.[30][31] This discovery was an important argument in support of the atomic theory of matter.
Indeed, for solid metallic chemical elements at room temperature, atom-molar heat capacities range from about 2.8 R to 3.4 R. Large exceptions at the lower end involve solids composed of relatively low-mass, tightly bonded atoms, such as beryllium (2.0 R, only of 66% of the theoretical value), and diamond (0.735 R, only 24%). Those conditions imply larger quantum vibrational energy spacing, thus many vibrational modes are “frozen out” at room temperature. Water ice close to the melting point, too, has an anomalously low heat capacity per atom (1.5 R, only 50% of the theoretical value).
At the higher end of possible heat capacities, heat capacity may exceed R by modest amounts, due to contributions from anharmonic vibrations in solids, and sometimes a modest contribution from conduction electrons in metals. These are not degrees of freedom treated in the Einstein or Debye theories.
Specific heat of solid elements[edit]
Since the bulk density of a solid chemical element is strongly related to its molar mass, there exists a noticeable inverse correlation between a solid’s density and its specific heat capacity on a per-mass basis.
This is due to a very approximate tendency of atoms of most elements to be about the same size, despite much wider variations in density and atomic weight. These two factors (constancy of atomic volume and constancy of mole-specific heat capacity) result in a good correlation between the volume of any given solid chemical element and its total heat capacity.
Another way of stating this, is that the volume-specific heat capacity (volumetric heat capacity) of solid elements is roughly a constant. The molar volume of solid elements is very roughly constant, and (even more reliably) so also is the molar heat capacity for most solid substances. These two factors determine the volumetric heat capacity, which as a bulk property may be striking in consistency. For example, the element uranium is a metal that has a density almost 36 times that of the metal lithium, but uranium’s specific heat capacity on a volumetric basis (i.e. per given volume of metal) is only 18% larger than lithium’s.
However, the average atomic volume in solid elements is not quite constant, so there are deviations from this principle. For instance, arsenic, which is only 14.5% less dense than antimony, has nearly 59% more specific heat capacity on a mass basis. In other words; even though an ingot of arsenic is only about 17% larger than an antimony one of the same mass, it absorbs about 59% more heat for a given temperature rise. The heat capacity ratios of the two substances closely follows the ratios of their molar volumes (the ratios of numbers of atoms in the same volume of each substance); the departure from the correlation to simple volumes, in this case, is due to lighter arsenic atoms being significantly more closely packed than antimony atoms, instead of similar size. In other words, similar-sized atoms would cause a mole of arsenic to be 63% larger than a mole of antimony, with a correspondingly lower density, allowing its volume to more closely mirror its heat capacity behavior.
Effect of impurities[edit]
Sometimes small impurity concentrations can greatly affect the specific heat, for example in semiconducting ferromagnetic alloys.[32]
Specific heat of liquids[edit]
A general theory of the heat capacity of liquids has not yet been achieved, and is still an active area of research. It was long thought that phonon theory is not able to explain the heat capacity of liquids, since liquids only sustain longitudinal, but not transverse phonons, which in solids are responsible for 2/3 of the heat capacity. However, Brillouin scattering experiments with neutrons and with X-rays, confirming an intuition of Yakov Frenkel,[33] have shown that transverse phonons do exist in liquids, albeit restricted to frequencies above a threshold called the Frenkel frequency. Since most energy is contained in these high-frequency modes, a simple modification of the Debye model is sufficient to yield a good approximation to experimental heat capacities of simple liquids.[34]
Because of high crystal binding energies, the effects of vibrational mode freezing are observed in solids more often than liquids: for example the heat capacity of liquid water is twice that of ice at near the same temperature, and is again close to the 3R per mole of atoms of the Dulong–Petit theoretical maximum.
Amorphous materials can be considered a type of liquid at temperatures above the glass transition temperature. Below the glass transition temperature amorphous materials are in the solid (glassy) state form. The specific heat has characteristic discontinuities at the glass transition temperature which are caused by the absence in the glassy state of percolating clusters made of broken bonds (configurons) that are present only in the liquid phase.[35] Above the glass transition temperature percolating clusters formed by broken bonds enable a more floppy structure and hence a larger degree of freedom for atomic motion which results in a higher heat capacity of liquids. Below the glass transition temperature there are no extended clusters of broken bonds and the heat capacity is smaller because the solid-state (glassy) structure of amorphous material is more rigid.
The discontinuities in the heat capacity are typically used to detect the glass transition temperature where a supercooled liquid transforms to a glass.
Effect of hydrogen bonds[edit]
Hydrogen-containing polar molecules like ethanol, ammonia, and water have powerful, intermolecular hydrogen bonds when in their liquid phase. These bonds provide another place where heat may be stored as potential energy of vibration, even at comparatively low temperatures. Hydrogen bonds account for the fact that liquid water stores nearly the theoretical limit of 3R per mole of atoms, even at relatively low temperatures (i.e. near the freezing point of water).
See also[edit]
- Quantum statistical mechanics
- Heat capacity ratio
- Statistical mechanics
- Thermodynamic equations
- Thermodynamic databases for pure substances
- Heat equation
- Heat transfer coefficient
- Heat of mixing
- Latent heat
- Material properties (thermodynamics)
- Joback method (Estimation of heat capacities)
- Specific heat of melting (Enthalpy of fusion)
- Specific heat of vaporization (Enthalpy of vaporization)
- Volumetric heat capacity
- Thermal mass
- R-value (insulation)
- Storage heater
- Frenkel line
References[edit]
- ^ International Bureau of Weights and Measures (2006), The International System of Units (SI) (PDF) (8th ed.), ISBN 92-822-2213-6, archived (PDF) from the original on 2021-06-04, retrieved 2021-12-16
- ^ W. Wagner, J. R. Cooper, A. Dittmann, J. Kijima, H.-J. Kretzschmar, A. Kruse, R. Mare, K. Oguchi, H. Sato, I. Stöcker, O. Šifner, Y. Takaishi, I. Tanishita, J. Trübenbach and Th. Willkommen (2000): “The IAPWS industrial formulation 1997 for the thermodynamic properties of water and steam”, ASME J. Eng. Gas Turbines and Power, volume 122, pages 150–182
- ^ International Union of Pure and Applied Chemistry, Physical Chemistry Division. “Quantities, Units and Symbols in Physical Chemistry” (PDF). Blackwell Sciences. p. 7.
The adjective specific before the name of an extensive quantity is often used to mean divided by mass.
- ^ Lange’s Handbook of Chemistry, 10th ed. p. 1524
- ^ Shuen-Chen Hwang, Robert D. Lein, Daniel A. Morgan (2005). “Noble Gases”. Kirk Othmer Encyclopedia of Chemical Technology. Wiley. pp. 343–383. |doi=10.1002/0471238961.0701190508230114.a01.pub2
- ^ Hwang, Shuen-Cheng; Weltmer, William R. (2000). “Helium Group Gases”. Kirk-Othmer Encyclopedia of Chemical Technology. Wiley. pp. 343–383. doi:10.1002/0471238961.0701190508230114.a01. ISBN 0-471-23896-1.
- ^ Feynman, R., Lectures in Physics, vol. I, chapter 40, pp. 7–8
- ^
Reif, F. (1965). Fundamentals of statistical and thermal physics. McGraw-Hill. pp. 253–254. ISBN 9780070518001. - ^
Charles Kittel; Herbert Kroemer (2000). Thermal physics. Freeman. p. 78. ISBN 978-0-7167-1088-2. - ^ Textbook: Young and Geller College Physics, 8e, Pearson Education, 2008
- ^ Steven T. Thornton and Andrew Rex (1993): Modern Physics for Scientists and Engineers, Saunders College Publishing, 1993
- ^ Quantum Physics and the Physics of large systems, Part 1A Physics, University of Cambridge, C.G. Smith, 2008.
- ^ a b “Nitrogen” NIST Chemistry WebBook, SRD 69, online. Accessed on 2019-05-18.
- ^ M.W. Chase Jr. (1998) NIST-JANAF Themochemical Tables, Fourth Edition, In Journal of Physical and Chemical Reference Data, Monograph 9, pages 1–1951.
- ^ “Hydrogen” NIST Chemistry WebBook, SRD 69, online. Accessed on 2019-05-18.
- ^ “Carbon monoxide” NIST Chemistry WebBook, SRD 69, online. Accessed on 2019-05-18.
- ^ “Chlorine”” NIST Chemistry WebBook, SRD 69, online. Accessed on 2019-05-18.
- ^ “Bromine” NIST Chemistry WebBook, SRD 69, online. Accessed on 2019-05-18.
- ^ Smith, C. G. (2008). Quantum Physics and the Physics of large systems, Part 1A Physics. University of Cambridge.
- ^ “Nitrous oxide” NIST Chemistry WebBook, SRD 69, online. Accessed on 2019-05-18.
- ^ “Cyanogen” NIST Chemistry WebBook, SRD 69, online. Accessed on 2019-05-18.
- ^ “Acetylene” NIST Chemistry WebBook, SRD 69, online. Accessed on 2019-05-18.
- ^ “Water” NIST Chemistry WebBook, SRD 69, online. Accessed on 2019-05-18.
- ^ “Methane” NIST Chemistry WebBook, SRD 69, online. Accessed on 2019-05-18.
- ^ “Ethane” NIST Chemistry WebBook, SRD 69
- ^ Kittel, Charles (2005). Introduction to Solid State Physics (8th ed.). Hoboken, New Jersey, USA: John Wiley & Sons. p. 141. ISBN 978-0-471-41526-8.
- ^ Blundell, Stephen (2001). Magnetism in Condensed Matter. Oxford Master Series in Condensed Matter Physics (1st ed.). Hoboken, New Jersey, USA: Oxford University Press. p. 27. ISBN 978-0-19-850591-4.
- ^ Kittel, Charles (2005). Introduction to Solid State Physics (8th ed.). Hoboken, New Jersey, USA: John Wiley & Sons. p. 141. ISBN 978-0-471-41526-8.
- ^ “The Heat Capacity of a Solid” (PDF). Archived from the original (PDF) on 2014-02-11.
- ^ Petit A.-T.; Dulong P.-L. (1819). “Recherches sur quelques points importants de la Théorie de la Chaleur”. Annales de Chimie et de Physique. 10: 395–413.
- ^ Petit A.-T., Dulong P.-L.: Recherches sur quelques points importants de la Théorie de la Chaleur. In: Annales de Chimie et de Physique 10, 395–413 (1819) (Translation)
- ^ Hogan, C. (1969). “Density of States of an Insulating Ferromagnetic Alloy”. Physical Review. 188 (2): 870. Bibcode:1969PhRv..188..870H. doi:10.1103/PhysRev.188.870.
- ^ In his textbook Kinetic Theory of Liquids (engl. 1947)
- ^ Bolmatov, D.; Brazhkin, V. V.; Trachenko, K. (2012). “The phonon theory of liquid thermodynamics”. Scientific Reports. 2: 421. arXiv:1202.0459. Bibcode:2012NatSR…2E.421B. doi:10.1038/srep00421. PMC 3359528. PMID 22639729.
- Hamish Johnston (13 June 2012). “Phonon theory sheds light on liquid thermodynamics”. Physics World.
- ^ Ojovan, Michael I.; Lee, William E. (2006). “Topologically disordered systems at the glass transition” (PDF). Journal of Physics: Condensed Matter. 18 (50): 11507–11520. Bibcode:2006JPCM…1811507O. doi:10.1088/0953-8984/18/50/007. S2CID 96326822.
Перевод термодинамической системы (например, порции идеального газа) из состояния `1` в состояние `2` можно осуществить разными способами. На рис. 12 показаны графики двух возможных процессов (`1-“а”-2` и `1-“в”-2`), позволяющих осуществить такой перевод. Изменение внутренней энергии системы в том и в другом случае одинаково (оно определяется положениями точек `1` и `2` на -диаграмме), а работа, совершённая системой над окружающими телами, различна (площадь фигур под графиками процессов `1-“а”-2` и `1-“в”-2` разная, площадь под графиком процесса `1-“в”-2` больше).
Следовательно, и количество теплоты, затраченное на перевод системы из состояния `1` в `2` ( $$ Q=Delta U+{A}^{text{‘}}$$ ), будет разным.
Теплоёмкостью $$ C$$ термодинамической системы (тела) называют отношение бесконечно малого количества теплоты $$ Delta Q$$, переданного системе, к изменению $$ Delta T$$ его температуры, вызванного этим количеством теплоты.
$$ C={displaystyle frac{Delta Q}{Delta T}}$$ — теплоёмкость тела (системы).
Единицей измерения этой величины будет $$ left[Cright]={displaystyle frac{1mathrm{Дж}}{mathrm{К}}}$$.
Численное значение теплоёмкости тела показывает, какое количество теплоты потребуется для изменения температуры всего тела на `1` градус по шкале Цельсия (Кельвина).
При расчётах чаще пользуются удельной теплоёмкостью (теплоёмкостью `1` кг вещества).
называют отношение теплоёмкости тела (системы) к массе этого тела (системы):
| $$ {c}_{mathrm{уд}}={displaystyle frac{C}{m}}={displaystyle frac{Delta Q}{m· Delta T}}$$ — удельная теплоёмкость тела (системы). | (1) |
Единицей измерения этой величины будет $$ left[cright]={displaystyle frac{1mathrm{Дж}}{mathrm{кг}·mathrm{К}}}$$.
называют отношение теплоёмкости тела (системы) к количеству вещества в этом теле (системе):
| $$ {c}_{mathrm{мол}}={displaystyle frac{C}{nu }}={displaystyle frac{Delta Q}{ Delta T·nu }}$$ — молярная теплоёмкость тела (системы). | (2) |
Единицей измерения этой величины будет $$ left[{c}_{mathrm{мол}}right]={displaystyle frac{1mathrm{Дж}}{mathrm{моль}·mathrm{К}}}$$.
Получим соотношение между удельной и молярной теплоёмкостями:
| $$ {c}_{mathrm{мол}}={displaystyle frac{Q}{ Delta T·frac{m}{M}}}={displaystyle frac{Q·M}{ Delta T·m}}={c}_{mathrm{уд}}·M$$ — соотношение между молярной и удельной теплоёмкостями | (3) |
Теперь найдём молярную теплоёмкость идеального газа при изобарном и при изохорном процессах.
При изобарном процессе присутствуют и $$ Delta U$$, и $$ {A}^{text{‘}}$$, следовательно:
$$ {c}_{p}={displaystyle frac{Q}{nu · Delta T}}={displaystyle frac{Delta U+Atext{‘}}{nu · Delta T}}={displaystyle frac{Delta U}{nu Delta T}}+{displaystyle frac{Atext{‘}}{nu Delta T}}={displaystyle frac{frac{i}{2}nu R Delta T}{nu Delta T}}+{displaystyle frac{nu R Delta T}{nu Delta T}}={displaystyle frac{iR}{2}}+R=R{displaystyle frac{i+2}{2}}$$,
$${c}_{p}=R{displaystyle frac{i+2}{2}}$$ — молярная теплоёмкость газа при изобарном процессе.
При изохорном процессе работа не совершается, $$ {A}^{text{‘}}=0$$, следовательно:
$$ {c}_{V}={displaystyle frac{Q}{nu Delta T}}={displaystyle frac{Delta U+{A}^{text{‘}}}{nu Delta T}}={displaystyle frac{Delta U}{nu Delta T}}={displaystyle frac{frac{i}{2}nu R Delta T}{nu Delta T}}={displaystyle frac{iR}{2}}$$
$$ {c}_{V}=R{displaystyle frac{i}{2}}$$ — молярная теплоёмкость газа при изохорном процессе.
Соотношение между $$ {c}_{V}$$ и $$ {c}_{р}$$ можно записать в двух формах:
1) $$ {c}_{p}={c}_{V}+R$$ — закон Майера, и
2) $$ gamma ={displaystyle frac{{c}_{p}}{{c}_{V}}}$$ — коэффициент Пуассона.
Т. к. мы уже знаем, чему равно число степеней свободы у разных молекул, то можем вычислить и значения $$ {с}_{р}$$ и $$ gamma $$:
|
формула |
Одноатомные `(i = 3)` |
Двухатомные `(i = 5)` |
|||
| `c_p` |
`R((i+2)/2)` |
`5/2 R` |
`20,775 “Дж”/(“моль”*”К”)` | `7/2 R` | `29,085 “Дж”/(“моль”*”К”)` |
|
`gamma` |
`(i+2)/i` |
`5/3` |
`1,66667` |
`7/5` |
`1,4` |
Воздух представляет собой смесь газов, преимущественно двухатомных азота и кислорода, потому для него эксперименты дают значение $$ gamma approx mathrm{1,4}$$.
Для твёрдых тел теплоёмкости $$ {с}_{р}$$ и $$ {c}_{V}$$ будут почти одинаковыми. Это можно показать следующим образом. По определению $$ C={displaystyle frac{Delta Q}{ Delta T}}$$, но $$ Delta Q= Delta U+pDelta V$$, тогда
$$ {C}_{p}={displaystyle frac{Delta U+pDelta V}{ Delta T}}={displaystyle frac{Delta U}{ Delta T}}+{displaystyle frac{pDelta V}{ Delta T}}={C}_{V}+{displaystyle frac{pDelta V}{ Delta T}}$$.
При нагревании твёрдых или жидких тел изменение объёма составляет около $$ {10}^{-6}$$ первоначального объёма, поэтому вторым слагаемым можно пренебречь по сравнению с первым, что и позволяет говорить о равенстве $$ {c}_{p}={c}_{V}$$.
Для газов $$ frac{ Delta V}{V}$$ на два порядка больше, чем для твёрдых или жидких тел, потому пренебрегать вторым слагаемым нельзя, более того, оно будет составлять заметную долю теплоёмкости $$ {c}_{p}$$.
Роберт Майер является одним из основоположников первого начала термодинамики и механической теории теплоты. В 1842 году он вычислил механический эквивалент теплоты, показывающий соотношение между теплотой и работой или механической энергией.
Уравнение Майера — какие процессы описывает
Уравнение Майера описывает соотношение теплоемкостей 1 моля идеального газа при его постоянном давлении (C_p) и неизменном объеме (C_V:)
(C_p-C_v=R,) где
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
(C_p)— постоянное давление газа;
(C_V) — постоянный объем газа;
R — универсальная газовая постоянная, равная:
R = 8,314 (Дж/(моль*Л).)
Идеальный газ состоит из молекул, взаимодействие между которыми пренебрежимо мало.
Моль — величина, описывающая количество вещества, которое содержит в себе количество частиц, равное постоянной Авогадро (Na):
(Na = 6,022cdot10^{23};моль^{-1})
Понятие теплоемкости
Теплоемкость С — количество тепла, которое нужно передать телу, чтобы повысить его температуру на 1 градус:
(С=d’Q/dT), где
С — удельная теплоемкость;
d’Q — теплота;
dT — температура, [К].
Величина С зависит от процесса, и без него данная формула не имеет смысла. То есть она является функцией.
Теплоемкость называется удельной, когда в системе используется тело с массой в 1 кг.
В зависимости от количественной единицы вещества теплоемкость делится на три вида:
- Мольная — (C_mu), [Дж/кмоль·К].
- Массовая — С, [Дж/кг·К].
- Объемная — С´, [Дж/м3·К].
Величина С зависит от температуры линейно и нелинейно.
В простейших инженерных расчетах может приниматься либо постоянная зависимость теплоемкости от температуры, либо принимают, что теплоемкость не меняется с ее изменением. Тогда ее не учитывают, но расчет получается приблизительным.
В варианте с линейной зависимостью с возрастанием температуры возрастает и величина С.
С возрастанием температуры необходимо больше подводить теплоты к газу, чтобы повысить температуру и теплоемкость на равный интервал. Теплота (q_2) будет больше, чем теплота (q_1.)
В данном интервале температур (t_1-t_2, t_3-t_4,t_n-t_{n+1}) рассчитывают среднюю теплоемкость:
(overline C=frac{q_1}{t_2-t_1}=frac{q_2}{t_4-t_3}), где
(overline C) — средняя теплоемкость, рассчитанная для интервала температур.
Формула для расчета линейной зависимости теплоемкости от температуры:
C=a+b·t,
где a, b — постоянные коэффициенты для конкретного газа,
t — данная температура для газа. Разным температурам соответствуют свои коэффициенты.
Для высчитывания средней теплоемкости при изменении температур от (t_1) до (t_2) (например, от 100⁰С до 160⁰С), пользуются соотношением:
( overline C=a+bfrac{t_1+t_2}2.)
Постоянные коэффициенты для конкретных газов в известных условиях приведены в справочных таблицах.
При нелинейной зависимости теплоемкость и температура могут возрастать различными интервалами. Для расчета нелинейной зависимости С от t применяют формулу:
( overline{C_{t_1}^{t_2}}=frac{C_0^{t_2}cdot t_2-C_0^{t_1}cdot t_1}{t_2-t_1})
( C_0) — начальные теплоемкости при некой температуре. Их можно найти в справочных таблицах «Средняя объемная теплоемкость газов при постоянном давлении».
Формула Майера для теплоемкостей, вывод из первого закона термодинамики
Формула Майера для теплоемкостей
Теплоемкости при постоянном давлении и при постоянном объеме обозначают следующим образом:
- (C_p) и (C_v) — массовые;
- (C’_p) и (C’_v) — объемные;
- (C_{pmu}) и (C_{vmu}) — мольные.
Уравнение Майера для массовых теплоемкостей имеет вид:
( C_p-C_v=R.)
Формулы для расчета этих теплоемкостей следующие:
(C_v=frac R{k-1}; C_p=frac{Rcdot k}{k-1}.)
Для выведения газовой постоянной (R_mu) и формулы Майера для мольных теплоемкостей необходимо все части уравнения умножить на молярную массу:
( mucdot C_p-mucdot C_v=R_mu.)
Для расчета теплоемкости не отдельных газов, а их смеси, применяют формулу для определения массовой теплоемкости газовой смеси, которая рассчитывается как сумма произведений массовых долей компонента, умноженная на массовую теплоемкость данного компонента:
(C_{см}=sum_{i=1}^nleft(g_icdot C_iright))
Мольная теплоемкость смеси рассчитывается как сумма произведений объемных долей, умноженная на (C_mu) этого компонента:
(C_{mucdot см}=sum_{i=1}^nleft(r_icdot C_{mucdot i}right).)
Понятие термодинамики, вывод формулы Майера из первого закона термодинамики
Термодинамика — общая теория теплоты. Она является постулатной наукой, то есть не рассматривает строение системы или вещества и физическую природу теплоты, но использует понятия и физические величины, относящиеся к системе в целом.
Термодинамика изучает макросистемы, состояние которых характеризуют термодинамические параметры: давление, объем, температура и т.д.
Формулировка первого закона термодинамики: при переходе из начального состояния 1 в конечное состояние 2 внутренняя энергия макросистемы складывается из работы, совершенной над системой внешними макроскопическими силами, и из тепла, переданного системе:
( U_2-U_1=Q+A’.)
Как правило, для расчетов используют ту работу А, которую совершила сама система над внешними телами, а не работу, проведенную по отношению к системе.
Вывод уравнения первого начала термодинамики производится с учетом того, что (A’=-A:)
(Q=triangle U+A), где
( triangle U=U_2-U_1.)
Первое начало термодинамики выражается этим правилом: количество теплоты Q, подведенное к макросистеме, идет на совершение системой работы A и изменение ее внутренней энергии (triangle U.)
Для вывода уравнения Майера из первого закона термодинамики учитывают уравнения:
(left(frac{partial U}{partial V_t}right)=0; {left(frac{partial V}{partial t}right)}_p=frac RP.)
Тогда уравнение Майера и количественное выражение первого закона термодинамики будет следующим:
(delta Q=C_vdt+PdV.)
Данное уравнение справедливо для газа, у которого (C_p) и (C_v = const)., и для газа, у которого (C_p=C_p(t)) и (C_p=C_v(t).)
Как записывается соотношение для молярных и массовых теплоемкостей
Опираясь на формулу теплоемкости (C=frac{delta Q}{dT}) и учитывая, что количество вещества Z (количество молей), содержащееся в теле, влияет на его теплоемкость, запишем соотношение для молярных теплоемкостей:
(C_m=frac CZ.)
Задачи на определение теплоемкостей
При расчете удельных теплоемкостей необходимо учитывать отличия между реальными и идеальными газами:
- На теплоемкость идеальных газов влияет не только температура, но и количество в них атомов, и характер процесса. То есть она будет разной, в зависимости от того, сколько атомов имеет тот или иной идеальный газ.
- На теплоемкость реальных газов влияют не только температура, давление и характер процесса, но и их природные свойства.
Теплоемкость принимают в большей степени для идеальных газов, поскольку в основном расчет и ориентация идут на них.
Примеры задач и их решение
Задача 1
Условия:
Один моль идеального газа нагрели. Давление стало пропорционально его объему:
(p=alpha V,)
где α — постоянная.
Найти теплоемкость газа.
Решение:
Помня о том, что газ при разных способах нагревания совершает разную работу, делаем вывод, что теплоемкость будет различной и при разных температурах.
Используя первое начало термодинамики для теплоемкости идеального газа:
( triangle Q=triangle U+triangle A), (1)
получим:
(C=C_v+frac{triangle A}{triangle T}.) (2)
Чтобы найти теплоемкость С необходимо определить работу ∆А, которую совершает газ в рассматриваемом процессе при нагревании его на ∆T.
Совершаемая газом работа ∆А при расширении в условиях постоянного давления вычисляется по формуле:
(triangle A=ptriangle V.) (3)
В условиях, когда давление не остается постоянным, для вычисления работы ∆A необходимо ∆V выбрать настолько малым, чтобы изменением давления газа при расширении можно было бы им пренебречь.
Для этого применим уравнение состояния:
(pV=RT.) (4)
Пусть при изменении температуры газа на ∆T его объем изменился на ∆V, а давление — на ∆p.
Уравнение (left(p+triangle pright)(V+triangle V)=R(T+triangle T)) (5) связывает эти изменения.
Вычитаем выражения (4) и (5) и пренебрегаем (triangle ptriangle V), получаем:
( ptriangle V=Vtriangle p=Rtriangle T) (6).
Возьмем во внимание формулу (1) и учтем, что в данном процессе давление газа пропорционально его объему. Получим:
( Vtriangle p=alpha Vtriangle V=ptriangle V) (7).
Подставляем V∆p из выражения (6) и (7), найдем
( triangle A=ptriangle V=frac12Rtriangle T).
С помощью формулы (2) найдем теплоемкость газа в этом процессе:
( C=C_v+frac R2.)
Поскольку (C_v) и (C_p) связаны, представим теплоемкость и получим ответ:
(C=frac12left(C_v+C_pright).)
Задача 2
Условия:
Имеется цилиндр, у которого стенки AC, BD, крышка CD и поршень MN не проводят тепло. Дно AB проводит тепло. Поршень движется в цилиндре без трения. Сверху и снизу поршня присутствует по одному молю идеального газа с показателем адиабаты γ. Молярная теплоемкость газа Cv постоянна по объему. При квазистатическом изменении температуры первого газа поршень начинает перемещение.
Выразите теплоемкость первого газа (C_1) при таком процессе через объемы газов (V_1) и (V_2). Чему равна теплоемкость второго газа (C_2?)
Решение:
Элементарное количество тепла, получаемое первым газом:
(delta Q=C_vdT_1+P_1dV_1=C_vdT_1+RT_1dV_1/V_1.)
А вторым газом — (delta Q_2=0.)
Поэтому (C_2=0) и (C_vdT_2+RT_2dV_2/V_2=0.)
Из равенства давлений (P_1) и (P_2) следует:
(V_1/V_2=T_1/T_2,)
откуда (dV_1/V_1+dV_2/V_1=dT_1/T_1-dT_2/T_2.)
Так как объем системы не изменяется, то
(dV_1+dV_2=0.)
Исключая (dV_2) и (dT_2), получим:(left(frac1{v_1}+frac1{v_2}+frac R{C_v}frac1{v_2}right)dV_1=frac{dT_1}{T_1}. ) Используя также уравнение Майера (C_p-C_v=R), найдем
(delta Q_1=left(C_v+Rfrac{V_2}{V_2+gamma V_1}right)dT_1.)
Следовательно:
(C_1=C_v+frac{V_2}{V_2+gamma V_1}R=frac{V_1+V_2}{V_2+gamma V_1}gamma Cv..)
При (V_1=V_2)
(C_1=2gamma C_v/left(gamma+1right).)
Задача 3
Условия:
Определите удельную теплоемкость кислорода при постоянном объеме. Газ нагрет до очень высокой температуры, приблизительно до нескольких килоэлектрон-вольт.
Решение:
(C_v=frac{27}{32}R=1,68;кал/(гcdot К)approx7,0;Дж/(гcdot К).)
Задача 4
Условие:
Посчитайте по классической теории удельной теплоемкости при постоянном давлении газа следующего молярного состава:
He — 20 %, H2 — 30 %, CH4 — 50 %.
Молярный состав — количество молей данного газа по отношению к общему числу молей газовой смеси.
Решение:
( C_p=frac{71}{188}Rapprox0,75;кал/(гcdot К)approx3,14;Дж/(гcdot К))
Задача 5
Условие:
Найдите полярную теплоемкость водорода (C_v). Коэффициент диссоциации α = 0,25. Молярная теплоемкость атомарного водорода (C_{v1} = 2,94) (кал/(моль·⁰С)). (C_{v2})молекулярного водорода (= 4,9) (кал/(моль·⁰С).)
Решение:
( C_v=(2C_{v1}-C_{v2})alpha+C_{v2}=5,15;кал/(мольcdot К)approx21,5;Дж/(мольcdot К).)



