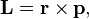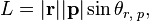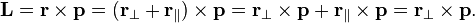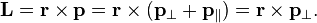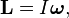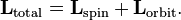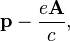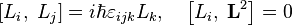| Момент импульса | |
|---|---|
 |
|
| Размерность | L2MT−1 |
| Единицы измерения | |
| СИ | м2·кг/с |
| СГС | см2·г/с |
| Примечания | |
| псевдовектор |
Моме́нт и́мпульса (момент импульса относительно точки, также: кинетический момент, угловой момент, орбитальный момент, момент количества движения) — физическая величина, характеризующая количество вращательного движения и зависящая от того, сколько массы вращается, как она распределена в пространстве и с какой угловой скоростью происходит вращение[1].
Для одной материальной точки момент импульса равен векторному произведению радиус-вектора точки на её импульс, для системы точек — сумме таких произведений. Стандартное обозначение: 

Момент импульса замкнутой системы сохраняется. Он является одним из трёх аддитивных (энергия, импульс, момент импульса) интегралов движения. При наличии внешних сил производная момента импульса по времени равна моменту сил (относительно того же начала O).
Основное использование понятия момента импульса относится к задачам, связанным с реальным вращением (особенно при наличии центральной или осевой симметрии; тогда О обычно выбирается в центре или на оси). Но величина 
В случае вращения твёрдого тела вокруг фиксированной оси часто используется не сам момент импульса, а его проекция 
Понятие момента импульса было изначально введено в классической механике, но имеет обобщения в квантовой механике и электродинамике.
Момент импульса в классической механике[править | править код]

Связь между силой F, моментом силы τ, импульсом 
Определение[править | править код]
Момент импульса 
,
где 

Из определения момента импульса следует его аддитивность: для системы, состоящей из нескольких материальных точек, выполняется
.
Количество частиц может быть бесконечным, например в случае твёрдого тела с распределённой массой.
Так как момент импульса задаётся векторным произведением, он является псевдовектором, перпендикулярным обоим векторам 

Момент импульса можно вычислить относительно любого начала отсчета O (получающиеся при этом разные значения 
Выбор точки O иногда связан с характером задачи. Так, при рассмотрении орбитального движения планеты вокруг Солнца за начало отсчёта естественно взять Солнце, а при анализе её же собственного вращения — центр этой планеты. Естественно, получатся два разных момента импульса: 

Вычисление в общем случае[править | править код]
Если имеется материальная точка массой 



.
Чтобы рассчитать момент импульса тела, его надо разбить на бесконечно малые кусочки 

.
На практике 
.
Если считать, что 
Случай фиксированной оси[править | править код]
Важным случаем использования понятия «момент импульса» является движение вокруг неизменной оси. В такой ситуации часто рассматривают не сам момент импульса (псевдовектор), а его проекцию на ось как псевдоскаляр, знак которого зависит от направления вращения:
.
Параллельность-перпендикулярность (




.
Если при этом все точки тела движутся по окружностям (вращаются) с одинаковой угловой скоростью 


или
.
Величину 

Для абсолютно твёрдого тела, величина последнего интеграла называется моментом инерции относительно оси вращения и обозначается 


Сохранение момента импульса[править | править код]
Закон сохранения момента импульса: суммарный момент импульса относительно любой неподвижной точки для замкнутой системы остается постоянным со временем.
Производная момента импульса по времени есть момент силы:
,
Таким образом, требование замкнутости системы может быть ослаблено до требования равенства нулю главного (суммарного по всем частицам 
,
где 
По теореме Нётер закон сохранения момента импульса следует из изотропии пространства, то есть из инвариантности пространства по отношению к повороту на произвольный угол. При повороте на произвольный бесконечно малый угол 




С учётом 


Теперь, пользуясь свойством смешанного произведения, совершим циклическую перестановку векторов, в результате чего получим, вынося общий множитель:
где 



Смежные понятия[править | править код]
При рассмотрении задач, связанных с вращением, фигурируют понятия, частично упоминавшиеся выше:
- момент импульса относительно оси (термин состоит из четырёх слов) — проекция момента импульса на ось;
- момент инерции твёрдого тела (см. также моменты инерции некоторых тел);
- момент силы (он же: крутящий момент, вращательный момент, вертящий момент);
- импульс момента силы
(единица измерения — Н·м·с) — мера воздействия момента силы относительно данной оси за данный промежуток времени (во вращательном движении).
Несмотря на созвучность с «моментом импульса», эти понятия не синонимичны термину «момент импульса» и несут самостоятельный смысл.
Момент импульса в электродинамике[править | править код]
При описании движения заряженной частицы в электромагнитном поле канонический импульс 

где 



где 
Момент импульса в квантовой механике[править | править код]
Оператор момента[править | править код]
В квантовой механике момент импульса квантуется, то есть он может изменяться только по «квантовым уровням» между точно определёнными значениями. Проекция на любую ось момента импульса частиц, обусловленного их пространственным движением, должна быть целым числом, умноженным на 


Эксперименты показывают, что большинство частиц имеют постоянный внутренний момент импульса, который не зависит от их движения через пространство. Этот спиновый момент импульса всегда кратен 


В классическом определении момент импульса зависит от 6 переменных 





Математически полный момент импульса в квантовой механике определяется как оператор физической величины из суммы двух частей, связанных с пространственным движением — в атомной физике такой момент называют орбитальным, и внутренним спином частицы — соответственно, спиновым. Первый оператор действует на пространственные зависимости волновой функции:
,
где 

,
где 
,
где 
и даже более важные подстановки с гамильтонианом частицы без заряда и спина:
.
Симметрия вращения[править | править код]
Операторы момента импульса обычно встречаются при решении задач сферической симметрии в сферических координатах. Тогда момент импульса в пространственном отображении:
Когда находят собственные значения этого оператора, получают следующее:
где 


— сферические функции.
Примечания[править | править код]
- ↑ Pivarski, Jim Spin. Symmetry Magazine (март 2013). Дата обращения: 28 апреля 2014. Архивировано 15 апреля 2014 года.
- ↑ [Информация с сайта Нобелевского комитета (англ.). Дата обращения: 3 ноября 2017. Архивировано 18 мая 2008 года. Информация с сайта Нобелевского комитета (англ.)]
Литература[править | править код]
- Биденхарн Л., Лаук Дж. Угловой момент в квантовой физике. Теория и приложения. — М.: Мир, 1984. — Т. 1. — 302 с.
- Блохинцев Д. И. Основы квантовой механики. — М.: Наука, 1976. — 664 с.
- Боум А. Квантовая механика: основы и приложения. — М.: Мир, 1990. — 720 с.
- Варшалович Д. А., Москалев А. Н., Херсонский В. К. Квантовая теория углового момента. — Л.: Наука, 1975. — 441 с.
- Зар Р. Теория углового момента. О пространственных эффектах в физике и химии. — М.: Мир, 1993. — 352 с.
При решении задач на движение тел в пространстве часто используют формулы сохранения кинетической энергии и импульса. Оказывается, что аналогичные выражения существуют и для вращающихся тел. В данной статье подробно рассматривается закон сохранения момента импульса (формулы соответствующие также приводятся) и дается пример решения задачи.
Процесс вращения и момент импульса
Перед тем как перейти к рассмотрению формулы закона сохранения момента импульса, необходимо познакомиться с этим физическим понятием. Проще всего его можно ввести, если воспользоваться рисунком ниже.
 Вам будет интересно:Нарративный анализ: понятие и применение
Вам будет интересно:Нарративный анализ: понятие и применение
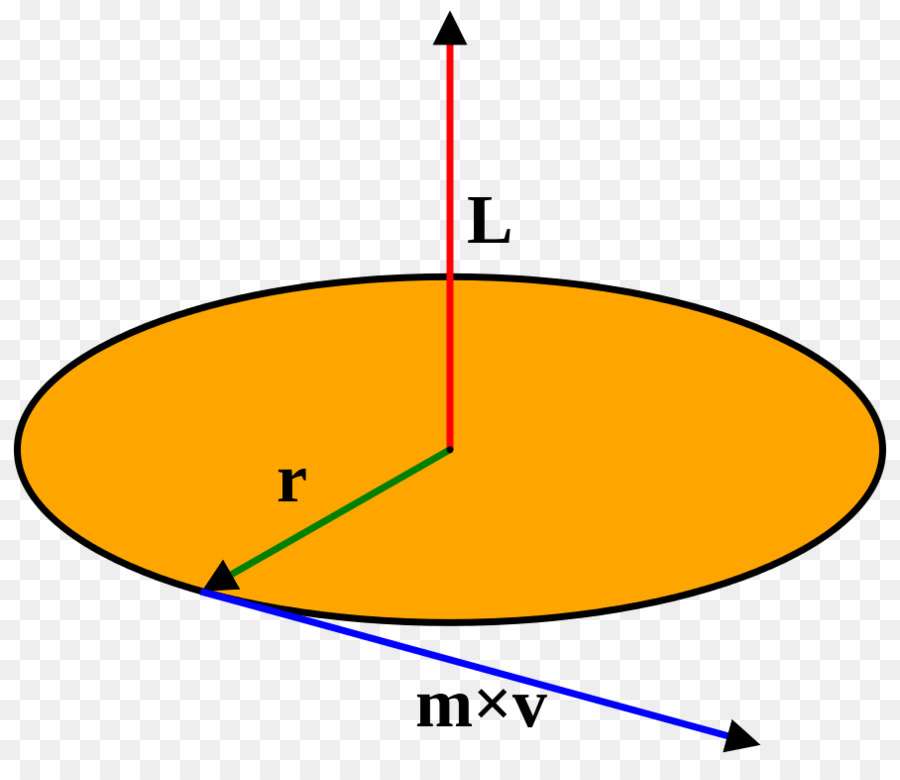
На рисунке видно, что на конце вектора r¯, направленного от оси вращения и перпендикулярного ей, имеется некоторая материальная точка массой m. Эта точка движется по окружности названного радиуса с линейной скоростью v¯. Из физики известно, что произведение массы на линейную скорость называется импульсом (p¯). Теперь стоит ввести новую величину:
 Вам будет интересно:Сульфат стронция: нахождение в природе, растворимость, применение
Вам будет интересно:Сульфат стронция: нахождение в природе, растворимость, применение
L¯ = r¯*m*v¯ = r¯*p¯.
Здесь векторная величина L¯ представляет собой момент импульса. Чтобы перейти к скалярной форме записи, необходимо знать модули соответствующих значений r¯ и p¯, а также угол θ между ними. Скалярная формула для L имеет вид:
L = r*m*v*sin(θ) = r*p*sin(θ).
На рисунке выше угол θ является прямым, поэтому можно просто записать:
L = r*m*v = r*p.
Из записанных выражений следует, что единицей измерения для L будут кг*м2/с.
Направление вектора момента импульса
Поскольку рассматриваемая величина является вектором (результат векторного произведения), то она будет иметь определенное направление. Из свойств произведения двух векторов следует, что их результат даст третий вектор, перпендикулярный плоскости, образованной первыми двумя. При этом направлен он будет таким образом, что если смотреть с его конца, то тело будет вращаться против часовой стрелки.
 Вам будет интересно:Самые старые горы в мире: где находятся, фото, названия
Вам будет интересно:Самые старые горы в мире: где находятся, фото, названия
Результат применения этого правила показан на рисунке в предыдущем пункте. Из него видно, что L¯ направлен вверх, поскольку, если смотреть на тело сверху, его движение будет происходить против хода стрелки часов. При решении задач важно учитывать направление во время перехода к скалярной форме записи. Так, рассмотренный момент импульса считается положительным. Если бы тело вращалось по часовой стрелке, тогда в скалярной формуле перед L следовало бы поставить знак минуса (-L).
Аналогия с линейным импульсом
Рассматривая тему момента импульса и закона его сохранения, можно проделать один математический трюк – преобразовать выражение для L¯, помножив и поделив его на r2. Тогда получится:
L¯ = r*m*v¯*r2/r2 = m*r2*v¯/r.
В этом выражении отношение скорости к радиусу вращения называется угловой скоростью. Она обычно обозначается буквой греческого алфавита ω. Эта величина показывает, на сколько градусов (радиан) сделает поворот тело по орбите своего вращения за единицу времени. В свою очередь, произведение массы на квадрат радиуса – это тоже физическая величина, имеющая собственное название. Обозначают ее I и называют моментом инерции.
В итоге формула для момента импульса преобразуется в следующую форму записи:
L¯ = I *ω¯, где ω¯= v¯/r и I=m*r2.
Выражение демонстрирует, что направление момента импульса L¯ и угловой скорости ω¯ совпадают для системы, состоящей из вращающейся материальной точки. Особый интерес представляет величина I. Ниже она рассмотрена подробнее.
Момент инерции тела
Введенная величина I характеризует “сопротивляемость” тела любому изменению скорости его вращения. То есть она играет точно такую же роль, что и инерция тела при линейном перемещении объекта. По сути I для кругового движения с физической точки зрения означает то же самое, что и масса при линейном движении.
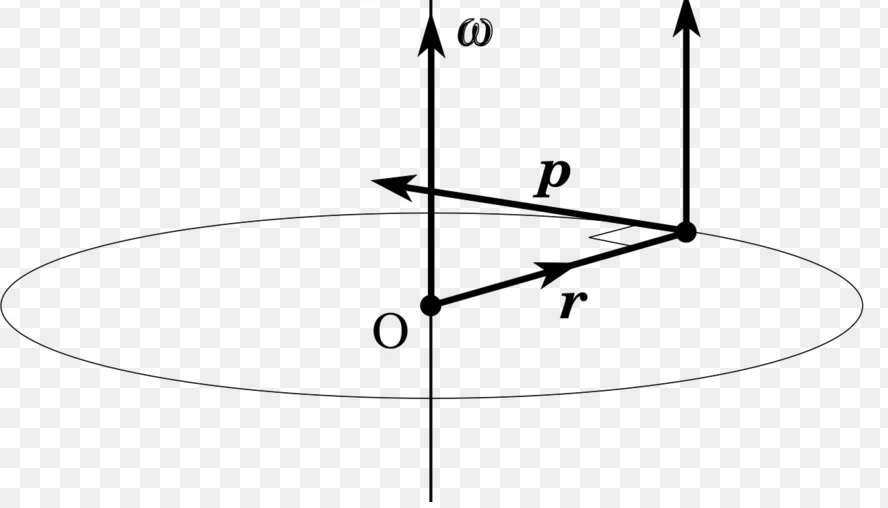
Как было показано, для материальной точки с массой m, вращающейся вокруг оси на расстоянии от нее r, момент инерции рассчитать просто (I = m*r2), однако для любых других тел этот расчет будет несколько сложным, поскольку предполагает использование интеграла.
Для тела произвольной формы I можно определить при помощи следующего выражения:
 Вам будет интересно:Архаический период Древней Греции (IX–VIII вв. до н.э.)
Вам будет интересно:Архаический период Древней Греции (IX–VIII вв. до н.э.)
I = ∫m(r2*dm) = ∫V(r2*ρ*dV), где ρ – плотность материала.
Выражения выше означают, что для вычисления момента инерции следует разбить все тело на бесконечно малые объемы dV, умножить их на квадрат расстояния до оси вращения и на плотность и просуммировать.
Для тел разной формы эта задача решена. Ниже приводятся данные для некоторых из них.
Материальная точка: I = m*r2.
Диск или цилиндр: I = 1/2*m*r2.
Стержень длиной l, закрепленный по центру: I = 1/12*m*l2.
Шар: I = 2/5*m*r2.
Момент инерции зависит от распределенной массы тела относительно оси вращения: чем дальше от оси будет находиться большая часть массы, тем больше будет I для системы.
Изменение момента импульса во времени
Рассматривая момент импульса и закон сохранения момента импульса в физике, можно решить простую проблему: определить, как и за счет чего он будет изменяться во времени. Для этого следует взять производную по dt:
dL¯/dt = d(r¯*m*v¯)/dt = m*v¯*dr¯/dt+r*m*dv¯/dt.
Первое слагаемое здесь равно нулю, поскольку dr¯/dt = v¯ и произведение векторов v¯*v¯ = 0 (sin(0) = 0). Второе же слагаемое может быть переписано следующим образом:
dL¯/dt =r*m*a¯, где ускорение a = dv¯/dt, откуда:
dL¯/dt =r*F¯=M¯.
Величина M¯, согласно определению, называется моментом силы. Она характеризует действие силы F¯ на материальную точку массой m, расположенную на расстоянии r от оси вращения.
Что показывает полученное выражение? Оно демонстрирует, что изменение момента импульса L¯ возможно только за счет действия момента силы M¯. Эта формула – закон сохранения момента импульса точки: если M¯=0, то dL¯/dt = 0 и L¯ является постоянной величиной.
Какие моменты сил могут изменить L¯ системы?
Существует два вида моментов сил M¯: внешние и внутренние. Первые связаны с силовым воздействием на элементы системы со стороны любых внешних сил, вторые же возникают за счет взаимодействия частей системы.
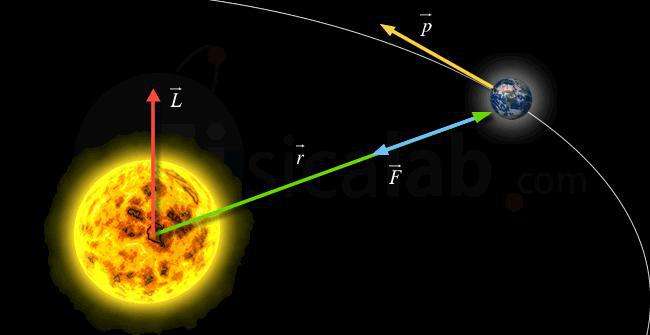
Согласно третьему закону Ньютона, любой силе действия соответствует направленная противоположно сила противодействия. Это означает, что суммарный момент силы любых взаимодействий внутри системы всегда равен нулю, то есть он не может повлиять на изменения момента импульса.
Величина L¯ может измениться только за счет внешних моментов сил.
Формула закона сохранения момента импульса
Формула для записи выражения сохранения величины L¯ в случае, если сумма внешних моментов сил равна нулю, имеет следующий вид:
I1*ω1 = I2*ω2.
Любые изменения момента инерции системы пропорционально отражаются на изменении угловой скорости таким образом, что произведение I*ω не меняет своего значения.
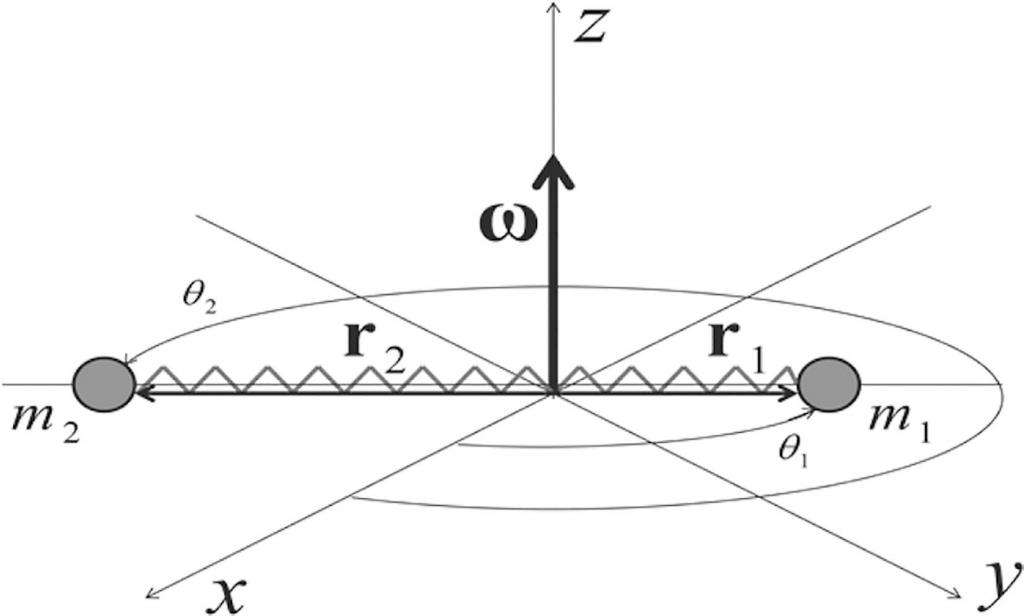
Вид этого выражения аналогичен закону сохранения линейного импульса (роль массы играет I, а роль скорости – ω). Если развивать аналогию дальше, то, помимо этого выражения, можно записать еще одно, которое будет отражать сохранение кинетической энергии вращения:
E = I *(ω)2/2 = const.
Применение закона сохранения момента импульса находит себя в целом ряде процессов и явлений, которые кратко охарактеризованы ниже.
Примеры использования закона сохранения величины L¯
Следующие примеры закона сохранения момента импульса имеют важное значение для соответствующих сфер деятельности.
- Любой вид спорта, где необходимо совершать прыжки с вращением. Например, балерина или спортсмен по фигурному катанию начинает исполнение пируэта с вращением, разведя широко руки и отодвинув ногу от центра тяжести своего тела. Затем он прижимает ногу ближе к опорной и руки ближе к телу, уменьшая тем самым момент инерции (большая часть точек тела расположена близко к оси вращения). По закону сохранения величины L, должна увеличиться его угловая скорость вращения ω.

- Для изменения направления ориентации относительно Земли какого-либо искусственного спутника. Выполняется это так: спутник имеет специальный тяжелый “маховик”, его приводит в движение электромотор. Общий момент импульса должен сохраняться, поэтому сам спутник начинает вращаться в противоположную сторону. Когда он примет нужную ориентацию в пространстве, маховик останавливают, и спутник также перестает вращаться.
- Эволюция звезд. По мере того как звезда сжигает свое водородное топливо, силы гравитации начинают преобладать над давлением ее плазмы. Этот факт приводит к уменьшению радиуса звезды до небольших размеров и, как следствие, к сильному увеличению скорости вращения угловой. Например, установлено, что нейтронные звезды, имеющие диаметр несколько километров, вращаются с гигантскими скоростями, делая один оборот за доли миллисекунды.

Решение задачи на закон сохранения L¯
Учеными установлено, что через несколько миллиардов лет Солнце, исчерпав энергетические запасы, превратится в “белого карлика”. Необходимо рассчитать, с какой скоростью оно будет вращаться вокруг оси.
Для начала необходимо выписать значения необходимых величин, которые можно взять из литературы. Итак, сейчас данная звезда имеет радиус 696 000 км и один оборот вокруг своей оси делает за 25,4 земных суток (значение для области экватора). Когда она подойдет к концу своего эволюционного пути, то сожмется до размеров 7000 км (порядка радиуса Земли).

Полагая, что Солнце – идеальный шар, можно воспользоваться формулой закона сохранения момента импульса для решения этой задачи. Нужно перевести сутки в секунды и километры в метры, получается:
L = I*ω = 2/5*m*r12*ω1 = 2/5*m*r22*ω2.
Откуда следует:
ω2 = (r1/r2)2*ω1 = (696000000/7000000)2*2*3,1416/(25,4*24*3600)= 0,0283 рад/с.
Здесь использовалась формула для угловой скорости (ω = 2*pi/T, где T – период вращения в секундах). При выполнении вычислений также было сделано предположение, что масса Солнца остается постоянной (это не верно, поскольку она будет уменьшаться. Тем не менее полученное значение ω2 является нижней границей, то есть в действительности Солнце-карлик будет вращаться еще быстрее).
Поскольку полный оборот – это 2*pi радиан, тогда получится:
T2 = 2*pi/ω2 = 222 с.
То есть в конце своего жизненного цикла данная звезда будет делать один оборот вокруг своей оси быстрее, чем за 222 секунды.
Импульс
тела
(или
количество
движения)
− это векторная физическая величина,
равная произведению массы тела на его
скорость.
![]()
Единица
измерения импульса в СИ – кг*м/с
Закон
сохранения импульса:
если сумма внешних сил, действующих на
точки системы, равна нулю, то сумма
импульсов всех точек системы остается
величиной постоянной.
15. Энергия. Кинетическая и потенциальная энергия. Теорема об изменении кинетической энергии. Закон сохранения энергии в механики.
Работа
− это
количественная характеристика процесса
обмена энергией между взаимодействующими
телами.
Кинетическая
энергия
− это энергия
тела, обусловленная его механическим
движением ![]()
Теорема
об изменении кинетической энергии:
![]()
Потенциальная
энергия
− часть общей механической энергии
системы, зависящей от взаимного
расположения материальных точек системы
и их положения во внешнем силовом поле.
К1
+ П1
= К2
+ П2
= const (1)
Величину
E
=
К + П называют полной
механической энергией
системы.
Из
соотношения (1) следует закон
сохранения полной механической энергии:
полная механическая энергия системы,
на материальные точки которой действуют
только консервативные силы, с течением
времени не изменяется:
E
= const.
16. Момент импульса материальной точки относительно некоторого центра. Чему равен модуль вектора момента импульса? Что называется плечом импульса? Момент импульса в си.
Момент
импульса
−
векторная величина, равная векторному
произведению радиус-вектора
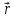
точки,
проведенного из центра на ее импульс
 .
.
![]()
Модуль
вектора момента импульса
относительно центра или оси − есть
скалярная величина, равная произведению
им-пульса p на плечо импульса d
относительно
этой оси.
Модуль
вектора момента импульса равен:
![]()
где
d
−
плечо импульса относительно точки О.
Плечо
импульса
− это расстояние, измеряемое по
перпендикуляру от оси вращения до
линии, вдоль которой направлен импульс.
В
системе СИ момент
импульса измеряется в единицах джоуль-секунда;
Дж·с.
17. Как определяется направление вектора момента импульса.
Направление
момента импульса совпадает с направлением
поступательного движения правого винта
при его вращении от радиус-вектора
 к импульсу
к импульсу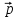 ,
,
и
он перпендикулярен как вектор
 ,
,
так и вектору .
.

18.
Момент силы материальной точки
относительно некоторого центра.
Момент
силы
– векторная
величина, равная векторному произведению
радиус-вектора
 точки, проведенному из полюса в точку
точки, проведенному из полюса в точку
приложения силы, на силу :
:
![]()
19.
Формула для определения модуля вектора
момента силы. Плечо силы. Момент силы
в СИ.
Модуль
вектора момента силы равен:
![]()
где
d
=
r
sin
α − плечо силы относительно точки О.
Плечо
силы
−
это расстояние, измеряемое по
перпендикуляру от оси вращения до
линии, вдоль которой действует сила.
Момент
силы измеряется
в ньютон-метрах. 1
Н·м
20.
Как определяется направление вектора
момента силы.
Направление
момента силы

совпадает
с направлением поступательного движения
правого винта при его вращении от
радиус-вектора
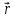 к силе
к силе ,
,
и он перпендикулярен как вектору ,
,
так и вектору

21.
Момент инерции тела относительно данной
оси. Физический смысл момента инерции.
Момент инерции в СИ
Моментом
инерции
твердого
тела относительно данной оси называется
физическая величина, являющаяся мерой
инертности тела во вращательном движении
вокруг этой оси и равная сумме произведений
масс всех частиц тела на квадраты их
расстояний от той же оси:

[I]
= 1 кг · м2
Физический
смысл момента инерции
можно
определить из выражения:
![]()
Момент
инерции тела является мерой инерции
тела при вращательном движении.
22.
Теорема Штейнера. Правило аддитивности
для момента инерции.
Теорема
Штейнера:
момент инерции тела Iz
относительно
произвольной оси равен сумме момента
инерции Ic
относительно
оси, параллельной данной и проходящей
через центр масс тела, и произведения
массы тела m
на квадрат расстояния a между осями:
![]()
Правило
аддитивности:
сумма моментов инерции частей системы
относительно оси равен моменту инерции
системы относительно данной оси:
![]()
23.
Формула для расчета работы силы при
вращении тела.
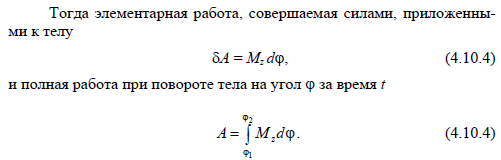
24.
Основное уравнение динамики вращательного
движения относительно точки. Закон
сохранения момента импульса.
Уравнение
динамики вращательного движения
относительно точки
(или
иначе закон
изменения момента импульса механической
системы)
![]()
Производная
по времени от момента импульса системы
относительно точки равна сумме моментов
внешних сил относительно этой точки.
Закон
сохранения момента импульса:
если момент внешних сил действующих
на механическую систему относительно
центра оси равен нулю, то момент импульса
системы остаётся величиной постоянной.
25.
Основное уравнение динамики вращательного
движения относительно неподвижной
оси. Закон сохранения проекции момента
импульса.
Основное
уравнение динамики вращательного
движения относительно неподвижной
оси:
![]()
Закон
сохранения проекции момента импульса:
![]()
Если
проекцию моментов внешних сил относительно
оси z равна нулю, то момент импульса
тела относительно этой оси остаётся
величиной постоянной.
26.
Кинетическая энергия тела вращающегося
вокруг неподвижной оси. Кинетическая
энергия тела при плоском движении.


27.
Свободные
гармонические колебания и их
характеристики( смещение, амплитуда,
частота и период колебаний, циклическая
частота фаз и начальная фаза колебаний).
Колебания
−
это движения или процессы, обладающие
той или иной степенью повторяемости
во времени.
Периодические
колебания
− значения физических величин,
изменяющихся в процессе колебания,
повторяются через равные промежутки
времени.
Гармонические
колебания
−
это периодическое изменение во времени
физической величины, происходящее по
закону косинуса или синуса. Уравнение
гармонических колебаний имеет вид:


28.
Дать определение частоты
обращения
тела. Дайте определение периода
обращения
тела.
Равномерное
движение по окружности характеризуют
периодом и частотой
обращения.
Период обращения – это время,
за которое совершается один оборот.
Если, например, за время t = 4 с тело,
двигаясь по окружности, совершило n = 2
оборота, то легко сообразить, что один
оборот длился 2 с. Это
и
есть период обращения.
29.Характеристики
колебательной системы. Коэффициент
затухания и логарифмический декремент
затухания. Время релаксации. Добротность
колебательной системы.
Во
всякой реальной колебательной системе
имеются силы сопротивления, действие
которых приводит к уменьшению энергии
системы. Если убыль энергии не восполняется
за счет работы внешних сил, то колебания
будут затухать.



30.
Уравнение состояния идеального
газа(Клапейрона – Менделеева).
Уравнением
состояния идеального газа или
уравнение
Менделеева − Клапейрона.
![]()
31.
Внутренняя энергия идеального газа.
Дать определение числа степеней свободы
молекулы газа. Работа газа при изменении
его объёма.

Число
степеней свободы
− это число
независимых координат (переменных),
которые полностью определяют положение
системы в пространстве.
Молекулу
одноатомного
газа
рассматривают как материальную точку,
которой приписывают три степени свободы
поступательного движения. Молекула
двухатомного
газа рассматривается как совокупность
двух материальных точек,
связанных
недеформированной связью. Эта система
кроме трех степеней свободы поступательного
движения имеет еще две степени свободы
вращательного движения. Трехатомная
молекула имеет шесть степеней свободы:
три поступательные и три вращательные.
Столько же степеней свободы будут иметь
и многоатомные молекулы (четырех, пяти
и т. д.).

как определить направление момента импульса тела
Влад Шориков
Ученик
(118),
закрыт
5 лет назад
Дивергент
Высший разум
(1537974)
9 лет назад
Направление момента импульса L определяется как направление векторного произведения импульса p и радиус-вектора r: p х r=L. В векторном произведении а х b=с вектор с направлен так, что тройка векторов аbc является правой. Проще простого. Указательный палец ПРАВОЙ руки направляешь по вектору а, средний – по вектору b, Оттопыренный большой палец покажет направление вектора с.

Главная
»
Самолетостроение
»
Физика
»
Момент импульса. Закон сохранения момента импульса. Основной закон динамики вращательного движения.
Момент импульса. Закон сохранения момента импульса. Основной закон динамики вращательного движения.
Моме́нт и́мпульса (кинетический момент, угловой момент, орбитальный момент, момент количества движения) характеризует количество вращательного движения. Величина, зависящая от того, сколько массы вращается, как она распределена относительно оси вращения и с какой скоростью происходит вращение.
Замечание: момент импульса относительно точки — это псевдовектор, а момент импульса относительно оси — скалярная величина.
Следует учесть, что вращение здесь понимается в широком смысле, не только как регулярное вращение вокруг оси. Например, даже при прямолинейном движении тела мимо произвольной воображаемой точки оно также обладает моментом импульса. Наибольшую роль момент импульса играет при описании собственно вращательного движения.
Момент импульса замкнутой системы сохраняется.
Момент импульса в классической механике
Связь между импульсом  и моментом
и моментом 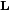
Определение
Момент импульса 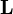 частицы относительно некоторого начала отсчёта определяется векторным произведением её радиус-вектора и импульса:
частицы относительно некоторого начала отсчёта определяется векторным произведением её радиус-вектора и импульса:
где  — радиус-вектор частицы относительно выбранного неподвижного в данной системе отсчёта начала отсчёта,
— радиус-вектор частицы относительно выбранного неподвижного в данной системе отсчёта начала отсчёта, 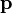 — импульс частицы.
— импульс частицы.
В системе СИ момент импульса измеряется в единицах джоуль-секунда; Дж·с.
Из определения момента импульса следует его аддитивность. Так, для системы частиц выполняется выражение:
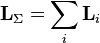 .
.
Вычисление момента
Так как момент импульса определяется векторным произведением, он является псевдовектором, перпендикулярным обоим векторам  и
и 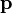 . Однако, в случаях вращения вокруг неизменной оси, бывает удобно рассматривать не момент импульса как псевдовектор, а его проекцию на ось вращения как скаляр, знак которого зависит от направления вращения. Если выбрана такая ось, проходящая через начало отсчёта, для вычисления проекции углового момента на неё можно указать ряд рецептов в соответствии с общими правилами нахождения векторного произведения двух векторов.
. Однако, в случаях вращения вокруг неизменной оси, бывает удобно рассматривать не момент импульса как псевдовектор, а его проекцию на ось вращения как скаляр, знак которого зависит от направления вращения. Если выбрана такая ось, проходящая через начало отсчёта, для вычисления проекции углового момента на неё можно указать ряд рецептов в соответствии с общими правилами нахождения векторного произведения двух векторов.
где  — угол между
— угол между  и
и 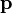 , определяемый так, чтобы поворот от
, определяемый так, чтобы поворот от  к
к 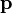 производился против часовой стрелки с точки зрения наблюдателя, находящегося на положительной части оси вращения. Направление поворота важно при вычислении, так как определяет знак искомой проекции.
производился против часовой стрелки с точки зрения наблюдателя, находящегося на положительной части оси вращения. Направление поворота важно при вычислении, так как определяет знак искомой проекции.
Запишем  в виде
в виде 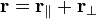 , где
, где 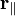 — составляющая радиус-вектора, параллельная вектору импульса, а
— составляющая радиус-вектора, параллельная вектору импульса, а  — аналогично, перпендикулярная ему.
— аналогично, перпендикулярная ему.  является, по сути, расстоянием от оси вращения до вектора
является, по сути, расстоянием от оси вращения до вектора 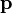 , которое обычно называют «плечом». Аналогично можно разделить вектор импульса на две составляющие: параллельную радиус-вектору
, которое обычно называют «плечом». Аналогично можно разделить вектор импульса на две составляющие: параллельную радиус-вектору 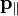 и перпендикулярную ему
и перпендикулярную ему  . Теперь, используя линейность векторного произведения, а также свойство, согласно которому произведение параллельных векторов равно нулю, можно получить еще два выражения для
. Теперь, используя линейность векторного произведения, а также свойство, согласно которому произведение параллельных векторов равно нулю, можно получить еще два выражения для 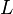 .
.
Для систем, совершающих вращение вокруг одной из осей симметрии (вообще говоря, вокруг так называемых главных осей инерции), справедливо соотношение
где 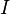 — момент инерции относительно оси вращения,
— момент инерции относительно оси вращения, 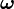 — вектор угловой скорости.
— вектор угловой скорости.
В общем случае вектор момента связан с вектором угловой скорости линейным оператором момента инерции:
Сохранение углового момента
Закон сохранения момента импульса (закон сохранения углового момента): векторная сумма всех моментов импульса относительно любой оси для замкнутой системы остается постоянной. В соответствии с этим, момент импульса замкнутой системы относительно любой неподвижной точки не изменяется со временем.
Производная момента импульса по времени есть момент силы:
Таким образом, требование системы быть «замкнутой», означает равенство нулю главного (суммарного) момента внешних сил:
где 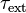 — момент одной из сил, приложенных к системе частиц.
— момент одной из сил, приложенных к системе частиц.
Математически закон сохранения момента импульса следует из изотропии пространства, то есть из инвариантности пространства по отношению к повороту на произвольный угол. При повороте на произвольный бесконечно малый угол 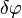 , радиус-вектор частицы с номером
, радиус-вектор частицы с номером 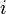 изменятся на
изменятся на 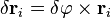 , а скорости —
, а скорости —  . Функция Лагранжа
. Функция Лагранжа 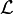 системы при таком повороте не изменится, вследствие изотропии пространства. Поэтому
системы при таком повороте не изменится, вследствие изотропии пространства. Поэтому
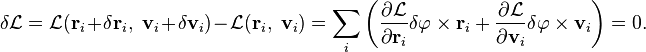
С учетом 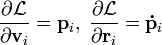 , где
, где 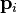 — обобщенный импульс
— обобщенный импульс 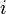 -той частицы, каждое слагаемое в сумме из последнего выражения можно переписать в виде
-той частицы, каждое слагаемое в сумме из последнего выражения можно переписать в виде
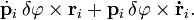
Теперь, пользуясь свойством смешанного произведения, совершим циклическую перестановку векторов, в результате чего получим, вынося общий множитель:
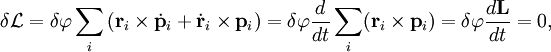
где, 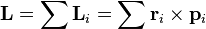 — момент импульса системы. Ввиду произвольности
— момент импульса системы. Ввиду произвольности  , из равенства
, из равенства  следует
следует 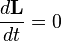 .
.
На орбитах момент импульса распределяется между собственным вращением планеты и момента импульса ее орбитального движения:
Момент импульса в электродинамике
При описании движения заряженной частицы в электромагнитном поле, канонический импульс 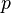 не является инвариантным. Как следствие, канонический момент импульса
не является инвариантным. Как следствие, канонический момент импульса  тоже не инвариантен. Тогда берем реальный импульс, который также называется «кинетическим импульсом»:
тоже не инвариантен. Тогда берем реальный импульс, который также называется «кинетическим импульсом»:
где  — электрический заряд,
— электрический заряд,  — скорость света,
— скорость света,  — векторный потенциал. Таким образом, гамильтониан (инвариантный) заряженной частицы массы m в электромагнитном поле:
— векторный потенциал. Таким образом, гамильтониан (инвариантный) заряженной частицы массы m в электромагнитном поле:
где 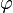 — скалярный потенциал. Из этого потенциала следует закон Лоренца. Инвариантный момент импульса или «кинетический момент импульса» определяется:
— скалярный потенциал. Из этого потенциала следует закон Лоренца. Инвариантный момент импульса или «кинетический момент импульса» определяется:
Момент импульса в квантовой механике
Оператор момента
В квантовой механике момент импульса квантуется, то есть он может изменяться только по «квантовым уровням» между точно определенными значениями. Проекция на любую ось момента импульса частиц, обусловленного их пространственным движением, должна быть целым числом, умноженным на  (h с чертой), определяемой, как постоянная Планка, поделенная на 2π. Эксперименты показывают, что большинство частиц имеют постоянный внутренний момент импульса, который не зависит от их движения через пространство. Этот спиновой момент импульса всегда кратен
(h с чертой), определяемой, как постоянная Планка, поделенная на 2π. Эксперименты показывают, что большинство частиц имеют постоянный внутренний момент импульса, который не зависит от их движения через пространство. Этот спиновой момент импульса всегда кратен  . Например, электрон в состоянии покоя имеет момент импульса
. Например, электрон в состоянии покоя имеет момент импульса  .
.
В классическом определении момент импульса зависит от 6 переменных 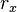 ,
, 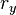 ,
, 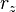 ,
, 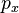 ,
, 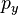 , и
, и 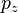 . Переводя это на квантовомеханические определения, используя принцип неопределенности Гейзенберга, получаем, что невозможно вычислить все шесть переменных одновременно с любой точностью. Поэтому есть ограничение на то, что мы можем узнать или подсчитать о практическом моменте импульса. Это значит, что лучшее, что мы можем сделать — это подсчитать одновременно величину вектора момента импульса и его компоненты по осям.
. Переводя это на квантовомеханические определения, используя принцип неопределенности Гейзенберга, получаем, что невозможно вычислить все шесть переменных одновременно с любой точностью. Поэтому есть ограничение на то, что мы можем узнать или подсчитать о практическом моменте импульса. Это значит, что лучшее, что мы можем сделать — это подсчитать одновременно величину вектора момента импульса и его компоненты по осям.
Математически полный момент импульса в квантовой механике определяется как оператор физической величины из суммы двух частей, связанных с пространственным движением — в атомной физике такой момент называют орбитальным, и внутренним спином частицы — соответственно, спиновым. Первый оператор действует на пространственные зависимости волновой функции:
где 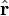 и
и  — координатный и импульсный оператор, соответственно, а второй — на внутренние, спиновые. В частности, для одной частицы без электрического заряда и без спина, оператор углового момента может быть записан как:
— координатный и импульсный оператор, соответственно, а второй — на внутренние, спиновые. В частности, для одной частицы без электрического заряда и без спина, оператор углового момента может быть записан как:
где  — оператор набла. Это часто встречающаяся форма оператора момента импульса, но не самая главная, она имеет следующие свойства:
— оператор набла. Это часто встречающаяся форма оператора момента импульса, но не самая главная, она имеет следующие свойства:
и даже более важные подстановки с гамильтонианом частицы без заряда и спина:
Друзья! Приглашаем вас к обсуждению. Если у вас есть своё мнение, напишите нам в комментарии.