Осевые моменты инерции простых сечений (фигур)
На этой странице указаны формулы для расчёта моментов инерции простых сечений (фигур). Данные формулы используются при проведении прочностных расчётов при изгибе и расчётов на жёсткость. А также для расчёта геометрических характеристик более сложных сечений.
Формулы для расчёта осевых моментов инерции
Традиционно, моменты инерции обозначаются буквой – I. Также в литературе, часто используют букву – J.
На сайте – ssopromat.ru, ты также можешь найти другую справочную информацию.
| Момент инерции | |
|---|---|
 |
|
| Размерность | L2M |
| Единицы измерения | |
| СИ | кг·м² |
| СГС | г·см² |
Моме́нт ине́рции — тензорная физическая величина, мера инертности во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении. Характеризуется распределением масс в теле. Момент инерции равен сумме произведений элементарных масс на квадрат их расстояний до базового множества, которое, формально, может представлять собой не обязательно ось вращения (т.е. прямую), но и точку или плоскость. В последних случаях говорят о моменте инерции относительно точки или плоскости, а возникать такие величины могут в формальных вычислениях, например, при расчете тензора инерции.
Единица измерения в Международной системе единиц (СИ): кг·м².
Обозначение: I или J.
Различают несколько моментов инерции — в зависимости от типа базового множества до которого отсчитываются расстояния от элементарных масс.
Осевой момент инерции[править | править код]
Осевые моменты инерции некоторых тел
Моментом инерции механической системы относительно неподвижной оси («осевой момент инерции») называется величина Ja, равная сумме произведений масс всех n материальных точек системы на квадраты их расстояний до оси[1]:
где:
- mi — масса i-й точки,
- ri — расстояние от i-й точки до оси.
Осевой момент инерции тела Ja является мерой инертности тела во вращательном движении вокруг оси подобно тому, как масса тела является мерой его инертности в поступательном движении.
где:
- dm = ρ dV — масса малого элемента объёма тела dV,
- ρ — плотность,
- r — расстояние от элемента dV до оси a.
Если тело однородно, то есть его плотность всюду одинакова, то
Теорема Гюйгенса — Штейнера[править | править код]
Момент инерции твёрдого тела относительно какой-либо оси зависит от массы, формы и размеров тела, а также и от положения тела по отношению к этой оси. Согласно теореме Гюйгенса — Штейнера, момент инерции тела J относительно произвольной оси равен сумме момента инерции этого тела Jc относительно оси, проходящей через центр масс тела параллельно рассматриваемой оси, и произведения массы тела m на квадрат расстояния d между осями[1]:
где m — полная масса тела.
Например, момент инерции стержня относительно оси, проходящей через его конец, равен:
Осевые моменты инерции некоторых тел[править | править код]
| Тело | Описание | Положение оси a | Момент инерции Ja |
|---|---|---|---|
| Материальная точка массы m | На расстоянии r от точки, неподвижная | 
|
|

|
Полый тонкостенный цилиндр или кольцо радиуса r и массы m | Ось цилиндра | 
|

|
Сплошной цилиндр или диск радиуса r и массы m | Ось цилиндра | 
|

|
Полый толстостенный цилиндр массы m с внешним радиусом r2 и внутренним радиусом r1 | Ось цилиндра |  [Комм 1] [Комм 1]
|
|
Сплошной цилиндр длины l, радиуса r и массы m | Ось перпендикулярна образующей цилиндра и проходит через его центр масс | 
|
|
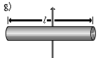
Полый тонкостенный цилиндр (кольцо) длины l, радиуса r и массы m | Ось перпендикулярна к цилиндру и проходит через его центр масс | 
|
|
Прямой тонкий стержень длины l и массы m | Ось перпендикулярна к стержню и проходит через его центр масс | 
|

|
Прямой тонкий стержень длины l и массы m | Ось перпендикулярна к стержню и проходит через его конец | 
|

|
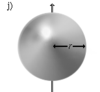
Тонкостенная сфера радиуса r и массы m | Ось проходит через центр сферы | 
|
|
Шар радиуса r и массы m | Ось проходит через центр шара | 
|
|
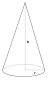
Конус радиуса r и массы m | Ось конуса | 
|
| Равнобедренный треугольник с высотой h, основанием a и массой m | Ось перпендикулярна плоскости треугольника и проходит через вершину (при высоте) | 
|
|
| Правильный треугольник со стороной a и массой m | Ось перпендикулярна плоскости треугольника и проходит через центр масс | 
|
|
| Квадрат со стороной a и массой m | Ось перпендикулярна плоскости квадрата и проходит через центр масс | 
|
|
| Прямоугольник со сторонами a и b и массой m | Ось перпендикулярна плоскости прямоугольника и проходит через центр масс | 
|
|
| Правильный n-угольник радиуса r и массой m | Ось перпендикулярна плоскости и проходит через центр масс | ![{displaystyle {frac {mr^{2}}{6}}left[1+2cos(pi /n)^{2}right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6bf60937eb16b822e5b6212250fa8f13c794f3cb)
|
|

|
Тор (полый) с радиусом направляющей окружности R, радиусом образующей окружности r и массой m | Ось перпендикулярна плоскости направляющей окружности тора и проходит через центр масс | 
|
Вывод формул[править | править код]
Тонкостенный цилиндр (кольцо, обруч)
Вывод формулы
Момент инерции тела равен сумме моментов инерции составляющих его частей. Разобьём тонкостенный цилиндр на элементы с массой dm и моментами инерции dJi. Тогда
Поскольку все элементы тонкостенного цилиндра находятся на одинаковом расстоянии от оси вращения, формула (1) преобразуется к виду
Толстостенный цилиндр (кольцо, обруч)
Вывод формулы
Пусть имеется однородное кольцо с внешним радиусом R, внутренним радиусом R1, толщиной h и плотностью ρ. Разобьём его на тонкие кольца толщиной dr. Масса и момент инерции тонкого кольца радиуса r составит
Момент инерции толстого кольца найдём как интеграл
Поскольку объём и масса кольца равны
получаем окончательную формулу для момента инерции кольца
Однородный диск (сплошной цилиндр)
Вывод формулы
Рассматривая цилиндр (диск) как кольцо с нулевым внутренним радиусом (R1 = 0), получим формулу для момента инерции цилиндра (диска):
Сплошной конус
Вывод формулы
Разобьём конус на тонкие диски толщиной dh, перпендикулярные оси конуса. Радиус такого диска равен
где R – радиус основания конуса, H – высота конуса, h – расстояние от вершины конуса до диска.
Масса и момент инерции такого диска составят
Интегрируя, получим
Сплошной однородный шар
Вывод формулы
Разобьём шар на тонкие диски толщиной dh, перпендикулярные оси вращения. Радиус такого диска, расположенного на высоте h от центра сферы, найдём по формуле
Масса и момент инерции такого диска составят
Момент инерции шара найдём интегрированием:
Тонкостенная сфера
Вывод формулы
Для вывода воспользуемся формулой момента инерции однородного шара радиуса R:
Вычислим, насколько изменится момент инерции шара, если при неизменной плотности ρ его радиус увеличится на бесконечно малую величину dR.
Тонкий стержень (ось проходит через центр)
Вывод формулы
Разобьём стержень на малые фрагменты длиной dr. Масса и момент инерции такого фрагмента равна
Интегрируя, получим
Тонкий стержень (ось проходит через конец)
Вывод формулы
При перемещении оси вращения из середины стержня на его конец, центр тяжести стержня перемещается относительно оси на расстояние l⁄2. По теореме Штейнера новый момент инерции будет равен
Безразмерные моменты инерции планет и их спутников[2][3][4]
Безразмерные моменты инерции планет и спутников[править | править код]
Большое значение для исследований внутренней структуры планет и их спутников имеют их безразмерные моменты инерции. Безразмерный момент инерции тела радиуса r и массы m равен отношению его момента инерции относительно оси вращения к моменту инерции материальной точки той же массы относительно неподвижной оси вращения, расположенной на расстоянии r (равному mr2). Эта величина отражает распределение массы по глубине. Одним из методов её измерения у планет и спутников является определение доплеровского смещения радиосигнала, передаваемого АМС, пролетающей около данной планеты или спутника. Для тонкостенной сферы безразмерный момент инерции равен 2/3 (~0,67), для однородного шара — 0,4, и вообще тем меньше, чем большая масса тела сосредоточена у его центра. Например, у Луны безразмерный момент инерции близок к 0,4 (равен 0,391), поэтому предполагают, что она относительно однородна, её плотность с глубиной меняется мало. Безразмерный момент инерции Земли меньше, чем у однородного шара (равен 0,335), что является аргументом в пользу существования у неё плотного ядра[5][6].
Центробежный момент инерции[править | править код]
Центробежными моментами инерции тела по отношению к осям прямоугольной декартовой системы координат называются следующие величины[1][7]:
где x, y и z — координаты малого элемента тела объёмом dV, плотностью ρ и массой dm.
Ось OX называется главной осью инерции тела, если центробежные моменты инерции Jxy и Jxz одновременно равны нулю. Через каждую точку тела можно провести три главные оси инерции. Эти оси взаимно перпендикулярны друг другу. Моменты инерции тела относительно трёх главных осей инерции, проведённых в произвольной точке O тела, называются главными моментами инерции данного тела[7].
Главные оси инерции, проходящие через центр масс тела, называются главными центральными осями инерции тела, а моменты инерции относительно этих осей — его главными центральными моментами инерции. Ось симметрии однородного тела всегда является одной из его главных центральных осей инерции[7].
Геометрические моменты инерции[править | править код]
Геометрический момент инерции объёма относительно оси — геометрическая характеристика тела, выражаемая формулой[8]:
где, как и ранее r — расстояние от элемента dV до оси a.
Размерность JVa — длина в пятой степени (
Геометрический момент инерции площади относительно оси — геометрическая характеристика тела, выражаемая формулой[8]:
где интегрирование выполняется по поверхности S, а dS — элемент этой поверхности.
Размерность JSa — длина в четвёртой степени (
Через геометрический момент инерции площади выражается момент сопротивления сечения:
Здесь rmax — максимальное расстояние от поверхности до оси.
| Геометрические моменты инерции площади некоторых фигур | |
|---|---|
Прямоугольника высотой  и шириной и шириной  : :
|

|
Прямоугольного коробчатого сечения высотой и шириной по внешним контурам  и и  , а по внутренним , а по внутренним  и и  соответственно соответственно
|

|
Круга диаметром 
|

|
Момент инерции относительно плоскости[править | править код]
Моментом инерции твёрдого тела относительно некоторой плоскости называют скалярную величину, равную сумме произведений массы каждой точки тела на квадрат расстояния от этой точки до рассматриваемой плоскости[9].
Если через произвольную точку 




В случае сплошного тела суммирование заменяется интегрированием.
Центральный момент инерции[править | править код]
Центральный момент инерции (момент инерции относительно точки O, момент инерции относительно полюса, полярный момент инерции) 
где:
Центральный момент инерции можно выразить через главные осевые моменты инерции, а также через моменты инерции относительно плоскостей[9]:
Тензор инерции и эллипсоид инерции[править | править код]
Момент инерции тела относительно произвольной оси, проходящей через центр масс и имеющей направление, заданное единичным вектором 
(1)
где 

Выбором соответствующей системы координат матрица тензора инерции может быть приведена к диагональному виду. Для этого нужно решить задачу о собственных значениях для матрицы тензора 
где 

откуда получается уравнение эллипсоида в собственных координатах. Разделив обе части уравнения на 
и произведя замены:
получаем канонический вид уравнения эллипсоида в координатах 
Расстояние от центра эллипсоида до некоторой его точки связано со значением момента инерции тела вдоль прямой, проходящей через центр эллипсоида и эту точку:
См. также[править | править код]
- Кинематика твёрдого тела
- Метод главных компонент
- Сопротивление материалов
- Теорема Штейнера
- Теорема Кёнига (механика)
- Механические приложения тройного интеграла
- Механические приложения двойного интеграла
- Полярный момент инерции
- Список моментов инерции
- Момент силы
- Момент импульса
Комментарии[править | править код]
- ↑ При получении этой формулы путём вычитания момента инерции сплошного цилиндра радиусом r1 из цилиндра радиусом r2 необходимо обратить внимание, что их массы при этом не будут одинаковыми или равны m. При этом должно выполняться условие
. Из формулы для массы соответствующего цилиндра можно определить, что в этом случае
и
. В правильности использования знака «+» в этой формуле также можно убедиться, если сравнить моменты инерции полого толстостенного и сплошного цилиндров с одинаковыми массами. Действительно, у первого из этих цилиндров масса в среднем сосредоточена дальше от оси, чем у второго, поэтому и момент инерции этого цилиндра должен быть больше, чем у сплошного. Именно такое соотношение моментов инерции и обеспечивает знак «+». С другой стороны, в пределе при стремлении r1 к r2 формула для полого толстостенного цилиндра должна приобрести тот же вид, что и формула для полого тонкостенного цилиндра. Очевидно, что такой переход происходит только при использовании формулы со знаком «+».
Примечания[править | править код]
- ↑ 1 2 3 Тарг С. М. Момент инерции // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Большая Российская энциклопедия, 1992. — Т. 3. — С. 206—207. — 672 с. — 48 000 экз. — ISBN 5-85270-019-3.
- ↑ Planetary Fact Sheet. Дата обращения: 31 августа 2010. Архивировано 14 марта 2016 года.
- ↑ Showman, Adam P.; Malhotra, Renu. The Galilean Satellites (англ.) // Science. — 1999. — Vol. 286, no. 5437. — P. 77—84. — doi:10.1126/science.286.5437.77. — PMID 10506564.
- ↑ Margot, Jean-Luc; et al. Mercury’s moment of inertia from spin and gravity data (англ.) // Journal of Geophysical Research (англ.) (рус. : journal. — 2012. — Vol. 117. — doi:10.1029/2012JE004161.
- ↑ Галкин И.Н. Внеземная сейсмология. — М.: Наука, 1988. — С. 42-73. — 195 с. — (Планета Земля и Вселенная). — 15 000 экз. — ISBN 502005951X.
- ↑ Пантелеев В. Л. Физика Земли и планет. Гл. 3.4 — Гравитационное поле планеты. Дата обращения: 31 августа 2010. Архивировано 3 октября 2013 года.
- ↑ 1 2 3 Тарг С. М. Краткий курс теоретической механики. — М.: «Высшая школа», 1995. — С. 269—271. — 416 с. — ISBN 5-06-003117-9.
- ↑ 1 2 Бухгольц Н. Н. Основной курс теоретической механики. — 4-е изд. — М.: «Наука», 1966. — Т. 2. — С. 131.
- ↑ 1 2 3 Яблонский А. А. Динамика // Курс теоретической механики. — 3-е изд. — М.: «Высшая школа», 1966. — Т. II. — С. 102—103. — 411 с.
Литература[править | править код]
- Матвеев. А. Н. Механика и теория относительности. М.: Высшая школа, 1986. (3-е изд. М.: ОНИКС 21 век: Мир и Образование, 2003. — 432с.)
- Трофимова Т. И. Курс физики. — 7-е изд. — М.: Высшая школа, 2001. — 542 с.
- Алешкевич В. А., Деденко Л. Г., Караваев В. А. Механика твердого тела. Лекции. Архивная копия от 7 января 2014 на Wayback Machine Издательство Физического факультета МГУ, 1997.
- Павленко Ю. Г. Лекции по теоретической механике. М.: ФИЗМАТЛИТ, 2002. — 392с.
- Яворский Б. М., Детлаф А. А. Физика для школьников старших классов и поступающих в вузы: учебное пособие — М.: Дрофа, 2002, 800с. ISBN 5-7107-5956-3
- Сивухин Д. В. Общий курс физики. В 5 т. Том I. Механика. 4-е изд. М.: ФИЗМАТЛИТ; Изд-во МФТИ, 2005. — 560 с.
- Беляев Н. М. Сопротивление материалов. Главная редакция физико-математической литературы изд-ва «Наука», 1976. — 608 с.
Ссылки[править | править код]
- Определение момента инерции тел простой формы.
Таблица. Изгиб. Осевые моменты инерции сечений (статические моменты сечений), осевые моменты сопротивления и радиусы инерции плоских фигур. Версия для печати.
(Моменты инерции сечений = статические моменты сечений J даны для главных центральных осей. Радиус инерции i=(J/F)1/2, где F – площадь сечения).
Легенда:
|
Легенда:
|
||
|
Форма поперечного сечения |
Осевой момент инерции, J, см4 |
Момент сопротивления W, см3 |
Радиус инерции i, см |
Круг.gif) |
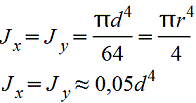 |
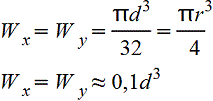 |
.gif) |
Кольцо.gif) c=d1/d |
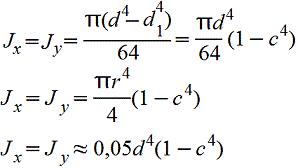 |
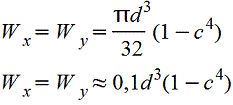 |
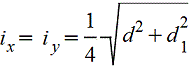 |
Тонкостенное кольцо.gif) s≤(D/10) |
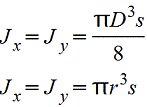 |
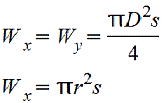 |
.gif) |
Полукруг.gif) Vo=2d/3π=0,2122d=0,4244r |
.gif) |
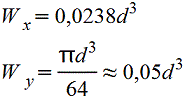 |
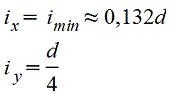 |
Круговой сегмент.gif) 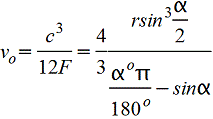 |
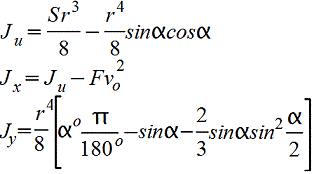 |
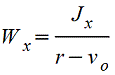 |
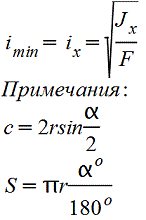 |
Круговой сектор.gif) 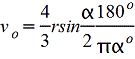 |
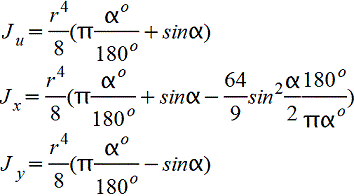 |
— | 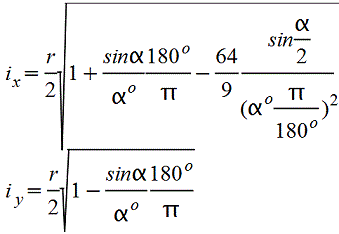 |
Круговое полукольцо.gif) .gif) |
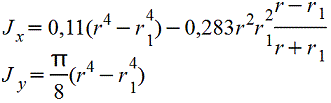 |
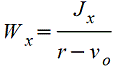 |
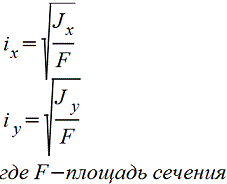 |
Сектор кругового кольца.gif) 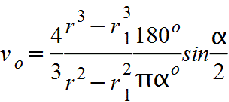 |
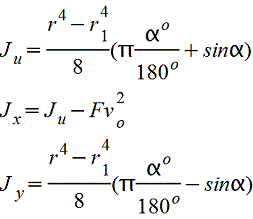 |
— | 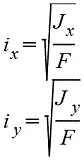 |
Профиль с симметричными закруглениями.gif) |
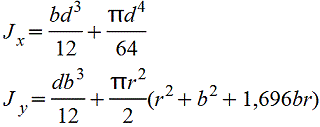 |
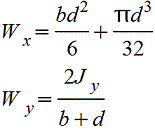 |
— |
|
Эллипс |
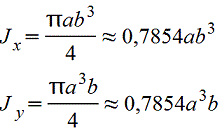 |
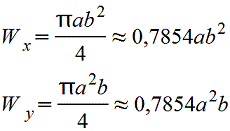 |
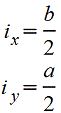 |
|
Квадрат |
 |
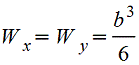 |
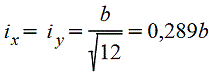 |
|
Полый квадрат |
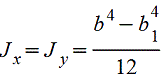 |
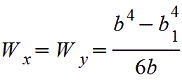 |
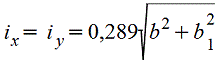 |
|
Полый тонкостенный квадрат
|
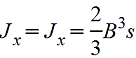 |
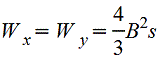 |
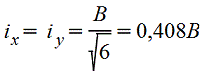 |
Квадрат, поставленный на ребро.gif) |
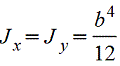 |
Срез верхнего и нижнего углов увеличивает Wx; при срезе углов на С=1/18 диагонали с каждой стороны момент сопротивления увеличивается до Wx=0,124b3 |
|
Полый квадрат, поставленный на ребро.gif) |
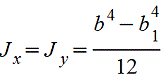 |
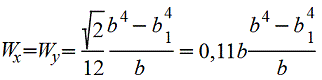 |
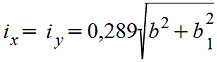 |
|
Прямоугольник |
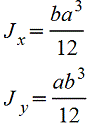 |
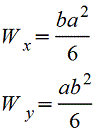 |
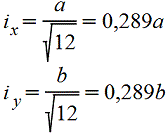 |
Прямоугольник повернутый.gif) 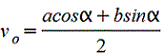 |
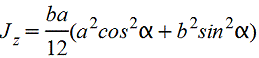 |
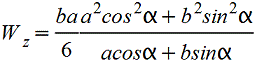 |
|
|
Полый прямоугольник |
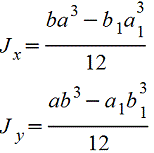 |
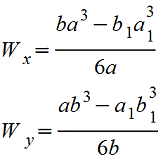 |
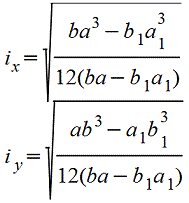 |
|
Полый тонкостенный прямоугольник |
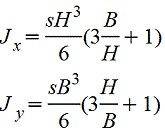 |
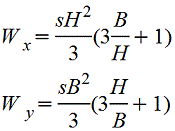 |
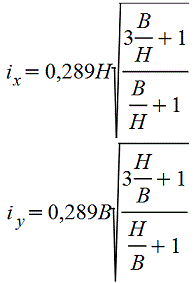 |
|
Сечение из двух равных прямоугольников |
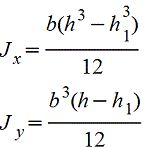 |
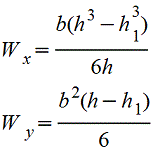 |
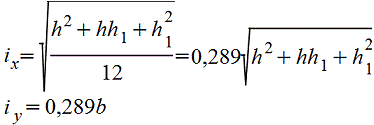 |
|
Треугольник |
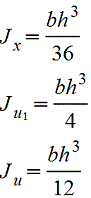 |
При вычислении напряжения в вершине треугольника |
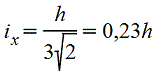 |
|
Поставленный на ребро треугольник |
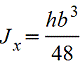 |
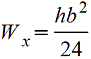 |
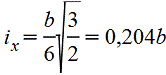 |
|
Трапеция |
.gif) |
При вычислении напряжений в точках верхнего основания |
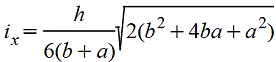 |
|
Трапеция |
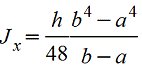 |
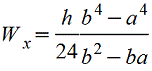 |
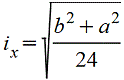 |
|
Тавр |
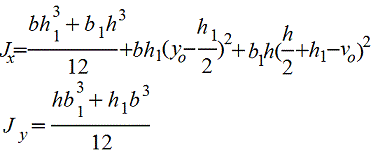 |
Для нижних волокон_25.gif) Для верхних волокон _25.gif) |
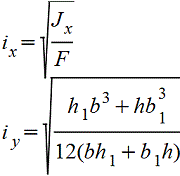 |
|
Корытное сечение |
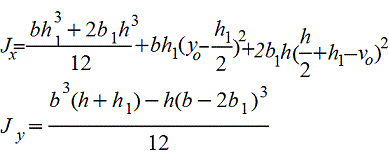 |
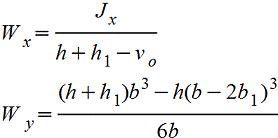 |
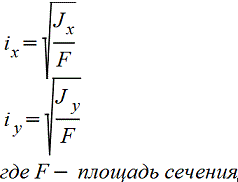 |
|
Крестообразное сечение |
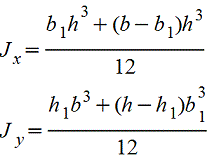 |
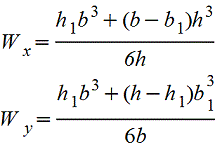 |
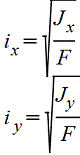 |
|
Правильный шестиугольник |
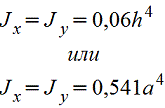 |
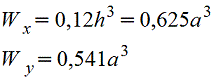 |
|
|
Правильный восьмиугольник |
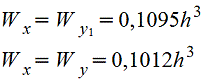 |
Как уже отмечалось выше, к числу простых
плоских фигур относятся три фигуры:
прямоугольник, треугольник и круг.
Простыми эти фигуры считаются потому,
что положение центра тяжести этих фигур
заранее известно. Все остальные фигуры
могут быть составлены из этих простых
фигур и считаются сложными. Вычислим
осевые моменты инерции простых фигур
относительно их центральных осей.
1. Прямоугольник.Рассмотрим сечение
прямоугольного профиля размерами(Рис.4.6). Выделим элемент сечения двумя
бесконечно близко расположенными
сечениями на расстоянииот
центральной оси.
Рис.4.6
Вычислим момент инерции прямоугольного сечения относительно оси :
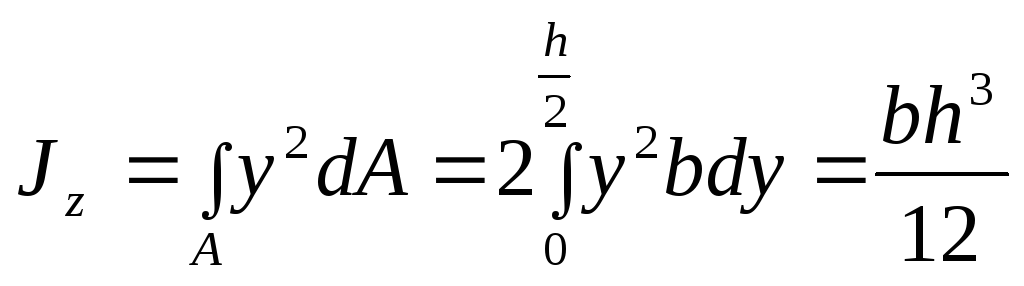
(4.10)
Момент
инерции прямоугольного сечения
относительно оси
найдем аналогично. Здесь вывод не
приводится.
.
(4.11)
Центробежный
момент инерции относительно осей
и
равен нулю, так как оси
и
являются осями симметрии, а, следовательно,
главными осями.
2. Равнобедренный треугольник.Рассмотрим сечение треугольного профиля
размерами(Рис.4.7). Выделим элемент сечения двумя
бесконечно близко расположенными
сечениями на расстоянииот центральной оси
.
Центр тяжести треугольника находится
на расстояниот основания. Треугольник принимается
равнобедренным, так что осьсечения является осью симметрии.
Рис.4.7
Вычислим
момент инерции сечения относительно
оси :

(4.12)
Величину
определим из подобия треугольников:

откуда
.
Подставляя
выражения для
в (4.12) и интегрируя, получим:
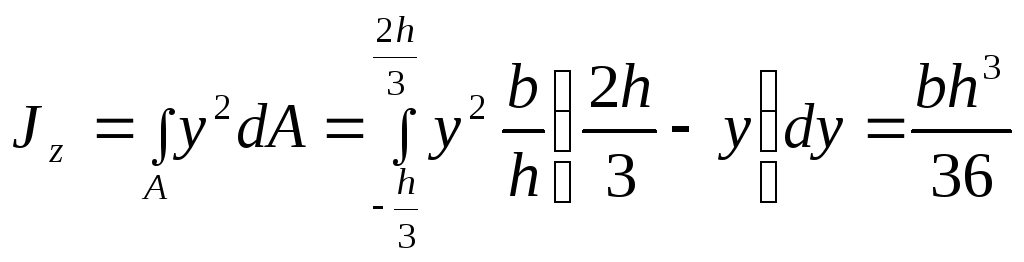
(4.13)
Момент
инерции для равнобедренного треугольника
относительно оси
находится аналогичным образом и равен:
(4.14)
Центробежный
момент инерции относительно осей
и
равен нулю, так как ось
является осью симметрии сечения.
3. Круг. Рассмотрим сечение круглого
профиля диаметром(Рис.4.8).
Выделим элемент сечения двумя бесконечно
близко расположенными концентрическими
окружностями, расположенными на
расстоянииот центра тяжести круга
.
Рис.4.8
Вычислим полярный момент инерции круга,
воспользовавшись выражением (4.5):

(4.15)
Используя условие инвариантности для
суммы осевых моментов инерции относительно
двух взаимно перпендикулярных осей
(4.6) и учитывая, что для круга в силу
симметрии
,
определяем величину осевых моментов
инерции:
.
(4.16)
Откуда:
.
(4.17)
Центробежный
момент инерции относительно осей
и
равен нулю, так как оси
и
являются осями симметрии сечения.
4.4. Зависимости между моментами инерции относительно параллельных осей
При
вычислении моментов инерции для сложных
фигур следует запомнить одно правило:
значения для моментов инерции можно
складывать, если
они вычислены относительно одной и той
же оси. Для
сложных фигур чаще всего центры тяжести
отдельных простых фигур и всей фигуры
не совпадают. Не совпадают, соответственно,
и центральные оси для отдельных простых
фигур и всей фигуры. В связи с этим
существуют приемы приведения моментов
инерции к одной оси, например, центральной
оси всей фигуры. Это может быть связано
с параллельным переносом осей инерции
и дополнительными вычислениями.
Рассмотрим
определение моментов инерции относительно
параллельных осей инерции, изображенных
на рис.4.9.
Рис.4.9
Пусть
осевые и центробежный моменты инерции
изображенной на рис.4.9. фигуры относительно
произвольно выбранных осей
и
с началом координат в точке
известны. Требуется вычислить осевые
и центробежный моменты инерции фигуры
относительно произвольных параллельных
осейи
с началом координат в точке
.
Осии
проведены на расстояниях
и
соответственно от осей
и
.
Воспользуемся
выражениями для осевых моментов инерции
(4.4) и для центробежного момента инерции
(4.7). Подставим в эти выражения вместо
текущих координат
и
элемента с бесконечно малой площадью
координатыи
в новой системе координат. Получим:
.
(4.18)
.
(4.19)
.
(4.20)
Анализируя полученные выражения,
приходим к выводу, что при вычислении
моментов инерции относительно параллельных
осей к моментам инерции, вычисленных
относительно исходных осей инерции,
следует призводить добавки в виде
дополнительных членов, которые могут
оказаться намного больше значений для
моментов инерции относительно исходных
осей. Поэтому пренебрегать этими
дополнительными членами ни в коем случае
нельзя.
Рассмотренный случай представляет
собой самый общий случай параллельного
переноса осей, когда в качестве исходных
были взяты произвольные оси инерции. В
большинстве расчетов встречаются
частные случаи определения моментов
инерции.
Первый частный случай. Исходные оси
являются центральными осями инерции
фигуры. Тогда, используя основное
свойство для статического момента
площади, можно исключить из уравнений
(4.18)(4.20) члены
уравнений, в которые входит статический
момент площади фигуры. В результате
получим:
.
(4.21)
.
(4.22)
.
(4.23)
Здесь оси
и
центральные оси
инерции.
Второй частный случай. Исходные оси
являются главными осями инерции. Тогда,
учитывая, что относительно главных осей
инерции центробежный момент инерции
равен нулю, получим:
.
(4.24)
.
(4.25)
.
(4.26)
Здесь оси
и
главные оси инерции.
Воспользуемся полученными выражениями
и рассмотрим несколько примеров
вычисления моментов инерции для плоских
фигур.
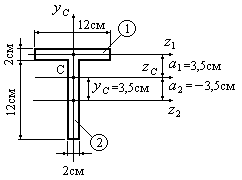
Пример 4.2.Определить осевые моменты
инерции фигуры, приведенной на рис.
4.10, относительно центральных осейи
.
Рис.4.10
Решение:
В предыдущем примере 4.1 для изображенной
на рис.4.10 фигуры было определено положение
центра тяжести С. Координата центра
тяжести откладывалась от оси
и составила
.
Вычислим расстоянияи
между осями
и
и осями
и
.
Эти расстояния составили соответственнои
.
Так как исходные осии
являются центральными осями для простых
фигур в виде прямоугольников, для
определения момента инерции фигуры
относительно осивоспользуемся выводами для первого
частного случая, в частности, формулой
(4.21).
см4.
Момент инерции относительно оси
получим путем сложения моментов инерции
простых фигур относительно этой же оси,
так как осьявляется общей центральной осью для
простых фигур и для всей фигуры.
см4.
Центробежный момент инерции относительно
осей
и
равен нулю, так как ось инерции
является главной осью (осью симметрии
фигуры).
Пример
4.3. Чему равен
размер b
(в см) фигуры,
изображенной на рис. 4.11, если момент
инерции фигуры относительно оси
равен 1000 см4?
Рис.4.11
Решение:
Выразим момент инерции относительно
оси
через неизвестный размер сечения
,
воспользовавшись формулой (4.21), учитывая,
что расстояние между осямии
равно 7см:
см4.
(а)
Решая выражение (а) относительно размера
сечения
,
получим:

Пример.4.4.
Какая из фигур, изображенных на рис.4.12
, имеет больший момент инерции относительно
оси
,
если обе фигуры имеют одинаковую площадьсм2?
Рис.4.12
Решение:
1. Выразим площади фигур через их размеры
и определим:
а) диаметр сечения для круглого сечения:
см2; Откуда
см.
б) размер стороны квадрата:
;
Откудасм.
2. Вычисляем момент инерции для круглого
сечения:
см4.
3. Вычисляем момент инерции для сечения
квадратной формы:
см4.
Сравнивая полученные результаты,
приходим к выводу, что наибольшим
моментом инерции будет обладать сечение
квадратной формы по сравнению с сечение
круглой формы при одинаковой у них
площади.
Пример 4.5.Определить полярный момент
инерции (в см4) сечения прямоугольной
формы относительно его центра тяжести,
если ширина сечения
см,
высота сечениясм.
Решение:
1. Найдем моменты инерции сечения
относительно горизонтальной
и вертикальной
центральных осей инерции:
см4;
см4.
2. Определяем полярный момент инерции
сечения как сумму осевых моментов
инерции:
см4.
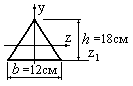
Пример
4.6. Определить
момент инерции фигуры треугольной формы
изображенной на рис.4.13, относительно
центральной оси
,
если момент инерции фигуры относительно
осиравен 2400 см4.
Рис.4.13
Решение:
Момент инерции сечения треугольной
формы относительно главной оси инерции
будет меньше по сравнению с моментом
инерции относительно осина величину
.
Поэтому присм
момент инерции сечения относительно
осинайдем следующим образом:
см4.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Часто мы слышим выражения: «он инертный», «двигаться по инерции», «момент инерции». В переносном значении слово «инерция» может трактоваться как отсутствие инициативы и действий. Нас же интересует прямое значение.
Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.
Что такое инерция
Согласно определению инерция в физике – это способность тел сохранять состояние покоя или движения в отсутствие действия внешних сил.
Если с самим понятием инерции все понятно на интуитивном уровне, то момент инерции – отдельный вопрос. Согласитесь, сложно представить в уме, что это такое. В этой статье Вы научитесь решать базовые задачи на тему «Момент инерции».
Определение момента инерции
Из школьного курса известно, что масса – мера инертности тела. Если мы толкнем две тележки разной массы, то остановить сложнее будет ту, которая тяжелее. То есть чем больше масса, тем большее внешнее воздействие необходимо, чтобы изменить движение тела. Рассмотренное относится к поступательному движению, когда тележка из примера движется по прямой.
По аналогии с массой и поступательным движением момент инерции – это мера инертности тела при вращательном движении вокруг оси.
Момент инерции – скалярная физическая величина, мера инертности тела при вращении вокруг оси. Обозначается буквой J и в системе СИ измеряется в килограммах, умноженных на квадратный метр.
Как посчитать момент инерции? Есть общая формула, по которой в физике вычисляется момент инерции любого тела. Если тело разбить на бесконечно малые кусочки массой dm, то момент инерции будет равен сумме произведений этих элементарных масс на квадрат расстояния до оси вращения.
Это общая формула для момента инерции в физике. Для материальной точки массы m, вращающейся вокруг оси на расстоянии r от нее, данная формула принимает вид:
Теорема Штейнера
От чего зависит момент инерции? От массы, положения оси вращения, формы и размеров тела.
Теорема Гюйгенса-Штейнера – очень важная теорема, которую часто используют при решении задач.
Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы
Теорема Гюйгенса-Штейнера гласит:
Момент инерции тела относительно произвольной оси равняется сумме момента инерции тела относительно оси, проходящей через центр масс параллельно произвольной оси и произведения массы тела на квадрат расстояния между осями.
Для тех, кто не хочет постоянно интегрировать при решении задач на нахождение момента инерции, приведем рисунок с указанием моментов инерции некоторых однородных тел, которые часто встречаются в задачах:
Пример решения задачи на нахождение момента инерции
Рассмотрим два примера. Первая задача – на нахождение момента инерции. Вторая задача – на использование теоремы Гюйгенса-Штейнера.
Задача 1. Найти момент инерции однородного диска массы m и радиуса R. Ось вращения проходит через центр диска.
Решение:
Разобьем диск на бесконечно тонкие кольца, радиус которых меняется от 0 до R и рассмотрим одно такое кольцо. Пусть его радиус – r, а масса – dm. Тогда момент инерции кольца:
Массу кольца можно представить в виде:
Здесь dz – высота кольца. Подставим массу в формулу для момента инерции и проинтегрируем:
В итоге получилась формула для момента инерции абсолютного тонкого диска или цилиндра.
Задача 2. Пусть опять есть диск массы m и радиуса R. Теперь нужно найти момент инерции диска относительно оси, проходящей через середину одного из его радиусов.
Решение:
Момент инерции диска относительно оси, проходящей через центр масс, известен из предыдущей задачи. Применим теорему Штейнера и найдем:
Кстати, в нашем блоге Вы можете найти и другие полезные материалы по физике и решению задач.
Надеемся, что Вы найдете в статье что-то полезное для себя. Если в процессе расчета тензора инерции возникают трудности, не забывайте о студенческом сервисе. Наши специалисты проконсультируют по любому вопросу и помогут решить задачу в считанные минуты.
Иван Колобков, известный также как Джони. Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.






















































.gif)
.gif)
.gif)
.gif)
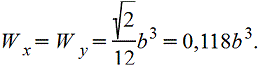
.gif)
.gif)
.gif)
.gif)
.gif)
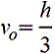
_21.gif)
_21.gif)
.gif)
.gif)

_23.gif)
_23.gif)
.gif)
.gif)
.gif)
.gif)

.gif)
.gif)
.gif)