Содержание материала
- Что это такое?
- Видео
- Вычисление мощности алфавита
- Что такое мощность алфавита: начальное понятие
- Как определить объем информации в тексте?
- Рассчитываем мощность
- Правильные названия единиц измерения данных
- Как найти мощность алфавита и использование его в компьютерных терминов
Что это такое?
Понятие «мощность алфавита» лежит в основе изучения информатики. Многочисленный набор символов принято называть — алфавит. Сумма всех символов выбранного языка называется мощностью. Следует вывод: мощность алфавита — это количество символов, которое используется в выбранном языке. Весь перечень используемых значков может содержать числа, различного характера скобки, специальные символы, запятые, двоеточия, точки, пробел и т.д.
Все же обобщенное понятие в информатике не учитывает расчеты информационной величины сообщения, которое содержит знаки препинания, числа и другое. Здесь необходим другой метод. Суть в том, что отдельная литера, цифра или скобка содержит собственный информационный объем данных. По этому информационному коду мозг компьютера опознает, что было напечатано. Машина разбирает введенные данные только в двоичном коде в виде единицы и нуля, в этом и заключается суть компьютерной науки.
В результате выходит, что любой символ можно закодировать путем различной расстановки нулей и единиц. Наименьшая последовательность, которая обозначает какую-либо букву или цифру, содержит всего два элемента. Информационный вес одного символа принято представлять в виде стандартной информационной единицы измерения, наименование которой «бит». Восемь битов равны одному байту.
Для определения количество информации, содержащейся в сообщении используют формулу Хартли: N=2i.
Формула предназначена для расчета мощности используемого языка, которая обозначается буквой N (информационный вес, или объем), i – количество бит (в единице слова. Т.е. вес символа).
Формулировка теории о количестве информации в набранной фразе: I=K*i. Здесь К – это количество символов в сообщении, I- информационная масса значка.
Что такое url адрес и его структура
Количество символов входящих в русский алфавит — 33 буквы. Выходит, что мощность взятого языка N=33. Английский язык содержит 26 букв и его мощность — 26. Но есть и клавиатурный язык, состоящий из букв русского языка и дополнительных знаков: 33 буквы, 10 чисел, 11 знаков препинания, скобки и пробел = 57.
Видео
Вычисление мощности алфавита
Численность знаков в коде и мощность алфавита всегда выражают определённую зависимость. Для того чтобы определить информационный объём, который заключается в сообщении, прибегают к специальному способу измерения, которое выражается в формуле мощности алфавита: N = 2 в n -ной степени.
Эта формула была изобретена американским инженером Ральфом Хартли более сотни лет тому назад. Она применяется для работы с равновероятными событиями и используется для определения мощности конкретного буквенного набора, которая обозначается буквой N (информационная масса или объём). n означает численность бит в словесной единице, иными словами, количество знаков внутри двоичного кода. Так, если n равен 1, то N тоже равен 1, при n = 2 N = 4, при n = 3 N = 8, при n = 4 N = 16.
Чтобы сформулировать теорию о численности информации в набранном словосочетании, пользуются формулой I=K*i. В этом случае К обозначает численность всех символов в предложении, а i — это информационная масса символа.
При ответе на вопрос, как найти мощность алфавита, нужно сказать, что в русском языке 33 буквы, поэтому это можно выразить как N = 33. Для сравнения, аналогичный показатель в английском, немецком и французском языках равняется 26, в испанском — 27. Венгерский язык, например, является 40-символьным.
Существует также и клавиатурный язык, куда входят не только буквы, но и дополнительные знаки. Так, в русском языке есть ещё 10 цифр и 11 символов, а также пробел и пара скобок. Их мощность прибавляется к аналогичному буквенному показателю, и на выходе получается N = 33+10+11+1+2=57. В некоторых случаях букву «ё» не выделяют в качестве отдельного самостоятельного символа, и в таком случае полная мощность русского алфавита становится равна 56.
Что такое мощность алфавита: начальное понятие
Итак, если следовать общепринятому правилу, что конечное значение какой-либо величины представляет собой параметр, определяющий, какое количество раз эталонная единица уложена в измеряемой величине, можно сделать вывод: мощность алфавита есть полное количество символов, использующихся для того или иного языка.
Чтобы было понятнее, оставим пока вопрос о том, как находить мощность алфавита, в стороне, и обратим внимание на сами символы, естественно, с точки зрения информационных технологий. Грубо говоря, полный список используемых символов содержит литеры, цифры, всевозможные скобки, специальные символы, знаки препинания, и т.д. Однако, если подходить к вопросу о том, что такое мощность алфавита именно компьютерным способом, сюда следует включить еще и пробел (единичный разрыв между словами или другими символами).
Возьмем в качестве примера русский язык, вернее, клавиатурную раскладку. Исходя из вышесказанного, полный перечень содержит 33 литеры, 10 цифр и 11 специальных знаков. Таким образом, полная мощность алфавита равна 54.
Как определить объем информации в тексте?
Обычно всегда при наборе текста можно использовать жирные, заглавные, и буквы с курсивом, знаки препинания, разнообразные скобы, операции вычисления и т.д. По расчетам получается, что мощность компьютерного алфавита — это 256 символов и вариантов. Следуя формуле Хартли, N=256, тогда масса каждого значка (i) в клавиатурном алфавите равна восьми битам, то есть один байт.
Рассчитываем мощность
Скорее всего, вам уже известно из школьного курса информатики, что в современных вычислительных системах, построенных на архитектуре фон Неймана, используется двоичная система кодировки информации. Так кодируются как программы, так и данные.
Для того чтобы представить текст в вычислительной системе, используют равномерный код из восьми разрядов. Равномерным код считается потому, что содержит фиксированный набор элементов — 0 и 1. Значения в таком коде задаются определенным порядком этих элементов. С помощью восьмиразрядного кода мы можем закодировать сообщения весом 256 бит, ведь по формуле Хартли: M8=28= 256 бит информации.
Такая ситуация с кодировкой символов двоичным кодом сложилась исторически. Но теоретически мы могли бы использовать и другие алфавиты для представления данных. Так, к примеру, в четырехзнаковом алфавите у каждого символа был бы вес не один, а два бита, в восьмизнаковом — 3 бита и так далее. Это рассчитывается с помощью двоичного логарифма, который был приведен выше (i = log2M).
Так как в алфавите мощностью 256 бит для обозначения одного символа отводится восемь двоичных разрядов, было решено ввести дополнительную меру информации — байт. Один байт содержит один символ кодовой таблицы ASCII и содержит в себе восемь бит.
Правильные названия единиц измерения данных
Для того чтобы устранить некорректности и неудобства, в марте 1999 года Международной комиссией в области электротехники были утверждены новые приставки к единицам, которые используются для определения объема информации в электронной вычислительной технике. Такими приставками стали «меби», «киби», «гиби», «теби», «эксби», «пети». Пока эти единицы еще не прижились, так что, скорее всего, необходимо время для введения этого стандарта и начала широкого применения. Как осуществлять переход от классических единиц к новоутвержденным, вы можете определить по следующей таблице:
Предположим, что мы имеем текст, который содержит K символов. Тогда, используя алфавитный подход, можно вычислить объем информации V, который в нем содержится. Он будет равен произведению мощности алфавита на информационный вес одного символа в нем.
По формуле Хартли мы знаем, как вычислить объем информации через двоичный логарифм. Предположив, что количество знаков алфавита равно N и количество знаков в записи информационного сообщения равняется K, получим такую формулу для вычисления информационного объема сообщения:
V = K ⋅ log2 N
Алфавитный подход свидетельствует о том, что информационный объем будет зависеть только лишь от мощности алфавита и размера сообщений (то есть количества символов в нем), но никак не будет связан со смысловым содержанием для человека.
Как найти мощность алфавита и использование его в компьютерных терминов
А теперь попробуем взглянуть на зависимость, которая выражает количество цифр в коде и мощности алфавита. Формула, где N-мощность алфавита, алфавитный и B-количество цифр в двоичный код, будет выглядеть так:
Н=2В
Это, 21=2, 22=4, 23=8, 24=16 и т. д. грубо говоря, нужное количество цифр двоичного кода веса персонажа. В информационном плане это выглядит так:
|
Мощность алфавита, Н |
2 |
4 |
8 |
16 |
|
Количество код символа, б |
1 бит |
2 биты |
3 бита |
4 бита |
Теги
Содержание материала
- Что такое мощность алфавита
- Определение информационного объёма в тексте
- Что такое мощность алфавита: начальное понятие
- Отображение символов в двоичном коде
- Как находить мощность алфавита и использовать ее в компьютерном выражении
- Представление символов в двоичный код
- Описание термина
- Правильные названия единиц измерения данных
- Как определить объем информации в тексте?
- Примеры расчёта мощности
Что такое мощность алфавита
Под мощностью алфавита мы подразумеваем общее количество символов в нем. Для того чтобы узнать, какова мощность алфавита, необходимо просто посчитать количество символов в нем. Давайте разбираться. Для русского алфавита мощность алфавита равна 33 или же 32 символам, если не использовать «ё».
Давайте предположим, что все символы в нашем алфавите встречаются с равной вероятностью. Это предположение можно понимать так: допустим, у нас есть мешок с подписанными кубиками. Число кубиков в нем бесконечно, и каждый подписан лишь одним символом. Тогда при равномерном распределении, сколько бы мы кубиков ни доставали из мешка, количество кубиков с разными символами будет одинаково, или будет стремиться к этому при росте числа кубиков, которые мы достаем из мешка.
Определение информационного объёма в тексте
Почти всегда при наборе текста на компьютерах и других электронных устройствах приходится сталкиваться с написанием различных символов. К ним следует отнести:
- заглавные и жирные буквы;
- курсив;
- скобки;
- знаки препинания;
- вычислительные операции и прочее.
По всем расчётам получается, что мощность компьютерного алфавита составляет 256 различных символов и вариантов. В соответствии с формулой Хартли, N = 256, а i — масса любого из значков в клавиатурном алфавите соответствует одному байту, или восьми битам.
Размер любой напечатанной фразы может быть вычислен по формуле V=K ⋅ log2N. В этом случае N обозначает количество всех символов в алфавите, а K — это численность знаков непосредственно в напечатанной фразе. Так, например, имеется произвольный текст объёмом в 25 листов. На каждом из них расположено по 45 строчек текста, содержащих по 58 символов.
Исходя из этого, на любой отдельной странице будет 45*58 = 2610 байт информации. В целом же по всему тексту этот объём будет равен 2610*25 = 65250 байт. Для обозначения мощности алфавита в информатике общепринятым вариантом является буква N из формулы Хартли. Именно ее чаще всего указывают в большинстве учебников и профессиональной литературе.
В кодовой таблице ASCII используют восьмибитную кодировку текстовых сообщений. Она позволяет полностью вместить основной набор символов кириллического и латинского алфавитов как в строчном, так и в прописном вариантах. Также с её помощью можно отобразить знаки препинания, цифры и прочие базовые знаки. Часто пользователям приходится иметь дело с более крупными объёмами, состоящими из триллионов байтов.
Для удобства их всегда переводят в увеличенные величины — кило-, мега-, гигабайты и прочее. Для их упрощённого обозначения используются специальные сокращения: Кб, Мб, Гб и так далее. 1 Кб равняется 1024 байтам (2 байта в десятой степени), 1 Мб составляет 1024 Кб (2 Кб в десятой степени) и так далее. Исходя из этого, 65250 байт будут составлять 63,72 килобайта.
Поскольку один отдельный символ состоит из 8 битов, то устанавливать их кодировку целиком не представляется возможным. Вместо этого предпочтительнее образовать кодировку трёхбитовых комбинаций. Расчёт этого действия проводится по формуле Хартли, где n-ная степень будет равняться трём. В результате получается N, равная 8.
При определении мощности чаще всего используют алфавитный подход. Он говорит о том, что объём информации, заложенной в тексте, зависит исключительно от мощности самого алфавита и размера сообщения (то есть количества символов, содержащихся в нём). Этот показатель не имеет никакой связи со смысловым наполнением для человека.
Что такое мощность алфавита: начальное понятие
Итак, если следовать общепринятому правилу, что конечное значение какой-либо величины представляет собой параметр, определяющий, какое количество раз эталонная единица уложена в измеряемой величине, можно сделать вывод: мощность алфавита есть полное количество символов, использующихся для того или иного языка.
Чтобы было понятнее, оставим пока вопрос о том, как находить мощность алфавита, в стороне, и обратим внимание на сами символы, естественно, с точки зрения информационных технологий. Грубо говоря, полный список используемых символов содержит литеры, цифры, всевозможные скобки, специальные символы, знаки препинания, и т.д. Однако, если подходить к вопросу о том, что такое мощность алфавита именно компьютерным способом, сюда следует включить еще и пробел (единичный разрыв между словами или другими символами).
Возьмем в качестве примера русский язык, вернее, клавиатурную раскладку. Исходя из вышесказанного, полный перечень содержит 33 литеры, 10 цифр и 11 специальных знаков. Таким образом, полная мощность алфавита равна 54.
Отображение символов в двоичном коде
Алфавитная мощность может быть использована на практике только при наличии двоичного кода. В качестве примера можно использовать упрощённый алфавит, состоящий всего из четырёх символов. В этом случае разрядность их и информационное представление описываются следующим образом:
- 1 — 00;
- 2 — 01;
- 3 — 10;
- 4 — 11.
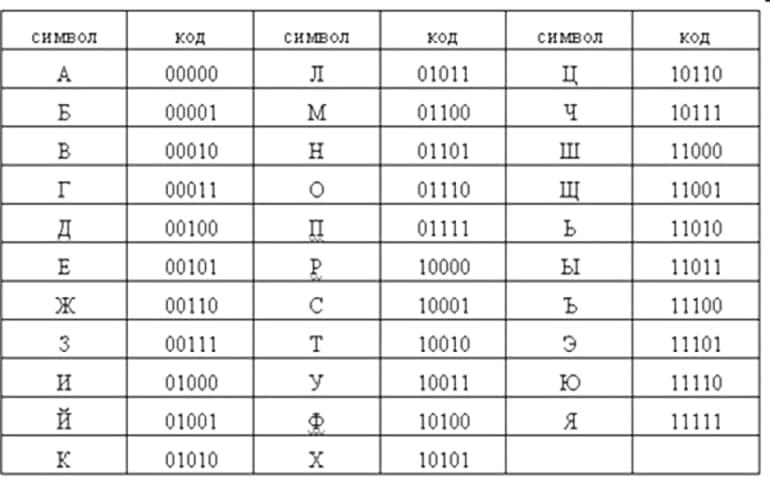
Из этого списка можно сделать вывод о том, что если алфавитная мощность равняется 4, то масса отдельного единичного символа будет составлять 2 бита. Если же есть алфавит, состоящий из 8 символов, то при подборе двоичного трёхзначного кода для него комбинационное количество будет следующим:
- 1 — 000;
- 2 — 001;
- 3 — 010;
- 4 — 011;
- 5 — 100;
- 6 — 101;
- 7 — 110;
- 8 — 111.
Иными словами, если алфавитная мощность равна 8, то вес отдельно взятого символа для двоичного трёхзначного кода составит 3 бита.
Как находить мощность алфавита и использовать ее в компьютерном выражении
Теперь попробуем посмотреть на зависимость, которую выражает количество знаков в коде и мощность алфавита. Формула, где N – алфавитная мощность алфавита, а b – количество знаков в двоичном коде, будет выглядеть так:
N=2b
То есть, 21=2, 22=4, 23=8, 24=16 и т.д. Грубо говоря, искомое количество знаков самого двоичного кода и есть вес символа. В информационном выражении это выглядит так:
|
Мощность алфавита, N |
2 |
4 Читайте также: Калькулятор расчет зарплаты по окладу 2021 |
8 |
16 |
|
Количество знаков кода, b |
1 бит |
2 бита |
3 бита |
4 бита |
Представление символов в двоичный код
Итак, что такое мощность алфавита, Я думаю, немного понятно. Теперь посмотрим на другой аспект, в частности, практической деятельности власти, используя двоичный код. В качестве примера, для простоты, мы принимаем алфавит, содержащий только 4 символа.
В двухразрядный двоичный код и вид информации, можно описать следующим образом:
|
Серийный номер |
1-й |
2-й |
3-й |
4-й |
|
Двоичный код |
00 |
01 |
10 |
11 |
Отсюда простой вывод: С мощность алфавита Н=4, символ удельный вес составляет 2 бита.
Если вы используете три-значный двоичный код для алфавита, например, 8 символов, то количество комбинаций будет выглядеть следующим образом:
|
Серийный номер |
1-й |
2-й |
3-й |
4-й |
5-й |
6-й |
7-й |
8-й |
|
Двоичный код |
000 |
001 |
010 |
011 |
100 |
101 |
110 |
111 |
Другими словами, когда мощность алфавита Н=8 вес одного символа трехзначный двоичный код будет равен 3 битам.
Описание термина
Понятие мощности алфавита находится в основании изучения информатики. Алфавитом принято называть набор многочисленных символов. Сумма всех их в определённом языке и есть алфавитная мощность. Иными словами, это количество всех символов, входящих в конкретно взятый язык. Сюда входят не только буквы, но и прочие обозначения, в частности:
- числа;
- спецсимволы;
- двоеточия;
- пробел;
- скобки;
- запятые;
- точки;
- многоточия и прочее.
Правильные названия единиц измерения данных
Для того чтобы устранить некорректности и неудобства, в марте 1999 года Международной комиссией в области электротехники были утверждены новые приставки к единицам, которые используются для определения объема информации в электронной вычислительной технике. Такими приставками стали «меби», «киби», «гиби», «теби», «эксби», «пети». Пока эти единицы еще не прижились, так что, скорее всего, необходимо время для введения этого стандарта и начала широкого применения. Как осуществлять переход от классических единиц к новоутвержденным, вы можете определить по следующей таблице:
Предположим, что мы имеем текст, который содержит K символов. Тогда, используя алфавитный подход, можно вычислить объем информации V, который в нем содержится. Он будет равен произведению мощности алфавита на информационный вес одного символа в нем.
По формуле Хартли мы знаем, как вычислить объем информации через двоичный логарифм. Предположив, что количество знаков алфавита равно N и количество знаков в записи информационного сообщения равняется K, получим такую формулу для вычисления информационного объема сообщения:
V = K ⋅ log2 N
Алфавитный подход свидетельствует о том, что информационный объем будет зависеть только лишь от мощности алфавита и размера сообщений (то есть количества символов в нем), но никак не будет связан со смысловым содержанием для человека.
Как определить объем информации в тексте?
Обычно всегда при наборе текста можно использовать жирные, заглавные, и буквы с курсивом, знаки препинания, разнообразные скобы, операции вычисления и т.д. По расчетам получается, что мощность компьютерного алфавита — это 256 символов и вариантов. Следуя формуле Хартли, N=256, тогда масса каждого значка (i) в клавиатурном алфавите равна восьми битам, то есть один байт.
Размер нужно вычислять по формуле: V=K⋅log2N, N — это численность символов в алфавите, а количество знаков в напечатанной фразе – K. Например, дан любой текст, который уместился на 30 страницах. На каждой из них расположено по 55 строчек, в них по 65 символов. Получается, что на странице будет 50 х 65= 3 575 байт информации.
Примеры расчёта мощности
От пользователей или обучающихся в задачах часто требуют научиться определять информационный объём какого-либо сообщения, приняв информационный вес символа за один байт. Так, в отрывке из поэмы Н. Н. Некрасова «Крестьянские дети»:
«Однажды, в студеную зимнюю пору,
Я из лесу вышел; был сильный мороз»
Теги
Вспомним некоторые известные нам факты:
 Множество символов, с помощью которых записывается текст, называется алфавитом. Число символов в алфавите – это его мощность. Формула определения количества информации: N=2 i , где N – мощность алфавита (количество символов), i – количество бит (информационный вес символа). В алфавит мощностью 256 символов можно поместить практически все необходимые символы. Такой алфавит называется достаточным. Т.к. 256 = 28, то вес 1 символа – 8 бит. Единице измерения 8 бит присвоили название 1 байт: 1 байт = 8 бит. Двоичный код каждого символа в компьютерном тексте занимает 1 байт памяти. |
Задачи: 1) Алфавит содержит 32 буквы. Какое количество информации несет одна буква? Дано: Мощность алфавита N = 32
Решение: 1. 32 = 2 5, значит вес одного символа i = 5 бит. Ответ: одна буква несет 5 бит информации. 2) Сообщение, записанное буквами из 16 символьного алфавита, содержит 10 символов. Какой объем информации в битах оно несет? Дано: Мощность алфавита N = 16 текст состоит из 10 символов.
Решение: 1. 16 = 2 4 2. Всего символов 10, значит объем информации 10 * 4 = 40 бит. Ответ: сообщение несет 40 бит информации (8 байт). 3) Информационное сообщение объемом 300 бит содержит 100 символов. Какова мощность алфавита? Дано: Объем сообщения = 300 бит текст состоит из 100 символов
Решение: 1. Определим вес одного символа: 300 / 100 = 3 бита. 2. Мощность алфавита определяем по формуле: 2 3 = 8 Ответ: мощность алфавита N = 8. |
Современные компьютерные технологии, информатика, мощность алфавита, системы исчисления и многие другие понятия имеют самые непосредственные связи между собой. Очень немногие пользователи сегодня достаточно хорошо разбираются в этих вопросах. Попробуем прояснить, что такое мощность алфавита, как ее вычислять и применять на практике. В дальнейшем это, вне всякого сомнения, может пригодиться на практике.
Как измеряется информация
Прежде чем приступить к изучению вопроса о том, какова мощность алфавита, и вообще, что это такое, следует начать, так сказать, с азов.

Наверняка всем известно, что сегодня существуют специальные системы измерения каких-либо величин, на основе эталонных значений. Например, для расстояний и аналогичных величин это метры, для массы и веса – килограммы, для временных промежутков – секунды и т.д.
Но как же измерить информацию в смысле объема текста? Именно для этого и было введено понятие мощности алфавита.
Что такое мощность алфавита: начальное понятие
Итак, если следовать общепринятому правилу, что конечное значение какой-либо величины представляет собой параметр, определяющий, какое количество раз эталонная единица уложена в измеряемой величине, можно сделать вывод: мощность алфавита есть полное количество символов, использующихся для того или иного языка.

Чтобы было понятнее, оставим пока вопрос о том, как находить мощность алфавита, в стороне, и обратим внимание на сами символы, естественно, с точки зрения информационных технологий. Грубо говоря, полный список используемых символов содержит литеры, цифры, всевозможные скобки, специальные символы, знаки препинания, и т.д. Однако, если подходить к вопросу о том, что такое мощность алфавита именно компьютерным способом, сюда следует включить еще и пробел (единичный разрыв между словами или другими символами).
Возьмем в качестве примера русский язык, вернее, клавиатурную раскладку. Исходя из вышесказанного, полный перечень содержит 33 литеры, 10 цифр и 11 специальных знаков. Таким образом, полная мощность алфавита равна 54.
Информационный вес символов
Однако общее понятие мощности алфавита не определяет сущности вычислений информационных объемов текста, содержащего литеры, цифры и символы. Здесь требуется особый подход.
В принципе, задумайтесь, ну вот каким может быть минимальный набор с точки зрения компьютерной системы, сколько символов он может содержать? Ответ: два. И вот почему. Дело в том, что каждый символ, будь то буква или цифра, имеет свой информационный вес, по которому машина и распознает, что именно перед ней. Но компьютер понимает лишь представление в виде единиц и нулей, на чем, собственно, и основана вся информатика.
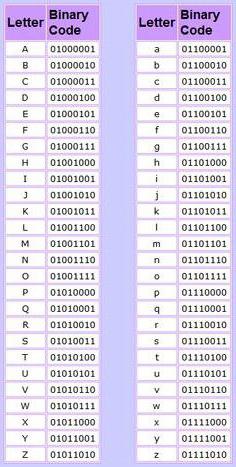
Таким образом, любой символ можно представить в виде последовательностей, содержащих цифры 1 и 0, то есть, минимальная последовательность, обозначающая букву, цифру или символ, состоит из двух компонентов.
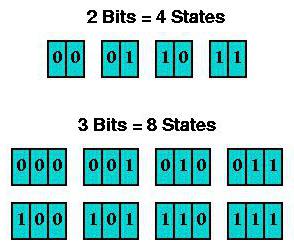
Сам же информационный вес, принятый за стандартную информационную единицу измерения, называется битом (1 бит). Соответственно, 8 бит составляют 1 байт.
Представление символов в двоичном коде
Итак, что такое мощность алфавита, думается, уже немного понятно. Теперь посмотрим на другой аспект, в частности, практическое представление мощности с использованием двоичного кода. В качестве примера для простоты возьмем алфавит, содержащий всего 4 символа.
В двузначном двоичном коде последовательность и их информационное представление можно описать следующим образом:
Отсюда – простейший вывод: при мощности алфавита N=4 вес единичного символа составляет 2 бита.
Если использовать трехзначный двоичный код для алфавита, например, с 8 символами, количество комбинаций будет следующим:
Иными словами, при мощности алфавита N=8 вес одного символа для трехзначного двоичного кода будет равен 3 битам.
Как находить мощность алфавита и использовать ее в компьютерном выражении
Теперь попробуем посмотреть на зависимость, которую выражает количество знаков в коде и мощность алфавита. Формула, где N – алфавитная мощность алфавита, а b – количество знаков в двоичном коде, будет выглядеть так:
То есть, 2 1 =2, 2 2 =4, 2 3 =8, 2 4 =16 и т.д. Грубо говоря, искомое количество знаков самого двоичного кода и есть вес символа. В информационном выражении это выглядит так:
Мощность алфавита, N
Количество знаков кода, b
Измерение информационного объема
Однако это были всего лишь простейшие примеры, так сказать, для начального понимания того, что такое мощность алфавита. Перейдем непосредственно к практике.

На данном этапе развития компьютерной техники для набора текста с учетом заглавных, прописных и строчных букв, кириллических и латинских литер, знаков препинания, скобок, знаков арифметических действий и т.д. используется 256 символов. Исходя из того, что 256 это 2 8 , нетрудно догадаться, что вес каждого символа в таком алфавите равен 8, то есть, 8 битам или 1 байту.
Если исходить из всех известных параметров, можно с легкостью получить нужное нам значение информационного объема любого текста. Например, у нас есть компьютерный текст, содержащий 30 страниц. На одной странице располагается 50 строк по 60 любых знаков или символов, включая и пробелы.
Таким образом, одна страница будет содержать 50 х 60= 3 000 байт информации, а весь текст – 3000 х 50=150000 байт. Как видим даже небольшие тексты измерять в байтах неудобно. А что говорить о целых библиотеках?

В данном случае лучше переводить объем в более мощные величины – килобайты, мегабайты, гигабайты и т.д. Исходя из того, что, например, 1 килобайт равен 1024 байта (2 10 ), а мегабайт – 2 10 килобайт (1024 килобайта), нетрудно посчитать, что объем текста в информационно-математическом выражении для нашего примера составит 150000/1024=146,484375 килобайт или приблизительно 0,14305 мегабайт.
Вместо послеловия
В общем и целом, это вкратце и все, что касается рассмотрения вопроса, что такое мощность алфавита. Остается добавить, что в данном описании был использован чисто математический подход. Само собой разумеется, что смысловая нагрузка текста в данном случае не учитывается.
Но, если подходить к вопросам рассмотрения именно с позиции, которая дает человеку что-то для осмысления, набор бессмысленного сочетания или последовательностей символов в этом плане будет иметь нулевую информационную нагрузку, хотя, с точки зрения понятия информационного объема, результат все равно можно вычислить.
В целом же, знания о мощности алфавита и сопутствующих понятиях не так уж и сложны для понимания и элементарно могут применяться в смысле практических действий. При этом любой пользователь практически каждый день сталкивается с этим. Достаточно привести в пример популярный редактор Word или любой другой такого же уровня, в котором используется такая система. Но не путайте его с обычным «Блокнотом». Здесь мощность алфавита ниже, поскольку при наборе текста не используются, скажем, прописные буквы.
Для решения задач нам понадобится формула, связывающая между собой информационный вес каждого символа, выраженный в битах (b), и мощность алфавита (N):
N = 2 b
Задача 1:
Алфавит содержит 32 буквы. Какое количество информации несет одна буква?
Мощность алфавита N = 32 Какое количество информации несет одна буква?
1. 32 = 2 5 , значит вес одного символа b = 5 бит.
Ответ: одна буква несет 5 бит информации.
Задача 2:
Сообщение, записанное буквами из 16 символьного алфавита, содержит 10 символов. Какой объем информации в битах оно несет?
Мощность алфавита N = 16
текст состоит из 10 символов
Определить объем информации в битах.
1. 16 = 2 4 , значит вес одного символа b = 4 бита.
2. Всего символов 10, значит объем информации 10 * 4 = 40 бит.
Ответ: сообщение несет 40 бит информации (8 байт).
Задача 3:
Информационное сообщение объемом 300 бит содержит 100 символов. Какова мощность алфавита?
Объем сообщения = 300 бит
текст состоит из 100 символов
Какова мощность алфавита?
1. Определим вес одного символа: 300 / 100 = 3 бита.
2. Мощность алфавита определяем по формуле: 2 3 = 8.
Ответ: мощность алфавита N = 8.
Попробуйте следующие задачи решить самостоятельно.
Задача 4:
Объем сообщения, содержащего 20 символов, составил 100 бит. Каков размер алфавита, с помощью которого записано сообщение?
Проверить решение
Задача 5:
Сколько символов содержит сообщение, записанное с помощью 8 символьного алфавита, если объем его составил 120 бит?
Проверить решение
Задача 6:
В книге 100 страниц. На каждой странице 60 строк по 80 символов в строке. Вычислить информационный объем книги.
 Развитие высоких технологий привело к появлению большого количества терминов и понятий, с которыми сталкиваются все пользователи в процессе работы с компьютерами. Продвинутые юзеры имеют представление о большинстве из них, однако, для новичков разобраться со всеми терминами очень сложно. Одним из таковых терминов, о которых имеют представление не все даже опытные пользователи, является мощность алфавита. Что подразумевается под этим понятием и как она рассчитывается?
Развитие высоких технологий привело к появлению большого количества терминов и понятий, с которыми сталкиваются все пользователи в процессе работы с компьютерами. Продвинутые юзеры имеют представление о большинстве из них, однако, для новичков разобраться со всеми терминами очень сложно. Одним из таковых терминов, о которых имеют представление не все даже опытные пользователи, является мощность алфавита. Что подразумевается под этим понятием и как она рассчитывается?
Методы измерения информации в электронном виде
Мощность алфавита может пригодиться очень многим пользователям в процессе работы. Однако перед тем как дать определение этому термину и разобраться в методах его расчета необходимо немного поговорить о том, как измеряется электронная информация, поскольку это является материальной базой, на основании которой базируется дальнейшая теория.
Каждый человек знает о том, что любая величина имеет свою систему измерений. Например, температура измеряется в градусах, расстояние выражается в метрах, временные интервалы строятся из секунд и так далее. Однако немногие пользователи знают о том, в каких величинах измеряется текстовая информация в электронном виде. Для этих целей в информатике и было создано определение мощность алфавита.
Определение термина
Исходя из того, что значение абсолютно любой величины, известной в наши дни человечеству, является неким параметром, состоящим из набора измерительных единиц, то определение понятию мощности алфавита проще всего сделать следующим образом: мощность алфавита — это количество символов, которое входит в состав любого языка.
Однако это всего-лишь общее определение, которое отражает только поверхностное значение мощности алфавита, поскольку само определение носит более глубокий характер. Чтобы понять всю его суть необходимо разобраться с тем, что представляют собой символы, с точки зрения высоких технологий. Все символы, используемые в компьютере, включают в себя буквы, цифры, знаки препинания и набор специальных символов. Однако это еще не все, поскольку для определения мощности алфавита необходимо еще учитывать и пробел, который предназначен для разделения слов между собой.
Давайте в качестве примера рассмотрим русскую раскладку клавиатуры, которая используется для печати русскоязычного текста и состоит из 34 букв, 10 цифр и 11 дополнительных символов, суммарное количество которых составляет 54, что, в свою очередь, классифицируется как мощность алфавита русской раскладки клавиатуры..
Информационный вес символов
Давайте постепенно продвигаться далее. Мощность алфавита не заключается в одном лишь числе букв и цифр, которые используются в напечатанном тексте. Для определения этого параметра необходим более глубокий подход.
Давайте на секунду задумаемся о том, какой минимальный объем символов входит в состав одной буквы, цифры или специального знака? Правильный ответ — два. Каждый символ в компьютере обладает своим информационным весом, благодаря которому машина способна распознавать какую информацию ввел пользователь. Все дело в том, что машина не способна распознавать информацию в том виде, в котором ее представляют люди. Вместо этого, он использует специальный машинный язык, состоящий из нулей и единиц, при помощи которых происходит преобразование текстовой информации в двоичный код, понятный компьютерной системе.
Что касается информационного веса, то он выражается в битах и является стандартной единицей для измерения информации в электронном виде.
Немного о двоичном коде
Теперь мы имеем более-менее доступным для понимания определением мощности алфавита. Однако для понимания всей глубины теории представления электронной информации машинами необходимо иметь представление о двоичном коде. Давайте рассмотрим этот вопрос на примере мощности алфавита, состоящей из четырех любых символов, каждый из которых имеет вес два бита.
Следуя из всего вышесказанного, четыре символа будут иметь весь четыре бита, восемь — три и так далее. На основании этого принципа и происходит расчет веса текстовой информации, выраженной в электронном виде, компьютерными системами.
Вычисления мощности алфавита и ее практическое использование
С терминологией и основными теоретическими терминами мы разобрались, поэтому теперь давайте рассмотрим какая существует взаимосвязь между мощностью алфавита и его весом. Чтобы более наглядно провести взаимосвязь между ними давайте рассмотрим одну формулу: N=2b, в которой первая переменная соответствует количеству символов, а вторая — количеству знаков, используемых компьютерами в машинном языке.
Из этого математического выражения следует, что 21=2, 22=4, 23=8, 24=16 и так далее. На основании этого можно сделать весьма разумный и обоснованный вывод: число символов, используемых в машинном языке, представляет собой вес символа.
Как измеряется объем информации?
Рассмотренные выше примеры являются очень простыми, на примере которых можно дать общее представление мощности алфавита. Однако на деле все выглядит намного сложнее, поскольку каждый пользователь в процессе набора текста использует не только строчные, но и заглавные буквы, а также различные шрифты, языковую раскладку, знаки препинания, специальные символы, цвета и многое другое. Исходя из этого можно предположить, что общее число всех суммарных символов равняется 256. Поскольку 256 равняется 28 в двоичном коде, то в этом случае вес каждого символа составляет 8 битам или одному байту.
Таким образом, обладая всеми необходимыми параметрами, мы можем рассчитать объем электронной информации. Например, мы напечатали 30 страниц печатной информации, на каждой из которых содержится 50 строк по 60 различных символов. Используя известную нам формулу, производим необходимые вычисления:
— информационный вес одной строки будет равен: 50 х 60 = 3000 байт;
— а весь текст будет весить: 3000 х 50 = 150 000 байт.
Стоит отметить, что конечный результат можно выражать не только в байтах, а переводить стандартную единицу измерения в килобайты, мегабайты и другие. Для этого необходимо величину более младшего порядка разделить на 1024, поскольку именно столько единиц младшей величины образуют старшую единицу измерения.
Заключение
Прочитав эту статью, вы получили общее представление о том, что представляет собой мощность алфавита, а также о методах ее расчета. Однако был рассмотрен исключительно математический подход, в котором не учитываются некоторые другие параметры, основным из которых является смысловая нагрузка. Этот аспект является одним из наиболее важных для понимания, поскольку независимо от объема символов, если они не несут никакой информационной ценности, то его ценность равна нулю. Однако рассчитать вес бессмысленного набора символов все равно можно.
Если говорить в общем, то мощность алфавита, как один из терминов информатики, не представляет собой ничего сложного для понимания. Но многие пользователи пренебрегают этим терминов, поскольку считают его бесполезным, однако, на практике все обстоит совершенно иначе. В наши дни пользователи работают преимущественно с электронной информацией, которая со временем может полностью вытеснить печатную, поэтому необходимо иметь представление о том, как эта информация выражается в машинном виде и каким образом она рассчитывается.
Современные компьютерные технологии, информатика, мощность алфавита, системы исчисления и многие другие понятия имеют самые непосредственные связи между собой. Очень немногие пользователи сегодня достаточно хорошо разбираются в этих вопросах. Попробуем прояснить, что такое мощность алфавита, как ее вычислять и применять на практике. В дальнейшем это, вне всякого сомнения, может пригодиться на практике.
Как измеряется информация
Прежде чем приступить к изучению вопроса о том, какова мощность алфавита, и вообще, что это такое, следует начать, так сказать, с азов.

Наверняка всем известно, что сегодня существуют специальные системы измерения каких-либо величин, на основе эталонных значений. Например, для расстояний и аналогичных величин это метры, для массы и веса – килограммы, для временных промежутков – секунды и т.д.
Но как же измерить информацию в смысле объема текста? Именно для этого и было введено понятие мощности алфавита.
Что такое мощность алфавита: начальное понятие
Итак, если следовать общепринятому правилу, что конечное значение какой-либо величины представляет собой параметр, определяющий, какое количество раз эталонная единица уложена в измеряемой величине, можно сделать вывод: мощность алфавита есть полное количество символов, использующихся для того или иного языка.

Чтобы было понятнее, оставим пока вопрос о том, как находить мощность алфавита, в стороне, и обратим внимание на сами символы, естественно, с точки зрения информационных технологий. Грубо говоря, полный список используемых символов содержит литеры, цифры, всевозможные скобки, специальные символы, знаки препинания, и т.д. Однако, если подходить к вопросу о том, что такое мощность алфавита именно компьютерным способом, сюда следует включить еще и пробел (единичный разрыв между словами или другими символами).
Возьмем в качестве примера русский язык, вернее, клавиатурную раскладку. Исходя из вышесказанного, полный перечень содержит 33 литеры, 10 цифр и 11 специальных знаков. Таким образом, полная мощность алфавита равна 54.
Информационный вес символов
Однако общее понятие мощности алфавита не определяет сущности вычислений информационных объемов текста, содержащего литеры, цифры и символы. Здесь требуется особый подход.
В принципе, задумайтесь, ну вот каким может быть минимальный набор с точки зрения компьютерной системы, сколько символов он может содержать? Ответ: два. И вот почему. Дело в том, что каждый символ, будь то буква или цифра, имеет свой информационный вес, по которому машина и распознает, что именно перед ней. Но компьютер понимает лишь представление в виде единиц и нулей, на чем, собственно, и основана вся информатика.

Таким образом, любой символ можно представить в виде последовательностей, содержащих цифры 1 и 0, то есть, минимальная последовательность, обозначающая букву, цифру или символ, состоит из двух компонентов.

Сам же информационный вес, принятый за стандартную информационную единицу измерения, называется битом (1 бит). Соответственно, 8 бит составляют 1 байт.
Представление символов в двоичном коде
Итак, что такое мощность алфавита, думается, уже немного понятно. Теперь посмотрим на другой аспект, в частности, практическое представление мощности с использованием двоичного кода. В качестве примера для простоты возьмем алфавит, содержащий всего 4 символа.
В двузначном двоичном коде последовательность и их информационное представление можно описать следующим образом:
|
Порядковый номер |
1-ый |
2-ой |
3-ий |
4-ый |
|
Двоичный код |
00 |
01 |
10 |
11 |
Отсюда – простейший вывод: при мощности алфавита N=4 вес единичного символа составляет 2 бита.
Если использовать трехзначный двоичный код для алфавита, например, с 8 символами, количество комбинаций будет следующим:
|
Порядковый номер |
1-ый |
2-ой |
3-ий |
4-ый |
5-ый |
6-ой |
7-ой |
8-ой |
|
Двоичный код |
000 |
001 |
010 |
011 |
100 |
101 |
110 |
111 |
Иными словами, при мощности алфавита N=8 вес одного символа для трехзначного двоичного кода будет равен 3 битам.
Как находить мощность алфавита и использовать ее в компьютерном выражении
Теперь попробуем посмотреть на зависимость, которую выражает количество знаков в коде и мощность алфавита. Формула, где N – алфавитная мощность алфавита, а b – количество знаков в двоичном коде, будет выглядеть так:
N=2b
То есть, 21=2, 22=4, 23=8, 24=16 и т.д. Грубо говоря, искомое количество знаков самого двоичного кода и есть вес символа. В информационном выражении это выглядит так:
|
Мощность алфавита, N |
2 |
4 |
8 |
16 |
|
Количество знаков кода, b |
1 бит |
2 бита |
3 бита |
4 бита |
Измерение информационного объема
Однако это были всего лишь простейшие примеры, так сказать, для начального понимания того, что такое мощность алфавита. Перейдем непосредственно к практике.

На данном этапе развития компьютерной техники для набора текста с учетом заглавных, прописных и строчных букв, кириллических и латинских литер, знаков препинания, скобок, знаков арифметических действий и т.д. используется 256 символов. Исходя из того, что 256 это 28, нетрудно догадаться, что вес каждого символа в таком алфавите равен 8, то есть, 8 битам или 1 байту.
Если исходить из всех известных параметров, можно с легкостью получить нужное нам значение информационного объема любого текста. Например, у нас есть компьютерный текст, содержащий 30 страниц. На одной странице располагается 50 строк по 60 любых знаков или символов, включая и пробелы.
Таким образом, одна страница будет содержать 50 х 60= 3 000 байт информации, а весь текст – 3000 х 50=150000 байт. Как видим даже небольшие тексты измерять в байтах неудобно. А что говорить о целых библиотеках?

В данном случае лучше переводить объем в более мощные величины – килобайты, мегабайты, гигабайты и т.д. Исходя из того, что, например, 1 килобайт равен 1024 байта (210), а мегабайт – 210 килобайт (1024 килобайта), нетрудно посчитать, что объем текста в информационно-математическом выражении для нашего примера составит 150000/1024=146,484375 килобайт или приблизительно 0,14305 мегабайт.
Вместо послеловия
В общем и целом, это вкратце и все, что касается рассмотрения вопроса, что такое мощность алфавита. Остается добавить, что в данном описании был использован чисто математический подход. Само собой разумеется, что смысловая нагрузка текста в данном случае не учитывается.
Но, если подходить к вопросам рассмотрения именно с позиции, которая дает человеку что-то для осмысления, набор бессмысленного сочетания или последовательностей символов в этом плане будет иметь нулевую информационную нагрузку, хотя, с точки зрения понятия информационного объема, результат все равно можно вычислить.
В целом же, знания о мощности алфавита и сопутствующих понятиях не так уж и сложны для понимания и элементарно могут применяться в смысле практических действий. При этом любой пользователь практически каждый день сталкивается с этим. Достаточно привести в пример популярный редактор Word или любой другой такого же уровня, в котором используется такая система. Но не путайте его с обычным «Блокнотом». Здесь мощность алфавита ниже, поскольку при наборе текста не используются, скажем, прописные буквы.

