Мосты
Определение
Пусть дан неориентированный граф. Мостом называется такое ребро, удаление которого делает граф несвязным (или, точнее, увеличивает число компонент связности). Требуется найти все мосты в заданном графе.
Неформально, эта задача ставится следующим образом: требуется найти на карте такие дороги, при удалении которых пропадает путь между какими-либо двумя точками.
Суть алгоритма
Идея
Мы можем заметить тот факт, что ребро между точками v и u является мостом тогда и только тогда, когда из вершины u и её потомков нельзя вернуться в вершину v или подняться выше нее. Осталось лишь понять, как нам это выяснить.
Алгоритм
Разобьём ребра на ориентированные и будем хранить их в отдельной структуре. Пусть мы будем запоминать номер вершины, в которую направлено ребро, номер данного ребра (номер ребра равен номеру обратного ребра) и ссылку на его обратное ребро.
Заведём граф ссылок на рёбра и заполним его.
Запустим обход графа в глубину (DFS).
Будем для каждой вершины v хранить два значения:
-
dp[v] – минимально возможная вершина в которую мы можем опуститься из этой вершины в процессе обхода в глубину (по умолчанию текущая глубина)
-
d[v] – глубина текущей вершины
В процессе обхода:
-
Если встречаем вершину u, в которой еще не были, то спускаемся в неё и тогда dp[v] = min(dp[v], dp[u]). Тем самым проверяем опустились ли мы из вершины u и её потомков выше v.
-
Если встречаем вершину v, в которой уже были, то dp[v] = min(dp[v], d[u]). Тем самым проверяем не встретили ли мы вершину выше по обходу графа, чем вершина v.
По завершении обхода вершины v и её потомков:
Если из вершины v нельзя опуститься выше нее самой и мы знаем проверяемое ребро (dp[v] == d[v] && p != nullptr(текущее ребро)), то ребро из этой вершины – есть мост.
Тогда:
p->is_bridge = true – вершина v
p->bck->is_bridge = true – вершина другого конца ребра
Реализация
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define fast_cin() ios_base::sync_with_stdio(false); cin.tie(NULL); cout.tie(NULL)
struct Edge{
ll v,num;
bool is_bridge;
Edge* bck;
Edge(){}
Edge(ll v, ll num):v(v),num(num){}
};
vector<vector<Edge*>> gr;
vector<ll> dp,d,bridges;
vector<bool> used;
void dfs(ll v, ll depth = 0, Edge* p = nullptr){
used[v] = true;
dp[v] = d[v] = depth;
for(auto u : gr[v]){
if(!used[u->v]){
dfs(u->v,depth+1,u);
dp[v] = min(dp[v],dp[u->v]);
}
else if (p && p->num != u->num){
dp[v] = min(dp[v],d[u->v]);
}
}
if(p != nullptr && dp[v] == d[v]){
p->is_bridge = true;
p->bck->is_bridge = true;
bridges.push_back(p->num+1);
}
}
int main(){
fast_cin();
ll n,m;
cin >> n >> m;
gr.resize(n);
dp.resize(n);
d.resize(n);
used.resize(n);
ll v,u;
for(ll i = 0;i < m;i++){
cin >> v >> u;
v--;
u--;
Edge* a = new Edge(u,i);
Edge* b = new Edge(v,i);
a->bck = b;
b->bck = a;
gr[v].push_back(a);
gr[u].push_back(b);
}
for(ll i = 0;i < n;i++)
if(!used[i])
dfs(i);
sort(bridges.begin(),bridges.end());
cout << bridges.size() << endl;
for(auto i : bridges){
cout << i << " ";
}
}Задачи по теме
https://informatics.mccme.ru/mod/statements/view.php?id=31311#1
https://informatics.mccme.ru/mod/statements/view.php?id=40111&chapterid=389#
https://informatics.mccme.ru/mod/statements/view.php?id=28842#1
https://informatics.mccme.ru/mod/statements/view.php?id=28842&chapterid=3586#1
Точки сочленения
Определение
Точкой сочленения называется вершина, удаление которой делает граф несвязным.
Суть алгоритма
Идея
Мы можем заметить два факта:
-
Рассмотрим ребро между вершинами v и u. Тогда если из вершины u и ее потомков нельзя попасть в какого-либо предка вершины v и притом вершина v не является корнем дерева, то данная вершина и есть точка сочленения
-
Если вершина v – корень дерева, то она является точкой сочленения тогда и только тогда, когда эта точка имеет более одного сына в обходе графа в глубину
Алгоритм
Заведем общий счетчик времени входа timer и два массива:
-
tin[v] – время входа в вершину v
-
fup[v] – минимально достижимая вершина из вершины v
Запустим обход графа в глубину (DFS).
В процессе обхода:
-
Если встречаем уже посещенную вершину u, то fup[v] = min(fup[v], tin[u]). Проверяем не спустились ли мы выше v.
-
Если встречаем не посещенную вершину v, то спускаемся в неё. Затем fup[v] = min(fup[v], fup[u]). Тем самым проверим не спустились ли мы выше v из вершины u и ее потомков. И наконец если из вершины u нельзя спуститься ниже вершины v и вершины v – не корень дерева обхода графа (v fup[u] >= tin[v] && p != -1), то вершина v и есть искомая точка сочленения. Добавляем 1 к количеству сыновей вершины v (children++)
По завершении обхода:
Если вершина v является корнем обхода графа в глубину и имеет более одного сына, то она также является точкой сочленения (p == -1 && children > 1)
Реализация
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define fast_cin() ios_base::sync_with_stdio(false); cin.tie(NULL); cout.tie(NULL)
ll timer = 0;
vector<vector<ll>> gr;
vector<ll> tin,fup;
set<ll> points_of_connectebility;
vector<bool> used;
void dfs(ll v,ll p = -1){
used[v] = true;
tin[v] = fup[v] = timer++;
ll children = 0;
for(auto u : gr[v]){
if(u == p){
continue;
}
if(used[u]){
fup[v] = min(fup[v],tin[u]);
}
else{
dfs(u,v);
fup[v] = min(fup[v],fup[u]);
if(fup[u] >= tin[v] && p != -1){
points_of_connectebility.insert(v+1);
}
children++;
}
}
if(p == -1 && children > 1){
points_of_connectebility.insert(v+1);
}
}
int main() {
fast_cin();
ll n, m;
cin >> n >> m;
gr.resize(n);
tin.resize(n);
fup.resize(n);
used.resize(n);
ll v, u;
for (ll i = 0; i < m; i++) {
cin >> v >> u;
v--;
u--;
gr[v].push_back(u);
gr[u].push_back(v);
}
for (ll i = 0; i < n; i++)
if (!used[i])
dfs(i);
cout << points_of_connectebility.size() << endl;
for(auto i : points_of_connectebility){
cout << i << " ";
}
}Задачи по теме
https://informatics.mccme.ru/mod/statements/view3.php?id=40111&chapterid=111690#1
https://informatics.mccme.ru/mod/statements/view.php?id=40111&chapterid=111795#1
https://informatics.mccme.ru/mod/statements/view.php?id=40111&chapterid=3883#1
https://informatics.mccme.ru/mod/statements/view.php?id=40111&chapterid=3586#1
Дан неориентированный граф . Найти все мосты в за время
Содержание
- 1 Алгоритм
- 1.1 Функция [math]ret(v)[/math]
- 1.2 Лемма
- 1.3 Псевдокод
- 2 См. также
- 3 Источники информации
Алгоритм
| Теорема: |
|
Пусть — дерево обхода в глубину графа . Ребро является мостом тогда и только тогда, когда и из вершины и любого ее потомка нет обратного ребра в вершину или предка |
| Доказательство: |
|
Удалим из . Докажем, что мы не сможем достичь ни одного из предков (в частности ). Докажем этот факт от противного. Пусть существует удовлетворяющее условию обратное ребро . Тогда лежит на цикле и не может быть мостом. |
Функция
Определим функцию , где , как минимум из следущих величин
- время входа в вершину
- , где — потомок
- , где — обратное ребро, а — потомок (в нестрогом смысле)
Лемма
| Лемма: |
|
Ребро является мостом тогда и только тогда, когда принадлежит дереву обхода в глубину и |
| Доказательство: |
|
Рассмотрим вершину или её потомка. Из нее есть обратное ребро в предка тогда и только тогда, когда найдется такой сын , что . Если , то найдется обратное ребро, приходящее точно в . Если же , то это означает наличие обратного ребра в какого-либо предка вершины . Таким образом, если для текущего ребра (принадлежащего дереву поиска) выполняется , то это ребро является мостом; в противном случае оно мостом не является. |
| Утверждение: |
|
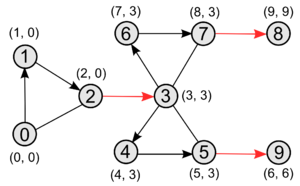
= , , |
|
В скобах у вершины указаны и . Мостами будут красные ребра
|
Псевдокод
function dfs(v):
time = time + 1
enter[v] = time
ret[v] = time
for всех u смежных с v
if (v, u) — обратное ребро
ret[v] = min(ret[v], enter[u])
if вершина u — белая
dfs(u)
ret[v] = min(ret[v], ret[u])
if ret[u] > enter[v]
ребро (v, u) — мост
См. также
- Обход в глубину, цвета вершин
- Лемма о белых путях
Источники информации
- MAXimal :: algo :: Поиск мостов
- Wikipedia — Bridge
- Визуализация поиска мостов
- Седжвик Р. Фундаментальные алгоритмы на C++. Часть 5: Алгоритмы на графах. Пер. с англ. — СПб.: ООО «ДиаСофтЮП», 2002. — С. 123-128
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 10 ноября 2021 года; проверки требует 1 правка.
Граф с 6 мостами (выделены красным)

Неориентированный связный граф, не имеющий разрезающих рёбер
Мост — ребро в теории графов, удаление которого увеличивает число компонент связности[1]. Такие рёбра также известны как разрезающие рёбра, разрезающие дуги или перешейки. Эквивалентное определение — ребро является мостом в том и только в том случае, если оно не содержится ни в одном цикле.
Деревья и леса[править | править код]
Граф с 


В любом неориентированном графе существует отношение эквивалентности вершин, согласно которому две вершины эквивалентны, если существует два соединяющих их пути, которые не пересекаются по рёбрам (любая вершина считается эквивалентной себе). Классы эквивалентности этого отношения называются рёберно 2-связными компонентами и мосты графа — это в точности те рёбра, концы которых принадлежат различным компонентам. Мостовая блок-схема графа имеет вершину для любой нетривиальной компоненты и ребро для каждого моста[2].
Связь с вершинной связностью[править | править код]
Мосты тесно связаны с концепцией шарниров — вершин, которые входят в любой путь, соединяющий некоторые две вершины.
Две конечные вершины моста являются шарнирами, если они не имеют степень 1, хотя рёбра, не являющиеся мостами, тоже могут с обоих концов иметь шарниры. Аналогично графам без мостов, которые рёберно 2-связны, графы без шарниров вершинно 2-связны.
В кубических графах любой шарнир является конечной вершиной хотя бы одного моста.
Графы без мостов[править | править код]
Как понятно из названия, граф без мостов — это граф, в котором нет мостов. Эквивалентные условия — что каждая компонента связности графа имеет открытое ушное разложение[3], что каждая связная компонента является рёберно 2-связной или (по теореме Роббинса) что каждая связная компонента имеет строгую ориентацию[en][3].
Важной открытой проблемой, связанной с мостами, является гипотеза о двойном покрытии циклами, высказанная Сеймуром и Секерешем (в 1978 году и 1979 году, независимо), которая утверждает, что любой граф без мостов можно покрыть простыми циклами, содержащими каждое ребро дважды[4].
Алгоритм поиска мостов Тарьяна[править | править код]
Первый алгоритм для нахождения мостов в графе, имеющий линейное время работы, описан Робертом Тарьяном в 1974 году[5]. Алгоритм работает следующим образом:
Будем обозначать ребро (v,w), содержащееся в дереве, как 

- Для каждой вершины
при прямом обходе выполняем:



Если 



Поиск мостов с помощью разложения на цепочки[править | править код]
Очень простой алгоритм поиска мостов[6] опирается на разложение на цепи.
Разложение на цепи не только позволяет получить все мосты, оно также даёт возможность получить все шарниры (и двусвязные компоненты) графа G, давая тем самым базу для проверки рёберной и вершинной 2-связности (и этот метод можно распространить на линейную по времени проверку рёберной и вершинной 3-связности).
Разложение на цепочки — это специальный случай разложения на уши, основанный на поиске в глубину по дереву T графа G и оно может быть выполнено очень просто:
пусть все вершины помечены как непосещённые. Для всех вершин v в восходящем порядке номеров обхода 1…n, проходим каждое обратное ребро (то есть ребро, не принадлежащее дереву обхода), инцидентное вершине v, и проследуем по рёбрам дерева к корню пока не встретим посещённую вершину. Во время этого прохода помечаем все пройденные вершины как посещённые. Этот проход закончится образованием либо пути, либо цикла, начинающегося в v, мы назовём это путь или цикл цепочкой. Будем обозначать i-ю цепочку, полученную такой процедурой, как Ci. C=C1,C2,… является тогда разбиением графа G на цепочки.
Следующие свойства дают возможность получить некоторую информацию о графе G из C эффективно, включая все мосты[6]:
Пусть C — разложение на цепочки простого связного графа G=(V,E).
- G является рёберно 2-связным в том и только в том случае, когда цепочки C содержат все рёбра из E.
- Ребро e в G является мостом в том и только в том случае, когда e не содержится ни в одной цепочке из C.
- Если G является рёберно 2-связным, C является разложением на уши.
- G является вершинно 2-связным в том и только в том случае, когда G имеет минимальную степень 2 и C1 является единственным циклом в C.
- Вершина v в рёберно 2-связном графе G является шарниром в том и только в том случае, когда v является первой вершиной в цикле из C – C1.
- Если G является вершинно 2-связным, C является открытым разложением на уши[en].
Примечания[править | править код]
- ↑ Béla Bollobás. Modern Graph Theory. — New York: Springer-Verlag, 1998. — Т. 184. — С. 6. — (Graduate Texts in Mathematics). — ISBN 0-387-98488-7. — doi:10.1007/978-1-4612-0619-4.
- ↑ Jeffery Westbrook, Robert E. Tarjan. Maintaining bridge-connected and biconnected components on-line // Algorithmica. — 1992. — Т. 7, вып. 5—6. — С. 433—464. — doi:10.1007/BF01758773.
- ↑ 1 2 H. E. Robbins. A theorem on graphs, with an application to a problem of traffic control // The American Mathematical Monthly. — 1939. — Т. 46. — С. 281—283.
- ↑ F. Jaeger. Annals of Discrete Mathematics 27 — Cycles in Graphs. — 1985. — Т. 27. — С. 1—12. — (North-Holland Mathematics Studies). — doi:10.1016/S0304-0208(08)72993-1.
- ↑ R. Endre Tarjan. A note on finding the bridges of a graph // Information Processing Letters. — Т. 2, вып. 6. — С. 160—161. — doi:10.1016/0020-0190(74)90003-9.
- ↑ 1 2 Jens M. Schmidt. A Simple Test on 2-Vertex- and 2-Edge-Connectivity // Information Processing Letters. — 2013. — Т. 113, вып. 7. — С. 241—244. — doi:10.1016/j.ipl.2013.01.016.
Improve Article
Save Article
Like Article
Improve Article
Save Article
Like Article
Given an undirected Graph, The task is to find the Bridges in this Graph.
An edge in an undirected connected graph is a bridge if removing it disconnects the graph. For a disconnected undirected graph, the definition is similar, a bridge is an edge removal that increases the number of disconnected components.
Like Articulation Points, bridges represent vulnerabilities in a connected network and are useful for designing reliable networks.
Examples:
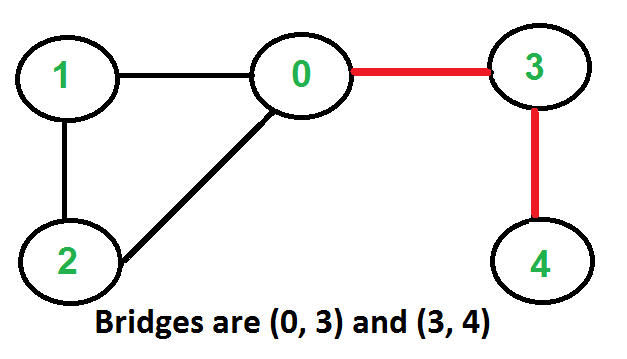
Input:
Output: (0, 3) and (3, 4)
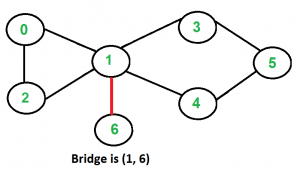
Input:
Output: (1, 6)
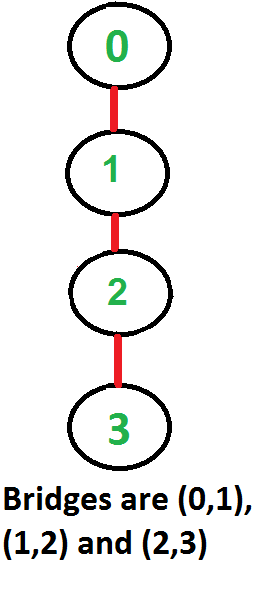
Input:
Output: (0, 1), (1, 2), and (2, 3)
Naive Approach: Below is the idea to solve the problem:
One by one remove all edges and see if the removal of an edge causes a disconnected graph.
Follow the below steps to Implement the idea:
- For every edge (u, v), do the following:
- Remove (u, v) from the graph
- See if the graph remains connected (either uses BFS or DFS)
- Add (u, v) back to the graph.
Time Complexity: O(E*(V+E)) for a graph represented by an adjacency list.
Auxiliary Space: O(V+E)
Find Bridges in a graph using Tarjan’s Algorithm.
Before heading towards the approach understand which edge is termed as bridge. Suppose there exists a edge from u -> v, now after removal of this edge if v can’t be reached by any other edges then u -> v edge is bridge. Our approach is based on this intuition, so take time and grasp it.
ALGORITHM: –
To implement this algorithm, we need the following data structures –
- visited[ ] = to keep track of the visited vertices to implement DFS
- disc[ ] = to keep track when for the first time that particular vertex is reached
- low[ ] = to keep track of the lowest possible time by which we can reach that vertex ‘other than parent’ so that if edge from parent is removed can the particular node can be reached other than parent.
We will traverse the graph using DFS traversal but with slight modifications i.e. while traversing we will keep track of the parent node by which the particular node is reached because we will update the low[node] = min(low[all it’s adjacent node except parent]) hence we need to keep track of the parent.
While traversing adjacent nodes let ‘v’ of a particular node let ‘u’ 3 cases arise –
1. v is parent of u then,
- skip that iteration.
2. v is visited then,
- update the low of v i.e. low[u] = min( low[u] , disc[v]) this arises when a node can be visited by more than one node, but low is to keep track of the lowest possible time so we will update it.
3. v is not visited then,
- call the DFS to traverse ahead
- now update the low[u] = min( low[u], low[v] ) as we know v can’t be parent cause we have handled that case first.
- now check if ( low[v] > disc[u] ) i.e. the lowest possible to time to reach ‘v’ is greater than ‘u’ this means we can’t reach ‘v’ without ‘u’ so the edge u -> v is a bridge.
Below is the implementation of the above approach:
C++
#include<bits/stdc++.h>
using namespace std;
class Graph
{
int V;
list<int> *adj;
void bridgeUtil(int u, vector<bool>& visited, vector<int>& disc,
vector<int>& low, int parent);
public:
Graph(int V);
void addEdge(int v, int w);
void bridge();
};
Graph::Graph(int V)
{
this->V = V;
adj = new list<int>[V];
}
void Graph::addEdge(int v, int w)
{
adj[v].push_back(w);
adj[w].push_back(v);
}
void Graph::bridgeUtil(int u, vector<bool>& visited, vector<int>& disc,
vector<int>& low, int parent)
{
static int time = 0;
visited[u] = true;
disc[u] = low[u] = ++time;
list<int>::iterator i;
for (i = adj[u].begin(); i != adj[u].end(); ++i)
{
int v = *i;
if(v==parent)
continue;
if(visited[v]){
low[u] = min(low[u], disc[v]);
}
else{
parent = u;
bridgeUtil(v, visited, disc, low, parent);
low[u] = min(low[u], low[v]);
if (low[v] > disc[u])
cout << u <<" " << v << endl;
}
}
}
void Graph::bridge()
{
vector<bool> visited (V,false);
vector<int> disc (V,-1);
vector<int> low (V,-1);
int parent = -1;
for (int i = 0; i < V; i++)
if (visited[i] == false)
bridgeUtil(i, visited, disc, low, parent);
}
int main()
{
cout << "nBridges in first graph n";
Graph g1(5);
g1.addEdge(1, 0);
g1.addEdge(0, 2);
g1.addEdge(2, 1);
g1.addEdge(0, 3);
g1.addEdge(3, 4);
g1.bridge();
cout << "nBridges in second graph n";
Graph g2(4);
g2.addEdge(0, 1);
g2.addEdge(1, 2);
g2.addEdge(2, 3);
g2.bridge();
cout << "nBridges in third graph n";
Graph g3(7);
g3.addEdge(0, 1);
g3.addEdge(1, 2);
g3.addEdge(2, 0);
g3.addEdge(1, 3);
g3.addEdge(1, 4);
g3.addEdge(1, 6);
g3.addEdge(3, 5);
g3.addEdge(4, 5);
g3.bridge();
return 0;
}
Java
import java.io.*;
import java.util.*;
import java.util.LinkedList;
class Graph
{
private int V;
private LinkedList<Integer> adj[];
int time = 0;
static final int NIL = -1;
@SuppressWarnings("unchecked")Graph(int v)
{
V = v;
adj = new LinkedList[v];
for (int i=0; i<v; ++i)
adj[i] = new LinkedList();
}
void addEdge(int v, int w)
{
adj[v].add(w);
adj[w].add(v);
}
void bridgeUtil(int u, boolean visited[], int disc[],
int low[], int parent[])
{
visited[u] = true;
disc[u] = low[u] = ++time;
Iterator<Integer> i = adj[u].iterator();
while (i.hasNext())
{
int v = i.next();
if (!visited[v])
{
parent[v] = u;
bridgeUtil(v, visited, disc, low, parent);
low[u] = Math.min(low[u], low[v]);
if (low[v] > disc[u])
System.out.println(u+" "+v);
}
else if (v != parent[u])
low[u] = Math.min(low[u], disc[v]);
}
}
void bridge()
{
boolean visited[] = new boolean[V];
int disc[] = new int[V];
int low[] = new int[V];
int parent[] = new int[V];
for (int i = 0; i < V; i++)
{
parent[i] = NIL;
visited[i] = false;
}
for (int i = 0; i < V; i++)
if (visited[i] == false)
bridgeUtil(i, visited, disc, low, parent);
}
public static void main(String args[])
{
System.out.println("Bridges in first graph ");
Graph g1 = new Graph(5);
g1.addEdge(1, 0);
g1.addEdge(0, 2);
g1.addEdge(2, 1);
g1.addEdge(0, 3);
g1.addEdge(3, 4);
g1.bridge();
System.out.println();
System.out.println("Bridges in Second graph");
Graph g2 = new Graph(4);
g2.addEdge(0, 1);
g2.addEdge(1, 2);
g2.addEdge(2, 3);
g2.bridge();
System.out.println();
System.out.println("Bridges in Third graph ");
Graph g3 = new Graph(7);
g3.addEdge(0, 1);
g3.addEdge(1, 2);
g3.addEdge(2, 0);
g3.addEdge(1, 3);
g3.addEdge(1, 4);
g3.addEdge(1, 6);
g3.addEdge(3, 5);
g3.addEdge(4, 5);
g3.bridge();
}
}
Python3
from collections import defaultdict
class Graph:
def __init__(self,vertices):
self.V= vertices
self.graph = defaultdict(list)
self.Time = 0
def addEdge(self,u,v):
self.graph[u].append(v)
self.graph[v].append(u)
def bridgeUtil(self,u, visited, parent, low, disc):
visited[u]= True
disc[u] = self.Time
low[u] = self.Time
self.Time += 1
for v in self.graph[u]:
if visited[v] == False :
parent[v] = u
self.bridgeUtil(v, visited, parent, low, disc)
low[u] = min(low[u], low[v])
if low[v] > disc[u]:
print ("%d %d" %(u,v))
elif v != parent[u]:
low[u] = min(low[u], disc[v])
def bridge(self):
visited = [False] * (self.V)
disc = [float("Inf")] * (self.V)
low = [float("Inf")] * (self.V)
parent = [-1] * (self.V)
for i in range(self.V):
if visited[i] == False:
self.bridgeUtil(i, visited, parent, low, disc)
g1 = Graph(5)
g1.addEdge(1, 0)
g1.addEdge(0, 2)
g1.addEdge(2, 1)
g1.addEdge(0, 3)
g1.addEdge(3, 4)
print ("Bridges in first graph ")
g1.bridge()
g2 = Graph(4)
g2.addEdge(0, 1)
g2.addEdge(1, 2)
g2.addEdge(2, 3)
print ("nBridges in second graph ")
g2.bridge()
g3 = Graph (7)
g3.addEdge(0, 1)
g3.addEdge(1, 2)
g3.addEdge(2, 0)
g3.addEdge(1, 3)
g3.addEdge(1, 4)
g3.addEdge(1, 6)
g3.addEdge(3, 5)
g3.addEdge(4, 5)
print ("nBridges in third graph ")
g3.bridge()
C#
using System;
using System.Collections.Generic;
public class Graph
{
private int V;
private List<int> []adj;
int time = 0;
static readonly int NIL = -1;
Graph(int v)
{
V = v;
adj = new List<int>[v];
for (int i = 0; i < v; ++i)
adj[i] = new List<int>();
}
void addEdge(int v, int w)
{
adj[v].Add(w);
adj[w].Add(v);
}
void bridgeUtil(int u, bool []visited, int []disc,
int []low, int []parent)
{
visited[u] = true;
disc[u] = low[u] = ++time;
foreach(int i in adj[u])
{
int v = i;
if (!visited[v])
{
parent[v] = u;
bridgeUtil(v, visited, disc, low, parent);
low[u] = Math.Min(low[u], low[v]);
if (low[v] > disc[u])
Console.WriteLine(u + " " + v);
}
else if (v != parent[u])
low[u] = Math.Min(low[u], disc[v]);
}
}
void bridge()
{
bool []visited = new bool[V];
int []disc = new int[V];
int []low = new int[V];
int []parent = new int[V];
for (int i = 0; i < V; i++)
{
parent[i] = NIL;
visited[i] = false;
}
for (int i = 0; i < V; i++)
if (visited[i] == false)
bridgeUtil(i, visited, disc, low, parent);
}
public static void Main(String []args)
{
Console.WriteLine("Bridges in first graph ");
Graph g1 = new Graph(5);
g1.addEdge(1, 0);
g1.addEdge(0, 2);
g1.addEdge(2, 1);
g1.addEdge(0, 3);
g1.addEdge(3, 4);
g1.bridge();
Console.WriteLine();
Console.WriteLine("Bridges in Second graph");
Graph g2 = new Graph(4);
g2.addEdge(0, 1);
g2.addEdge(1, 2);
g2.addEdge(2, 3);
g2.bridge();
Console.WriteLine();
Console.WriteLine("Bridges in Third graph ");
Graph g3 = new Graph(7);
g3.addEdge(0, 1);
g3.addEdge(1, 2);
g3.addEdge(2, 0);
g3.addEdge(1, 3);
g3.addEdge(1, 4);
g3.addEdge(1, 6);
g3.addEdge(3, 5);
g3.addEdge(4, 5);
g3.bridge();
}
}
Javascript
<script>
class Graph
{
constructor(v)
{
this.V = v;
this.adj = new Array(v);
this.NIL = -1;
this.time = 0;
for (let i=0; i<v; ++i)
this.adj[i] = [];
}
addEdge(v,w)
{
this.adj[v].push(w);
this.adj[w].push(v);
}
bridgeUtil(u,visited,disc,low,parent)
{
visited[u] = true;
disc[u] = low[u] = ++this.time;
for(let i of this.adj[u])
{
let v = i;
if (!visited[v])
{
parent[v] = u;
this.bridgeUtil(v, visited, disc, low, parent);
low[u] = Math.min(low[u], low[v]);
if (low[v] > disc[u])
document.write(u+" "+v+"<br>");
}
else if (v != parent[u])
low[u] = Math.min(low[u], disc[v]);
}
}
bridge()
{
let visited = new Array(this.V);
let disc = new Array(this.V);
let low = new Array(this.V);
let parent = new Array(this.V);
for (let i = 0; i < this.V; i++)
{
parent[i] = this.NIL;
visited[i] = false;
}
for (let i = 0; i < this.V; i++)
if (visited[i] == false)
this.bridgeUtil(i, visited, disc, low, parent);
}
}
document.write("Bridges in first graph <br>");
let g1 = new Graph(5);
g1.addEdge(1, 0);
g1.addEdge(0, 2);
g1.addEdge(2, 1);
g1.addEdge(0, 3);
g1.addEdge(3, 4);
g1.bridge();
document.write("<br>");
document.write("Bridges in Second graph<br>");
let g2 = new Graph(4);
g2.addEdge(0, 1);
g2.addEdge(1, 2);
g2.addEdge(2, 3);
g2.bridge();
document.write("<br>");
document.write("Bridges in Third graph <br>");
let g3 = new Graph(7);
g3.addEdge(0, 1);
g3.addEdge(1, 2);
g3.addEdge(2, 0);
g3.addEdge(1, 3);
g3.addEdge(1, 4);
g3.addEdge(1, 6);
g3.addEdge(3, 5);
g3.addEdge(4, 5);
g3.bridge();
</script>
Output
Bridges in first graph 3 4 0 3 Bridges in second graph 2 3 1 2 0 1 Bridges in third graph 1 6
Time Complexity: O(V+E),
- The above approach uses simple DFS along with Tarjan’s Algorithm.
- So time complexity is the same as DFS which is O(V+E) for adjacency list representation of the graph.
Auxiliary Space: O(V) is used for visited, disc and low arrays.
Last Updated :
02 May, 2023
Like Article
Save Article
Сайт переезжает. Большинство статей уже перенесено на новую версию.
Скоро добавим автоматические переходы, но пока обновленную версию этой статьи можно найти там.
Обходы графов
В этой статье рассмотрены основные применения обхода в глубину: топологическая сортировка, нахождение компонент сильной связности, решение задачи 2-SAT, нахождение мостов и точек сочленения, а также построение эйлерова пути и цикла в графе.
Поиск в глубину
Поиском в глубину (англ. depth-first search, DFS) называется рекурсивный алгоритм обхода дерева или графа, начинающий в корневой вершине (в случае графа её может быть выбрана произвольная вершина) и рекурсивно обходящий весь граф, посещая каждую вершину ровно один раз.
const int maxn = 1e5;
bool used[maxn]; // тут будем отмечать посещенные вершины
void dfs(int v) {
used[v] = true;
for (int u : g[v])
if (!used[u])
dfs(v);
}Немного его модифицируем, а именно будем сохранять для каждой вершины, в какой момент мы в неё вошли и в какой вышли — соответствующие массивы будем называть (tin) и (tout).
Как их заполнить: заведем таймер, отвечающий за «время» на текущем состоянии обхода, и будем инкрементировать его каждый раз, когда заходим в новую вершину:
int tin[maxn], tout[maxn];
int t = 0;
void dfs(int v) {
tin[v] = t++;
for (int u : g[v])
if (!used[u])
dfs(u);
tout[v] = t; // иногда счетчик тут тоже увеличивают
}У этих массивов много полезных свойств:
- Вершина (u) является предком (v) (iff tin_v in [tin_u, tout_u)). Эту проверку можно делать за константу.
- Два полуинтервала — ([tin_v, tout_v)) и ([tin_u, tout_u)) — либо не пересекаются, либо один вложен в другой.
- В массиве (tin) есть все числа из промежутка от 0 до (n-1), причём у каждой вершины свой номер.
- Размер поддерева вершины (v) (включая саму вершину) равен (tout_v – tin_v).
- Если ввести нумерацию вершин, соответствующую (tin)-ам, то индексы любого поддерева всегда будут каким-то промежутком в этой нумерации.
Эти свойства часто бывают полезными в задачах на деревья.
Мосты и точки сочленения
Определение. Мостом называется ребро, при удалении которого связный неориентированный граф становится несвязным.
Определение. Точкой сочленения называется врешина, при удалении которой связный неориентированный граф становится несвязным.
Пример задачи, где их интересно искать: дана топология сети (компьютеры и физические соединения между ними) и требуется установить все единые точки отказа — узлы и связи, без которых будут существовать два узла, между которыми не будет пути.
Наивный алгоритм поочередного удаления каждого ребра ((u, v)) и проверки наличия пути (u leadsto v) потребует (O(m^2)) операций. Чтобы научиться находить мосты быстрее, сначала сформулируем несколько утверждений, связанных с обходом в глубину.
Запустим DFS из произвольной вершины. Введем новые виды рёбер:
-
Прямые рёбра — те, по которым были переходы в dfs.
-
Обратные рёбра — то, по которым не было переходов в dfs.
Заметим, что никакое обратное ребро ((u, v)) не может являться мостом: если его удалить, то всё равно будет существовать какой-то путь от (u) до (v), потому что подграф из прямых рёбер является связным деревом.
Значит, остается только проверить все прямые рёбра. Это уже немного лучше — такой алгоритм будет работать за (O(n m)).
Сооптимизировать его до линейного времени (до одного прохода dfs) поможет замечание о том, что обратные рёбра могут вести только «вверх» — к какому-то предку в дереве обхода графа, но не в другие «ветки» — иначе бы dfs увидел это ребро раньше, и оно было бы прямым, а не обратным.
Тогда, чтобы определить, является ли прямое ребро (v to u) мостом, мы можем воспользоваться следующим критерием: глубина (h_v) вершины (v) меньше, чем минимальная глубина всех вершин, соединенных обратным ребром с какой-либо вершиной из поддерева (u).
Для ясности, обозначим эту величину как (d_u), которую можно считать во время обхода по следующей формуле:
[
d_v = min begin{cases}
h_v, &\
d_u, &text{ребро } (v to u) text{ прямое} \
h_u, &text{ребро } (v to u) text{ обратное}
end{cases}
]
Если это условие ((h_v < d_u)) не выполняется, то существует какой-то путь из (u) в какого-то предка (v) или саму (v), не использующий ребро ((v, u)), а в противном случае — наоборот.
const int maxn = 1e5;
bool used[maxn];
int h[maxn], d[maxn];
void dfs(int v, int p = -1) {
used[u] = true;
d[v] = h[v] = (p == -1 ? 0 : h[p] + 1);
for (int u : g[v]) {
if (u != p) {
if (used[u]) // если рябро обратное
d[v] = min(d[v], h[u]);
else { // если рябро прямое
dfs(u, v);
d[v] = min(d[v], d[u]);
if (h[v] < d[v]) {
// ребро (v, u) -- мост
}
}
}
}
}Примечание. Более известен алгоритм, вместо глубин вершин использующий их (tin), но автор считает его чуть более сложным для понимания.
Точки сочленения
Задача поиска точек сочленения не сильно отличается от задачи поиска мостов.
Вершина (v) является точкой сочленения, когда из какого-то её ребёнка (u) нельзя дойти до её предка, не используя ребро ((v, u)). Для конкретного прямого ребра (v to u) этот факт можно проверить так: (h_v leq d_u) (теперь нам нам достаточно нестрогого неравенства, так как если из вершины можно добраться до нее самой, то она все равно будет точкой сочленения).
Используя этот факт, можно оставить алгоритм практически прежним — нужно проверить этот критерий для всех прямых рёбер (v to u):
void dfs(int v, int p = -1) {
used[u] = 1;
d[v] = h[v] = (p == -1 ? 0 : h[p] + 1);
int children = 0; // случай с корнем обработаем отдельно
for (int u : g[u]) {
if (u != p) {
if (used[u])
d[v] = min(d[v], h[u]);
else {
dfs(u, v);
d[v] = min(d[v], d[u]);
if (dp[v] >= tin[u] && p != -1) {
// u -- точка сочленения
}
children++;
}
}
}
if (p == -1 && children > 1) {
// v -- корень и точка сочленения
}
}Единственный крайний случай — это корень, так как в него мы по определению войдём раньше других вершин. Но фикс здесь очень простой — достаточно посмотреть, было ли у него более одной ветви в обходе (если корень удалить, то эти поддеревья станут несвязными между собой).
Топологическая сортировка
Задача топологической сортировки графа звучит так: дан ориентированный граф, нужно упорядочить его вершины в массиве так, чтобы все графа рёбра вели из более ранней вершины в более позднюю.
Это может быть полезно, например, при планировании выполнения связанных задач: вам нужно одеться, в правильном порядке надев шорты (1), штаны (2), ботинки (3), подвернуть штаны (4) — как хипстеры — и завязать шнурки (5).
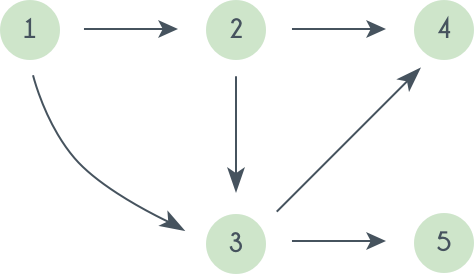
Во-первых, сразу заметим, что граф с циклом топологически отсортировать не получится — как ни располагай цикл в массиве, все время идти вправо по ребрам цикла не получится.
Во-вторых, верно обратное. Если цикла нет, то его обязательно можно топологически отсортировать — сейчас покажем, как.
Заметим, что вершину, из которой не ведет ни одно ребро, можно всегда поставить последней, а такая вершина в ациклическом графе всегда есть (иначе можно было бы идти по обратным рёбрам бесконечно). Из этого сразу следует конструктивное доказательство: будем итеративно класть в массив вершину, из которой ничего не ведет, и убирать ее из графа. После этого процесса массив надо будет развернуть.
Этот алгоритм проще реализовать, обратив внимание на времена выхода вершин в dfs. Вершина, из которой мы выйдем первой — та, у которой нет новых исходящих ребер. Дальше мы будем выходить только из тех вершин, которые если имеют исходящие ребра, то только в те вершины, из которых мы уже вышли.
Следовательно, достаточно просто выписать вершины в порядке выхода из dfs, а затем полученный список развернуть, и мы получим какую-то из корректных топологических сортировок.
Компоненты сильной связности
Мы только что научились топологически сортировать ациклические графы. А что же делать с циклическими графами? В них тоже иногда требуется найти какую-то структуру.
Для этого можно ввести понятие сильной связности.
Определение. Две вершины ориентированного графа связаны сильно (англ. strongly connected), если существует путь из одной в другую и наоборот. Иными словами, они обе лежат в каком-то цикле.
Понятно, что такое отношение транзитивно: если (a) и (b) сильно связны, и (b) и (c) сильно связны, то (a) и (c) тоже сильно связны. Поэтому все вершины распадаются на компоненты сильной связности — такое разбиение вершин, что внутри одной компоненты все вершины сильно связаны, а между вершинами разных компонент сильной связности нет.

Самый простой пример сильно-связной компоненты — это цикл. Но это может быть и полный граф, или сложное пересечение нескольких циклов.
Часто рассматривают граф, составленный из самих компонент сильной связности, а не индивидуальных вершин. Очевидно, такой граф уже будет ациклическим, и с ним проще работать. Задачу о сжатии каждой компоненты сильной связности в одну вершину называют конденсацией графа, и её решение мы сейчас опишем.
Если мы знаем, какие вершины лежат в каждой компоненте сильной связности, то построить граф конденсации несложно: дальше нужно лишь провести некоторые манипуляции со списками смежности. Поэтому сразу сведем исходную задачу к нахождению самих компонент.
Лемма. Запустим dfs. Пусть (A) и (B) — две различные компоненты сильной связности, и пусть в графе конденсации между ними есть ребро (A to B). Тогда:
[
maxlimits_{a in A}(tout_a) > maxlimits_{bin B}(tout_b)
]
Доказательство. Рассмотрим два случая, в зависимости от того, в какую из компонент dfs зайдёт первым.
Пусть первой была достигнута компонента (A), то есть в какой-то момент времени dfs заходит в некоторую вершину (v) компоненты (A), и при этом все остальные вершины компонент (A) и (B) ещё не посещены. Но так как по условию в графе конденсаций есть ребро (A to B), то из вершины (v) будет достижима не только вся компонента (A), но и вся компонента (B). Это означает, что при запуске из вершины (v) обход в глубину пройдёт по всем вершинам компонент (A) и (B), а, значит, они станут потомками по отношению к (v) в дереве обхода, и для любой вершины (u in A cup B, u ne v) будет выполнено (tout_v] > tout_u), что и утверждалось.
Второй случай проще: из (B) по условию нельзя дойти до (A), а значит, если первой была достигнута (B), то dfs выйдет из всех её вершин ещё до того, как войти в (A).
Из этого факта следует первая часть решения. Отсортируем вершины по убыванию времени выхода (как бы сделаем топологическую сортировку, но на циклическом графе). Рассмотрим компоненту сильной связности первой вершины в сортировке. В эту компоненту точно не входят никакие рёбра из других компонент — иначе нарушилось бы условие леммы, ведь у первой вершины (tout) максимальный . Поэтому, если развернуть все рёбра в графе, то из этой вершины будет достижима своя компонента сильной связности (C^prime), и больше ничего — если в исходном графе не было рёбер из других компонент, то в транспонированном не будет ребер в другие компоненты.
После того, как мы сделали это с первой вершиной, мы можем пойти по топологически отсортированному списку дальше и делать то же самое с вершинами, для которых компоненту связности мы ещё не отметили.
vector<int> g[maxn], t[maxn];
vector<int> order;
bool used[maxn];
int component[maxn];
int cnt_components = 0;
// топологическая сортировка
void dfs1(int v) {
used[v] = true;
for (int u : g[v]) {
if (!used[u])
dfs1(u);
order.push_back(v);
}
// маркировка компонент сильной связности
void dfs2(int v) {
component[v] = cnt_components;
for (int u : t[v])
if (cnt_components[u] == 0)
dfs2(u);
}
// в содержательной части main:
// транспонируем граф
for (int v = 0; v < n; v++)
for (int u : g[v])
t[u].push_back(v);
// запускаем топологическую сортировку
for (int i = 0; i < n; i++)
if (!used[i])
dfs1(i);
// выделяем компоненты
reverse(order.begin(), order.end());
for (int v : order)
if (component[v] == 0)
dfs2(v);TL;DR:
-
Сортируем вершины в порядке убывания времени выхода.
-
Проходимся по массиву вершин в этом порядке, и для ещё непомеченных вершин запускаем dfs на транспонированном графе, помечающий все достижимые вершины номером новой компонентой связности.
После этого номера компонент связности будут топологически отсортированы.
2-SAT
Ликбез. Конъюнкция — это «правильный» термин для логического «И» (обозначается (wedge) или &). Конъюкция возвращает true тогда и только тогда, когда обе переменные true.
Ликбез. Дизъюнкция — это «правильный» термин для логического «ИЛИ» (обозначается (vee) или |). Дизъюнкция возвращает false тогда и только тогда, когда обе переменные false.
Рассмотрим конъюнкцию дизъюнктов, то есть «И» от «ИЛИ» от каких-то перемений или их отрицаний. Например, такое выражение:
(a | b) & (!c | d) & (!a | !b)Если буквами: (А ИЛИ B) И (НЕ C ИЛИ D) И (НЕ A ИЛИ НЕ B).
Можно показать, что любую логическую формулу можно представить в таком виде.
Задача satisfiability (SAT) заключается в том, чтобы найти такие значения переменных, при которых выражение становится истинным, или сказать, что такого набора значений нет. Для примера выше такими значениями являются a=1, b=0, c=0, d=1 (убедитесь, что каждая скобка стала true).
В случае произвольных формул эта задача быстро не решается. Мы же хотим решить её частный случай — когда у нас в каждой скобке ровно две переменные (2-SAT).
Казалось бы — причем тут графы? Заметим, что выражение (a , | , b) эквивалентно (!a rightarrow b ,| , !b rightarrow a). Здесь «(rightarrow)» означает импликацию («если (a) верно, то (b) тоже верно»). С помощью это подстановки приведем выражение к другому виду — импликативному.
Затем построим граф импликаций: для каждой переменной в графе будет по две вершины, (обозначим их через (x) и (!x)), а рёбра в этом графе будут соответствовать импликациям.

Заметим, что если для какой-то переменной (x) выполняется, что из (x) достижимо (!x), а из (!x) достижимо (x), то задача решения не имеет. Действительно: какое бы значение для переменной (x) мы бы ни выбрали, мы всегда придём к противоречию — что должно быть выбрано и обратное ему значение.
Оказывается, что это условие является не только достаточным, но и необходимым. Доказательством этого факта служит описанный ниже алгоритм.
Переформулируем данный критерий в терминах теории графов. Если из одной вершины достижима вторая и наоборот, то эти две вершины находятся в одной компоненте сильной связности. Тогда критерий существования решения звучит так: для того, чтобы задача 2-SAT имела решение, необходимо и достаточно, чтобы для любой переменной (x) вершины (x) и (!x) находились в разных компонентах сильной связности графа импликаций.
Пусть решение существует, и нам надо его найти. Заметим, что, несмотря на то, что решение существует, для некоторых переменных может выполняться, что из (x) достижимо (!x) или из (!x) достижимо (x) (но не одновременно). В таком случае выбор одного из значений переменной (x) будет приводить к противоречию, в то время как выбор другого — не будет. Научимся выбирать из двух значений то, которое не приводит к возникновению противоречий. Сразу заметим, что, выбрав какое-либо значение, мы должны запустить из него обход в глубину/ширину и пометить все значения, которые следуют из него, т.е. достижимы в графе импликаций. Соответственно, для уже помеченных вершин никакого выбора между (x) и (!x) делать не нужно, для них значение уже выбрано и зафиксировано. Нижеописанное правило применяется только к непомеченным ещё вершинам.
Утверждается следующее. Пусть (space{rm comp}[V]) обозначает номер компоненты сильной связности, которой принадлежит вершина (V), причём номера упорядочены в порядке топологической сортировки компонент сильной связности в графе компонентов (т.е. более ранним в порядке топологической сортировки соответствуют большие номера: если есть путь из (v) в (w), то (space{rm comp}[v] leq space{rm comp}[w])). Тогда, если (space{rm comp}[x] < space{rm comp}[!x]), то выбираем значение !x, иначе выбираем x.
Докажем, что при таком выборе значений мы не придём к противоречию. Пусть, для определённости, выбрана вершина (x) (случай, когда выбрана вершина (!x), доказывается также).
Во-первых, докажем, что из (x) не достижимо (!x). Действительно, так как номер компоненты сильной связности (space{rm comp}[x]) больше номера компоненты (space{rm comp}[!x]) , то это означает, что компонента связности, содержащая (x), расположена левее компоненты связности, содержащей (!x), и из первой никак не может быть достижима последняя.
Во-вторых, докажем, что из любой вершины (y), достижимой из (x) недостижима (!y). Докажем это от противного. Пусть из (x) достижимо (y), а из (y) достижимо (!y). Так как из (x) достижимо (y), то, по свойству графа импликаций, из (!y) будет достижимо (!x). Но, по предположению, из (y) достижимо (!y). Тогда мы получаем, что из (x) достижимо (!x), что противоречит условию, что и требовалось доказать.
Итак, мы построили алгоритм, который находит искомые значения переменных в предположении, что для любой переменной (x) вершины (x) и (!x) находятся в разных компонентах сильной связности. Выше показали корректность этого алгоритма. Следовательно, мы одновременно доказали указанный выше критерий существования решения.
Эйлеров цикл
Определение. Эйлеров путь — это путь в графе, проходящий через все его рёбра.
Определение. Эйлеров цикл — это эйлеров путь, являющийся циклом.
Для простоты в обоих случаях будем считать, что граф неориентированный.
Также существует понятие гамильтонова пути и цикла — они посещают все вершины по разу, а не рёбра. Нахождение гамильтонова цикла (задача коммивояжера, англ. travelling salesman problem) — одна из самых известных NP-полных задач, в то время как нахождение эйлерового цика решается за линейное время — и мы сейчас покажем, как.
Теорема. Эйлеров цикл существует тогда и только тогда, когда степени всех вершин чётны.
Доказательство. Необходимость показывается так: можно просто взять эйлеров цикл и ориентировать все его ребра в порядке обхода. Тогда из каждой вершины будет выходить столько же рёбер, сколько входить, а значит степень у всех вершин исходного неориентированного графа была четной.
Достаточность докажем конструктивно — предъявим алгоритм нахождения.
const int maxn = 1e5;
set<int> g[maxn];
void euler(int v) {
while (!g[v].empty()) {
u = *g[v].begin();
g[v].erase(g[v].begin());
dfs(u);
}
cout << v << " ";
}Если условие на четность степеней вершин выполняется, то этот алгоритм действительно выводит эйлеров цикл, то есть последовательность из ((m+1)) вершин, между соседними есть связи.
Следствие. Эйлеров путь существует тогда и только тогда, когда количество вершин с нечётными степенями не превосходит 2.
Кстати, аналогичная теорема есть и для ориентированного графа (можете сами попытаться сформулировать).
Доказать это можно например через лемму о рукопожатиях.
Как теперь мы будем решать задачу нахождения цикла в предположении, что он точно есть. Давайте запустимся из произвольной вершины, пройдем по любому ребру и удалим его.
void euler(int v){
stack >s;
s.push({v, -1});
while (!s.empty()) {
v = s.top().first;
int x = s.top().second;
for (int i = 0; i < g[v].size(); i++){
pair e = g[v][i];
if(!u[e.second]){
u[e.second]=1;
s.push(e);
break;
}
}
if (v == s.top().first) {
if (~x) {
p.push_back(x);
}
s.pop();
}
}
}Упражнение. Сформулируйте и докажите аналогичные утверждения для случая ориентированного графа.