Производная положительна только тогда, когда функция возрастает. То есть, нам необходимо найти точки, в которых функция растет. Смотрим на график нашей функции: функция растет на промежутках: от (x=-7) до (x=0) и от (x = 6) до (x=12).
Так как по условию нам нужны только ЦЕЛЫЕ точки, в которых производная положительна, то это будут: (x=—6); (x=-5), (x=-4), (x=-3), (x=-2), (x=-1), (x=7), (x=8), (x=9), (x=10), (x=11). Всего точек получилось (11). Я отметил их зеленым цветом.
Обратите внимание, что точки (x=-7), (x=0), (x=6), (x=12) мы не считаем, так как в этих точках у нас будут минимумы и максимумы функции, а в них производная равна нулю, то есть не положительна.
Ответ: (11.)
Пример 2
На рисунке 6 изображен график функции, определенной на промежутке ((-10;12)). Найдите количество точек, в которых производная функции равна нулю.
было в ЕГЭ
в условии
в решении
в тексте к заданию
в атрибутах
Категория
Атрибут
Всего: 660 1–20 | 21–40 | 41–60 | 61–80 …
Добавить в вариант
Найдите наименьшее значение функции на отрезке
Найдите наибольшее значение функции на отрезке
Найдите наименьшее значение функции на отрезке
Найдите наибольшее значение функции на отрезке
Найдите наименьшее значение функции на отрезке
Найдите наименьшее значение функции на отрезке
Найдите наибольшее значение функции на отрезке
Найдите наибольшее значение функции на отрезке
Найдите наименьшее значение функции на отрезке
Найдите наименьшее значение функции на отрезке
Найдите наибольшее значение функции на отрезке
Найдите наибольшее значение функции на отрезке
Найдите точку минимума функции
Найдите точку минимума функции
Найдите точку максимума функции
Найдите точку минимума функции
Найдите точку максимума функции
Найдите наименьшее значение функции на отрезке [−2,5; 0].
Найдите наибольшее значение функции на отрезке [−4,5; 0].
Найдите наименьшее значение функции на отрезке
Всего: 660 1–20 | 21–40 | 41–60 | 61–80 …
Исследование графика функции
На рисунке изображен график функции . Посмотрим, как исследовать функцию с помощью графика. Оказывается, глядя на график, можно узнать всё, что нас интересует, а именно:
- область определения функции;
- область значений функции;
- нули функции;
- промежутки возрастания и убывания;
- точки максимума и минимума;
- наибольшее и наименьшее значение функции на отрезке.

Уточним терминологию:
Абсцисса — это координата точки по горизонтали.
Ордината — координата по вертикали.
Ось абсцисс — горизонтальная ось, чаще всего называемая ось X.
Ось ординат — вертикальная ось, или ось Y.
Аргумент — независимая переменная, от которой зависят значения функции. Чаще всего обозначается x.
Другими словами, мы сами выбираем x, подставляем в формулу функции и получаем y.
Область определения функции — множество тех (и только тех) значений аргумента x, при которых функция существует.
Обозначается: D(f) или D(y).
На нашем рисунке область определения функции — это отрезок
. Именно на этом отрезке нарисован график функции. Только здесь данная функция существует.
Область значений функции — это множество значений, которые принимает переменная . На нашем рисунке это отрезок
— от самого нижнего до самого верхнего значения
.
Нули функции — точки, где значение функции равно нулю, то есть . На нашем рисунке это точки
и
.
Значения функции положительны там, где . На нашем рисунке это промежутки
и
.
Значения функции отрицательны там, где . У нас это промежуток (или интервал) от
до
.
Важнейшие понятия — возрастание и убывание функции на некотором множестве . В качестве множества
можно взять отрезок
, интервал
, объединение промежутков или всю числовую прямую.
Функция возрастает на множестве
, если для любых
и
, принадлежащих множеству
, из неравенства
следует неравенство
.
Иными словами, чем больше , тем больше
, то есть график идет вправо и вверх.
Функция убывает на множестве
, если для любых
и
, принадлежащих множеству
, из неравенства
следует неравенство
.
Для убывающей функции большему значению соответствует меньшее значение
. График идет вправо и вниз.
На нашем рисунке функция возрастает на промежутке
и убывает на промежутках
и
.
Определим, что такое точки максимума и минимума функции.
Точка максимума — это внутренняя точка области определения, такая, что значение функции в ней больше, чем во всех достаточно близких к ней точках.
Другими словами, точка максимума — такая точка, значение функции в которой больше, чем в соседних. Это локальный «холмик» на графике.
На нашем рисунке — точка максимума.
Точка минимума — внутренняя точка области определения, такая, что значение функции в ней меньше, чем во всех достаточно близких к ней точках.
То есть точка минимума — такая, что значение функции в ней меньше, чем в соседних. На графике это локальная «ямка».
На нашем рисунке — точка минимума.
Точка — граничная. Она не является внутренней точкой области определения и потому не подходит под определение точки максимума. Ведь у нее нет соседей слева. Точно так же и
на нашем графике не может быть точкой минимума.
Точки максимума и минимума вместе называются точками экстремума функции. В нашем случае это и
.
А что делать, если нужно найти, например, минимум функции на отрезке
? В данном случае ответ:
. Потому что минимум функции — это ее значение в точке минимума.
Аналогично, максимум нашей функции равен . Он достигается в точке
.
Можно сказать, что экстремумы функции равны и
.
Иногда в задачах требуется найти наибольшее и наименьшее значения функции на заданном отрезке. Они не обязательно совпадают с экстремумами.
В нашем случае наименьшее значение функции на отрезке равно
и совпадает с минимумом функции. А вот наибольшее ее значение на этом отрезке равно
. Оно достигается в левом конце отрезка.
В любом случае наибольшее и наименьшее значения непрерывной функции на отрезке достигаются либо в точках экстремума, либо на концах отрезка.
Спасибо за то, что пользуйтесь нашими публикациями.
Информация на странице «Исследование графика функции» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.
Публикация обновлена:
08.05.2023
Задание №7 (ЕГЭ)
Как работать если
-
на рисунке изображен график функции y = f(x), надо ответить на вопросы, связанные с производной,
-
или на рисунке изображен график первообразной y = F(x) (это график функции), надо ответить на вопросы, связанные с функцией y = f(x) (это производная y = F(x)),
-
или изображен график пройденного расстояния S = S(t) (это формула функции), надо ответить на вопросы, связанные со скоростью (производная пути).
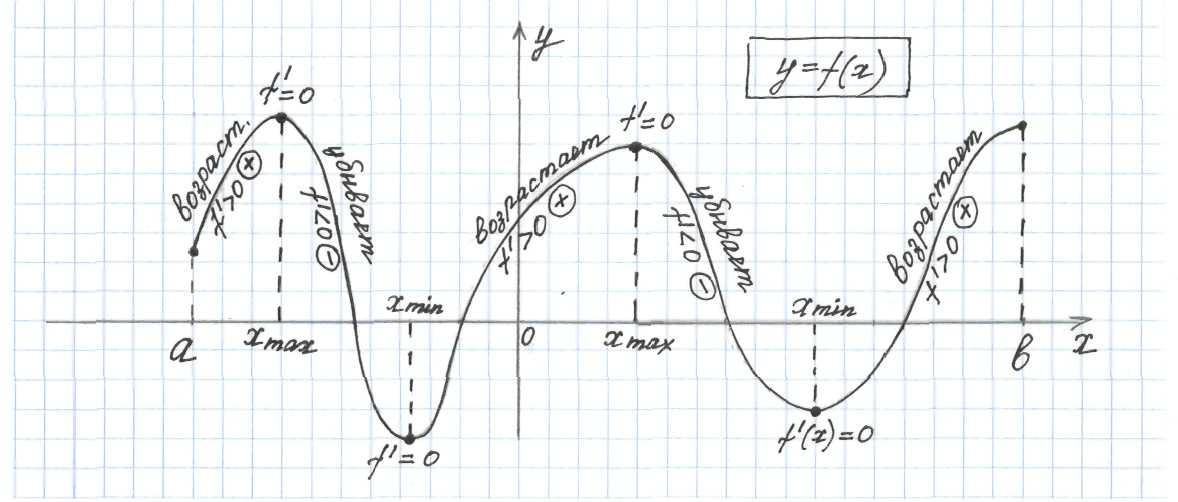
-
Если график задан на промежутке [a; b], то через числа a и b провести вертикальные пунктирные линии.
-
Жирно выделить часть графика на этом отрезке.
-
Обводить график слева направо.
-
Если поднимаемся вверх, то над графиком записать функция возрастает, под графиком f ‘(x) 0 (производная положительная «+»).
-
Если опускаемся вниз, то над графиком записать функция убывает, под графиком f ‘(x) (производная отрицательная « – »).
-
Если слева на право, функция меняет возрастание на убывание, то это точка максимума и производная в этой точке равна нулю (f ‘(x) = 0).
-
Если слева на право, функция меняет убывание на возрастание, то это точка минимума и производная в этой точке равна нулю (f ‘(x) = 0).
Внимание!!!
Если изображен график функции и несколько чисел на оси OX, просят найти наименьшее или наибольшее значение производной, то
-
Если наибольшее: выбрать числа, где производная положительная, через точки касания провести касательную и луч параллельный оси OX (вправо), где угол больше там и производная больше.
-
Если наименьшее: выбрать числа, где производная отрицательная, через точки касания провести касательную и луч параллельный оси OX (вправо), где угол меньше там и производная меньше.

Задание №7 (ЕГЭ)
Как дать правильный ответ, если сказано:
На рисунке изображен график производной функции f(x). Значит, изображен график y = f ‘(x).
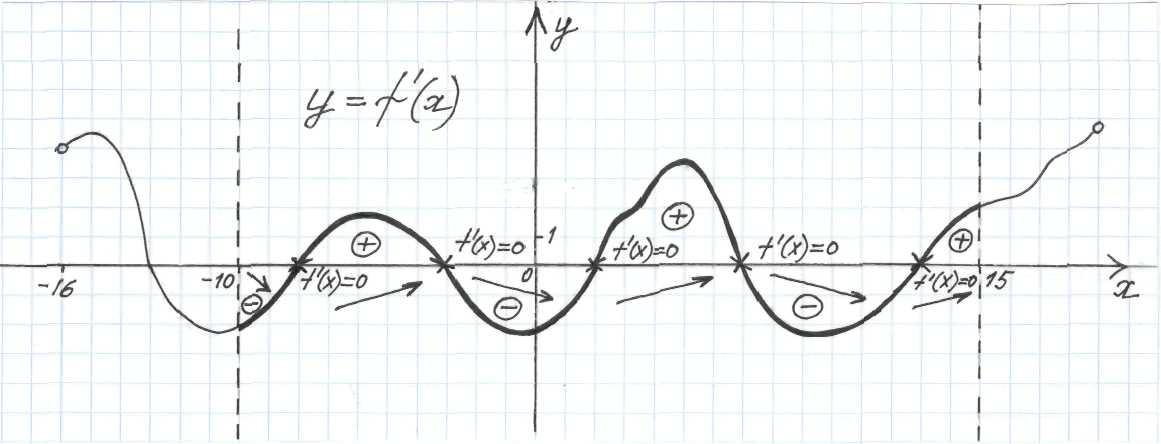
На рисунке изображен график производной функции f(x) на интервале (-16; 19). Отвечать на вопросы на отрезке [-10; 15].
-
Через концы заданного отрезка (найти числа на оси OX) провести вертикальные линии (это пунктирные).
-
Жирно выделить часть графика на этом отрезке.
-
Крестиком отметить точки пересечения графика с осью OX, здесь производная равна нулю. На чертеже около крестика записать f ‘(x) = 0.
-
Ось Ox (горизонтальная) делит график производной функции на части:
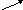
-
Если часть графика лежит выше оси Ox, здесь производная положительная (вверху поставить знак плюс «+», внизу нарисовать стрелку вверх (это значит, функция возрастает)).
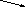
-
Если часть графика лежит ниже оси Ox, здесь производная отрицательная (внизу поставить знак «-»), здесь внизу изобразить стрелку вниз (это значит, функция убывает).
-
Если двигаться по оси Ox от левого конца заданного отрезка (левый пунктирный конец) к правому концу, то:
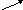
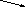
-
Если при переходе через точку, где производная равна нулю (это крестик) производная меняет знак с минуса «-» на плюс «+», а функция убывание на возрастание , то эта точка (смотрят какой у этой точки x) минимума.
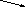
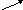
-
Если до точки (слева) стоял знак производной плюс «+», а после этой точки знак производной минус «-», при переходе через эту точку функция меняет возрастание на убывание , то эта точка (смотрим какой у этой точки x) максимума.
-
Если просят найти точки экстремума: это точки максимума и минимума вместе.
-
Если по графику производной надо выяснить, в какой точке заданного отрезка функция принимает наибольшее или наименьшее значение, то надо посмотреть на график и выделить вертикальными пунктирными линиями отрезок.
-
Если производная на этом отрезке отрицательная «-», а функция убывает , то наибольшее значение будет в левой точке, наименьшее в правой точке заданного отрезка.
-
Если производная положительная «+», а функция возрастает , то наименьшее значение в левой точке, наибольшее значение в правой точке заданного отрезка.
-
Если просят найти количество точек, в которых касательная параллельна прямой y = a (y =6; y =-2; и т.д.), формула без x (нет x), это значит угловой коэффициент (число перед x, его нет так как нет x) равен нулю. k = 0, но k = f ‘(x) = tgα. Если k = 0, то f ‘(x) = 0 (производная равна нулю). Тогда считаем точки, где производная равна нулю (крестики).


-
Если просят найти количество точек, в которых касательная параллельна заданной прямой y = kx +m (у = -2 x + 4; y = 3 x -6) тогда надо обвести кружком число, стоящее перед x вместе со знаком (угловой коэффициент), записать k = -2 или k = 3. Но k = f ‘(x), значит, производная равна этому числу f ‘(x) = -2; f ‘(x) = 3. Дальше на оси Oy найти это число и через него провести прямую, параллельную оси Ox. Посчитать количество точек пересечения, проведенной прямой с жирно выделенным графиком, это число записать в ответ.
Внимание!!!
Несколько раз внимательно прочитайте задание, жирно обведите вопрос, постарайтесь понять, что Вас просят найти, а дальше ищите и не забывайте записать ответ, проверив три раза!!!

Задание №7 (ЕГЭ)
I способ
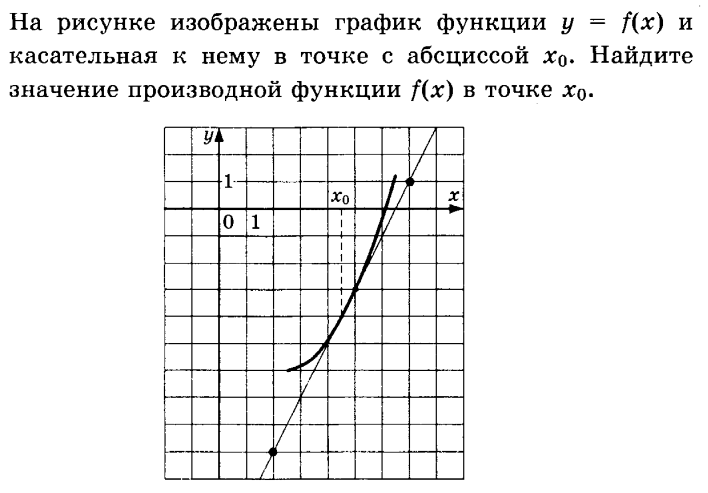
Знаем!!! f ‘(x₀) = tgα = k
Чтобы найти f ‘(x₀) найдем tgα. tgα = 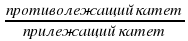
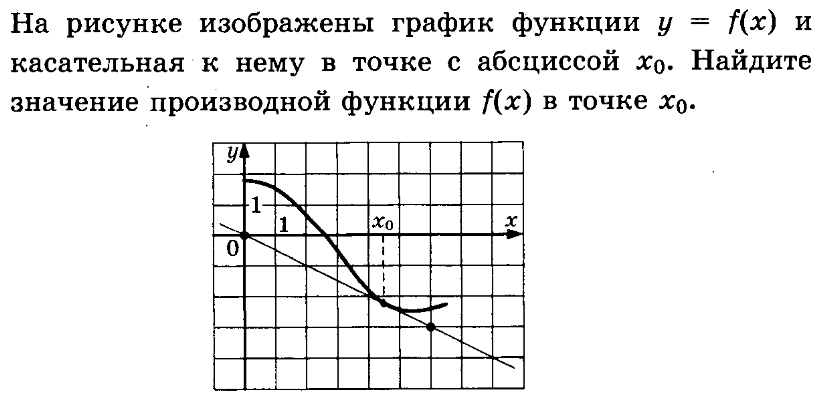
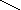
-
Если прямая убывающая (имеет вид ), то f ‘(x₀) = – tgα
-
На прямой найти две жирные точки. Если таких нет, то на прямой надо выделить жирно две точки, которые будут вершиной клетки (узловые точки).
-
Через верхнею точку, провести вертикальную (параллельную оси Oy) прямую.
-
Через нижнею точку горизонтальную (параллельную оси Ox) прямую.
-
Проведенные прямые вместе с касательной образуют прямоугольный треугольник, его нужно жирно выделить.
-
В прямоугольном треугольнике выделить острый угол около горизонтального катета, обозначить его буквой α.
-
Записать tgα =
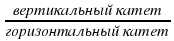 (длины катетов посчитать по клеткам).
(длины катетов посчитать по клеткам). -
Полученную дробь заменить десятичной.
-
Записать ответ f ‘(x₀) = – tgα
-
Перенести в бланк ответов.
Задание №7 (ЕГЭ)
I способ
Знаем!!! f ‘(x₀) = tgα = k
Чтобы найти f ‘(x₀) найдем tgα. tgα = 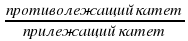
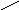
-
Если прямая возрастающая (имеет вид ), то f ‘(x₀) = tgα
-
На прямой найти две жирные точки. Если таких нет, то на прямой надо выделить жирно две точки, которые будут вершиной клетки (узловые точки).
-
Через верхнею точку, провести вертикальную (параллельную оси Oy) прямую.
-
Через нижнею точку горизонтальную (параллельную оси Ox) прямую.
-
Проведенные прямые вместе с касательной образуют прямоугольный треугольник, его нужно жирно выделить.
-
В прямоугольном треугольнике выделить острый угол около горизонтального катета, обозначить его буквой α.
-
Записать tgα =
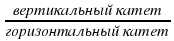 (длины катетов посчитать по клеткам).
(длины катетов посчитать по клеткам). -
Полученную дробь заменить десятичной.
-
Записать ответ f ‘(x₀) = tgα (без минуса)
-
Перенести в бланк ответов.
Задание №7 (ЕГЭ)
II способ
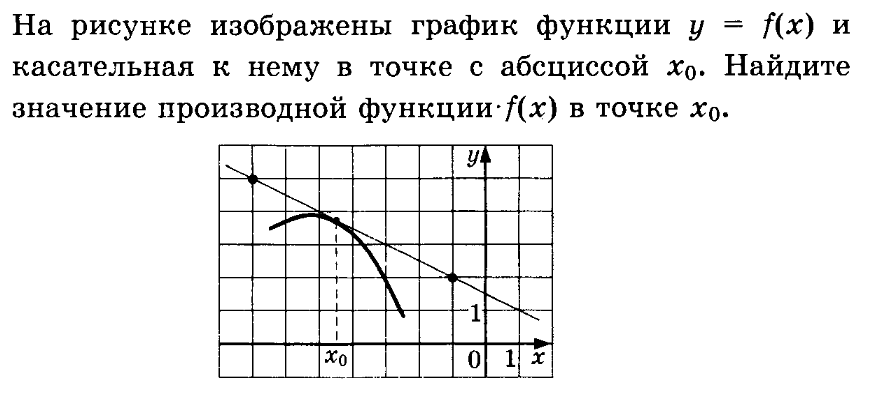
Знаем, что f ‘(x₀) = tgα = k , где k – угловой коэффициент касательной
-
Записать уравнение прямой y = k∙x + m
-
На касательной выбрать две точки А (-7; 5) и В (-1; 2)
-
В уравнение прямой подставить координаты точек
y = k∙x + m А (-7; 5) x =-7; y = 5 5 = k∙(-7) + m
y = k∙x + m В (-1; 2) x =-1; y = 2 2 = k∙(-1) + m
-
Составить систему
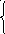
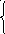 -7∙k + m = 5, -6∙k = 3, k = –
-7∙k + m = 5, -6∙k = 3, k = –
-1∙k + m = 2; -1∙k + m = 2;
Т.к. k = f ‘(x₀), то f ‘(x₀) = –
Тема 11.
Исследование функций с помощью производной
11
.
08
Поиск наибольшего/наименьшего значения у сложных функций
Вспоминай формулы по каждой теме
Решай новые задачи каждый день
Вдумчиво разбирай решения
ШКОЛКОВО.
Готовиться с нами – ЛЕГКО!
Подтемы раздела
исследование функций с помощью производной
Решаем задачи
Найдите наименьшее значение функции
Показать ответ и решение
Выпишем ОДЗ:
1) Обозначим тогда
Найдем производную функции по
Найдём критические точки, то есть внутренние точки области определения
функции, в которых её производная равна 0 или не существует:
Отсюда При этом производная существует всюду на ОДЗ.
Для того, чтобы найти наибольшее/наименьшее значение функции, нужно
понять, как схематично выглядит её график.
2) Найдём промежутки знакопостоянства и промежутки монотонности

3) Эскиз графика
Таким образом, наименьшее значение функции достигается в точке
минимума
Найдите наименьшее значение функции
на
отрезке .
Показать ответ и решение
Найдем ОДЗ: — любое число.
1) Найдем производную:
Найдём критические точки (то есть внутренние точки области определения функции, в которых её
производная равна 0 или не существует):
Таким образом, при
. Производная существует при любом
.
2) Найдём промежутки знакопостоянства и промежутки монотонности
:

3) Найдём промежутки знакопостоянства и промежутки монотонности
на отрезке
:

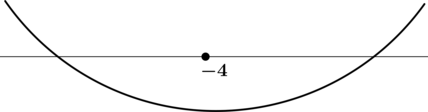
4) Эскиз графика на отрезке
:
Таким образом, наименьшего на отрезке значения функция достигает в точке
.
Тогда — наименьшее значение функции
на отрезке
.
Найдите наименьшее значение функции
на отрезке
Показать ответ и решение
Найдем ОДЗ: — любое число.
1) Найдем производную:
Найдём критические точки, то есть внутренние точки области определения функции, в которых её производная равна 0 или не
существует:
Производная существует при любом
2) Найдём промежутки знакопостоянства и промежутки монотонности

Здесь бесконечное число промежутков, в которых чередуются знаки производной.
3) Найдём промежутки знакопостоянства и промежутки монотонности
на отрезке

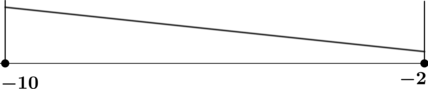
4) Эскиз графика на отрезке
Таким образом, наименьшего на отрезке значения функция достигает в точке минимума
Найдите наименьшее значение функции
Показать ответ и решение
Способ 1.
Функцию можно переписать в виде
Эта функция является композицией двух функций: возрастающей и
возрастающей при и убывающей при
функции
Следовательно, исходная функция возрастает при и убывает при
то есть является точкой минимума.
Следовательно, в этой точке достигается наименьшее значение функции:
P.S. Композиция двух возрастающих или двух убывающих функций —
возрастающая, а возрастающей и убывающей — убывающая.
Способ 2.
Функция определена при всех Исследуем функцию и найдем ее
промежутки возрастания и убывания, для этого найдем ее производную:
Найдем нули производной:
Нули производной и точки, в которых она не существует, разбивают область
определения производной на промежутки, на каждом из которых она непрерывна и
принимает значения одного знака. Найдем знаки производной на каждом из таких
промежутков:
При производная отрицательна, то есть функция
убывает; при производная положительна, то есть функция
возрастает. Следовательно, является точкой минимума и наименьшего
значения функция достигает в этой точке:
Найдите наименьшее значение функции
Показать ответ и решение
Преобразуем исходную функцию:
Заметим, что Значит,
Мы доказали, что Значит, если мы докажем, что существует такая точка
что
то 3 будет
наименьшим значением функции
Для этого найдем точку, в которой
Пусть тогда
Значит, наименьшее значение функции равно 3.
Найдите наименьшее значение функции
на отрезке
Показать ответ и решение
Найдем критические точки функции Для этого посчитаем производную:
Теперь найдем нули производной:
При этом то есть данная точка лежит на отрезке
Наименьшее значение функции на отрезке достигается в точке экстремума или на концах отрезка. Сравним значения
функции во всех таких точках:
Таким образом, наименьшее значение функции на отрезке равно -7.
Найдите наибольшее значение функции
на отрезке
Показать ответ и решение
Найдем ОДЗ: — любое число.
1) Найдем производную:
Найдём критические точки, то есть внутренние точки области определения функции, в которых её производная равна 0 или не
существует:
Производная существует при любом
2) Найдём промежутки знакопостоянства и промежутки монотонности

3) Найдём промежутки знакопостоянства и промежутки монотонности
на отрезке

4) Эскиз графика на отрезке
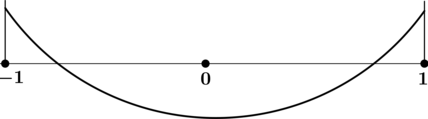
Таким образом, наибольшего на отрезке значения функция
достигает в точке
или в точке
Сравним
значения функции в этих точках:
Тогда наибольшее значение функции на отрезке
равно 2.
Найдите наибольшее значение функции
.
Показать ответ и решение
1) Обозначим , тогда
.
Найдём критические точки (то есть внутренние точки области определения функции, в которых её
производная равна или не существует):
(так
как , но
при любом
), откуда находим корень
. Для того, чтобы
найти наибольшее/наименьшее значение функции, нужно понять, как схематично выглядит её
график.
2) Найдём промежутки знакопостоянства :
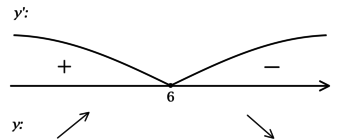
3) Эскиз графика:
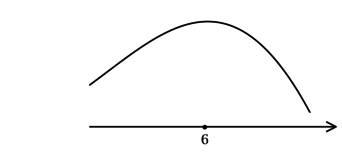
Таким образом, – точка максимума функции
и наибольшее значение достигается в
ней:
.
Итого: – наибольшее значение функции
.
Найдите наибольшее значение функции
Показать ответ и решение
Найдем ОДЗ: .
1) Обозначим , тогда
.
Найдем производную:
Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна
или не существует):
— на ОДЗ, откуда находим корень .
Производная функции не существует при
, но у данного уравнения отрицательный
дискриминант, следовательно, у него нет решений.
Для того, чтобы найти наибольшее/наименьшее значение функции, нужно понять, как схематично выглядит её
график.
2) Найдём промежутки знакопостоянства и промежутки монотонности
:
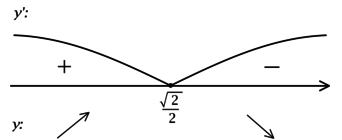
3) Эскиз графика :
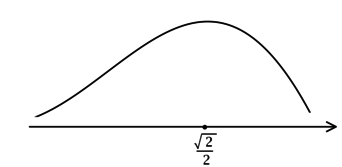
Таким образом, наибольшего значение функция достигает в точке
:
Найдите наибольшее значение функции
на отрезке
Показать ответ и решение
Найдем критические точки функции Для этого посчитаем производную:
Теперь найдем нули производной:
При этом то есть данная точка лежит на отрезке
Наибольшее значение функции на отрезке достигается в точке экстремума или на концах отрезка. Сравним значения
функции во всех таких точках:
Таким образом, наибольшее значение функции на отрезке равно 7.
Найдите наибольшее значение функции
.
Показать ответ и решение
1) Обозначим , тогда
.
Найдём критические точки (то есть внутренние точки области определения функции, в которых её
производная равна или не существует):
(так
как , но
при любом
), что равносильно
при
, откуда
находим корни . Для того, чтобы найти наибольшее/наименьшее значение функции,
нужно понять, как схематично выглядит её график.
2) Найдём промежутки знакопостоянства : (их бесконечно много, но они чередуются)
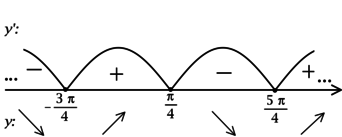
3) Эскиз графика:
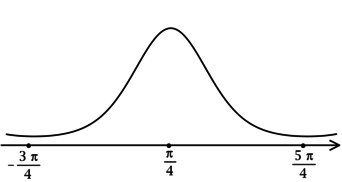
Таким образом, – точки локальных максимумов функции
и наибольшее значение
достигается в одной из них:
.
Итого: – наибольшее значение функции
.
