- Учебники
- 2 класс
- Математика 👍
- Петерсон
- №5
авторы: Петерсон.
издательство: Ювента
Раздел:
- ЧАСТЬ 3
- Урок 35. Решение задач
ГДЗ учебник по математике 2 класс Петерсон. Урок 35. Решение задач. Номер №5
- Предыдущее
- Следующее
Найди площадь закрашенной фигуры:
reshalka.com
ГДЗ учебник по математике 2 класс Петерсон. Урок 35. Решение задач. Номер №5
Решение а
1) 7 * 5 = 35
(
м
2
)
− площадь прямоугольника;
2) 4 * 4 = 16
(
м
2
)
− площадь квадрата;
3) 35 + 16 = 51
(
м
2
)
− площадь закрашенной фигуры.
Ответ: 51
м
2
Решение б
1) 5 * 6 = 30
(
д
м
2
)
− площадь всего прямоугольника;
2) 2 * 1 = 2
(
д
м
2
)
− площадь не закрашенного прямоугольника;
3) 30 − 2 = 28
(
д
м
2
)
− площадь закрашенной фигуры.
Ответ: 28
д
м
2
- Предыдущее
- Следующее
Нашли ошибку?
Если Вы нашли ошибку, неточность или просто не согласны с ответом, пожалуйста сообщите нам об этом
было в ЕГЭ
в условии
в решении
в тексте к заданию
в атрибутах
Категория
Атрибут
Всего: 85 1–20 | 21–40 | 41–60 | 61–80 …
Добавить в вариант
На клетчатой бумаге с размером клетки 
изображён круг. Найдите площадь закрашенного сектора. Ответ дайте в квадратных сантиметрах.
На клетчатой бумаге с размером клетки изображён круг. Найдите площадь закрашенного сектора. Ответ дайте в квадратных сантиметрах.
На клетчатой бумаге с размером клетки изображён круг. Найдите площадь закрашенного сектора. Ответ дайте в квадратных сантиметрах.
На клетчатой бумаге с размером клетки изображён круг. Найдите площадь закрашенного сектора. Ответ дайте в квадратных сантиметрах.
На клетчатой бумаге с размером клетки изображён круг. Найдите площадь закрашенного сектора. Ответ дайте в квадратных сантиметрах.
На клетчатой бумаге с размером клетки изображён круг. Найдите площадь закрашенного сектора. Ответ дайте в квадратных сантиметрах.
Найдите площадь закрашенной фигуры на координатной плоскости.
Найдите площадь закрашенной фигуры на координатной плоскости.
На клетчатой бумаге с размером клетки изображён круг. Найдите площадь закрашенного сектора. Ответ дайте в квадратных сантиметрах.
Найдите площадь закрашенной фигуры на координатной плоскости.
На клетчатой бумаге с размером клетки изображён круг. Найдите площадь закрашенного сектора. Ответ дайте в квадратных сантиметрах.
На клетчатой бумаге с размером клетки изображён круг. Найдите площадь закрашенного сектора. Ответ дайте в квадратных сантиметрах.
На клетчатой бумаге с размером клетки изображён круг. Найдите площадь закрашенного сектора. Ответ дайте в квадратных сантиметрах.
На клетчатой бумаге с размером клетки изображён круг. Найдите площадь закрашенного сектора. Ответ дайте в квадратных сантиметрах.
На клетчатой бумаге с размером клетки изображён круг. Найдите площадь закрашенного сектора. Ответ дайте в квадратных сантиметрах.
На клетчатой бумаге с размером клетки изображён круг. Найдите площадь закрашенного сектора. Ответ дайте в квадратных сантиметрах.
На клетчатой бумаге с размером клетки изображён круг. Найдите площадь закрашенного сектора. Ответ дайте в квадратных сантиметрах.
На клетчатой бумаге с размером клетки изображён круг. Найдите площадь закрашенного сектора. Ответ дайте в квадратных сантиметрах.
На клетчатой бумаге с размером клетки изображён круг. Найдите площадь закрашенного сектора. Ответ дайте в квадратных сантиметрах.
На клетчатой бумаге с размером клетки изображён круг. Найдите площадь закрашенного сектора. Ответ дайте в квадратных сантиметрах.
Всего: 85 1–20 | 21–40 | 41–60 | 61–80 …
Приветствую вас, дорогие читатели!
Предлагаю вам решить две геометрических задачи. Задания очень простые и от вас требуется только вспомнить несколько формул на нахождение площадей. Здесь нужно найти площадь закрашенной фигуры.
Надеюсь, вы быстро найдете решение)
Задание первое
Задание второе
Как вам задания? Обе площади удалось найти?
Ответы и свои решения оставляйте в комментариях.
Не забудьте подписаться на мой канал, чтобы не пропустить новые задания)
Благодарю за внимание!
Я позволю себе также нетривиальный метод решения без использования теоремы Пифагора.
Дострою прямоугольник жёлтым цветом ABCD. Как мы видим на моём эскизе его площадь равна произведению клеток длинной стороны на клетки короткой стороны, точнее 4 х 3 = 12 клеток.
Далее я дострою голубой прямоугольник fBgh недостающего треугольника Bgh он занимает площадь 2 клетки или 1 х 2 = 2, но следует заметить, что недостающий треугольник занимает ровно половину от прямоугольника, а точнее 1 клетку или 2 : 2 = 1.
Осталось ещё немного. Я дострою малиновый прямоугольник CDeg недостающего треугольника Deg он занимает площадь в 6 клеток или 3 х 2 = 6, но следует заметить, что недостающий треугольник занимает ровно половину от прямоугольника а точнее 3 клетки или 6 : 2 = 3.
А теперь завершим расчёт:
Я отниму от площади большого прямоугольника ABCD 2 треугольника Bgh и Deg. Решаем:
12 – 1 – 3 = 8.
Мой ответ 8 клеток
Задача решена нетривиальным эксклюзивным методом с использованием не только логического, но и абстрактного мышления. Без квадратов катетов и квадрата гипотенузы.
ЕГЭ профильный уровень. №7 Первообразная. Задача 6
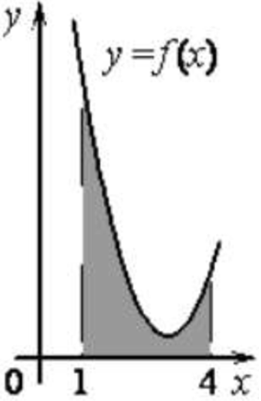Задача6 . На рисунке изображён график некоторой функции (y = fleft( x right)). Функция (Fleft( x right) = frac{1}{2}{x^3} — frac{9}{2}{x^2} + 14x — 12) — одна из первообразных функции (fleft( x right)). Найдите площадь закрашенной фигуры.
ОТВЕТ: 6.
Площадь закрашенной фигуры равна интегралу (intlimits_1^4 {left( x right)dx} = Fleft( 4 right) — Fleft( 1 right).) Найдём значение первообразной в точках 4 и 1:
(Fleft( 4 right) = frac{1}{2} cdot {4^3} — frac{9}{2} cdot {4^2} + 14 cdot 4 — 12 = 32 — 72 + 56 — 12 = 4)
(Fleft( 1 right) = frac{1}{2} cdot {1^3} — frac{9}{2} cdot {1^2} + 14 cdot 1 — 12 = frac{1}{2} — frac{9}{2} + 14 — 12 = — 2)
Тогда площадь закрашенной фигуры: (S = Fleft( 4 right) — Fleft( 1 right) = 4 — left( { — 2} right) = 6)
Ответ: 6.
Комментарии для сайта Cackle
