Найди равные фигуры. Сколько клеток содержит каждая фигура на этом рисунке?


reshalka.com
ГДЗ учебник по математике 3 класс Дорофеев. Часть 1 страница 81. Номер №6
Решение
1) 4 * 2 + 2 * 2 = 8 + 4 = 12 (клеток) − в первой фигуре;
2) 3 * 4 = 12 (клеток) − во второй фигуре;
3) 5 * 2 + 2 * 1 = 10 + 2 = 12 (клеток) − в третьей фигуре;
4) 5 * 1 + 3 * 2 = 5 + 6 = 11 (клеток) − в четвертой фигуре;
5) 6 * 1 + 4 * 2 = 6 + 8 = 14 (клеток) − в пятой фигуре;
6) 4 * 2 + 2 * 2 = 8 + 4 = 12 (клеток) − в шестой фигуре;
7) 2 * 8 + 3 * 2 = 16 + 6 = 22 (клетки) − в седьмой фигуре.
Равные фигуры 1 и 6, так как их можно наложить друг на друга.
ГДЗ и решебники
вип уровня
- ГДЗ
- 5 класс
- Математика
- Виленкин
- Задание 712

Условие
Найдите равные фигуры на рисунке 67. Сколько клеточек содержит каждая фигура на этом рисунке?
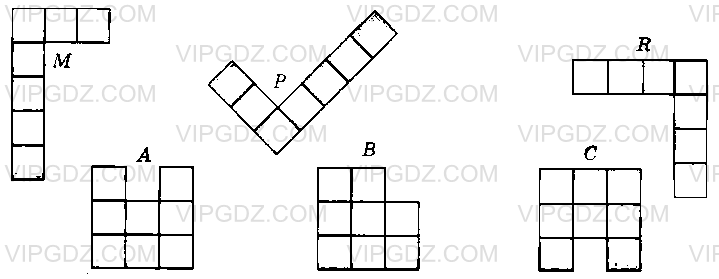
Решение 1

Решение 2
Решение 3

Популярные решебники
В детстве с друзьями часто покупали одну шоколадку на двоих и делили. Разрезать нужно было поровну иначе война и конец дружбы. А как проверить? Совместить две части и посмотреть. Это интуитивно понятное действие. Если два объекта совместились, они равны. Если одни уместился в другой, он меньше.
Неудивительно, что в “Началах” Евклида содержится соответствующая аксиома:
И совмещающиеся друг с другом равны между собой.
А в школьном курсе равные фигуры определяются, как фигуры, которые совмещаются при наложении. Определение понятное, но неудобное. При попытке наложить нарисованные фигуры, возникают сложности. Вырезать ее, что ли. А кроме того, нет гарантий, что нарисованные фигуры отражают реальность. Может повезло с рисунком.
Движение
Изучая алгебру, дети проходят функции. Правило, по которому каждому числу из множества ставится в соответствие единственное число множества. В геометрии аналогом функций является преобразование плоскости. Правило, по которому каждой точке плоскости ставится в соответствие точка этой же плоскости. Среди преобразований плоскости выделяют движения. Это преобразования, которых сохраняют расстояние. То есть, если точки лежат на расстоянии 5 см, то образы (точки, в которые они перейдут) тоже будут лежать на этом же расстоянии друг от друга.
Самый известный вид движения – осевая симметрия.
Также к движениям относится поворот, параллельный перенос и центральная симметрия, хотя это частный случай поворота.
Любопытно, что любое движение раскладывается в композицию осевых симметрий. То есть, грубо говоря, все движения на плоскости это производные от осевой симметрии.
Движение обладает рядом свойств. Отрезок переходит в отрезок, прямая – в прямую, луч – в луч, а угол – в угол такой же градусной меры. Эти свойства выводятся из определения движения. Если расстояние между точками остается неизменным, то отрезок не может перейти в ломаную. Иначе расстояние между концами отрезка увеличится по неравенству треугольника.
Равные фигуры
Две фигуры равны, если существует движение, которое переводит одну фигуру в другую. Это определение очень близко по духу к наложению, но имеет преимущество. Им удобно пользоваться при решении задач.
Доказать, что две трапеции равны, если четыре стороны одной из них соответственно равны сходственным элементам другой.
Чтобы доказать, что фигуры равны необходимо привести пример движения, который переводит одну фигуру в другую.
Рассмотрим первый случай расположения трапеций.
Построим вектор соединяющий две сходственные вершины. Совершим параллельный перенос вершин трапеции. Тогда отрезок АВ перейдет в отрезок EN, отрезок ВС в NM, CD в MH и AD в EH. Таким образом трапеция АВСD равна трапеции ENMH.
Второй случай.
Тогда сначала применим центральную симметрию относительно точки В, а затем перейдем к первому случаю. Точка В, как центр поворота останется на месте. Точнее перейдет в себя.
Третий случай. Основания не параллельны.
Продлим большие основания до пересечения и повернем трапецию на угол равный углу между основаниями. И опять переходим к первому случаю.
-
Главная
-
ГДЗ
- 1 класс
- Математика
-
Петерсон. Учебник
- Страница 36. Урок 19. Часть 2
Вернуться к содержанию учебника
Страница 31. Урок 16
Страница 32. Урок 17
Страница 33. Урок 17
Страница 34. Урок 18
Страница 35. Урок 18
Страница 36. Урок 19
Страница 37. Урок 19
Страницы 38. Урок 20
Страница 39. Урок 20
Страница 40. Урок 21
Страница 41. Урок 21
Вопрос
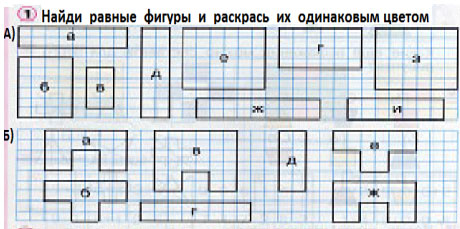
Задание № 1. Найди равные фигуры и раскрась их одинаковым цветом.
Подсказка
Повтори материал о геометрической фигуре прямоугольнике.
Ответ

Страница 31. Урок 16
Страница 32. Урок 17
Страница 33. Урок 17
Страница 34. Урок 18
Страница 35. Урок 18
Страница 36. Урок 19
Страница 37. Урок 19
Страницы 38. Урок 20
Страница 39. Урок 20
Страница 40. Урок 21
Страница 41. Урок 21
Вопрос
Задание № 2. Раскрась.
Подсказка
Повтори материал о треугольниках и многоугольниках.
Ответ

Страница 31. Урок 16
Страница 32. Урок 17
Страница 33. Урок 17
Страница 34. Урок 18
Страница 35. Урок 18
Страница 36. Урок 19
Страница 37. Урок 19
Страницы 38. Урок 20
Страница 39. Урок 20
Страница 40. Урок 21
Страница 41. Урок 21
Вопрос
Задание № 3.
Подсказка
Повтори состав чисел 2, 4, 6 и 8.
Ответ
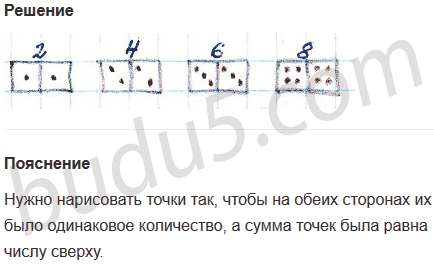
Страница 31. Урок 16
Страница 32. Урок 17
Страница 33. Урок 17
Страница 34. Урок 18
Страница 35. Урок 18
Страница 36. Урок 19
Страница 37. Урок 19
Страницы 38. Урок 20
Страница 39. Урок 20
Страница 40. Урок 21
Страница 41. Урок 21
Вернуться к содержанию учебника
Цель: формирование понятия “равные
фигуры”.
Задачи:
- сформировать способность к фиксированию
понятия “равные фигуры”, к фиксированию умения
нахождения равных фигур; - развивать математическую речь, геометрическое
мышление; тренировать мыслительные операции; - совершенствовать навыка счета в пределах 9;
- воспитывать в учащихся дисциплинированность,
умение совместной деятельности.
Ход урока
1. Организационный момент
Вступительное слово учителя.
Пираты – это морские разбойники, главной их цель
всегда была поиск клада. Мы будем добрыми
пиратами и отправимся в морское путешествие на
поиски нашего клада. Мне в руки попала старинная
пиратская карта.
Она очень запутанная, на ней отмечено множество
островов, чтобы запутать искателей, но нужно
попасть на остров, на котором спрятаны сокровища.
Чтобы его найти, нам нужно будет преодолеть
множество препятствий. Вы готовы? Тогда в путь.
Путешествовать мы будем на корабле.
Отправляемся на первый остров.
2. Устные счет
Итак, следуя нашей карте, мы оказались на
острове под названием “Устный счет”. И чтобы
двинуться дальше, нам необходимо выполнить
задания:
– назови соседей чисел: 3, 6, 8;
– заполни пропуски:
7,….,….,….,…, 12
10,…,…., 7,….,…,….,…., 2
– реши пример по числовому отрезку.
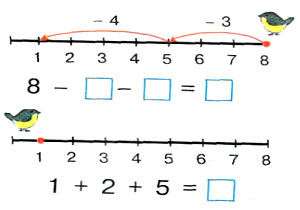
3. Актуализация знаний
Следующий остров, встретившийся нам на пути,
это “Геометрический остров”. Он таит в себе свои
тайны и загадки, которые нам необходимо раскрыть!
Задания.
– Ребята нужно вспомнить и нарисовать все
известные нам геометрические фигуры. (Круг,
квадрат, ромб, овал, прямоугольник)
– Посмотрите на рисунок, какие фигуры
изображены?
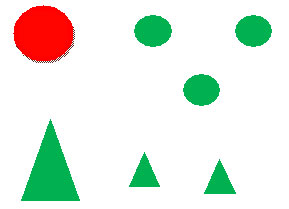
– По каким признакам можно разбить все фигуры на
группы? (Цвет, форма, размер). Назови эти
группы.
4. Ознакомление с новым материалом
Мы удачно справились с заданием и можем
отправиться на следующий остров. На третьем
острове я нашла тайные послания для нас с вами. У
каждого на парте есть конверт. Давайте откроем их
и посмотрим, какое на этот раз испытание нас ждёт.
(В каждом конверте находятся большой и
маленький зеленый квадрат, большой и маленький
синий треугольник, большой и маленький желтый
прямоугольник, два красных круга одинакового
размера)
– Ребята, вспомним, по каким признакам делятся
все фигуры? (Цвет, форма, размер)
Задание: разбейте по парам фигуры,
находящиеся в конверте, так, чтобы менялся только
один признак – размер.
– Смогли ли вы разбить все предметы по парам? (Нет)
– Почему? (Потому что два круга одинаковы по
размеру, цвету и форме)
– Докажите, что эти фигуры одинаковы. (Наложением)
– Давайте подумаем, как можно такие фигуры
назвать? (Из предложенных вариантов учитель
выбирает понятие “равные фигуры”)
– Итак, ребята, тема нашего урока “Равные
фигуры”. (Тема фиксируется на доске)
Давайте поближе познакомимся с ними. Для этого
нам нужно отправиться на следующий остров,
который так и называется: “Равные фигуры”.
Прибыв на остров, я сразу заметила на песке
различные фигуры, зарисовала их, так как волна
могла в любой момент их смыть.
– Посмотрите на доску, вот эти фигуры:
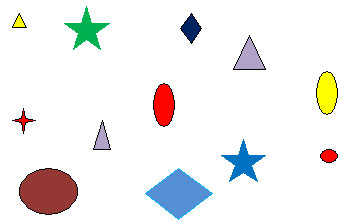
– Если среди них равные? (Дети сначала
определяют визуально равные фигуры, затем к
доске вызывается ученик)
– Как мы узнаем, действительно эти фигуры равны
или нет? (Путем наложения одной фигуры на
другую). Выполняется практическое действие.
– Итак, какие же фигуры мы можем назвать равными?
(Равными фигурами являются те, которые
совпадают при наложении).
– Определим, какие признаки у равных фигур
должны совпадать.
Под темой урока на доске фиксируется краткая
запись рассуждений детей.
Ф![]() Ф
Ф
Р![]() Р
Р
Ц![]() или
или![]() Ц
Ц
(Равные фигуры всегда одинаковой формы и
одинакового размера, а цвет может различаться)
Далее к доске приглашаются три ученика, каждому
учитель выдаёт большую модель фигуры. Весь класс
участвует в обсуждении.
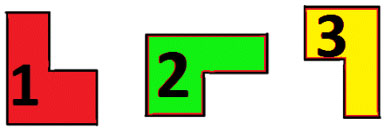
– Как вы считаете, 1 и 2 фигуры – равные?
– Как мы это проверим? (Ученики совмещают
фигуры и убеждаются, что они равны)
– А как вы думаете, 2 и 3 фигуры равны? (Выполняется
аналогичная работа)
– Ребята, а 1 и 3 фигура равны?
– Почему? (Они обе равны фигуре 2, значит, равны
друг другу)
– Давайте проверим наложением.
Ребята делают вывод, учитель кратко фиксирует
на доске 1=2 и 2=3, то 1=3 (Если первая фигура равна
второй, а вторая третьей, то первая фигура равна
третьей)
– У меня возникла проблема, а если я не могу
наложить фигуры, например, они нарисованы в
тетради, как проверить, равны они или нет? (Можно
посчитать по клеткам)
Отправляемся на следующий остров.
5. Первичное закрепление
Работа с учебником.
1) Стр. 36 №1. Найди равные фигуры и раскрась их
одинаковым цветом. Работа выполняется по
вариантам:
1 вариант – №1 а)
2 вариант – №1 б)
– Ребята, и с этим заданием вы справились, но
продолжить наше путешествие мы не можем, корабль
наткнулся на риф, нам необходимо его снова
собрать. Потому что по карте последний остров
именно тот, который нам нужен!
2) Стр. 36 №2.
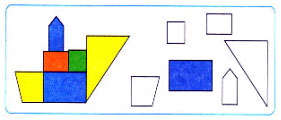
6. Повторение пройденного
Вы сегодня были храбры и не боялись сложных
испытаний, которые встречались нам на островах. И
в награду за это вы можете стать
учителями-капитанами корабля. Но быть капитаном
не просто, вам нужно многое знать и уметь, поэтому
постарайтесь справиться со следующими
заданиями:
1) Учащимся предлагается стать учителем:
придумать задание к рисунку, проконтролировать
выполнение, оценить.
![]()
2) Раздаются карточки. Нужно найти все ошибки.
Взаимопроверка по парам.
8=8 4+3=8 8-2>8-3
7>4 3+1<6 5+1<5+4
3<1 5<5+4 9-7=9-6
7. Итог урока, рефлексия
Мы прибыли на последний остров, а вот и клад! Наш
путь оказался не напрасным, ведь нам в награду
достались такие сокровища!

– Ребята, как вы понимаете фразу “Знания – наше
богатство”?
– Перед вами на столе два смайлика – грустный и
веселый. Если у вас хорошее настроение, приклейте
к кораблю желтый веселый смайлик, если плохое –
красный.
Мы с вами теперь опытные путешественники и
кладоискатели, и в следующий раз нас будут ждать
новые приключения! Спасибо за работу на уроке!

