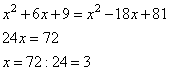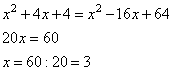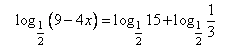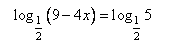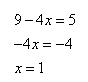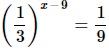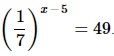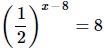Найдите корень уравнения егэ как решать

В задании №5 варианта ЕГЭ вам встретятся всевозможные уравнения: квадратные и сводящиеся к квадратным, дробно-рациональные, иррациональные, степенные, показательные и логарифмические и даже тригонометрические. Видите, как много нужно знать, чтобы справиться с заданием! И еще ловушки и «подводные камни», которые ждут вас в самом неожиданном месте.

Вот список тем, которые стоит повторить:

Квадратные уравнения

Арифметический квадратный корень

Корни и степени

Показательная функция

Показательные уравнения

Логарифмическая функция

Логарифмические уравнения

Тригонометрический круг

Формулы приведения

Формулы тригонометрии

Простейшие тригонометрические уравнения 1

Уравнения, сводящиеся к квадратным

1. Решите уравнение . Если уравнение имеет более одного корня, в ответе запишите меньший из корней.

Кажется, что уравнение очень простое. Но иногда здесь ошибаются даже отличники. А вот шестиклассник бы не ошибся.

С левой частью уравнения все понятно. Дробь умножается на А в правой части — смешанное число Его целая часть равна 19, а дробная часть равна Запишем это число в виде неправильной дроби:

Получим:

или

Выбираем меньший корень.

Ответ: -6,5.

2. Решите уравнение

Возведем в квадрат левую часть уравнения. Получим:

Ответ: -6.

Дробно-рациональные уравнения

3. Найдите корень уравнения

Перенесем единицу в левую часть уравнения. Представим 1 как и приведем дроби к общему знаменателю:

Ответ: -2.

Это довольно простой тип уравнений. Главное – внимательность.

Иррациональные уравнения

Так называются уравнения, содержащие знак корня – квадратного, кубического или n-ной степени.

4. Решите уравнение:

Выражение под корнем должно быть неотрицательно, а знаменатель дроби не равен нулю.

Значит, .

Возведём обе части уравнения в квадрат:

Решим пропорцию:

Условие  при этом выполняется.

Ответ: 87.

5. Решите уравнение Если уравнение имеет более одного корня, в ответе запишите меньший из корней.

А в этом уравнении есть ловушка. Решите его самостоятельно и после этого читайте дальше.

Выражение под корнем должно быть неотрицательно. И сам корень — величина неотрицательная. Значит, и правая часть должна быть больше или равна нуля. Следовательно, уравнение равносильно системе:

.

Решение таких уравнений лучше всего записывать в виде цепочки равносильных переходов:

.

Мы получили, что . Это единственный корень уравнения.

Типичная ошибка в решении этого уравнения такая. Учащиеся честно пишут ОДЗ, помня, что выражение под корнем должно быть неотрицательно:

Возводят обе части уравнения в квадрат. Получают квадратное уравнение: Находят его корни: или Пишут в ответ: -9 (как меньший из корней). В итоге ноль баллов.

Теперь вы знаете, в чем дело. Конечно же, число -9 корнем этого уравнения быть не может.

Ответ: 8.

6. Решите уравнение . Если уравнение имеет более одного корня, в ответе запишите больший из корней.

Запишем решение как цепочку равносильных переходов:

.

Ответ: 9.

Показательные уравнения

При решении показательных уравнений мы пользуемся свойством монотонности показательной функции.

7. Решите уравнение

Вспомним, что Уравнение приобретает вид: Функция монотонно возрастает и каждое свое значение принимает только один раз. Степени равны, их основания, значит, и показатели равны.

откуда

Ответ: 4.

8. Решите уравнение

Представим как

Функция монотонно возрастает и каждое свое значение принимает только один раз. Степени равны, их основания, значит, и показатели равны.

Ответ: 7,5.

9. Решите уравнение

Представим в виде степени с основанием 3 и воспользуемся тем, что

Ответ: 12,5.

Логарифмические уравнения

Решая логарифмические уравнения, мы также пользуемся монотонностью логарифмической функции: каждое свое значение она принимает только один раз. Это значит, что если логарифмы двух чисел по какому-либо основанию равны, значит, равны и сами числа.

И конечно, помним про область допустимых значений логарифма:

Логарифмы определены только для положительных чисел.

Основание логарифма должно быть положительно и не равно единице.

10. Решите уравнение:

Область допустимых значений: . Значит, 

Представим 2 в правой части уравнения как , чтобы слева и справа в уравнении были логарифмы по основанию 5.

Функция монотонно возрастает и каждое свое значение принимает ровно один раз. Логарифмы равны, их основания равны. «Отбросим» логарифмы! Конечно, при этом 

Ответ: 21.

11. Решите уравнение:

Запишем решение как цепочку равносильных переходов. Записываем ОДЗ и «убираем» логарифмы:

.

Ответ: -4.

12. Решите уравнение:

Перейдем от логарифма по основанию 4 (в показателе) к логарифму по основанию 2. Мы делаем это по формуле перехода к другому основанию:

Записываем решение как цепочку равносильных переходов.

.

Ответ: 19.

13. Решите уравнение. Если уравнение имеет более одного корня, в ответе запишите меньший из корней.

В этом уравнении тоже есть ловушка. Мы помним, что основание логарифма должно быть положительно и не равно единице.

Получим систему:

Первое уравнение мы получили просто из определения логарифма.

Квадратное уравнение имеет два корня: и

Очевидно, корень является посторонним, поскольку основание логарифма должно быть положительным. Значит, единственный корень уравнения:

Ответ: 12.

Тригонометрические уравнения (Часть 1 ЕГЭ по математике)

Тригонометрические уравнения? В первой части вариантов ЕГЭ? – Да. Причем это задание не проще, чем задача 13 из второй части варианта Профильного ЕГЭ.

14. Найдите корень уравнения: В ответе запишите наибольший отрицательный корень.

Типичная ошибка — решать это уравнение в уме. Мы не будем так делать! Несмотря на то, что это задание включено в первую части варианта ЕГЭ, оно является полноценным тригонометрическим уравнением, причем с отбором решений.

Сделаем замену Получим:

Получаем решения: Вернемся к переменной x.

Поделим обе части уравнения на и умножим на 4.

Первой серии принадлежат решения

Вторая серия включает решения

Наибольший отрицательный корень — тот из отрицательных, который ближе всех к нулю. Это

Ответ: -2.

15. Решите уравнение: В ответе напишите наименьший положительный корень.

Решение:

Сделаем замену Получим: Решения этого уравнения:

Вернемся к переменной х:

Умножим обе части уравнения на 4 и разделим на .

Выпишем несколько решений уравнения и выберем наименьший положительный корень:

Наименьший положительный корень

Ответ: 2.

Мы разобрали основные типы уравнений, встречающихся в задании №5 Профильного ЕГЭ по математике. Конечно, это не все, и видов уравнений в этой задаче существует намного больше. Именно поэтому мы рекомендуем начинать подготовку к ЕГЭ по математике не с задания 1, а с текстовых задач на проценты, движение и работу и основ теории вероятностей.
Успеха вам в подготовке к ЕГЭ!

Для начала немного поговорим о самом задании и критерии его оценивания.

В методических рекомендациях указано, что входить будут логарифмические, тригонометрические и показательные уравнения. А там – что попадется.

Задание состоит из двух вопросов:

1. Найти корни данного уравнения

2. Из всех корней выделить необходимые по условию корни, обосновать выбор

От правильного решения и обоснования своего ответа зависит итоговый балл, который можно получить за решение этого задания.

Под верными ответами подразумевается не просто написать слово “ответ” и числа, которые могут быть правильными, но и безошибочное, логически верное решение.

Во второй части задания с отбором корней также просто написать какие корни подойдут – не прокатит. Нужно именно показать, что корни подходят.

Отбор корней может быть произведён любым способом: с помощью числовой окружности, графика, решения двойных неравенств и т.п. При отборе корней с помощью числовой (тригонометрической) окружности на числовой окружности должно быть: отмечены и обозначены концы числового отрезка, выделена дуга, отмечены и обозначены корни, принадлежащие данному отрезку. На окружности могут быть отмечены вспомогательные числа, принадлежащие числовому отрезку

Конечно, говоря о решении уравнений, подразумевается, что простейшие уравнения (линейные, квадратные) уже решать умеем. На них я здесь подробно останавливаться не буду.

Логарифмические уравнения. Теория

Показательные уравнения. Теория

Тригонометрические уравнения. Теория

Сначала нужно научиться решать простейшие уравнения. Для их решения достаточно знать значения тригонометрических функций. Можно либо выучить, либо определять по единичной окружности. Лично мне удобнее пользоваться окружностью.

Кроме того, нужно уметь преобразовывать тригонометрические выражения

Самое главное, что нужно понимать – то, что все тригонометрические уравнения так или иначе сводятся к решению простейших тригонометрических уравнений. В табличку ниже я запишу в общем виде все типы простейших тригонометрических уравнений и формулы для обозначения ответов к ним.

В принципе, не сложно. Достаточно восстановить угол по значению одной из функций и правильно записать ответ. В этом очень помогает тригонометрическая окружность. Однако, сами уравнения изначально даны «хитрые». Нужно каким-нибудь способом привести их к простейшему виду. И вот об этих способах мы поговорим далее.

После того, как мы посмотрели теорию с примерами, рассмотрим несколько уравнений из №12 из пособий Ященко и Лысенко:

Сайты, меню, вход, новости

Сегодня мы будем тренировать навык решения задания 5 ЕГЭ – найдите корень уравнения. Будем искать корень уравнения. Рассмотрим примеры решения такого рода заданий. Но для начала, давайте вспомним – что значит – найти корень уравнения?

Это значит найти такое, зашифрованное под х число, которое мы подставим вместо x и наше уравнение будет верным равенством.

Например, 3x=9 – это уравнение, а 3^.3=9 – это уже верное равенство. То есть в данном случае, мы вместо x подставили число 3 – получили верное выражение или равенство, это означает, что мы решили уравнение, то есть нашли данное число x=3, которое превращает уравнение в верное равенство.

Вот этим мы и займемся  – будем находить корень уравнения.

Задание 1 – найдите корень уравнения 2^1-4x=32

Это показательное уравнение. Оно решается следующим образом – нужно чтобы и слева, и справа от знака “равно” была степень с одинаковым основанием.

Слева у нас основание степени 2, а справа – степени нет вовсе. Но мы знаем, что 32 – это 2 в пятой степени. То есть, 32=2⁵

Таким образом, наше уравнение будет выглядеть так: 2^1-4х=2⁵

Слева и справа у нас основания степени одинаковы, значит, чтобы у нас было равенство, должны быть равны и показатели степени:

1-4х=5

Получаем обыкновенное уравнение. Решаем обычным способом – все неизвестные оставляем слева, а известные переносим вправо, получим:

-4х=5-1

-4х=4

х=-1.

Делаем проверку: 2^1-4(-1)=32

2⁵=32

32=32

Мы нашли корень уравнение. Ответ: х=-1.

Самостоятельно найдите корень уравнения в следующих заданиях:

а) 2^5-х=64

б) 2^1-3х=128

Задание 2 – найдите корень уравнения 2^5-x = 1/16

Уравнение решаем аналогично – путем приведения левой и правой частей уравнения к одному основанию степени. В нашем случае – к основанию степени 2.

Используем следующее свойство степени:

По этому свойству мы получим для правой части нашего уравнения:

Тогда наше уравнение запишется в виде:

Если равны основания степени, значит, равны и показатели степени:

5-х=-4

-х=-4-5

х=9

Ответ: х=9.

Сделаем проверку – подставим найденное значение х в исходное уравнение – если мы получим верное равенство, значит, мы решили уравнение правильно.

2^5-9=1/16

2^-4=1/16

1/16=1/16

Мы нашли корень уравнения правильно.

Задание 3 – найдите корень уравнения

Заметим, что справа у нас стоит 1/8, а 1/8 – это

Тогда наше уравнение запишется в виде:

Если основания степени равны, значит, равны и показатели степени, получим простое уравнение:

3х-12=3

3х=15

х=5

Ответ: х=5. Проверку сделайте самостоятельно.

Задание 4 – найдите корень уравнения log₃(15-х)=log₃2

Это уравнение решается также как и показательное. Нам нужно, чтобы основания логарифмов слева и справа от знака “равно” были одинаковыми. Сейчас они одинаковы, значит, приравниваем те выражения, которые стоят под знаком логарифмов:

15-х=2

-х=2-15

-х=-13

х=13

Ответ: х=13

Задание 5 – найдите корень уравнения log₃(3-x)=3

Число 3 – это log₃27. Чтобы было понятно внизу нижним индексом под знаком логарифма стоит число которое возводится в степень, в нашем случае 3, под знаком логарифма стоит число, которое получилось при возведении в степень – это 27, а сам логарифм – это показатель степени, в которую нужно возвести 3, чтобы получить 27.

Смотрите на картинке:

Таким образом, любое число можно записать в виде логарифма. В данном случае очень удобно записать число 3 в виде логарифма с основанием 3. Получим:

log₃(3-x)=log₃27

Основания логарифмов равны, значит, равны и числа, стоящие под знаком логарифма:

3-х=27

Получим,

-х=27-3

-х=24

х=-24

Сделаем проверку:

log₃(3-(-24))=log₃27

log₃(3+24)= log₃27

log₃27=log₃27

3=3

Ответ: x=-24.

Задание 6. Найдите корень уравнения log(x+3)=log₂(3x-15).

log₂(x+3)=log₂(3x-15)

Решение:

x+3=3x-15

x-3x=-3-15

-2x=-18

x=9

Проверка: log₂(9+3)=log₂(27-15)

log₂12=log₂12

Ответ: x=9.

Задание 7. Найдите корень уравнения log₂(14-2x)=2log₂3

log₂(14-2x)=2log₂3

log₂(14-2x)=log₂3²

14-2x=3²

14-2x=9

-2x=9-14

-2x=-5

x=2,5

Проверка: log₂(14-5)=2log₂3

log₂9=2log₂3

log₂3²=2log₂3

2log₂3=2log₂3

Ответ: x=2,5

Подготовьтесь к ЕГЭ и к ОГЭ -посмотрите предыдущие темы Найдите значение выражения и Как решать неравенства .

---

Простейшие уравнения

---

В задании №7 базового уровня ЕГЭ по математике необходимо решить простейшие уравнения. Для этого нам понадобятся знания логарифмов, степеней и методы решения квадратных уравнений. Перейдем к рассмотрению и разбору подобных примеров.

---

Разбор типовых вариантов заданий №7 ЕГЭ по математике базового уровня

---

Вариант 7МБ1

[su_note note_color=”#defae6″]

Найдите корень уравнения 

[/su_note]

Алгоритм выполнения

1. Раскрыть скобки с левой и с правой стороны равенства, применив формулы приведения.
2. Все, выражения, содержащие переменную перенести в левую часть, а не содержащие в правую.
3. Преобразовать левую часть.
4. Преобразовать правую часть.
5. Решить уравнение относительно x, то есть найти неизвестный множитель.

Решение:

Раскроем скобки с левой и с правой стороны равенства, применив формулы приведения.

Квадрат суммы двух выражений равен сумме квадратов этих выражений плюс удвоенное произведение первого и второго выражений.

(x + 3)² = x² + 2 · x · 3 + 3² = x² + 6x + 9

Квадрат разности двух выражений равен сумме квадратов этих выражений минус удвоенное произведение первого и второго выражений.

(x – 9)² = x² – 2 · x · 9 + 9² = x² – 18x + 81

После преобразования выражение примет вид:

x² + 6x + 9 = x² – 18x + 81

Все выражения, содержащие переменную перенесем в левую часть, а не содержащие – в правую.

При переносе из одной части равенства в другую знак меняется на противоположный.

x² + 6x – x² + 18x = 81 – 9

Преобразуем левую часть. Приведем подобные слагаемые. Объединим в скобки, сохранив знаки, те выражения, где содержится x² и x.

x² + 6x – x² + 18x = (x² – x²) + (6x +18x) = 0 + 24x = 24x

Выражение примет вид:

24x = 81 – 9

Преобразуем правую часть. 81 – 9 = 72

Выражение примет вид:

24x = 72

Решим уравнение относительно x, то есть найдем неизвестный множитель. Для того чтобы найти неизвестный множитель нужно произведение разделить на известный множитель.

x = 72 : 24

x = 3

Решение в общем виде:

Раскроем скобки в уравнении, получим:

 

 

 

Ответ: 3.

---

Вариант 7МБ2

[su_note note_color=”#defae6″]

Найдите корень уравнения 

[/su_note]

Алгоритм выполнения

1. Раскрыть скобки с левой и с правой стороны равенства, применив формулы приведения.
2. Все, выражения, содержащие переменную перенести в левую часть, а не содержащие в правую.
3. Преобразовать левую часть.
4. Преобразовать правую часть.
5. Решить уравнение относительно x, то есть найти неизвестный множитель.

Решение:

Раскроем скобки с левой и с правой стороны равенства, применив формулы приведения.

Квадрат суммы двух выражений равен сумме квадратов этих выражений плюс удвоенное произведение первого и второго выражений.

(x + 2)² = x² + 2 · x · 2 + 2² = x² + 4x + 4

Квадрат разности двух выражений равен сумме квадратов этих выражений минус удвоенное произведение первого и второго выражений.

(x – 8)² = x² – 2 · x · 8 + 8² = x² – 16x + 64

После преобразования выражение примет вид:

x² + 4x + 4 = x² – 16x + 64

Все выражения, содержащие переменную перенесем в левую часть, а не содержащие – в правую.

При переносе из одной части равенства в другую знак меняется на противоположный.

x² + 4x – x² + 16x = 64 – 4

Преобразуем левую часть. Приведем подобные слагаемые. Объединим в скобки, сохранив знаки, те выражения, где содержится x² и x.

x² + 4x – x² + 16x = (x² – x²) + (4x +16x) = 0 + 20x = 20x

Выражение примет вид:

20x = 64 – 4

Преобразуем правую часть. 64 – 4 = 60

Выражение примет вид:

20x = 60

Решим уравнение относительно x, то есть найдем неизвестный множитель. Для того чтобы найти неизвестный множитель нужно произведение разделить на известный множитель.

x = 60 : 20

x = 3

Решение в общем виде:

Раскроем скобки, получим:

Ответ: 3.

---

Вариант 7МБ3

[su_note note_color=”#defae6″]

Найдите корень уравнения 

[/su_note]

Алгоритм выполнения

1. Перенести вычитаемое в правую сторону равенства с противоположным знаком.
2. Преобразовать правую часть с учетом свойства: log_a x + log_a y = log_a (x · y).
3. Приравнять логарифмические выражения. Можно так поступить, так как основания логарифмов в левой и правой части одинаковы.
4. Решить уравнение относительно x.

Решение:

Перенесем вычитаемое в правую сторону равенства с противоположным знаком.

Преобразуем правую часть с учетом свойства: log_a x + log_a y = log_a (x · y).

Выполним преобразование:

Приравняем логарифмические выражения. Можно так поступить, так как основания логарифмов в левой и правой части одинаковы.

Решим уравнение относительно x.

Ответ: 1.

---

Вариант 7МБ4

[su_note note_color=”#defae6″]

Найдите корень уравнения 3^{x− 3} = 81.

[/su_note]

Алгоритм выполнения

1. Привести выражения в степенях к одинаковому основанию. В данном случае – это 3. Теперь необходимо вспомнить, какой степенью тройки является 81.
2. Когда основания равны, можно приравнять значения степеней

Если вы забыли, то для этого необходимо делить 81 на 3 до тех пор, пока не получим 3. Чтобы получить три из 81, нам нужно поделить 81 на 3 три раза: при первом делении мы получим 27, при втором – 9, при третьем – три.

Значит, 81 это три в четвертой степени. Запишем это:

Решение:

3^{x− 3} = 3⁴

х – 3 = 4

Откуда:

х = 7

Ответ: 7

---

Вариант 7МБ5

[su_note note_color=”#defae6″]

Найдите корень уравнения log₂( x − 3) = 6 .

[/su_note]

Алгоритм выполнения

1. Логарифм по основанию два показывает нам число, в степень которого нам необходимо возвести основание, то есть двойку, чтобы получить число под логарифмом.

Решение:

x − 3 = 2⁶

x − 3 = 64

x = 67

Ответ: 67

---

Вариант 7МБ6

[su_note note_color=”#defae6″]

Найдите отрицательный корень уравнения x² − x − 6 = 0.

[/su_note]

Алгоритм выполнения

1. Вычислить дискриминант
2. Найти корни
3. Выбрать необходимый корень

D = b² − 4ac

Решение:

D = -(1)² − 4 • 1 • (-6) = 25

x = (- b ±√D) : 2a

x = (1 + 5) : 2 = 3

x = (1 – 5) : 2 = -2

Так как нам необходим отрицательный корень – ответ -2

Ответ: -2.

---

Вариант 7МБ7

[su_note note_color=”#defae6″]

Решите уравнение х² = –2х + 24.

Если уравнение имеет больше одного корня, в ответе укажите больший из них.

[/su_note]

Алгоритм выполнения

1. Переносим влево часть ур-ния, стоящую справа от знака «=». Получаем кв.уравнение стандартного вида.
2. Поскольку уравнение является приведенным, используем для нахождения корней т.Виета.
3. Записываем в качестве ответа большее из полученных 2 чисел.

Решение:

х² = –2х +24

х² +2х – 24 = 0

По т.Виета х₁+х₂=–b, x₁·x₂=c. В нашем ур-нии b=2, c=24. Подбираем подходящую пару чисел, получаем: х₁=–6, х₂=4.

Поскольку требуется указать больший из корней, то ответом будет 4.

Ответ: 4

---

Вариант 7МБ8

[su_note note_color=”#defae6″]

Найдите корни уравнения 4^х–6 = 64.

[/su_note]

Алгоритм выполнения

1. Представляем 64 как степень с основанием 4, т.е. приводим выражения справа и слева к степеням с одинаковым основанием.
2. Опускаем одинаковые основания и переходим к равенству показателей. Ур-ние стало простейшим линейным.
3. Находим корень ур-ния.

Решение:

4^х–6 = 64

4^х–6 = 4³

х – 6 = 3

х = 9

Ответ: 9

---

Вариант 7МБ9

[su_note note_color=”#defae6″]

Найдите корень уравнения log₃ (2x – 5) = 2.

[/su_note]

Алгоритм выполнения

1. Преобразуем часть уравнения справа от знака «=», используя св-ва логарифмов log_xx=1 и log_xyⁿ=nlog_xy.
2. Переходим от равенства логарифмов к равенству выражений, стоящих под их знаками.
3. Решаем полученное линейное ур-ние.

Решение:

log₃ (2x – 5) = 2

log₃ (2x – 5) = 2 · log₃3

log₃ (2x – 5) = log₃3²

2x – 5 = 3²

2x – 5 = 9

2x = 14

x=7

Ответ: 7

---

Вариант 7МБ10

[su_note note_color=”#defae6″]

Найдите корень уравнения

[/su_note]

Алгоритм выполнения

1. Преобразовываем обе части ур-ния: приводим их к степеням с основанием 3. Для этого используем св-во степеней (1/а)^х=а^–х.
2. Поскольку основания степеней слева и справа в ур-нии теперь одинаковы, то можем их опустить и приравнять показатели.
3. Решаем полученное линейное ур-ние.

Решение:

–x + 9 = –2

–x = –2–9

x = 11

Ответ: 11

---

Вариант 7МБ11

[su_note note_color=”#defae6″]

Найдите корень уравнения (х – 8)² = (х – 2)².

[/su_note]

Алгоритм выполнения

1. Раскрываем скобки слева и справа, используя ф-лу сокращенного умножения (х–у)²=х²–2ху–у².
2. Переносим влево часть уравнения справа от знака «=». Справа получаем 0.
3. Приводим подобные слагаемые. В результате уравнение стало линейным.
4. Решаем полученное уравнение.

Решение:

(х – 8)² = (х – 2)²

х² – 2 · х ·8 + 8² = х² – 2 · х · 2 + 2²

х² – 16х + 64 = х² – 4х + 4

х² – 16х +64 – х² + 4х – 4 = 0

–12х + 60 = 0

–12х = –60

х = 5

Ответ: 5

---

Вариант 7МБ12

[su_note note_color=”#defae6″]

Найдите корень уравнения

[/su_note]

Алгоритм выполнения

1. Преобразовываем обе части ур-ния так, чтобы привести их к степеням с одинаковым основанием 7. Для выражения слева применяем св-во степеней (1/а)^х=а^–х.
2. Применяем св-во показат.уравнений: если степени с одинаковыми основаниями равны, то равны и их показатели. Отсюда переходим к линейному ур-нию.
3. Решаем его.

Решение:

–(x–5) = 2

5 – x = 2

–x = 2 – 5

x = 5 – 2

x = 3

Ответ: 3

---

Вариант 7МБ13

[su_note note_color=”#defae6″]

Решите уравнение х² – 25 = 0

[/su_note]

Алгоритм выполнения

1. Переносим 25 в правую часть ур-ния.
2. Выражаем из ур-ния х путем извлечения корня из 25.
3. Определяем корни, сравниваем их, определяем больший.

Решение:

х² – 25 = 0

х² = 25

х = ±√25

х₁ = –5, х₂ = 5

Для ответа берем 5.

Ответ: 5

---

Вариант 7МБ14

[su_note note_color=”#defae6″]

Найдите корень уравнения

[/su_note]

Алгоритм выполнения

1. Применим св-во логарифмических равенств: если логарифмы с одинаковыми основания равны, то равны и их подлогарифменные выражения. В результате получаем равенство из выражений, стоящих под знаком логарифма.
2. Решаем полученное линейное ур-ние.

Решение:

log₅ (24 – 7x) = log₅ 3

24 – 7x = 3

–7x = 3 – 24

7x = 21

x = 3

Ответ: 3

---

Вариант 7МБ15

[su_note note_color=”#defae6″]

Найдите корень уравнения

[/su_note]

Алгоритм выполнения

1. Приводим обе части ур-ния к степеням с основанием 2. При этом для преобразования выражения слева используем св-во степеней (1/а)^х=а^–х.
2. Получив слева и справа степени с одинаковым основанием, опускаем это основание и приравниваем показатели этих степеней. Получаем линейное ур-ние.
3. Решаем его.

Решение:

2^–(x–8) = 2³

–x+8 = 3

–x = 3–8

x = 5

Ответ: 5

---

Вариант 7МБ16

[su_note note_color=”#defae6″]

Найдите корень уравнения

[/su_note]

Алгоритм выполнения

1. К левой части уравнения применяем св-во логарифмов log_a(x/y)=log_ax–log_ay.
2. Поскольку в обеих частях ур-ния имеем логарифмы по одинаковым основаниям, то можем их знаки, оставив только подлогарифменные выражения. Получаем линейное ур-ние.
3. Решаем его.

Решение:

log₃ (2x + 4) – log₃ 2 = log₃ 5

log₃ (2x + 4)/2 = log₃ 5

log₃ (x + 2) = log₃ 5

x + 2 = 5

x = 3

Ответ: 3

Даниил Романович | Просмотров: 11.6k