Уравнения бывают разные. Вы изучите их многие виды в курсе математике, но все они решаются по одним правилам, эти правила мы сейчас рассмотрим подробно.
Что такое уравнение? Смысл и понятия.
Узнаем сначала все понятия, связанные с уравнением.
Определение:
Уравнение – это равенство, содержащее переменные и числовые значения.
Переменные (аргументы уравнения) или неизвестные уравнения – их обозначают в основном латинскими буквами (x, y, z, f и т.д.). При подстановки числового значения переменной в уравнение получаем верное равенство – это корень уравнения.
Решить уравнение – это значит найти все корни уравнения или доказать, что у данного уравнения нет корней.
Корни уравнения – это значение переменной при котором уравнение превращается в верное равенство.
Рассмотрим теперь, все термины на простом примере:
x+1=3
В данном случае x – переменная или неизвестное значение уравнения.
Можно устно решить данное уравнение. Какое надо число прибавить к 1, чтобы получить 3? Конечно, число 2. То есть наша переменная x =2. Корень уравнения равен 2. Проверим правильно ли мы решили уравнение? Чтобы проверить уравнение, нужно вместо переменной подставить полученный корень уравнения.
2+1=3
Получили верное равенство. Значит, правильно нашли корни уравнения.
Но бывают более сложные уравнения, которые устно не решить. Нужно прибегать к правилам решения уравнений. Рассмотрим правила решения уравнений ниже, которые объяснят нам как решать уравнения.
Правила уменьшения или увеличения уравнения на определенное число.
Чтобы понять правило рассмотрим подробно простой пример:
Решите уравнение x+2=7
Решение:
Чтобы решить данное уравнение нужно левую и правую часть уменьшить на 2. Это нужно сделать для того, чтобы переменная x осталась слева, а известные (т.е. числа) справа. Что значит уменьшить на 2? Это значит отнять от левой части двойку и одновременно от правой части отнять двойку. Если мы делаем какое-то действие, например, вычитание применяя его одновременно к левой части уравнения и к правой, то уравнение не меняет смысл.
x+2-2=7-2
x+0=7-2
x=7-2
Нужно остановиться на этом моменте подробно. Другими словами, мы +2 перенесли с левой части на правую и знак поменяли стало число -2.

x=5
Как проверить правильно ли вы нашли корень уравнения? Ведь не все уравнения будут простыми как данное. Чтобы проверить корень уравнения его значение нужно поставить в само уравнение.
Проверка:
Вместо переменной x подставим 5.
x+2=7
5+2=7
Получили верное равенство, значит уравнение решено верно.
Ответ: 5.
Разберем следующий пример:
Решите уравнение x-4=12.
Решение:
Чтобы решить данное уравнение нужно увеличить левую и правую часть уравнения на 4, чтобы переменная x осталось в левой стороне, а известные (т.е. числа) в правой стороне. Прибавим к левой и правой части число 4. Получим:
x-4+4=12+4
x=12+4
Другими словами, мы -4 перенесли из левой части уравнения в правую и получили +4. При переносе через равно знаки меняются на противоположные.

x=16
Теперь выполним проверку, вместо переменной x подставим в уравнение полученное число 16.
x-4=12
16-4=12
Ответ: 16
Очень важно понять правила переноса частей уравнения через знак равно. Не всегда нужно переносить числа, иногда нужно перенести переменные или даже целые выражения.
Рассмотрим пример:
Решите уравнение 4+3x=2x-5
Решение:
Чтобы решить уравнение необходимо неизвестные перенести в одну сторону, а известные в другую. То есть переменные с x будут в левой части, а числа в правой части.
Сначала перенесем 2x с правой стороны в левую сторону уравнения и получим -2x.
4+3x=2x-5
4+3x-2x=-5
Далее 4 с левой стороны уравнения перенесем на правую сторону и получим -4
4+3x-2x=-5
3x-2x=-5-4
Теперь, когда все неизвестные в левой стороне, а все известные в правой стороне посчитаем их.
(3-2)x=-9
1x=-9 или x=-9
Сделаем проверку, правильно ли решено уравнение? Для этого вместо переменной x в уравнение подставим -9.
4+3x=2x-5
4+3⋅(-9)=2⋅(-9)-5
4-27=-18-5
-23=-23
Получилось верное равенство, уравнение решено верно.
Ответ: корень уравнения x=-9.
Правила уменьшения или увеличения уравнения в несколько раз.
Данное правило подходит тогда, когда вы уже посчитали все неизвестные и известные, но какой-то коэффициент остался перед переменной. Чтобы избавится от не нужного коэффициента мы применяем правило уменьшения или увеличения в несколько раз коэффициент уравнения.
Рассмотрим пример:
Решите уравнение 5x=20.
Решение:
В данном уравнение не нужно переносить переменные и числа, все компоненты уравнения стоят на месте. Но нам мешает коэффициент 5 который стоит перед переменной x. Мы не можем его просто взять и перенести в правую сторону уравнения, потому что между число 5 и переменно x стоит умножение 5⋅х. Если бы между переменной и числом стоял знак плюс или минус, мы могли бы 5 перенести вправо. Но мы так поступить не можем. За то мы можем все уравнение уменьшить в 5 раз или поделить на 5. Обязательно делим правую и левую сторону одновременно.
5x=20
5x:5=20:5
5:5x=4
1x=4 или x=4
Делаем проверку уравнения. Вместо переменной x подставляем 4.
5x=20
5⋅4=20
20=20 получили верное равенство, корень уравнение найден правильно.
Ответ: x=4.
Рассмотрим следующий пример:
Найдите корни уравнения .
Решение:
Так как перед переменной x стоит коэффициент необходимо от него избавиться. Надо все уравнение увеличить в 3 раза или умножить на 3, обязательно умножаем левую часть уравнения и правую часть.
1x=21 или x=21
Сделаем проверку уравнения. Подставим вместо переменной x полученный корень уравнения 21.
7=7 получено верное равенство.
Ответ: корень уравнения равен x=21.
Следующий пример:
Найдите корни уравнения
Решение:
Сначала перенесем -1 в правую сторону уравнения относительно знака равно, а в левую сторону и знаки у них поменяются на противоположные.
Теперь нужно все уравнение умножить на 5, чтобы в коэффициенте перед переменной x убрать из знаменателя 5.
3x=45
Далее делим все уравнение на 3.
3x:3=45:3
(3:3)x=15
1x=15 или x=15
Сделаем проверку. Подставим в уравнение найденный корень.
5=5
Ответ: x=15
Как решать уравнения? Алгоритм действий.
Подведем итог разобранной теме уравнений, рассмотрим общие правила решения уравнений:
- Перенести неизвестные в одну сторону, а известные в другую сторону уравнения относительно равно.
- Преобразовать и посчитать подобные в уравнении, то есть переменные с переменными, а числа с числами.
- Избавиться от коэффициента при переменной если нужно.
- В итоге всех действий получаем корень уравнение. Выполняем проверку.
Эти правила действуют на любой вид уравнения (линейный, квадратный, логарифмический, тригонометрический, рациональные, иррациональные, показательные и другие виды). Поэтому важно понять эти простые правила и научиться ими пользоваться.
- Главная
- Справочники
- Справочник по математике 5-9 класс
- Натуральные числа и действия над ними
- Уравнения
Уравнение – это равенство, содержащее букву, значение которой надо найти. Например:  + 5 = 10. Чтобы решить данное уравнение, требуется найти такое число, при подстановке которого в данное равенство вместо буквы (то есть найти значение переменной), числовое равенство будет верным. В нашем случае вместо
+ 5 = 10. Чтобы решить данное уравнение, требуется найти такое число, при подстановке которого в данное равенство вместо буквы (то есть найти значение переменной), числовое равенство будет верным. В нашем случае вместо  необходимо подставить 5. Говорят, что число 5 – корень уравнения
необходимо подставить 5. Говорят, что число 5 – корень уравнения  + 5 = 10.
+ 5 = 10.
Корень уравнения – это число, которое при подстановке вместо буквы обращает уравнение в верное числовое равенство.
Корень уравнения – это решение уравнения. Уравнение может иметь один и более корней или не иметь их вообще. Тогда говорят, что решить уравнение – значит найти все его корни или показать, что их нет вообще.
Для решения уравнений используют правило нахождения неизвестного:
1) слагаемого: чтобы найти неизвестное слагаемое, надо из суммы вычесть известное слагаемое.
Решим уравнение  + 125 = 200;
+ 125 = 200;
 = 200 – 125;
= 200 – 125;
 = 75.
= 75.
Ответ:  = 75.
= 75.
2) уменьшаемого: чтобы найти неизвестное уменьшаемое, надо к разности прибавить вычитаемое.
Решим уравнение  – 24 = 36;
– 24 = 36;
 = 36 + 24;
= 36 + 24;
 = 60.
= 60.
Ответ:  = 60.
= 60.
3) вычитаемого: чтобы найти неизвестное вычитаемое, надо из уменьшаемого вычесть разность.
Решим уравнение 135 –  = 115;
= 115;
 = 135 – 115;
= 135 – 115;
 = 20.
= 20.
Ответ:  = 20.
= 20.
4) множителя: чтобы найти неизвестный множитель, надо произведение разделить на известный множитель.
Решим уравнение 
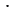 6 = 42;
6 = 42;
 = 42 : 6;
= 42 : 6;
 = 7.
= 7.
Ответ:  = 7.
= 7.
5) делимого: чтобы найти неизвестное делимое, надо частное умножить на делитель.
Решим уравнение  : 12 = 5;
: 12 = 5;
 = 5
= 5 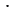 12;
12;
 = 60.
= 60.
Ответ:  = 60.
= 60.
6) делителя: чтобы найти неизвестный делитель, надо делимое разделить на частное.
Решим уравнение 184 :  = 46;
= 46;
 = 184 : 46;
= 184 : 46;
 = 4.
= 4.
Ответ:  = 4.
= 4.
При решении уравнений проводится проверка решения, для этого найденный корень (или корни) подставляются в уравнение вместо переменной. Если числовое равенство получается верным, то решение найдено верно. При оформлении решения проверка записывается под чертой после решения, а затем пишется ответ, при этом каждое действие записывается на новой строке (т.е. одна строка один знак равенства).
Например, решим уравнение  + 36 = 45 и проведем проверку:
+ 36 = 45 и проведем проверку:
 + 36 = 45;
+ 36 = 45;
 = 45 – 36;
= 45 – 36;
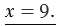
9 + 36 = 45;
45 = 45 – верно.
Ответ:  = 9.
= 9.
Советуем посмотреть:
Понятие о натуральном числе
Сложение натуральных чисел
Вычитание натуральных чисел
Умножение натуральных чисел
Деление натуральных чисел
Порядок выполнения действий
Степень числа. Квадрат и куб числа
Меньше или больше
Меньше или больше на сколько? во сколько раз?
Формулы
Натуральные числа и действия над ними
Правило встречается в следующих упражнениях:
5 класс
Задание 623,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1381,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1459,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1593,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1663,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Номер 292,
Мерзляк, Полонский, Якир, Учебник
Номер 365,
Мерзляк, Полонский, Якир, Учебник
Номер 497,
Мерзляк, Полонский, Якир, Учебник
Номер 508,
Мерзляк, Полонский, Якир, Учебник
Номер 8,
Мерзляк, Полонский, Якир, Учебник
6 класс
Номер 646,
Мерзляк, Полонский, Якир, Учебник
Номер 738,
Мерзляк, Полонский, Якир, Учебник
Номер 824,
Мерзляк, Полонский, Якир, Учебник
Номер 1165,
Мерзляк, Полонский, Якир, Учебник
Номер 1191,
Мерзляк, Полонский, Якир, Учебник
Задание 426,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 803,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 832,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1310,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1514,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
7 класс
Номер 50,
Мерзляк, Полонский, Якир, Учебник
Номер 51,
Мерзляк, Полонский, Якир, Учебник
Номер 54,
Мерзляк, Полонский, Якир, Учебник
Номер 61,
Мерзляк, Полонский, Якир, Учебник
Номер 83,
Мерзляк, Полонский, Якир, Учебник
Номер 95,
Мерзляк, Полонский, Якир, Учебник
Номер 106,
Мерзляк, Полонский, Якир, Учебник
Номер 871,
Мерзляк, Полонский, Якир, Учебник
Номер 918,
Мерзляк, Полонский, Якир, Учебник
Номер 1189,
Мерзляк, Полонский, Якир, Учебник
8 класс
Номер 142,
Мерзляк, Полонский, Якир, Учебник
Номер 208,
Мерзляк, Полонский, Якир, Учебник
Номер 214,
Мерзляк, Полонский, Якир, Учебник
Номер 218,
Мерзляк, Полонский, Якир, Учебник
Номер 219,
Мерзляк, Полонский, Якир, Учебник
Номер 394,
Мерзляк, Полонский, Якир, Учебник
Номер 401,
Мерзляк, Полонский, Якир, Учебник
Номер 403,
Мерзляк, Полонский, Якир, Учебник
Номер 406,
Мерзляк, Полонский, Якир, Учебник
Номер 416,
Мерзляк, Полонский, Якир, Учебник
Время чтения: 7 минут.
Если уравнения вызывают страх и ужас, то эта статья точно для тебя. Разберемся, что такое линейные уравнения и как быстро находить их корни.
Что такое линейные уравнения?
Для начала разберемся, что такое линейные уравнения и какой вид они имеют.
Линейное уравнение имеет вид: ax + b = 0, где a и b – это некоторые числа, а x – неизвестное.
Чтобы решить уравнение, нужно найти все его корни, либо доказать, что корней нет. Решением линейного уравнения является то число, которое обращает это уравнение в верное равенство (то есть правая часть становится равной левой части).
Правила переноса и деления
Чтобы научиться решать линейные уравнения, необходимо знать правила переноса членов уравнения из одной части в другую, а также правило деления всех частей уравнения на одно и то же число.
Правило переноса: При переносе члена уравнения из одной части уравнения в другую нужно менять знак на противоположный. Все члены с Х оставляем слева, а все числа – переносим вправо.
Правило деления: В уравнении можно разделить правую и левую часть на одно и то же число.
Алгоритм решения
Коротко алгоритм решения линейных уравнений можно записать так:
- Раскрыть все скобки (если они есть);
- Члены с Х перенести влево, а все числа – вправо;
- Сложить/вычесть все, что возможно, в каждой части уравнения;
- Найти корень уравнения.
Примеры решения линейных уравнений
Далее разберем примеры решения линейных уравнений, а после ты сможешь проверить свои знания и самостоятельно решить несколько подобных заданий.
А теперь проверь свои знания на заданиях ниже:
На этом все! Остались вопросы? Напиши о них в комментариях!👇
Обязательно подпишись на канал, чтобы не пропустить больше полезных статей!🧠
#впр #огэ #егэ #математика #репетитор #алгебра #геометрия #7класс #уравнения #линейныеуравнения
Уравнение представляет собой многочлен переменных (неизвестных величин) вида:
f(x1,x2,…,xn)=0fleft(x_1,x_2,ldots,x_nright)=0
Степень уравнения определяется степенью входящего в него неизвестного.
Линейные уравнения
Линейные уравнения – уравнения типа ax=bax=b.
Например, 103x+18=4103x+18=4.
Для решения таких уравнений необходимо перенести неизвестные в одну сторону, числовые значения в другую, затем привести подобные и выразить неизвестное.
Решить уравнение 4x–8=2+3x+44x – 8 = 2 + 3x + 4
Решение
- Перенесем неизвестные в левую часть, числа – в правую (с противоположными знаками):
4x–3x=2+4+84x – 3x = 2 + 4 + 8
- Приведем подобные (сложим и вычтем неизвестные и числа):
x=14x = 14
Ответ: x=14x = 14
Противоположный знак – знак обратный исходному при переноси числа или выражения через знак =. Для знака плюс, противоположным будет знак «–» и наоборот, для частного произведение и соответственно для произведения – частное.
Выразить xx в уравнении 18x+2x–4=10x+1618x + 2x – 4 = 10x + 16
Решение
- Перенесем неизвестные в левую часть, числа – в правую
18x+2x–10x=16+418x + 2x – 10x = 16 + 4
- Приведем подобные
10∗x=2010*x = 20
x=20/10=2x = 20/10 = 2
Ответ: x=2x = 2.
Квадратные уравнения
Квадратные уравнения – уравнения вида ax2+bx+c=0ax^2+bx+c=0. Наиболее универсальной формулой решения таких уравнений является следующая:
x1.2=−b∓b2−4ac2ax_{1.2}=-bmpfrac{sqrt{b^2-4ac}}{2a}
где a,b,ca,b,c – коэффициенты уравнения.
Найти корни уравнения x2+2x–1=–9–3хx^2 + 2x – 1 = –9 – 3х
Решение
- Приведем уравнение к виду квадратного
x2+2x–1+9+3х=0x^2 + 2x – 1 + 9 + 3х = 0
1×2+5x+8=01x^2 + 5x + 8 = 0
- Найдем корни
x1.2=−5∓52−4∗1∗82∗1=−5∓−72∗1x_{1.2}=-5mpfrac{sqrt{5^2-4ast1ast8}}{2ast1}=-5mpfrac{sqrt{-7}}{2ast1}
Поскольку подкоренное выражение отрицательно, уравнение корней не имеет.
Решить уравнение 2×2+3x–2=02x^2 + 3x – 2 = 0
Решение
x1.2=−3∓32−4∗2∗(−2)2∗2=−3∓9+164=3∓54×1=3+54=4,25×2=3−54=1,75x_{1.2}=-3mpfrac{sqrt{3^2-4ast2astleft(-2right)}}{2ast2}=-3mpfrac{sqrt{9+16}}{4}=3mpfrac{5}{4}
x_1=3+frac{5}{4}=4,25
x_2=3-frac{5}{4}=1,75
Ответ: уравнение имеет 2 корня: 4,25 и 1,75.
Кубические уравнения
Кубические уравнения – уравнения вида ax3+b=0ax^3 + b = 0 или ax3+сx2+dx=0ax^3 + сx^2 + dx = 0.
Для решения таких уравнений xx выносится за скобку, записывается корень х=0х = 0, решается оставшееся в скобках квадратное уравнение.
Сколько корней имеет уравнение 3×3+2×2–1x=03x^3 + 2x^2 – 1x = 0
Решение
- Вынесем xx
x(3×2+2x–1)=0x(3x^2 + 2x – 1) = 0
Первый корень x=0x = 0
- Решаем уравнение 3×2+2x–1=03x^2 + 2x – 1 = 0
x2.3=−2∓42−4∗3∗(−1)2∗3=−2∓16+126=−2∓286=−2∓276×2=−2+73×3=−2−73x_{2.3}=-2mpfrac{sqrt{4^2-4ast3astleft(-1right)}}{2ast3}=-2mpfrac{sqrt{16+12}}{6}=-2mpfrac{sqrt{28}}{6}=-2mpfrac{2sqrt7}{6}
x_2=-2+frac{sqrt7}{3}
x_3=-2-frac{sqrt7}{3}
Ответ: 3 корня.
Решить уравнение 2×3−16=02x^3 – 16 = 0
Решение
- Упростим уравнение делением на общий делитель 2
2×3− 16 2=x3−8×3−8=0x3=8x=83=2frac{2x^3- 16 }{2}=x^3-8
x^3-8=0
x^3=8
x=sqrt[3]{8}=2
Ответ: x=2x = 2
Существуют и другие виды уравнений (дробно-рациональные, трансцендентные), однако их решение сводится к упрощению и приведению к линейному, квадратному или кубическому виду.
Например, дробно-рациональное уравнение вида
x2+2x+1x+1=0frac{x^2+2x+1}{x+1}=0
решается путем сокращения дроби и преобразованию к линейному виду
(x+1)∗(x+1)x+1=0frac{left(x+1right)astleft(x+1right)}{x+1}=0
x+1=0x+1=0
х=−1х = -1
Трансцендентные уравнения (логарифмические, показательные, тригонометрические) решаются заменой сложных выражений знакомым нам х, его нахождением и обратной заменой на найденное значение.
Тест по теме «Примеры решения уравнений»
п.1. Определение уравнения и его корня
Уравнением с одной переменной x называют равенство f(x)=g(x), для которого поставлена задача найти все значения переменной x, которые обращают это равенство в истинное числовое равенство.
Значение переменной, при котором выражения f(x) и g(x) принимают равные числовые значения, называют корнем уравнения f(x)=g(x).
Например, для уравнения 15x+8=23 корнем является значение x=1.
В уравнении x(x + 5)(x – 3) = 0 три корня, $x_1 = 0,x_2 = -5,x_3 = 3$.
Уравнение $x^2 = -1$ действительных корней не имеет.
В уравнении 5(x + 3)=5x + 15 бесконечное количество корней, т.к. оно превращается в истинное равенство при любом $x in Bbb R$, т.е. является тождеством.
Решить уравнение означает найти все его корни или доказать, что их нет.
п.2. Примеры
Пример 1. Решите уравнение и выполните проверку x – (3 – 2x) = 9
Решение:
x-(3-2x)=9 $iff$ x-3+2x=9 $iff$ x+2x=9+3 $iff$ 3x=12 $iff$ x=4
Проверка:
$4 -(3 – 2 cdot 4)=9 implies 4 – 3 + 8 = 9 implies 9 equiv 9$
Ответ: x = 4
Пример 2. Решите уравнение и выполните проверку 7(x + 3) = 56
Решение:
7(x + 3)=56 |:7 $iff$ x + 3 = 8 $iff$ x = 8 – 3 $iff$ x=5
Проверка:
$7(5 + 3) = 56 implies 7 cdot 8 = 56 implies 56 equiv 56$
Ответ: x = 5
Пример 3. Решите уравнение и выполните проверку (3x + 4) : 2 = 14
Решение:
(3x + 4) : 2=14 |$times$2 $iff$ 3x + 4 = 28 $iff$ 3x = 28 – 4 $iff$ 3x = 24 $iff$ x=8
Проверка:
$(3 cdot 8 + 4) : 2 = 14 implies (24 + 4) : 2 = 14 implies 28 : 2 = 14 implies 14 equiv 14$
Ответ: x = 8
Пример 4. Решите уравнение $ frac{3x-7}{3} – frac {5x-11}{5} = 0$
Решение:
$frac {3x-7}{3} – frac {5x-11}{5} = 0 | times 15 iff5(3x-7)-3(5x-11)=0 iff$
$ iff 15x-35-15x+33=0 iff 0x=2 iff x in varnothing $
Решений нет.
Ответ: $x in varnothing $
Пример 5. Решите уравнение $frac {2x – 7}{2} = frac {3x+6}{3}$
Решение:
$frac {2x-7}{2}=frac {x+6}{3} | times 6 iff 3(2x-7)=2(x+6) iff 6x-21=2x+12 iff $
$iff 6x-2x=12+21 iff 4x=33 iff x= frac {33}{4} =8 frac 14$
Ответ: $8 frac 14$
Пример 6. Решите уравнение |x+1|=5
Решение:
$$|x+1|=5 iff left[ begin{array}{cc} {x+1=-5}\ {x+1=5} end{array} right. iff left[ begin{array}{cc} {x=-5-1}\ {x=5-1} end{array} right. iff left[ begin{array}{cc} {x_1=-6}\ {x_2=4} end{array} right. $$
Ответ: $ x_1=-6, x_2=4$
Пример 7*. Решите уравнение и выполните проверку |x + 1| = x + 3
Решение:
$$ |x + 1| = x + 3 iff left[ begin{array}{cc} {left{ begin{array}{c} x+1 ge 0 \ x+1=x+3 end{array} right.}\ {left{ begin{array}{c} x+1<0 \ -(x+1)=x+3 end{array} right.} end{array} right. iff left[ begin{array}{cc} {left{ begin{array}{c} x ge -1 \ 1=3 end{array} right.}\ {left{ begin{array}{c} x<-1 \ -x-1=x+3 end{array} right.} end{array} right. iff $$
$$ iff left[ begin{array}{cc} {emptyset}\ {left{ begin{array}{c} x<-1 \ -x-x=3+1 end{array} right.} end{array} right. iff left[ begin{array}{cc} {x<-1}\ {-2x=4} end{array} right. iff left[ begin{array}{cc} {x<-1}\ {x=-2} end{array} right. iff x=-2 $$
Проверка:
$$|-2+1|=-2+3 implies |-1|=1implies 1 equiv 1$$
Ответ: x = -2
Пример 8. При каком значении a уравнение 5ax + 18 = 3 будет иметь корень x = -3?
Решение:
Подставляем x=-3 в уравнение и решаем его относительно параметра a:
5a $cdot$ (-3) + 18 = 3 $iff$ -15a = 3 – 18 $iff$ -15a = -15 $iff$ a = -15:(-15)=1
a=1
Ответ: a = 1
