Найдите нули функции это как - Сайт, где вы сможете решить свои вопросы

Прежде чем перейти к изучению темы «Нули функции»
внимательно изучите уроки
«Что такое функция в математике»
и
«Как решать задачи на функцию».

Запомните!

Нули функции — это
значения « x »
(аргумента функции),

при которых « y = 0 ».

В заданиях «Найдите нули функции» чаще всего сама функция задана через формулу

(аналитически). Разберем алгоритм решения

подобных задач.

Как найти нули функции, заданной формулой

Важно!

Чтобы найти нули функции, нужно:

в формулу функции вместо

« у » (или « f(x) »,
« g(x) » и т.п.)
подставить «0»;
решить полученное уравнение
относительно « x »;
записать полученные решения уравнения для « x » в ответ.

По традиции разберемся на примере.

Разбор примера

Найдите нули функции:

Подставим вместо значения функции « f(x) » ноль.

0 = 0,2x + 3

Решаем полученное линейное уравнение
и записываем полученный ответ
для « x ».

Перенесем неизвестное « 0,2x » из правой части уравнения в левую с
противоположным
знаком.

−0,2x = 3 | · (−1)

0,2x = −3

Переведем десятичную дробь «0,2» в
обыкновненную для упрощения дальнейших расчетов.

0,2x = −3

· x = −3 | · 10

· x · 10 = −3 · 10

· x = −30

2x = −30

x =

x = −15

Ответ: x = −15 является нулем
функции f(x) = 0,2x + 3

Разбор примера

Найдите нули функции:

Вместо « f(x) » подставим ноль.

0 = x ³ − 4x

−x ³ + 4x = 0 | · (−1)

(−1) · (−x ³ + 4x) = 0 · (−1)

x ³ − 4x = 0

Вынесем общий множитель
« x » за скобки.

В левой части полученного уравнения у нас два множителя:
« x »
и «(x ² − 4)». Результат их умножения равен нулю.

Это возможно, когда любой
из множителей равен нулю. Поэтому рассмотрим оба варианта: когда множитель
« x » равен нулю и когда множитель «(x ² − 4)»
равен нулю.

Решаем квадратное уравнение
«x ² − 4 = 0».
Используем формулу
для решения квадратного уравнения с дискриминантом.

a · x ² + b · x + c = 0

x_1;2 =

x ² − 4 = 0

x_1;2 =

0 ±
√0² − 4 · 1 · (−4)

2 · 1

x_1;2 =

Запишем все полученные корни уравнений в ответ в порядке возрастания. Они будут являться нулями функции.

Ответ: x = −2; x = 0; x = 2 являются нулями функции
f(x) = x ³ − 4x

Разбор примера

Найдите нули функции:

Подставим вместо « h(x) » ноль.

Перенесем правую часть

в левую, изменив ее знак на минус.

Единственный вариант, когда дробь будет равна нулю, только если
ее числитель
«x ² − x − 6» будет равен нулю. Знаменатель
«x + 3» не может быть равен нулю, так как на ноль делить нельзя.

Решим полученное квадратное уравнение через формулу с дискриминантом.

a · x ² + b · x + c = 0

x_1;2 =

x ² − x − 6 = 0

x_1;2 =

−(−1) ±
√(−1)² − 4 · 1 · (−6)

2 · 1

x_1;2 =

x₁ =	x₂ =
x₁ =	x₂ =
x₁ = 3	x₂ = −2

Ответ: x = −2; x = 3 являются нулями функции

h(x) =

Разбор примера

Найдите нули функции:

Заменим «f(x)» на ноль.

Единственное число, квадратный корень которого равен нулю — это сам ноль.
Поэтому, квадратный корень
«√ x ² − 4 = 0 »

будет равен нулю, когда его подкоренное выражение
« x ² − 4 »
будет равно нулю.

Осталось решить полученное квадратное уравнение, чтобы найти нули функции
«f(x) = √x ² − 4».

x_1;2 =

x ² − 4 = 0

x_1;2 =

−(−0) ±
√(−0)² − 4 · 1 · (−4)

2 · 1

x_1;2 =

Ответ: x = −2; x = 2 являются нулями
функции f(x) = √x ² − 4

Как найти нули функции на графике функции

Важно!

Графически нули функции — это точки пересечения графика функции
с осью «Ox»
(осью абсцисс).

По определению
нули функции — это значения « x »,
при которых
« y = 0 ». Другими словами, у точек
графика функции, которые являются нулями функции,
координата « x » равна нулю.

Чтобы найти нули функции на графике
нам остается, только найти, какая у них
координата
по оси « Ox ».

Рассмотрим на примере.

Разбор примера

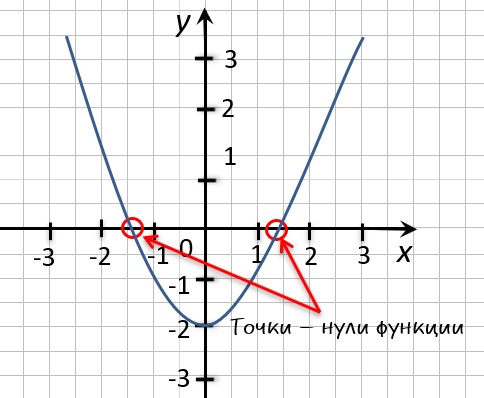
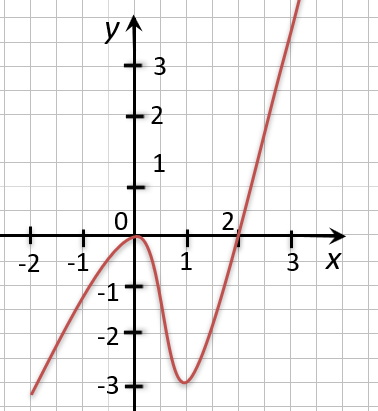
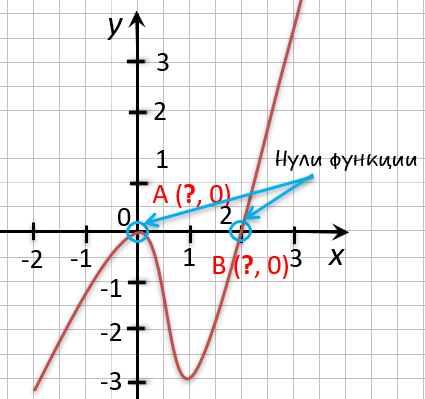
На рисунке ниже изображен график функции « y = f(x) », определенной на множестве действительных чисел. Используя график,
найдите нули функции.

Отметим на графике функции его точки пересечения с осью « Ox ».

Назовем полученные точки «(·)А» и «(·)B».
В точках «(·)А» и «(·)B» график функции пересекает
ось

« Ox » , то есть координаты точки «(·)А» и «(·)B»
по оси « Oy »
равны нулю.

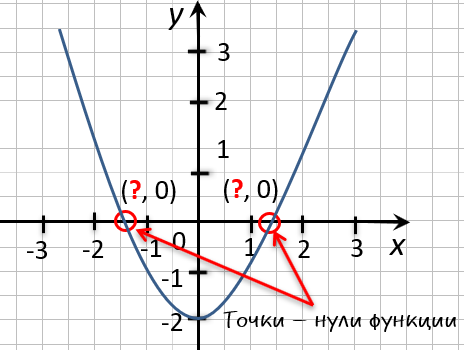
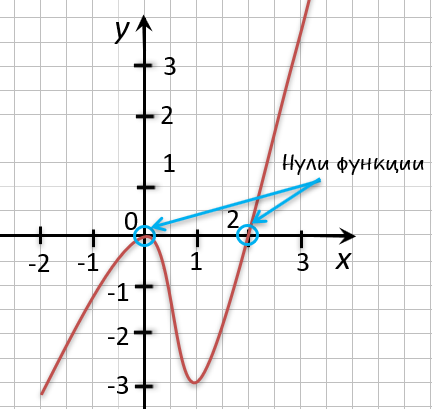
Точки «(·)А» и «(·)B»
— нули функции. Теперь определим, чему равны их координаты по оси « Ox ».

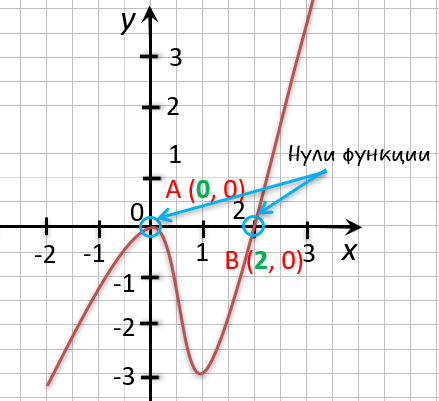
На графике видно, что у точки «(·)А» координата « x » равна
« 0 », а у точки «(·)B» координата « x » равна
« 2 ».

Запишем полученные значения координат « x » в ответ.

Ответ: x = 0; x = 2 являются нулями функции.

Как найти нули функции, заданной таблицей

В некоторых заданиях, где требуется найти нули функции, сама функция задана не вполне привычно с помощью формулы,
а с помощью таблицы. Поиск нулей в таких примерах является легкой задачей.

Разбор примера

Найдите нули функции, заданной таблицей.

x	−2	−1	0	1	2	3
y	−3	−1,5	0	2	1	0

Вспомним определение нулей функции.

Запомните!

Нули функции — это
значения « x » в функции,
при которых « y = 0 ».

Согласно определению нулей функции нам достаточно найти значения « x » в таблице,
где
« y = 0 ». Выделим их цветом.

x	−2	−1	0	1	2	3
y	−3	−1,5	0	2	1	0

Остаётся только записать в ответ значения « x » из таблицы.

Ответ: x = 0; x = 3 являются нулями функции, заданной таблицей.

Ваши комментарии

Важно!

Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи

«ВКонтакте».

Оставить комментарий:

Источник

Каждый из нас встречался с разными графиками, как на уроках, так и в жизни. Например, рассматривали, как изменяется температура воздуха в определенный период времени.

На рисунке видно, что температура воздуха была отрицательной с 0 часов до 6 часов, а также с 20 до 24 часов. Еще можем сказать, что температура повышалась до 14 часов, а затем понижалась. То есть по данному графику мы смогли определить некоторые свойства зависимости температуры воздуха от времени суток.

Свойства функции. Возрастание и убывание, наибольшее и наименьшее значения, нули, промежутки знакопостоянства

Остановимся подробнее на свойствах функций.

Нули функции

Определение

Нули функции – это значение аргумента, при которых функция обращается в нуль. Если смотреть нули функции на графике, то берем точки, где график пересекает ось х.

На рисунке он пересекает ось х при х=-1; х=4; х=6. Эти точки пересечения выделены красным цветом.Внимание!

Существует функция, которая не будет иметь нули функции. Это гипербола. Вспомним, что функция имеет вид у=k/x, где х не равное 0 число.

График функции у=k/x выглядит следующим образом: По данному рисунку видно, что нулей функции не существует.Как найти нули функции?

Для того чтобы найти нули функции, которая задана формулой, надо подставить вместо у число нуль и решить полученное уравнение.
Если график функции дан на рисунке, то ищем точки пересечения графика с осью х.

Рассмотрим примеры нахождения нулей функции. Пример №1. Найти нули функции (если они существуют):

а) у= –11х +22
б) у= (х + 76)(х – 95)
в) у= – 46/х

а) Для нахождения нулей функции необходимо в данную формулу вместо у подставить число 0, так как координаты точки пересечения графика с осью х (х;0). Нам нужно найти значение х. Получаем 0 = –11х +12. Решаем уравнение. Переносим слагаемое, содержащее переменную, в левую часть, меняя знак на противоположный: 11х=22

Находим х, разделив 22 на 11: х=22:11
Получим х=2.
Таким образом, мы нашли нуль функции: х=2

б) Аналогично во втором случае. Подставляем вместо у число 0 и решаем уравнение вида 0=(х + 76)(х – 95). Вспомним, что произведение двух множителей равно 0 тогда и только тогда, когда хотя бы один из множителей равен 0.

Таким образом, так как у нас два множителя, составляем два уравнения: х + 76 = 0 и х – 95 = 0. Решаем каждое, перенося числа 76 и -95 в правую часть, меняя знаки на противоположные. Получаем х = – 76 и х = 95.

Значит, нули функции это числа (-76) и 95.

в) в третьем случае: если вместо у подставить 0, то получится 0 = – 46/х, где для нахождения значения х нужно будет -46 разделить на нуль, что сделать невозможно. Значит, нулей функции в этом случае нет.

Пример №2. Найти нули функции у=f(x) по заданному графику.

Находим точки пересечения графика с осью х и выписываем значения х в этих точках. Это (-4,9); (-1,2); 2,2 и 5,7. У нас на рисунке точки пересечения выделены красным цветом.

Промежутки знакопостоянства

Определение

Промежутки, где функция сохраняет знак (то есть значение y либо положительное на этом промежутке, либо отрицательное), называется промежутками знакопостоянства.

Рассмотрим по нашему рисунку, на какие промежутки разбивается область определения данной функции [-3; 7] ее нулями. По графику видно, что это 4 промежутка: [-3; -1), (-1;4), (4; 6) и (6; 7]. Помним, что значения из области определения смотрим по оси х.

На рисунке синим цветом выделены части графика в промежутках [-3; -1) и (4; 6), которые расположены ниже оси х. Зеленым цветом выделены части графика в промежутках (-1;4) и (6; 7], которые расположены выше оси х.

Значит, что в промежутках [-3; -1) и (4; 6) функция принимает отрицательные значения, а в промежутках (-1;4) и (6; 7] она принимает положительные значения. Это и есть промежутки знакопостоянства.

Пример №3. Найдем промежутки знакопостоянства по заданному на промежутке [-2; 10] графику функции у=f(x).

Функция принимает положительные значения в промежутках [-2; -1) и (3; 8). Обратите внимание, что эти части на рисунке выделены зеленым цветом.

Функция принимает отрицательные значения в промежутках (-1; 3) и (8; 10]. Обратите внимание на линии синего цвета.

Возрастание и убывание функции

Значения функции могут уменьшаться или увеличиваться. Это зависит от того, как изменяются значения х. Рассмотрим это свойство по рисунку.

На графике видно, что с увеличением значения х от -3 до 2 значения у тоже увеличиваются. Также с увеличением значения х от 5 до 7 значения у опять увеличиваются. Проще говоря, слева направо график идет вверх (синие линии). То есть в промежутках [-3; 2] и [5; 7] функция у=f(x) является возрастающей.

Посмотрим на значения х, которые увеличиваются от 2 до 5. В этом случае значения у уменьшаются. На графике эта часть выделена зеленым цветом. Слева направо эта часть графика идет вниз. То есть в промежутке [2;5] функция у=f(x) является убывающей.

Определение

Функция называется возрастающей в некотором промежутке, если большему значению аргумента из этого промежутка соответствует большее значение функции; функция называется убывающей в некотором промежутке, если большему значению аргумента из этого промежутка соответствует меньшее значение функции.

Метод интервалов: примеры, решения

Метод интервалов принято считать универсальным для решения неравенств. Иногда этот метод также называют методом промежутков. Применим он как для решения рациональных неравенств с одной переменной, так и для неравенств других видов. В нашем материале мы постарались уделить внимание всем аспектам вопроса.

Что ждет вас в данном разделе? Мы разберем метод промежутков и рассмотрим алгоритмы решения неравенств с его помощью. Затронем теоретические аспекты, на которых основано применение метода.

Особое внимание мы уделяем нюансам темы, которые обычно не затрагиваются в рамках школьной программы. Например, рассмотрим правила расстановки знаков на интервалах и сам метод интервалов в общем виде без его привязки к рациональным неравенствам.

Алгоритм

Кто помнит, как происходит знакомство с методом промежутков в школьном курсе алгебры? Обычно все начинается с решения неравенств вида f(x) или ≥). Здесь f(x) может быть многочленом или отношением многочленов. Многочлен, в свою очередь, может быть представлен как:

произведение линейных двучленов с коэффициентом 1 при переменной х;

произведение квадратных трехчленов со старшим коэффициентом 1 и с отрицательным дискриминантом их корней.

Приведем несколько примеров таких неравенств:

(x+3)·(x2−x+1)·(x+2)3≥0,
(x-2)·(x+5)x+3>0 ,
(x−5)·(x+5)≤0,
(x2+2·x+7)·(x-1)2(x2-7)5·(x-1)·(x-3)7≤0 .

Запишем алгоритм решения неравенств такого вида, как мы привели в примерах, методом промежутков:

находим нули числителя и знаменателя, для этого числитель и знаменатель выражения в левой части неравенства приравниваем к нулю и решаем полученные уравнения;
определяем точки, которые соответствуют найденным нулям и отмечаем их черточками на оси координат;
определяем знаки выражения f(x) из левой части решаемого неравенства на каждом промежутке и проставляем их на графике;
наносим штриховку над нужными участками графика, руководствуясь следующим правилом: в случае, если неравенство имеет знаки или ≥, то выделяем штриховкой участки, отмеченные знаком «+».

Четреж, с которым мы будем работать, может иметь схематический вид. Излишние подробности могут перегружать рисунок и затруднять решение. Нас будет мало интересовать маштаб. Достаточно будет придерживаться правильного расположения точек по мере роста значений их координат.

При работе со строгими неравенствами мы будем использовать обозначение точки в виде круга с незакрашенным (пустым) центром. В случае нестрогих неравенств точки, которые соответствуют нулям знаменателя, мы будем изображать пустыми, а все остальные обычными черными.

Отмеченные точки разбивают координатную прямую на несколько числовых промежутков. Это позволяет нам получить геометрическое представление числового множества, которое фактически является решением данного неравенства.

Научные основы метода промежутков

Основан подход, положенный в основу метода промежутков, основан на следующем свойстве непрерывной функции: функция сохраняет постоянный знак на интервале (a, b), на котором эта функция непрерывна и не обращается в нуль. Это же свойство характерно для числовых лучей (−∞, a) и (a, +∞).

Приведенное свойство функции подтверждается теоремой Больцано-Коши, которая приведена во многих пособиях для подготовки к вступительным испытаниям.

Обосновать постоянство знака на промежутках также можно на основе свойств числовых неравенств. Например, возьмем неравенство x-5x+1>0 . Если мы найдем нули числителя и знаменателя и нанесем их на числовую прямую, то получим ряд промежутков: (−∞, −1), (−1, 5) и (5, +∞).

Возьмем любой из промежутков и покажем на нем, что на всем промежутке выражение из левой части неравенства будет иметь постоянный знак. Пусть это будет промежуток (−∞, −1). Возьмем любое число t из этого промежутка. Оно будет удовлетворять условиям t

Источник

Нули функции — это значения аргумента, при которых функция равна нулю.

Чтобы найти нули функции, заданной формулой y=f(x), надо решить уравнение f(x)=0.

Если уравнение не имеет корней, нулей у функции нет.

Примеры.

1) Найти нули линейной функции y=3x+15.

Решение:

Чтобы найти нули функции, решим уравнение 3x+15=0.

3x=-15; x= -5.

Таким образом, нуль функции y=3x+15 — x= -5.

Ответ:x= -5.

2) Найти нули квадратичной функции f(x)=x²-7x+12.

Решение:

Для нахождения нулей функции решим квадратное уравнение

x²-7x+12=0.

Его корни x1=3 и x2=4 являются нулями данной функции.

Ответ: x=3; x=4.

Инструкция

1. Нуль функции – это такое значение довода х, при котором значение функции равно нулю. Впрочем нулями могут быть лишь те доводы, которые входят в область определения исследуемой функции. То есть в такое уйма значений, для которых функция f(x) имеет толк.

2. Запишите заданную функцию и приравняйте ее к нулю, скажем f(x) = 2х?+5х+2 = 0. Решите получившееся уравнение и обнаружьте его действительные корни. Корни квадратного уравнения вычисляются с поддержкой нахождения дискриминанта. 2х?+5х+2 = 0;D = b?-4ac = 5?-4*2*2 = 9;х1 = (-b+?D)/2*а = (-5+3)/2*2 = -0,5;х2 = (-b-?D)/2*а = (-5-3)/2*2 = -2.Таким образом, в данном случае получены два корня квадратного уравнения, соответствующих доводам начальной функции f(x).

3. Все обнаруженные значения х проверьте на принадлежность к области определения заданной функции. Обнаружьте ООФ, для этого проверьте начальное выражение на наличие корней четной степени вида ?f (х), на присутствие дробей в функции с доводом в знаменателе, на наличие логарифмических либо тригонометрических выражений.

4. Рассматривая функцию с выражением под корнем четной степени, примите за область определения все доводы х, значения которых не обращают подкоренное выражение в негативное число (напротив функция не имеет смысла). Уточните, попадают ли обнаруженные нули функции в определенную область допустимых значений х.

5. Знаменатель дроби не может обращаться в нуль, следственно исключите те доводы х, которые приводят к такому итогу. Для логарифмических величин следует рассматривать лишь те значения довода, при которых само выражение огромнее нуля. Нули функции, обращающие подлогарифмическое выражение в нуль либо негативное число, обязаны быть отброшены из финального итога.

Обратите внимание!
При нахождение корней уравнения, могут возникнуть лишние корни. Проверить это легко: довольно подставить полученное значение довода в функцию и удостовериться обращается ли функция в нуль.

Полезный совет
Изредка функция не выражается в очевидном виде через свой довод, тогда легко нужно знать, что представляет собой эта функция. Примером этому может служить уравнение окружности.

Нулями функции называются значение абсциссы, при котором значение функции равно нулю.

Если функция задана своим уравнением, то нулями функции будут решения уравнения . Если задан график функции , то нули функции — это значения , в которых график пересекает ось абсцисс.

Примеры нахождения нулей функции

ПРИМЕР 1

Источник

Нули функции – это такое значение х, при котором функция y=f(x) равна нулю (то есть график функции пересекается с осью Х) .
Для того, чтобы найти нули функции, надо функцию приравнять к нулю.
Например, дана функция f(x) = х2 – 4 (икс в квадрате минус четыре)
Приравниваем к нулю:
х2 – 4 = 0
А теперь решаем как квадратное уравнение, находим х (первое) = – 2, х (второе) = 2
При этих значениях х функция y=f(x) = 0

Это можно сделать и графически. Просто построить функцию по точкам и начертить, точки пересечения графика с осью Х и будут нулями функции.

Посмотрите еще здесь:

[ссылка заблокирована по решению администрации проекта]
http://www.mathematics.ru/courses/function/content/chapter1/section3/paragraph3/theory.html
http://fgraphiks.narod.ru/svoistva.html

Источник

Нули функции

Что такое нули функции? Как определить нули функции аналитически и по графику?

Нули функции — это значения аргумента, при которых функция равна нулю.

Чтобы найти нули функции, заданной формулой y=f(x), надо решить уравнение f(x)=0.

Если уравнение не имеет корней, нулей у функции нет.

Примеры.

1) Найти нули линейной функции y=3x+15.

Решение:

Чтобы найти нули функции, решим уравнение 3x+15=0.

3x=-15; x= -5.

Таким образом, нуль функции y=3x+15 — x= -5.

Ответ:x= -5.

2) Найти нули квадратичной функции f(x)=x²-7x+12.

Решение:

Для нахождения нулей функции решим квадратное уравнение

x²-7x+12=0.

Его корни x1=3 и x2=4 являются нулями данной функции.

Ответ: x=3; x=4.

3)Найти нули функции

$[g(x) = frac{{{x^2} + 5x + 4}}{{{x^2} - 1}}]$

Решение:

Дробь имеет смысл, если знаменатель отличен от нуля. Следовательно, x²-1≠0,x²≠1,x≠±1. То есть область определения данной функции (ОДЗ)

x ∈ (-∞; -1)U(-1; 1)U(1;∞).

Решаем уравнение

$[frac{{{x^2} + 5x + 4}}{{{x^2} - 1}} = 0 Leftrightarrow left{ begin{array}{l} {x^2} + 5x + 4\ {x^2} - 1 ne 0 end{array} right.]$

Из корней уравнения x²+5x+4=0 x1=-1 x2=-4 в область определения входит только x=-4.

Ответ: x=-4.

Чтобы найти нули функции, заданной графически, надо найти точки пересечения графика функции с осью абсцисс.

Если график не пересекает ось Ox, функция не имеет нулей.

Например,

функция, график которой изображен на рисунке,имеет четыре нуля —

$[{x_1} = - 2;{x_2} = - 1;{x_3} = 1;{x_4} = 3.]$

В алгебре задача нахождения нулей функции встречается как в виде самостоятельного задания, так и при решения других задач, например, при исследовании функции, решении неравенств и т.д.

Источник

Как найти нули функции, заданной формулой

Разбор примера

Разбор примера

Разбор примера

Разбор примера

Как найти нули функции на графике функции

Разбор примера

Как найти нули функции, заданной таблицей

Разбор примера

Ваши комментарии

Свойства функции. Возрастание и убывание, наибольшее и наименьшее значения, нули, промежутки знакопостоянства

Нули функции

Промежутки знакопостоянства

Возрастание и убывание функции

Метод интервалов: примеры, решения

Алгоритм

Научные основы метода промежутков

Вам также может понравиться

Как найти работника инженера

Как найти архивный чат в вотсап

Как найти квадратичную функцию при

Добавить комментарий Отменить ответ