было в ЕГЭ
в условии
в решении
в тексте к заданию
в атрибутах
Категория
Атрибут
Всего: 657 1–20 | 21–40 | 41–60 | 61–80 …
Добавить в вариант
Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см
1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
На клетчатой бумаге с клетками размером 1 см
1 см
изображен треугольник (см. рис.). Найдите его площадь в квадратных
сантиметрах.
Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см
1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см
1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см
1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
На клетчатой бумаге с клетками размером 1 см
1 см
изображен треугольник (см. рис.). Найдите его площадь в квадратных
сантиметрах.
Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см
1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
На клетчатой бумаге с клетками размером 1 см х 1 см изображен треугольник (см. рис.). Найдите его площадь в квадратных сантиметрах.
На клетчатой бумаге с клетками размером 1 см
1 см изображен треугольник (см. рис.). Найдите его площадь в квадратных сантиметрах.
Найдите площадь трапеции, изображенной на клетчатой бумаге с размером клетки 1 см
1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
На клетчатой бумаге с клетками размером 1 см
1 см изображена трапеция (см. рис.). Найдите ее площадь в квадратных сантиметрах.
Найдите площадь трапеции, изображенной на клетчатой бумаге с размером клетки 1 см
1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
Найдите площадь трапеции, изображенной на клетчатой бумаге с размером клетки 1 см
1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
Найдите площадь трапеции, изображенной на клетчатой бумаге с размером клетки 1 см
1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
Найдите площадь трапеции, изображенной на клетчатой бумаге с размером клетки 1 см
1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
Найдите площадь трапеции, изображенной на клетчатой бумаге с размером клетки 1 см
1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
На клетчатой бумаге с размером клетки
изображён круг. Найдите площадь закрашенного сектора. Ответ дайте в квадратных сантиметрах.
На клетчатой бумаге с размером клетки
изображён круг. Найдите площадь закрашенного сектора. Ответ дайте в квадратных сантиметрах.
На клетчатой бумаге с размером клетки
изображён круг. Найдите площадь закрашенного сектора. Ответ дайте в квадратных сантиметрах.
На клетчатой бумаге с размером клетки
изображён круг. Найдите площадь закрашенного сектора. Ответ дайте в квадратных сантиметрах.
Всего: 657 1–20 | 21–40 | 41–60 | 61–80 …
18. Площади геометрических фигур
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Площадь трапеции
Найдите площадь прямоугольной трапеции, основания которой равны (6) и (2), большая боковая сторона составляет с основанием угол (45^circ).

Проведем высоту (CH).
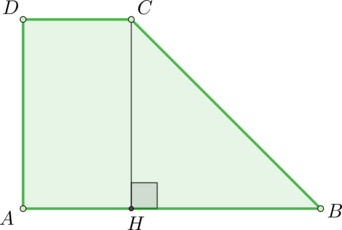
Так как (angle HBC=45^circ), то (angle HCB=45^circ). Следовательно, (triangle HBC) равнобедренный и (HB=HC).
(ADCH) – прямоугольник, следовательно, (AH=DC=2). Тогда (CH=HB=6-2=4). Тогда площадь трапеции равна [S=dfrac{AB+DC}2cdot CH=dfrac{2+6}2cdot 4=16]
Ответ: 16
Основания прямоугольной трапеции равны (12) и (4). Ее площадь равна (64). Найдите острый угол этой трапеции. Ответ дайте в градусах.

Проведем высоту (CH).

(ADCH) – прямоугольник, следовательно, (AH=DC=4). Тогда (HB=12-4=8). Площадь трапеции равна [64=dfrac{AB+DC}2cdot CH=dfrac{4+12}2cdot CHquadRightarrowquad
CH=8] Заметим, что мы получили, что (CH=HB=8). То есть (triangle
CHB) равнобедренный, значит, углы при основании равны, то есть (angle HCB=angle HBC). Так как сумма острых углов в прямоугольном треугольнике равна (90^circ), то (angle B=angle
HBC=90^circ:2=45^circ).
Ответ: 45
Основания трапеции равны (18) и (6), боковая сторона, равная (7), образует с одним из оснований угол (150^circ). Найдите площадь трапеции.
Пусть (AD=7), тогда (angle ADC=150^circ). По свойству трапеции (angle DAB=180^circ-150^circ=30^circ). Проведем (DHperp
AB).
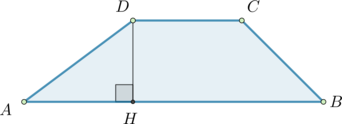
Рассмотрим (triangle ADH). Катет, лежащий против угла (30^circ), равен половине гипотенузы, следовательно, (DH=AD:2=3,5). Тогда площадь трапеции равна [S=dfrac{AB+DC}2cdot DH=dfrac{18+6}2cdot 3,5=42]
Ответ: 42
Основания трапеции равны (27) и (9), боковая сторона равна (8). Площадь трапеции равна (72). Найдите острый угол трапеции, прилежащий к данной боковой стороне. Ответ дайте в градусах.

Пусть (AD=8). Проведем (DHperp AB).

Тогда площадь трапеции равна [72=dfrac{AB+DC}2cdot DH=dfrac{27+9}2cdot DHquadRightarrowquad
DH=4] Рассмотрим прямоугольный (triangle ADH). Так как катет (DH) равен половине гипотенузы (AD), то угол (DAH) равен (30^circ).
Ответ: 30
Основания равнобедренной трапеции равны (14) и (26), а ее боковые стороны равны (10). Найдите площадь трапеции.

Проведем высоту (BH). По свойству равнобедренной трапеции (AH=(AD-BC):2=(26-14):2=6).

Тогда из прямоугольного треугольника (ABH): [BH=sqrt{AB^2-AH^2}=sqrt{10^2-6^2}=8] Тогда площадь трапеции: [S=dfrac{AD+BC}2cdot BH=dfrac{26+14}2cdot 8=160]
Ответ: 160
Основания равнобедренной трапеции равны (7) и (13), а ее площадь равна (40). Найдите боковую сторону трапеции.

Проведем высоту (BH).

Площадь трапеции равна [40=dfrac{AD+BC}2cdot BH=dfrac{7+13}2cdot BHquadRightarrowquad BH=
4] Рассмотрим прямоугольный (triangle ABH). По свойству равнобедренной трапеции (AH=(AD-BC):2=(13-7):2=3). Следовательно, [AB=sqrt{AH^2+BH^2}=5]
Ответ: 5
Основания равнобедренной трапеции равны (14) и (26), а ее периметр равен (60). Найдите площадь трапеции.

Проведем высоту (BH). По свойству равнобедренной трапеции (AH=(AD-BC):2=(26-14):2=6).

Так как периметр трапеции равен (60), а боковые стороны равны, то [AB=dfrac{60-14-26}2=10] Тогда из прямоугольного треугольника (ABH): [BH=sqrt{AB^2-AH^2}=sqrt{10^2-6^2}=8] Тогда площадь трапеции: [S=dfrac{AD+BC}2cdot BH=dfrac{26+14}2cdot 8=160]
Ответ: 160

УСТАЛ? Просто отдохни
Лучшие онлайн-курсы для подготовки к ЕГЭ
Лучшие репетиторы для сдачи ЕГЭ
Задания по теме «Трапеция»
Открытый банк заданий по теме трапеция. Задания B6 из ЕГЭ по математике (профильный уровень)
Производная и первообразная функции
Задание №1067
Тип задания: 6
Тема:
Трапеция
Условие
Большее основание равнобедренной трапеции равно 24. Боковая сторона равна 7. Синус острого угла равен frac{sqrt{33}}{7}. Найдите меньшее основание.
Показать решение
Решение
Рассмотрим равнобедренную трапецию ABCD, в которой BC и AD — основания, AD = 24, AB = CD = 7. Проведём высоты CK и BH. BCKH — прямоугольник, BC = KH.
.png)
Треугольник ABH прямоугольный, cos A = frac{AH}{AB}. Вычислим cos A= sqrt{1-sin^2A}= sqrt{1-left (frac{sqrt{33}}{7}right)^2}= frac47. AH= ABcos A= 7cdotfrac47= 4. Треугольники ABH и DCK равны по гипотенузе и острому угу, откуда AH=KD=4, BC=24-4-4=16.
Ответ
16
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №1065
Тип задания: 6
Тема:
Трапеция
Условие
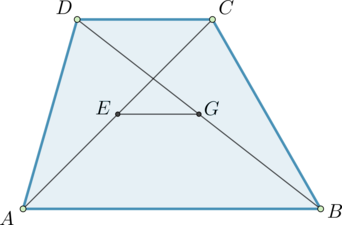
Площадь треугольника МРЕ равна 68, KT — средняя линия, параллельная стороне MP. Найдите площадь трапеции MPTK.
Показать решение
Решение
S_{MPTK}=S_{MPE}-S_{KTE}. KT — средняя линия, параллельная стороне MP, поэтому K и T — середины сторон и ET=frac12EP, KE=frac12 EM.
triangle MPE sim triangle KTE по двум углам: angle E — общий, MP parallel KT Rightarrow angle MPE= angle KTE. S_{KTE}= frac14S_{MPE}= frac{68}{4}= 17. S_{MPTK}= 68-17= 51.
Ответ
51
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №1064
Тип задания: 6
Тема:
Трапеция
Условие
Площадь треугольника АВС равна 76, DE — средняя линия, параллельная стороне AB. Найдите площадь трапеции ABED.
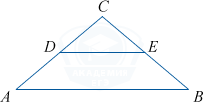
Показать решение
Решение
S_{ABED}=S_{ABC}-S_{CDE}. DE — средняя линия, параллельая стороне AB, поэтому D и E — середины сторон.
CD=frac12CA, CE=frac12CB, S_{ABC} =frac12CAcdot CBsin C,
S_{CDE}= frac12CDcdot CEsin C= frac12cdotfrac12CAcdotfrac12CBsin C= frac14cdotfrac12CAcdot CBsin C= frac14 S_{ABC}= frac{76}{4}=19
S_{ABED}= S_{ABC}-S_{CDE}= 76-19=57.
Ответ
57
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №1061
Тип задания: 6
Тема:
Трапеция
Условие
Основания равнобедренной трапеции равны 10 и 90, а её боковые стороны равны 41. Найдите площадь трапеции.
Показать решение
Решение
Рассмотрим равнобедренную трапецию ABCD, в которой BC = 10, AD = 90 — основания, AB = CD = 41.
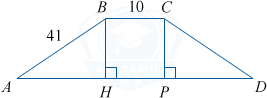
Проведём высоты CP и BH. BCPH — прямоугольник, BC = PH = 10. Прямоугольные треугольники ABH и DCP равны по гипотенузе и катету (AB = CD, BH = CP), тогда AH = PD = (90 – 10) : 2 = 40.
Треугольник ABH прямоугольный, BH = sqrt{41^2-40^2} = 9.
Площадь трапеции равна S = frac{BC+AD}{2}cdot BH= frac{10+90}{2}cdot 9= 450.
Ответ
450
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №895
Тип задания: 6
Тема:
Трапеция
Условие
Основания равнобедренной трапеции равны 15 и 43. Косинус острого угла трапеции равен 0,7. Найдите боковую сторону.
Показать решение
Решение
Рассмотрим равнобедренную трапецию ABCD, в которой BC=15, AD=43 — основания, AB=CD.
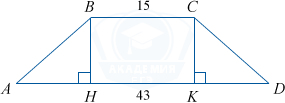
Проведём высоты CK и BH. BCKH — прямоугольник, BC=KH=15. Треугольники ABH и DCK равны по гипотенузе и острому углу, откуда AH=KD=(43-15):2=14. Треугольник ABH прямоугольный, cos A=frac{AH}{AB}. Боковая сторона трапеции AB=AH:cos A=14:0.7=20.
Ответ
20
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №888
Тип задания: 6
Тема:
Трапеция
Условие
Найдите площадь прямоугольной трапеции, основания которой равны 16 и 22, большая боковая сторона составляет с основанием угол 45^{circ}.
Показать решение
Решение
Рассмотрим прямоугольную трапецию ABCD с основаниями BC=16 и AD=22, angle A=90^{circ}, angle D=45^{circ}. Проведём высоту CH. ABCH — прямоугольник, BC=AH=16, тогда HD=22-16=6.
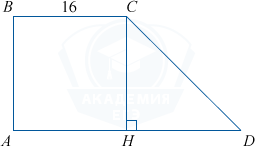
Треугольник CDH прямоугольный и равнобедренный (т.к. angle CHD=90^{circ}, angle HCD=45^{circ}=angle D). HD=HC=6.
Площадь трапеции S=frac{BC+AD}{2}cdot CH=frac{16+22}{2}cdot6=114.
Ответ
114
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №297
Тип задания: 6
Тема:
Трапеция
Условие
Основания равнобедренной трапеции равны 9 и 53. Тангенс острого угла равен frac{6}{11}. Найдите высоту трапеции.
Показать решение
Решение
Рассмотрим рисунок:
.png)
BKperp AD и CMperp AD, тогда AK=MD=frac{53-9}{2}=22.
frac{BK}{AK}=tgangle BAK=frac{6}{11}, поэтому BK=AKcdotfrac{6}{11}=22cdotfrac{6}{11}=12.
Ответ
12
Источник: «Математика. Подготовка к ЕГЭ-2016. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №293
Тип задания: 6
Тема:
Трапеция
Условие
Основания прямоугольной трапеции имеют длины 4 и 8. Ее большая сторона с основанием образуют угол равный 45^{circ}. Найдите площадь трапеции.
.png)
Показать решение
Решение
Пусть CH — высота трапеции ABCD. Тогда в прямоугольном треугольнике CHD острый угол CHD = 45^{circ}. Значит, этот треугольник равнобедренный, то есть CH=DH=AD-BC=8-4=4.
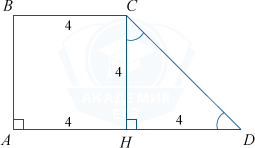
Тогда S_{ABCD}=frac{AD+BC}{2}cdot CH=frac{8+4}{2}cdot4=24.
Ответ
24
Источник: «Математика. Подготовка к ЕГЭ-2016. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Лучшие репетиторы для сдачи ЕГЭ
Ситуация вынудила стать учителем онлайн. Пришлось многому научиться. Понравилось. Теперь здесь на канале каждый день пишу краткое содержание одного онлайн урока на 45 минут или просто какую-нибудь фишку для онлайна .
Итак, что нужно знать про трапецию:
1)
2)
3)
4)
5)
6)
7)
8) Случай равнобедренной трапеции, в которую вписана окружность
9) Формула Буракова
10) Дополнительные построения:
Первая задача:
Вторая задача:
Третья задача:
Задание 972
Основания равнобедренной трапеции равны 7 и 13, а ее площадь равна 40. Найдите периметр трапеции.
Ответ: 30
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Скрыть
Площадь трапеции вычисляется по формуле $$S=frac{a+b}{2}*h$$. Получаем $$40=frac{7+13}{2}*CH$$. Отсюда CH = 4.
Из треугольника CHD по теореме Пифагора находим CD = 5. Отсюда периметр равен 7 + 13 + 5 + 5 = 30
Задание 1858
Найдите больший угол равнобедренной трапеции ABCD, если диагональ AC образует с основанием AD и боковой стороной AB углы, равные 30° и 45° соответственно.
Ответ: 105
Скрыть

$$angle A=angle BAC+angle CAD=30+45=75^{circ}$$, тогда по свойству углов трапеции: $$angle B=180-angle A=105^{circ}$$
Задание 1859
Найдите угол АDС равнобедренной трапеции ABCD, если диагональ АС образует с основанием ВС и боковой стороной АВ углы, равные 30° и 50° соответственно.
Ответ: 80
Скрыть

$$angle A=angle BAC+angle CAD=30+50=80^{circ}$$
Задание 1860
Сумма двух углов равнобедренной трапеции равна 140°. Найдите больший угол трапеции. Ответ дайте в градусах.
Ответ: 110
Скрыть

Так как дана равнобедренная трапеция, то сумма острых углов при большем основании будет составлять 140 градусов, $$angle A=angle B=frac{140}{2}=70^{circ}$$, по свойству углов трапеции: $$angle D=180-angle A=110^{circ}$$
Задание 1861
Найдите меньший угол равнобедренной трапеции, если два ее угла относятся как 1:2. Ответ дайте в градусах.
Ответ: 60
Скрыть
Пусть меньший угол равен х, тогда больший угол равен 2х. По свойству углов трапеции получаем, что $$x+2x=180Leftrightarrow$$$$x=60$$, то есть меньший угол составляет $$60^{circ}$$
Задание 1863
Тангенс острого угла прямоугольной трапеции равен $$frac{5}{6}$$. Найдите её большее основание, если меньшее основание равно высоте и равно 15.
Ответ: 33
Скрыть
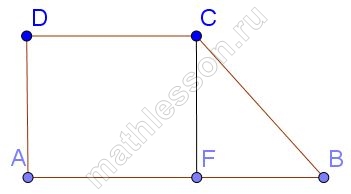
Опустим высоту CF, тогда из прямоугольного треугольника CFB: $$FB=frac{CF}{tgB}=frac{15}{frac{5}{6}}=18$$. DC=AF=15, тогда AB=15+18=33.
Задание 1864
В равнобедренной трапеции известны высота 4, меньшее основание 8 и угол при основании $$45^{circ}$$. Найдите большее основание.
Ответ: 16
Скрыть
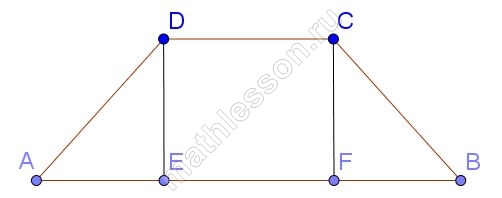
Опустим высоты DE=CF=4, тогда из прямоугольного треугольника ADE: так как $$angle A=45^{circ}$$, то $$angle ADE=90-45=45^{circ}$$, следовательно, реугольник AED – равнобедренный, и AE=DE=4, аналогично FB=4. Но EF=DC=8, тогда AB=4+4+8=16.
Задание 1865
Основания трапеции равны 4 и 10. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из её диагоналей.
Ответ: 5
Скрыть

EG – средняя линия треугольника ADB, тогда $$EG=frac{1}{2}=AB=5$$, аналогично GF – средняя линия треугольника DCB, тогда $$GF=frac{1}{2}DC=2$$, наибольший в таком случае равен 5
Примечение: больший из отрезков всегда будет равен половине большего основания
Задание 1866
Основания равнобедренной трапеции равны 50 и 104, боковая сторона 45. Найдите длину диагонали трапеции.
Ответ: 85
Скрыть
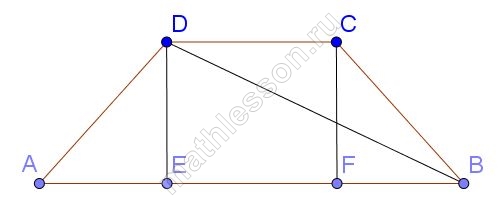
Опустим две высоты DE=CF, тогда AE=FB (из равенства прямоугольных треугольников ADE и CFB по катету и гипотенузе), и DC=EF=50, тогда $$AE=FB=frac{104-50}{2}=27$$. Тогда из прямоугольного треугольника ADE : $$DE=sqrt{AD^{2}-AE^{2}}=sqrt{45^{2}-27^{2}}=36$$, следовательно, EB=AB-AE=104-27=77. Тогда из прямоугольного треугольника DEB: $$DB=sqrt{DE^{2}+EB^{2}}=sqrt{77^{2}+36^{2}}=85$$
Задание 1867
Около трапеции, один из углов которой равен 49°, описана окружность. Найдите остальные углы трапеции.
Запишите величины углов в ответ через точку с запятой в порядке неубывания.
Ответ: 49; 131; 131
Скрыть
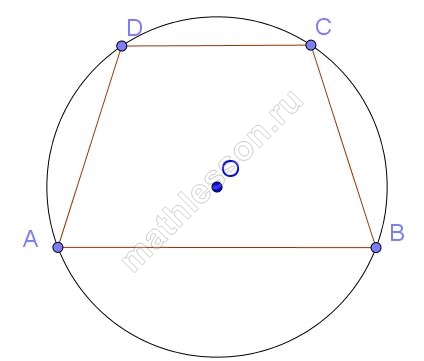
По свойству вписанного четырехугольник $$angle A+angle C=180^{circ}$$, пусть $$angle A=49^{circ}Rightarrow$$$$angle C=180-49=131^{circ}$$. По свойству углов трапеции $$angle B=180-angle C=180-131=49^{circ}$$, аналогично $$angle D=180-angle A=131^{circ}$$
Задание 1868
В трапецию, сумма длин боковых сторон которой равна 24, вписана окружность. Найдите длину средней линии трапеции.
Ответ: 12
Скрыть
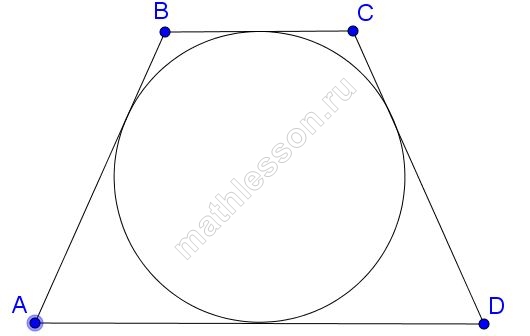
По свойству описанного четырехугольника AD+BC=AB+CD, тогда сумма оснований тоже 24, средняя линия же равна полусумме оснований, то есть 24/2=12.
Задание 1965
Основания трапеции равны 18 и 12, одна из боковых сторон равна 6, а синус угла между ней и одним из оснований равен $$frac{1}{3}$$. Найдите площадь трапеции.
Ответ: 30
Скрыть

- Опустим высоту CE. Пусть $$sin D=frac{1}{3}$$, тогда из прямоугольного треугольника CED: $$CE=CD*sin D=2$$
- Из формулы площади трапеции: $$S_{ABCD}=frac{18+12}{2}*2=30$$
Задание 1966
Основания трапеции равны 18 и 12, одна из боковых сторон равна 6, а косинус угла между ней и одним из оснований равен $$frac{2sqrt{2}}{3}$$. Найдите площадь трапеции.
Ответ: 30
Скрыть

- Пусть $$cos D =frac{2sqrt{2}}{3}$$, опустим высоту CE. Тогда из треугольника CED: $$ED=CD*cos D=6*frac{2sqrt{2}}{3}=4sqrt{2}$$
- По теореме Пифагора из треугольника CED: $$CE=sqrt{6^{2}-(4sqrt{2})^{2}}=2$$
- Из формулы площади трапеции $$S_{ABCD}=frac{18+12}{2}*2=30$$
Задание 1967
Средняя линия трапеции равна 11, а меньше основание равно 5. Найдите большее основание трапеции.
Ответ: 17
Скрыть
Пусть a – большее основание, тогда из формулы длины средней линии трапеции : $$a=2*11-5=17$$
Задание 1968
Боковая сторона трапеции равна 5, а один из прилегающих к ней углов равен 30°. Найдите площадь трапеции, если её основания равны 3 и 9.
Ответ: 15
Скрыть

- Пусть $$angle D=30^{circ}$$. Опустим высоту CE, тогда из прямоугольного треугольника CED: $$CE=CD*sin D=2,5$$
- По формуле площади трапеции $$S_{ABCD}=frac{3+9}{2}*2,5=15$$
