Здравствуйте, дорогие читатели, подписчики и гости канала. В этой статье рассмотрим различные вычисления с дробями, которые встречаются в шестом задании ОГЭ по математике. В июле 2.07.2021 года состоится последняя пересдача по математике в основной этап. Дополнительный этап будет уже в сентябре.
Давайте начнем разбор заданий.
1) Умножение дробь на дробь. Чтобы умножить дробь на дробь, нужно числитель умножить на числитель, знаменатель на знаменатель, при возможности сократить.
2) Деление дроби на дробь. При делении дробь на дробь, первая дробь переписывается, вторая дробь переворачивается, а деление заменяется на умножение.
3) Вычитание и умножение дробей. Несколько действий.
Способ №1. Находим общий знаменатель при вычитании. Чтобы найти общий знаменатель, нужно найти такое число, которое будет делиться на первое и второе число. В нашем случае это числа 10 и 20. Общий знаменатель 20.
Способ №2. Распределительный закон умножения. Чтобы умножить число на сумму можно умножить это число на каждое слагаемое, и результат сложить. Также это действует и при вычитании.
Также встречаются выражения, в которых не стоит находить общий знаменатель, поскольку это будет сложно. Приведу два примера:
Пример №1
Пример №2
4) Умножение целого числа на дробь. При умножении целого числа на дробь, целое число умножается на числитель, а знаменатель остается без изменений.
5) Сложение, деление и умножение смешанных чисел.
При сложении, вычитании, умножении и делении смешанных чисел иногда легче перевести смешанное число в неправильную дробь. Чтобы смешанное число перевести в неправильную дробь, нужно целую часть умножить на знаменатель, к полученному значению прибавить числитель дробной части и записать это в числитель, а знаменатель оставить прежним.
6) Вынесение общего множителя за скобку.
7) Действия с десятичными дробями
В итоге у нас получилось, что числитель дроби умножили на 100 (10*10=100), значит и знаменатель дроби тоже умножаем на 100, чтобы значение дроби не изменилось.
И еще один пример:
8) Десятичные дроби и действия со степенями
При возведении отрицательного числа в четную степень, получится число положительное. При возведении отрицательного числа в нечетную степень, получится число отрицательное.
И последнее выражение
Для отработки этих примеров, можно воспользоваться сайтом. Там много аналогичных задания, а эта статья вам будет в помощь при их решений.
Спасибо, что дочитали. Вы меня очень поддержите, если поставите лайк и подпишитесь на мой блог.
Каталог заданий.
Действия с обыкновенными дробями
Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Тип 6 № 314127 

i
Найдите значение выражения
Аналоги к заданию № 311234: 314127 32 311235 … Все
Источник: Банк заданий ФИПИ
Решение
·
Помощь
2
Тип 6 № 314264 

i
Вычислите:
Аналоги к заданию № 314262: 314264 314265 383596 … Все
Источник: Банк заданий ФИПИ
Решение
·
Помощь
3
Тип 6 № 314265 

i
Вычислите:
Аналоги к заданию № 314262: 314264 314265 383596 … Все
Источник: Банк заданий ФИПИ
Решение
·
Помощь
4
Тип 6 № 314288 

i
Найдите значение выражения
Аналоги к заданию № 314282: 314288 333111 314283 … Все
Источник: Банк заданий ФИПИ
Решение
·
Помощь
5
Тип 6 № 333006 

i
Найдите значение выражения
Аналоги к заданию № 333006: 337375 353450 Все
Решение
·
Помощь
Пройти тестирование по этим заданиям
Найдите значения выражений
| 1 | frac{7}{2} cdot frac{5}{4} – frac{3}{8} | Смотреть видеоразбор >> |
| 2 | frac{22}{3}:frac{2}{15} cdot frac{6}{5} | Смотреть видеоразбор >> |
| 3 | (frac{9}{14}-frac{10}{21}) cdot 42 | Смотреть видеоразбор >> |
| 4 | (frac{11}{10}+frac{11}{13}):frac{22}{39} | Смотреть видеоразбор >> |
| 5 | (frac{11}{10}-frac{13}{15}):frac{7}{60} | Смотреть видеоразбор >> |
| 6 | frac{19}{6}:(frac{5}{6}+frac{3}{4}) | Смотреть видеоразбор >> |
| 7 | frac{0,9+0,7}{3,2} | Смотреть видеоразбор >> |
| 8 | frac{3,2-5,7}{2,5} | Смотреть видеоразбор >> |
| 9 | frac{4,7-1,4}{7,5} | Смотреть видеоразбор >> |
| 10 | frac{2,4}{1,2-0,4} | Смотреть видеоразбор >> |
| 11 | frac{5,6}{1,9-7,5} | Смотреть видеоразбор >> |
| 12 | (1,7+2,8) cdot 4,8 | Смотреть видеоразбор >> |
| 13 | 4,1 cdot 7,7 + 0,86 | Смотреть видеоразбор >> |
| 14 | 1,2 : 0,6 cdot 1,5 | Смотреть видеоразбор >> |
| 15 | 1 + frac{1}{7} cdot 0,77 | Смотреть видеоразбор >> |
| 16 | frac{5}{3}:frac{2}{7}-frac{11}{6} | Смотреть видеоразбор >> |
| 17 | frac{5}{6}+frac{5}{2} cdot frac{2}{3} | Смотреть видеоразбор >> |
| 18 | (frac{5}{12}-frac{3}{20}) cdot frac{45}{2} | Смотреть видеоразбор >> |
| 19 | (frac{17}{35}+frac{3}{8}):frac{5}{28} | Смотреть видеоразбор >> |
| 20 | (frac{11}{5}-frac{13}{6}):frac{1}{90} | Смотреть видеоразбор >> |
| 21 | frac{12}{7}:(frac{6}{7}-frac{3}{4}) | Смотреть видеоразбор >> |
| 22 | frac{7,9+3,4}{0,2} | Смотреть видеоразбор >> |
| 23 | frac{2,6-8,4}{2,5} | Смотреть видеоразбор >> |
| 24 | frac{2,6-2,6}{7,8} | Смотреть видеоразбор >> |
| 25 | frac{5,6}{1,7-1,6} | Смотреть видеоразбор >> |
| 26 | frac{9,2}{0,5-2,8} | Смотреть видеоразбор >> |
| 27 | (1,7+2,8) cdot 24 | Смотреть видеоразбор >> |
| 28 | 5,6 cdot 5,5 – 4,1 | Смотреть видеоразбор >> |
| 29 | frac{1}{4} cdot 0,48 + 1 | Смотреть видеоразбор >> |
| 30 | frac{1}{frac{1}{5}-frac{1}{30}} | Смотреть видеоразбор >> |
| 31 | frac{14}{9} cdot frac{3}{2}:frac{7}{6} | Смотреть видеоразбор >> |
| 32 | frac{5}{4}+frac{7}{6}:frac{2}{3} | Смотреть видеоразбор >> |
| 33 | (frac{11}{9}+frac{4}{9}):frac{5}{36} | Смотреть видеоразбор >> |
| 34 | (frac{5}{7}-frac{3}{7}):frac{2}{21} | Смотреть видеоразбор >> |
| 35 | (frac{8}{25}-frac{13}{38}):frac{6}{19} | Смотреть видеоразбор >> |
| 36 | 3:(frac{6}{7}-frac{3}{4}) | Смотреть видеоразбор >> |
| 37 | frac{6,9+4,1}{0,2} | Смотреть видеоразбор >> |
| 38 | frac{0,5-1,5}{0,8} | Смотреть видеоразбор >> |
| 39 | frac{3,8}{2,6+1,2} | Смотреть видеоразбор >> |
| 40 | frac{2,6}{3,1-0,6} | Смотреть видеоразбор >> |
| 41 | frac{6,9}{3,2-5,7} | Смотреть видеоразбор >> |
| 42 | (6,9-3,4) cdot 8,4 | Смотреть видеоразбор >> |
| 43 | 5,4 cdot 1,9 – 2,15 | Смотреть видеоразбор >> |
| 44 | frac{1}{6} cdot 9,6 – 1 | Смотреть видеоразбор >> |
| 45 | frac{1}{frac{1}{2}+frac{1}{3}} | Смотреть видеоразбор >> |
| 46 | frac{18}{7} cdot frac{14}{3} : frac{4}{5} | Смотреть видеоразбор >> |
| 47 | (frac{5}{6}+frac{7}{15}) cdot frac{30}{13} | Смотреть видеоразбор >> |
| 48 | (frac{3}{22}+frac{2}{11}):frac{5}{33} | Смотреть видеоразбор >> |
| 49 | (frac{13}{6}-frac{11}{6}):frac{1}{90} | Смотреть видеоразбор >> |
| 50 | frac{13}{7}:(frac{1}{3}+frac{2}{7}) | Смотреть видеоразбор >> |
| 51 | frac{1,8+1,9}{3,7} | Смотреть видеоразбор >> |
| 52 | frac{7,5+3,5}{2,5} | Смотреть видеоразбор >> |
| 53 | frac{7,3-2,5}{1,2} | Смотреть видеоразбор >> |
| 54 | frac{9,4}{2,1+2,6} | Смотреть видеоразбор >> |
| 55 | frac{4,4}{5,8-5,3} | Смотреть видеоразбор >> |
| 56 | frac{0,6}{1,7-2,9} | Смотреть видеоразбор >> |
| 57 | (5,3-2,8)cdot38 | Смотреть видеоразбор >> |
| 58 | 1,32:1,2-0,8 | Смотреть видеоразбор >> |
| 59 | 3-frac{1}{4}cdot5,6 | Смотреть видеоразбор >> |
| 60 | frac{1}{frac{1}{4}-frac{1}{5}} | Смотреть видеоразбор >> |
| 61 | frac{15}{2}:frac{5}{21}cdotfrac{4}{3} | Смотреть видеоразбор >> |
| 62 | (frac{4}{15}+frac{1}{20})cdot60 | Смотреть видеоразбор >> |
| 63 | (frac{13}{21}+frac{3}{14}):frac{10}{27} | Смотреть видеоразбор >> |
| 64 | (frac{17}{8}-frac{1}{16}):frac{11}{48} | Смотреть видеоразбор >> |
| 65 | 13:(frac{1}{3}+frac{2}{7}) | Смотреть видеоразбор >> |
| 66 | frac{4,2+3,3}{0,3} | Смотреть видеоразбор >> |
| 67 | frac{2,7+5,8}{6,8} | Смотреть видеоразбор >> |
| 68 | (frac{6,8-4,7}{1,4}) | Смотреть видеоразбор >> |
| 69 | frac{5,6}{8,5-2,9} | Смотреть видеоразбор >> |
| 70 | frac{2,1}{6,6-2,4} | Смотреть видеоразбор >> |
| 71 | frac{7,7}{3,7-8,7} | Смотреть видеоразбор >> |
| 72 | 3,5cdot6,6+1,6 | Смотреть видеоразбор >> |
| 73 | 2,7+1,32:1,2 | Смотреть видеоразбор >> |
| 74 | 0,15:frac{3}{7}+1 | Смотреть видеоразбор >> |
| 75 | frac{1}{frac{1}{10}-frac{1}{15}} | Смотреть видеоразбор >> |
Шестое задание проверяет наши умения проведения вычислений. Это самое простое задание из всего модуля и требует от нас только знания арифметики. В первом задании арифметические действия будут самыми простыми. В демонстрационном варианте ОГЭ предлагается сложить две дроби: обыкновенную и десятичную. Тем не менее, в соответствии с документами о проведении ОГЭ, учащиеся должны быть готовы и к выполнению некоторых других несложных заданий. Ответом в первом задании является целое число или конечная десятичная дробь.
Итак, для успешного выполнения необходимо помнить:
- порядок проведения арифметических операций – сначала производятся действия в скобках, затем возведение в степень или извлечение корня, затем умножения и деления, а затем вычитания и сложения.
- правила умножения и деления в столбик
- правила вычисления обыкновенных дробей
Напоминаем правила операций с обыкновенными дробями:

Рекомендуем вычислить отдельно числитель и знаменатель, а затем разделить числитель на знаменатель. Остальные рекомендации смотрите ниже при разборе типовых вариантов первого задания ОГЭ по математике. 🙂
Задание 6OM21R
Найти значение выражения 4,9 – 9,4.
Выполним вычитание десятичных дробей, где 9,4 больше по модулю, значит, ответ будет отрицательным. Итак, – (9,4 – 4,9)= – 4,5
Ответ: -4,5
pазбирался: Даниил Романович | обсудить разбор
Задание OM0606o
Найдите значение выражения:
–0,3·(–10)4+4·(–10)2–59
Для получения результата необходимо последовательно выполнить математические действия в соответствии с их приоритетом.
–0,3·(–10)4+4·(–10)2–59 =
Выполняем возведение в степень. Получаем числа, состоящие из единицы и следующего за ней количества нулей, равного показателю степени. При этом знаки «–» в скобках исчезают, поскольку показатели степеней четные. Получаем:
= –0,3·10000+4·100–59 =
Выполняем умножение. Для этого в числе 0,3 переносим десятичную запятую на 4 знака вправо (так как в 10000 четыре нуля), а к 4 дописываем, соответственно, 2 нуля. Получаем:
= –3000+400–59 =
Выполняем сложение –3000+400. Поскольку это числа с разными знаками, то вычитаем из большего модуля меньший и перед результатом ставим «–», поскольку число с большим модулем отрицательное. Получаем:
= –2600–59 =
Так как оба числа отрицательные, то складываем их модули и перед результатом ставим «–». Получаем:
= –(2600+59) = –2659
Ответ: -2659
pазбирался: Даниил Романович | обсудить разбор
Задание OM0605o
Найдите значение выражения:
–13•(–9,3)–7,8
Это задание требует простого умения выполнять арифметические действия с десятичными дробями.
–13·(–9,3)–7,8 =
Сначала выполняем умножение. Умножаем –13 и –9,3 в столбик без учета знаков «–» перед сомножителями. В полученном произведении отделяем одну – последнюю – цифру десятичной запятой:
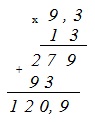
Знак произведения будет положительным, поскольку умножаются два отрицательных числа. Получаем:
= 120,9–7,8 =
Эту разность можно вычислить в столбик, но можно и устно. Выполним это действие в уме: вычитаем отдельно целые части и десятичные. Получаем:
= 113,1
Ответ: 113,1
pазбирался: Даниил Романович | обсудить разбор
Задание OM0604o
Найдите значение выражения: ¼ + 0,07
К данному заданию, как и к большинству заданий 1 модуля Алгебры, подход к решению заключается в переводе дроби от одного вида к другому. В нашем случае это переход от обыкновенной дроби к десятичной.
Переводим ¼ из обыкновенной дроби в десятичную. Делим 1 на 4, получаем 0,25. Затем переписываем выражение с использованием только десятичных дробей и вычисляем:
0,25 + 0,07 = 0,32
Ответ: 0,32
pазбирался: Даниил Романович | обсудить разбор
Задание OM0603o
Найдите значение выражения: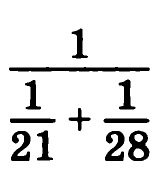
Аналогично предыдущим заданиям вычисляем знаменатель: для этого приводим дроби к общему знаменателю — это 84. Для этого первую дробь умножаем на 4, а вторую на 3, получим:
1/21 + 1/28 = 4/84 + 3/84
Затем складываем:
4/84 + 3/84 = 7/84
Итак, мы получили в знаменателе 7/84, теперь делим числитель на знаменатель — это все равно что умножить 1 на обратную 7/84 дробь:
1 / ( 7 / 84 ) = 1 •84/7 = 84/7
Далее остается поделить 84 на 7:
84 / 7 = 12
Ответ: 12
pазбирался: Даниил Романович | обсудить разбор
Задание OM0602o
Найдите значение выражения:![]()
Можно решать задачу напрямую — вычисляя значения последовательно, это не должно составить труда, однако решение будет долгим и с большими вычислениями. Здесь можно заметить, что 1/3 присутствует как в уменьшаемом — 6 • (1/3)², так и в вычитаемом — 17 • 1/3, поэтому её можно легко вынести за скобку.
1/3 • (6 • (1/3) — 17 )
Проведя вычисления в скобках, получим:
1/3 • ( 6 • (1/3) — 17 ) = 1/3 • (6 /3 — 17 ) = 1/3 • ( 2 — 17 ) = 1/3 • ( -15 )
Теперь умножим полученное значение -15 на 1/3:
1/3 • ( -15 ) = -5
Ответ: -5
pазбирался: Даниил Романович | обсудить разбор
Задание OM0601o
Найдите значение выражения:![]()
Задачу можно решать разными путями, а именно менять последовательность действий, но этот вариант решения рекомендуется для тех, кто уверен в своих возможностях и знает математику на отлично. Для остальных мы рекомендуем выполнить последовательно действия в числителе и знаменателе, а затем разделить числитель на знаменатель. Числитель вычислять в данном примере нет необходимости, это число 9.
Вычислим значение знаменателя:
4,5 • 2,5
Можно произвести вычисления в столбик, тогда получим:
4,5 • 2,5 = 11,25
Либо перевести дробь к простому виду:
4,5 • 2,5 = 4½ • 2 ½ = 9 / 2 • 5 / 2 = 45 / 4
Последний случай предпочтительней, так как для дальнейшей операции – деления числителя на знаменатель задача упрощается. Делим числитель на знаменатель, умножая числитель на перевернутую дробь в знаменателе:
9 / ( 45 / 4 ) = ( 9 / 1 ) • ( 4 / 45 ) = ( 9 • 4 ) / (1 • 45 )
9 и 45 можно сократить на 9:
( 9 • 4 ) / (1 • 45 ) = ( 1 • 4 )/ (1 • 5 ) = 4 / 5 = 8 / 10 = 0,8
Ответ: 0,8
pазбирался: Даниил Романович | обсудить разбор
Задача 6 ОГЭ по математике называется «Числа и вычисления». Это действия с обыкновенными и с десятичными дробями. Действия со степенями. Сравнение чисел.
Приступим к решению задач.
Пример 1. Найдите значение выражения
Решение. Вспоминаем, что при вычитании дробей нужно их привести к общему знаменателю, а при делении дробей первую из них умножаем на перевёрнутую вторую.
Посчитаем, чему равен знаменатель.
Получим:
Ответ: 0,9.
Пример 2. Соотнесите обыкновенные дроби с равными им десятичными дробями.
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
Решение. Каждую из данных обыкновенных дробей можно представить в виде десятичной, например, используя деление в столбик.

Итак, деление выполнено. Сопоставим полученные результаты:
Ответ: 4312.
Замечание 1. Преобразование обыкновенных дробей в десятичные можно произвести и без деления в столбик. Т. к. любая десятичная дробь записывается как обыкновенная со знаменателем 10, 100, 1000 и т. д., то данные обыкновенные дроби можно «доделать» до десятичных. Для этого используем основное свойство дроби: дробь не изменится, если её числитель и знаменатель домножить на одно и тоже число.

Замечание 2. В этой задаче можно было, наоборот, преобразовывать заданные десятичные дроби в обыкновенные путём упрощения, т. е. сокращения числителя и знаменателя.

Выбирайте любой способ. Здесь важен правильный результат!
Для выполнения следующих заданий нам потребуются свойства степеней. Напомним основные из них.
Степенью называется выражение вида
Здесь a — основание степени, c — показатель степени.
По определению,
Возвести число в квадрат — значит умножить его само на себя:
Возвести число в куб — значит умножить его само на себя три раза:
Возвести число в натуральную степень n — значит умножить его само на себя n раз:
По определению,
Это верно для Выражение
не определено.
Определим, что такое степень с целым отрицательным показателем.
Конечно, все это верно для поскольку на ноль делить нельзя.
Соберем свойства степеней и основные формулы в одной таблице.
| При перемножении степеней с одинаковыми основаниями показатели степеней складываются. | |
|
|
При делении степеней с одинаковыми основаниями показатели степеней вычитаются. |
|
|
При возведении степени в степень показатели степеней перемножаются. |
|
|
При возведении в отрицательную степень получаем дробь, где единица делится на степень с положительным показателем. |
| При возведении произведения двух множителей в степень каждый из этих множителей возводится в заданную степень. | |
| При возведении дроби в степень получается дробь, числитель и знаменатель которой возведены в заданную степень. | |
|
|
При возведении дроби в отрицательную степень дробь переворачивается, а показатель степени становится положительным. |
Пример 3. Найдите значение выражения
Решение. Вычислим, используя свойства степеней:
Ответ: 3328.
Пример 4. Найдите значение выражения
Решение. Вычислим, используя свойства степеней:
Ответ: 0,5604.
Пример 5. Найдите значение выражения
Решение. Вычислим, используя свойства степеней:
Ответ: 81.
Спасибо за то, что пользуйтесь нашими статьями.
Информация на странице «Задание 6 ОГЭ по математике. Числа и вычисления.» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.
Публикация обновлена:
08.05.2023
