Найти частное способом подбора это как

Математика. 3 класс

Конспект урока

Математика, 3 класс

Урок № 43. Приём деления для случаев вида 87 : 29, 66 : 22

Перечень вопросов, рассматриваемых в теме:

1. Как разделить двузначное число на двузначное?

2. Как выполнить деление вида 87 : 29, 66 : 22?

3. Как проверить правильность результата деления?

Глоссарий по теме:

Деление – это обратное действие умножению

Умножение – это сложение одинаковых слагаемых.

Метод подбора – это способ деления двузначного числа на двузначное, при котором частное подбираем последовательно и проверяем умножением.

Обязательная и дополнительная литература:

1. Моро М. И., Бантова М. А. и др. Математика 3 класс. Учебник для общеобразовательных организаций М.; Просвещение, 2017, C-18.

2. Петерсон Л. Г. Математика 3 класс. Часть 2. – М.: Ювента, 2013– 96 C., С-86.

3. Марченко И.С. Справочник школьника по математике: 1 – 4 классы. – М.: Эксмо, 2014. С. 160, (Светлячок) С. 50.

Теоретический материал для самостоятельного изучения

Рассмотрим решение задачи.

Высота дома тридцать два метра, а высота дерева – шестнадцать метров. Во сколько раз дом выше дерева?

Чтобы узнать во сколько раз дом выше, надо тридцать два разделить на шестнадцать. Получится два, в два раза. Выполнить такое деление можно

используя взаимосвязь умножения и деления. Это поможет научиться делить двузначное число на двузначное методом подбора частного.

Рассмотрим пример 48 : 12

Пробуем в частном два и проверяем. Двенадцать умножить на два получится двадцать четыре — не подходит. Пробуем- три. Двенадцать умножить на три равно тридцать шесть, тоже не подходит. Пробуем четыре. Двенадцать умножаем на четыре, получается сорок восемь, подходит. Значит, сорок восемь разделить на двенадцать получится четыре.

12 ∙ 2 = 24 не подходит

12 ∙ 3 = 36 не подходит

12 ∙ 4 = 48 подходит

В случае деления числа шестьдесят шесть на двадцать два, подбираем число, на которое надо умножить двадцать два, чтобы получилось шестьдесят шесть. Это число три.

66 : 22 = 3, так как 22 ∙ 3 = 66

Умножение нужно использовать для проверки правильности вычислений.

88 : 11 = 8, так как 11 ∙ 8 = 88

Чтобы делать меньше проб при подборе частного, нужно обратить внимание на последнюю цифру в делимом и делителе. В делимом цифра один , в делителе — цифра семь. В таблице умножения на семь находим число двадцать один (ведь один последняя цифра в делимом). Чтобы получить двадцать один, нужно семь умножить на три. Три – пробное число. Выполняем проверку.

Делимое 81 — последняя цифра 1

Делитель 27 — последняя цифра 7

7 ∙ 3 = 21 Проверка: 27 ∙ 3 = 81

Частное найдено, верно.

Выполним тренировочные задания

Вставьте пропущенные числа:

54 : 27 = ____ , так как 27 ∙ ___ = 54;

Ответ: 54 : 27 = 2 , так как 27∙ 2 = 54.

Зачеркните пример с ошибкой:

Ошибка в примере 42 : 14 = 2 и 64 : 16 = 3

Расшифруйте, расставляя ответы в порядке возрастания, название одного из самых высоких деревьев в мире:

Источник

Приёмы нахождения частного и остатка способом подбора

Тема: Приёмы нахождения частного и остатка.

Учитель: Ожогина С.В.

Цели: учить выполнять деление с остатком методом подбора; закреплять вычислительные навыки, умение решать задачи изученных видов.

Планируемые результаты: учащиеся научатся выполнять деление с остатком разными способами и оформлять запись в столбик; решать задачи изученных видов; работать в парах; выполнять задания творческого и поискового характера.

1) Организационный момент. Мотивационный настрой.

-Ребята, класс – это одна семья, а в семье необходимо друг друга поддерживать. Давайте дружно потрудимся, совместно преодолевая трудности. Сегодня на уроке нам нужно показать всё то, чему мы научились на уроках математики.

-Вы готовы к работе? Удачи вам.

-Свои математические умения, оценивать вы будете самостоятельно на листе самооценки. Подпишите их.

Знание таблицы умножения

Знание названий компонентов умножения и деления

Умение выполнять деление с остатком

Умение решать задач

Умение находить значение числовых выражений

Умение дружно трудиться

Оценка за урок, которую поставил бы я себе

2) Актуализация теоретических знаний.

-О каком математическом действии больше всего мы говорили на последних уроках математики? (делении)

-Какое математическое действие является основой для действия деления? (умножение)

-Давайте вспомним названия компонентов действия деления. (делимое, делитель, частное)

3) Устный счёт. Минутка чистописания.

-Давайте немного разомнёмся, как спортсмены перед началом демонстрации своих умений. Проведём устный счёт, совместив его с минуткой чистописания. Запишите в тетрадях число, классная работа. Я диктую примеры, ваша задача правильно и аккуратно записывать ответы в тетрадь. (Проверка: после записи каждого ответа, один ученик называет ответ)

7*4, 5*3, 8*8, 9*2, 48:6, 4*5, 30*1, 14:2, 25:5, 7*7, 0*1, 17:17, 54:6, 18:3, 3*3, 4*2, 56:7, 24:6, 50:10, 8*9, 3*2, 30:3, 40:2, 8*5.

-Какие знания пригодились? (знания таблицы умножения)

-Оцените свои умения в оценочном листе в графе «Знание таблицы умножения и названий компонентов».

4) Самоопределение к деятельности.

-Ребята, на доске записан пример 34:9 . В чём его особенность? (пример на деление с остатком)

-По какому правилу, алгоритму мы с вами находим значение таких числовых выражений? (Подбираем самое большое число к делителю, которое делится на делитель без остатка. Сколько не поделилось нацело, т.е. остаток, ищем вычитанием.)

-Два ученика решали этот пример. У них завязался спор, один сказал, что самое большое число, которое делится нацело без остатка – это 30. А другой сказал, что это 32. Как вы думаете, почему у ребят могли возникнуть разные варианты? ( Кто-то из них не смог вспомнить самое большое число)

-А у вас могут возникнуть такие затруднения?

— Какой вы предложите выход из данного спора?

-Как вы думаете, чем мы сейчас заниматься? (Искать выход из таких ситуаций)

5) Работа по теме урока.

5.1 Знакомство с новым способом.

— Когда вы не можете вспомнить самое большое число, тогда можно воспользоваться способом подбора частного.

— Прочитайте, как выполнить деление с остатком методом подбора, на с. 29.

— Как определить, правильно ли подобрано частное?

— Какой должен получиться остаток?

9*2=18, 34-18=16, 16>9 (не подходит)

— Когда можно воспользоваться этим способом? (когда не можешь вспомнить самое большое число)

— А ещё, ребята, такой способ можно применять, когда случай не табличный.

5.2 Применение нового способа.

— На доске примеры: 53:8, 78:9, 25:10, 38:11, 50:20.

— Давайте решим данные примеры, где нужно, будем применять способ подбора частного.

5.3 Самостоятельная работа в парах.

-Решите примеры самостоятельно, работая в парах: 43:8=, 64:7=

— Давайте оценим себя на листах самооценки в графе «Умение выполнять деление с остатком»

5.4 Решение задач.

— Назовите общее количество самолетов.

— Что значит «сколько троек может подняться в небо»? По сколько их надо разделить?

— Сделаем схематический рисунок.

— Сколько троек самолетов поднялось в небо? (6.)

— Сколько самолетов осталось? (2.)

— Запишите решение задачи выражением. (20:3 = 6(ост. 2).)

— Какими еще способами можно узнать, сколько троек в 20 самолетах? (Вспомнить наибольшее число до 20, которое делится на 3, или найти частное методом подбора.)

— Как оформить краткую запись? (С помощью таблицы.)

— Что надо узнать в задаче? (На сколько дней хватит 80мешков муки.)

— Что такое 48 мешков, 80 мешков? (Общий расход муки.)

— Что обозначает число 3? (Количество дней, за которые расходуют 48 мешков.)

— Какого столбца не хватает? (Расход муки в день.)

Расход муки в день

Общий расход муки

— Составьте программу решения.

— Запишите решение задачи одним выражением. (80:(48:3) = 5 (д.).)

( Тем, кто справится с заданием быстрее остальных, дополнительно можно предложить выполнить № 6 (с. 29). Ответ:1-ая ваза у Пети, 2-ая ваза у Кати, 3-ья — у Оли.)

— Давайте оценим себя на листах самооценки в графе «Умение решать задачи»

5.4 Решение числовых выражений на порядок действий.

№ 5 (с.29) – три ученика у доски, представители каждого ряда. Решаем по строкам: 1-ый ряд -1-ая строка, 2-ой ряд –вторая строка, 3-ий ряд – третья строка.

38:19+42:3= (47+8):11= 3*(72-60)=

28:2*3+8= 90-9:9= 82-25:5=

— Оцените свою работу на уроке. Ответьте на вопрос. Над чем мне ещё нужно поработать, чтобы преодолеть трудности……

— Оцените своё умение дружно работать, поставьте себе оценку за урок. Сдайте листы самооценки учителю.

VIII . Подведение итогов урока

— Какой метод деления с остатком мы использовали сегодня на уроке?

— Как проверить, правильно ли подобрано число?

— Почему остаток не может быть больше делителя?

— Полезен ли вам новый способ деления с остатком?

Учебник: № 5 (с. 29)- если не успеем на уроке.

— Рабочая тетрадь: № 95 (с. 36).

— Творческое задание по желанию: придумать примеры на деление с остатком для своих одноклассников.

Источник

Конспект урока математики в 3 классе «Деление на двузначное число способом подбора цифры частного»

Муниципальное бюджетное общеобразовательное учреждение

«Средняя общеобразовательная школа № 29»

Конспект урока математики

«Деление на двузначное число

способом подбора цифры частного»

универсальных учебных действий

ТЕМА: Деление на двузначное число (нахождение однозначного частного способом подбора цифры частного). Формирование умения выполнять пробные действия, фиксировать затруднение, выявлять причину и находить способ решения

ЦЕЛЬ: сформировать представление о последовательности действий на первом шаге УД (повторить необходимое для изучения нового: таблица умножения и деления, взаимопроверяемые действия), научить выполнять новое задание; фиксируя затруднение (если не смог выполнить), устанавливать причину затруднения (понять, почему не получилось), находить способ выхода из затруднения и закреплять умение.

1. Организационный момент: проверка готовности к уроку, настрой на работу.

2. Устный счёт (презентация, слайд № 1): Вычислить, используя приёмы

поразрядного умножения и деления, и определить проверочное действие

(УУД ПОЗНАВАТЕЛЬНЫЕ: логические – анализ, классификация).

33 х 3 = 99 12 х 2 = 24 304 х 2 = 602 120 х 3 = 360

360 : 3 = 120 99 : 3 = 33 602 : 2 = 304 24 : 2 = 12

Какие знания и умения нам пригодились?

— знание таблицы умножения и деления пригодилось?

— поразрядные способы умножения и деления повторили?

— взаимообратные действия определили?

А как вы думаете, зачем мы выполняли эти задания, проверяли умения?

Эти знания и умения нам сегодня потребуются.

3. А пока нам, юным экологам, нужно срочно вмешаться в ситуацию (слайд № 2):

Решить задачу «Детская площадка во дворе одного дома имеет прямоугольную форму. Её площадь равна 117 кв. м, а длина 13 метров. По ширине площадки требуется поставить забор, потому что водители повадились машинами заезжать на край площадки».

Чтобы закупить строительный материал (рейки), нужно вычислить, ширину забора.

Напомните друг другу, как узнать ширину, если известна площадь

и длина прямоугольника?

(Слайд № 3, картинки в презентации взяты из Интернет ресурсов, спасибо!).

Формула нахождения площади: повторяют, проговаривают (актуализация изученных способов): S = a х b b = S : a

(УУД ОБЩЕУЧЕБНЫЕ: знаково-символические, моделирование)

Значит, нам надо значение площади разделить на значение длины и получится значение ширины: 117 = 13 х b, b = 117 : 13, b = __

Это, надеюсь, нетрудно. (Слайд № 4)

117 : 13 – выполнение пробных действий в тетради. Не получается?

( УУД ПОЗНАВАТЕЛЬНЫЕ — логические – выдвижение гипотез, их обоснование, фиксирование затруднения)

— Зафиксировали затруднение (место причины затруднения, что и почему не смогли разделить?) – не делится, не изучали, мы делили на однозначное число, и др. (Слайд № 5 картинка из презентации Интернет ресурсов))

4. Оказывается, это новый способ деления, способ подбора частного,

Актуализация (мотивация): — А надо делить? может кому-то это не интересно?

— (хочу), или слишком трудно? (могу).

— Какая будет цель урока? – научиться делить, т. е. находить частное при делении на двузначное число

(УУД ПОЗНАВАТЕЛЬНЫЕ: общеучебные: формирование познавательной цели).

(Надо, хочу и могу, а то всю площадку испортят).

Значит, будем делить. Это и есть цель урока: не получилось, значит, будем учиться.

5. Определите свой выбор (Индивидуальная программа в приложении), как и сколько будете учиться? (Определяют и проговаривает несколько человек: что выбрали и почему)

(УУД РЕГУЛЯТИВНЫЕ – своя цель, планирование результатов, прогнозирование)

Слайд № 6 — белый (чтобы ничего не отвлекало)

6. Продолжим работу, чтобы, наконец, вычислить и обнести забором ширину площадки. Где можем узнать, как разделить 117 : 13? (в учебнике):

— На стр. 71 по работе зайца и волка попробуйте объяснить, почему у зайца все примеры записаны на умножение, а надо разделить 144 : 24?

– Так он подбирал частное (УУД — соотнесение своих действий с предлагаемым способом и выявление причины, почему у меня не получилось? — не делал так раньше, не знал правила и др.)

— Какие числа подбирал заяц?

— А как проще было? — по последней цифре делимого и таблице умножения?

(чтобы получить на конце цифру 4, надо на 4 умножить только 1 и 6).

(УУД ПОЗНАВАТЕЛЬНЫЕ – поиск и выделение информации, логические – построение логической цепи рассуждения)

— Какие действия заяц использовал для проверки? Взаимообратные.

— Каков ваш план действий? (Проект будущих действий – по алгоритму на стенде): (УУД КОММУНИКАТИВНЫЕ – планирование, постановка вопросов):

1) Изучаем правило о подборе частного (УУД фиксирование нового учебного действия – подбора частного).

2) Пробуем снова самостоятельно вычислить ширину забора 117 : 13=

(УУД использование нового учебного действия для выполнения задания).

3) Если не получится, то по алгоритму правила подбираем частное коллективно, записываем решение задачи на доске и в тетради и строим забор по ширине площадки – 9 метров.

4) Можно вычислить ещё быстрее, если использовать знание таблицы умножения и деления делимое заканчивается на 7, значит, при подборе цифры частного надо подобрать… (проговаривают) такое число, которое при умножении на число 3 даёт произведение, оканчивающееся на 7, а это только число 9 (3 х 9 = 27).

(УУД Личностные – нравственно-этического оценивания).

7. Молодцы, поняли и попробовали. Но все площадки заборами не обнести, а как ещё можно бороться с недобросовестными водителями? – размышляют: беседовать, обращаться с просьбой, писать письма – обращения, листовки, садить на газонах цветы, кусты и др.

(Слайд № 8 – белый слайд).

— Вам понравилось так долго находить ширину прямоугольника?

— Надо научиться делить быстрее.

8. Комментирование решения типовых примеров № 000 (1-й столбик) и № 000 (1-й столбик) решение их с проговариванием алгоритма УУД.

8. Самостоятельная работа: № 000 (2-й, 3-й столбики) (использование изучаемого УУД и осуществление его самопроверки, пошагово сравнивая с эталоном).

9. Проверка по эталону-образцу. (Слайд № 9).

(Сравнить выбор уровня в индивидуальной программе с результатом самостоятельной работы)

10. Уточнение особенностей нового УУД, его роли и места в системе изученных учебных действий. (Слайд № 10)

— Выбрать из примеров новые, на нахождение частного способом подбора и найти значения выражений: 36 : 9 (табличный), 36:18 (подбор частного), 590 : 10 (деление на 10), 60: 6 (поразрядное), 404: 4 (поразрядное), 72: 36 (подбор частного), 72: 18 (подбор частного) 120: 2 (а ещё на сколько можно разделить 120?), 126: 14 (подбор частного).

11. Рефлексия. Соотношение поставленной цели и результата (проверка по эталону), фиксирование степени их соответствия в индивидуальной программе и намётка дальнейшей цели работы;

— Какую цель ставили в начале урока (и по индивидуальной программе)?

— Как справились? (обозначить в индивидуальной программе).

— Кто удовлетворён своей работой, почему? (Комментируют)

— Что дальше будем делать? Ваши планы? – тренироваться дома.

Д/З — № в рабочей тетради, решить столько примеров, сколько считаете нужным, чтобы закрепить приобретённое умение

Индивидуальная программа изучения темы

«Нахождение однозначного частного (способом подбора частного)».

Цель: научиться делить на двузначное число, находить однозначное

частное способом подбора цифры.

Научиться соотносить поставленную цель и результат,

фиксировать степень их соответствия и намечать дальнейшую

Источник

Математика, 3 класс

Урок № 43. Приём деления для случаев вида 87 : 29, 66 : 22

Перечень вопросов, рассматриваемых в теме:

1. Как разделить двузначное число на двузначное?

2. Как выполнить деление вида 87 : 29, 66 : 22?

3. Как проверить правильность результата деления?

Глоссарий по теме:

Деление – это обратное действие умножению

Умножение – это сложение одинаковых слагаемых.

Метод подбора – это способ деления двузначного числа на двузначное, при котором частное подбираем последовательно и проверяем умножением.

Обязательная и дополнительная литература:

1. Моро М. И., Бантова М. А. и др. Математика 3 класс. Учебник для общеобразовательных организаций М.; Просвещение, 2017, C-18.

2. Петерсон Л. Г. Математика 3 класс. Часть 2. – М.: Ювента, 2013– 96 C., С-86.

3. Марченко И.С. Справочник школьника по математике: 1 – 4 классы. – М.: Эксмо, 2014. С. 160, (Светлячок) С. 50.

Теоретический материал для самостоятельного изучения

Рассмотрим решение задачи.

Высота дома тридцать два метра, а высота дерева – шестнадцать метров. Во сколько раз дом выше дерева?

Чтобы узнать во сколько раз дом выше, надо тридцать два разделить на шестнадцать. Получится два, в два раза. Выполнить такое деление можно

используя взаимосвязь умножения и деления. Это поможет научиться делить двузначное число на двузначное методом подбора частного.

Рассмотрим пример 48 : 12

Пробуем в частном два и проверяем. Двенадцать умножить на два получится двадцать четыре – не подходит. Пробуем- три. Двенадцать умножить на три равно тридцать шесть, тоже не подходит. Пробуем четыре. Двенадцать умножаем на четыре, получается сорок восемь, подходит. Значит, сорок восемь разделить на двенадцать получится четыре.

48 : 12

12 ∙ 2 = 24 не подходит

12 ∙ 3 = 36 не подходит

12 ∙ 4 = 48 подходит

Значит,

48 : 12 = 4

В случае деления числа шестьдесят шесть на двадцать два, подбираем число, на которое надо умножить двадцать два, чтобы получилось шестьдесят шесть. Это число три.

66 : 22

22 ∙ 3 = 66

66 : 22 = 3, так как 22 ∙ 3 = 66

Умножение нужно использовать для проверки правильности вычислений.

88 : 11 = 8, так как 11 ∙ 8 = 88

Чтобы делать меньше проб при подборе частного, нужно обратить внимание на последнюю цифру в делимом и делителе. В делимом цифра один , в делителе – цифра семь. В таблице умножения на семь находим число двадцать один (ведь один последняя цифра в делимом). Чтобы получить двадцать один, нужно семь умножить на три. Три – пробное число. Выполняем проверку.

81 : 27 = 3

Делимое 81 – последняя цифра 1

Делитель 27 – последняя цифра 7

7 ∙ 3 = 21 Проверка: 27 ∙ 3 = 81

Частное найдено, верно.

Выполним тренировочные задания

Вставьте пропущенные числа:

54 : 27 = ____ , так как 27 ∙ ___ = 54;

Ответ: 54 : 27 = 2 , так как 27∙ 2 = 54.

Зачеркните пример с ошибкой:

38 : 19 = 2

42 : 14 = 2

64 : 16 = 3

Ошибка в примере 42 : 14 = 2 и 64 : 16 = 3

Расшифруйте, расставляя ответы в порядке возрастания, название одного из самых высоких деревьев в мире:

Я 78 : 26

С 99 : 33

В 78 : 13

Й 64 : 16

К 84: 12

О 70 : 14

Е 88 : 11

Ответ:

11 8 7 6 5 4 3

С Е К В О Й Я

№ п/п

ЭТАПЫ УРОКА

Методы и приемы

Хронометраж

СОДЕРЖАНИЕ УРОКА

ФОРМИРУЕМЫЕ

УУД

ДЕЯТЕЛЬНОСТЬ УЧИТЕЛЯ

ДЕЯТЕЛЬНОСТЬ УЧАЩИХСЯ

1.

Этап самоопределения к деятельности

Словесный метод:

беседа

1-2 мин

– Здравствуйте ребята! Меня зовут Маргарита Валерьевна и сегодня я проведу у вас урок математики. Тихо сели мальчики. Ещё тише сели девочки. 

– Предлагаю сегодняшний урок провести под девизом: «Не говори – не умею, а говори – научусь».

– Ребята, а для чего мы с вами изучаем математику?

–  Откройте свои тетрадки, запишите число и классная работа.

ОТВЕЧАЮТ НА ВОПРОСЫ УЧИТЕЛЯ

– Она нам помогает в жизни, чтобы правильно считать

Р: саморегуляция

2.

Актуализация знаний и мотивация

Словесный метод: речь учителя

Наглядный метод: презентация

Практический метод: работа в тетрадях

4-5 мин

– Сегодня на уроке нас ждёт большая работа. Но вначале мы проведём устный счёт. На доске появляются примеры, ваша задача записывать в тетрадь только ответы, через запятую.

8*2;

9*3;

3*6;

6*6;

10*2;

7*2;

9*9;

(6+36):6;

(8+2)*3

32:(4+4)

– Ребята, сейчас возьмите в руки простой карандаш и поменяйтесь тетрадкой с соседом. На доске записан ряд чисел, который должен был получиться у вас в тетрадках. Над каждым правильно записанным числом ставим плюсик. Посчитайте кол-во плюсиков. У кого 10 плюсиков поставьте 5, у кого 8-9 четвёрку, 6-7 тройку, и у кого менее 6 плюсиков – два. Верните тетрадку своему соседу. Поднимите руку, кто получил 5 и 4. Молодцы.

РАБОТАЮТ САМОСТОЯТЕЛЬНО

16

27

18

36

20

14

81

7

30

4

Р: саморегуляция

П: синтез

К: планирование учебного сотрудничества с учителем и сверст-ми

Р: саморегуляция

П: анализ, подведение под понятие

3.

Постановка учебной задачи

Словесный метод: беседа

Наглядный метод: презентация

Практический метод: работа в тетрадях

4-5 мин

– Посмотрите на примеры, которые я вывела на экран. Запишите их в тетрадку и решите:

56:7        

68:4

40:2        

98:14

– Ребята, какой пример вызвал у вас затруднения? Почему?

– Кто мне назовет компоненты деления?

– Предположите, какова тема нашего урока?

– Совершенно верно, сегодня мы с вами познакомимся с нахождением частного путём подбора.

– Какую цель на урок мы с вами поставим?

РАБОТАЮТ В ТЕТРАДЯХ

8

17

20

7

– У нас вызвал затруднения последний пример, потому что мы не умеем делить двузначное число на двузначное

– Делимое, делитель, частное

– Деление двузначного числа на двузначное; нахождение частного

– Научиться делить двузначные числа способом подбора

Р: саморегуляция

П: синтез

Р: оценка, целеполагание

П: осознание и произвольное построение речевого высказывания, анализ, синтез, подведение под понятие, формулирование проблемы

4.

Открытие детьми нового знания

Словесный метод: работа с учебником, беседа

Практический метод: работа в тетрадях

Наглядный метод: доска

7-8 мин

– Ребята, откройте учебник на стр.18. Кто прочитает, что написано рядом с красной чертой.

– Подумайте и скажите, так как нам 98:14?

– Как называется данный метод?

– Сейчас мы с вами решим пример, в котором у вас возникли затруднения. Давайте попробуем взять в частное 2, 14*2 сколько получится?

– 28<98, значит частное 2 нам не подходит

– Какое число возьмём следующее?

– Давайте его проверим. 14*3

– Берём следующее число. 14*4

– Берём следующее число. 14*5

– Берём следующее число. 14*6

– Берём следующее число. 14*7

– Это что значит?

– Ребята, так как можно разделить двузначное число на двузначное?

– Каким методом мы будем это делать?

ОТВЕЧАЮТ НА ВОПРОСЫ УЧИТЕЛЯ

– Надо найти число, которое при умножении на 14 давало 98

– Метод подбора

– 28

– 3

– Получится 42, не подходит

– Получится 56, не равно 98

– Получится 70, не равно 98

– Получится 84, не равно 98

– Получится 98, равно 98

– Это означает, что число 7 нам подходит

– Надо найти такое число, которое бы при умножении на делитель, давало бы делимое

– Методом подбора

Р: саморегуляция

П: поиск и выделение необходимой информации, подведение под понятие, установление причинно-следственных связей, выдвижение гипотез и их обоснование

К: постановка вопросов, умение с достаточной полнотой и точностью выражать свои мысли

5.

Первичное закрепление

Словесный метод: работа с учебником, беседа

Практический метод: физминутка

4-5 мин

– Сейчас посмотрите в учебнике на №1. Прочитайте задание

– Сейчас мы с вами будем решать, комментируя свой ответ. Начинаем по цепочке с первой парты 2-го ряда

– Молодцы. Сейчас прорешаем №2 первый столбик. Продолжаем на ком остановились.

– Хорошо, кому было не понятно, что мы с вами делали?

– Давайте мы сейчас сделаем физминутку. Все встаем и повторяем за мной:

По дороге Петя шел, 

Он горошину нашел, 

А горошина упала, 

Покатилась и пропала. 

Ох, ох, ох, ох! 

Где-то вырастет горох.

– Молодцы, садимся на места.

– Реши с устным объяснением

– 24:12, пробуем в частном 2 и проверяем 12*2=24, 24=24, значит 24:12=2;

45:15, пробуем в частном 2 и проверяем 15*2=30, 30<45, пробуем 3, 15*3=45, 45=45, значит 45:15=3;

88:44, пробуем в частном 2 и проверяем 44*2=88, 88=88, значит 88:44=2

– 48:24, пробуем в частном 2 и проверяем 24*2=48, 48=48, значит 48:24=2;

32:16, пробуем в частном 2 и проверяем 16*2=32, 32=32, значит 32:16=2;

88:11, пробуем в частном 2 и проверяем 11*2=22, 22<88,…….пробуем в частном 8 и проверяем 11*8=88, 88=88, значит 88:11=8

ВЫПОЛНЯЮТ ФИЗ.УПРАЖНЕНИЯ

Ходьба на месте

Упор присев, встать

Поворот туловища вправо, правую руку в сторону, левую на пояс, и наоборот

Наклоны головы вправо-влево

Руки на голову

Прогибаясь назад, руки развести в стороны

Р: саморегуляция

П: осознание и произвольное построение речевого высказывания, анализ, синтез, подведение под понятие

Р: саморегуляция

6.

Самостоятельная работа с самопроверкой

Практический метод: работа в тетрадях

Словесный метод: работа с учеб.

Наглядный метод: презентация 

4-5 мин

– Сейчас самостоятельно в тетрадях решите №2 (4столбик) и №3 1-ый вариант первое уравнение, 2-ой вариант – второе.

– Кто готов, руку на локоток. Сейчас посмотрите на доску и сравните ответы, у кого все правильно поставьте на полях плюсик, у кого на половину правильно – плюс минус, и у кого совсем все неправильно – минус.

РАБОТАЮТ САМОСТОЯТЕЛЬНО

72:3=24; 92:4=23; 76:2=36.

8*Х=24; Х=24:8; Х=3.

32:Х=8; Х=32:8; Х=4.

Р: саморегуляция

П: подведение под понятие, установление причинно-следственных связей

7.

Включение в систему знаний, повторение

Словесный метод: работа с учебником, беседа

Наглядный метод: доска

Практический метод: работа в тетрадях

7-8 мин

– Ребята, посмотрите сейчас на №4. Кто прочитает задачу?

– Скажите, что нам известно в задаче?

– Что нам необходимо найти?

– Давайте составим кр.запись и запишем её в тетрадку

– Посмотрите на нашу кр.запись и скажите, как мы будем решать задачу?

– Что нам необходимо знать, чтобы ответить на вопрос задачи?

– Каким будет первое действие?

– Зная это, что мы можем узнать? И как?

– Что мы узнали?

– Молодцы, запишите ответ.

– Ребята, откройте дневники и запишите д/з: стр. 18 №2 (2,3 столбик) и № 6. Кто скажет, что вы должны будете сделать?

– Сколько масла получится из 75 л молока, если из 50 л молока получается 2 кг масла.

– Нам известно, что из 50 л молока получается 2 кг масла

– Сколько масла получится из 75 л молока

На 1 кг масла	Масса масла	Масса молока
Один.	2 кг	50 л
?	75 л

– Нам нужно знать, сколько л молока потребуется для 1 кг масла. Из этого мы сможем ответить на вопрос задачи.

– 50:2=25 (л) – молока потребуется для 1 кг масла

– 75:25=3 (кг)

– Мы узнали, сколько кг масла получится из 75 л молока

– Решить примеры и решить задачу

Р: саморегуляция

П: подведение под понятие, установление причинно-следственных связей, осознание и построение речевого высказывания

8.

Рефлексия деятельности  

Словесный метод: беседа

Практический метод: работа с карточками

2-3 мин

– Ребята, что нового вы узнали на уроке? Чему научились?

–    На партах у вас есть карточки, в которой нужно подчеркнуть фразы, которые характеризуют вашу работу на уроке по трем направлениям:

урок	я на уроке	итог
интересно	работал	понял материал
скучно	отдыхал	узнал больше, чем знал
безразлично	помогал другим	Не понял

– Мы научились делить двузначное число на двузначное

Р: саморегуляция, оценка

П: структурирование знаний, осознание и произвольное построение речевого высказывания, синтез

К: умение с достаточной полнотой и точностью выражать свои мысли

УРОК МАТЕМАТИКИ 4 класс по теме: Письменное деление на двузначное число, когда цифру частного находят способом подбора.
план-конспект урока (математика, 4 класс) по теме

Разработка урока для 4 класса ,УМК «Школа России «

Скачать:

Вложение	Размер
mat.ppt	1.03 МБ
urok_matematiki4_klass.docx	24.76 КБ

Предварительный просмотр:

Подписи к слайдам:

Математику, друзья, Не любить никак нельзя. Очень точная наука, Очень строгая наука, Интересная наука – Это математика!

Письменное деление на двузначное число, когда цифру частного находят способом подбора. Тема:

а 640 280 650 в 12 40 50 а : в 32 60

в — 70 см S — 630 см 2 а — ?

V t S 13км/ ч ? 52км 4км/ч 2ч ? ? 3 ч 210км/ч

60 км / ч 70 км / ч 4 ч B A 4 ч 9 0 км ?

Алгоритм деления: 1.Нахожу первое неполное делимое. 2. Определяю количество цифр в частном. 3.Определяю первую цифру частного. 4.Нахожу второе неполное делимое. 5.Определяю вторую цифру частного…..

Алгоритм деления: 1.Нахожу первое неполное делимое. 2. Определяю количество цифр в частном. 3.Определяю первую цифру частного. 4 .Пробую подходит ли пробная цифра частного. 5.Нахожу второе неполное делимое. 6.Определяю вторую цифру частного…..

ПАМЯТКА Нахожу первое неполное делимое. Определяю количество цифр в частном. Определяю первую цифру частного (это пробная цифра). Пробую, подходит ли цифра…

Мы проверили осанку И свели лопатки, Мы походим на носках, А потом на пятках. Пойдём мягко, как лисята, И как мишка косолапый, И как заинька-трусишка, И как серый волк — волчишка. Вот свернулся ёж в клубок, Потому что он продрог. Лучик ёжика коснулся, Ёжик сладко потянулся. ФИЗКУЛЬТМИНУТКА

65км / ч 12км / ч Скорость V Время t Расстояние S 4 часа 4 часа ? км ? км ? км Гепард и зебра побежали одновременно в противоположных направлениях. Какое расстояние будет между ними через 4 часа, если скорость зебры равна 12км/ч, а гепарда – 65км/ч?

ЛОГИЧЕСКАЯ ЗАДАЧА По тропинке вдоль кустов Шло одиннадцать хвостов. Насчитать я также смог, Что шагало тридцать ног. Это вместе шли куда-то Индюки и жеребята. А теперь вопрос таков: Сколько было индюков? Спросим также у ребят: Сколько было жеребят?

Домашнее задание С.48 №232, 235

Определи своё настроение отличное я был(а) уверен(а) в себе мне было трудно я устал(а)

Источник

Математика. 4 класс

Конспект урока

Математика, 4 класс

Урок № 55. Деление на двузначное число

(цифра частного находится способом проб)

Перечень вопросов, рассматриваемых в теме:

— Как делить многозначное число на двузначное?

— Как подобрать цифру частного?

Глоссарий по теме:

Делимое – число, которое подвергается делению.

Делитель – число, на которое делят делимое.

Частное – результат деления одного числа на другое.

Неполное частное – результат деления с остатком, который показывает, какое максимальное число раз делитель содержится в делимом.

Основная и дополнительная литература по теме урока (точные библиографические данные с указанием страниц):

1.Демидова Т. Е., Козлова С. А. Математика. 4 класс. 3 ч. – М.: Баласс, 2008. – С. 32-35.

2. Моро М. И., Бантова М. А. Математика. Учебник для 4 кл. нач. шк. В 2 ч. – М.: Просвещение, 2017.

3. Аргинская И. И., Ивановская Е. И., Кормишина С. Н. Математика. 4 класс. Учебник. Часть1. Самара: Издательский дом «Федоров», 2012. – С. 126

4. Рудницкая В. Н., Юдачёва Т. В. Математика. Учебник для 3 класса нач. шк. Часть 2. – М.: Вентана-Граф, 2015. – С. 131

Теоретический материал для самостоятельного изучения

Подберем значение частного 273 : 39.

Рассмотрим несколько способов подбора частного ваших сверстников.

Соня сначала попробовала число 5, так как оно среднее среди однозначных чисел.

Источник

«Деление на двузначное число методом подбора» 4 класс

Онлайн-конференция

«Современная профориентация педагогов
и родителей, перспективы рынка труда
и особенности личности подростка»

Свидетельство и скидка на обучение каждому участнику

Описание презентации по отдельным слайдам:

Описание слайда:

Деление на двузначное число
4 б класс «Школа России»
Учитель Быстрова Т.В.

Описание слайда:

Представьте, что вы отправляетесь в магазин покупать шарики на День рождения, у вас есть 56 руб. Один шарик стоит 14 руб. Сколько шариков вы можете купить?

Описание слайда:

56:14=4 (шар.)
Ответ: 4 шарика

Описание слайда:

Представьте у вас в кармане не 56 руб, а 126 руб.
Сколько шариков вы купите?

Описание слайда:

Описание слайда:

ЦЕЛЬ УРОКА:
ОЗНАКОМИТЬСЯ С ПИСЬМЕННЫМ ДЕЛЕНИЕМ НА ДВУЗНАЧНОЕ ЧИСЛО МЕТОДОМ ПОДБОРА

Описание слайда:

Тема урока :
Деление на двузначное число

Описание слайда:

Алгоритм деления на двузначное
1. Нахожу пробную цифру.
2. Проверяю умножением.
3. Если она подходит, запишу эту цифру в частном.

Описание слайда:

Работа по учебнику
стр. 57 № 206

Описание слайда:

Работа по карточке. Задание на выбор.
Реши пример:
378 : 42 + 544 : 68

Реши уравнение:
224 : Х = 448 : 8

Реши задачу:
Из 224 литров молока получают 56 кг творога. Сколько литров нужно взять, чтобы получить тем же способом 250 кг творога?

Описание слайда:

Итоги:
— Какую цель мы поставили в начале урока?
-Нам удалось достичь результатов?
-Что нового для себя вы узнали на уроке?
— Как вы оцениваете свою работу на уроке?
-Что на уроке у вас хорошо получалось?
-Над чем ещё надо поработать?
-Где можно применить новые знания?
— Какую цель мы поставим на следующий урок?

Описание слайда:

Описание слайда:

Спасибо за урок

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 931 человек из 81 региона

Курс повышения квалификации

Скоростное чтение

• Сейчас обучается 881 человек из 79 регионов

Курс повышения квалификации

Актуальные вопросы теории и методики преподавания в начальной школе в соответствии с ФГОС НОО

• Курс добавлен 23.09.2021
• Сейчас обучается 283 человека из 62 регионов

Ищем педагогов в команду «Инфоурок»

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

также Вы можете выбрать тип материала:

Общая информация

Похожие материалы

Проверка знаний русский язык 2 класс словарные слова

Проверка знаний математика 4 класс

Проверка знаний русский язык 2 класс словарные слова

Презентация «Главные сражения Великой Отечественной войны»

Технологическая карта внеурочного занятия по литературе

Буклет «Сборник детских сказок»

Викторина «В мире спорта»

Динамические паузы для начальной школы

Не нашли то что искали?

Воспользуйтесь поиском по нашей базе из
5388889 материалов.

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

ЕГЭ в 2022 году пройдет в доковидном формате

Время чтения: 1 минута

Более 50 российских школ перешли на дистанционку из-за коронавируса

Время чтения: 1 минута

В Оренбурге школьников переведут на дистанционное обучение с 9 декабря

Время чтения: 1 минута

Путин поручил не считать выплаты за классное руководство в средней зарплате

Время чтения: 1 минута

В России утвердили новый порядок формирования федерального перечня учебников

Время чтения: 1 минута

Учителям предлагают 1,5 миллиона рублей за переезд в Златоуст

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Источник

Как найти частное подбором 4 класс

Ответ

Проверено экспертом

900:300=3
300*1=300 -нет
300*2=600 — нет
300*3=900 — да

420:105=4
105*1=105 — нет
105*2=210 — нет
105*3=315 — нет
105*4=420 — да

630:105=6
105*1=105 — нет
105*2=210 — нет
105*3=315 — нет
105*4=420 — нет
105*5=525 — нет
105*6=630 — да

812:116=7
116*1=116 — нет
116*2=232 — нет
116*3=348 — нет
116*4=464 — нет
116*5=580 — нет
116*6=696 — нет
116*7=812 — да

Ответ или решение 1

Исходя из условия нашей задачи нам необходимо выполнить несколько шагов по достижению результата нашей задачи среди которых нам необходимо найти значения выражение в данном примере. Для этого нам необходимо будет выполнить математические действия и записать наш окончательный ответ в задаче.

Математическая запись данного выражения будет представлена следующим образом в данной задаче.

Таким образом, мы нашли результат данной задачи, который будет равняться числу 3, это будет наш ответ.

Янв 18

3 класс. Рабочая тетрадь №2. Ответы к стр. 29

Числа от 1 до 100 (продолжение)
Внетабличное умножение и деление

72. Найди частное подбором.

64 : 16 = 4 42 : 14 = 3 90 : 18 = 5
96 : 24 = 4 63 : 21 = 3 84 : 12 = 7

73.

27 : 3 : 3 = 3 27 • 3 + 3 = 84
27 • 3 — 3 = 78 (27 + 3) • 3 = 90

Выполняя задания, восстанови, где это нужно, пропущенные скобки.

74. Реши задачи, составляя выражения.

1) В одном гараже 48 машин, в другом — 24, а на стоянке в 6 раз меньше машин, чем в этих двух гаражах. Сколько машин на стоянке?

(48 + 24) : 6 = 12 (м.)
О т в е т: 12 машин.

2) Витя посчитал, что в новом доме свет горел в 26 окнах, а тёмных окон было в нём в 2 раза больше. Сколько всего окон насчитал Витя в этом доме?

26 + 26 • 2 = 78 (ок.)
О т в е т: 78 окон.

75. В витрине магазина было 18 сумок и 3 чемодана. Во сколько раз больше было сумок, чем чемоданов, в этой витрине?

18 : 3 = 6 (р.)
О т в е т: в 6 раз.

Источник

Урок математики. Алгоритм нахождения однозначного частного

автор: Турчанинова Ирина Теодозиевна

Учитель начальных классов СОШ №5 г. Югорск ХМАО

Урок математики. Алгоритм нахождения однозначного частного

Урок математики «Алгоритм нахождения однозначного частного»

Цель: Сформировать умение делить трёхзначное число на двузначное путём подбора однозначного частного.

-совершенствовать вычислительные навыки;

-развивать внимание, память, математическую речь;

-воспитывать стремление вести ЗОЖ.

Поздоровайтесь с гостями. Желаю вам на уроке хорошего настроения и отличной работы. Пусть лучик солнышка заглянет сегодня в класс, придаст вам силу и уверенности в знаниях. Перед вами лежит оценочный лист, который вы будете заполнять на уроке, после каждого этапа урока. На доске дерево наших решений. Оно волшебное, на нём могут созреть плоды, а может не вырасти ничего. Всё зависит от вашего стремления хорошо работать на уроке.

1. Начинаем урок как обычно с устного счёта.

а) У речки гуляли 4 утёнка и 24 весёлых гусёнка. Во сколько раз больше было гусят? (24:4=6 раз).

Ты-капитан космического корабля, который отправляется на орбиту со скоростью 28260 км/ч. Сколько лет капитану?

б) Возьмите карточки, которые лежат у вас на партах, положите перед собой. Внимательно посмотрите, какая задача стоит перед вами? (повторить таблицу умножения и деления).

В тетрадь записывайте только ответы в строчку, через запятую, математические выражения переписывать не надо.

9х6=54, 42:7=6, 56:8=7, 32:4=8, 9х3=27, 7х4=28, 16:4=4, 8х5=40, 72:8=9, 7х9=63, 24:3=8, 7:7=1, 8х6=48, 9х4=36, 6:1=6.

(ученики читают по цепочке ответы).

Самопроверка. Давайте согласуем критерии оценивания:

0 ошибок = 5, 1-2 ошибки = 4, 3 и более = 3.

Возьмите оценочный лист, найдите 1 этап, оцените свою работу.

Переворачиваю карточку на доске «Здоровое питание».

Какое питание считается здоровым? (разнообразное, витамины, регулярно, без спешки).

Для чего мы с вами повторяли таблицу умножения и деления? (поможет нам в вычислении).

Посмотрите на примеры на доске. Найдите лишний. 49:7, 8х100, 35х10, 45х2, 144:24 . Почему? (Не можем решить). А кто умеет? Как вы думаете, как называется тема нашего урока? (Деление на двузначное число). Точнее: Нахождение однозначного частного. А какую задачу поставите перед собой? Научиться делить на двузначное число и находить частное.

А как называются компоненты действия деления?

Кто объяснит как разделить 144 на 24?

1. Определим количество цифр в частном 144:24 будет 1 цифра.
2. Начнём проверку цифр с 5 24х5=120(мало)
3. Перебираем цифры через 1, берём 7 24х7=168 (много)

Пробуем 6 24х6=144, значит 144:24=6, нашли частное, оно равно 6.

Кто понял, как находить однозначное частное, поднимите руки. Каким способом мы будем его находить? (подбором).

3.Чтобы все ребята научились, поработаем в группах.

Ваша задача? (Помочь товарищу, научиться у него.)

На партах лежат листы с заданием.

234:26=9; 512:64=8; 108:18=6.

Послушайте план работы:

1. Выяснить, кто в группе не понял, как находить однозначное частное, объяснить ему ещё раз на данном примере.
2. Составить алгоритм нахождения однозначного частного.

Алгоритм. ( на доску вывешиваю).

1. Определить количество цифр в частном.
2. Находить частное способом подбора, начиная с 5.
3. Перебирать цифры через 1.
4. Подходящее число и есть искомое частное.

Поднимите руки, кому помогла работа в группе. Чему вы учились, работая в группе? (делить на двузначное число, слушать товарища, согласовывать свою работу). Оценочный лист заполняем.

Спасибо за работу. Переворачиваю листок «Движение это жизнь».

Почему нужно больше двигаться? (для здоровья).

Что это значит? (бегать, играть в подвижные игры, заниматься физкультурой).

1. Предлагаю отдохнуть, выполнить физминутку.

– утром рано умывались (вращаем головой)

– полотенцем растирались (ножницы)

-ногами потопали, руками похлопали, вправо-влево наклонялись и друг другу улыбались. Вот здоровья в чём секрет. Всем друзьям физкультпривет.

1. Итак, чему же мы учились сегодня на уроке? (находить однозначное частное, решать примеры на деление), каким способом? (подбором).
2. Предлагаю применить свои знания для выполнения самостоятельной работы.

Взаимопроверка. Обменяйтесь тетрадями.

Проверяем работу товарища. Слайд с ответами перед вами.

Оцените работу. Согласуем критерии оценивания.

Верните тетради, зафиксируйте свои баллы в оценочном листе.

Переворачиваю лист «Хорошее настроение».

Почему? (быстрее справлялись с трудностями). Что может повлиять на наше настроение? (стыд, обида, плохое самочувствие).

Можно ли исправить настроение? Чем? (улыбка, хорошие мысли, уверен в себе).

Проведём итог вашей работы на уроке.

Сосчитайте свои баллы, суммируйте их и запишите в последнюю строку оценочного листа, поставьте оценку.

Кто оценил свою работу на 5?, на 4?, на 3?.

Хорошо. Вы отлично справились с работой на уроке. А чему учились? (находить однозначное частное). Каким способом? (подбором). Какой алгоритм составили? (проговорили).

А что же такое ЗОЖ? Зачем его вести? (Он укрепляет здоровье, воспитывает характер человека).

Источник

В этой статье мы рассмотрим правила и алгоритмы деления натуральных чисел. Сразу отметим, что здесь мы смотрим только на деление нацело, то есть без остатка. О делении натуральных чисел с остатком читайте в нашем отдельном материале.

Перед тем, как формулировать правило деления натуральных чисел, нужно понять связь деления с умножением. После того, как мы установим эту связь, последовательно рассмотрим самые простые случаи: деление натурального числа на себя и на единицу. Далее разберем деление с помощью таблицы умножения, деление методом последовательного вычитания, деление на числа, кратные числу 10, различные степени числа 10.

Для каждого случая приведем и подробно рассмотрим примеры. В конце статьи покажем, как проводить проверку результата деления.

Связь деления с умножением

Чтобы проследить связь между делением и умножением, вспомним, что деление представляется, как разбиение исходного делимого множества на несколько одинаковых множеств. Умножение связано с объединением нескольких одинаковых множеств в одно. 

Деление – действие, обратное умножению. Что это значит? Приведем аналогию. Представим, что у нас есть b множеств, в каждом из которых – по с предметов. Общее количество предметов во всех множествах равно a. Умножение – это объединение всех множеств в одно. Математически оно запишется так:

b·c=a.

Обратный процесс разбиения полученного общего множества на b множеств по с предметов в каждом соответствует делению:

a÷b=c.

На основе сказанного можно перейти к следующему утверждению:

Если произведение натуральных чисел c и b равно a, то частное чисел a и b равно c. Перепишем в буквенном виде. 

Если b·c=a, то a÷b=c

Пользуясь переместительным свойством умножения, можно записать:

c·b=a

Отсюда также следует, что a÷с=b. 

На основании сказанного можно сформулировать общий вывод. Если произведение чисел c и b равно a, то соответственно частные a÷b и a÷c равны c и b.

Подытожим все изложенное выше и дадим определение деления натуральных чисел.

Деление – нахождение неизвестного множителя по известному произведению и другому известному множителю.

Это определение станет базой, на основе которой мы будем строить правила и методы деления натуральных чисел.

Деление методом последовательного вычитания

Только что мы говорили о делении в контексте умножения. На основе этого знания можно проводить операцию деления. Однако, существует еще один, достаточно простой и достойный внимания подход – деление методом последовательного вычитания. Этот способ понятен интуитивно, поэтому рассмотрим его на примере, не приводя теоретических выкладок.

Работая с числами, не нужно каждый раз проводить аналогию с предметами. Что мы делали с делимым и делителем? Последовательно вычитали делитель из делимого, пока не получили нуль в остатке.

При делении методом последовательного вычитания количество операций вычитания до получения нулевого остатка и есть частное от деления.

Для закрепления рассмотрим еще один, более сложный пример.

Отметим, что данный метод удобен только в случаях, когда необходимое количество последовательных вычитаний невелико. В остальных случаях целесообразно применять правила деления, которые мы рассмотрим ниже.

Деление равных натуральных чисел

Согласно свойствам натуральных чисел, сформулируем правило, как делить равные натуральные числа.

Например:

1÷1=1; 141÷141=1; 2589÷2589=1; 100000000÷100000000=1.

Деление на единицу

Основываясь на свойствах натуральных чисел, можно также сформулировать правило деление натурального числа на единицу.

Например: 

1÷1=1; 141÷1=141; 2589÷1=2589; 100000000÷1=100000000.

Деление с помощью таблицы умножения

Таблица умножения – удобный инструмент, который позволяет найти произведения однозначных натуральных чисел. Однако, ее можно использовать и для деления.

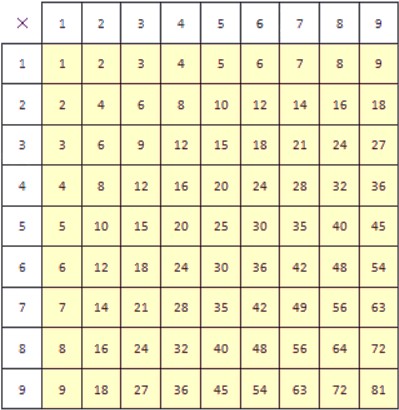
Таблица умножения позволяет находить не только результат произведения множителей, но и множитель по известному произведению и другому множителю. Как мы выяснили ранее, деление – это как раз и есть нахождение неизвестного множителя по известному произведению и еще одному множителю. 

С помощью таблицы умножения можно проводить деление любого числа на желтом фоне на любое однозначное натуральное число. Покажем, как это делать. Есть два способа, применение которых мы будем рассматривать на примерах.

Разделим 48 на 6.

Способ первый.

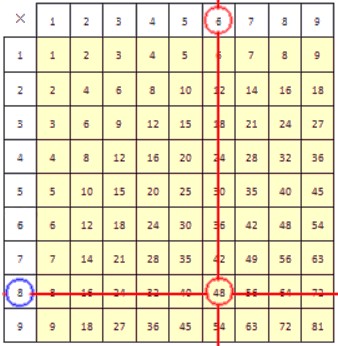
В столбце, верхняя ячейка которого содержит делитель 6, находим делимое 48. Результат деления при этом находится в крайней левой ячейке строки, содержащей делимое. Он обведен синей окружностью.

Способ второй. 

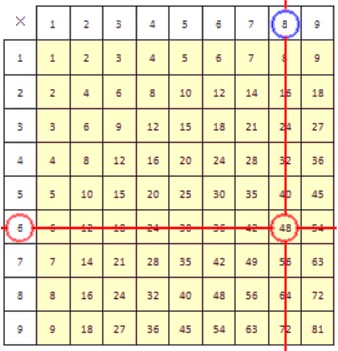
Сначала в строке с делителем 6 находим делимое 48. Результат деления при этом находится в крайней верхней ячейке столбца, содержащем делимое. Он обведен синей окружностью.

Итак, мы разделили 48 на 6 и получили 8. Результат был найден по таблице умножения двумя способами. Оба способа абсолютно идентичны.

Для закрепления рассмотрим еще один пример. Разделим 7 на 1. Приведем рисунки, иллюстрирующие процесс деления.

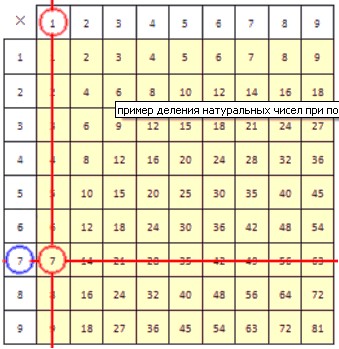
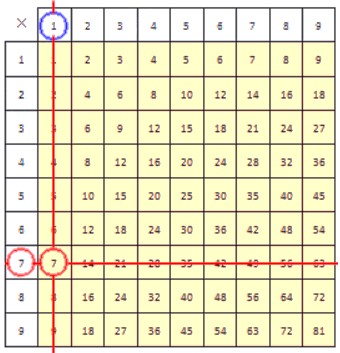
В результате деления числа 7  на  1, как вы уже догадались, получается число 7. В делении с помощью таблицы умножения очень важно знать эту таблицу наизусть, так как не всегда можно иметь ее под рукой.

Настоятельно рекомендуем выучить таблицу умножения!

Деление на 10, 100, 1000 и т.д.

Сразу сформулируем правило деления на натуральных чисел на 10, 100, 1000 и т.д. Сразу будем считать, что деление без остатка возможно.

Например, 30÷10=3. От числа 30 мы отбросили один нуль.

Частное 120000÷1000 равно 120 – от числа 120000 отбрасываем справа три нуля, именно столько их содержится в делителе.

Обоснование правила строится на правиле умножения натурального числа на 10, 100, 1000 и т.д. Приведем пример. Пусть нужно разделить 10200 на 100.

10200=102·100

10200÷100=102·100100=102.

Представление делимого в виде произведения

При делении натуральных чисел не стоит забывать о свойстве деления произведения двух чисел на натуральное число. Иногда делимое можно представить в виде произведения, один из множителей в котором делится на делитель. 

Рассмотрим типичные случаи.

Приведем еще несколько аналогичных примеров.

В более сложных примерах удобно пользоваться таблицей умножения. Проиллюстрируем это.

Для закрепления данного материала рассмотрим еще один пример, уже без подробных словесных пояснений.

Деление натуральных чисел, оканчивающихся на нуль

При делении чисел, записи которых оканчиваются цифрой 0, полезно помнить свойство деления натурального числа на произведение двух чисел. При этом, делитель представляется в виде произведения двух множителей, после чего указанное свойство находит применение в совокупности с таблицей умножения.

Как всегда, поясним это на примерах.

Для закрепления разберем еще один, более сложный пример.

Подведем итог по изложенному в данном пункте.

Метод подбора частного

Прежде чем рассматривать этот способ деления, введем некоторые условия.

Пусть числа a и b делятся друг на друга, причем произведение b·10 дает число, большее, чем a. В таком случае частное a÷b является однозначным натуральным числом. Иными словами, это число от 1 до 9. Это типичная ситуация, когда метод подбора частного удобен и применим. Последовательно умножая делитель на 1, 2, 3, .. , 9 и сравнивая результат с делимым, можно найти частное.

Рассмотрим пример.

Отметим, что в случаях, когда b·10>a частное также удобно находить методом последовательного вычитания.

Представление делимого в виде суммы

Еще один способ, который может помочь найти частное – это представить делимое в виде суммы нескольких натуральных чисел, каждое из которых легко делится на делитель. После этого нам пригодится свойство деления суммы натуральных чисел на число. Вместе с примером рассмотрим алгоритм и ответим на вопрос: в виде каких слагаемых представлять делимое?

Пусть делимое равно 8551, а делитель равен 17.

1. Вычислим, на сколько в записи делимого больше знаков, чем в записи делителя. В нашем случае делитель содержит два знака, а делимое – четыре. Значит в записи делимого на два знака больше. Запоминаем число 2.
2. Справа в делителе дописываем два нуля. Почему два? В предыдущем пункте мы как раз и определили это число. Однако, если записанное в результате число окажется больше делителя, из числа, полученного в предыдущем пункте, нужно вычесть 1. В нашем примере, дописав нули к делителю, мы получили число 1700<8551. Таким образом, отнимать единицу из двойки, полученной в первом пункте, не нужно. В памяти так же оставляем число 2.
3. К числу 1 справа приписываем нули в количестве, определенном числом из предыдущего пункта. Тем самым мы получаем рабочую единицу разряда, с которым будем оперировать далее. В нашем случае, к единице приписываются два нуля. Рабочий разряд – сотни. 
4. Проводим последовательное умножения делителя на 1, 2, 3 и т.д. единицы рабочего разряда до того момента, пока не получим число, большее, чем делимое. 17·100=1700; 17·200=3400; 17·300=5100; 17·400=6400; 17·500=8500; 17·600=10200Нас интересует предпоследний результат, так как следующий после него результат произведения больше делимого. Число 8500, которое получено на предпоследнем шаге при умножении, и является первым слагаемым. Запоминаем равенство, которое мы будем использовать далее: 8500=17·500.
5. Вычисляем разность между делимым и найденным слагаемым. Если она не равна нулю, возвращаемся к первому пункту и начинаем поиск второго слагаемого, используя вместо делимого уже полученную разность. Повторяем пункты до тех пор, пока в результате не получим нуль. В нашем примере разность равна 8551-8500=51. 51≠0, поэтому, переходим к пункту 1.

Повторяем алгоритм:

1. Сравниваем количество знаков в новом делимом 51 и делителе 17. В обоих записях по две цифры, разность количества знаков равно нулю. Запоминаем число 0.
2. Так как мы запомнили число 0, в записи делителя не нужно дописывать дополнительных нулей.
3. К единице также не будем добавлять нулей. Опять же, потому что в первом пункте мы запоминали число 0. Таким образом, нашим рабочим разрядом являются единицы
4. Последовательно умножаем 17 на 1, 2, 3,.. и т.д. Получаем: 17·1=17; 17·2=34; 17·3=51.
5. Очевидно, на третьем шаге мы получили число, равное делителю. Это и есть второе слагаемое. Так как 51-51=0, на этом этапе останавливаем поиск слагаемых – он завершен.

Теперь осталось найти частное. Делимое 8551 мы представили в виде суммы 8500+51. Запишем:

8500+51÷17=8500÷17+51÷17.

Результаты делений в скобках известны нам из проведенных ранее действий.

8500+51÷17=8500÷17+51÷17=500+3=503.

Результат деления: 8551÷17=503.

Рассмотрим еще несколько примеров, уже не комментируя каждое действие столь детально.

Постепенно увеличиваем сложность примеров.

Казалось бы, мы рассмотрели практически все возможные способы деления натуральных чисел. На этом, тему можно считать закрытой. Однако, есть способ, который в ряде случаев позволяет провести деление быстрее и рациональнее.

Рассмотрим его напоследок.

Представление делимого в виде разности натуральных чисел

Иногда делимое проще и удобнее представлять в виде разности, а не суммы. Это может значительно ускорить и облегчить процесс деления. Как именно? Покажем на примере.

Решим еще один пример тем же методом. Отметим, что важно уметь правильно заметить, какую манипуляцию сделать с числами, чтобы провести деление легко. Скажем даже, что в этом присутствует некоторый элемент искусства.

Проверка результата деления

Проверка никогда не бывает лишней, особенно, если мы делили большие числа. Как проверять, правильно ли выполнено деление натуральных чисел? При помощи умножения!

Смысл этого действия очень прост. Например, у нас было a предметов, и эти a предметов мы разложили на b кучек. В каждой кучке оказалось по с предметов. Математически это выглядит так:

a÷b=c.

Теперь объединим обратно все b кучек по с предметов. В результате должно получится та же совокупность предметов a.

b·c=a.

Рассмотрим проведение проверки на двух примерах.

Проверка результата деления чисел делением

Рассмотренный выше способ проверки основан на умножении. Существует также проверка делением. Как ее проводить?

Правило основано на той же связи между делимым, делителем и частным, что и правило из предыдущего пункта.

Рассмотрим примеры.