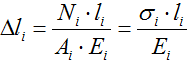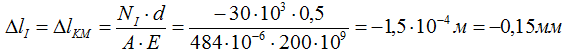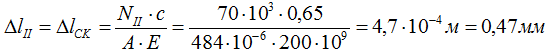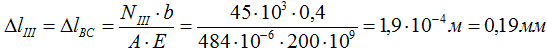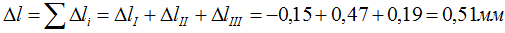Пример решения задачи на расчет деформаций участков и изменение общей длины стального стержня при его растяжении-сжатии.
Задача
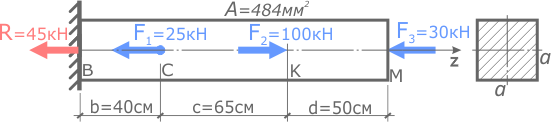
Рассчитать деформации участков и общее изменение длины прямого стержня постоянного сечения.
Другие примеры решений >
Помощь с решением задач >
Модуль продольной упругости стали E=200ГПа.
Пример решения
Предыдущие пункты решения задачи
- Определение опорных реакций,
- Построение эпюр внутренних продольных сил,
- Подбор размеров поперечного сечения стержня,
- Построение эпюр нормальных напряжений.
Стержень имеет три силовых участка, на которых площадь сечения одинакова, но внутренние силы и нормальные напряжения отличаются, поэтому определим абсолютные деформации всех участков в отдельности, после чего сложив их, получим изменение длины всего стержня в целом.
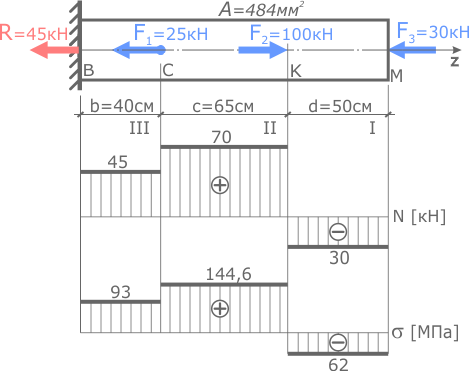
Изменение длины участков стержня при растяжении-сжатии рассчитывается по формуле:
где N – величина внутренней продольной силы,
l – длина рассматриваемого участка,
A – площадь его поперечного сечения,
E – модуль Юнга (продольной упругости) для материала стержня,
σ — значение нормальных напряжений на рассматриваемом участке.
Значения внутренних сил и напряжений принимаются с построенных эпюр N (σ).
По эпюрам видно, что первый участок сжимается, а участки II и III растягиваются, следовательно, деформации Δl второго и третьего участков будут положительны (их длина увеличивается), а первого отрицательны (продольный размер уменьшается).
Рассчитаем их:
Деформация I участка (KM)
II участок (CK)
Удлинение третьего участка BC
Сложив (с учетом их знака) деформации всех участков получим величину изменения длины всего стержня в целом:
В результате деформации общая длина стержня увеличится на 0,51мм.
Расчет и построение эпюры перемещения сечений >
Другие примеры решения задач >
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее
Добавил:
Uman
Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Предмет:
Файл:
Скачиваний:
577
Добавлен:
04.03.2014
Размер:
1.33 Mб
Скачать
С учетом того что ε =N/EF, вторая формула (3.13) принимает вид:
|
∆ l = |
N l |
, |
(3.14) |
|
|
E F |
||||
где EF – жёсткость при растяжении-сжатии (этот параметр зависит от свойств материала (Е) стержня и площади его поперечного сечения).
Формула (3.14) может быть получена непосредственно из закона Гука (3.5) с учетом формул (3.9) и (2.1). Поэтому выражение (3.14) определяют как закон Гука для участка бруса при постоянной деформации на участке.
Если на участке бруса действует распределенная нагрузка постоянной интенсивности q (рис. 3.5,б), то нормальная сила в произвольном сечении при известном значении в начальном сечении (Nн ) рав-
|
на: |
||||||
|
N = Nн – qz . |
(3.15) |
|||||
|
При z = l |
Nк = Nн |
– q l. |
||||
|
Подставляя выражение (3.15) в формулу (3.10), после интегриро- |
||||||
|
вания при wo = wн получаем: |
||||||
|
w = wн + |
N н z |
− |
qz2 |
. |
(3.16) |
|
|
EF |
2EF |
|||||
|
Следовательно, эпюра w (см. рис. 3.5,б) ограничена параболой |
||||||
|
выпуклостью вверх (d2w/dz2< 0). Если на участке эпюра N |
пересекает |
ось, то в этом сечении функция w имеет экстремум (dw/dz = 0). Этот случай на рис. 3.5,б показан штриховыми линиями. При z = l перемещение концевого сечения участка равно:
|
wк = wн + |
N |
н |
l |
− |
q l2 |
. |
|
|
EF |
2EF |
||||||
Изменение длины стержня может вызываться различными причинами: силовым воздействием, изменением температуры, отклонением от номинальной длины стержня.
Если на стержень действуют заданные нагрузки, то изменение длины любого его участка с постоянной деформацией (рис. 3.6,а) определяется по формуле (3.14).
40

Рис 3.6
При изменении температуры стержня на ∆ T° (температурное воздействие) любой его участок изменяет длину (рис. 3.6,б) на величину
|
∆ lT = α T ∆ T l , |
(3.17) |
где α T – температурный коэффициент линейного расширения мате-
риала. (Например, для стали α T =1,25 10-5 1/град.) Соответственно возникают температурные деформации:
|
ε ò = |
∆ lT |
= |
α T ∆ T . |
(3.18) |
|
l |
Если силовое и температурное воздействия осуществляются одновременно, то изменение длины и деформация определяются с использованием принципа суперпозиции:
|
∆ l = |
N l |
+ |
α T ∆ T l ; |
ε |
= |
σ + |
αα Τ ∆ Τ . |
(3.19) |
|
|
EF |
|||||||||
|
E |
Использование принципа суперпозиции, при котором силовая и температурная деформации рассматриваются как независимые, справедливо в том случае, когда модуль упругости Е и температурный коэффициент α T не зависят от температуры. Практически это имеет место при умеренном температурном воздействии. Например, для малоуглеродистой стали при Т < 300° C (cм. рис. 2.10).
Кроме того, изменение длины стержня или его участка может быть связано и с тем, что он изготовлен длиннее или короче своей номинальной длины на величину ∆ o= l – lo (рис. 3.6,в). Отклонение от номинального размера положительно (∆ o> 0), если стержень длиннее,
иотрицательно (∆ o< 0), если – короче.
Сучетом всех перечисленных факторов изменение длины участка стержня определяется выражением
|
∆ l = |
N l |
+ |
α Τ ∆Τ∆Τ l+ |
∆ 0 . |
(3.20) |
|
|
EF |
||||||
Полное изменение длины стержня равно сумме изменений длин его участков.
41
3.5. Расчет стержня на прочность
Прочностной анализ стержня заключается в определении напряжений для стержня в целом, выявлении максимальных напряжений и сопоставлении их с допускаемыми или предельными напряжениями.
Сечение стержня, в котором возникают максимальные напряжения, называется опасным. Если максимальные напряжения действуют на всем участке стержня, то такой участок также называется опасным. При расчете на прочность стержня из пластичного материала ис-
пользуется условие прочности:
|
σ max ≤ [σ ]; [σ ] = σ т / nт или [σ ] = σ 0,2 / nт . |
(3.21) |
Максимальные напряжения σ max = (N/F)max в опасном сечении могут быть как растягивающими (положительными), так и сжимающими (отрицательными). В последнем случае величина напряжения берется по модулю. Допускаемые напряжения [σ ] либо заданы, либо вычисляются по второй формуле (3.21) при известном пределе текучести σ т (или σ 0,2) и коэффициенте запаса nт.
При расчете на прочность стержня из хрупкого материала используется система условий прочности:
|
σ |
р,max ≤ |
[σ ]р; |
[σ ]р = σ вр / nв, |
|
|
σ |
с,max ≤ |
[σ ]с; |
[σ ]с = σ вс / nв. |
(3.22) |
Расчет ведется как для опасного сечения, в котором возникают максимальные растягивающие напряжения σ р,max, так и для опасного сечения с максимальными сжимающими напряжениями σ с,max.
Условия прочности (3.21), (3.22) подробно рассмотрены в разде-
ле 2.5.
При известных допускаемых напряжениях для материала стержня могут проводиться три варианта расчетов.
1. Если заданы нагрузки и размеры сечений стержня, то проводится поверочный расчет.
2.Если заданы нагрузки, то могут быть определены размеры сечений стержня (проектировочный расчет).
3.Если заданы размеры сечений, то могут быть определены допускаемые нагрузки.
Эти варианты расчета на конкретном примере рассмотрены в следующем разделе.
42

3.6. Расчёт статически определимого стержня
Для статически определимого стержня (рис. 3.7) реакция в за-
делке (или нормальная сила в любом сечении) может быть определена с использованием уравнений статики. Если реакция в заделке предварительно не определена, то построение эпюры N рациональнее начинать со свободного конца стержня. При этом, используя метод сечений, необходимо отбрасывать часть стержня с заделкой. Последовательно применяя метод сечений на каждом участке (i =1, 2, 3, 4), определяются нормальные силы на участках. По полученным значениям строится эпюра N. Скачки на эпюре N по величине равны силам, приложенным в соответствующих сечениях. Участок АВ не деформируется, участки ВС и DM растягиваются, а участок СD сжимается.
Рис. 3.7
Для построения эпюры σ определяются нормальные напряжения на каждом участке по формуле (3.9)
|
σ ( i) = |
Ni |
; |
i = 1, 2, 3, 4 |
(3.23) |
|
Fi |
с учётом того, что F1=F2=F3=F и F4=2F.
Если стержень изготовлен из пластичного материала, то участки 3 и 4 равноопасны. Если стержень изготовлен из хрупкого материала, то более опасным может оказаться участок 4 (как правило, хрупкий материал хуже работает на растяжение).
Линейные деформации на участках определяются из закона Гука
|
(3.5): |
σ ( i) |
|||
|
ε (i) = |
; |
i = 1, 2, 3, 4. |
(3.24) |
|
|
E( i) |
43
Если стержень выполнен из одного материала (E(i) = E), то эпюра ε имеет такой же вид, как и эпюра σ .
Эпюра осевых перемещений w строится, начиная с сечения, где известно перемещение. Для рассматриваемого стержня – от сечения
М, так как wМ= 0.
В соответствии с формулами (3.13), (3.14) и учитывая, что wн = wМ= 0, а wк = wD, получим перемещение сечения D:
|
w |
= ∆ l = |
4Pl |
= |
2Pl |
. |
|
|
D |
||||||
|
4 |
E 2F |
EF |
||||
Если на i-ом участке стержня определена деформация ε (i) = const, то проще вычислять ∆ li по второй формуле (3.13):
Аналогично определяем перемещения других сечений по участ-
кам:
|
wC = wD +∆ l3 |
= 2 |
P l |
+ (−− 2 |
P |
) 1,5l== −− |
Pl |
; |
||||||
|
EF |
EF |
EF |
|||||||||||
|
wB = wC + ∆ l2 |
= − |
P l |
+ ( |
P |
) 1,5l= |
0,5 |
P l |
; wA = wB. |
|||||
|
EF |
EF |
EF |
Участок АВ перемещается как жесткое тело, не деформируясь. Поэтому перемещения всех сечений на этом участке одинаковы. Сечение А перемещается вверх. Направления перемещения просто определить по участку 4. Так как этот участок растягивается (N4 > 0), то при wD > 0 сечение D перемещается вверх. Отсюда следует, что сечения, у которых w > 0, перемещаются вверх, и наоборот.
Полное изменение длины стержня (удлинение или укорочение), а значит и перемещение его концевого сечения относительно начального сечения, может быть определено суммированием изменений длин участков:
|
∆ l = ∑m |
∆∆ l |
i |
, |
(3.26) |
|
i = |
1 |
|||
|
где m – число участков. |
В данном случае ∆ l = wA = ∆ l1 +∆ l2 + ∆ l3 + ∆ l4.
Из построенной эпюры w видно, что наибольшее перемещение
имеет сечение D (wmax = wD).
Отметим, что в соответствии с формулой (3.4) значение деформации ε является производной от функции перемещений w. Двигаясь в положительном направлении оси z (вверх) от сечения М (см. рис.3.7), значения на эпюре ε определяют возрастание или убывание
44

функции перемещений w. И наоборот, перемещения являются интегральной функцией от деформаций ε формула (3.11). Например, перемещение произвольного сечения w(z) на участке 4 равно площади прямоугольника длиной z на эпюре ε (w(z) = ε 4 z).
Рассмотрим различные варианты расчета стержня на прочность.
Вариант 1. Проверить прочность стержня при заданных параметрах:
F = 2 см2, Р=10 кН, σ T = 320 МПа, nТ = 2.
Определяем максимальные напряжения σ max (см. эпюру σ на рис. 3.7) и допускаемые напряжения (3.21):
|
3 |
||||||
|
σ max= σ |
(2) |
=σ (3)=2 |
P |
, σ max=2 |
10 10 |
=108 Па = 100 МПа; |
|
F |
− 4 |
|||||
|
2 10 |
[σ ]= 320 = 160 МПа. 2
Сравнивая максимальные напряжения с допускаемыми, делаем заключение, что условие прочности (3.21) для стержня удовлетворяется. Вариант 2. Определить параметр F при следующих исходных дан-
ных:
Р = 20 кН; [σ
Учитывая что σ
2FP ≤ [σ ] .
] = 160 MПа.
mах = 2P/F, условие прочности (3.21) примет вид:
Решая это неравенство относительно параметра F, находим:
|
F ≥ |
2P |
; |
Fmin = 2 |
2 20 103 |
= 2,5 10− 4м2=2,5 см2. |
|
160 106 |
|||||
|
[σ ] |
Вариант 3. Определить максимально допустимое значение параметра нагрузкиРдлястержняизхрупкогоматериала, используятакиеданные:
F = 2 см2; σ вр =240 МПа; σ вс = 960 МПа; nв = 4 .
Материал стержня хуже работает при растяжении, поэтому наиболее опасным является участок 3 (см. эпюру σ на рис. 3.7). Подставляя σ p,max= 2P/F в первое неравенство (3.22), получим:
|
2 |
P |
≤ [σ ]р; [σ ]р = 240/4 = 60 МПа. |
|
|
F |
|||
Решая это неравенство, находим:
Р ≤ [σ ]р F/ 2; Pдоп = 60 106 2 10 –4/2 = 6 кН.
Определимизменениедлиныстержняпризначенияхпараметров:
F = 2 см2; P = 20 кН ; l = 1м; E = 2 105 МПа.
45

Как следует из эпюры w (см. рис. 3.7,б), стержень удлиняется, так как wA > 0 (сечение А перемещается вверх):
|
wA = |
0,5 |
20 10− 4 1 |
= 2,5 10− 3 |
м= 2,5 ìì . |
|
|
2 1011 |
2 10− 4 |
||||
При расчете стержня не учитывался его собственный вес. Считается, что им можно пренебречь по сравнению с действующими силами. Но в ряде практических случаев необходимо учитывать напряжения от собственного веса.
Рассмотрим стержень постоянного сечения (рис. 3.8,а), нагруженный собственным весом. Следует отметить, что расчетная схема стержня с сосредоточенной силой, равной силе веса стержня и приложенной в его центре тяжести (рис. 3.8,б), является весьма приближённой, так как нагруженной является половина стержня (см эпюру N на рис. 3.8,б). Тогда как очевидно, что в произвольном сечении 1-1 нормальная сила равна силе веса отсеченной части.
Рис. 3.8
Для расчётной схемы стержня (рис. 3.8,в) объемную нагрузку, определяемую собственным весом стержня P, заменим погонной нагрузкой интенсивности q = P/l. С учетом соотношения P = γ Fl, где γ – удельный вес материала стержня, получим q = γ F. Тогда N и σ в произвольном сечении стержня (рис. 3.8,в) определяются выражениями:
N = q (l – z) = γ F (l – z); σ = N/F = γ (l – z).
Соответствующие эпюры N и σ представлены наэтом жерисунке. Найдем предельную длину стержня lпр, при которой максимальные напряжения в стержне у заделки достигнут предела прочности и
стержень разрушится:
σ max = σ вр; γ lпр = σ вр; lпр = σ вр/γ .
46
Как видим, предельная длина стержня постоянного сечения не зависит от его площади поперечного сечения. Например, для стального стержня с γ = 7,8 104 Н/м3 и σ вр= 780 МПа получим lпр= 104м.
Более эффективно применять материал, у которого высокие прочностные характеристики (σ вр) и/или наименьший удельный вес (γ ), т.е. материал, имеющий большее значение lпр=σ вр/γ . В наибольшей степени таким условиям удовлетворяют волокнистые композитные материалы (углепластик, органопластик и др.).
Осевые перемещения сечений стержня определяются по формуле (3.18) при wн = 0 (в заделке):
|
w (z) = − |
q z2 |
+ |
Níz |
= − |
q z2 |
++ |
ql z |
. |
|
2EF |
||||||||
|
2EF |
EF |
EF |
Функция w(z) является квадратичной параболой. Перемещение концевого сечения стержня (при z = l и c учетом ql = P) равно:
w = Pl/2EF.
Отметим, что этот же результат получается и с использованием приближённой расчетной схемы на рис. 3.8,б. Следует также отметить, что при использовании этой схемы правильно определяются максимальные напряжения в стержне у заделки, однако распределение N , σ и w по длине стержня описываются неверно.
3.7. Расчёт статически неопределимого стержня
Статически неопределимым является стержень с двумя заделками (рис. 3.9). Две реакции не могут быть определены из одного уравне-
|
ния статики: |
|
|
Σ Fz = 0; RA + P – 5P + RD = 0. |
(3.27) |
Второе уравнение должно быть получено из рассмотрения деформирования стержня. Для этого условно сделаем стержень статически определимым, удалив одну из заделок, например правую. Вместо удаленной заделки приложим неизвестную реакцию X1=RA. Получим
стержень, аналогичный (статически эквивалентный) заданному. При этом нужно учитывать, что из-за наличия двух заделок изменение полной длины стержня равно нулю (деформационное условие). В со-
|
ответствии с формулой (3.26) запишем: |
|
|
∆ l1 +∆ l2 +∆ l3 = 0. |
(3.28) |
|
Для определения ∆ li (3.14) получим нормальные силы Ni в сече- |
|
|
ниях каждого участка: |
|
|
N1 = X1; N2 = X1 + P ; N3 = X1 + P – 5P = X1 – 4P . |
(3.29) |
47

Используя формулу (3.14), значения Ni (3.29) и физико-геомет- рические параметры участков (Ei, Fi, li), уравнение (3.28) запишем в виде:
|
X1l |
+ |
( X1 + P) l |
+ |
( X1 − 4P) l |
|
EF |
E2F |
E2F |
||
Это уравнение является дополнительным к уравнению статики
(3.27).
Уравнение (3.30) может быть преобразовано к виду :
Первое слагаемое в этом уравнении определяет для эквивалентного стержня перемещение концевого сечения А от неизвестной реакции Х1, а второе слагаемое – перемещение от заданных сил. При этом коэффициент при Х1 численно равен перемещению сечения А от силы
Х1=1.
Решая уравнение (3.31), находим Х1 = RA = 3/4P, а затем из (3.29) – усилия на участках. После чего строятся эпюры N, σ и w, которые представлены на рис. 3.9. Эпюра w построена, начиная с сечения D. Правильность решения контролируется равенством нулю перемещения сечения А.
Для статически неопределимого стержня практическое значение имеет вычисление температурных и монтажных напряжений.
48
При изменении температуры статически определимого стержня в нем не возникают усилия и напряжения. Стержень просто удлиняется или укорачивается. Если же нагревать или охлаждать статически неопределимый стержень, то в нем возникают температурные усилия и напряжения. Это объясняется тем, что жесткие заделки не позволяют изменяться длине стержня. В результате при нагреве возникают сжимающие усилия и напряжения, а при охлаждении стержня – растягивающие усилия и напряжения.
Если длина стержня имеет отклонение от номинального размера (например, стержень выполнен длиннее на величину ∆ 0 = l – l0), то после принудительной установки такого стержня между жесткими опорами в нем возникают так называемые монтажные усилия и на-
пряжения.
Учет вышеуказанных факторов покажем для стержня, рассмотренного в предыдущем примере (см. рис.3.9). Предположим, что стержень нагрет на ∆ T° C и выполнен короче своей номинальной длины на ∆ 0 (рис. 3.10). При нагреве стержень получил бы удлинение ∆ T=α T∆ T.3l при отсутствии правой заделки. Если ∆ 0 ≥ ∆ T, то усилия и напряжения в стержне не возникают. Если же ∆ 0 < ∆ T, то в заделках возникают реакции RA и RD, которые не могут быть определены из одного уравнения статики:
|
RD – RA = 0; RD= RA. |
(3.32) |
Отметим, что возникающие реакции самоуравновешены.
Удалим правую заделку и вместо неё в сечении А приложим неизвестную реакцию X1 = RA. Учитывая, что изменение длины стержня (или перемещение сечения А) равно ∆ 0, запишем:
|
∆ l1 + ∆ l2 = ∆ 0. |
(3.33) |
Нормальные силы на участках стержня равны:
Используя первую формулу (3.19) для определения ∆ li и значения Ni , уравнение (3.33) запишем в виде:
|
( |
− |
X1l |
+ α |
T |
∆ Tl)++ |
(− |
− |
X1 2l |
++ αα |
∆ |
∆ T2l)== ∆ |
0 |
. |
(3.35) |
||
|
EF |
EF |
T |
||||||||||||||
|
Решая это уравнение, получим: |
||||||||||||||||
|
X1 |
= |
EF |
( ∆ |
Τ − ∆∆ |
0 ) ; |
∆ 0 ≤ ∆ |
T, |
(3.36) |
||||||||
|
2l |
где ∆ T = 3α T∆ Tl – температурное удлинение стержня.
49
Если ∆ T = ∆ 0, то X1 = 0. На рис. 3.10 представлены эпюры N, σ и w. Эпюра w построена от сечения D (wD = 0). При этом получим:
|
w |
B |
= ∆ l |
== |
− X1 2l |
+ α |
∆∆ T2l |
; w |
A |
= |
w |
B |
++ |
∆ l |
== |
w |
B |
+ |
− X1l |
+ α |
∆∆ Tl . |
|
|
2 |
E2F |
T |
1 |
EF |
T |
||||||||||||||||
|
С учетом формулы(3.36) получим: |
|||||||||||||||||||||
|
wВ = (∆ |
О + α T∆ T l)/2 ; |
wA = ∆ |
0. |
Последнее равенство является проверкой расчёта. Из этого условия исходили, решая задачу.
При одновременном воздействии на стержень нагрузки, температуры и наличии монтажных отклонений в соответствии с принципом суперпозиции усилия, напряжения и перемещения, полученные при соответствующем расчете стержня (см. рис. 3.9) и (см. рис. 3.10), суммируются.
50
Соседние файлы в папке Книги и методические указания
- #
04.03.201414.07 Mб253Кочетов Сопротивление материалов.pdf
- #
Ученик
(105),
закрыт
6 лет назад
Валентина Вавилова(Серкова)
Гений
(62183)
11 лет назад
По релятивистской формуле длины:
L=L0*корень квадратный из (1 – v^2 / c^2.) ( L0 -начальная длина, L-длина, при скорости v, c- скорость света)
L0 / L= 1 / кор. кв. из (1 – v^2 / c^2).
L0 / L= 1 / ор. кв. из ( 1 – (0,99с) ^2 / c^2) =7. Длина уменьшиться в 7 раз.
Рассчитать деформации участков и общее изменение длины прямого стержня постоянного сечения.
Предыдущие пункты решения задачи
Стержень имеет три силовых участка, на которых площадь сечения одинакова, но внутренние силы и нормальные напряжения отличаются, поэтому определим абсолютные деформации всех участков в отдельности, после чего сложив их, получим изменение длины всего стержня в целом.
Изменение длины участков стержня при растяжении-сжатии рассчитывается по формуле:
где N – величина внутренней продольной силы,
l – длина рассматриваемого участка,
A – площадь его поперечного сечения,
E – модуль Юнга (продольной упругости) для материала стержня,
σ — значение нормальных напряжений на рассматриваемом участке.
Значения внутренних сил и напряжений принимаются с построенных эпюр N ( σ ).
По эпюрам видно, что первый участок сжимается, а участки II и III растягиваются, следовательно, деформации Δ l второго и третьего участков будут положительны (их длина увеличивается), а первого отрицательны (продольный размер уменьшается).
Деформация I участка (KM)
Удлинение третьего участка BC
Сложив (с учетом их знака) деформации всех участков получим величину изменения длины всего стержня в целом:
В результате деформации общая длина стержня увеличится на 0,51мм.
Разобранные примеры показывают, что критическое значение сжимающего осевого усилия на стержень можно выразить по формуле
где 




Формула (207) называется обобщенной формулой Эйлера. Напомним, что она справедлива, если напряжения и деформации в стержне в момент потери устойчивости находятся в упругой области:
где 
называется минимальным радиусом инерции поперечного сечения.
Введем еще одно важное понятие — гибкость стержня
Тогда обобщенную формулу Эйлера можно представить в простой форме:
Условие (208) ограничивает область применения формулы Эйлера.
Минимальное значение гибкости, ниже которой формула Эйлера перестает быть пригодной, равно
Например, для малоуглеродистой стали при 
Формулу Эйлера можно применять, если 
Замечание. Критическое напряжение, конечно, является сжимающим. В задачах устойчивости по традиции, чтобы устранить знак «минус» в расчетных формулах, критические сжимающие напряжения считаются положительными.
Рис. 12.40. Устойчивость стержня переменного сечения
В момент потери устойчивости сжатый стержень выпучивается, поворачивается вокруг центров соответствующих узлов и вследствие жесткости фасонок заставляет поворачиваться и изгибаться в плоскости фермы остальные стержни.
Примыкающие стержни сопротивляются изгибу и повороту узла и препятствуют свободному изгибу стержня, теряющего устойчивость.
Наибольшее сопротивление повороту узла оказывают растянутые стержни. Сжатые стержни слабо сопротивляются изгибу.
Таким образом, чем больше растянутых стержней примыкает к сжатому стержню и чем они мощнее (больше их погонная жесткость), тем выше степень защемления стержня и меньше его расчетная длина; влиянием сжатых стержней на защемление можно пренебречь.
Сжатый пояс оказывается слабо защемленным в узлах, так как с каждой стороны к нему примыкает только по одному растянутому раскосу, погонная жесткость которых значительно меньше погонной жесткости пояса. Поэтому защемлением сжатого пояса в запас устойчивости можно пренебречь и принимать его расчетную длину равной расстоянию между смежными узлами.
Таким образом, при большей степени защемления меньше расчетная длина стержня фермы: 
где 

По нормам коэффициент приведения длины “

Исключение составляет опорный восходящий раскос, условия работы которого в плоскости фермы такие же, как и у верхнего пояса, поэтому расчетная длина опорного раскоса в плоскости фермы принимается равной расстоянию между центрами узлов.
Расчетная длина пояса в плоскости, перпендикулярной плоскости фермы, принимается равной расстоянию между узлами, закрепленными связями от смещения из плоскости фермы.
В беспрогонных покрытиях верхний пояс стропильных ферм закреплен в плоскости кровли плитами или панелями настила, прикрепленными к поясам ферм в каждом узле. В этом случае за расчетную длину пояса из плоскости фермы принимают ширину одной плиты.
Расчетная длина стержней решетки при выгибе их из плоскости фермы принимается равной расстоянию между геометрическими центрами узлов, так как фасонки очень гибки и рассматриваются как листовые шарниры.
В трубчатых фермах с бесфасонными узлами расчетная длина раскоса, как в плоскости фермы, так и из нее, с учетом повышенной крутильной жесткости замкнутых сечений применятся равной 0,9.
В других случаях расчетная длина элементов ферм принимается по нормали.
9.7. Предельные гибкости стержней
Элементы конструкций должны проектироваться из жестких стержней. Особенно существенное значение имеет гибкость “
Даже при незначительных сжимающих усилиях гибкость сжатых стержней не должна быть слишком большой, так как гибкие стержни легко искривляются от случайных воздействий, провисают, вибрируют при динамических нагрузках. Поэтому для сжатых стержней устанавливается предельная гибкость, зависящая от назначения стержня и степени его нагружения 

сжатые пояса, а также опорные стойки и раскосы,
передающие опорные реакции……………………………………………… 180-60
прочие сжатые стержни фермы………………………………………………… 210-60
При этом 
Растянутые стержни конструкций так же не должны быть слишком гибкими, так как могут прогнуться при транспортировании и монтаже.
Стержни должны иметь достаточную жесткость особенно в конструкциях подверженных динамическим воздействиям.
Для растянутых стержней ферм, подвергающихся действию динамической нагрузки, установлены следующие значения предельной гибкости:
растянутые пояса и опорные раскосы………………………………………250
прочие растянутые стержни ферм………………………………………….350
растянутые стержни связей………………………………………………….400
В конструкциях, не подвергающихся динамическим воздействиям, гибкость растянутых стержней ограничивают только в вертикальной плоскости (чтобы предотвратить чрезмерное провисание), установив для всех растянутых стержней предельную гибкость 
32. Типы, подбор и проверка сечений стержней ферм. Конструирование, особенности работы и расчета узлов ферм из парных уголков.
Изменение – длина – стержень
Cтраница 3
Для того чтобы при подсчете изменения полной потенциальной энергии воспользоваться зависимостями типа (2.45) или (2.46), необходимо ввести в рассматриваемую систему дополнительный упругий элемент, аккумулирующий энергию в докрити-ческом состоянии равновесия. Причем в соответствии с принятыми выше ограничениями жесткость пружины должна быть достаточно большой, чтобы можно было пренебречь изменением длины стержня в докритическом состоянии.
[31]
Возьмем деревянную чертежную линейку и приложим к ней продольную сжимающую нагрузку. Постепенно ее увеличивая, заметим, что ось сначала остается почти прямолинейной, а затем при некоторой нагрузке она внезапно искривляется и может сломаться. Заметим, что с изменением длины стержня изменяется и разрушающая нагрузка, чем длиннее стержень, тем при меньшей нагрузке он разрушается. Кроме того, при сжатии длинных стержней изменение формы поперечного сечения ( при прочих равных условиях) так же вызывает изменение разрушающей нагрузки.
[32]
При увеличении магнитного поля вектор намагниченности каждого кристаллика отклоняется от направления оси легкого намагничивания и поворачивается по направлению приложенного поля. В результате они приводят к изменению длины стержня в направлении приложенного поля.
[33]
При деформации тела взаимное положение его отдельных точек меняется, точки получают перемещения. Например, под действием груза Q ( рис. 1) нижний конец стержня перемещается ( опускается) на величину и, в то время как верхний конец остается неподвижным. Различие в перемещениях связано с изменением длины стержня под нагрузкой. Абсолютное удлинение Д / 1 – / с в данном примере равно перемещению и и зависит от длины стержня.
[35]
Для компенсации упругого последействия применено следящее устройство, основой которого является стержень из магнитострикционного материала [73], установленный между кареткой подачи и гайкой винта. Стержень помещен в катушку индуктивности и вместе с кожухом из мягкого магнитного материала образует почти замкнутый магнитопривод. Сила тока в катушке и, следователно, изменение длины стержня автоматически регулируются сигналом от муаровых полос, благодаря чему обеспечивается неподвижность решетки при нанесении на нее штрихов.
[36]
По своей физической природе сила реакции стержня – это, конечно, упругая сила. Используемая здесь физическая модель, т.е. идеализация свойств стержня, заключается в пренебрежении его возможной деформацией. Другими словами, жесткость стержня считается настолько большой, что при действующих здесь силах деформация практически отсутствует: можно не учитывать изменения длины стержня при подсчете потенциальной энергии груза в поле тяжести и пренебречь потенциальной энергией упругой деформации самого стержня.
[38]
Чаще применяется и перспективнее размерная ультразвуковая обработка абразивом, зерна которого получают энергию от специального инструмента ( фиг. В рабочую зону между торцом инструмента / и обрабатываемой деталью 3 подается взвешенный в жидкости абразив 2 ( карбид бора), зерна которого под действием ударов колеблющегося инструмента производят обработку. Источником энергии инструмента является достаточно мощный ( обычно ламповый) генератор электрических колебаний. Электрические колебания преобразуются в механические с помощью вибраторов – пьезоэлектрических или чаще магнитострикционных. В последнем случае используется эффект продольной магнитострикции, заключающийся в изменении длины стержня из ферромагнитного материала, помещенного в магнитном поле.
[39]
Известно несколько типов регуляторов температуры, в которых применяется тепловое расширение жидких и твердых тел. К первым относятся известные жидкостные пружинные термометры, снабженные для per улирова-ния контактными устройствами. Вместо упругой пружины могут применяться эластичные камеры расширения [55], служащие резервуарами давления. Для поддержания постоянства температуры часто применяются термометры с удлиняющимися стержнями [ 57 J. Стержень и трубка, в которую он вставлен, изготовлены из материалов с различными коэффициентами линейного расширения. Обусловленное температурой изменение длины стержня в большинстве случаев поворачивает ртутный контакт, который при этом замыкает цепь тока нагревателя. В таких терморегуляторах специальное устройство позволяет устанавливать стержни в любой рабочей точке.
[41]
Другими словами, оптимальное решение лежит на границе всех ограничений. На рисунке точки соответствуют металлическим элементам. Масса узлов соединений не учитывается. При уменьшении длины стержня роль осевого модуля снижается, соответственно возрастает влияние предела прочности при сжатии, и более эффективным оказывается боропластик, имеющий очень высокий предел прочности при сжатии. Это обстоятельство является важной отличительной чертой процесса проектирования элементов ферменных конструкций из композиционных материалов. В результате анализа геометрических параметров и нагрузок выбирают тип и структуру композиционного материала, оптимального для заданных условий эксплуатации. В табл. 3 для сравнения приведена масса двух стержней различной длины и из различных материалов. Изменение длины стержня полностью меняет порядок расположения материалов по степени эффективности.
[43]
Страницы:
1
2
3