Решение:
В данном случае нужно представленный на картинке треугольник поделить одним отрезком пополам, начиная из верхней вершины к противоположной стороне.
![]()
И тогда мы получим максимально возможно количество треугольников, а именно 6 треугольников.
Рассмотрим еще несколько аналогичных примеров. Если необходимо сделать один разрез так, чтобы получилось как можно больше треугольников.
![]()
Для решения данной задачи также проведем отрезок из верхней вершины вниз.
![]()
В результате такого разделения мы получим 8 треугольников
Рассмотрим еще один пример, когда в треугольнике, изображенном на рисунке нужно сделать один разрез, чтобы получилось максимально возможное количество треугольников.
![]()
Для решения данной задачи снова проведем отрезок из верхней вершины к нижней стороне, поделив треугольник пополам, и получим 9 треугольников.
![]()
Предлагаем решить еще одну аналогичную задачу. Дан треугольник, нужно сделать в нем один разрез так, чтобы получилось максимальное количество треугольников и назвать данное количество.
![]()
Что такое “степень треугольника” — вполне понятно. Из данного выше определения следует, что у прямоугольного треугольника эта степень равна двум, у тупоугольного — меньше двух, у остроугольного — больше двух. Задача станет вполне корректной, если определить, в каком смысле следует понимать слово “больше”. Это можно сделать в терминах геометрической вероятности. Иными словами, речь идёт о том, каких треугольников “больше” среди “случайных” — тупоугольных или остроугольных.
Если числам позволено принимать неограниченные значения, то определить геометрические вероятности довольно затруднительно. Поэтому, с учётом того, что всякий треугольник подобен треугольнику со сторонами, ограниченными некой константой, удобно рассматривать в качестве длин сторон числа отрезка $%[0,1]$%, выбираемые в некотором роде “случайно”.
В частности, можно поставить такой вопрос: если мы равномерно бросаем точку в отрезок три раза (независимо) и получаем три числа $%x,y,z$%, то какова вероятность, что из полученных длин можно составить треугольник? Это известная задача, и на моей памяти она где-то обсуждалась. Ответ там можно найти при помощи многомерных интегралов, и он оказывается равен $%1/2$%.
В предложенной здесь задаче уже накладываются условия, скажем, $%x+y>z>x,y$%, что определяет подмножество $%Phi$% единичного куба. Далее в этом подмножестве выбирается одна “случайная” точка при “равномерном” выборе. Это стандартная для таких случаев операция. Здесь вероятность попадания в фигуру $%Phi’$%, содержащуюся в $%Phi$%, полагается равной отношению объёмов фигур $%Phi’$% и $%Phi$%.
Пусть далее $%(x,y,z)in[0,1]^3$%. Очевидно, что величина $%sqrt{x^2+y^2}$% будет удовлетворять неравенствам $%x+ygesqrt{x^2+y^2}ge x,y$%, и тогда нужно сравнить “шансы” на то, что $%z$% будет больше или меньше $%sqrt{x^2+y^2}$%, что будет относиться к случаю тупоугольного или остроугольного треугольника, соответственно, составленного из сторон с длинами $%x,y,z$%.
Итак, пусть $$Phi=left{(x,y,z)in[0,1]^3mid x+y>z>x,yright}.$$ Объём $%Phi$% равен трёхмерному интегралу $$iiintlimits_Phi,dx,dy,dz=iiintlimits_{Phi_1},dx,dy,dz+iiintlimits_{Phi_2},dx,dy,dz,$$ где $%Phi_1$% относится к случаю $%x+y<1$%, а $%Phi_2$% — к случаю $%x+y>1$%. Из соображений симметрии, можно дополнительно считать, что $%y>x$%, удваивая все величины.
Для фигуры $%Phi_1$% область интегрирования будет задаваться неравенствами $%x+y>z>y>x$%, причем $%y<1-x$%, откуда $%x<1/2$%. Поэтому $$iiintlimits_{Phi_1},dx,dy,dz=2intlimits_0^{1/2},dxintlimits_x^{1-x},dyintlimits_y^{x+y},dz=2intlimits_0^{1/2}x(1-2x),dx=frac1{12}.$$
Аналогично, для фигуры $%Phi_2$% имеем неравенства $%1>z>y>x,1-x$%. Ввиду симметрии между $%x$% и $%1-x$%, полагаем $%x<1-x$%, то есть $%x<1/2$%, что ведёт к ещё одному удвоению. Поэтому $$iiintlimits_{Phi_2},dx,dy,dz=4intlimits_0^{1/2},dxintlimits_{1-x}^1,dyintlimits_y^1,dz=4intlimits_0^{1/2}frac{x^2}2,dx=frac1{12}.$$ Суммируя, получаем, что объём фигуры $%Phi$% равен $%1/12+1/12=1/6$%.
(Объём фигуры $%Phi$% можно найти проще, но я не буду переписывать уже написанное.)
Теперь положим $$Phi’=left{(x,y,z)in[0,1]^3mid sqrt{x^2+y^2}>z>x,yright}.$$ Это соответствует случаю остроугольного треугольника. Здесь так же получаем, что объём фигуры $%Phi’$% равен $$iiintlimits_{Phi’},dx,dy,dz=iiintlimits_{Phi_1′},dx,dy,dz+iiintlimits_{Phi_2′},dx,dy,dz,$$ где $%Phi_1’$% относится к случаю $%x^2+y^2<1$%, а $%Phi_2’$% — к случаю $%x^2+y^2>1$%. Как и выше, из соображений симметрии считаем, что $%y>x$%, удваивая соответствующие величины.
Для первого случая имеем неравенства $%sqrt{x^2+y^2}>z>y>x$%, причём $%y<sqrt{1-x^2}$%, откуда $%x<1/sqrt{2}$%. Поэтому
$$iiintlimits_{Phi_1′},dx,dy,dz=2intlimits_0^{1/sqrt{2}}dxintlimits_x^{sqrt{1-x^2}}dyintlimits_y^{sqrt{x^2+y^2}}dz=intlimits_0^{1/sqrt{2}}dxintlimits_x^{sqrt{1-x^2}}left(sqrt{x^2+y^2}-yright),dy,$$ что удобнее всего вычислить в полярных координатах. После замены переменных, с учётом того, что якобиан замены равен $%r$%, а область интегрирования представляет собой верхний из двух секторов, на которые прямая $%y=x$% делит четверть круга из первого координатного угла, получаем $$2intlimits_{pi/4}^{pi/2}dvarphiintlimits_0^1(r-rsinvarphi)r,dr=2intlimits_{pi/4}^{pi/2}(1-sinvarphi),dvarphicdotintlimits_0^1r^2,dr=frac{pi}6-frac{sqrt{2}}3.$$
Чтобы найти объём фигуры $%Phi_2’$%, заметим, что у нас выполняются при этом неравенства $%1>z>y>x,sqrt{1-x^2}$%, с учётом необходимости произвести удвоение. Так как $%z$% меняется от $%y$% до $%1$%, мы должны проинтегрировать фукнцию $%1-y$% по двумерной области, ограниченной прямыми $%y=1$%, $%y=x$% и единичной окружностью. После перехода к полярным координатам, мы получаем $$iiintlimits_{Phi_2′},dx,dy,dz=2intlimits_{pi/4}^{pi/2}dvarphiintlimits_1^{1/sinvarphi}(1-rsinvarphi)r,dr,$$ то есть $$frac13intlimits_{pi/4}^{pi/2}frac{d{varphi}}{sin^2varphi}+frac23intlimits_{pi/4}^{pi/2}sinvarphi,d{varphi}-intlimits_{pi/4}^{pi/2}dvarphi=frac13+frac{sqrt{2}}3-frac{pi}4.$$ Складывая найденные объёмы фигур $%Phi_1’$% и $%Phi_2’$%, мы находим объём фигуры $%Phi’$%, равный $$left(frac{pi}6-frac{sqrt{2}}3right)+left(frac13+frac{sqrt{2}}3-frac{pi}4right)=frac13-frac{pi}{12}.$$
Таким образом, осталось поделить объём фигуры $%Phi’$% на объём фигуры $%Phi$%, равный $%1/6$%. Это даст нам вероятность того, что “случайный” треугольник окажется остроугольным. Эта величина равна $$2-frac{pi}2approx0.429203673.$$ Соответственно, вероятность возникновения тупоугольного треугольника составит $%pi/2-1$%, то есть приблизительно $%0.570796327$%.
Поскольку ответ получился “хороший”, это говорит о том, что его, скорее всего, можно получить при помощи более простых вычислений. Однако, использованный подход довольно стандартен, и мне проще было применить его, а не искать что-то более “элегантное”.
Сколько треугольников видно на картинке?

Сначала насчитала 8, потом 9, а потом пошло и поехало. Не уверена что правильно посчитала, но у меня всего получилось 22 треугольника. Интересно сколько их на самом деле. Хорошее упражнение на внимательность.
Давайте попробуем считать треугольники по каким-тот правилам. Итак, треугольников которые имеют общую вершину на самом верху всего 18. Действительно из этой вершины исходят три луча, которые пересекаются с двумя прямыми, образуя на каждом уровне по 6 треугольников (3 маленьких, 2 средних и один большой).
Теперь перейдем к вершине на втором уровне, там можно найти 3 треугольника (большой, средний и маленький). Те же 3 треугольника можно найти на нижнем уровне. Итак всего 24 треугольника: 18+3+3 = 24.
Как вычислить количество треугольников?
Вот я криво нарисовал треугольник и разбил его на несколько маленьких, а затем задумался: можно ли как-нибудь без банального пересчета узнать общее количество получившихся треугольников? Немного подумав я разделил все треугольники на несколько типов: одинарные, двойные и т. д. То есть формула должна быть суммой всех треугольников каждого типа. На рисунке сторона самого большого треугольника поделена на 7 отрезков. Практическим методом я понял, что при любом количестве этих отрезков число одинарных треугольников равно квадрату числа отрезков. То есть, самых маленьких треугольничков на рисунке 49. Так же разобрался с двойными, их количество находится по формуле 3(n-1), где n- опять же число отрезков. К этой сумме можно прибавить число самых больших треугольников — всегда 1. Вот и все: для остальных треугольников не могу закономерности увидеть. Может из здесь присутствующих кто нибудь увидит?
/>
считай не треугольники, а ВЕРХНИЕ/НИЖНИЕ ВЕРШИНЫ (как вариант- ПАРЫ точек, задающих горизонтальное основание)
_________
Сколько есть горизонтальных отрезков длины 1?
1+2+. +(n-1)+n
Каждый, кроме последних n,задает 2 треугольника.
2*(1+2+. +(n-1))+n
________________
Сколько есть горизонтальных отрезков длины 2?
1+2+. +(n-2)+(n-1)
Каждый, кроме последних (n-1) и (n-2),задает 2 треугольника.
только не бросайся сразу складывать.)))
Просто пойми сначала, что можно смотреть на задачу с разных сторон.
____________________
вторая идея тебе:
попробуй идти не от мелкого к крупному, а наоборот- от самого большого размера уменьшать понемногу.
Задачи «на подсчет треугольников»
5.3.2. Опишем проведенную работу при решении задач «на подсчет треугольников». В первых геометрических задачах будет применяться термин «взаимопроникающие фигуры», предложенный И.С. Якиманской. Вслед за ней взаимопроникающими мы называем такие фигуры, которые имеют часть общей площади: одними своими частями они перекрывают друг друга, другими частями не совпадают [196].
Посмотрите на рис. 5.2, а: треугольник АВС можно разделить на составляющие его фигуры: треугольники АЕО, О DC, АОС и четырехугольник BEOD (рис. 5.2, б).
Можно рассмотреть и другие имеющиеся в треугольнике АВС треугольники: ABD, ЕВС, АЕС, ADC (рис. 5.2, в). В этом случае мы получаем «взаимопроникающие» фигуры.
Исследование И.С. Якиманской [196] было направлено на изучение того, как учащийся анализирует геометрический чертеж, какие фигуры выступают для него более явно, бросаются в глаза, а какие трудны для выделения, на что опирается учащийся при рассмотрении чертежа, какие умственные процессы обеспечивают возможность различного видения чертежа. Результаты, полученные И.С. Якиманской, очень интересны, к сожалению, их недостаточно используют при работе с учащимися.

Задачи с взаимопроникающими элементами использовал в своей работе и В. А. Крутецкий. С помощью этих задач он исследовал особенности аналитико-синтетического восприятия геометрических фигур учащимися, в частности умения рассматривать и оценивать взаимопроникающие элементы геометрических фигур с различных точек зрения, выделять элементы фигур и фигуры из фона, включать один и тот же элемент в разные фигуры и соответственно давать им различную интерпретацию.
Рассмотрим некоторые задачи по подсчету треугольников с учетом взаимопроникающих фигур.
Задача 5.8. Сколько отрезков вы видите на рис. 5.3? Назовите их.

Задача 5.9. Сколько треугольников изображено на рис. 5.4? Назовите их.
Задача 5.10. Сколько углов вы видите на рис. 5.5? Назовите их.


В.А. Крутецкий ограничивал исследование тем, что фиксировал, «насколько полный ответ дают испытуемые, какую роль играют „видение» и „рассуждение»» [98].
Учитывая вышеизложенное, рассмотрим, как можно использовать «цепочки задач на подсчет треугольников» для выявления «геометрического зрения», уровней владения приемами анализа и синтеза, алгоритмических способностей учащихся, причем не будем ограничиваться только окончательным ответом, а приведем качественный анализ выполнения задания.
Б.М. Теплов подчеркивал, что «не следует вовсе исключать возможность количественного подхода при исследовании способностей. Он возможен, однако, только в том случае, когда он следует за качественным анализом, вытекает из него, им определяется» [171].
Количественная характеристика применялась нами при оценке:
- • геометрического зрения — насколько полно и точно учащийся увидел искомые фигуры; количество выделенных фигур из фона;
- • аналитико-синтетической деятельности — наличие и количество «идей» при решении задач, выбор наиболее рационального способа решения;
- • алгоритмические способности — количество шагов, приводящих к правильному решению.
Ниже приведены некоторые из предлагаемых учащимся заданий по подсчету треугольников и дан анализ их решения.
Задача 5.11. Сосчитайте, сколько треугольников изображено на рис. 5.6.
Цепочка задач построена таким образом, что при переходе к каждой последующей фигуре увеличивается число искомых треугольников (принцип нарушается при переходе от слу-

чая 5.6, в к случаю, изображенному на рис. 5.6, г, но в случае 5.6, г усложняется «геометрический фон», т. е. появляются такие взаимопроникающие треугольники, которые состоят, например, из треугольника и четырехугольника, а в случае 5.6, в все взаимопроникающие треугольники можно рассматривать состоящими только из треугольников).
Оценка выполнения задания (а)
- 1. Если учащийся увидел на рис. 5.6, а большой треугольник, состоящий из двух маленьких, т. е. всего три треугольника, то он получает 1 балл.
- 2. Если учащийся не видит какой-либо из трех треугольников, то он получает 0 баллов.
Оценка выполнения задания (б)
На рис. 5.6, б изображен большой треугольник, состоящий из трех маленьких, всего четыре треугольника. Такое решение оценивается в 1 балл.
Схема рассуждений и ход решения (в)
1. Воспроизведем рис. 5.6, в. Пронумеруем треугольники (рис. 5.7, а). Сосчитаем все маленькие треугольники, их всего шесть (рис. 5.7, б).
- 2. Сосчитаем треугольники, состоящие из двух маленьких, их всего три (рис. 5.7, в).
- 3. Сосчитаем треугольники, состоящие из трех маленьких, их всего шесть (рис. 5.7, г).
- 4. Треугольник, состоящий из шести маленьких треугольников, — один (рис. 5.7, а).
Всего получилось 16 треугольников.

Оценка выполнения задания (в)
- 1. Учащиеся сосчитали (увидели) все взаимопроникающие треугольники, подсчет вели с помощью алгоритма — 2 балла.
- 2. Задача решалась без применения алгоритма (какие треугольники учащийся увидел, такие и сосчитал, но нашел больше семи треугольников — 1 балл).
- 3. Учащийся при решении насчитал меньше семи треугольников, т. е. не увидел взаимопроникающих треугольников, — оценка 0 баллов.
Схема рассуждений и ход решения (г)
- 1. Сосчитаем треугольники в «нижней» части рис. 5.6, г, их всего шесть, причем все они состоят только из треугольников (рис. 5.8, а, б, в).
- 2. Добавляем «верхнюю» часть, получаем треугольники, состоящие из треугольников и четырехугольника, решение аналогично решению в случае а, треугольников тоже шесть (рис. 5.9, а, б, в).

Всего получилось: (3 + 2 + 1) + (3 + 2+ 1) = 12 треугольников.
Оценка выполнения задания (г)
- 1. Учащийся подсчитал все треугольники с помощью алгоритма (выбор алгоритма значения не имеет) — оценка 3 балла.
- 2. Учащийся применил для решения алгоритм, не позволивший выделить все имеющиеся на рисунке треугольники — оценка 2 балла.
- 3. Учащиеся, сосчитавшие только треугольники на рис. 5.8, а, в и рис. 5.9, а, в, т. е. не увидевшие взаимопроникающих треугольников, получают 1 балл.
4. Учащиеся, увидевшие на рисунке меньше семи треугольников, получают О баллов.
Схема рассуждений и ход решения (д)
В этой задаче (как, впрочем, и в других) при подсчете числа треугольников без алгоритма есть опасность «потерять» треугольники, поэтому полезно обозначить треугольники цифрами (рис. 5.10).
- 1. Начнем подсчет с маленьких треугольников, их всего 12 (рис. 5.10).
- 2. Считаем треугольники, состоящие из трех маленьких (два маленьких треугольника образуют ромб), таких треугольников шесть (рис. 5.11).
3. Четыре, пять, шесть, семь, восемь маленьких треугольников не образуют новых треугольников, а треугольников, состоящих из девяти маленьких треугольников, — два (рис. 5.12).

Всего получилось 12 + 6 + 2 = 20 треугольников.
Оценка выполнения задания (д)
- 1. Учащиеся, предложившие алгоритм подсчета и сосчитавшие все треугольники, получают 3 балла.
- 2. Учащиеся, сосчитавшие все треугольники, но не предложившие алгоритм подсчета, получают 2 балла.
- 3. Учащиеся, увидевшие случаи, изображенные на рис. 5.11 и рис. 5.12, но пропустившие некоторые треугольники, получают 1 балл.
- 4. Учащиеся, не увидевшие случаи, изображенные на рис. 5.11, 5.12, получают 0 баллов.
Схема рассуждений и ход решения (е)
Эта задача самая сложная в цепочке, выявляющей «уровни видения» взаимопроникающих треугольников, так как в ней появляются треугольники, состоящие из треугольников и пятиугольника. Пронумеруем все элементы пятиугольника (рис. 5.13).
1. Десять маленьких треугольников (1-10) (рис. 5.13).

- 2. Десять треугольников, состоящих из двух маленьких треугольников (1-2, 2-3,
- 3-4, 4-5, 5-6, 6-7, 7-8, 8-9, 9-10, 10-1).
- 3. Пять треугольников, состоящих из трех маленьких треугольников (1-2-3,
- 3-4-5, 5-6-7, 7-8-9, 9-10-1).
- 4. Пять треугольников, состоящих из двух маленьких треугольников и пятиугольника (2-11-6, 4-11-8, 6-11-10, 8-11-2,10-11-4).
- 5. Пять треугольников, состоящих из четырех маленьких треугольников и пятиугольника (1-2-10-11-6, 3-4-2-11-8, 5-6-4-11-10,7-8-6-11-2,9-8-10-11-4).
Всего получилось 10 + 10 + 5 + 5 + 5 = 35 треугольников.
Оценка выполнения задания (д)
- 1. Учащийся увидел все взаимопроникающие треугольники, предложил алгоритм подсчета (не обязательно рассмотренный нами) — оценка 4 балла.
- 2. Учащийся увидел треугольники, соответствующие пп. 1, 2, 3, 4 или 1, 2, 3, 5 и какие-то треугольники, соответствующие пп. 4 или 5, — оценка 3 балла.
- 3. Учащийся увидел треугольники, соответствующие пп. 1, 2, 3, но не увидел ни одного треугольника, соответствующего пп. 4 и 5, — оценка 2 балла.
- 4. Учащийся увидел какие-то треугольники, соответствующие пп. 1, 2, 3, но не все — оценка 1 балл.
- 5. Учащийся увидел только треугольники, соответствующие п. 1, — оценка 0 баллов.
При рассмотрении предложенных в предыдущей задаче случаев видно, что можно пользоваться «методом проб и ошибок», но без подключения «анализа» (причем иногда довольно углубленного) успеха добиться трудно.
Задача 5.12. Сосчитайте, сколько треугольников изображено на рис. 5.14.
Ответ: на рис. 5.14, а изображено 13 треугольников; 5.14,6 — 27 треугольников; 5.14, в — 47 треугольников; 5.14, г —27 треугольников; 5.14, д — 32 треугольника; 5.14, е — 48 треугольников.
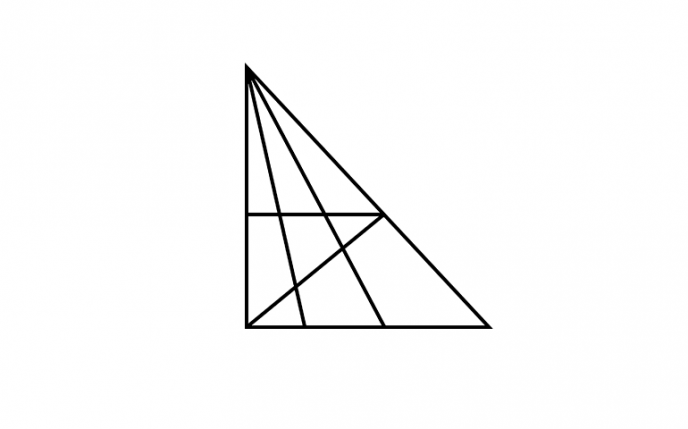
Внимательно посмотрите на картинку, представленную далее.
Сможете отыскать на ней 18 треугольников и больше? Если да, поздравляем! Ваш IQ выше 120.
Проверь свой IQ
Даже если геометрия никогда не была вашей сильной стороной в школе, попробуйте отыскать на картинке 18 треугольников.
Изображение, которое первоначально было опубликовано в издании People’s Daily China, представляет треугольник с несколькими вариантами треугольников внутри него… Мнения пользователей о том, сколько треугольников скрыто на картинке, разошлись.
По мнению экспертов, только те, у кого значение 120 или выше, могут видеть 18 треугольников и более.
Итак, вам удалось рассмотреть 18 треугольников? А, может, вы смогли найти большее количество фигур на рисунке?
Некоторые пользователи социальной сети Twitter поделились своими достижениями. Кто-то сообщил, что ему удалось справиться с задачей всего лишь за 12 секунд. Истинный гений, не так ли?
Другой же утверждал, что нашел 24 треугольников и даже предоставил этому доказательства.
Третий же придумал удобную систему кодирования букв для поиска всех фигур.

А теперь попробуйте потренировать свои способности с помощью несложных логических задач, с которыми вполне способен справиться и смышленый ребенок.
Задачи на логику с ответами
Ответы указаны в конце постаЗадача № 1:

Перед вами стол. Сколько углов останется у него, если один из них отпилить?
a) 3 угла;
b) 4 угла;
c) 5 углов;
d) 6 углов.
Задача №2:

В холодильнике имеется 3 яблока и 4 морковки. Одну морковь хозяйка взяла для салата. Сколько всего фруктов осталось в холодильнике в итоге?
а) 3 фрукта;
b) 4 фрукта;
c) 6 фруктов;
d) 7 фруктов.
Задача №3:

На ипподроме вы видите 6 пар лошадиных ног. Сколько всего лошадей находится на ипподроме?
a) 3 лошади;
b) 4 лошади;
c) 8 лошадей;
d) 12 лошадей.
Задача №4:

Близнецам Джеймсу и Джону друзья подарили на День рождения по коробке сладостей. В каждой коробке имеется 12 конфет. Джеймс съел несколько конфет из своей упаковки. Джон сделал то же самое, съев из своей коробки столько конфет, сколько осталось в коробке у Джеймса.
Вопрос: сколько всего конфет осталось на двоих у ребят в итоге?
Задача на внимательность
Задача № 5: Найди ошибку

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Ответы:
Ответ № 1: При отпиливании одного угла, в результате образуется 5 углов.
Ответ № 2: В холодильнике по-прежнему останется 3 фрукта. Ведь морковь-это овощ, а яблоко- это фрукт.
Ответ № 3: На ипподроме 3 лошади. Логично: 6 пар ног- это 12 ног. У каждого животного по 4 конечности. Если мы 12 поделим на 4, получится 3.
Ответ № 4: 12 конфет.
Ответ № 5: Ошибка в слове «Можеш». Оно написано без мягкого знака после буквы Ш.
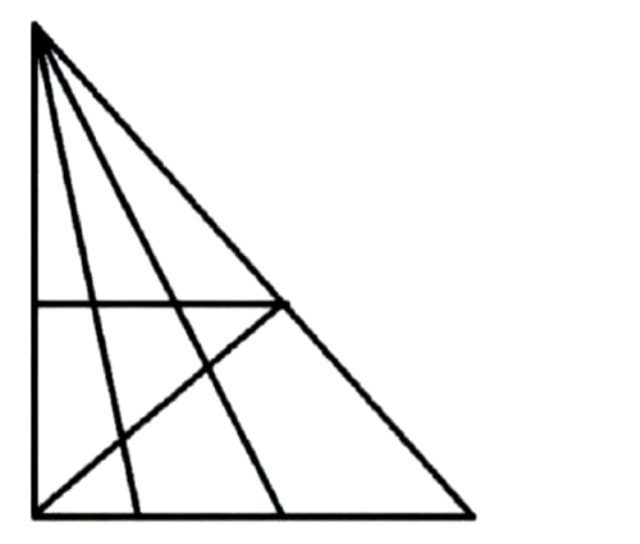
Задача, которую решают единицы: сколько треугольников на картинке?
Если у вас нашлась свободная минутка, то почему бы вам не проверить свои силы и не попробовать решить довольно простую задачу. Хотя простой она может показаться уже после того, как вы узнаете ответ. Итак, сколько треугольников вы можете найти на этой картинке?
Считается, что найти все зашифрованные треугольники могут только люди с высоким IQ. Если вы думаете, что действительно нашли все треугольники, то попробуйте сравнить свой ответ с нашим.
Число треугольников на картинке 24. Эта цифра может показаться невозможной, но это единственно верный ответ.
Считаем треугольники — разбор задания
Неделю назад дал ученикам своих мини-групп задание посчитать все треугольники, из которых состоят два рисунка:
Легкий треугольник
Сложный треугольник
Задание 1.
К выполнению подобных заданий нужно подходить системно. (Именно этому я учу детей, которые собираются поступать в 5 класс математических гимназий и лицеев, на моем математическом кружке и в мини-группах в Новых Черемушках.)
Пронумеруем все элементы легкого треугольника.
Выпишем поочередно треугольники, состоящие из одного элемента, из двух, из трех и т.д.
1. Из 1 элемента: 1, 2, 3, 5 — всего 4 треугольника (некоторые дети автоматически зачисляют в треугольники элементы № 4 и № 6 — это неправильно!).
2. Из 2 элементов: 12, 34, 56, 13, 35, 24 — всего 6 треугольников.
3. Из 3 элементов: 135, 246 — 2 треугольника.
4. Из 4 элементов: 1234 и 3456 — 2 треугольника.
5. Из 5 элементов — ничего нет.
6. Из 6 элементов — единственный 123456.
Итого: 15 треугольников.
Задание 2.
Сложное задание, требующее от детей внимательности, усидчивости и аккуратности в подсчетах. Пронумеруем все элементы легкого треугольника, причем цифр от 1 до 9 нам не хватит. Задействуем 10, 11 и 12.
Выпишем поочередно треугольники, состоящие из одного элемента, из двух, из трех и т.д.
1. Из 1 элемента: все от 1 до 12 — это треугольники. Их 12 штук.
2. Из 2 элементов. Начинаем считать от вершины и движемся по часовой стрелке. 12, 17, 18, 9 11, 11 12, 12 10, 56, 54, 43. Не забудем про внутренние треугольники: 28, 9 10, 36. Насчитали снова 12 штук.
3. Из 3 элементов — отыщем их только во внутреннем треугольнике. 289, 36 10, 823, 9 10 6, 10 98, 632. Их 6 штук.
4. Из 4 элементов: 1234, 1236, 789 10, 789 11, 12 10 63, 12 10 65, 289 11, 4328, 56 10 9. Набрали еще 9 треугольников.
5. Из 5 элементов — ничего не нашел. Кто найдет — напишите, объявлю благодарность.
6. Из 6 элементов: 123456, 789 10 11 12, 12789 11, 12 10 6345, 56 10 9 11 12, 432178 — нарыли еще 6 штук. Плюс центральный: 236 10 98. Итого — 7 треугольников.
7. Ну и самый большой, из 12 элементов — 1 треугольник.
Кратко:
1 — 12
2 — 12
3 — 6
4 — 9
6 — 7
12 — 1
Итого: 47 треугольников. (Огромное спасибо мамам Антона и Маруси, которые помогли мне найти недостающие треугольники из 4-х элементов).
Бедные мои ученики…
Сочувствую. Но если им нужно сдавать вступительные экзамены в наши математические школы Юго-Запада (1533, 1534, 1543, 2007, Л2Ш, 1514 и т.д.) или участвовать в олимпиадах, то такая тренировка мозгов пойдет им только на пользу.
Так что их ждут новые задания. Что-то — полегче, что-то — потяжелее. Поступление в хорошую школу стоит того, чтобы усердно работать над заданиями, чуть-чуть выходящими за рамки школьной программы.
С этой задачкой для первоклашек не могут справиться даже опытные учителя: проверьте свои знания
Эта банальная логическая задача стара как мир. Все очень просто: посчитайте каждый отдельный треугольник, затем сложите все различные комбинации маленьких треугольников и обязательно не забудьте про большую общую фигуру. Вы ведь так делаете? При всей своей простоте, эта задача всегда вызывает массу споров и сотни комментариев с ответами в диапазоне от четырех до 45 (боже, откуда столько?).
Давайте сначала вспомним из школьной программы, что же такое треугольник. В евклидовом пространстве это геометрическая фигура (он же многоугольник с фиксированным числом углов), образованная тремя отрезками (стороны треугольника), которые соединяют три точки (вершины треугольника), не лежащие на одной прямой. Возможно, мы повторно взорвем ваш мозг, но есть так называемый вырожденный треугольник, вершины которого таки лежат на одной прямой. Живите теперь с этим.
Отрезок, соединяющий вершину с точкой на противоположной стороне, называется чевианой. Обычно под чевианой понимают не один такой отрезок, а один из трех отрезков, проведенных из трех разных вершин треугольника и пересекающихся в одной точке. В нашем случае есть две чевианы, которые спускаются из верхнего угла на нижнюю сторону большой фигуры. Благодаря треугольнику появилась тригонометрия, планиметрия, а еще используя эту простую фигуру, люди научились составлять карты, измерять участки и конструировать. Даже «Черный квадрат» Малевича должен был называться «Черный китайский треугольник», и не спрашивайте, почему. Казимир Северинович унес эту тайну с собой на тот свет. В общем, при всей своей простоте полезная штука. Но мы отвлеклись.
Итак, еще раз посмотрим на нашу задачу. Те из вас, кто везде торопится, выдают сразу варианты ответов: шесть треугольников, 16, 22. Многие насчитывают 18 искомых фигур. Кто подотошнее считает, что на изображении нет ни одной прямой линии, а некоторые углы — не углы вовсе. Ну, конечно, это же нарисовано от руки! Для таких тут вообще нет ни одного треугольника. Зануды. Если вы все еще не нашли ответ и пытаетесь прочитать его в этом тексте, то остановитесь и просто посчитайте чертовы треугольники.
Ладно, давайте не будем играть в «Поле Чудес», а посмотрим на задачу с точки зрения науки. Единственный способ образовать треугольники на рисунке — это если верхний угол является частью каждого треугольника. Основание треугольника должно быть одним из трех горизонтальных уровней ниже. Получается, три уровня, на каждом вы можете выбрать базу для шести разных способов построения фигуры. В сумме выходит восемнадцать или три раза по шесть треугольников. Все варианты научного решения так или иначе крутятся вокруг этого способа. И да, вы же не забыли посчитать треугольник у стрелочки? Ладно, это была шутка. Или все же посчитали?
[spoiler title=”источники:”]
http://www.popmech.ru/science/587343-zadacha-dlya-pervoklashki-a-vy-spravites/
[/spoiler]
