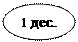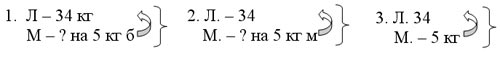Математика 3 класс Урок №58.
Приёмы письменных вычислений
Перечень вопросов, рассматриваемых в теме:
Как контролировать пошагово правильность применения алгоритмов арифметических действий при письменных вычислениях?
Как использовать различные приёмы проверки правильности вычислений?
Глоссарий по теме:
Каждая цифра в записи многозначного числа занимает определённое место – позицию. Место (позицию) в записи числа, на котором стоит цифра, называют разрядом.
Единицы, десятки, сотни, тысячи и т. д. иначе ещё называют разрядными единицами: единицы называют единицами 1-го разряда
десятки называют единицами 2-го разряда
сотни называют единицами 3-го разряда и т. д.
Сложение – арифметическое действие в математике, в результате которого два или более чисел объединяется в единое целое, оно обозначается знаком «+». Слагаемое, слагаемое, сумма – главные составляющие математического действия сложения.
Вычитание – арифметическое действие, обратное сложению и обозначается оно знаком «-». Уменьшаемое, вычитаемое, разность- главные составляющие математического действия вычитания.
Основная и дополнительная литература по теме урока:
1. Моро М. И. Учебник для 3 класса четырехлетней начальной школы. М. «Просвещение» — 2017. с. 70-72.
2. Волкова С. И. Проверочные работы. 3 кл. — М.: Просвещение, 2018. с. 72-75.
3. Волкова С. И. математика. Тесты. 3 кл. — М.: Просвещение, 2018. с. 54-59.
4. Рудницкая В. Н. Математика. Дидактические материалы.Ч.1 3 кл. – М. «Вентана- Граф», 2016, с. 10-12.
Теоретический материал для самостоятельного изучения
Не любой пример с трёхзначными числами можно быстро решить в уме
Как быть в таком случае?
Уже давно люди научились пользоваться письменным приёмом вычислений. И не только трёхзначных, а любых многозначных чисел.
Если вы хорошо усвоите приёмы письменных вычислений с трёхзначными числами, то без труда сможешь решать примеры с любыми числами.
Для того чтобы освоить приёмы письменных вычислений трёхзначных чисел необходимо вспомнить действия с двузначными числами.
При этом действия записываются столбиком и выполняются поразрядно, начиная с первого разряда (единиц).
При работе с трёхзначными числами разрядов уже не два, а три. И в алгоритм соответственно добавляется ещё один шаг – работа с сотнями.
Сегодня мы попробуем выполнять письменные вычисления трёхзначных чисел, опираясь на умение работать с двузначными числами.
Найдём сумму чисел 427 и 196 в столбик.
- Сначала запишем одно число под другим так, чтобы единицы были под единицами, десятки под десятками, а сотни под сотнями.
2. Складываем единицы: 7 + 6 = 13
3 пишем под единицами, а 1 дес. запомним и прибавим к десяткам.
3. Складываем все десятки: 2 + 9 + 1 = 12
2 пишем под десятками, а 1 сот. запомним и прибавим к сотням.
4. Складываем все сотни:
6 пишем под сотнями.
Ответ: 623
Найдём разность чисел 846 и 561 в столбик.
1. Сначала запишем одно число под другим так, чтобы единицы были под единицами, десятки под десятками, а сотни под сотнями.
2. Вычитаем единицы.5 пишем под единицами.
3. Вычитаем десятки
Из 4 дес. вычесть 6 дес. нельзя. Занимаем 1 сот.у 8 сот. и ставим точку над цифрой 8,
чтобы знать, что на 1 сотню осталось меньше.
Из 14 дес. вычитаем 6 дес.
8 пишем под десятками.
4. Вычитаем все сотни: 2 пишем под сотнями.
Ответ: 285
Главное при выполнении письменных вычислений строго следовать алгоритму.
Если при выполнении сложения в разряде появились единицы другого разряда, их надо запомнить и прибавить к следующему разряду.
Если при вычитании в разряде недостаточно единиц чтобы выполнить действие, надо занять у разряда слева, а потом не забыть, что 1 десяток, или 1 сотню занимали, значит единиц в этом разряде на 1 меньше.
Не забывайте про алгоритм и у вас всё получится.
Задания тренировочного модуля:
- Укажите правильно вычисленную разность чисел 723 и 474
Правильные варианты ответов:
- Введите результат вычислений.
Правильные варианты ответов:
284, 0, 106, 660, 214
- Подчеркните ошибки в вычислениях
Правильный вариант:
Привет, ребята!
Ну как, вы готовы слушать объяснение новой темы?
Во время прошлой нашей встречи я рассказывал вам, как можно устно складывать и
вычитать двузначные и трёхзначные числа.
Но иногда считать устно бывает довольно сложно. И
тогда можно использовать приёмы письменных вычислений. Сегодня я
хочу вам рассказать, как складывать трёхзначные числа письменно, то есть записывая
их столбиком.
Итак, начнём. Запись оформим на разлиновке в
клеточку, ведь вы же помните, как важно при письменном приёме вычислений
аккуратно выполнять записи. Если чуть сдвинуть число в сторону, или вписать две
цифры в одну клеточку, при вычислении легко допустить ошибку. Вспоминаем, как складывать
двузначные числа. Находим сумму чисел сорок шесть и тридцать девять.
Единицы записаны под единицами, десятки под десятками. Знак плюс. Черта. Складываем
единицы. Шесть и девять – пятнадцать. Это пять единиц и один десяток. Под единицами
записываем пять, а десяток запоминаем. Складываем десятки. Четыре и три – семь,
да ещё один – восемь. Ответ – восемьдесят пять.
Теперь к трёхзначному числу прибавим двузначное. Двести
сорок шесть плюс тридцать девять. Опять строго записываем единицы под
единицами, десятки под десятками. Под сотнями не пишем ничего, ведь во втором
слагаемом сотен нет. Конечно, вычисление начинаем с единиц. Шесть и девять –
пятнадцать. Под единицами записываем пять, а десяток запоминаем. Складываем
десятки. Четыре и три – семь, да ещё один – восемь. А сотни просто переносим из
первого слагаемого в сумму. Ответ: двести восемьдесят пять.
Переходим к сложению трёхзначных чисел.
Двести сорок шесть плюс пятьсот тридцать девять. Не забываем: единицы под
единицами, десятки под десятками, сотни под сотнями. Складываем единицы,
теперь десятки, не забывая про десяток, который получился при сложении единиц.
А теперь складываем сотни. Ответ: семьсот восемьдесят пять.
А вот теперь опять вернёмся к двузначным
числам. Давайте сложим числа сорок шесть и девяносто четыре. Складываем
единицы. Шесть и четыре – десять. Нуль пишем под единицами, один десяток
запоминаем. Складываем десятки. Четыре десятка и девять десятков – тринадцать
десятков. Да ещё один десяток – четырнадцать десятков. Четыре десятка
записываем под десятками, а ещё десяток десятков – это одна сотня. Записываем
слева от десятков. И ответ – сто сорок.
Попробуем сложить числа триста сорок шесть и
четыреста девяносто четыре. Складываем единицы. Шесть и четыре – десять. Нуль
пишем под единицами, один десяток запоминаем. Складываем десятки. Четыре
десятка и девять десятков – тринадцать десятков. Да ещё один десяток –
четырнадцать десятков. Четыре десятка записываем под десятками, а цифра один
показывает количество образовавшихся сотен. Запоминаем. Складываем сотни. Три
сотни плюс четыре сотни, да ещё сотня, которая получилась в результате сложения
десятков – это восемь сотен. И ответ – восемьсот сорок.
Обратите внимание на то, что последовательность
выполнения вычислений во всех решённых примерах одинакова.
Пишу числа одно под другим. Единицы записаны под единицами, десятки под
десятками, сотни под сотнями. Знак плюс. Черта.
Складываю единицы. Если при сложении единиц получается двузначное
число, его единицы записываю под единицами, а полученный десяток добавлю к
десяткам.
Складываю десятки. Если при сложении десятков получается двузначное
число, цифру, которая находится справа, записываю под десятками, а вторая цифра
обозначает количество полученных сотен.
Складываю сотни. Не забываю про ту, которая получилась при сложении десятков.
Читаю ответ.
Вот у нас и получилась последовательность
выполнения действий при сложении трёхзначных чисел. А если сказать короче – алгоритм
сложения трёхзначных чисел.
Я думаю, сложение вы поняли. Не забудьте его алгоритм.
А в следующий раз мы с вами поговорим о том, как
правильно выполнять вычитание столбиком трёхзначных чисел. До встречи, друзья!
Одной из главных задач преподавания арифметики в начальных классах школы является обучение детей письменным вычислениям. Письменные вычисления — это необходимая составная часть математической грамоты. Наряду с решением задач они составляют главное содержание программы 3 класса. Кроме того, письменные вычисления имеются также в программе 4 класса, где они повторяются.
Ученик, оканчивающий 4 класс, должен хорошо владеть навыками письменных вычислений.
Каждое вычисление в целом и каждую вычислительную операцию в отдельности он должен выполнять сознательно. Правила должны быть для ученика понятными и обоснованными.
Письменные вычисления всегда должны приводить к пр ав ил ь ны м , б ез оши б о чным результатам. Ошибки в вычислениях нетерпимы в такой же мере, как орфографические ошибки в письме.
Навыки письменных вычислений должны быть твёрдыми, устой – чив ыми . Раз приобретённые, они не должны утрачиваться. Навык, скоро утрачиваемый, — неполноценный навык.
Письменные вычисления должны выполняться не только правильно, но и достаточно быстро , увер енно . Вычисления, производимые медленно и сбивчиво, свидетельствуют о незрелости навыка, о недостаточной работе над его развитием и закреплением.
Письменные вычисления всегда должны выполняться р аци о нал ь – н ы ми с п о с о б ами , т. е. такими, при которых вычисления не содержат в себе ничего лишнего, выполняются с минимальной затратой времени и на основании разумно используемых законов арифметических действий, лежащих в основе вычислительных приёмов.
Записи вычислений должны быть кр атки , уд о б ны , л е гко о б о – зр имы . Располагать их на странице тетради надо в определённом порядке и симметрично.
Обстоятельное о бъяснение правила письменного выполнения каждого арифметического действия достигается путём: а) умелого расчленения сложного навыка на его составные элементы — на отдельные «случаи», б) расположения этих случаев в порядке их постепенного усложнения, в) выделения в каждом новом случае особенного , единичного, г) подчёркивания элементов схо д с тв а нового случая с ранее изученными и д) применения наглядности. При помощи р ас сужд е ний , сопутствующих вычислениям, обосновывается каждая операция в отдельности и правило в целом. Ясному пониманию механизма письменных вычислений способствует применение в объяснении ан алитич е ско го приёма (см. примеры на стр. 471), при котором сложное целое расчленяется на его составные элементы. Общепринятые, стандартные формы записи вычислений в некоторых случаях вводятся не сразу, а постепенно, через промежуточные формы.
Первы е упр аж н е ния в навыке, направленные на углубление понимания вычислительных операций, выполняются учеником с подробными рассуждениями при непосредственной помощи учителя. В по следую – щ их упражнениях, направленных на автоматизацию навыка, происходит постепенный переход: а) от подробных рассуждений к кратким, схематичным, с допущением в языке принятых условностей; б) от упражнений с прямой помощью учителя к вполне самостоятельным упражнениям; в) от лёгких примеров к трудным; г) от медленных темпов в вычислениях к более скорым. Упражнения проводятся на таком колич е с тв е примеров, которое обеспечивает получение навыка, отвечающего указанным выше требованиям Объективным показателем достаточности или недостаточности упражнений являются результаты письменной контрольной работы. Допущенные в контрольной работе ошибки регистрируются и классифицируются, устанавливаются их причины, и вслед за этим ведётся работа над их ликвидацией. Если причина ошибок кроется в недостаточно ясном понимании вычислительной операции, даётся объяснение, углубляющее это понимание; если же она лежит в нетвёрдом навыке, даются дополнительные упражнения тренировочного характера.
Закрепление полученного навыка производится при помощи систематического повторения, причём большое внимание уделяется трудным вычислительным операциям.
Источник:
Начальная школа. Настольная книга учителя – 1950, под редакцией проф.. М.А. Мельникова
Способы письменных вычислений ( в столбик)
Способы письменных вычислений
( в столбик)
В основе выполнения письменных способов вычислений лежит использование правила сложения суммы с суммой. В явном виде в современных учебниках математики для начальных классов данное правило не изучается, оно заменено упрощенным вариантом правила поразрядного сложения: единицы складываются с единицами, десятки с десятками.
Письменный алгоритм сложения содержит:
1. Правило записи слагаемых при письменном сложении: разряд записывается под соответствующим разрядом.
2. Указание на порядок выполнения действий: сложение начинаем с разряда единиц (справа налево).
3. Прием добавления накапливающихся единиц старших разрядов в соответствующий разряд после выполнения основного сложения.
Алгоритм письменного сложения и вычитания в начальной школе вводится во 2 классе на примере сложения и вычитания двузначных чисел в пределах сотни.
На самом же деле, уже при знакомстве со случаями вида 45 + 23, учитель знакомит детей со способами записи вычислительных действий «в столбик» и приемом поразрядного сложения, применяемым при письменных вычислениях:
Сначала предлагается устный способ вычислений:

Затем отмечается, что удобно записать этот пример столбиком:
Далее в учебнике приводятся подробные объяснения приема вычислений:
1. Пишу десятки под десятками, а единицы под единицами.
2. Складываю единицы: 5 + 3 = 8. Пишу 8 под единицами.
3. Складываю десятки: 4 + 2 = 6. Пишу 6 под десятками.
4. Читаю ответ: сумма равна 68.
Главным отличием письменных вычислений от устных является порядок складывания (или вычитания) разрядных единиц. При устных вычислениях всегда начинают со старших разрядов (в данном случае – с разряда десятков) и выполняют действие, двигаясь слева направо. При письменных вычислениях всегда начинают с разряда единиц и выполняют действие, двигаясь справа налево.
Методическое обоснование знакомства детей со способами письменных вычислений при формировании вычислительной деятельности в пределах 100:
1. Многие дети с большим трудом осваивают устные вычислительные действия с двузначными числами. Письменный прием вычислений облегчает им вычислительную деятельность.
2. Полноценное освоение устной вычислительной деятельности требует от ребенка свободного владения результатами табличных вычислений в пределах 10 и 20, свободного владения разрядным составом чисел, десятичным составом чисел, умением гибко и свободно применять разнообразные вычислительные действия, выбирая способ вычислений в каждом случае. Далеко не все дети могут это делать. Письменный способ вычислений требует более простых вычислительных действий, выполняемых по единому жесткому правилу (называемому «алгоритмом письменных вычислений»).
3. Знакомство со способами оформления вычислений «в столбик» при изучении вычислений в пределах 100 рассматривается как подготовка к использованию этой вычислительной технологии в дальнейшем (при вычислениях с трехзначными и многозначными числами).
Запись и способ вычисления « в столбик» для многих детей, с трудом усваивающих устные приемы сложения и вычитания (особенно с переходом через десяток), является более легким и доступным. Запись «в столбик» и применяемые при этом вычислительные приемы позволяет создать для ребенка «систему промежуточных опор», так как на каждом шаге вычислений ребенок фактически действует не более чем в пределах второго десятка, что значительно облегчает вычисления.
| 1) 217 +439 | 2) 217 +439  56 1 дес. + 3.дес. = 4дес. 56 1 дес. + 3.дес. = 4дес.
|
3) 217 2сот. + 4дес. = 6сот. +439  656 656 |
В основе письменного сложения и вычитания лежат:
1) прочное знание таблицы сложения и соответствующих случаев вычитания в пределах 10;
2) умение складывать и вычитать в пределах 20 (с переходом через десяток);
3) знание разрядного состава чисел и соотношение разрядных единиц;
Алгоритм письменного вычитания строится на тех же принципах. Сначала детей знакомят со способом записи чисел при выполнении письменных вычислений и определяют порядок выполнения вычислений (справа налево, начиная с разряда единиц).
1. Пишу десятки под десятками, а единицы под единицами.
2. Вычитаю единицы из единиц: 6 – 2 = 4. Пишу 4 под единицами.
3. Вычитаю десятки из десятков: 5дес. – 4дес. = 1дес. Пишу 1 под десятками.
4. Читаю ответ: разность равна 14.
Наиболее трудны для многих детей, как и при устных вычислениях, случаи вида 50 – 24 и 52 — 24, где для выполнения вычислений необходимо выполнить «заем» десятка из старшего разряда.
Например: 5дес. = 4дес. + 1дес.
1. Пишу единицы под единицами, десятки под десятками.
2. Вычитаю единицы. Из 0 нельзя вычесть 4. Занимаю 1дес. из 5дес.
1дес. = 10; 10 – 4 = 6.Пишу под единицами 6.
3. Вычитаю десятки. Было 5 дес., но 1дес. занятии при вычитании единиц. Осталось 4дес. 4дес. – 2 дес. = 2дес. Пишу 2 под десятками.
4. Читаю ответ: разность равна 26.
Для того чтобы не забывать о заемной единице, над разрядом десятков можно ставить точку, черточку, или подписывать число оставшихся после заема разрядных единиц.
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Источник
Вопрос 7. «Технологии формирования устных и письменных вычислений»
Характеристика видов вычислений и вычислительных приемов
1. Виды вычислений
2. Характеристика вычислительного приема
3. Этапы формирования вычислительных умений
4. Виды вычислений
Формирование у школьников 1-4 классов вычислительных умений и навыков традиционно считается одной из основных задач курса математики в начальной школе
По способу производства действий вычисления делятся на три вида: устные, письменные и полуписьменные.
Устные вычисления в сформированном виде выполняются мысленно, совсем без записи чисел или с записью данных и результата в строчку. При этом сами вычисления выполняются разными способами и начинаются с единиц высшего разряда. Устные вычисления в процессе усвоения могут быть доведены до уровня навыка. Вычисления протекают в форме автоматизированного (неосознаваемого) психического регулирования, а обращение к развернутому алгоритму выполнения действия происходит только в случаях затруднений или по требованию учителя, желающего проверить степень осознанности выполняемого действия или для осуществления контроля за выполняемым действием.
Устные вычисления в свою очередь делятся на табличные и внетабличные. К табличным вычислениям относят все случаи выполнения сложения и умножения с однозначными числами и соответствующие им случаи вычитания и деления. К устным внетабличным приемам вычислений относят все случаи вычислений в пределах сотни, кроме табличных, и, сводимые к ним, вычисления с многозначными числами.
Письменные вычисления характеризуются тем, что в процессе вычислений производится запись, как результата действия, так и промежуточных операций, которая имеет особую форму записи «в столбик». Вычисления выполняются по установленным правилам (алгоритмам) и начинаются с единиц низших разрядов (кроме деления). Письменные вычисления формируются на уровне умений и выполняются с опорой на усвоенный алгоритм действия, который постепенно сокращается, приобретая некоторые операциональные характеристики, но усвоенный алгоритм всегда остается регулирующей основой вычислительного действия.
Полуписьменные вычисления характеризуются частичным использованием признаков устных и письменных вычислений и чаще всего используются в особых приемах вычислений
328 * 25 = 328 * 100 : 4 = 328 : 4 * 100 = 8200
К полуписьменным вычислениям относят и деление в столбик, поскольку этот вид вычислений начинается с единиц старшего разряда, а значит, обладает признаками письменных и устных вычислений.
2. Характеристика вычислительного приема
Под вычислительным приемом (ВП) понимают совокупность операций, приводящую к нахождению результата вычислений в выражениях определенного типа. В устных вычислениях чаще всего эта совокупность операций содержит:
· разбивку одного из чисел на части, что приводит к получению составного выражения;
· применение свойства арифметического действия для изменения порядка действий в полученном составном выражении;
· выполнение во вновь полученном составном выражении вычислений по правилу порядка действий.
Подробное проговаривание этих операций составляют полный, развернутый алгоритм рассуждений. Например, для вычислительного приема вида 40+12 он будет следующим. «Чтобы к 42 прибавить 12 можно, 12 разложить на сумму разрядных слагаемых 10 и 2 и эту сумму прибавить к числу 40. Получим составное выражение 40+(10+2). Чтобы вычислить значение этого составного выражения можно изменить в выражении порядок действий применив правило прибавления суммы к числу. Удобно, к числу40 прибавить 10 и к полученному результату прибавить второе слагаемое 2. Получим второе составное выражение (40+10)+2. Вычислим значение этого выражения, применив правило порядка действий. Вычисляем, к 50+10=60, к 60+2=62. Значение суммы чисел 40 и12 равно 62.» Символическая запись этого рассуждения имеет вид:
Такой алгоритм должен быть представлен детям на уроке ознакомления с вычислительным приемом, затем он постепенно сокращается и переходит в умственный план.
Овладеть вычислительным приемом, значит, для каждого случая знать, какие операции и в каком порядке следует выполнять, чтобы найти результат арифметического действия и выполнять эти операции достаточно быстро в развёрнутом и свёрнутом виде.
Вычислительный приём имеет название, теоретическую основу, алгоритм рассуждений и совокупность базовых знаний.
Название вычислительного приёма складывается из названия вида вычислений (письменные, устные), действия, которое используется в вычислении (сложение, вычитание, умножение или деление) и названия чисел по их значности (однозначное, двузначное).
Например: 371*8 – письменное (вид вычисления) умножение (действие) трёхзначного числа на однозначное (названия чисел по их значности).
В основе методики формирования вычислительных умений и навыков положен принцип сведения нового вычислительного приема к ранее изученным. Это значит, что каждый ВП требует знания определенной совокупности базовых знаний, опираясь на которую можно организовать самостоятельную деятельность детей по открытию нового ВП и его осознанное усвоение. Например, для вычислительного приема вида «умножение двузначного числа на однозначное» базовой может быть следующая совокупность знаний:
· разрядный состав чисел;
· свойство умножения суммы на число;
· правило порядка действий; умножение круглых десятков на однозначное число;
· табличные случаи умножения;
· сложение двузначных чисел.
Теоретической основой ВП могут служить свойства арифметических действий или следствия из них, с помощью которых данный вычислительный прием сводится к ранее изученным, и таким образом находят значение данного выражения.
Например, для вычислительного приема вида 13-5 можно использовать, по меньшей мере, две теоретические основы.
В первом случае теоретической основой является свойство вычитания суммы из числа, а во втором – вычитание числа из суммы. То есть один и тот же вычислительный прием может иметь несколько теоретических основ, которые и задают алгоритм вычислений.
Ниже приводится таблица, в которой указана теоретическая основа изучаемых вычислительных приемов.
| Устные вычислительные приемы | Теоретическая основа устных вычислительных приемов |
| 40+20 50 — 30 | Разрядный состав двузначного числа. Табличные случаи сложения (вычитания) |
| 34 + 20 34 + 2 26 +4 | Прибавление числа к сумме |
| 47 + 5 | Прибавление суммы к числу |
| 42 — 5 | Вычитание суммы из числа |
| 40 + 16 40 — 16 | Прибавление суммы к числу .Вычитание суммы из числа. |
| 45 + 12 45 — 12 | Прибавление суммы к числу. Вычитание суммы из числа. |
1.3. Этапы формирования вычислительных умений
Формирование вычислительных умений и навыков – одна из основных задач начального курса математики.
Вычислительные умения – это развёрнутое осуществление действия, в котором каждая операция осознаётся и конкретизируется. В отличие от умения вычислительные навыки характеризуются свёрнутым, в значительной мере автоматизированным выполнением действия, с пропуском промежуточных операций, когда контроль переносится на конечный результат.
Принято считать, что процесс вычислений требует только репродуктивного воспроизведения соответствующего алгоритма. Поэтому в педагогической практике преобладает такой подход, при котором обучение вычислительным приемам идет репродуктивным путем. Деятельность детей состоит во внимательном слушании учителя, выполнении практических действий по заданной инструкции или образцу, объяснении готового решения. В этих условиях вычислительные навыки формируются в результате выполнения большого числа однообразных заданий, и не приобретают необходимых качественных характеристик. При таком обучении не происходит и существенного умственного развития.
Формирование полноценного вычислительного навыка должно обеспечиваться созданием ряда специальных условий. Первостепенное значение имеет систематическая работа по формированию мотивов учебной деятельности, организация поисковой, эвристической деятельности учащихся на этапе восприятия вычислительного приема, целенаправленный отбор заданий для обеспечения осознания и осмысления вновь вводимого вычислительного приема, насыщение всего процесса формирования заданиями на развитие приемов умственных действий, учет индивидуальных особенностей усвоения.
При формировании вычислительных навыков необходимо исходить из того, что мышление — это активная, целенаправленная деятельность, в процессе которой осуществляется переработка имеющейся и вновь поступающей информации, отчленение внешних случайных или второстепенных ее элементов от основных или внутренних, отражающих сущность исследуемых ситуаций, раскрывается закономерная связь между ними.
Задача учителя заключается в умелом руководстве этой деятельностью. Управлять — не значит подавлять, навязывать процессу мышления ход, противоречащий его природе, а, наоборот, максимально учитывать эту природу, согласовывать каждое воздействие на процесс с его логикой и особенностями усвоения учащихся. В связи с этим, оптимально подобранная совокупность заданий на каждом этапе формирования вычислительного навыка становится средством управления мышлением и практическими действиями школьников.
Формирование вычислительных умений и навыков можно осуществлять, придерживаясь следующих этапов: подготовка к восприятию вычислительного приема, восприятие нового материала, осознание и осмысление всех характеристик вычислительного приема, закрепление и применение сформированного вычислительного умения.
Этап подготовки к восприятию нового вычислительного приема предполагает проведение тщательной перспективной и непосредственной подготовки. Перспективная подготовкапредполагает, что учащиеся предварительно изучают все знания, которые являются базовыми для нового вычислительного приема. Этому способствует основополагающий принцип изучения вычислительных приемов: сведение нового вычислительного приема к ранее изученным.
Непосредственная подготовка к изучению нового ВП традиционно предполагает: актуализацию опорных знаний из числа тех, которые входят в базовые для нового вычислительного приема. Актуализация знаний предполагает решение трех задач:
· воспроизведение понятий и алгоритмов, необходимых и достаточных для «открытия» нового знания;
· создание положительной мотивации к изучению нового ВП;
· отработка логических приемов мышления.
При отборе упражнений для данного этапа важны все три составляющих: первая позволяет содержательно подготовить этап открытия нового знания. Вторая положительную эмоциональную направленность на его включение в следующий этап урока. Третья активизировать мыслительные способности учащихся: способность к анализу, синтезу, сравнению, классификации, аналогии, обобщению.
Этапы формирования вычислительных умений
| Подготовка к восприятию | Восприятие материала | Осознание и осмысление | Закрепление и применение |
| 1.Перспективная подготовка. 2.Непосредственная подготовка к восприятию · актуализация опорных знаний; · мотивация деятельности; · создание проблемной ситуации. | 1.Фиксация затруднения 2. Постановка учебной проблемы 3. Поиск решения учебной проблемы 4. Выделение общего способа действия, фиксация его в виде различных моделей | 1. Выполнение упражнений, удовлетворяющих принципам: полноты, однотипности, контрпримеров, сравнения, непрерывного повторения, вариативности. 2.Пооперационный контроль и коррекция | 1, Введение ВП в систему ранее изученных знаний 2. Отработка качеств ВН 3. Формирование действий контроля 4. Итоговый тематический контроль |
Следует подчеркнуть значимость создания ситуации успеха для каждого ребенка на этапе актуализации знаний, поскольку положительный результат, зафиксированный ребенком в сознании, создает положительную эмоциональную направленность на его включение в следующий этап урока.
Этап восприятия нового знания будет организован с большим развивающим эффектом, если введение нового материала будет организовано через проблемную ситуацию. Этот метод в большей степени активизирует процесс мышления и требует высокой степени теоретического обобщения.
В современных УМК предоставляются условия для использования технологии проблемно диалогического обучения, которая позволяет учащимся самостоятельно «открывать» знания, а значит включать детей в продуктивные виды деятельности. (сноска на первую часть)
Известно, что новое знание принимает четкие формы в сознании ученика, если оно зафиксировано в форме алгоритма, схемы или языковой записи, принятой в данной дисциплине и в данной технологии. В связи с чем, на этом этапе происходит оформление нового алгоритма, фиксирование его как вербально, так и графически, что создает основу для развития способности к новому виду математической деятельности – моделированию.
Этап восприятия нового вычислительного приема заканчивается первичным закреплением алгоритма выполнения вычислительного действия.
С этой целью несколько аналогичных примеров выполняются детьми у доски. Выполнение первых заданий полезно сопровождать полным теоретическим обоснованием, затем, перейти к поиску путей сокращения алгоритма и записи вычислений. Переход к выполнению вычислений по сокращенному алгоритму и сокращенной записи должен осуществляться индивидуально по мере усвоения и осознания значения каждой операции учеником.
Ознакомление детей с новым ВП в основном происходит на одном уроке, в конце которого полезно провести небольшое тестирование для выявления уровня усвоения ВП каждым учеником. Полученные в результате тестирования результаты помогут учителю осуществить дифференцированный подход в обучении и с учетом данных тестирования определить содержание следующего урока, с которого начинается следующий этап формирования ВП.
Завершая этот этап, следует особое внимание уделить подведению итога, обсуждению процесса получения результата, различным видам моделирования вновь спроектированного алгоритма выполнения действия, его проговариванию в свернутой и развернутой форме. Именно на этот образец будет ориентироваться ученик на следующих этапах и при самостоятельных вычислениях.
На этапе осознания и осмысления школьниками ВП полезно предложить совокупность упражнений, удовлетворяющую принципам полноты, однотипности, сравнения, вариативности, контрпримеров, непрерывности, единственного различия.
Эти принципы или требования к процессу отбора упражнений необходимо реализовать как для осознания и осмысления приема вычислений, так и для развития логических приемов мышления.
Раскроем принципы отбора совокупности упражнений, которую полезно предлагать учащимся на этапе осознания и осмысления вычислительного приема.
Реализация принципа полноты предполагает, что совокупность упражнений будет содержать задания, обеспечивающие осознанное применение всех операций, связанных с усвоением изучаемого вычислительного приема. К ним мы относим упражнения:
· на отбор выражений, значение которых можно находить с помощью изученного вычислительного приема;
· на отработку каждой операции, входящей в состав вычислительного приема;
· на понимание математического смысла и последовательности выполнения каждой операции входящей в состав алгоритма;
· на осуществление контроля и оценки выполненного вычислительного приема.
Совокупность упражнений будет соответствовать принципу однотипности, если на каждую из выше перечисленных операций будет выполнено достаточное число однотипных упражнений. При этом достаточность определяется индивидуальными особенностями скорости усвоения материала каждым учеником класса. Для осознания и осмысления операции некоторым детям достаточно выполнить одно упражнение, для других, этого количества бывает недостаточно. Здесь нужно подходить дифференцированно, ориентируясь на уровень развития детей в классе и организовать работу так, чтобы одним стало понятно, а другим было интересно.
Принцип контрпримеров предполагает включение в совокупность таких заданий, которые провоцируют ученика на ошибку. Умение увидеть ошибку это уже определенный уровень освоения алгоритма вычислительного приема. В связи с этим такие упражнения могут служить как для осознания и осмысления вычислительного приема, так и для диагностики уровня сформированности вычислительного приема и самоконтроля. Кроме того, такие задания дети воспринимают как своеобразную игру, с интересом включаются в диалог по обоснованию причин возникновения ошибки и правильному выполнению действия, что способствует повышению познавательной мотивации.
Применение принципа сравнения предполагает включение некоторого ряда взаимосвязанных заданий, позволяющих подчеркнуть сходство и различие нового и ранее изученного вычислительных приемов. Алгоритм вычислительных приемов дает для сравнения богатейший материал. Сравнивать можно, опираясь на схематическую, математическую модель выполнения действия, на теоретическую основу вычислительного приема и другие его характеристики. В процессе формирования вычислительных навыков скрыты немалые возможности для существенного развития мышления детей путем использования заданий на сравнение, классификацию, подведение под понятие, выведения следствия из факта принадлежности объекта к понятию. Задача учителя — реализовать их в полной мере через совокупность упражнений, предполагающих использование логических приемов мышления.
Принцип вариативности полезно использовать двояко: варьировать формы выполнения вычислительного приема (варьируя модели вычислительного приема, осуществляя переход от одной модели к другой) и видоизменять форму подачи заданий (используя формулировки: вычисли, допиши, прочитай разными способами, сравни, назови вычислительный прием и т. д.).
Принцип непрерывного повторения предполагает включение вновь изученного вычислительного приема в контекст ранее изученного материала. Это могут быть задачи, уравнения, вычисления на нахождение значений величин и другие, ранее изученные понятия.
Следует понимать, что реализация всех этих принципов вовсе не требует большого числа упражнений, разумно подбирать такие задания, выполнение которых предусматривает реализацию сразу нескольких принципов.
На этапе закрепления и применениядетям предлагается совокупность упражнений, удовлетворяющая принципу непрерывного повторения, т. е., вновь изученный ВП будет включаться в систему ранее усвоенных знаний. Кроме того, на этом этапе учитель предусматривает решение следующих обучающих задач:
· доведения изученного ВП до уровня умения или навыка со всеми присущими им качествами;
· формирование умения проверять правильность вычислений.
В процессе обучения детей работе над ошибками, можно выделить шесть этапов, на каждом из которых используются специальные методические приёмы, формирующие у детей учебные действия контроля и оценки. Результатом такой работы может быть составленный ребенком справочник вычислительных ошибок.
1. Выяснение, какие ошибки можно допустить при выполнении заданий на вычисления и каков характер этих ошибок. Это могут быть ошибки по содержанию (неправильное использование алгоритма вычисления, сложения или вычитание единиц в разряде) и ошибки на невнимание (неверно списал цифры при записи чисел, поставил не тот знак, знак поставил правильно, но выполнял другое действие и т.д.).
2. Знаковая фиксация ошибок. Следующий этап связан с поиском знаковых форм фиксации ошибок. Ученики при участии учителя разрабатывают и придумывают значки для обозначения каждой ошибки.
3. Упорядочивание ошибок. Ученики, прежде чем начать выполнять то, или иное задание, представляли, какие ошибки можно допустить при его выполнении. Такая работа учит мысленно составлять план собственных действий раньше, чем ребенок приступит к выполнению заданий.
4. Работа с контролирующей карточкой. Упорядочивая ошибки, ученики должны осмыслить и выстроить, в какой последовательности и как они будут обнаруживать эти ошибки. В результате учащиеся составляют «Справочник ошибок», где находятся карточки, в которых с помощью созданной символики фиксируют последовательность действий при проверке: первое – проверь вот это, второе – проверь вот это, третье – проверь – вот это.
Ученик выполняет задание сначала до конца, затем возвращается в начало, читает карточку и на каждом этапе проверяет, нет ли у него ошибок. При работе с карточкой очень эффективна работа в паре.
5. Выявление собственных проблем. Когда ученики совместно с учителем составили карточки для самоконтроля и начали работать с ними, то каждому ученику необходимо зафиксировать, где у него появляются ошибки, на каком шаге и отметить эти шаги на карточке.
6. Предвидение ошибки и её предупреждение. На заключительном этапе ученик сначала должен посмотреть, где он может сделать ошибку, и только после этого начинать действовать.
В настоящее время существующие учебно методические комплексы преуспели в разработке совокупности заданий, направленных на отработку как устных, так и письменных вычислений. Наиболее последовательно и обоснованно как с психологической, так и с методической точки зрения разработана совокупность упражнений в системе Д.Б. Эльконина — В.В. Давыдова.
Автор этой совокупности Э. И. Александрова. Всю совокупность упражнений она делит на 10 блоков, в некоторых из них выделяются еще и уровни.
Первый блок – это задания, которые уже выполнены кем-то, а ребёнку нужно их оценить. (Учителями этот блок называется оценочным, ученик узнает информацию и оценивает ее). Этот блок включает в себя задания двух уровней.
1-ый уровень – задания, выполненные кем-то с использованием символической модели. Ученик должен оценить правильность выполненных заданий.
2–ой уровень – задания, выполненные кем-то без использования символической модели. Для того чтобы оценить правильность выполнения заданий, ребёнку сначала нужно выполнить символическую модель.
Второй блок – исполнительный. Эти задания ребёнку нужно выполнить самому.
1-й уровень – ребёнок выполняет задание сам, но ему дан готовый ответ, с которым он сравнивает свое выполнение.
2-й уровень – ребёнок выполняет задание сам, но ему даётся несколько ответов, среди которых один правильный, а остальные получены в результате типичных ошибок.
3-й уровень – ребёнок сам выполняет задание и сам доказывает правильность его выполнения.
Третий блок – рефлексивный. Это задания на придумывание самим ребёнком таких же заданий, как те, которые ему предложены учителем. Этот блок позволяет выяснить, умеет ли ребёнок выделять существенные связи и отношения в заданиях, которые даны учителем и составить такие же.
Четвёртый блок – рефлексивно-методический. Это задания типа: «как научить других, придумывать такие же задания».
Пятый блок – диагностический. Это задания с «ловушками» (можно выделить несколько типов «ловушек»: «ловушки на способ», «ловушки, связанные с недостающими или лишними данными» и др.).
Шестой блок – рефлексивно-диагностический. Это задания на придумывание детьми таких же «ловушек», что позволяет определить, насколько ученик видит «ошибко-опасные» места.
Седьмой блок – методико-диагностический, в котором ребёнок думает над вопросом, как научить других, придумывать задания с «ловушками».
Восьмой блок – это так называемые олимпиадные задачи, к которым относятся задачи, не выходящие за рамки изучаемых понятий по годам обучения, но требующие нестандартных способов решения.
Девятый блок – это задания на придумывание детьми своих олимпиадных заданий по аналогии с данными в восьмом блоке.
Десятый блок – содержит задания, где ребенку предлагается научить других, придумывать олимпиадные задания.
Данная совокупность заданий, предлагаемая в системе, нацелена на формирование компонентов учебной деятельности (осознание учебной задачи, планирование ее выполнения, осуществление самоконтроля и самооценки).
Технологии изучения табличных случаев умножения и
соответствующих им случаев деления
1. Характеристика табличного умножения
2. Этапы формирования табличных вычислений
3. Способы запоминания таблиц
4. Особенности изучения материала в различных системах обучения
1. Характеристика табличного умножения
К табличнымотносят случаи умножения однозначных чисел и соответствующие им случаи деления.
Все знают «Таблицу умножения», которая нередко печатают на обложках тетрадей по математике. Там даются случаи умножения однозначного числа, начиная с числа 2 до числа 9, на последовательно увеличивающиеся однозначные числа от 1 до 10. Запомнив эти табличные случаи умножения, мы без труда для каждого случая из таблицы умножения находим результаты трех других, связанных с ним, случаев умножения и деления. Например, зная, что 6*3=18, мы, не особенно задумываясь, можем найти результаты следующих выражений: 3*6, 18:6, 18:3. Происходит это потому, что между этими четырьмя случаями вычислений существует связь, которая обеспечивается математическими положениями (правилами, свойствами действий или связями между производимыми действиями). Рассмотрим эти положения.
Значение 3*6 мы находим, применяя переместительное свойство суммы (Для любых а, в, принадлежащих множеству целых неотрицательных чисел верно равенство а*в=в*а). Значения следующих двух выражений 18:6 и 18: 3 находят, используя связь между действиями умножения и деления. Поскольку деление есть действие обратное умножению, то из равенства а*в=с, вытекают верные равенства: с:а=в и с:в=а. То есть деление – это действие, с помощью которого по известному значению произведения и одному из множителей мы находим другой множитель.
Из названных математических положений вытекают методические особенности изучения табличных случаев умножения и соответствующих им случаев деления.
Изучение табличных случаев умножения и соответствующих им случаев деления предусматривает рассмотрение 4-х столбцов. Первый из них отражает последовательное умножение некоторого числа, например числа 6, на однозначные числа от 2 до 9. Второй — умножение однозначных чисел от 2 до 9 на данное число 6, третий – деление результатов первого столбика на данное число 6 и четвертый – деление результатов первого столбика на однозначные числа от 2 до 9, где в результате получается число 6-ть.
Каждый из этих столбцов в методике обучения математике имеет свое название. Первый столбец – умножение 6- ти, второй – умножение на 6-ть, третий деление на 6-ть, четвертый — деление результатов первого столбика на однозначные числа со значением частного равным 6-ти.
2. Этапы формирования табличных вычислений
Формирование навыка сложный и длительный процесс, который осуществляется по тем же этапам, что и другие виды вычислений: подготовка к восприятию табличных вычислений, восприятие нового материала, осознание и осмысление всех характеристик табличных случаев умножения и соответствующих им случаев деления, закрепление и применение сформированного вычислительного навыка.
Цель перспективной подготовки – обеспечить усвоение теоретических вопросов, являющихся основой вычислительных приемов, которыми учащиеся будут пользоваться при составлении табличных случаев умножения и деления. К этим вопросам следует отнести:
· смысл действия умножения как сложения одинаковых слагаемых;
· переместительное свойство умножения;
· распределительное свойство умножения относительно сложения (правило умножения числа на сумму);
· смысл действия деления.
· взаимосвязь между действиями умножения и деления;
· рассмотрение особых случаев умножения и деления ( а*1; а:а; а*10)
На втором этапе дети знакомятся с табличными случаями умножения и соответствующими случаями деления. Составляют соответствующие столбики табличных случаев умножения и деления, опираясь на изученные теоретические положения. Знакомятся с сокращенной формой таблицы умножения (таблица Пифагора) и правилами пользования этой формой таблицы. В разных УМК табличное умножение и деление изучается по своему сценарию. Мы излагаем один из возможных вариантов.
Рассмотрим, как может быть введена таблица умножения и деления с числом 6-ть.
На доске записывается два столбца.
В процессе диалога устанавливается, что значения первых четырех случаев умножения в первом и втором столбцах можно легко найти, т.к. дети знают таблицу умножения 2-х, 3-х, 4-х, 5-ти и переместительное свойство умножения.
Значение выражения 6*6 дети могут найти, опираясь на смысл действия умножения. В начальных классах действие умножения трактуется как действие, с помощью которого можно найти значение суммы одинаковых слагаемых. Следовательно, 6*3=6+6+6=18. Для нахождения значения следующих выражений можно использовать распределительное свойство умножения относительно сложения. Например, чтобы найти результат умножения 6*7, можно 7 представить в виде суммы ( 6+1) и число 6 умножить на эту сумму, получим 6*7=6*(6+1)= 6*6+6*1=36+6=42. В этом случае используется распределительное свойство умножения относительно сложения и знание табличных случаев умножения 6*6 и 6*1. Обычно в практике устанавливают закономерность получения каждого следующего результата в таблице умножения, подчеркивая, что каждый следующий результат в таблице умножения увеличивается на первый множитель. (Если 6*7=42, то 6*8=42+6=48).
Далее уточняется, какие случаи умножения 6-ти дети должны запомнить и как знание этих случаев использовать для нахождения случаев умножения на 6-ть и соответствующих случаев деления.
Два следующих столбца деление на 6-ть и деление на однозначные числа со значением частного равным 6-ти дети составляют самостоятельно с последующей проверкой, опираясь на взаимосвязь между действиями умножения и деления.
На третьем этапе осуществляется отработка навыка со всеми присущими ему качествами: правильность, скорость, осознанность, обобщенность, полнота, рациональность, поскольку в соответствии со стандартом табличные случаи умножения и соответствующие им случаи деления должны быть усвоены на уровне сознательного вычислительного навыка.
Под вычислительным навыком будем понимать автоматизированное выполнение учеником вычислительного действия.
Полноценно усвоенные вычислительные навыки характеризуются шестью качествами: правильностью, прочностью, осознанностью, обобщенностью, рациональностью и скоростью (автоматизацией).
Качество правильности проявляется в том, что ученик, верно выбирает и выполняет вычислительные операции входящие в состав действия, что позволяет ему получать верный результат. Наличие такого качества обычно устанавливается в процессе устного опроса или математического диктанта.
Осознанность проявляется в том, что ученик осознает, на основе каких знаний осуществляется переход от одной операции к другой, какое правило определяет порядок выполнения операций. Ученик в любой момент может объяснить, как он вычислял и почему так можно находить значение выражения. Наличие данного качества можно выявить с помощью устного опроса, или специально составленных тестов.
Прочностьвыражается в том, насколько долго удерживается в памяти вычислительный прием и не утрачивается в тот период, когда он практически не используется. Данное качество обычно проверяется в начале нового учебного года, когда учитель дает тот же математический диктант, который проводился в конце предыдущего года. Сравнив результаты можно установить, какие из вычислительных приемов усвоены прочно, а какие требуют доработки или повторения.
Качество обобщенности проявляется в умении переносить известный вычислительный прием в новые условия. Обычно это можно выявить при открытии сходного вычислительного приема в новом числовом концентре.
Рациональностьпроявляется в умении выбирать те способы вычисления, которые быстрее приводят к нахождению результата. Проверить наличие этого качества можно, предложив ученику вычислить значение выражения разными способами и выбрать из них рациональный способ.
Автоматизм (скорость) проявляется в качественном и быстром выполнении вычислительного действия за счет свертывания операций входящих в его состав. Автоматизм (скорость) ВП проверяют с помощью специально организованных математических диктантов «на скорость» и последующим сравнением результатов выполнения работы с нормой.
Наиболее распространенной теорией усвоения, на которую ориентируются существующие технологии обучения, является теория поэтапного формирования умственных действий (Л.С. Выготский, П.Я. Гальперин, Н.Ф. Талызина). В ее основе лежит идея о принципиальной общности внутренней и внешней деятельности человека. Согласно этой идеи, умственное развитие, как и усвоение знаний, навыков и умений, происходит путем интериоризации, т.е. поэтапном переходе внешней материальной деятельности во внутренний умственный план. В результате такого перехода, действия с внешними предметами преобразуются в умственные и интериоризируются. При этом они подвергаются обобщению, вербализуются, сокращаются и становятся готовыми к дальнейшему внутреннему развитию, которое может превышать возможности внешней деятельности.
Последовательность усвоения алгоритма ВП на основе теории поэтапного формирования умственных действий слагается из этапов.
1. Предварительное знакомство с ВП, т.е. с совокупностью операций, которая является ориентировочной основой вычислительного действия (ООД). Знакомство осуществляется с помощью различных видов моделей (материальной, графической, математической) и проговаривается система условий его выполнения.
2. Выполнение действия в материальном или материализованном виде. На данном этапе учащиеся самостоятельно в соответствии с заданием выполняют действие в развернутой материальной (оперируя реальными предметами) или материализованной (преобразовывая модели) форме.
3. Этап внешней речи. Здесь функцию ООД выполняет речь. Учащиеся проговаривают вслух в определенной последовательности ту совокупность операций, которая входит в ВП. При этом в их сознании происходит обобщение, сокращение учебной информации, а алгоритм выполнения действия начинает автоматизироваться.
4. Этап внутренней речи. Обучаемые проговаривают алгоритм выполняемого действия про себя. При этом делается акцент только на наиболее сложные значимые операции, что способствует дальнейшему мысленному свертыванию и обобщению алгоритма.
5. Этап автоматизированного действия. Учащиеся автоматически выполняют вычислительное действие. Это свидетельствует о том, что действие интериоризировалось, т.е. перешло во внутренний план, и необходимость во внешней опоре отпала.
3. Способы запоминания таблиц.
При организации деятельности детей по выработке навыка со всеми присущими ему качествами необходимо соблюдать психологические закономерности заучивания материала, а именно:
1. Давать установку на запоминание, поскольку восприятие материала без установки на заучивание часто вообще не дает никаких результатов.
Данная закономерность у
Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций.
Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим.
Опора деревянной одностоечной и способы укрепление угловых опор: Опоры ВЛ — конструкции, предназначенные для поддерживания проводов на необходимой высоте над землей, водой.
Источник
Цели:
- Образовательные. Повторить и
закрепить умение выполнять письменные приемы
сложения и вычитания двузначных чисел с
переходом через десяток, совершенствовать
умение решать задачи, вырабатывать навыки
устного счета, закреплять знание о
геометрических фигурах, формировать навык
правильного письма цифр и выражений. - Развивающие. Развивать мыслительные
операции, навыки логического мышления, речь
учащихся. Способствовать развитию внимания и
смекалки. - Воспитательные. Пробуждать интерес
к предмету через дидактическую игру, воспитывать
чувство коллективизма, любви к математике,
интерес к истории своей страны, своего края.
Оборудование: учебник М.И.Моро,
А.А.Бантова, Г.В.Бельтюкова и др. «Математика 2
класс»
(2 часть); плакат для физминутки; изображение
танкиста, моряка, летчика, дорожного знака
«Сан.часть»; геометрических фигур, чисел, 3
варианта примеров, 3 варианта краткой записи
задач; иллюстрация реки Кубань; карта
краснодарского края; лодочки с заданиями;
магнитофон.
ХОД УРОКА
I. Организационный момент
Громко прозвенел звонок
Начинается урок.
Наши ушки на макушке
Глазки широко открыты.
Слушаем, запоминаем.
Ни минутки не теряем.
Проверка домашнего задания.
– Дома вы решали № 5. Вопросов нет по домашнему
заданию?
II. Сообщение темы и цели урока
– Тема нашего урока «Письменные приемы
сложения и вычитания».
– Мы сегодня закрепляем приемы сложения и
вычитания чисел разного вида. Решим задачи,
числовые выражения, поработаем с геометрическим
материалом и выполним самостоятельную работу,
при этом будем учиться быть сообразительными и
внимательными.
– Откройте тетради, запишите число, классная
работа.
III. Минута чистописания
1. На доске записан ряд чисел: 5, 7, 23, 8,1
– Посмотрите на ряд чисел.
– Найдите лишнее число. (23).
– Почему оно лишнее? (двухзначное).
– Какие цифры использованы для записи этого
числа? (2 и 3).
– Сколько в этом числе отдельных единиц?
Десятков?
– Увеличьте число 23 на 10 (33).
– Уменьшите число 23 на 12 (11).
– А теперь запишите число 23 в тетради. (На доске
число 23).
– Обратите внимание на правильность написания
цифр.
2. Историческая справка.
– С каким праздником связано число 23?
– А вы знаете, что 23 февраля 1918 года только что
созданная Красная армия (так в те годы называли
нашу армию) вступила в бой с немецкими
оккупантами и преградила им путь к Петрограду
(сейчас это Санкт-Петербург). Этот день стал
рождением Красной армии.
После ВОВ наши вооруженные силы стали называться
Советской армией, а день 23 февраля – День
Советской армии и Военно-Морского флота.
С распадом Советского Союза с марта 1995 года 23
февраля стал отмечаться, как День защитника
Отечества.
Вы, пока что, маловаты,
Но вы, в будущем солдаты
И сегодня мы проверим
Кому Родину доверим.
В нашем классе 3 отряда (на доске появляется
изображение танкиста, моряка и летчика):
1 – танкисты
2 – моряки
3 – летчики
– Мы отправляемся на военные учения.
IV. Устный счет
1. Задача.
– Решаем задачу. Называем только ответ.
– На военные учения прибыли 6 танкистов, 6
моряков, 5 летчиков. Сколько всего человек
прибыло на военные учения? (17)
2. Геометрический материал.
– Итак. Сориентируемся на местности.
– Какие геометрические фигуры вы видите на
плакате? (Треугольники, квадраты,
прямоугольники и круги.)
– Какая из них лишняя? (Круг)
– Почему? (Все фигуры кроме круга –
многоугольники).
– Найдите сумму чисел, записанных в кругах. (65)
– Найдите разность чисел, записанных в
квадратах. (27)
– Сложите числа, записанные в треугольниках. (64)
– Сравните числа в прямоугольниках и узнайте, на
сколько одно больше другого. (На 32)
– Что вы знаете о прямоугольнике? (У
прямоугольника углы прямые, противоположные
стороны равны).
3. Продолжи ряд чисел.
– На военных учениях, ребята, мы должны
проявить не только смекалку. Нам необходимо
обойти ловушки, а обнаружить их мы сможем, если
определим закономерность в ряде чисел и
продолжим ряд.
11, 22, 33, …, 99
83, 80, 77, …
– Какую закономерность обнаружили в первом
ряду? (Числа увеличиваются на 11).
– Во втором ряду? (Числа уменьшаются на 3).
– Молодцы, ребята, в ловушки никто не попался!
4. Задача на смекалку.
– А теперь задача на смекалку.
– К празднику зимой в саду расцвели тюльпаны.
Сначала распустились 19 тюльпанов, а потом еще 4.
Сколько всего тюльпанов распустилось? (Зимой
тюльпаны не цветут).
– А в какое время года цветут тюльпаны?
– Так сколько бы их зацвело весной? (23)
– Замечательно справились со всеми заданиями.
V. Физминутка
– С целью улучшения физподготовки проводим
физкультминутку.
– Встаньте, ребята. Выполняем упражнения под
музыку. Повторяем за мной (под мелодию песни
«Солдатушки, бравы ребятушки»).
– Теперь мы полны сил и энергии можем продолжить
учение.
VI. Закрепление пройденного
1. Работа по учебнику (с.29 №8, 1–2 пр).
– Основная цель военных учений – закрепить
умения письменно выполнять сложение и вычитание
двузначных чисел с переходом через десяток.
– Заняли удобную позицию, приступаем к
выполнению данной цели.
– откройте учебники на с.29 (№ 8, 1–2 пр.)
– Примеры выполняем с комментированием у доски и
в тетради, записывая решение столбиком. (У
доски 4 человека).
– Закройте учебники. Отложите в сторону.
2. Самостоятельная работа. (Дифференцированный
подход.)
– А сейчас выполняем задание, которое
приготовили военные.
– Перед вами несколько вариантов.
– Каждый из вас должен выбрать только одно
задание, с которым он справится (повтор) и решит
только 2 примера.
– Кто решил, сядьте правильно. Положите ручку на
стол.
– Итак, кто выбрал первое задание?
– Кто второе?
– Кто третье?
3. Самопроверка.
– Проверяем. (Открываю ответы.
– У кого нет ошибок? Молодцы!
– Остальные ребята исправили ошибки?
– В следующий раз будьте внимательнее.
4. Домашнее задание.
– Ребята, дома попробуйте составить вот такие
же 2 примера с пропущенными числами и завтра на
уроке вы их решите.
5. Решение задачи.
– Мы отправляемся дальше.
– На пути следования солдатская кухня.
– Слушаем задачу.
– Для солдатской кухни доставили 34 килограмма
лука, а моркови на 5 килограмм меньше. Сколько
всего килограмм овощей привезли на солдатскую
кухню.
– Разбор задачи.
– О чем говорится в задаче? (Об овощах).
– О каких овощах?
– Что нам известно? (Лука 34 килограмма, а
моркови на 5 килограмм меньше).
– Какой вопрос в задаче?
– Можем ли мы сразу ответить на вопрос задачи?
– Почему?
– А можем ли мы узнать, сколько привезли моркови?
– Каким действием «+» или «–»?
– После этого мы сможем ответить на вопрос
задачи?
– Каким действием: сложением или вычитанием?
– Посмотрите на доску и назовите номер краткой
записи, которая соответствует нашей задачи. (2).
– Правильно, давайте повторим условие задачи по
краткой записи.
– Запишем решение задачи с комментированием (с
места)
– Закройте тетради.
– Молодцы, ребята. Отправляемся дальше
VII. Физминутка (санчасть)
1. – Ребята, следующая остановка «Пункт первой
медицинской помощи» (На доске – дорожный знак).
– Представьте, что я медсестра.
– Чтобы ваши глазки лучше видели, выполним
гимнастику для глаз.
– Я буду водить указкой по стрелкам, а вы следите
за бабочкой.
2. Упражнения на релаксацию.
VIII. Закрепление пройденного
(Продолжение).
1. Решение числовых выражений. Работа в парах.
– Мы подошли к главной реку Краснодарского
края. (Иллюстрируются реки)
– Как она называется? (Кубань)
– Нам необходимо переправиться через нее.
– Посмотрите на карту Краснодарского края.
Кубань протекает через всю территорию нашего
края. Берет начало в горах Эльбруса и впадает в
Азовское море.
– Переправляться через реку мы будем на
лодочках. (Показываю разные лодочки).
– На каждой парте – лодочка с заданием, которое
необходимо выполнить. Вставьте в выражение знаки
«+» или «–». Работаем в паре.
| I. 6 * 7 * 2 = 11 63 * 20 * 7 = 50 |
II. 8 * 4 * 9 = 13 26 * 30 * 8 = 48 |
III. 5 * 7 * 8 =20 78 * 9 * 9 = 60 |
2. Взаимопроверка.
– Проверьте, правильно ли ваши товарищи
выполнили задание. Если неверно, исправьте
карандашом. Верните лодочки друг другу. У кого
нет ошибок? Молодцы!
– А у остальных я работы посмотрю и увижу, какие
вы допустили ошибки.
3. Подготовка к умножению.
– Мы переправлялись на лодочках и катерах.
– Танкисты на 3-х лодочках, моряки на 3-х, летчики
на 3-х.
– Сколько троек лодочек нам понадобилось? (3)
– Сколько раз по 3? (3)
– Сколько это всего лодочек? (9)
– Как нашли? (3 + 3 + 3)
IX. Итог урока. Рефлексия
– Наши учения проходят к концу.
– Как правильно выполнять письменные вычисления
столбиком?
– Что получилось лучше всего? Что не получилось?
Почему? С каким настроением уходите с урока?
– Сегодня на уроке вы проявили находчивость.
Смелость, сообразительность, показали свои
знания.
– Спасибо вам ребята. За работу.
– А кто из вас знает, как у военных определяют
звание? (По звездочкам на погонах.)
– А у меня есть одна большая генеральская звезда.
– И сегодня за достойную работу, я каждому из вас
подарю звездочку. Но пока, что сладкую. (Из
красивой коробки с большой красной звездой
достаю леденцы на палочке в форме пятиконечной
звезды и раздаю каждому учащемуся).
– Урок окончен, можно идти на перемену.
Литература: Журнал «Начальная
школа» № 1 2005 год.