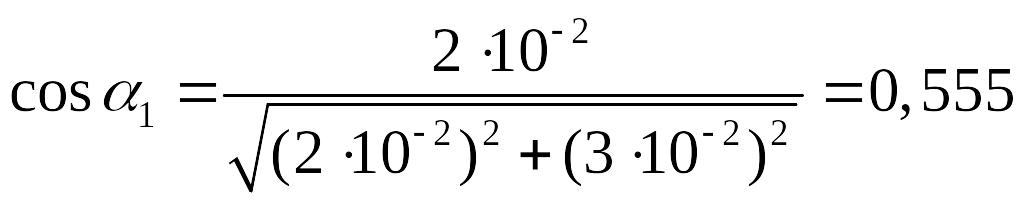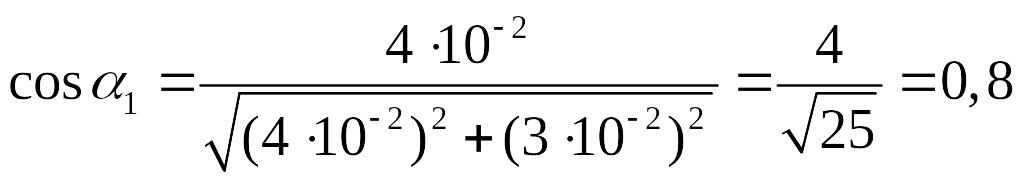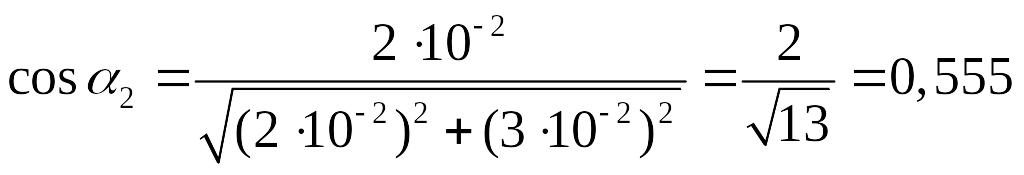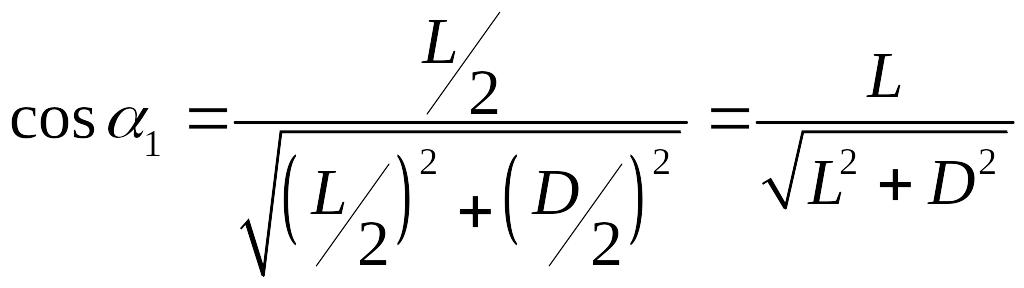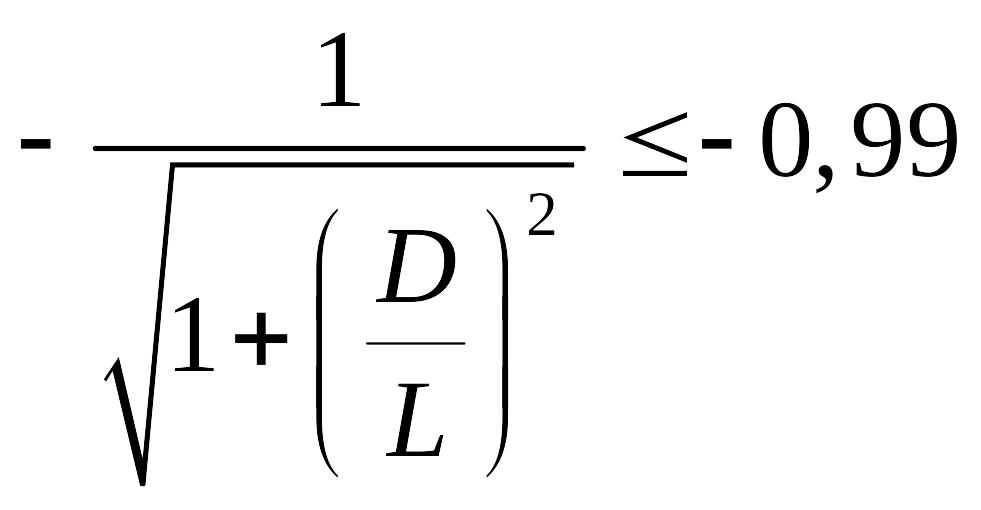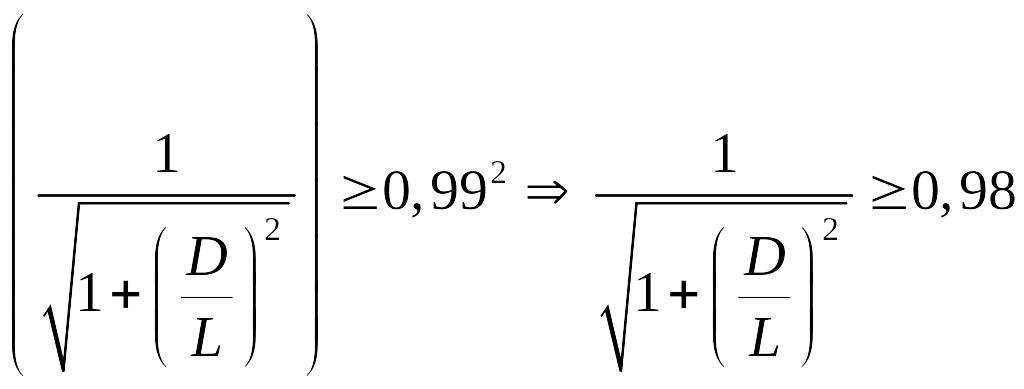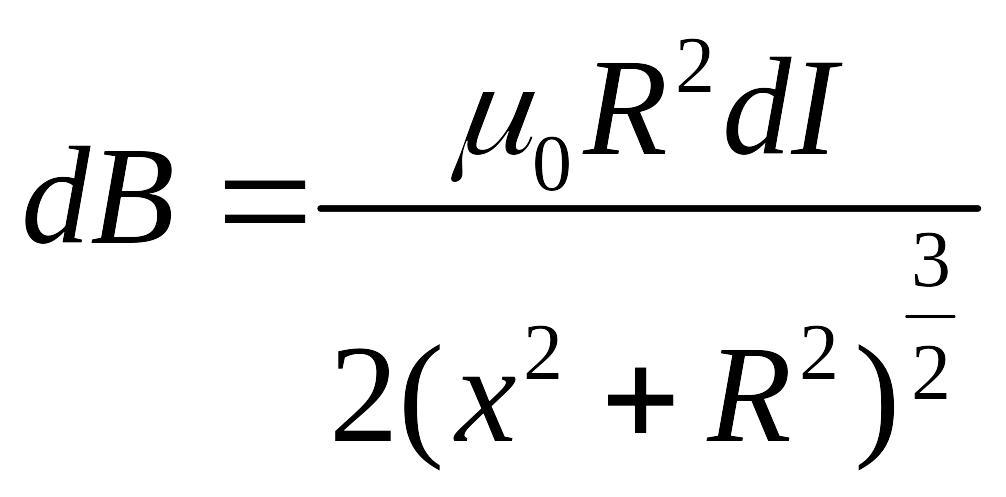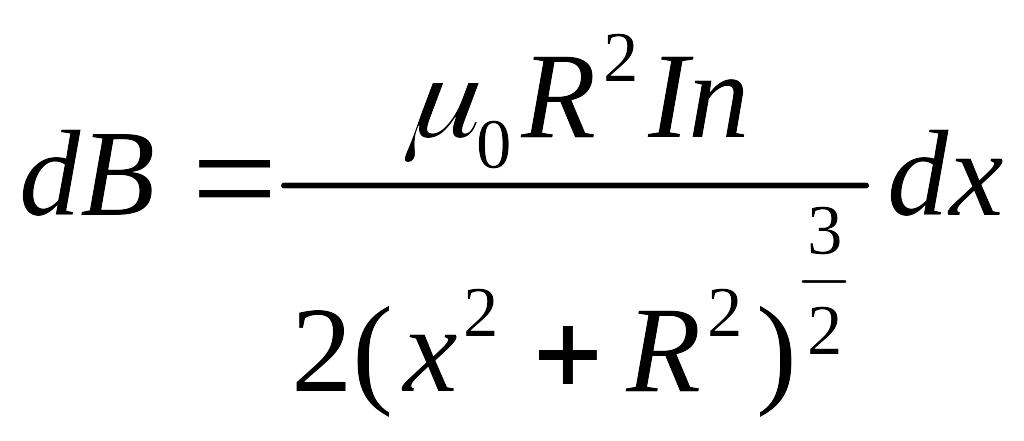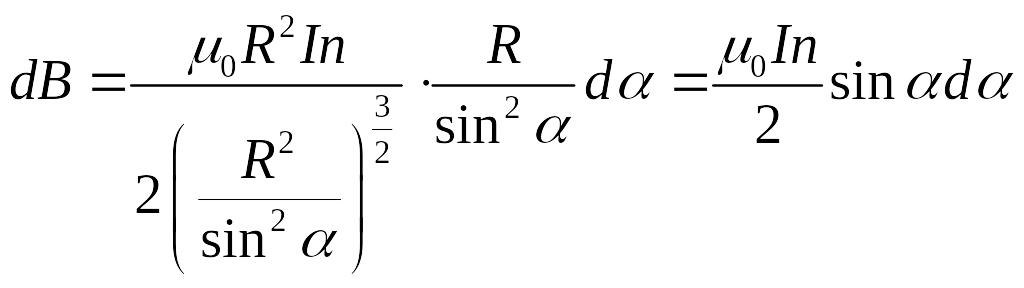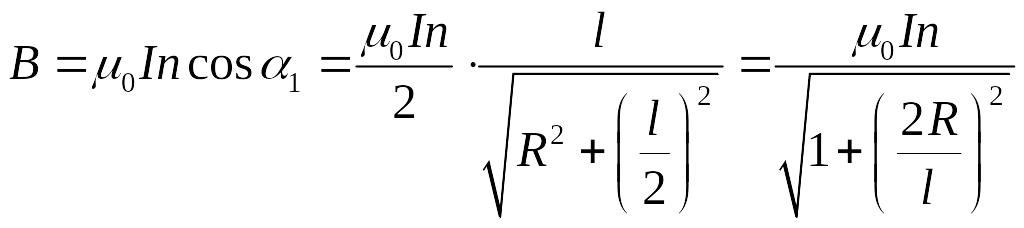Решебник
ВСЕ
ФИЗИКА
МАТЕМАТИКА
ХИМИЯ
Задача по физике – 7526
Очень длинный проводник с током $I = 5,0 А$ изогнут в форме прямого угла. Найти индукцию магнитного поля в точке, которая отстоит от плоскости проводника на $l = 35 см$ и находится на перпендикуляре к проводникам, проходящем через точку изгиба.
Подробнее
Задача по физике – 7527
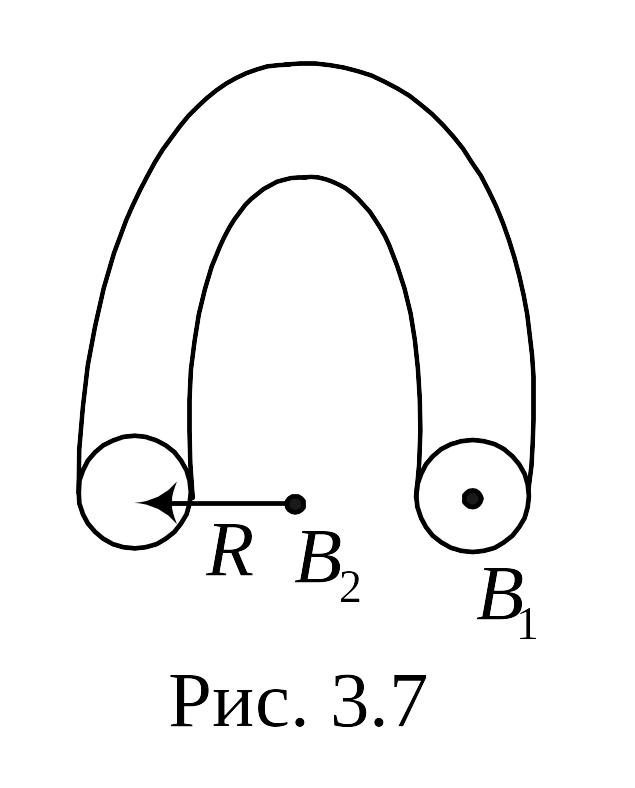
Найти индукцию магнитного поля в точке О, если проводник с током $I = 8,0 А$ имеет вид, показанный на рис. а, б, в. Радиус изогнутой части проводника $R = 100 мм$, прямолинейные участки проводника очень длинные.
Подробнее
Задача по физике – 7528
Определить модуль и направление вектора $vec{B}$ магнитного поля:
а) безграничной плоскости, По которой течет ток с линейной плотностью $vec{i}$, одинаковой во всех точках плоскости;
б) двух параллельных безграничных плоскостей, по которым текут токи с линейными плотностями $vec{i}$ и $- vec{i}$, одинаковыми во всех точках каждой плоскости.
Подробнее
Задача по физике – 7529
Однородный ток плотности $j$ течет внутри неограниченной пластины толщины $2d$ параллельно ее поверхности. Найти индукцию магнитного поля этого тока как функцию расстояния $x$ от средней плоскости пластины. Магнитную проницаемость всюду считать равной единице.
Подробнее
Задача по физике – 7530
Постоянный ток $I$ течет по длинному прямому проводу. Из точки О (рис.) он растекается радиально-симметрично по безграничной проводящей плоскости, перпендикулярной к проводу. Найти индукцию магнитного поля во всех точках пространства.
Подробнее
Задача по физике – 7531
Имеется круговой виток с током $I$. Найти интеграл $int vec{B} d vec{r}$ вдоль оси витка в пределах от $ – infty$ до $+ infty$. Объяснить полученный результат.
Подробнее
Задача по физике – 7532
По круглому однородному прямому проводу, радиус сечения которого $R$, течет постоянный ток плотности $vec{j}$. Найти вектор индукции магнитного поля этого тока в точке, положение которой относительно оси провода определяется радиус-вектором $vec{r}$. Магнитную проницаемость всюду считать равной единице.
Подробнее
Задача по физике – 7533
Внутри однородного длинного прямого провода круглого сечения имеется круглая длинная цилиндрическая полость, ось которой параллельна оси провода и смещена относительно последней на расстояние $vec{l}$. По проводу течет постоянный ток плотности $vec{j}$. Найти вектор индукции магнитного поля внутри полости. Рассмотреть, в частности, случай $vec{l} = 0$.
Подробнее
Задача по физике – 7534
Найти плотность тока как функцию расстояния $r$ от оси аксиально-симметричного параллельного потока электронов, если, индукция магнитного поля внутри потока зависит от $r$ как $B = br^{ alpha}$, где $b$ и $alpha$ — положительные постоянные.
Подробнее
Задача по физике – 7535
Однослойная катушка (соленоид) имеет длину $l$ и радиус сечения $R$. Число витков на единицу длины $n$. Найти индукцию магнитного поля в центре катушки при пропускании через нее тока $I$.
Подробнее
Задача по физике – 7536
Очень длинный прямой соленоид имеет радиус сечения $R$ и $n$ витков на единицу длины. По соленоиду течет постоянный ток $I$. Пусть $x$ — расстояние, отсчитываемое вдоль оси соленоида от его торца. Найти:
а) индукцию магнитного поля на оси как функцию $x$; изобразить примерный график зависимости индукции $B$ от отношения $x/R$;
б) расстояние $x_{0}$ до точки на оси, в которой индукция поля отличается от индукции в глубине соленоида на $eta = 1$%.
Подробнее
Задача по физике – 7537
Обмоткой очень длинного прямого соленоида с радиусом сечения $R = 2,5 см$ служит тонкая лента-проводник шириной $h = 2,0 см$, намотанная в один слой практически вплотную. По ленте течет постоянный ток $I = 5,0 А$. Найти индукцию магнитного поля внутри и вне соленоида как функцию расстояния $r$ от его оси.
Подробнее
Задача по физике – 7538
На деревянный тороид малого поперечного сечения намотано равномерно $N = 2,5 cdot 10^{3}$ витков провода, по которому течет ток $I$. Найти отношение $eta$ индукции магнитного поля внутри тороида к индукции магнитного поля в центре тороида.
Подробнее
Задача по физике – 7539
Постоянный ток $I = 10 А$ течет по длинному прямому проводнику круглого сечения. Найти магнитный поток через одну из половин осевого сечения проводника в расчете на один метр его длины.
Подробнее
Задача по физике – 7540
Имеется очень длинный прямой соленоид с током $I$. Площадь поперечного сечения соленоида равна $S$, число витков на единицу длины — $n$. Найти поток вектора $vec{B}$ через торец соленоида.
Подробнее
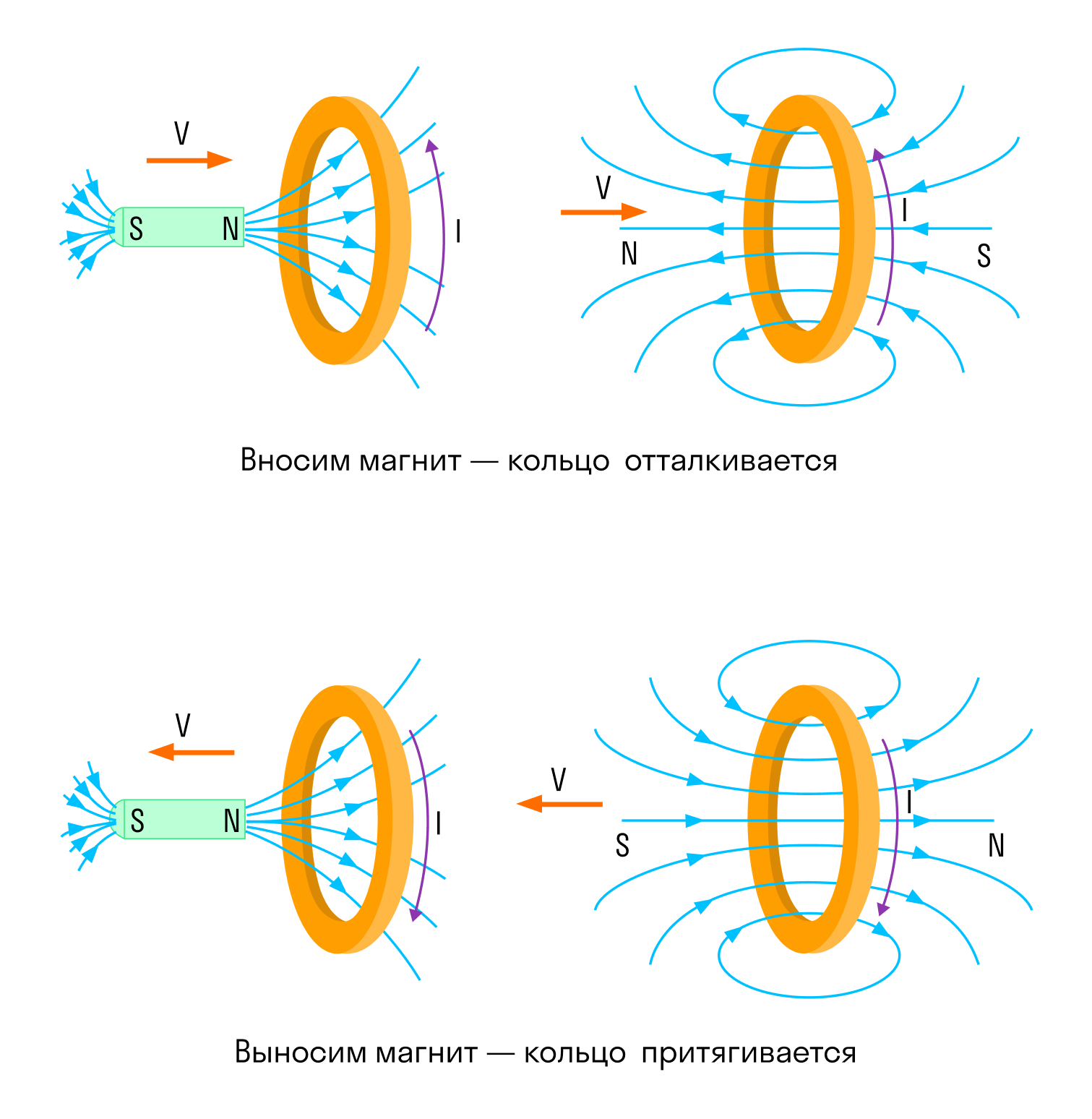
Электромагнитная индукция — это очень важное физическое явление, используемое в работе многих устройств, таких как трансформатор, генератор переменного напряжения, индукционная плита. Оно также имело большое теоретическое значение — привело к открытию электромагнитной волны.
Фарадея, первооткрывателя явления электромагнитной индукции, посетил в своей лаборатории министр финансов Великобритании и спросил:
- » Какую пользу человечество получит от вашего исследования? «
Фарадей ответил:
- » Трудно судить, но я уверен, что вы будете собирать с этого налоги. «
Он не ошибся — НДС в той же Великобритании добавляется к цене электроэнергии, поставляемой в дом.
Приведенный выше список применений, хотя и неполный, впечатляет. Они, безусловно, присутствуют в нашей жизни и являются инженерными разработками явления электромагнитной индукции.
В чем заключается явление электромагнитной индукции?
В общем смысле явление электромагнитное индукции заключается в генерации электрического тока с помощью магнитного поля.
Скажем точнее, явление электромагнитной индукции заключается в образовании электродвижущей силы (ЭДС) в проводнике в результате изменения потока магнитного поля, пронизывающего поверхность, охватывающую проводник. В замкнутой цепи электродвижущая сила (ЭДС) вызывает протекание электрического тока.
В приведенном выше определении явления могут быть неясными два понятия — ЭДС индукции и магнитный поток.
ЭДС индукции.
Абсолютная величина электродвижущей силы ( ЭДС индукции с символом εинд ) есть работа внешней силы Az, которая вызывает перемещение единичного заряда по цепи. Следовательно: | εинд | = Az / q .
Как видите, в определении мы использовали абсолютное значение ЭДС индукции. Это потому, что оно может быть отрицательным, при определенных ситуациях. С другой стороны, работа внешних сил, согласно принципу сохранения энергии, всегда, при генерации электрического тока, должна быть положительной.
Определение потока магнитной индукции.
Поток магнитной индукции B через поверхность S называется скалярным произведением векторов B и S: dФ = B * S * cos α , где α — угол между двумя векторами, а S — вектор, перпендикулярный поверхности S с величиной, равной площади этой поверхности.
Магнитный поток будет меняться при изменении любой величины, входящей в формулу — площади поверхности, значения магнитной индукции, угла между площадью поверхности и вектором индукции — при сохранении постоянства остальных переменных. Конечно, все эти величины могут изменяться одновременно, но таким образом, что их произведение не остается постоянным.
О том, что электрический ток является источником магнитного поля, было известно с 1820 года (работа Орстеда). Фарадей задался вопросом, не верно ли и обратное — не может ли магнитное поле быть источником (причиной) электрического тока. Однако дело оказалось не таким простым. Только в 1831 году ученый наблюдал это явление при определенных особых обстоятельствах. Оказалось, что при стабильных условиях электрический ток не возникает.
Почему это происходит? Даже в очень сильном, но постоянном во времени магнитном поле электрический ток не будет течь в замкнутой цепи «сам по себе». Он течет только тогда, когда мы соответствующим образом перемещаем контур или изменяем магнитное поле, в котором находится контур.
Когда Фарадей обратил внимание на условия, при которых в присутствии магнитного поля возникает электрический ток, он провел десятки экспериментов, которые обобщил и из которых сделал количественные выводы в виде закона электромагнитной индукции. Мы не будем здесь говорить об этом законе, а сосредоточимся только на сути явления электромагнитной индукции. Мы попытаемся увидеть двойственность этого явления, т.е. то, что оно имеет две разновидности, и ответить на вопрос, почему электрический ток течет при определенных условиях.
Мы рассмотрим, какие силы вызывают индукционный ток, т.е. какие силы действуют на свободные заряды в проводнике, заставляя их двигаться.
Эксперимент Фарадея 1831 года, демонстрирующий электромагнитную индукцию между двумя катушками (см. рисунок 1).
Справа находится аккумулятор, питающий меньшую из двух катушек (A), которая создает магнитное поле. Когда эта катушка находится в состоянии покоя, индукционный ток не наблюдается. Однако если переместить его внутрь большей катушки (B), переменный магнитный поток индуцирует в ней ток. Мы обнаруживаем это, наблюдая за колебаниями стрелки гальванометра (G) слева.
Закон электромагнитной индукции Фарадея
Явление электромагнитной индукции описывается законом Фарадея, первооткрывателя и исследователя этого явления.
Представьте себе простейший контур с подвижной стороной, помещенный в магнитное поле так, чтобы поверхность контура была перпендикулярна линиям магнитного поля (рис. 2.).
Мы перемещаем контур со скоростью v вправо. Это изменяет поток магнитной индукции, пронизывающий поверхность, охватываемую контуром, обозначенным на рисунке более темным цветом.
Вспоминая определение магнитного потока индукции, мы можем понять, почему изменяется поток ФB (рис. 2) — потому что, значение площади S поверхности увеличивается .
Вследствие изменения потока магнитной индукции в рассматриваемой цепи возникнет электродвижущая сила индукции и, следовательно, потечет электрический ток.
В рассматриваемом нами случае легко вычислить работу внешней силы, предполагая постоянную скорость движения контура. Внешняя сила Fz действует в соответствии со смещением контура (и вектором скорости) и в любой момент уравновешивает электродинамическую силу (силу Ампера) Fed, действующую в противоположном направлении (рис. 3.). Согласно определению работы Az = F * Δx где Δx — смещение контура во времени Δt.
Величина силы Fz равна величине электродинамической силы (силе Ампера) Fed, действующей на контур. Поэтому Az = I * L * B * Δx, где — I сила индукционного тока, протекающего в цепи (и в контуре), L — длина контура (той части, где протекает электрический ток), B — величина магнитной индукции. Давайте введем наше выражение в определение ЭДС индукции. Зная, что q = I * Δt, получаем:
| εинд | = Az / q = I * L * B * Δx / I * Δt = B * L * Δx / Δt = B * ΔS / Δt = dФB / dt.
Мы получили интересный результат. Абсолютное значение ЭДС индукции равно скорости изменения потока магнитной индукции.
В рассматриваемом здесь случае поток магнитной индукции изменяется равномерно во времени. В общем случае это совсем не обязательно. Вот почему мы пишем: εинд = ΔФB / Δt , где Δt → 0, который в сокращенном виде записывается как dФB / dt . Это производная магнитного потока по времени.
Хотя наш вывод формулы относится к одному примеру, оказывается, что выведенное отношение является общим. Необходимо сделать лишь небольшую поправку. Это знак минус, который связан с определенной условностью и принципом сохранения энергии.
Таким образом, закон электромагнитной индукции Фарадея записывается следующим образом: εинд = — dФB / dt и формулируется так:
Для любого контура индуцированная электродвижущая сила (ЭДС) равна скорости изменения магнитного потока, проходящего через этот контур, взятой со знаком минус.
Википедия
Знак «минус» означает, что ЭДС индукции действует так, что индукционный ток препятствует изменению потока. Этот факт отражён в правиле Ленца.
Этот закон верен независимо от того, как изменяется поток магнитного поля; когда изменение вызвано относительным движением источника магнитного поля и контура, или когда движения вообще нет, но значение магнитной индукции меняется.
Закон Фарадея — это универсальный, всеобъемлющий и полный математический отчет о явлении электромагнитной индукции.
Вернемся на мгновение к нашему примеру и отметим, что скорость изменения потока, а значит и абсолютное значение ЭДС индукции, в данном случае равна произведению B*L*v. Это следует из ранее написанных соотношений, а именно:
| εинд | = Az / q = I * L * B * Δx / I * Δt = B * L * Δx / Δt = B * L * ( Δx / Δt ) = B * L * v .
Правило Ленца.
Правило Ленца позволяет быстро и легко определить направление индукционного тока. Это действительно одна из форм принципа сохранения энергии. Правило гласит, что индукционный ток, наведенный в проводнике под действием переменного потока магнитной индукции, всегда имеет такое направление, что магнитное поле, создаваемое этим индукционным током, противодействует причине (т.е. изменению потока магнитного поля), которая его вызвала.
Пример задачи
Дано:
Контур в форме квадрата со стороной d = 0,5 м «втягивается» с постоянной скоростью v = 4 м/с в область однородного магнитного поля, величина индукции которого B = 1 Тл (см. рис. 4). Электрическое сопротивление цепи равно R = 2 Ом.
Нам нужно найти ответы на следующие вопросы:
a) Когда (в какой момент/моменты) в рамке будет протекать электрический ток?
б) Определите направление этого электрического тока.
(в) Вычислите значение силы, действующей на рамку при ее перемещении в соответствии с направлением вектора скорости. Предположите отсутствие механического сопротивления движению.
Решение.
(a) Индукционный ток протекает при изменении потока магнитной индукции через поверхность, охваченную контуром. В ситуации, показанной на рисунке 4, магнитный поток равен нулю и будет оставаться таковым до тех пор, пока правый край контура не коснется границы области магнитного поля. Затем, по мере движения контура, он будет все больше и больше заполняться магнитным полем — магнитный поток будет увеличиваться. Поэтому выполняется условие электромагнитной индукции, т.е. начинает протекать индукционный ток. Как долго? Это легко вычислить, поскольку движение рамы равномерно:
t = d / v = 0,5 / 2 = 0,25 секунд
Ток будет течь до тех пор, пока весь квадрат не войдет в магнитное поле. Тогда поток будет ненулевым, но больше не будет меняться.
б) Воспользуемся правилом Ленца. Мы уже заметили, что поток магнитной индукции при «втягивании» контура в магнитное поле увеличивается. Поэтому индукционный ток будет протекать в таком направлении, чтобы противодействовать увеличению потока.
Магнитное поле, создаваемое индукционным током с вектором индукции Bинд, будет противоположно вектору B.
Таким образом, вектор Bинд направлен в нашу сторону. Если расположить таким образом большой палец правой руки, остальные согнутые пальцы покажут направление индукционного тока. Ток будет течь против часовой стрелки.
(в) Снова воспользуемся равномерностью движения рамы. Обратите внимание, что сила, которая действует на рамку при ее перемещении по вектору скорости (например, сила моей руки), не может быть единственной силой, действующей на квадрат. Если бы это было так, он бы двигался с ускорением. Поскольку движение равномерное, это означает, что в каждый момент времени существует сила, которая уравновешивает силу моей руки. Это и есть электродинамическая сила. Ведь теперь в рамке течет ток, и часть его протекает в магнитном поле (см. рис. 5).
Красная стрелка показывает направление электрического тока. Электродинамическая сила (сила Ампера) действует слева (я определил ее с помощью правила трех пальцев). На верхнюю часть рамки и нижнюю часть также действуют электродинамические силы, но они аннулируют друг друга.
Подведем итог: электродинамическая сила уравновешивает силу моей руки. Таким образом, я могу сравнить значения обеих сил, то есть F = Fed = B * I * d, где I — сила индукционного тока. Теперь достаточно рассчитать значение силы этого тока. Мы будем использовать закон Фарадея и закон Ома для участка цепи. Давайте начнем с последнего: поскольку нас интересует только значение I, мы напишем
I = εинд / R .
| εинд | = ΔФB / Δt = Δx * d * B / Δt = ( Δx / Δt ) * d * B = v * d * B .
После подстановки в I получаем: I = εинд / R = v * d * B / R .
В конечном итоге искомое значение силы будет выражено через: Fed = B * I * d = ( B * d * v * d * B ) / R = ( B2 * d2 * v ) / R .
Подставляя численные значения получим: Fed = F = ( 12 * 0,52 * 4 ) / 2 = 0,5 Н .
Список использованной литературы
- Миллер М. А., Пермитин Г. В. Электромагнитная индукция // Физическая энциклопедия : [в 5 т.] / Гл. ред. А. М. Прохоров. — М.: Большая российская энциклопедия, 1999. — Т. 5: Стробоскопические приборы — Яркость. — С. 537—538. — 692 с. — 20 000 экз. — ISBN 5-85270-101-7.
- М. Лившиц. Закон электромагнитной индукции или «правило потока»? // Квант. — 1998. — № 3. — С. 37—38.
- Физика, базовый уровень, 11 класс, учебник — Пурышева Н.С., Важеевская Н.Е., Исаев Д.А., Чаругин В.М
Свойством поля магнитного в любой его точке с позиции силы выступает вектор магнитной индукции [overrightarrow{mathrm{B}}].
Вектор индукции магнитного поля: главные понятия
Рассмотрим определение вектора индукции магнитного поля. Индукцию определяют как предел отношения F силы, воздействующий на магнитное поле, на ток [text { Idl }] к произведению элементарного тока [text { I }] со значением элемента проводника [text { dl }]. Другими словами, магнитная индукция действует по направлению перпендикулярно [perp] по направлению тока (или по-другому к элементу проводника [text { dl }Rightarrow] из (1), а также вектор магнитной индукции поля перпендикулярен [perp] к направлению силы, которая действует с магнитного поля.
Вектор магнитной индукции однородного поля и неоднородного
Если [overrightarrow{mathrm{B}}=mathrm{const}], то поле является однородным. Если оно не изменяется с течением времени, то про него говорят, что поле постоянное.
Вектор индукции магнитного поля: важные формулы
Важно!
Формула с векторами преобразуется в модульную форму, потому что векторы задают направление, а модульная форма — значения, которые необходимы для решения задачи.
Формула
Модуль вектора индукции однородного поля находят следующим образом:
[mathrm{B}=frac{mathrm{M}_{max }}{mathrm{P}_{mathrm{m}}}].
где [mathrm{M}_{max }] — вращающий момент в максимуме действует на контур с элементарным током, помещенный в магнитное поле, где в данном случае [mathrm{P}_{mathrm{m}}=mathrm{I} cdot mathrm{S}] — магнитный момент контура (S — площадь определенного контура).
Модуль вектора индукции магнитного поля: производные формулы
Есть еще формулы для определения модуля магнитной индукции. Она определяется как отношение силы в максимуме [mathrm{F}_{max }], которое реагирует на проводник длины (при этом L= 1 м) к силе элементарного тока [text { I }] в проводнике:
[B=frac{F_{max }}{I cdot L}]
В вакууме модуль индукции будет равен:
[mathrm{B}=mu 0 cdot mathrm{H}]
Чтобы найти вектор индукции через силу Лоренца, следует преобразовать формулу: [overrightarrow{mathrm{F}}=mathrm{q} cdot[overrightarrow{mathrm{V}} times overrightarrow{mathrm{B}}]] (Крестом обозначается произведение векторов)
[vec{F}=B cdot q cdot v cdot sin alpha]
[B=frac{F}{sin alpha cdot q v}]
В данном случае угол α — это угол между вектором индукции и скорости. Стоит отметить, что направление силы Лоренца [overrightarrow{mathrm{F}}] перпендикулярно [perp] каждому вектору, направлено по правилу Буравчика. Под символом q подразумевается заряд в магнитном поле.
Интересно
В СИ единицей модуля магнитной индукции принимается 1 Тесла (кратко — Тл), где [1 Tл=frac{H}{Aм}]
Как определяется направление вектора индукции магнитного поля?
За направление вектора индукции магнитного поля [overrightarrow{mathrm{B}}] используют направление, в котором устанавливается под воздействием поля утвердительного нормали к току с контору. Другими словами объясняют так: вектор идет в направление поступательного перемещения правого винта при вращении по направлению передвижения тока внутри контура.
Вектор индукции [overrightarrow{mathrm{B}}] обладает направлением, которое начинается со стрелки южного полюса [text { S }] (она свободна передвигается в поле) к полюсу северному [text { N }].
Магнитное поле возникает из-за электрических зарядов (элементарными токами), движущиеся в нем.
Для того чтобы определить направление вектора магнитной индукции в проводнике с элементарным током, используют правило правой руки (Буравчика). Они формулируются так:
- Для катушки с током: 4 согнутых пальца руки, которые обхватывают катушку, направляют по течению току. В это время оставленный большой палец на [90^{circ}] указывает на направление магнитной индукции [overrightarrow{mathrm{B}}] в середине катушки.
- Для прямого проводника с элементарным током: большой палец руки, который оставляется на [90^{circ}], направить по течению элементарного тока. В это время 4 согнутых пальца, которые держат проводник, показывают сторону, куда направлена индукция магнитного поля.
Задания по теме
Разберем примеры, в которых будет задействована данная формула и свойства.
Пример 1
Условие задачи:
Проводник представлен в квадратной форме. Каждая из сторон равна d. В данный момент по нему проходит элементарный ток силы I. Найдите индукцию магнитного поля в месте, где диагонали квадрата пересекаются.
Решение задачи следующее:
Сделаем рисунок, в котором плоскость совпадает с плоскостью проводника. Изобразим направление вектора индукции магнитного поля.
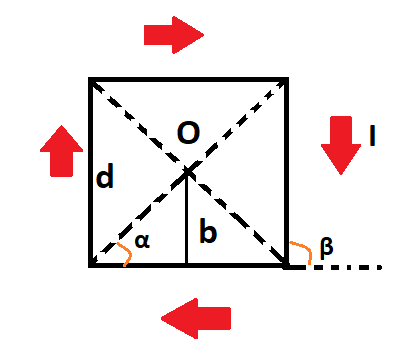
В данной точке О получаются проводники с элементарным током, которые расположены прямолинейно и вектор магнитной индукции поля перпендикулярен плоскости. Направления напряжености полей определяется в соответствием с правилом правого винта,то есть перпендикулярны плоскости изображения. Поэтому сумму векторов по принципу суперпозиции надо заменить на алгебраический вид. Получим следующее выражение: B=B1+B2+B3+B4
Из симметричности рисунка можно увидеть, что модули вектора индукции магнитного поля одинаковы. Получаем следующее: B=4B1
В разделе физике «Электромагнетизм» использовали одну из формул, чтобы рассчитать модуль индукции прямолинейного проводника с элементарным током.
Чтобы формула подошла к данной задачи, ее применяют в следующем виде:
[mathrm{B}_{1}=frac{mathrm{I} cdot mu_{0}}{4 mathrm{pi b}}(cos alpha-cos beta)]
углы α и β, которые отмечены на рисунке:
[beta=pi-alpha rightarrow cos beta=cos (pi-alpha)=-cos alpha]
Используем формулу [B_{1}=frac{I cdot mu_{0}}{4 pi b}(cos alpha-cos beta)] и преобразуем с применением тригонометрического свойства:
[mathrm{B}_{1}=frac{mathrm{I} cdot mu_{0}}{2 mathrm{pi b}} cdot cos alpha]
Поскольку у нас квадратная форма, то следует заметить следующее:
[mathrm{b}=mathrm{d} 2, alpha=frac{pi}{4} rightarrow cos alpha=frac{sqrt{2}}{2}]
Возьмем выведенные формулы и получим конечное выражение, то есть:
[mathrm{B}=4 cdot frac{mathrm{I} cdot mu_{0}}{pi mathrm{d}} cdot frac{sqrt{2}}{2}=frac{2 sqrt{2}}{pi mathrm{d}} cdot mathrm{I} cdot mu_{0}]
Ответ: [mathrm{B}=frac{2 sqrt{2}}{pi mathrm{d}} cdot mathrm{I} cdot mu_{0}]
Нет времени решать самому?
Наши эксперты помогут!
Пример 2
Условие задачи:
Бесконечно проводник с элементарным током (I) согнут под 90 градусов, который изображен на рисунке. Найдите вектор магнитной индукции однородного поля в точке А.
Решение задачи:
В точке А получается из двух частей проводника, то есть:
[overrightarrow{mathrm{B}}=mathrm{B}_{mathrm{II}}+mathrm{B}_{perp}]
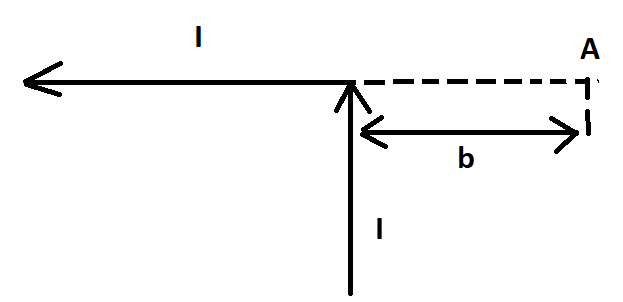
Теперь посмотрим горизонтальный участок, где расположена точка А. Данная область проводника с элементарным током формирует поле в этой точке. Вектор индукции магнитного поля [mathrm{B}_{mathrm{II}}] равен нулю, потому что в А все углы между с радиус-векторами и с элементарным током равны π.
Следовательно, произведение векторов [[mathrm{d} vec{ l } vec{r}]] и поток вектора индукции магнитного поля в законе Био-Савара-Лапласа будет равен нулю:
[overrightarrow{mathrm{B}}=frac{mu_{0}}{4 pi} oint frac{mathrm{I}[mathrm{d} vec{l} vec{r}]}{mathrm{r}^{3}}]
В этом случае [vec{r}] — радиус-вектор, который идет от элемента [mathrm{Idvec{l}}] к точке А, в которой находится индукция магнитного поля [overrightarrow{mathrm{B}}].
Индукция бесконечного проводника в точке А была бы равна:
[mathrm{B}^{prime}=frac{mu_{0}}{2 pi} frac{mathrm{I}}{mathrm{b}}]
Но так как полу бесконечный проводник, то следуя из принципа суперпозиции, получается следующее выражение для проводника магнитной индукций равна:
[mathrm{B}=mathrm{B}_{perp}=frac{1}{2} mathrm{~B}^{prime}=frac{mu_{0}}{Pi} frac{mathrm{I}}{mathrm{b}}]
Ответ: [mathrm{B}=frac{mu_{0}}{pi} frac{mathrm{I}}{mathrm{b}}]
Содержание
- Физический смысл магнитной индукции
- Формула магнитной индукции
- Формула магнитной индукции:
- Другие формулы, где встречается B
- Сила Ампера:
- Сила Лоренца:
- Магнитный поток:
- Магнитный поток
- Взаимодействие магнитов
- Направление вектора МИ
- Наглядное отображение линий МИ
- Основные формулы для вычисления вектора МИ
- Закон электромагнитной индукции
- Закон Био-Савара-Лапласа
- Принцип суперпозиции
- Правило Ленца
- Электромагнитная индукция
Физический смысл магнитной индукции
Физически это явление объясняется следующим образом. Металл имеет кристаллическую структуру (катушка состоит из металла). В кристаллической решетке металла расположены электрические заряды — электроны. Если на металл не оказывать ни какое магнитное воздействие, то заряды (электроны) находятся в покое и никуда не движутся.
Васильев Дмитрий ПетровичПрофессор электротехники СПбГПУ Если же металл попадает под действие переменного магнитного поля (из-за перемещения постоянного магнита внутри катушки – именно перемещения), то заряды начинают двигаться под действием этого магнитного поля.
В результате чего в металле возникает электрический ток. Сила этого тока зависит от физических свойств магнита и катушки и скорости перемещения одного относительно другого.
При помещении металлической катушки в магнитное поле заряженные частицы металлический решетки (в кашутке) поворачиваются на определенный угол и размещаются вдоль силовых линий магнитного поля.
Чем выше сила магнитного поля, тем больше количество частиц поворачиваются и тем более однородным будет являться их расположение.
Магнитные поля, ориентированные в одном направлении не нейтрализуют друг друга, а складываются, формируя единое поле.
Формула магнитной индукции
где, В — вектор магнитной индукции, F — максимальная сила действующая на проводник с током, I — сила тока в проводнике, l — длина проводника.
Формула магнитной индукции:
Формула магнитной индукции: B = Mmax/IS
Где:
- B — индукция магнитного поля (в Тл)
- Mmax — максимальный крутящий момент магнитных сил, приложенных к рамке (в Нм)
- l — длина проводника (в м)
- S — площадь рамки (в м²)
Другие формулы, где встречается B
Эти формулы также можно использовать для её расчёта.
Сила Ампера:
Сила Ампера: Fa=IBL sinα
Где:
- Fa — сила Ампера (в Н — ньютон)
- I — сила тока (в А — ампер)
- B — индукция магнитного поля (в Тл)
- L — длина проводника (в м)
- α — угол между вектором В и одним из направлений (силы тока, скорости или др.; измеряется в рад. или град.)
Сила Лоренца:
Сила Лоренца: Fл = qvB sinα
Где:
- Fл — сила Лоренца (в Н — ньютон)
- q — заряд частицы (в Кл — кулон)
- v — скорость (в м/с)
- B — индукция (в Тл)
- α — угол между вектором В и одним из направлений (силы тока, скорости, или др.; измеряется в рад. или град.))
Магнитный поток:
Магнитный поток: Ф = BS cosα
Где:
- Ф — магнитный поток (в Вб – вебер)
- B — индукция (в Тл)
- S — площадь рамки (в м²)
- α — угол между вектором В и одним из направлений (силы тока, скорости, или др.; измеряется в рад. или град.))
Магнитный поток
Магнитный поток это скалярная величина, которая характеризует действие магнитной индукции на некий металлический контур.
Магнитная индукция определяется числом силовых линий, проходящих через 1 см2 сечения металла.
Магнитометры, используемые для ее измерения, называют теслометрами.
Абрамян Евгений ПавловичДоцент кафедры электротехники СПбГПУ Единицей измерения магнитной индукции в системе СИ является Тесла (Тл).
После прекращения движение электронов в катушке сердечник, если он выполнен из мягкого железа, теряет магнитные качества. Если он изготовлен из стали, то он имеет способность некоторое время сохранять свои магнитные свойства.
Взаимодействие магнитов
Постоянный магнит (или магнитная стрелка) ориентируется вдоль магнитного меридиана Земли. Тот его конец, который указывает на север, называется северным полюсом (N), а противоположный конец — южным полюсом (S). Приближая два магнита друг к другу, заметим, что одноименные их полюсы отталкиваются, а разноименные — притягиваются (рис. 1).
Если разделить полюса, разрезав постоянный магнит на две части, то мы обнаружим, что каждая из них тоже будет иметь два полюса, т. е. будет постоянным магнитом (рис. 2). Оба полюса — северный и южный, — неотделимые друг от друга, равноправны.
Магнитное поле, создаваемое Землей или постоянными магнитами, изображается, подобно электрическому полю, магнитными силовыми линиями. Картину силовых линий магнитного поля какого-либо магнита можно получить, помещая над ним лист бумаги, на котором насыпаны равномерным слоем железные опилки. Попадая в магнитное поле, опилки намагничиваются — у каждой из них появляется северный и южный полюсы. Противоположные полюсы стремятся сблизиться друг с другом, но этому мешает трение опилок о бумагу. Если постучать по бумаге пальцем, трение уменьшится и опилки притянутся друг к другу, образуя цепочки, изображающие линии магнитного поля.
На рис. 3 показано расположение в поле прямого магнита опилок и маленьких магнитных стрелок, указывающих направление линий магнитного поля. За это направление принято направление северного полюса магнитной стрелки.
Направление вектора МИ
Направление магнитных полей может указать стрелка магнита, помещаемая в эти поля. Она будет крутиться до тех пор, пока не остановится. Северный конец стрелки покажет, куда ориентирован B→ орт того или иного поля.
Линии магнитной индукции
Таким же образом ведёт себя рамка с током, имеющая возможность без помех ориентироваться в МП. Направленность вектора индукции указывает ориентацию нормали к такому замкнутому электромагнитному контуру.
Внимание! Здесь используют правило буравчика (правого винта). Если винт вращать так, как направлен ток в рамке, то поступательное продвижение винта совпадёт с направлением положительной нормали.
В некоторых случаях, чтобы найти направление, применяют правило правой руки.
Наглядное отображение линий МИ
Линию, к которой можно провести касательную, совпадающую с B→, называют линией магнитной индукции (МИ). С помощью таких линий можно визуально отобразить магнитное поле. Это сомкнутые контурные чёрточки, которые охватывают токи. Их густота всегда пропорциональна величине B→ в конкретной точке МП.
Информация. Когда имеют дело с МП прямого движения заряженных частиц, то эти линии изображаются в виде концентрических окружностей. Они имеют свой центр, расположенный на прямой линии с током, и находятся в плоскостях, расположенных под прямым углом к нему.
С направлением магнитных линий также можно определиться, пользуясь правилом буравчика.
Основные формулы для вычисления вектора МИ
Вектор магнитной индукции, формула которого B = Fm/I*∆L, можно находить, применяя другие математические вычисления.
Закон электромагнитной индукции
Закон электромагнитной индукции (закон Фарадея) звучит так:
ЭДС индукции в замкнутом контуре равна и противоположна по знаку скорости изменения магнитного потока через поверхность, ограниченную контуром.
Математически его можно описать формулой:
Закон Фарадея
Ɛi — ЭДС индукции [В]
ΔФ/Δt — скорость изменения магнитного потока [Вб/с]
Знак «–» в формуле позволяет учесть направление индукционного тока. Индукционный ток в замкнутом контуре всегда направлен так, чтобы магнитный поток поля, созданного этим током сквозь поверхность, ограниченную контуром, уменьшал бы те изменения поля, которые вызвали появление индукционного тока.
Если контур состоит из N витков (то есть он — катушка), то ЭДС индукции будет вычисляться следующим образом.
Закон Фарадея для контура из N витков
Ɛi — ЭДС индукции [В]
ΔФ/Δt — скорость изменения магнитного потока [Вб/с]
N — количество витков [-]
Сила индукционного тока в замкнутом проводящем контуре с сопротивлением R:
Закон Ома для проводящего контура
Ɛi — ЭДС индукции [В]
I — сила индукционного тока [А]
R — сопротивление контура [Ом]
Если проводник длиной l будет двигаться со скоростью v в постоянном однородном магнитном поле с индукцией B ЭДС электромагнитной индукции равна:
ЭДС индукции для движущегося проводника
Ɛi — ЭДС индукции [В]
B — магнитная индукция [Тл]
v — скорость проводника [м/с]
l — длина проводника [м]
Возникновение ЭДС индукции в движущемся в магнитном поле проводнике объясняется действием силы Лоренца на свободные заряды в движущихся проводниках. Сила Лоренца играет в этом случае роль сторонней силы.
Движущийся в магнитном поле проводник, по которому протекает индукционный ток, испытывает магнитное торможение. Полная работа силы Лоренца равна нулю.
Количество теплоты в контуре выделяется либо за счет работы внешней силы, которая поддерживает скорость проводника неизменной, либо за счет уменьшения кинетической энергии проводника.
Изменение магнитного потока, пронизывающего замкнутый контур, может происходить по двум причинам:
- вследствие перемещения контура или его частей в постоянном во времени магнитном поле. Это случай, когда проводники, а вместе с ними и свободные носители заряда, движутся в магнитном поле
- вследствие изменения во времени магнитного поля при неподвижном контуре. В этом случае возникновение ЭДС индукции уже нельзя объяснить действием силы Лоренца. Явление электромагнитной индукции в неподвижных проводниках, возникающее при изменении окружающего магнитного поля, также описывается формулой Фарадея
Таким образом, явления индукции в движущихся и неподвижных проводниках протекают одинаково, но физическая причина возникновения индукционного тока оказывается в этих двух случаях различной:
- в случае движущихся проводников ЭДС индукции обусловлена силой Лоренца
- в случае неподвижных проводников ЭДС индукции является следствием действия на свободные заряды вихревого электрического поля, возникающего при изменении магнитного поля.
Закон Био-Савара-Лапласа
Формула ЭДС индукции
Описывает правила нахождения B→ магнитного поля, которое создаёт постоянный электроток. Это экспериментально установленная закономерность. Био и Савар в 1820 году выявили её на практике, Лапласу удалось сформулировать. Этот закон является основополагающим в магнитостатике. При практическом опыте рассматривался неподвижный провод с малым сечением, через который пропускали электроток. Для изучения выбирался малый участок провода, который характеризовался вектором dl. Его модуль соответствовал длине рассматриваемого участка, а направление совпадало с направлением тока.
Интересно. Лаплас Пьер Симон предложил считать током даже движение одного электрона и на этом утверждении, с помощью данного закона, доказал возможность определения МП продвигающегося точечного заряда.
Согласно этому физическому правилу, каждый сегмент dl проводника, по которому протекает электрический ток I, образовывает в пространстве вокруг себя на промежутке r и под углом α магнитное поле dB:
dB = µ0 *I*dl*sin α /4*π*r2,
где:
- dB – магнитная индукция, Тл;
- µ0 = 4 π*10-7 – магнитная постоянная, Гн/м;
- I – сила тока, А;
- dl – отрезок проводника, м;
- r – расстояние до точки нахождения магнитной индукции, м;
- α – угол, образованный r и вектором dl.
Важно! Согласно закону Био-Савара-Лапласа, суммируя векторы магнитных полей отдельных секторов, можно определить МП нужного тока. Оно будет равно векторной сумме.
Закон Био-Савара-Лапласа
Существуют формулы, описывающие этот закон для отдельных случаев МП:
- поля прямого перемещения электронов;
- поля кругового движения заряженных частиц.
Формула для МП первого типа имеет вид:
В = µ* µ0*2*I/4*π*r.
Для кругового движения она выглядит так:
В = µ*µ0*I/4*π*r.
В этих формулах µ – это магнитная проницаемость среды (относительная).
Рассматриваемый закон вытекает из уравнений Максвелла. Максвелл вывел два уравнения для МП, случай, где электрическое поле постоянно, как раз рассматривают Био и Савар.
Принцип суперпозиции
Для МП существует принцип, согласно которому общий вектор магнитной индукции в определённой точке равен векторной сумме всех векторов МИ, созданных разными токами в данной точке:
B→= B1→+ B2→+ B3→… + Bn→
Правило Ленца
Чтобы определить направление индукционного тока, нужно воспользоваться правилом Ленца.
Академически это правило звучит следующим образом: индукционный ток, возбуждаемый в замкнутом контуре при изменении магнитного потока, всегда направлен так, что создаваемое им магнитное поле препятствует изменению магнитного потока, вызывающего индукционный ток.
Давайте попробуем чуть проще: катушка в данном случае — это недовольная бабуля. Забирают у нее магнитный поток — она недовольна и создает магнитное поле, которое этот магнитный поток хочет обратно отобрать.
Дают ей магнитный поток, забирай, мол, пользуйся, а она такая — «Да зачем сдался мне ваш магнитный поток!» и создает магнитное поле, которое этот магнитный поток выгоняет.
Электромагнитная индукция
Электромагнитная индукция — явление возникновения тока в замкнутом проводящем контуре при изменении магнитного потока, пронизывающего его.
Явление электромагнитной индукции было открыто М. Фарадеем.
Майкл Фарадей провел ряд опытов, которые помогли открыть явление электромагнитной индукции.
Опыт раз. На одну непроводящую основу намотали две катушки: витки первой катушки были расположены между витками второй. Витки одной катушки были замкнуты на гальванометр, а второй — подключены к источнику тока.
При замыкании ключа и протекании тока по второй катушке в первой возникал импульс тока. При размыкании ключа также наблюдался импульс тока, но ток через гальванометр тек в противоположном направлении.
Опыт два. Первую катушку подключили к источнику тока, а вторую — к гальванометру. При этом вторая катушка перемещалась относительно первой. При приближении или удалении катушки фиксировался ток.
Опыт три. Катушка замкнута на гальванометр, а магнит движется вдвигается (выдвигается) относительно катушки
Вот, что показали эти опыты:
- Индукционный ток возникает только при изменении линий магнитной индукции.
- Направление тока будет различно при увеличении числа линий и при их уменьшении.
- Сила индукционного тока зависит от скорости изменения магнитного потока. Может изменяться само поле, или контур может перемещаться в неоднородном магнитном поле.
Почему возникает индукционный ток?
Ток в цепи может существовать, когда на свободные заряды действуют сторонние силы. Работа этих сил по перемещению единичного положительного заряда вдоль замкнутого контура равна ЭДС.
Значит, при изменении числа магнитных линий через поверхность, ограниченную контуром, в нем появляется ЭДС, которую называют ЭДС индукции.
Источники
- https://pue8.ru/elektrotekhnik/597-magnitnaya-induktsiya-opredelenie-i-opisanie-yavleniya.html
- https://www.uznaychtotakoe.ru/magnitnaya-indukciya/
- https://uchitel.pro/%D0%BC%D0%B0%D0%B3%D0%BD%D0%B8%D1%82%D0%BD%D0%BE%D0%B5-%D0%BF%D0%BE%D0%BB%D0%B5/
- https://amperof.ru/teoriya/vektor-magnitnoj-indukcii-formula.html
- https://skysmart.ru/articles/physics/zakon-elektromagnitnoj-indukcii
-
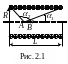
Индукция магнитного поля на оси соленоида
конечной длины (рис 2.1)
,
где – плотность витков; α1 и
α2 – углы, под которыми видны
края соленоида из точки А, где определяется
магнитная индукция.
-
Индукция магнитного поля на оси длинного
соленоида
.
-
Индукция поля тороида
,
где r – радиус выбранного
контура.
Если тороид имеет неограниченное число
витков, а его радиус R
стремится к бесконечности, то в пределе
получается выражение аналогичное
магнитному полю бесконечно длинного
соленоида
.
Примеры решения задач
1. Катушка длиною 2 см и радиусом
3 см состоит из 1000 витков. Ток,
проходящий по катушке равен 200 мА.
Найти магнитную индукцию на оси катушки
в точке:
а) равностоящей от торцов; б) на одном
из торцов; в) отстоящей от торца на
расстоянии 2см.
Решение.
Воспользуемся
формулой для расчета магнитной индукции
соленоида конечной длины ,
где
.
Согласно рис. 2.2.а ,
,
,
.
Согласно
рис. 2.2.б
,
,
,
.
В
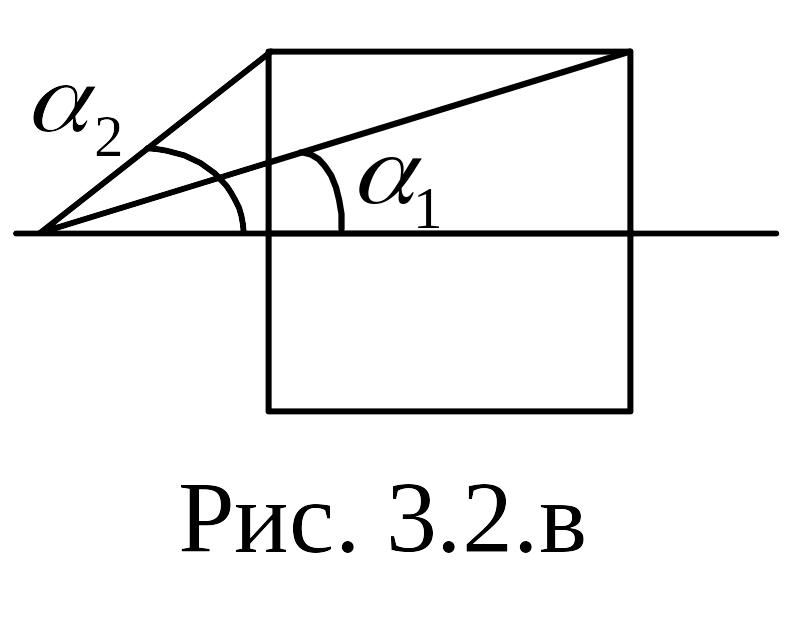
соответствии с рис. 2.2 в
,
Рис. 2.2 в
,
.
2.
Чему должно быть равно отношение длина
катушки к ее диаметру L/D,
чтобы магнитную индукцию в центре
катушки можно было найти по формуле для
поля бесконечно длинного соленоида?
Ошибка при таком допущении не должна
превышать 1%.
Р
ешение.
Относительная
ошибка ищется по следующей формуле
,
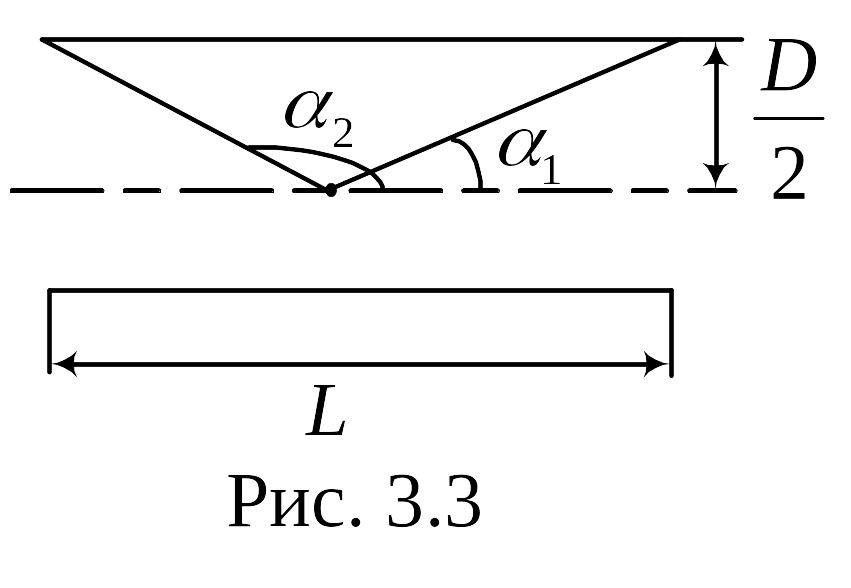
где
,
Рис. 2.3
–
магнитная индукция бесконечно длинного
соленоида.
–
магнитная индукция соленоида конечной
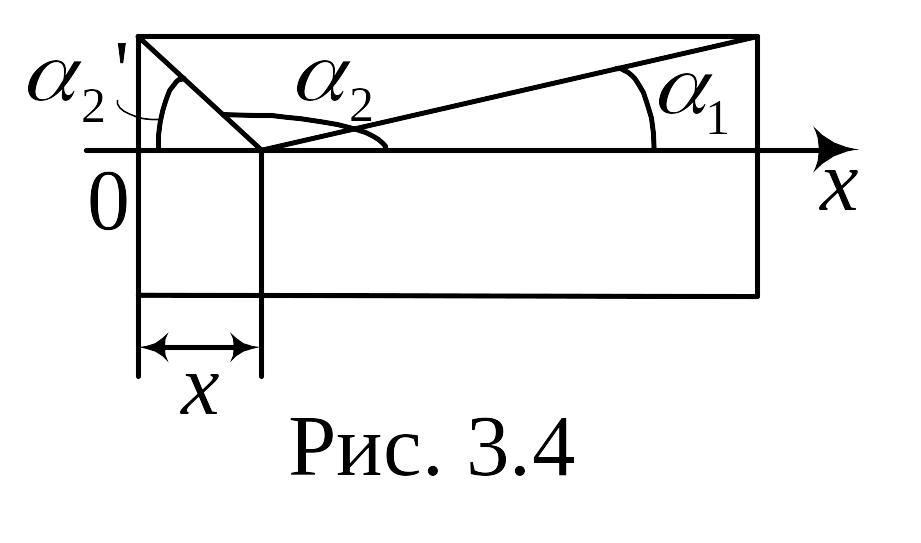
длины, где α
1
и α2
–
обозначены на рис. 2.3
,
,
.
Следовательно
.
После упрощения
,
,
,
.
3
.
Очень длинный прямой соленоид имеет
радиус сечения R
и n
витков на единицу длины. По соленоиду
течет постоянный ток I.
Пусть x
– расстояние, отсчитываемое вдоль оси
соленоида от его торца. Найти:
а)
индукцию магнитного поля на оси как
функцию x;
б
Рис. 2.4
) расстояние х0
до точки на оси, в которой индукция поля
отличается от В
в глубине соленоида на η=1%.
Решение.
а) Относительная
погрешность определяется по формуле
,
где
;
,
так как
.
,
где
.
Таким образом,
.
б) Воспользовавшись
соотношением для относительной
погрешности, получим:
;
.
;
;
;
.
;
,
.
4.
Однослойная катушка (соленоид) имеет
длину
и радиус сечения R.
Число витков на единицу длины равно n.
Найти индукцию магнитного поля в центре
катушки, если ток через нее равен I.
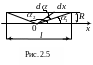
Решение.
Воспользуемся
формулой для расчета магнитной индукции
на оси витка с током
,
где
,
;
.
Знак
“-” показывает, что с увеличением угла
α dx
возрастает в отрицательном направлении
оси х (см. рис.2.5).
,
,
,
,
.
5.
Обмоткой длинного прямого соленоида с
радиусом сечения R=2,5
см служит
тонкая лента-проводник шириной h=5
см, намотанная
в один слой практически вплотную. По
ленте течет ток I=5
А. Найти
индукцию магнитного поля внутри и вне
соленоида как функцию расстояния r
от его оси.
Решение.
Изобразим
схематически
отрезок
ленты, образующий один виток (рис.2.6а).
Разложим ток текущий по ленте на две
составляющие – параллельную оси
соленоида I║
и
перпендикулярную I┴
(рис. 2.6 б).
Поле
внутри соленоида создается перпендикулярной
составляющей тока I┴,
а снаружи параллельной составляющей
I║.
Поле внутри соленоида рассчитывается
по известной формуле
,
где
– линейная плотность перпендикулярной
составляющей тока.
(рис.3.6 б), где
.
;
.
Для
нахождения индукции магнитного поля
вне соленоида необходимо использовать
теорему о циркуляции вектора магнитной
индукции ,
где
,
-линейная
плотность параллельной составляющей
тока.
(рис.2.6
б) =>
.
Следовательно
и
,
где
(рис. 2.6 а).
,
где
.
Таким
образом
.
6
.
На деревянный
тороид малого поперечного сечения
намотано равномерно N=2,5∙103
витков провода, по которому течет ток
I.
Найти отношение η индукции магнитного
поля внутри тороида к индукции в центре
тороида (рис.2.7).
Р
Рис. 2.7
ешение.
Индукция
магнитного поля внутри тороида рис. 2.7
ищется с использованием теоремы о
циркуляции вектора индукции
,
где
N
– число витков тороида; R
– радиус тороида.
Расчет индукции
в центре тороида производится по формуле
для кругового проводника с током.
,
.
7.
Имеется
очень длинный прямой соленоид с током
I.
Площадь поперечного сечения соленоида
S,
число витков на единицу длины n.
Найти поток вектора
через
торец соленоида.
Решение.
Поток
магнитной индукции в центре соленоида
определяется по формуле
.
На
концах соленоида
.
8.
Вычислить магнитный момент тонкого
проводника с током I=0,8
A,
плотно навитого на половину тора (рис.
2.8). Диаметр сечения тора d=5
см, число
витков N=500.
Решение.
Суммарный
магнитный момент формируется параллельными
составляющими
(рис. 2.8 б).
,
где
– число витков на 1 радиан,
–
число витков,
приходящихся на угловой интервал
.
В результате
интегрирования получим
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #