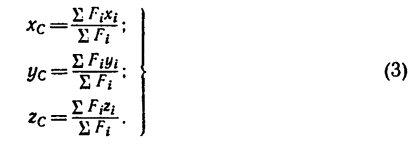
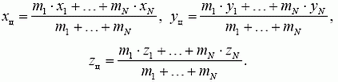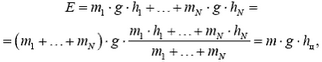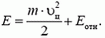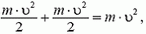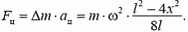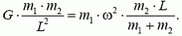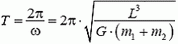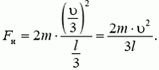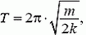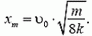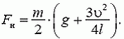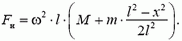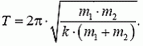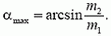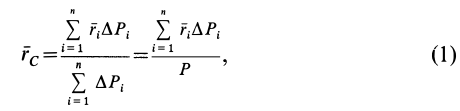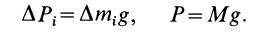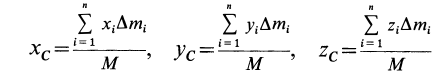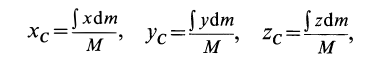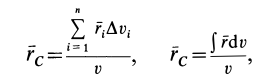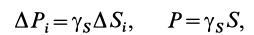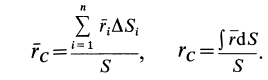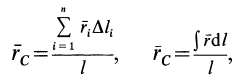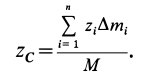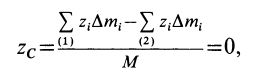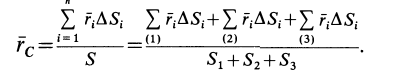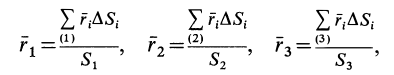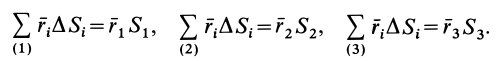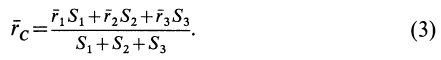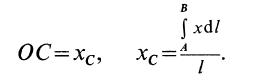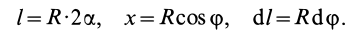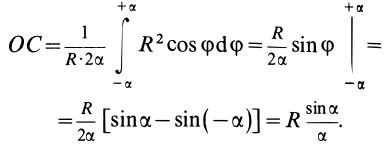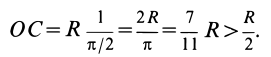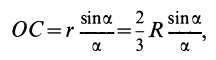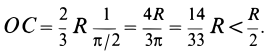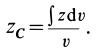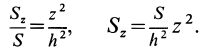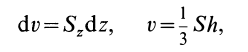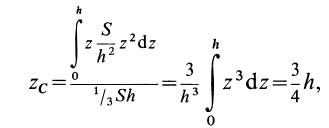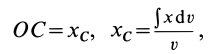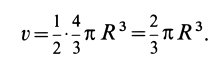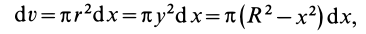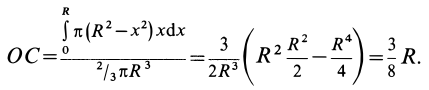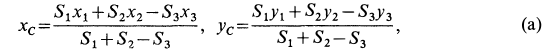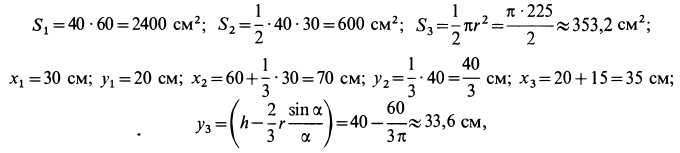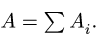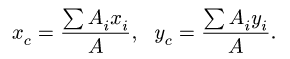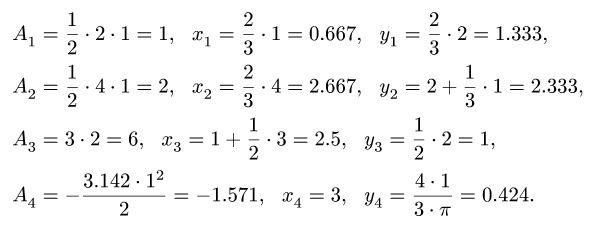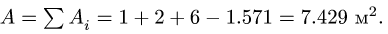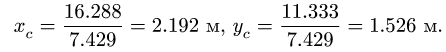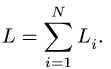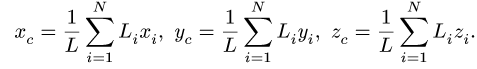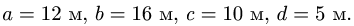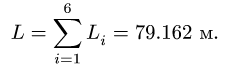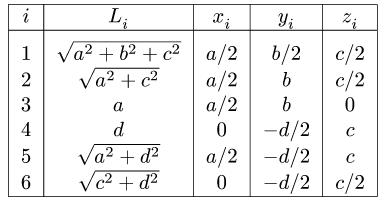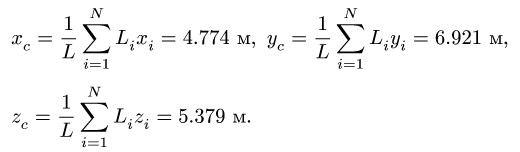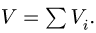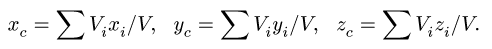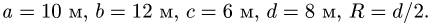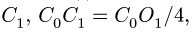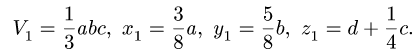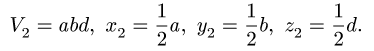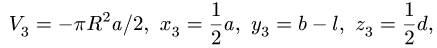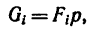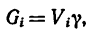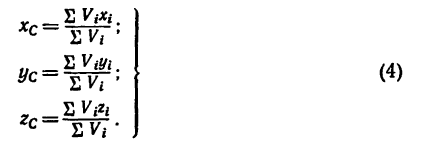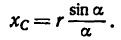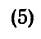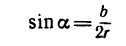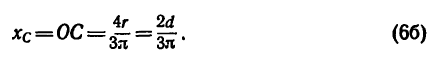1.4. Меры центра и разброса
Среднее, дисперсия и стандартное отклонение популяции
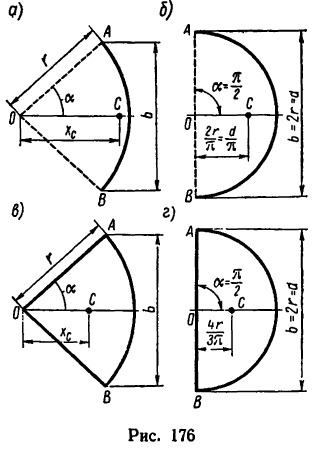
Важной характеристикой популяции наблюдений переменной (у) является её среднее y =
Рис.1.4.1. График функции плотности вероятности распределения и среднее Е(у)=y в качестве его центра.
Для рассматриваемых целей наиболее полезной такой мерой является обозначаемая s2 (сигма в квадрате) дисперсия популяции. Как сильно отличается отдельное наблюдение случайной переменной (у) от среднего y определяется разностью yi–y. Дисперсия s2 является средним квадратов таких разностей для всей популяции значений случайной переменной (у). Отсюда формула расчёта дисперсии имеет вид
s2=Е(у–y)2=
Как специальный символ Е(у) используется для обозначения среднего y, так и специальный символ D(у) используется для обозначения дисперсии, поэтому D(у)=s2.
Мерой разброса значений случайной переменной, которая имеет ту же единицу измерения, что и исходные наблюдения, является s. Она равна положительному значению квадратного корня из дисперсии s2. Эта мера называется стандартным отклонением и вычисляется по формуле
Рекомендуемые материалы
s=+



Иногда s снабжается подстрочным символом. Тогда обозначение sу не оставляет сомнений, что речь идёт о стандартным отклонении популяции наблюдений переменной (у), а не о какой либо другой популяции наблюдений переменной (х).
Усреднённое, дисперсия и стандартное отклонение выборки
Имеющиеся в действительности данные могут рассматриваться как малая выборка, состоящая из n результатов наблюдений взятых из большого множества N наблюдений, являющегося популяцией. Для данных точечной диаграммы на Рис.1.2.1 их усреднённое значение 
s2=



так как, в силу (1.2.3), 

Положительный квадратный корень из выборочной дисперсии даёт стандартное отклонение для этой выборки
s=+
которое имеет ту же единицу измерения, что и результаты наблюдений. Отсюда, для выборки из 10 наблюдений на Рис.1.2.1 её дисперсия получается
s2=

и стандартное отклонение для этой выборки s=1,36.
Также как это было для среднего y и усреднённого 
Таблица 1.4.1. Меры положения центра и разброса для популяции и выборки
|
Определения |
Популяция – очень большое множество N наблюдений, из которого может быть взята некоторая выборка наблюдений. |
Выборка – малая группа из n наблюдений, имеющихся в действительности. |
|
Параметры |
Статистики |
|
|
Меры центра |
Среднее популяции y = |
Усреднённое выборки |
|
Меры разброса |
Дисперсия популяции s2= Стандартное отклонение популяции s=+ |
Дисперсия выборки s2= Стандартное отклонение выборки s=+ |
Коэффициент вариации и медиана
Положим необходимо знать как велико стандартное отклонение s по сравнению со средним y. Их отношение s/y называется коэффициентом вариации. Представленным в процентах (s/y)100% его иногда называют выраженной в процентах ошибкой или вариацией. Коэффициент вариации равный 3% означает, что s составляет 3% от среднего y. Он очень близко связан со стандартным отклонением для log(y).
Коэффициент вариации выборки определяется отношением s/


Другой иногда полезной статистикой выборки является медиана. Она может быть получена посредством расположения членов выборки в ряд по мере возрастания их значений. Медианой будет среднее значение в ряду, если число членов выборки нечетное, а если чётное, то усреднённым между двумя средними значениями.
Остатки и степени свободы
Разности между результатами наблюдений и их усреднённым значением называются остатками. Сумма этих остатков всегда равна нулю. Отсюда, для n разностей выражение 





Обозначим число степеней свободы греческой буквой n (ню). Для данных точечной диаграммы на Рис.1.2.1 дисперсия выборки s2=1,86, её стандартное отклонение s=

Далее будут даны примеры, где для замены неизвестных параметров популяции необходимо вычислять несколько статистик выборки, и возникает необходимость накладывать несколько ограничений на разности. Когда имеется р независимых линейных ограничений на n остатков, то их сумма квадратов, а также получающиеся дисперсия и стандартное отклонение выборки – все имеют n =n–р степеней свободы.
«Натуральные» дисперсия и стандартное отклонение
Если среднее популяции y было бы известно, то дисперсия выборки вычислялась бы как обычная средняя величина квадратов отклонений от этого известного среднего


Эта статистика отмечена значком ~ для отличия её от s2. Сумма квадратов 



Люди также интересуются этой лекцией: 15 Пирамиды.
Упражнение 1.4.1. Вычислите усреднённое и выборочное стандартное отклонение для следующих данных по толщине эпитаксиального слоя в микрометрах: 16,8; 13,3; 11,8; 15,0; 13,2. Подтвердите, что сумма остатков у–
Ответ: 
Упражнение 1.4.2. Психолог измеряет (в секундах) периоды времени, требуемые для 10 крыс пройти по лабиринту, и получает следующие данные: 24, 37, 38, 43, 33, 35, 48, 29, 30, 38. Найдите усреднённое, а также дисперсию и стандартное отклонение выборки для этих данных.
Ответ: 
Упражнение 1.4.3. В последовательности испытаний в аэродинамической трубе получены следующие данные наблюдений поднятия аэродинамического профиля (в кг): 9072, 9148, 9103, 9084, 9077, 9111, 9096. Найдите усреднённое, выборочную дисперсию и выборочное стандартное отклонение для этих данных.
Ответ: 
Черноуцан А. Задачи на центр масс // Квант. — 1996. — № 2. — С. 43-45.
По специальной договоренности с редколлегией и редакцией журнала «Квант»
При решении механических задач неоценимую помощь может оказать использование понятия центра масс системы материальных точек. Одни задачи просто невозможно решить, не прибегая к этому понятию, решение других с его помощью может стать гораздо проще и нагляднее.
Перед тем как обсуждать конкретные задачи, напомним основные свойства центра масс и проиллюстрируем их примерами.
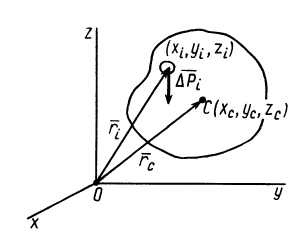
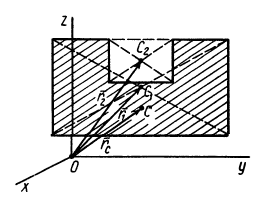
Центром масс (центром инерции) системы материальных точек назовем точку, характеризующую распределение масс в системе, координаты которой определяются формулами
Здесь mi — массы материальных точек, образующих систему, xi, yi, zi — координаты этих точек. Читатели, знакомые с понятием радиуса-вектора, предпочтут векторную запись:
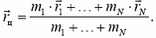
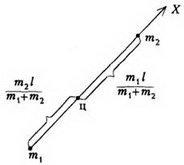
Пример 1. Найдем положение центра масс, простейшей системы, состоящей из двух точек, массы которых m1 и m2 и расстояние между ними l (рис. 1).
Рис. 1
Направив ось X от первой точки ко второй, получим, что расстояние от первой точки до центра масс (т.е. координата центра масс) равно 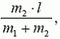
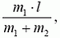
Обсудим некоторые свойства центра масс, что, как нам кажется, наполнит физическим содержанием приведенное выше несколько формальное определение этого понятия.
1) Положение центра масс не изменится, если какую-то часть системы заменить одной точкой с массой, равной массе этой подсистемы, и находящейся в ее центре масс.
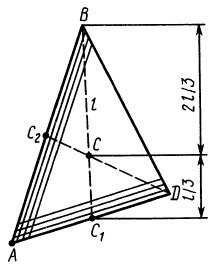
Пример 2. Рассмотрим плоский однородный треугольник и найдем положение его центра масс. Разделим треугольник на тонкие полоски, параллельные одной из сторон, и заменим каждую полоску точкой, расположенной в ее середине. Так как все такие точки лежат на медиане треугольника, центр масс тоже должен лежать на медиане. Повторяя рассуждения для каждой из сторон, получаем, что центр масс находится на пересечении медиан.
2) Скорость центра масс можно найти, взяв производную по времени от обеих частей равенства (1):
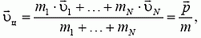
где 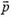
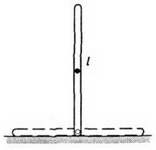
Пример 3. Поставим однородный стержень длиной l вертикально на гладкую плоскость (рис. 2) и отпустим. В процессе падения как горизонтальная составляющая его импульса, так и горизонтальная составляющая скорости центра масс будут оставаться равными нулю. Поэтому в момент падения центр стержня окажется в том месте, где первоначально стоял стержень, а концы стержня сместятся по горизонтали на 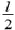
Рис. 2
3) Ускорение центра масс равно производной от его скорости по времени:

где в правой части равенства стоят только внешние силы, так как все внутренние силы сокращаются по третьему закону Ньютона. Получаем, что центр масс, движется так, как двигалась бы воображаемая точка с массой, равной массе системы, под действием результирующей внешней силы. Наверное, это самое физическое свойство центра масс.
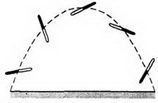
Пример 4. Если бросить палку, приведя ее при этом во вращение, то центр масс палки (ее середина) будет двигаться с постоянным ускорением 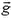
Рис. 3
4) Пусть система точек находится в однородном поле тяжести. Тогда суммарный момент сил тяжести относительно любой оси, проходящей через центр масс, равен нулю. Это значит, что равнодействующая сил тяжести проходит через центр масс, т.е. центр масс является также центром тяжести.
5) Потенциальная энергия системы точек в однородном поле тяжести вычисляется по формуле
где hц — высота центра масс системы.
Пример 5. При выкапывании в однородном фунте ямы глубиной h и разбрасывании грунта по поверхности его потенциальная энергия возрастает на 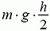
6) И еще одно полезное свойство центра масс. Кинетическая энергия системы точек может быть представлена в виде суммы двух слагаемых: кинетической энергии общего поступательного движения системы, равной 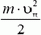
Пример 6. Кинетическая энергия обруча, катящегося без проскальзывания по горизонтальной поверхности со скоростью υ, равна
так как относительное движение в этом случае представляет собой чистое вращение, для которого линейная скорость точек обруча равна υ (полная скорость нижней точки должна быть равна нулю).
Теперь приступим к разбору задач на использование центра масс.
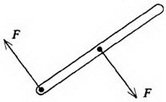
Задача 1. Однородный стержень лежит на гладкой горизонтальной поверхности. К стержню прикладывают две одинаковые по величине, но противоположные по направлению горизонтальные силы: одна сила приложена к середине стержня, другая — к его концу (рис. 4). Относительно какой точки начнет поворачиваться стержень?
Рис. 4
На первый взгляд может показаться, что осью вращения будет точка, лежащая посередине между точками приложения сил. Однако уравнение (3) показывает, что поскольку сумма внешних сил равна нулю, то равно нулю и ускорение центра масс. Значит, центр стержня будет оставаться в покое, т.е. служить осью вращения.
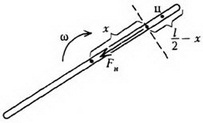
Задача 2. Тонкий однородный стержень длиной l и массой m привели в движение вдоль гладкой горизонтальной поверхности так, что он движется поступательно и одновременно вращается с угловой скоростью ω. Найдите, натяжение стержня в зависимости от расстояния x до его центра.
Перейдем в инерциальную систему отсчета, связанную с центром стержня. Рассмотрим движение куска стержня, заключенного между рассматриваемой точкой стержня (расположенной на расстоянии x от центра) и его концом (рис. 5).
Рис. 5
Единственной внешней силой для этого куска является искомая сила натяжения Fн, масса равна 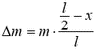
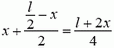
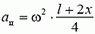
Задача 3. Двойная звезда состоит из двух звезд-компонентов массами m1 и m2, расстояние между которыми не меняется и остается равным L. Найдите период вращения двойной звезды.
Рассмотрим движение звезд-компонентов в инерциальной системе отсчета, связанной с центром масс двойной звезды. В этой системе отсчета звезды движутся с одной и той же угловой скоростью по окружностям разных радиусов (рис. 6).
Рис. 6
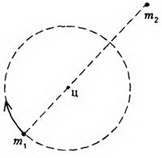
Радиус вращения звезды массой m1 равен 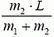
Видим, что период вращения двойной звезды равен
и определяется полной массой двойной звезды, независимо от того, как она распределена между звездами-компонентами.
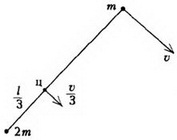
Задача 4. Две точечные массы m и 2m связаны невесомой нитью длиной l и движутся по гладкой горизонтальной плоскости. В некоторый момент времени скорость массы 2m равна нулю, а скорость массы m равна υ и направлена перпендикулярно нити (рис. 7). Найдите натяжение нити и период вращения системы.
Рис. 7
Центр масс системы находится на расстоянии 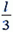
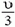
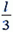
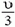
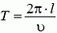
Задача 5. На гладкой горизонтальной плоскости лежат два одинаковых бруска массой m каждый, связанных легкой пружиной жесткостью k (рис. 8). Первому бруску сообщают скорость υ0 в направлении от второго бруска. Опишите движение системы. Через какое время деформация пружины впервые достигнет максимального значения?
Рис. 8
Центр масс системы будет перемещаться с постоянной скоростью 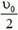
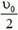
а амплитуда колебаний каждого бруска, которую можно найти из закона сохранения энергии, составляет
В первый раз деформация станет максимальной через четверть периода, т.е. через время 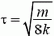
Задача 6. Шар массой m налетает со скоростью υ на покоящийся шар массой 2m. Найдите скорости обоих шаров после упругого центрального удара.
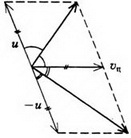
В системе отсчета, связанной с центром масс, полный импульс двух шаров равен нулю как до, так и после coyдарения. Легко догадаться, какой ответ для конечных скоростей удовлетворяет одновременно и этому условию, и закону сохранения энергии: скорости останутся такими же, как до удара, по величине, но изменят свои направления на противоположные. Скорость центра масс системы равна 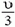
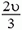
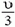
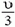
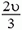
Отметим, что в системе центра масс очевидным является утверждение, что при ударе относительная скорость шаров не меняется по величине, но меняется по направлению. А так как разность скоростей при переходе в другую инерциальную систему отсчета не изменяется, можно считать, что мы вывели это важное соотношение и для первоначальной системы отсчета:
υ1 – υ2 = u1 – u2,
где буква υ используется для обозначения начальных скоростей, а u — для конечных. Это уравнение можно решать совместно с законом сохранения импульса вместо закона сохранения энергии (куда скорости входят во второй степени).
Задача 7. Известно, что при упругом нецентральном ударе двух одинаковых шаров, один из которых до удара покоился, угол разлета равен 90°. Докажите это утверждение.
В системе центра масс нецентральный удар можно описать следующим образом. До удара шары сближаются с одинаковыми импульсами, после удара они разлетаются с такими же по величине, но противоположно направленными импульсами, а прямая разлета поворачивается на некоторый угол относительно прямой сближения. Чтобы перейти обратно в начальную систему отсчета, надо каждую конечную скорость сложить (векторно!) со скоростью центра масс. В случае одинаковых шаров скорость центра масс равна 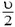
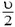
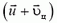
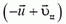
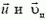
Рис. 9
Упражнения
1. Стержень массой m и длиной l шарнирно закреплен за один из концов. Стержень отклонили на некоторый угол от вертикального положения и отпустили. В момент прохождения вертикального положения скорость нижней точки равна υ. Найдите натяжение в средней точке стержня в этот момент времени.
2. Стержень массой m и длиной l вращают в горизонтальной плоскости с угловой скоростью ω вокруг одного из его концов. Найдите зависимость натяжения стержня от расстояния x до оси вращения, если на другом конце закреплен маленький грузик массой М.
3. Найдите период колебаний для системы, описанной в задаче 5 статьи, но для брусков различных масс m1 и m2.
4. Выведите известные общие формулы для упругого центрального удара двух шаров, используя переход в систему отсчета центра масс.
5. Шар массой m1 налетает на покоящийся шар меньшей массы m2. Найдите максимально возможный угол отклонения налетающего шара при упругом нецентральном ударе.
Ответы
1.
2.
3.
5.
Содержание:
Центр тяжести:
При рассмотрении движения тел, особенно таких, как самолеты, ракеты, космические корабли, важное значение имеет понятие центра тяжести.
Определения и формулы для вычисления центров тяжести
Для введения понятия центра тяжести разобьем мысленно рассматриваемое тело на достаточно большое число малых по сравнению с телом или элементарных его частей произвольной формы. Силу тяжести элементарной частицы тела с индексом
Радиус-вектор центра тяжести тела 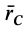
где 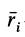

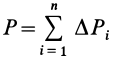

Рис. 88
Если в (1) перейти к пределу, увеличивая число элементарных частей 

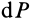
где 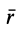
где 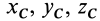
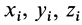
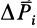
Используя понятие центра тяжести тела, введем понятие его центра масс. Силы тяжести элементарных частей тела и всего тела можно выразить через их массы 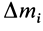
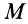

Подставляя эти значения сил тяжести в (1) и (1′) после сокращения на 
и соответственно
По формулам (2) и (2′) определяют радиус-вектор центра масс тела. Центр масс обычно определяют независимо от центра тяжести как геометрическую точку, радиус-вектор, которой вычисляется по формулам (2) или (2′). В проекциях на оси координат из (2) и (2′) получаем:
и
где 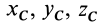
Для однородного тела силу тяжести элементарной частицы тела и ее массу можно вычислить по формулам
где 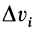


где 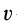


по которым определяют центр тяжести объема тела.
Если тело имеет форму поверхности, т. е. один из размеров мал по сравнению с двумя другими, как, например, у тонкого листа железа, то имеем
где 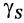
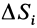
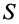
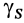
Для однородных тел типа проволоки, у которых два размера малы по сравнению с третьим, можно определить радиус-вектор центра тяжести длины линии по формулам
где 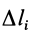
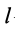
Методы определения центров тяжести (Центров масс)
Метод симметрии
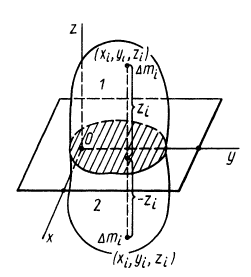
При определении центров тяжести широко используется симметрия тел. Докажем, что для однородного тела, имеющего плоскость симметрии, центр тяжести находится в плоскости симметрии. Для доказательства выберем начало координат в плоскости симметрии тела и одну из осей координат, ось 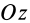
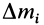
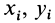
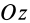
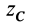
Разбивая сумму в числителе на две по симметричным частям тела, получаем, что
так как симметричные части тела 1 и 2 одинаковы.
Таким образом, центр масс расположен в плоскости симметрии и для его определения достаточно вычислить только две его координаты 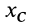
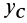
Аналогично доказывается, что для однородного тела, имеющего ось или центр симметрии, центр масс находится соответственно на оси симметрии или в центре симметрии.
Рис. 89
Метод разбиения на части (метод группировки)
Некоторые тела сложной формы можно разбить на части, центры тяжести которых известны или предварительно могут быть определены. В таких случаях центры тяжести сложных тел вычисляются по общим формулам, определяющим центр тяжести, только вместо элементарных частиц тела берутся его конечные части, на которые оно разбито. Покажем это на частном примере плоской фигуры, изображенной на рис. 90. Плоскую фигуру можно разбить на три части, центры тяжести которых 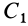
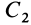
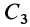
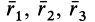
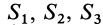
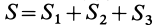
Используя определение центра тяжести и производя группировку слагаемых под знаком суммы по частям фигуры, на которые она разбита, получим
Радиусы-векторы центров тяжести частей тела выразятся в такой форме:
или
Используя эти формулы для радиуса-вектора всей фигуры, имеем
Полученная формула имеет ту же структуру, что и формула, определяющая радиус-вектор центра тяжести тела при разбиении его на элементарные частицы, только в нее входят величины для конечных частей тела.
Рис. 90
Метод отрицательных масс
Видоизменением метода разбиения на части является метод отрицательных масс. Проиллюстрируем его тоже на примере плоской фигуры (рис. 91). Для определения центра тяжести этой фигуры ее можно разбить на три части. Можно поступить по-другому. Для этого дополним нашу фигуру до прямоугольника и примем, что этот прямоугольник с площадью 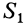
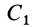
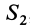
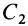
В отличие от обычного метода разбиения на части в формуле (4) массы и, следовательно, площади входят со знаком минус.
Метод отрицательных масс особенно удобен при вычислении положения центров тяжести тел, имеющих отверстия.
Рис. 91
Центры тяжести простейших тел
Для определения центров тяжести тел сложной формы методом разбиения на части или методом отрицательных масс необходимо уметь вычислять центры тяжести простейших тел, на которые разбивается тело сложной формы. Рассмотрим некоторые из тел, для определения центров тяжести которых известны простые способы их нахождения или вычисления по формулам.
Прямолинейный отрезок
Центр тяжести прямолинейного однородного отрезка располагается на его середине, а неоднородного— на самом отрезке и не может находиться вне отрезка.
Площадь треугольника
Для определения центра тяжести площади треугольника разобьем его прямыми линиями, параллельными одной из его сторон 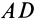

Затем разобьем треугольник на полоски прямыми линиями, параллельными другой стороне 
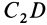

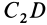
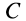

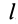
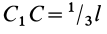
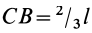
Рис. 92
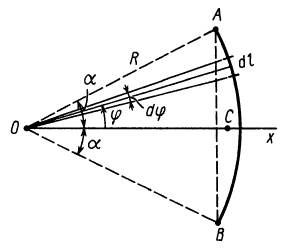
Дуга окружности
Дуга окружности 
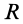
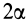
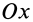

Рис. 93
В рассматриваемом случае
Подставляя эти значения в формулу для 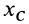
Таким образом,
Для полуокружности 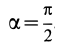
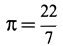
Площадь кругового сектора
Центр тяжести площади кругового сектора с радиусом 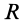
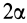
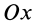
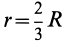
Рис. 94
Используя формулу для центра тяжести дуги окружности, получим
или
Для площади полукруга 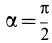
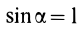
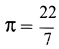
Объем пирамиды и конуса
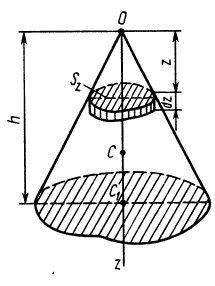
Определим положение центра тяжести объема конуса (рис. 95). Для простоты рассмотрим прямой конус, у которого высота является осью симметрии. Высотой конуса является отрезок, соединяющий его вершину 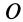
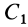
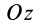
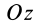
Разобьем конус плоскостями, перпендикулярными оси 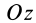
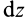
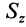
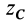
Отношения линейных размеров сечений к соответствующим размерам основания конуса пропорциональны их расстояниям до вершины конуса. Отношения площадей пропорциональны квадратам расстояний. Приняв 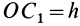
Учитывая, что
имеем
или
Таким образом, центр тяжести прямого конуса находится на расстоянии 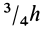
Рис. 95
Это справедливо для объема любого конуса и любой пирамиды, как прямых, так и наклонных, т. е. центр тяжести объема пирамиды или конуса находится на расстоянии 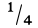
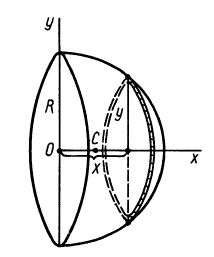
Объем полушара
Полушар имеет ось симметрии, которую примем за координатную ось 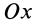
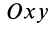
где 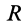
где 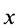
Объем элементарного диска
так как радиус диска 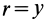
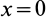
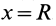
Таким образом, центр тяжести объема полушара находится от его центра на расстоянии
Это расстояние меньше половины радиуса полушара.
Рис. 96
Задача №1
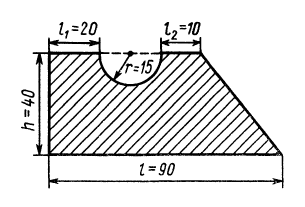
Определить координаты центра тяжести площади плоской фигуры, имеющей размеры, указанные на рис. 97.
Рис.97
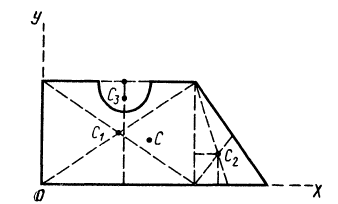
Рис. 98
Решение. Присоединим к заданной фигуре дополнительно полукруг 3 и разобьем полученную фигуру на прямоугольник 1 и треугольник 2. Получили три фигуры, две из которых имеют положительные площади (прямоугольник 1 и треугольник 2) и одна — отрицательную (полукруг 3). В выбранной системе координат для координат центра тяжести заданной фигуры имеем
где 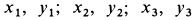
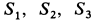
Вычислим площади и координаты центров тяжести отдельных фигур, учитывая рис. 98 Имеем:
так как 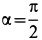
Подставляя полученные значения в (а), получим:
Центр тяжести плоской фигуры
постановка задачи. Найти площадь и координаты центра тяжести плоской фигуры.
План решения:
1. Разбиваем фигуру на простые отдельные части, положение центров тяжести которых известны.
2. Выбираем систему координат. Вычисляем площади и координаты 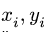
3. Находим общую площадь фигуры по формуле
4. Определяем координаты центра тяжести фигуры:
Задача №2
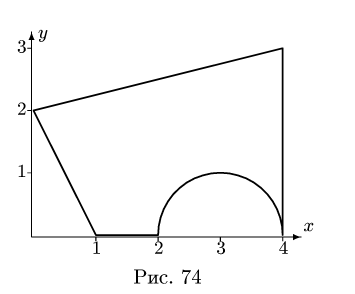
Найти площадь и координаты центра тяжести плоской фигуры. Криволинейный участок контура является половиной окружности с центром на оси Ох (рис. 74). Размеры на рисунке даны
Решение
1. Разбиваем фигуру на простые отдельные части, положение центров тяжести которых известны.
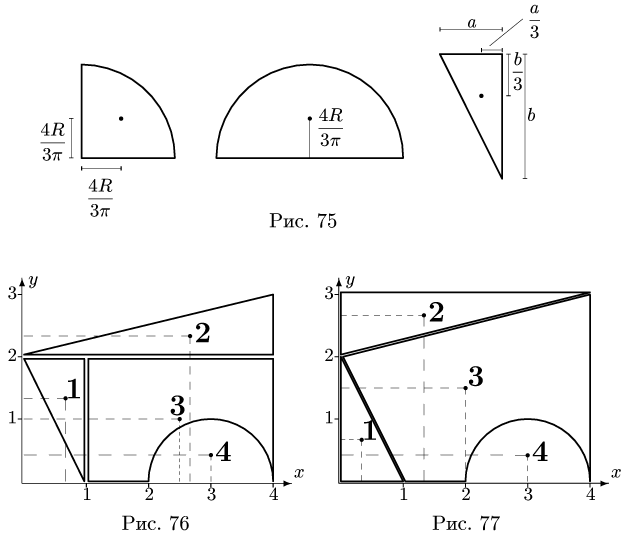
Центр тяжести прямоугольника находится в его геометрическом центре, положение центра тяжести других фигур, встречающихся в задачах, изображено на рис. 75
Представляем фигуру в виде двух треугольников 1,2, прямоугольника 3 и выреза 4 в виде полукруга (рис. 76).
2. Вычисляем площадь (в 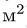
Площадь выреза берем со знаком минус.
3.Площадь фигуры
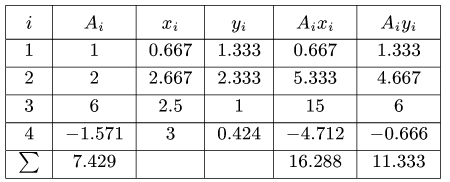
4. Находим координаты центра тяжести всей фигуры:
Вычисления удобно свести в таблицу:
Сначала заполняем столбцы 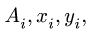
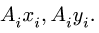
Замечание 1. Большинство задач на определение центра тяжести допускает несколько способов разбиения фигуры. Это можно использовать для проверки решения. Второй вариант разбиения фигуры в данном примере состоит из прямоугольника 3 с размерами 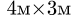
Замечание 2. Решение задачи в системе Maple V методом контурного интегрирования.
- Заказать решение задач по теоретической механике
Пространственная стержневая система
Постановка Задачи. Найти координаты центра тяжести пространственной фигуры, состоящей из N однородных стержней.
План решения:
1. Разбиваем фигуру на отдельные стержни.
2. Выбираем систему координат. Вычисляем длины и координаты 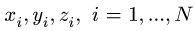
3. Находим суммарную длину стержней системы
4. Определяем координаты центра тяжести тела по формулам
Задача №3
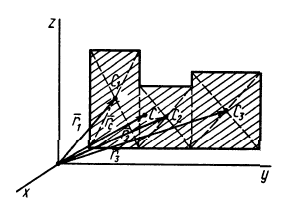
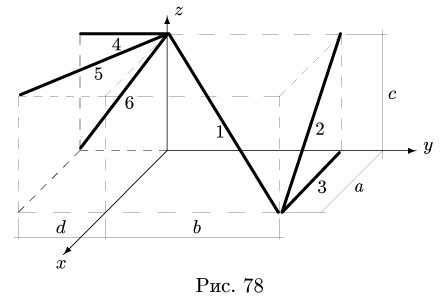
Найти координаты центра тяжести пространственной фигуры, состоящей из шести однородных стержней (рис. 78). Даны размеры:
Решение
1. Разбиваем фигуру на шесть стержней.
2. Выбираем систему координат (рис. 78). Вычисляем длины и координаты 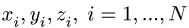
3. Находим суммарную длину стержней системы:
Промежуточные результаты удобно занести в таблицу:
4. Определяем координаты центра тяжести тела по формулам
Постановка задачи. Найти координаты центра тяжести однородного объемного тела.
План решения:
1. Разбиваем тело на простые части, положение центров тяжести которых известно.
2. Выбираем систему координат. Вычисляем объемы 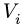
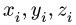
3. Находим общий объем тела по формуле
4. Определяем координаты центра тяжести тела:
Задача №4
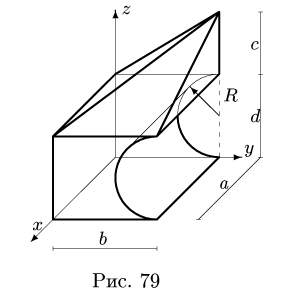
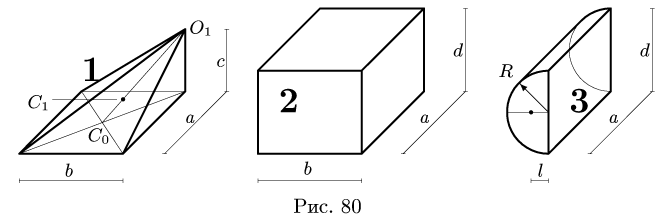
Найти координаты центра тяжести однородного объемного тела (рис.79);
Решение
1. Разбиваем тело на пирамиду 1, параллелепипед 2 и половину цилиндра 3 (рис. 80).
2. Выбираем систему координат. Вычисляем объемы 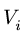
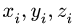
Центр тяжести параллелепипеда 2 совпадает с его геометрическим центром:
Объем половины цилиндра 3 берем со знаком минус:
где 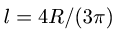
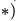
3. Находим общий объем тела:
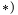
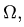
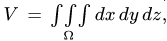
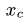
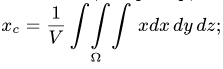
4. Определяем координаты центра тяжести тела:
Центр тяжести
Центр тяжести — точка, через которую проходит линия действия равнодействующей элементарных сил тяжести. Он обладает свойством центра параллельных сил. Поэтому формулы для определения положения центра тяжести различных тел имеют вид:
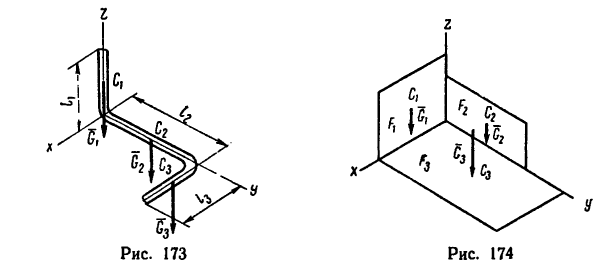
Если тело, центр тяжести которого нужно определить, можно отождествить с фигурой, составленной из линий (например, замкнутый или незамкнутый контур, изготовленный из проволоки, как на рис. 173), то вес 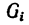
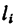
где d — постоянный для всей фигуры вес единицы длины материала.
После подстановки в формулы (1) вместо 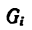
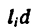
Если тело имеет вид фигуры, составленной из расположенных различным образом плоскостей или кривых поверхностей (рис. 174),
то вес каждой плоскости (поверхности) можно представить так:
где 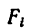
После подстановки этого значения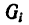
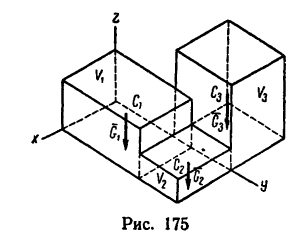
Если же однородное тело можно разделить на простые части определенной геометрической формы (рис. 175), то вес каждой части
где 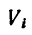
После подстановки значений 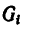
При решении некоторых задач на определение положения центра тяжести тел иногда необходимо знать, где расположен центр тяжести дуги окружности, кругового сектора или треугольника.
Если известен радиус дуги г и центральный угол 2а, стягиваемый дугой и выраженный в радианах, то положение центра тяжести С (рис. 176, а) относительно центра дуги О определится формулой
Если же задана хорда 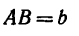
и тогда
В частном случае для полуокружности обе формулы примут вид (рис. 176, б)
Положение центра тяжести кругового сектора, если задан его радиус r (рис. 176, в), определяется при помощи формулы
Если же задана хорда сектора, то
В частном случае для полукруга обе последние формулы примут вид (рис. 176, г)
Центр тяжести площади любого треугольника расположен от любой стороны на расстоянии, равном одной трети соответствующей высоты.
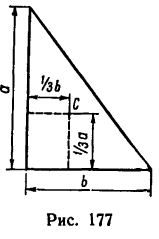
У прямоугольного треугольника центр тяжести находится на пересечении перпендикуляров, восставленных к катетам из точек, расположенных на расстоянии одной трети длины катетов, считая от вершины прямого угла (рис. 177).
При решении задач на определение положения центра тяжести любого однородного тела, й составленного либо из тонких стержней (линий), либо из пластинок (площадей), либо из объемов, целесообразно придерживаться следующего порядка:
- выполнить рисунок тела, положение центра тяжести которого нужно определить. Так как все размеры тела обычно известны, при этом следует соблюдать масштаб;
- разбить тело на составные части (отрезки линий или площади, или объемы), положение центров тяжести которых определяется исходя из размеров тела;
- определить или длины, или площади, или объемы составных частей;
- выбрать расположение осей координат;
- определить координаты центров тяжести составных частей;
- найденные значения длин или площадей, или объемов отдельных частей, а также координат их центров тяжести подставить в соответствующие формулы и вычислить координаты центра тяжести всего тела;
- по найденным координатам указать на рисунке положение центра тяжести тела.
- Кинематика точки
- Плоское движение твердого тела
- Мгновенный центр скоростей
- Мгновенный центр ускорений
- Условия равновесия системы сил
- Плоская система сил
- Трение
- Пространственная система сил
Центральные и вписанные углы
О чем эта статья:
Центральный угол и вписанный угол
Окружность — замкнутая линия, все точки которой равноудалены от ее центра.
Определение центрального угла:
Центральный угол — это угол, вершина которого лежит в центре окружности.
Центральный угол равен градусной мере дуги, на которую он опирается.
На рисунке: центральный угол окружности EOF и дуга, на которую он опирается EF
Определение вписанного угла:
Вписанный угол — это угол, вершина которого лежит на окружности.
Вписанный угол равен половине дуги, на которую опирается.
На рисунке: вписанный в окружность угол ABC и дуга, на которую он опирается AC
Свойства центральных и вписанных углов
Углы просты только на первый взгляд. Свойства центрального угла и свойства вписанного угла помогут решать задачки легко и быстро.
- Вписанный угол в два раза меньше, чем центральный угол, если они опираются на одну и ту же дугу:
Угол AOC — центральный, угол ABC — вписанный. Оба угла опираются на дугу AC, в этом случае центральный угол равен дуге AC, а угол ABC равен половине угла AOC.
- Теорема о центральном угле: центральный угол равен градусной мере дуги, на которую он опирается:
- Вписанные углы окружности равны друг другу, если опираются на одну дугу:
ㄥADC = ㄥABC = ㄥAEC, поскольку все три угла, вписанные в окружность, опираются на одну дугу AC.
- Вписанный в окружность угол, опирающийся на диаметр, — всегда прямой:
ㄥACB опирается на диаметр и на дугу AB, диаметр делит окружность на две равные части. Значит дуга AB = 180 ํ, ㄥCAB равен половине дуги, на которую он опирается, значит ㄥCAB = 90 ํ.
Если есть вписанный, обязательно найдется и описанный угол. Описанный угол — это угол, образованный двумя касательными к окружности. Вот так:
На рисунке: ㄥCAB, образованный двумя касательными к окружности. AO — биссектриса ㄥCAB, значит центр окружности лежит на биссектрисе описанного угла.
Для решения задачек мало знать, какой угол называется вписанным, а какой — описанным. Нужно знать, что такое хорда и ее свойство.
Нужно быстро привести знания в порядок перед экзаменом? Записывайтесь на курсы ЕГЭ по математике в Skysmart!
Хорда — отрезок, соединяющий две точки на окружности.
- Если две хорды в окружности пересекаются, то произведения отрезков одной равно произведению отрезков другой.
AB * AC = AE * AD
Получается, что стороны вписанного в окружность угла — это хорды.
- Если вписанные углы опираются на одну и ту же хорду — они равны, если их вершины находятся по одну сторону от хорды.
ㄥBAC = ㄥCAB, поскольку лежат на хорде BC.
- Если два вписанных угла опираются на одну и ту же хорду, то их суммарная градусная мера равна 180°, если их вершины находятся по разные стороны от хорды.
ㄥBAC + ㄥBDC = 180°
Примеры решения задач
Центральный, вписанные и описанные углы, как и любые другие, требуют тренировок в решении. Рассмотрите примеры решения задач и потренируйтесь самостоятельно.
Задачка 1. Дана окружность, дуга AC = 200°, дуга BC = 80°. Найдите, чему равен вписанный угол, опирающийся на дугу AB. ㄥACB = ?
Как решаем: окружность 360° − AC − CB = 360° − 200° − 80° = 80°
По теореме: вписанный угол равен дуге ½.
ㄥACB = ½ AB = 40°
Задачка 2. Дана окружность, ㄥAOC = 140°, найдите, чему равна величина вписанного угла.
Мы уже потренировались и знаем, как найти вписанный угол.
На рисунке в окружности центральный угол и дуга AC = 140°
Мы знаем, что вписанный угол равен половине центрального, то ㄥABC = ½ AC = 140/2 = 70°
Задачка 3. Чему равен вписанный в окружность угол, опирающийся на дугу, если эта дуга = ⅕ окружности?
СB = ⅕ от 360° = 72°
Вписанный угол равен половине дуги, поэтому ㄥCAB = ½ от CB = 72° / 2 = 36°
Геометрия
Именная карта банка для детей
с крутым дизайном, +200 бонусов
Закажи свою собственную карту банка и получи бонусы
План урока:
Центральный угол и градусная мера дуги
Любые две точки на окружности разбивают ее на две дуги. Чтобы отличать эти дуги, на каждой из них ставят точку, которую и указывают в обозначении дуги:
Здесь красным цветом показана⋃АСВ, а синим – ⋃ADB. Однако иногда для простоты указывают только концы дуги, то есть используют обозначение ⋃AВ. Это делается тогда, когда ясно, о какой дуге окружности идет речь. Обычно всегда подразумевается та дуга, которая меньше.
Можно заметить, что дуги отличаются по размеру, поэтому возникает потребность их измерения. Для этого используют такое понятие, как градусная мера дуги.
Для ее определения необходимо соединить концы дуги с центром окруж-ти. В результате получаются радиусы, которые пересекаются в центре окружности. Угол между ними именуется центральным углом окруж-ти.
Для каждой дуги можно построить единственный центральный угол, поэтому логично измерять дугу с помощью такого угла. Правда, обратное неверно. На рисунке видно, что центральному углу ∠АОВ соответствует сразу две дуги: ⋃АСВ и ⋃АDB:
Поэтому условно считают, градусная мера той из двух дуг, которая меньше, как раз и равна центральному углу:
Дуги, также как отрезки или углы, можно складывать или вычитать. Например, пусть есть две дуги, ⋃AВ и ⋃ВС, чьи градусные меры составляют 40° и 30°.
Как найти ⋃АС? Ей соответствует центральный угол ∠АОС, который в свою очередь равен сумме ∠АОВ и ∠ВОС:
Диаметр делит окруж-ть на две равные друг другу дуги, которые называются полуокружностями. При этом диаметр окружности можно рассматривать как угол между двумя радиусами, равный 180°. Получается, что градусная мера полуокружности составляет 180°:
Вместе две полуокружности образуют полную окруж-ть. Получается, что градусная мера всей окруж-ти составляет 180° + 180° = 360°.
Этот факт известен и из жизни – когда кто-то делает полный оборот вокруг своей оси, говорят, что он повернулся на 360°. Теперь мы можем вернуться к случаю, когда две точки делят окруж-ть на две неравные друг другу дуги. Градусная мера меньшей из них будет равна величине соответствующего центрального угла (обозначим его как α). В сумме две дуги должны дать 360°. Значит, градусная мера большей дуги будет составлять 360° – α:
Задание. Точки А, В, С и D лежат на одной окруж-ти. Известно, что ⋃АСВ составляет 107°. Какова величина ⋃ADB?
Решение. Вместе дуги ⋃АСВ и ⋃АDВ образуют полную окруж-ть, поэтому их сумма равна 360°. Это позволяет составить уравнение и найти из него ⋃АDB:
Задание. Найдите величину ∠АОС на рисунке, если известны ⋃AВ и ⋃ВС:
Решение. Сначала найдем ⋃АС, учтя, что все три дуги, показанные на рисунке, в сумме составляют 360°:
Для доказательства построим две одинаковые хорды AВ и СD в окруж-ти и соединим их концы с центром:
В результате получились ∆АОВ и ∆ОСD. У них равны все три стороны, значит, сами эти треугольники равны. Тогда
∠COD = ∠AOB
Но эти углы – центральные для дуг ⋃AВ и ⋃CD. Получается, что у этих дуг одинаковы их градусные меры, поэтому они также равны, ч. т. д.
Примечание. Всякая хорда окружности разбивает ее на две дуги – большую и меньшую. В данном правиле говорится именно равенстве меньших дуг.
Задание. На окруж-ти отмечены точки А, В и С так, что хорды AВ, ВС и АС равны. Найдите угол между радиусами окружности АО и ВО.
Дуги ⋃AВ, ⋃ВС и ⋃АС стянуты равными хордами AВ, ВС и АС. Значит, они одинаковы. Но в сумме эти три дуги образуют окруж-ть величиной в 360°. Значит, каждая из этих дуг втрое меньше:
⋃AВ = ⋃BC = ⋃AC = 360°:3 = 120°
∠АОВ – центральный для ⋃AВ, значит, он равен ее градусной мере, то есть он составляет 120°.
Вписанный угол
В окруж-ти можно построить ещё один угол, который именуют вписанным углом. Его отличие от центрального заключается в том, что его вершина лежит на окруж-ти, а не в ее центре. Сторонами же вписанного угла являются хорды окруж-ти.
Здесь дуга ⋃ВС находится внутри угла, а ее концы лежат на его сторонах. В таких случаях говорят, что ∠ВАС опирается на дугу ВС. Оказывается, что между величиной вписанного угла и дугой, на которую он опирается, есть взаимосвязь.
Обозначим вписанный угол ∠СAВ буквой α. Так как радиусы АО и ОС одинаковы, то ∆АОС – равнобедренный, и тогда углы при его основании будут одинаковы:
∠СОВ – внешний для ∆АОС. Напомним, что такой угол равен сумме тех 2 углов треуг-ка, которые с ним не смежны. В частности, в данном случае можно записать
∠СОВ = ∠OCA = ∠OAC = α + α = 2α
Но этот же угол – центральный, и его величина равна ⋃ВС:
Получается, что дуга вдвое больше вписанного угла.
Далее рассмотрим случай, когда диаметр, проведенный из вершины вписанного угла, делит его на две части:
В этом случае вписанный угол ∠СAВ можно представить как сумму углов ∠САD (обозначен как α)и ∠ВАD (обозначен как β). Мы уже доказали, что дуги, на которые опираются эти углы, вдвое больше самих углов:
Осталось рассмотреть третий случай, при котором обе стороны вписанного угла ∠ВАС лежат по одну сторону от диаметра:
Если здесь обозначить ∠САD как α, а ∠ВАD как β, то интересующий нас ∠СAВ можно представить как их разность:
Итак, во всех трех возможных случаях вписанный угол оказывается вдвое меньше дуги, на которую он опирается.
Задание. Найдите ∠ВАС на рисунке:
Задание. Найдите вписанный ∠AВС, сели прилегающие к нему дуги ⋃AВ и ⋃ВС равны 100° и 128°.
Решение. В сумме дуги ⋃АС, ⋃ВС и ⋃AВ образуют окруж-ть, поэтому их сумма составляет 360°. Тогда можно найти ⋃АС:
Задание. Найдите дугу ⋃SM на рисунке:
Решение. Сначала найдем дугу ⋃MN, она вдвое больше соответствующего ей вписанного угла:
⋃NM = 2*∠NSM = 2*35° = 70°
Заметим, что ⋃SN– это полуокружность, то есть она составляет 180°. При этом ⋃SM и ⋃MN вместе как раз образуют эту полуокружность, то есть их сумма также составляет 180°. Значит, ⋃МS можно найти, вычтя из полуокружности ⋃MN:
⋃MS = ⋃SN – ⋃MN = 180° – 70° = 110°
Заметим, что для одной дуги можно построить несколько вписанных углов. Каждый из них будет равен половине дуги, то есть все эти углы окажутся одинаковыми.
Задание. Найдите ∠АСD на рисунке:
Решение. Так как ∠ACD и ∠ABD опираются на одну дугу ⋃AD, то они должны быть одинаковыми:
∠ACD = ∠ABD = 63°
Задание. Докажите, что две дуги, находящиеся между двумя параллельными секущими окруж-ти, равны друг другу.
Нам надо доказать, что ⋃AВ и ⋃CD равны, если АС||BD. Проведем секущую ВС:
∠СВD и ∠АСВ равны, ведь они накрест лежащие. Получается, что ⋃AВ и ⋃CD являются основаниями равных вписанных углов. Отсюда вытекает, что эти дуги должны быть равными.
Напомним, что диаметр разбивает окруж-ть на две дуги по 180°. Отсюда можно сделать вывод – любой угол, опирающийся на полуокружность, должен составлять 180°:2 = 90°:
Задание. Диаметр окруж-ти AВ равен 17. Хорда ВС имеет длину 8. Какова длина хорды АС?
Так как ∠АСВ опирается на диаметр AВ, то он прямой. Значит, и ∆АСВ – прямоугольный, причем диаметр AВ в нем – гипотенуза. Неизвестный катет можно найти по теореме Пифагора:
Задание. Окруж-ть разбита на две дуги, ⋃AВС и ⋃СDA. Известно, что ∠AВС = 72°. Найдите ∠ADC.
Зная ∠AВС, мы легко найдем дугу ⋃ADC, она вдвое больше опирающегося на нее вписанного угла:
Углы между хордами и секущими
До этого мы рассматривали простые углы в окруж-ти, вершины которых лежали либо на самой окруж-ти, либо в ее центре. Однако иногда хорды и секущие пересекаются в другой точке, либо внутри, либо вне окруж-ти. Рассмотрим подобные задачи.
Более прост случай, когда необходимо найти угол между двумя пересекающимися хордами. Пусть хорды при пересечении образовали дуги ⋃AВ и ⋃СD величиной α и β. Каков угол между ними?
Проведем ещё одну хорду АD. В результате получим вписанные ∠САD и ∠ADB, которые будут равны половинам от соответствующих дуг, то есть α/2 и β/2. Интересующий нас ∠СPD оказывается внешним для ∆APD, и потому равен сумме двух углов в ∆APD (тех, которые с ним не смежны), то есть он составляет величину α/2 + β/2:
Величину α/2 + β/2 можно записать и иначе, вынеся множитель 1/2 за скобки:
Эту величину можно назвать полусуммой дуг, на которые опирается интересующий нас угол.
Задание. Найдите ∠МКВ на рисунке:
Решение. Интересующий нас угол опирается на хорды величиной 38° и 42°. Значит, он равен половине от их суммы:
∠MKB = (42° + 38°)/2 = 80°/2 = 40°
В более сложном случае необходимо найти угол между секущими, которые пересекаются вне окруж-ти. При этом известны дуги, образованные этими секущими:
Снова проведем хорду АD, чтобы у нас получились два вписанных угла, ∠ADB и ∠СAD, которые соответственно будут иметь величину β/2 и α/2:
Теперь уже ∠САD оказывается внешним для ∆ADK, а потому он является суммой двух других углов:
В итоге получили, что угол между секущими составляет половину от разности дуг, которые они отсекают от окруж-ти.
Задание. Найдите на рисунке величину∠К, если ⋃AВ и ⋃СD соответственно равны 42° и 130°:
Решение. В этой задаче просто используем доказанную теорему об углах между секущими. Искомый угол составляет половину от разности дуг, заключенных между секущими:
∠K = (130° – 42°):2 = 88°/2 = 44°
Теорема о произведении отрезков хорд
Можно заметить, что при пересечении двух хорд образуется пара подобных треугольников. Пусть хорды ADи ВС пересекаются в точке K. Добавим хорды AВ и СD и получим ∆AВК и ∆КСD:
На дугу ⋃BD опираются вписанные углы∠А и ∠С, значит, они одинаковы. Также на одну дугу АС опираются ∠D и∠В, поэтому и они одинаково. Равенство двух углов уже означает, что треугольники подобны по первому признаку подобия (дополнительно можно заметить, что ∠АКВ и ∠СКD равны как вертикальные углы).
Из подобия ∆AВК и ∆СКD вытекает пропорция между их сторонами:
Перемножив члены пропорции крест накрест, получим соотношение:
В результате нам удалось доказать следующее утверждение:
Задание. Хорды AВ и CD пересекаются в точке М. Известны, что АМ = 9, МВ = 3, МС = 2. Какова длина отрезка МD?
Хорда AВ разбивается на отрезки АМ и МВ, а хорда CD – на отрезки СМ и МD. Произведения этих отрезков одинаковы:
Подставим в это равенство известные величины
Рассмотрим ещё одну геометрическую конструкцию. Пусть из некоторой точки А к окруж-ти проведена как касательная к окружности АК, так и секущая, пересекающая окруж-ть в точках В и С:
Какие здесь есть взаимосвязи между углами и длинами отрезков? Для начала проведем хорды ВК и СК, а также радиусы ОК и ОВ. Обозначим буквой α угол ∠ВСК. Он вписанный, поэтому дуга, на которую он опирается (это ⋃ВК), вдвое больше и равна 2α. Тогда и центральный угол ∠ВОК также составляет 2α:
Теперь исследуем ∆ВОК. Он равнобедренный (ВО и ОК – одинаковые радиусы), поэтому углы при его основании совпадают:
Итак, углы при основании ∆ОВК, в частности ∠ОКВ, равны 90° – α. Заметим, что ∠ОКА – прямой, так как образован радиусом ОК и касательной АК, при этом он состоит из двух углов, ∠АКВ и ∠ВКО. Это позволяет найти ∠АКВ:
В результате мы получили важный промежуточный результат – угол между касательной и хордой, проведенной из точки касания, вдвое меньше образующейся при этом дуги.
Вернемся к картинке с секущей. Изначально как α мы обозначили ∠ВСК, но в результате получили, что и ∠АКВ = α.
Рассмотрим ∆AВК и ∆САК. У них есть общий∠А, а также одинаковые ∠AКВ и ∠ВСК, которые отмечены буквой α. Значит, ∆AВК и ∆САК подобны, поэтому мы имеем право записать пропорцию между его сторонами:
Здесь отрезок АС можно назвать секущей, а AВ – ее внешней частью. Тогда выведенное отношение можно сформулировать так:
Решение. Сначала находим длину всей секущей, пользуясь доказанной теоремой:
Решение. Проведем из точки А ещё и касательную АК к окруж-ти:
Величину квадрата касательной АК можно найти, используя секущую АС. Сначала вычислим длину АС:
Задачи на квадратной решетке
Рассмотрим несколько несложных задач, часто встречающихся на экзаменах.
Задание. Найдите ∠AВС на рисунке:
Решение. Здесь следует заметить, что расстояние между А и С составляет 8 клеток, при этом в окруж-ть как раз можно вписать квадрат со стороной 8.
Такой квадрат разобьет окруж-ть на 4 дуги, причем так как эти дуги опираются на хорды одинаковой длины, то они и сами равны. Вся окруж-ть составляет 360°, значит, каждая из этих дуг составляет 360°:4 = 90°. ∠AВС – вписанный, то есть он составляет половину дуги, на которую он опирается, а это⋃АС, равная 90°. Тогда
Задание. Найдите ∠AВС, используя рисунок:
Решение. Используя рассуждения из предыдущей задачи, легко определить, что∠А составляет 45°.При этом ∆AВС – равнобедренный, и ВС – его основание. Это следует хотя бы из того факта, что высота АН делит сторону ВН пополам.
Углы∠В и ∠С одинаковы, так как лежат при основании равнобедренного треуг-ка. Найдем их, используя тот факт, что все 3 угла в ∆AВС составляют в сумме 180°:
Задание. Вычислите ∠AВС:
Решение. Снова в окруж-ть можно вписать квадрат со стороной 8 клеток. Из этого следует что ⋃АВС составляет 90° (показана фиолетовым цветом):
Но ∠АВС опирается на синюю дугу. Так как вместе фиолетовая и синяя дуга составляют окружность, равную 360°, то синяя дуга должна быть равна 360° – 90° = 270°. ∠АВС как вписанный будет вдвое меньше, то есть он равен 270°:2 = 135°.
Задание. Чему равен ∠AВС на рисунке?
Если вписать в окруж-ть квадрат то он разобьет окруж-ти на дуги по 90°. В свою очередь точка А является серединой такой дуги, то есть она разбивает ее на две дуги по 45°.
∠AВС как вписанный будет вдвое меньше, то есть он равен 22,5°.
Углы, связанные с окружностью
Вписанные и центральные углы
Определение 1 . Центральным углом называют угол, вершина которого совпадает с центром окружности, а стороны являются радиусами радиусами (рис. 1).
Определение 2 . Вписанным углом называют угол, вершина которого лежит на окружности, а стороны являются хордами хордами (рис. 2).
Напомним, что углы можно измерять в градусах и в радианах. Дуги окружности также можно измерять в градусах и в радианах, что вытекает из следующего определения.
Определение 3 . Угловой мерой (угловой величиной) дуги окружности является величина центрального угла, опирающегося на эту дугу.
Теоремы о вписанных и центральных углах
Величина вписанного угла равна половине величины центрального угла, опирающегося на ту же дугу.
Середина гипотенузы прямоугольного треугольника является центром описанной
около этого треугольника окружности.
| Фигура | Рисунок | Теорема |
| Вписанный угол |  |
|
| Вписанный угол |  |
Вписанные углы, опирающиеся на одну и ту же дугу равны. |
| Вписанный угол |  |
Вписанные углы, опирающиеся на одну и ту же хорду, равны, если их вершины лежат по одну сторону от этой хорды |
| Вписанный угол |  |
Два вписанных угла, опирающихся на одну и ту же хорду, в сумме составляют 180° , если их вершины лежат по разные стороны от этой хорды |
| Вписанный угол |  |
Вписанный угол является прямым углом, тогда и только тогда, когда он опирается на диаметр |
| Окружность, описанная около прямоугольного треугольника |  |
Величина вписанного угла равна половине величины центрального угла, опирающегося на ту же дугу.
Вписанные углы, опирающиеся на одну и ту же дугу равны.
Вписанные углы, опирающиеся на одну и ту же хорду, равны, если их вершины лежат по одну сторону от этой хорды
Два вписанных угла, опирающихся на одну и ту же хорду, в сумме составляют 180° , если их вершины лежат по разные стороны от этой хорды
Вписанный угол является прямым углом, тогда и только тогда, когда он опирается на диаметр
Середина гипотенузы прямоугольного треугольника является центром описанной
около этого треугольника окружности.
Теоремы об углах, образованных хордами, касательными и секущими
| Вписанный угол |
| Окружность, описанная около прямоугольного треугольника |
Величина угла, образованного пересекающимися хордами, равна половине суммы величин дуг, заключённых между его сторонами.
Величина угла, образованного секущими, пересекающимися вне круга, равна половине разности величин дуг, заключённых между его сторонами
Величина угла, образованного касательной и хордой, проходящей через точку касания, равна половине величины дуги, заключённой между его сторонами
Величина угла, образованного касательной и секущей, равна половине разности величин дуг, заключённых между его сторонами
Величина угла, образованного двумя касательными к окружности, равна половине разности величин дуг, заключённых между его сторонами
| Фигура | Рисунок | Теорема | Формула |
| Угол, образованный пересекающимися хордами |  |
 |
|
| Угол, образованный секущими, которые пересекаются вне круга |  |
 |
|
| Угол, образованный касательной и хордой, проходящей через точку касания |  |
 |
|
| Угол, образованный касательной и секущей |  |
 |
|
| Угол, образованный двумя касательными к окружности |  |
 |
Величина угла, образованного пересекающимися хордами, равна половине суммы величин дуг, заключённых между его сторонами.
Величина угла, образованного касательной и хордой, проходящей через точку касания, равна половине величины дуги, заключённой между его сторонами
| Угол, образованный пересекающимися хордами хордами |
 |
Формула:  |
| Угол, образованный секущими секущими , которые пересекаются вне круга |
Формула:  |
|
Величина угла, образованного секущими, пересекающимися вне круга, равна половине разности величин дуг, заключённых между его сторонами |
| Угол, образованный касательной и хордой хордой , проходящей через точку касания |
 |
Формула:  |
| Угол, образованный касательной и секущей касательной и секущей |
Формула:  |
|
Величина угла, образованного касательной и секущей, равна половине разности величин дуг, заключённых между его сторонами |
| Угол, образованный двумя касательными касательными к окружности |
Формулы:  |
|
Величина угла, образованного двумя касательными к окружности, равна половине разности величин дуг, заключённых между его сторонами Доказательства теорем об углах, связанных с окружностьюТеорема 1 . Величина вписанного угла равна половине величины центрального угла, опирающегося на ту же дугу. Доказательство . Рассмотрим сначала вписанный угол ABC , сторона BC которого является диаметром окружности диаметром окружности , и центральный угол AOC (рис. 5). Таким образом, в случае, когда одна из сторон вписанного угла проходит через центр окружности, теорема 1 доказана. Теперь рассмотрим случай, когда центр окружности лежит внутри вписанного угла (рис. 6). В этом случае справедливы равенства и теорема 1 в этом случае доказана. Осталось рассмотреть случай, когда центр окружности лежит вне вписанного угла (рис. 7). В этом случае справедливы равенства что и завершает доказательство теоремы 1. Теорема 2 . Величина угла, образованного пересекающимися хордами хордами , равна половине суммы величин дуг, заключённых между его сторонами. Доказательство . Рассмотрим рисунок 8. Нас интересует величина угла AED , образованного пересекающимися в точке E хордами AB и CD . Поскольку угол AED – внешний угол треугольника BED , а углы CDB и ABD являются вписанными углами, то справедливы равенства что и требовалось доказать. Теорема 3 . Величина угла, образованного секущими секущими , пересекающимися вне круга, равна половине разности величин дуг, заключённых между сторонами этого угла. Доказательство . Рассмотрим рисунок 9. Нас интересует величина угла BED , образованного пересекающимися в точке E секущими AB и CD . Поскольку угол ADC – внешний угол треугольника ADE , а углы ADC , DCB и DAB являются вписанными углами, то справедливы равенства что и требовалось доказать. Теорема 4 . Величина угла, образованного касательной и хордой касательной и хордой , проходящей через точку касания, равна половине величины дуги, заключённой между его сторонами. Доказательство . Рассмотрим рисунок 10. Нас интересует величина угла BAC , образованного касательной AB и хордой AC . Поскольку AD – диаметр диаметр , проходящий через точку касания, а угол ACD – вписанный угол, опирающийся на диаметр, то углы DAB и DCA – прямые. Поэтому справедливы равенства что и требовалось доказать Теорема 5 . Величина угла, образованного касательной и секущей касательной и секущей , равна половине разности величин дуг, заключённых между сторонами этого угла. Доказательство . Рассмотрим рисунок 11. Нас интересует величина угла BED , образованного касательной AB и секущей CD . Заметим, что угол BDC – внешний угол треугольника DBE , а углы BDC и BCD являются вписанными углами. Кроме того, углы DBE и DCB , в силу теоремы 4, равны. Поэтому справедливы равенства что и требовалось доказать. Теорема 6 .Величина угла, образованного двумя касательными к окружности касательными к окружности , равна половине разности величин дуг, заключённых между его сторонами. Доказательство . Рассмотрим рисунок 12. Нас интересует величина угла BED , образованного касательными AB и CD . Заметим, что углы BOD и BED в сумме составляют π радиан. Поэтому справедливо равенство [spoiler title=”источники:”] http://100urokov.ru/predmety/urok-10-ugly-v-okruzhnosti http://www.resolventa.ru/spr/planimetry/cangle.htm [/spoiler] |
Содержание:
- Центр масс
- Центр параллельных сил
- Центр тяжести
- Центры тяжести некоторых плоских однородных фигур
- Центр тяжести дуги окружности
- Центр тяжести кругового сектора
- Центр тяжести кругового сегмента
- Центр тяжести треугольника
- Центр тяжести трапеции
- Примеры решения задач на тему: Центр масс
- Способы определения координат центра тяжести тела
- Метод симметрии
- Метод разбиения
- Метод дополнения
- Экспериментальные способы
- Центры тяжести некоторых однородных тел
- Центр тяжести дуги окружности
- Центр тяжести треугольника
- Центр тяжести сектора
Центр масс – это геометрическая точка, положение которой определяется распределением массы в теле, а перемещение характеризует движение тела или механической системы как целого.
На странице -> решение задач по теоретической механике собраны решения задач и заданий с решёнными примерами по всем темам теоретической механики.
Центр масс
Центр масс – это некоторое положение, определяемое относительно объекта или системы объектов и это среднее положение всех частей системы, взвешенное в соответствии с их массами.
Центр параллельных сил
Если на тело действует система параллельных сил 




Координаты центра параллельных сил определяются по зависимостям:
где 

Центр параллельных сил имеет ту особенность, что через него обязательно будет проходить линия действия равнодействующей при вращении линий действия всех сил системы вокруг точек их приложения на один и тот же угол в одну и ту же сторону. Модули сил при вращении не должны меняться.
Центр тяжести
Если твердое тело находится возле поверхности Земли, то на каждую материальную часть этого тела действует сила тяжести 


Координаты центра тяжести твердого тела можно определить как координаты центра параллельных сил:
где 



Если тело однородное, то есть удельный вес не меняется по объему 
где 

Тогда формулы для определения координат центра тяжести твердого тела приобретут вид:
Положение центра тяжести однородного тела зависит только от формы объема, что занимает тело, и называется центром тяжести этого объема.
Если однородное тело имеет форму тонкой пластины, то его можно рассматривать как материальную плоскую фигуру. В этом случае положение центра тяжести плоской фигуры определяется двумя координатами 

где 

Центр тяжести однородной пластины называется центром тяжести плоской фигуры.
Если выбранный элементарный объем 
а) для однородного твердого тела:
где 
б) для однородной поверхности:
где 
в) для однородной плоской фигуры, лежащей в плоскости xy:
г) для однородной линии:
где 
Центры тяжести некоторых плоских однородных фигур
Для упрощения определения центра тяжести используются следующие вспомогательные правилами:
1. Если тело имеет плоскость симметрии, то центр тяжести лежит на этой плоскости.
2. Если тело симметрично относительно оси, то центр тяжести лежит на этой оси.
3. Если тело симметрично относительно точки, то центр тяжести лежит в центре симметрии.
4. Если тело состоит из нескольких частей, центры тяжести которых можно определить, то центр тяжести такого тела находят как центр тяжести нескольких материальных точек, а именно тех, в которых расположены весы каждой отдельной части тела.
Центр тяжести дуги окружности
Центр тяжести дуги окружности 

где 


Центр тяжести кругового сектора
Центр тяжести кругового сектора лежит на оси симметрии и имеет координаты:
где 

Центр тяжести кругового сегмента
Центр тяжести кругового сегмента лежит на оси симметрии сегмента и имеет координаты:
где 

Центр тяжести треугольника
Центр тяжести треугольника (рис. 9.6) лежит в точке пересечения его медиан – на расстоянии 1/3 каждой медианы от соответствующего основания треугольника.
Центр тяжести трапеции
Центр тяжести трапеции (рис.9.7) с основаниями 



Расстояния 


Наиболее распространенный способ определения положения центра тяжести однородного тела сложной формы заключается в том, что его разбивают на такие части, положение центров тяжести которых известно, или может быть легко определено.
Например, однородную плоскую фигуру (рис.9.8) разбивают на три части 1,2 и 3, положения центров тяжести которых, 
Координаты центра тяжести фигуры 
где 


Этим способом удобно пользоваться и при определении положения центра тяжести плоской фигуры, из которой вырезана некоторая часть (рис.9.9).
В этом случае площадь плоской фигуры можно записать в виде разницы площадей сплошной фигуры 1 (площадь положительная) и вырезанной части 2 (площадь отрицательная), то есть 
Координаты центра тяжести фигуры равны:
где 



Первый из этих методов имеет название “метод разбиения”, второй – “метод дополнения”, или “метод отрицательных масс”. В общем случае формулы для определения центра тяжести плоской фигуры имеют вид:
где 
Примеры решения задач на тему: Центр масс
Задача № 1
Найти центр тяжести двутаврового профиля, размеры которого в сантиметрах указаны на рис.9.10.
Решение. Поскольку форма сечения имеет ось симметрии, ось 

В силу симметричности профиля относительно оси 
Линиями 

Запишем уравнение для определения абсциссы центра тяжести площади:
где 

Поскольку центры тяжести прямоугольников 

Площади этих прямоугольников соответственно равны:
Тогда:
Таким образом, центр тяжести фигуры лежит в точке 
Ответ:
Задача № 2
Найти координаты центра тяжести поперечного пересечения разностороннего угольника (рис.9.11), полки которого имеют ширину 
Решение. Разделим пересечение линией 


Запишем формулы для координат 

где 



С рис.9.11 видим, что
Тогда:
Ответ:
Задача № 3
Определить положение центра тяжести плоской фигуры (рис.9.12), ограниченной полуокружностью 



Решение. Данная площадь имеет ось симметрии, вдоль которой направим ось 

Разделим площадь 



Абсцисса центра тяжести площади 
где 





Для определения 
В случае половины круга
Площадь половины круга равна:
Центр тяжести треугольника лежит на пересечении его медиан (раздел 9.3.4). Поскольку треугольник 



Площадь треугольника 
Подставив найденные значения 




Ответ:
Задача № 4
Найти координаты центра тяжести квадратной пластины с вырезом в виде сегмента радиуса 
Решение. Осью симметрии рассматриваемой фигуры будет диагональ 
Поэтому направим ось 

Центр тяжести пластины будет лежать на оси 
Площадь фигуры 


Абсцисса центра тяжести фигуры будет равняться:
где 





Для квадрата 
Как следует из рис. 9.13, 
где 


Для кругового сектора (раздел 9.3.2) получим:
Поскольку 

Таким образом, абсцисса 
Площадь кругового сектора 
Подставив значение 




Ответ:
Задача № 5
Найти координаты центра тяжести площади, ограниченной (рис.9.14) правой веткой параболы 

Решение. На расстоянии 



Площадь выделенной элементарной площадки будет равняться:
Площадь фигуры, что ограничена заданными линиями:
Поскольку точка 


Отсюда:
Тогда:
Абсцисса центра тяжести
Для определения координаты 




Площадь выделенной площадки:
Ордината центра тяжести:
Тогда:
Ответ:
Способы определения координат центра тяжести тела
Существует несколько способов определения координат центра тяжести тел. среди них различают: метод симметрии, метод разбиения и дополнения, экспериментальные способы.
Рассмотрим последовательно эти способы.
Метод симметрии
Если однородное тело имеет плоскость, ось или центр симметрии, то его центр тяжести лежит соответственно в плоскости симметрии, или на оси симметрии, или в центре симметрии.
Таким образом, центр тяжести однородных симметричных тел, таких как кольца,
прямоугольные пластины, прямоугольные параллелепипеды, шары и другие тела, которые
имеют центр симметрии, расположенный в геометрических центрах (центры симметрии) этих тел.
Метод разбиения
Если тело можно разбить на конечное число таких частей, для каждой из которых положение центра тяжести нетрудно определяется, то координаты центра тяжести всего тела можно определить непосредственно по формулам выше. Причем количество слагаемых в числителе каждого из указанных выражений будет равно количеству частей, на которое разбивается тело.
Приведем пример определения центра тяжести тела методом разбиения его на отдельные тела, центры тяжести которых известны.
Пример:
Определить координаты центра тяжести однородной пластины. Размеры в
мм заданные на рис. 1.64
Решение.
Выберем оси координат x и y. Разбиваем пластину на отдельные прямоугольные части. Для каждого прямоугольника проводим диагонали, точки пересечения которых c1, c2 и c3 соответствуют центрам веса каждого прямоугольника. В принятой системе координат нетрудно получить значение координат этих точек. А именно: c1 (–1,1), c2 (1,5), c3 (5,9). Площади каждого тела соответственно равны: I — s1 = 4 см2; II — s2 = 20 см2; III — s3 = 12 см2. Площадь всей пластины равна: S = s1 + s2 + s3 = 36 см2.
Для определения координат центра тяжести заданной пластины используем выражение выше. Подставив значения всех известных величин в уравнения, получим
По вычисленным значениям координат центра тяжести пластины можно обозначить точку C на рисунке. Как видим, центр тяжести (геометрическая точка) пластины расположен за ее пределами.
Метод дополнения
Способ, о котором говорится далее, является некоторым случаем способа разбиения. Он может применяться к телам, которые имеют вырезы, полости, причем без учета выреза, или вырезанной части тела положение центра тяжести тела известно. Рассмотрим пример применения такого метода.
Пример. Определить положение центра тяжести круглой пластины радиусом R, имеет круговое отверстие радиуса r (рис. 1.65). Расстояние C1C2 = a.
Решение.
Как видно из рисунка, центр тяжести пластины находится на оси симметрии пластины x, то есть на прямой, проходящей через точки C1 и C2. Таким образом, для определения положения центра тяжести этой пластины необходимо вычислить только одну координату xC, поскольку вторая координата yC равна нулю. Покажем оси координат x, y. Примем, что пластина состоит из двух тел — с полного круга (без учета выреза) и тела,
образовано вырезом. В принятой системе координаты x для указанных тел будут равны: x1 = 0; x2 = C1C2 = a. Площади тел равны: 

заданной пластины используем первое уравнение выражения.
Подставив значения всех известных величин в это уравнение, получим
Таким образом, значение координаты xC отрицательное, а потому, поскольку вторая координата 0 yC = 0, то центр тяжести пластины C размещен на оси x слева от точки C1.
Экспериментальные способы
Эти способы нашли широкое применение при отыскании положения центра тяжести тел сложных форм и конфигураций, для которых другие способы почти непригодны вследствие громоздкости и сложности. К таким телам, в первую очередь, следует отнести комбайны, тракторы, сложные сельскохозяйственные машины и орудия. При применении экспериментальных способов отыскания положения
центра тяжести наиболее широко используют метод подвешивания и метод взвешивания тел.
При применении метода подвешивания тело на тросе подвешивают за различные его точки. Направление троса, будет давать каждый раз направление силы веса тела. Тогда точка пересечения этих направлений и дает положение центра тяжести тела.
Использование второго метода — взвешивание требует измерения веса всего тела, а также отдельных его частей. Рассмотрим пример применения этого метода.
Пример.
Определим продольную координату центра тяжести трактора, у которого продольная база составляет l (рис. 1.66).
Решение.
Сначала поставим на платформу весов задние колеса трактора, как это показано на рисунке. Итак, определяем силу давления задних колес на платформу, или реакцию 

Q = RA + RB.
Теперь составим алгебраическую сумму моментов всех сил относительно точки A. Она равна
Откуда определяем продольную координату центра тяжести:
xC = 
Для определения поперечной координаты центра тяжести трактора необходимо знать реакции левых колес (переднего и заднего) и правых, а также поперечную базу трактора. Дальше аналогичным выражением определяется эти координаты центра тяжести.
Центры тяжести некоторых однородных тел
Определим далее координаты центров тяжести некоторых простых однородных тел.
Центр тяжести дуги окружности
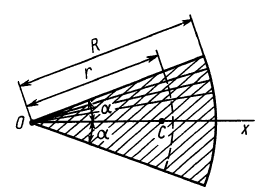
Рассмотрим дугу AB окружности радиусом R, в которой центральный угол OAB равен 2α (радиан) (рис. 1.67). Покажем оси координат x, y начало которых разместим в точке O. Вследствие того, что дуга имеет ось симметрии Ox, то центр ее тяжести будет расположен именно на этой оси (yC = 0). Остается только вычислить координату xC.
Используем для вычисления этой координаты первое уравнение выражения, а именно
Определим составляющие, которые необходимо подставить в это уравнение. Для этого выделим на дуге AB элемент M M1 длиной dl, равной:
dl = R · dφ.
Если φ — угол, определяющий положение элемента M M1 на дуге AB, то координата x элемента M M1 будет равна:
x = Rcosφ.
Общая длина дуги AB равна:
L = 2α · R.
Подставим эти значения в первое уравнение выражения. При этом считается, что интеграл в числителе данного выражения должен быть определенным по всей длине дуги. Будем иметь:
Таким образом, координата xC будет равняться
xC = 
Центр тяжести треугольника
Есть произвольный треугольник, вершины которого в принятой системе координат Oxy соответствуют точкам с координатами A1 (x1, y1), A2 (x2, y2), A3 (x3, y3) (рис. 1.68). Если провести прямые, которые будут параллельны основе A1A3 и провести их достаточное количество, то вся площадь треугольника будет состоять из полос бесконечно малой ширины, центры тяжести которых будут размещены посередине каждой полосы, а потому и центр тяжести треугольника будет расположенный на его медиане. А если провести линии, параллельные другой стороне треугольника, то и в этом случае центр тяжести будет размещен на соответствующей медиане. Таким образом, совершенно очевидно, что центр тяжести треугольника C будет расположен в точке пересечения его медиан.
Определим координаты этой точки. По курсу аналитической геометрии известно, что точка пересечения медиан треугольника в принятой системе координат определяется такими зависимостями
где x1, x2, …, y3 — координаты вершин треугольника.
Полезно также знать, что
Центр тяжести сектора
Рассмотрим круговой сектор OAB радиуса R, центральный угол которого равен 2α (радиан) (рис. 1.69). Центр тяжести сектора, вполне очевидно, лежит на оси его симметрии, то есть на биссектрисе угла AOB. Эту биссектрису примем за ось x и найдем на этой оси положение центра C. Разобьем площадь сектора на бесконечно большое число элементарных секторов с центральными углами ∆φ.
Будем рассматривать каждый сектор как треугольник с основанием R · ∆φ и высотой R. Центр тяжести каждого треугольника расположен на расстоянии 
Тогда учитывая, что
Будем иметь
Услуги по теоретической механике:
- Заказать теоретическую механику
- Помощь по теоретической механике
- Заказать контрольную работу по теоретической механике
Учебные лекции:
- Статика
- Система сходящихся сил
- Момент силы
- Пара сил
- Произвольная система сил
- Плоская произвольная система сил
- Трение
- Расчет ферм
- Расчет усилий в стержнях фермы
- Пространственная система сил
- Произвольная пространственная система сил
- Плоская система сходящихся сил
- Пространственная система сходящихся сил
- Равновесие тела под действием пространственной системы сил
- Естественный способ задания движения точки
- Центр параллельных сил
- Параллельные силы
- Система произвольно расположенных сил
- Сосредоточенные силы и распределенные нагрузки
- Кинематика
- Кинематика твердого тела
- Движения твердого тела
- Динамика материальной точки
- Динамика механической системы
- Динамика плоского движения твердого тела
- Динамика относительного движения материальной точки
- Динамика твердого тела
- Кинематика простейших движений твердого тела
- Общее уравнение динамики
- Работа и мощность силы
- Обратная задача динамики
- Поступательное и вращательное движение твердого тела
- Плоскопараллельное (плоское) движение твёрдого тела
- Сферическое движение твёрдого тела
- Движение свободного твердого тела
- Сложное движение твердого тела
- Сложное движение точки
- Плоское движение тела
- Статика твердого тела
- Равновесие составной конструкции
- Равновесие с учетом сил трения
- Колебания материальной точки
- Относительное движение материальной точки
- Статические инварианты
- Дифференциальные уравнения движения точки под действием центральной силы и их анализ
- Динамика системы материальных точек
- Общие теоремы динамики
- Теорема об изменении кинетической энергии
- Теорема о конечном перемещении плоской фигуры
- Потенциальное силовое поле
- Метод кинетостатики
- Вращения твердого тела вокруг неподвижной точки

 .
.