Как решать дифференциальные уравнения
СОДЕРЖАНИЕ ТЕКУЩЕЙ СТАТЬИ
- Основные понятия и определения
-
- Определения
- Типы уравнений
- Алгоритм решения
- Дифференциальные уравнения первого порядка
-
- ДУ с разделяющимися переменными
- Однородные ДУ
- Линейные неоднородные ДУ
- ДУ Бернулли
- ДУ в полных дифференциалах
- Дифференциальные уравнения второго порядка
-
- ДУ допускающие понижение порядка
- Линейные однородные ДУ с постоянными коэффицентами
- Линейные неоднородные ДУ с постоянными коэффициентами
- Метод Лагранжа
Введите уравнение
Условия к задаче (необязательно)
Пример 1 Пример 2 Правила ввода
Дифференциальные уравнения бывают обыкновенными и в частных производных. В этой статье мы будем говорить об обыкновенных уравнениях и о том, как их решать.
Основные понятия и определения
Определения
Обыкновенные дифференциальные уравнения – это уравнения, содержащие функцию $y(x)$ только от одной неизвестной переменной (например, $x$).
Рассмотрим это на следующих практических примерах. $$ y’ = xy $$ $$ y” = 1 $$
Итак, в первом диффуре присутствует независимая переменная $x$, неизвестная функция $y(x)$ и производная этой функции $y'(x)$. А во втором случае нет $x, y(x),y'(x)$, а есть только вторая производная функции $y”(x)$. Значит, для того, чтобы уравнение называлось дифференциальным необязательно иметь $y(x)$ и $x$, а должно быть производная $y(x)$ любого порядка.
Порядок дифференциального уравнения – это порядок старшей производной неизвестной функции $y(x)$ в уравнении.
В первом случае максимальная производная первого порядка, значит, и само ДУ первого порядка. А во втором случае уравнение имеет вторую производную $y”(x)$, поэтому это ДУ второго порядка.
Общее решение дифференциального уравнения – это семейство функций $y = f(x,C)$, при подстановке которых в заданное исходное уравнение мы получаем равенство левой и правой части. Здесь $C$ произвольная константа. Процесс нахождения таких решений называется интегрированием дифференциального уравнения.
Частное решение дифференциального уравнения – это решение, полученное из общего решения, путем нахождения константы $C$ из дополнительных условий в задаче.
Типы уравнений
- ДУ первого порядка
– с разделяющимися переменными
– однородные
– линейные неоднородные
– уравнение Бернулли - ДУ второго порядка
– уравнения допускающие понижение порядка
– однородные с постоянными коэффициентами
– неоднородные с постоянными коэффициентами
Алгоритм решения
- По старшей производной функции $y(x)$ определить порядок ДУ
- Зная порядок, определить тип уравнения
- Узнав тип, подобрать подходящий метод решения
- Используя метод, найти общее решение
- Получить частное решение из общего путем вычисления неизвестной $C$
В некоторых случаях для решения дифференциальных уравнений удобно переписать производные в таком виде (например, это нужно для ДУ с разделяющимися переменными). $$y’ = frac{dy}{dx}$$
ОБЯЗАТЕЛЬНО! Чтобы успешно решать дифференциальные уравнения необходимо уметь находить интегралы. Поэтому, если вы забыли данную тему, то её нужно вспомнить!
| Пример 1 |
| Дана функция $y = Ce^{frac{x^2}{2}} $. Проверить является ли функция решением дифференциального уравнения $y’ = xy$ |
| Решение |
|
Для того, чтобы проверить является ли функция решением нужно подставить её в исходное ДУ. Найдем производную функции. $$y’ = (Ce^{frac{x^2}{2}})’ = Ce^{frac{x^2}{2}} cdot (frac{x^2}{2})’ = Ce^{frac{x^2}{2}} cdot x = Cxe^{frac{x^2}{2}}$$ Теперь подставим $y’$ и $y$ в исходное уравнение. $$ Cxe^{frac{x^2}{2}} = x Ce^{frac{x^2}{2}} $$ Получили равенство левой и правой части, значит, функция $y = Ce^{frac{x^2}{2}} $ является общим решением ДУ. |
| Ответ |
| $$y = Ce^{frac{x^2}{2}} $$ |
Дифференциальные уравнения первого порядка
ДУ с разделяющимися переменными
Уравнения такого типа имеют следующий вид: $$ f_1(x)g_1(y)dy = f_2(x)g_2(y)dx$$ Общее решение такого ДУ нужно находить путем разделения переменных с иксами и с игреками: $$int frac{g_1(y)}{g_2(y)}dy = int frac{f_2(x)}{f_1(x)}dx$$
СОВЕТ: Если не удается определить тип диффура первого порядка, то рекомендуем мысленно попытаться разделить переменные иксы от игреков. Возможно перед вами хитрое дифференциальное уравнение с разделяющимися переменными.
Алгоритм нахождения общего решения:
- Переписываем производные через $y’ = frac{dy}{dx}$
- Разделяем все $y$ в левую часть уравнения, а все $x$ в правую
- Интегрируем обе части уравнения
| Пример 2 |
| Найти общее решение дифференциального уравнения первого порядка с разделяющимися переменными $y’ = xy$ |
| Решение |
|
Видим, что в условии задачи присутствует производная от неизвестной функции $y(x)$ первого порядка. Значит, перед нами диффур 1-го порядка. Забегая вперед скажем, что данный диффур из задачи является дифференциальным уравнением с разделяющимися переменными. Что это означает? Это означает, что можно в уравнении перенести всё что содержит $y$ в левую часть равенства, а то, что содержит $x$ перенести в правую часть. То есть разделить “игрики” от “иксов” по разные стороны. Но прежде, чем это делать стоит переписать производную таким образом: $$y’ = frac{dy}{dx}$$ После замены производной игрека исходное уравнение приобретает такой формат: $$frac{dy}{dx} = xy$$ Теперь, как сказали ранее, начинаем отделять игрики от иксов по разные стороны. Для этого обе части уравнения необходимо умножить на $dx$, а ещё разделить на $y$. $$ frac{dy}{y} = xdx $$ Теперь необходимо проинтегрировать обе части уравнения, чтобы получить функцию $y$. Для этого навешиваем значок интеграла на обе части уравнения. $$ int frac{dy}{y} = int xdx $$ Вспоминаем, что левый интеграл равен натуральному логарифму, а правый интеграл $frac{x^2}{2}$. А так как интеграл неопределенный, то необходимо прибавить константу $C$. $$ ln|y| = frac{x^2}{2} + C $$ Теперь необходимо вытащить $y$ для того, чтобы записать окончательный ответ в виде общего решения. Для этого вспоминаем, что игрик в $ln|y| = x$ равен $y = e^x$. Поэтому продолжая решать наше уравнение получаем. $$ y = e^{frac{x^2}{2} + C} $$ Далее вспоминаем свойство степеней $a^{x+y} = a^x cdot a^y$. Таким образом делаем преобразования нашего уравнения. Так как $e^C$ это константа, то её можно переписать следующим видом $e^C = C$. И после этого получаем окончательный ответ исходного уравнения, называемый общим решением. $$ y = Ce^{frac{x^2}{2}} $$ |
| Ответ |
| $$ y = Ce^{frac{x^2}{2}} $$ |
| Пример 3 |
| Найти частное решение дифференциального уравнения первого порядка с разделяющимися переменными $y’ = frac{2x}{1+x^2}$, если $y(0) = 0$. |
| Решение |
|
Начнем решать с того, что представим производную в исходном уравнении в виде $y’ = frac{dy}{dx}$: $$ frac{dy}{dx} = frac{2x}{1+x^2} $$ Теперь разделяем переменные иксы от игреков по разные стороны равенства путем умножения обеих частей уравнения на $dx$: $$ dy = frac{2x}{1+x^2} dx $$ Навешиваем знак интеграла на левую и правую часть, а затем решаем интегралы: $$ int dy = int frac{2x}{1+x^2} dx $$ $$ y = int frac{2x}{1+x^2} dx $$ Замечаем, что $(1+x^2)’ = 2x$. Поэтому $2x$ можно занести под знак дифференциала, чтобы решить интеграл: $$ y = int frac{d(1+x^2)}{1+x^2} = ln (1+x^2) + C $$ Получили общее решение $y = ln (1+x^2) + C$. В условии задачи просят найти частное решение при условии $y(0) = 0$. Это означает, что нужно из последного условия найти константу $C$. Из $y(0) = 0$ видно, что $x = 0$, а $y = 0$. Подставляем их в общее решение дифференциального уравнения и вычисляем $C$: $$ln(1+0^2)+C = 0$$ $$ln 1+C = 0$$ $$0 + C = 0$$ $$C=0$$ Теперь заменив в общем решении $C$ на ноль, получаем частное решение: $$y = ln(1+x^2)$$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$y = ln(1+x^2)$$ |
Однородные ДУ
Чтобы проверить является ли предложенное уравнение однородным нужно заменить $x$ и $y$ на $lambda x$ и $lambda y$. Производную $y’$ заменять не нужно. Если все $lambda$ после элементарных преобразований удастся уничтожить, то перед вами однородное дифференциальное уравнение первого порядка.
Решается по следующему алгоритму:
- Проверить уравнение на однородность с помощью $lambda$
- Привести уравнение к виду $y’ = f(frac{y}{x})$
- Выполнить замену $frac{y}{x} = t$ и $y’ = t’x+t$
- Решить уравнение методом разделяющихся переменных
| Пример 4 |
| Найти общее решение дифференциального уравнения первого порядка $$y’ = frac{y}{x} – 1$$ |
| Решение |
|
Так как разделить переменные не получается, то проверим уравнение на однородность. Для этого вместо $x$ и $y$ выполним подстановку $lambda x$ и $lambda y$: $$y’ = frac{lambda y}{lambda x} – 1$$ Выполняем сокращение $lambda$ в числителе и знаменателе: $$y’ = frac{y}{x} – 1$$ После сокращения все $lambda$ уничтожились, значит перед нами однородное дифференциальное уравнение первого порядка. Решим его с помощью замены $frac{y}{x} = t$ и $y’ = t’x + t$: $$ t’x + t = t – 1$$ Переносим $t$ в одну сторону и тем самым уничтожаем его: $$ t’x = -1 $$ Теперь это ДУ с разделяющимися переменными. Запишем его в привычном для него виде: $$ frac{dt}{dx} x = -1 $$ Разделим переменные домножением на $dx$ и делением на $x$ обеих частей равенства: $$dt = -frac{dx}{x}$$ Интегрируем обе части: $$int dt = – int frac{dx}{x}$$ $$t = -ln|x|+C$$ Выполняем назад замену $t = frac{y}{x}$: $$frac{y}{x} = -ln|x|+C$$ Умножаем обе части на $x$, чтобы получить окончательный ответ общего решения: $$y = -xln|x| +Cx$$ |
| Ответ |
| $$y = -xln|x| +Cx$$ |
| Пример 5 |
| Решить дифференциальное уравнение первого порядка $xy+y^2=(2x^2+xy)y’$ |
| Решение |
|
Сперва проверим уравнение на однородность. Подставляем $lambda$ вместо $x$ и $y$. $$lambda x cdot lambda y + (lambda y)^2 = (2 (lambda x)^2 + lambda xcdot lambda y)y’$$ После вынесения $lambda$ слева и справа за скобки получаем $$ lambda^2(xy+y^2) = lambda^2(2x^2+xy)y’,$$ где все $lambda$ сокращаются. А это подтвержает однородность уравнения. Перед тем, как выполнить замену $t = frac{y}{x}$ нужно привести исходное уравнение к виду $y = f(frac{y}{x})$. Для этого разделим левую и правую часть равенства на $x^2$: $$frac{y}{x}+frac{y^2}{x^2} = (2+frac{y}{x})y’.$$ Теперь производим замену $t = frac{y}{x}$ и $y’ = t’x+t$ в преобразованном уравнении: $$t+t^2=(2+t)(t’x+t).$$ Раскрываем скобки и сокращаем одинаковые слагаемые $$t+t^2 = 2t’x+2t+t’xt+t^2$$ $$2t’x+t’xt=-t.$$ Далее в полученном уравнении разделяем переменные $t$ и $x$ по разные стороны знака равенства. Для этого выносим за скобку $t’x$ $$t’x(2+t)=-t.$$ Делим на $t$ обе части уравнения $$t’xfrac{2+t}{t}=-1.$$ Представляем производную $t’ = frac{dt}{dx}$ и переносим $dx$ и $x$ в правую часть равенства $$frac{2+t}{t}dt = -frac{dx}{x}.$$ Интегрируем обе части уравнения $$int frac{2+t}{t}dt = – int frac{dx}{x}$$ $$int frac{2}{t}dt+int dt = -int frac{dx}{x}$$ $$2ln|t|+t = -ln|x|+C.$$ Выполняем обратную замену $t = frac{y}{x}$: $$2ln|frac{y}{x}|+frac{y}{x}=-ln|x|+C.$$ Упрощаем полученное равенство с помощью элементарных преобразований и свойств натурального логарифма $$2ln|y|-2ln|x|+frac{y}{x} = -ln|x|+C$$ $$2ln|y|+frac{y}{x}=ln|x|+C$$ $$2ln|y|+frac{y}{x}=ln|x|+ln|C|$$ $$2ln|y|+frac{y}{x}=ln|Cx|$$ $$ln y^2+frac{y}{x}=ln|Cx|$$ $$ln y^2 = ln|Cx|-frac{y}{x}$$ $$y^2 = Cxe^frac{-y}{x}.$$ Привели решение к такому виду через $y^2$. Это называется общим интегралом дифференциального уравнения. Ответ в таком виде остается в таком формате. Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$y^2 = Cxe^frac{-y}{x}$$ |
Линейные неоднородные ДУ
Линейное неоднородное дифференциальное уравнение 1-го порядка имеет следующий вид $$y’+p(x)y=q(x).$$
Для его решения существует два способа: метод Бернулли и вариация произвольной постоянной. В первом методе нужно сделать замену на произведение двух функций $y = uv$, а во втором способе необходимо найти неизвестную функцию $C(x)$.
Алгоритм метода Бернулли:
- Выполняем замену $y=uv$ и $y’ = u’v+uv’$
- Находим функции $u(x)$ и $v(x)$ с помощью решения системы двух уравнений
- Подставляем найденные $u(x)$ и $v(x)$ в уравнение $y=uv$, чтобы получить ответ
Алгоритм метода вариации произвольной постоянной:
- Решаем исходное уравнение в качестве однородного методом разделяющихся переменных
- В полученном общем решении заменяем константу $C$ на функцию $C(x)$
- Подставляем общее решение и его производную в исходное уравнение, чтобы найти $C(x)$
- Полученное $C(x)$ подставляем в общее решение однородного уравнения и записываем ответ
| Пример 6 |
| Найти частное решение дифференциального уравнения первого порядка методом Бернулли $xy’-2y=2x^4$, если $y(1)=0$. |
| Решение |
|
Приводим уравнение к виду $y’+p(x)y=q(x)$ путем деления на $x$ обеих частей равенства $$y’-2frac{y}{x}=2x^3.$$ Делаем замену в полученном уравнении на $y=uv$ и $y’=u’v+uv’$ $$u’v+uv’-2frac{uv}{x}=2x^3.$$Выносим за скобку $u$, чтобы в дальнейшем составить систему уравнений: $$u’v+u(v’-2frac{v}{x})=2x^3.$$ Теперь приравниваем к нулю выражение в скобках и составляем систему уравнений $$begin{cases} v’ – 2frac{v}{x} = 0 \ u’v = 2x^3 end{cases},$$ в которой начнем сначала решать первое уравнение для нахождения функции $v(x)$. Разделяем в нём переменные $$begin{cases} frac{dv}{dx} = 2frac{v}{x} \ u’v = 2x^3 end{cases} Leftrightarrow begin{cases} frac{dv}{v} = 2frac{dx}{x} \ u’v = 2x^3 end{cases}.$$ Интегрируем первое уравнение в системе, чтобы получить функцию $v(x)$ $$begin{cases} ln|v| = 2ln|x| \ u’v = 2x^3 end{cases} Leftrightarrow begin{cases} v = x^2 \ u’v = 2x^3 end{cases}.$$ Теперь, зная, чему равно $v$ подставляем его во второе уравнение $$begin{cases} v=x^2 \ u’x^2 = 2x^3 end{cases} Leftrightarrow begin{cases} v=x^2 \ u = x^2+C end{cases}.$$ Записываем общее решение дифференциального уравнения $$y = uv Rightarrow y = x^4+Cx^2.$$ В условии задачи требуется найти частное решение из условия $y(1)=0$. Подставим в найденное общее решение $x=1$ и $y=0$, чтобы вычислить $C$ $$1^4+Ccdot 1^2 = 0 Rightarrow C = -1. $$ С учётом, что $C=-1$ записываем частное решение дифференциального уравнения $$y = x^4 – x^2.$$ |
| Ответ |
| $$y = x^4 – x^2$$ |
| Пример 7 |
| Найти общее решение дифференциального уравнения первого порядка $y’sin x-ycos x = 1$ методом вариации произвольной постоянной $C$. |
| Решение |
|
Перепишем уравнение в виде $$ y’ – y frac{cos x}{sin x} = frac{1}{sin x} .$$ Теперь записываем однородное дифференциальное уравнение $$y’ – y frac{cos x}{sin x} = 0,$$ решим его методом разделяющихся переменных: $$frac{dy}{dx} = y frac{cos x}{sin x}$$ $$int frac{dy}{y} = int frac{cos x}{sin x} dx.$$ Слева получается натуральный логарифм, а справа заносим косинус под знак дифференциала, чтобы получить логарифм синуса: $$ln|y| = ln|sin x| + C$$ $$y = Csin x.$$ Теперь заменяем константу $C$ на функцию $C(x)$ в полученном решении и находим производную $$y = C(x)sin x Rightarrow y’ = C'(x)sin x+ C(x)cos x.$$ Подставляем $y$ и $y’$ в неоднородное уравнение и решаем его относительно $C(x)$: $$C'(x)sin x+ C(x)cos x – C(x)sin x frac{cos x}{sin x} = frac{1}{sin x}$$ $$C'(x)sin x = frac{1}{sin x}$$ $$C'(x) = frac{1}{sin^2 x}.$$ В последнем уравнении можно разделить переменные, что и делаем, а затем интегрируем: $$ d(C(x)) = int frac{dx}{sin^2 x}$$ $$C(x) = -ctg x + C.$$ Берем решение $y = C(x)sin x$ и подставляем в него найденное $C(x) = -ctg x + C$ $$y = (-ctg x + C) sin x = Csin x – cos x.$$ Таким образом получили общее решение дифференциального уравнения $y = Csin x – cos x$. Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$y = Csin x – cos x$$ |
ДУ Бернулли
Дифференциальное уравнение Бернулли имеет следующий вид $$y’ + g(x)y = f(x)y^alpha qquad (alpha neq 0), (alpha neq 1).$$
Алгоритм решения:
- Выполняем подстановку $y = z^frac{1}{1-alpha}$
- После подстановки получаем линейное уравнение $z’+p(x)z=q(x)$
- Решив линейное уравнение делаем обратную замену $z = y^{1-alpha}$
| Пример 8 |
| Найти общее решение дифференциального уравнения первого порядка $y’+y=xy^2$. |
| Решение |
|
Это уравнение Бернулли. Видим, что $alpha = 2$. Значит делаем замену на $y = z^frac{1}{1-alpha} = z^{-1}$. Отсюда $y’ = -frac{1}{z^2} cdot z’$. После подстановки в исходное уравнение имеем $$ -frac{z’}{z^2}+frac{1}{z}=frac{x}{z^2}.$$ Умножаем обе части равенства на $(-z^2)$, чтобы привести уравнение к линейному ДУ $$z’-z=-x, $$ которое можно решить методом Бернулли, либо вариацией произвольной постоянной. Выберем первый способ. Применяем подстановку $y=uv$ и $y’=u’v+uv’$ для последнего уравнения $$u’v+uv’-uv=-x.$$ Выносим за скобку $u$, чтобы затем построить систему уравнений для нахождения функций $u(x)$ и $v(x)$ $$u’v+u(v’-v) = -x.$$ Приравниваем к нулю скобку и получаем систему $$begin{cases} v’-v = 0 \ u’v = -x end{cases}.$$ Начинаем решать её с первого уравнения. Разделяем в нем переменные и затем интегрируем $$begin{cases} int frac{dv}{v} = int dx \ u’v = -x end{cases} Leftrightarrow begin{cases} ln|v| = x \ u’v = -x end{cases} Leftrightarrow begin{cases} v = e^x \ u’v = -x end{cases}. $$ Зная, что $v = e^x$ подставляем его во второе уравнение системы и решаем $$begin{cases} v = e^x \ u’ = -frac{x}{e^x} end{cases} Leftrightarrow begin{cases} v = e^x \ u = int (-x)e^{-x} dx end{cases}.$$ Для взятия интеграла воспользуемся методом интегрирования по частям $$u = int (-x)e^{-x} dx = begin{vmatrix} u = -x & du = -dx \ dv = e^{-x}dx & v = -e^{-x} end{vmatrix} = xe^{-x} – int e^{-x} dx = xe^{-x} +e^{-x} + C$$ Итак, получаем, что $$z = uv Rightarrow z = (xe^{-x} + e^{-x}+C) e^x = Ce^x +x + 1. $$ Вспоминаем, что была ещё одна замена в самом начале решения задачи $y = z^{-1}$, поэтому общее решение выглядит следующим образом $$y = frac{1}{Ce^x + x + 1}.$$ |
| Ответ |
| $$y = frac{1}{Ce^x + x + 1}$$ |
ДУ в полных дифференциалах
Дифференциальные уравнения в полных дифференциалах имеют следующий вид $$P(x,y) dx + Q(x,y) dy = 0, $$ при выполнении условия $frac{partial P}{partial y} = frac{partial Q}{partial x} $.
Алгоритм решения заключается в том, чтобы найти функцию $U(x,y)=C$, полный дифференциал которой, есть исходное ДУ:
- Проверяем условие, подтверждающее, что перед нами ДУ в полных дифференциалах
- Получаем $U(x,y)$ интегрируя функцию $P(x,y)$ по переменной $x$. В результате этого появится неизвестная функция $varphi(y)$
- Дифференцируем $U(x,y)$ по $y$ и приравниваем к $Q(x,y)$, чтобы найти $varphi(y)$
| Пример 9 |
| Найти общий интеграл $U(x,y)=C$ дифференциального уравнения $$(2x+5y)dx+(5x+3y^2)dy=0.$$ |
| Решение |
|
Убедимся, что данное уравнение в полных дифференциалах. Для этого проверим условие $frac{partial P}{partial y} = frac{partial Q}{partial x} $. Находим производные $$ P’_y = (2x+5y)’_y = 5, Q’_x = (5x+3y^2)’_x = 5, $$ и видим, что условие выполняется $P’_y=P’_x=5$. Находим функцию $U(x,y)$ беря интеграл по $x$ от функции $P(x,y)$ $$U(x,y) = int (2x+5y) dx = x^2 + 5yx + varphi(y).$$ Далее необходимо продифференцировать найденную $U(x,y)$ по $y$ $$U’_y = 5x + varphi'(y).$$ Осталось найти неизвестную функцию $varphi(y)$ приравняв $U’_y$ к $Q(x,y)$: $$5x + varphi'(y) = 5x+3y^2$$ $$varphi'(y) = 3y^2$$ $$varphi(y) = int 3y^2 dy = y^3 + C.$$ Теперь зная чему равна $varphi(y)$ подставляем её в $U(x,y)$ $$U(x,y)=x^2+5xy+y^3+C.$$ Записываем ответ в таком виде $$x^2+5xy+y^3 = C.$$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$x^2+5xy+y^3 = C.$$ |
Дифференциальные уравнения второго порядка
ДУ допускающие понижение порядка
Дифференциальные уравнения, допускающие понижение порядка бывают двух видов:
- Без функции $y$: $F(x,y’,y”)=0$
- Без переменной $x$: $F(y,y’,y”)=0$
Для решения таких диффуров в первом случае делаем замену $y’ = p(x)$, а во втором $y’ = p(y)$.
| Пример 10 |
| Найти частное решение дифференциального уравнения второго порядка $xy”+y’=0$ при условиях $y(1) = 0$ и $y'(1)=1$. |
| Решение |
|
Видим, что данный дифур попадает под первый случай, когда отсутствует в уравнении $y$, а есть только его производные. Значит, делаем замену $y’ = p(x)$ $$xp’+p=0.$$ Данное уравнение имеет разделяющиеся переменные. Начнем с того, что перепишем уравнение через $p’ = frac{dp}{dx}$ $$xfrac{dp}{dx} = -p.$$ Разделяем переменные налево и направо от знака равенства и затем интегрируем: $$ frac{dp}{p} = -frac{dx}{x}$$ $$ int frac{dp}{p} = -int frac{dx}{x}$$ $$ln|p| = -ln|x|+C_1.$$ Теперь избавимся от логарифмов, чтобы получить $p$: $$p = e^{-ln|x| + C_1}$$ $$p = frac{C_1}{x}.$$ Вспоминаем про ранее выполненную замену $$y’ = p(x) = frac{C_1}{x}.$$ Интегрируем для того, чтобы найти $y$ $$y = int frac{C_1}{x} dx = C_1 ln|x| + C_2.$$ Таким образом, общее решение дифференциального уравнения $$y = C_1 ln|x| + C_2.$$ Займемся поиском частного решения. Для этого используем два дополнительных равенства из условия задачи: $$y(1) = 0 Rightarrow C_1 ln|1| + C_2 = 0 Rightarrow C_2 = 0$$ $$y'(1)=1 Rightarrow frac{C_1}{1} = 1 Rightarrow C_1 = 1.$$ Записываем частное решение дифференциального уравнения $$y = ln|x|.$$ |
| Ответ |
| $$y = ln|x|$$ |
| Пример 11 |
| Найти частное решение дифференциального уравнения второго порядка $$yy”+y’^2 = 1, qquad y(0) = 1, y'(0) = 1.$$ |
| Решение |
|
Видим, что в диффуре отсутствует в явном виде переменная $x$, поэтому необходимо сделать замену $y’ = p(y)$ и отсюда $y” = p'(y)cdot y’ = p'(y)p$. Делаем замену и получаем уравнение $$yp'(y)p + p^2 = 1,$$ которое решим методом разделения переменных: $$ypfrac{dp}{dy} = 1-p^2$$ $$frac{p}{1-p^2}dp = frac{1}{y}dy.$$ Далее по плану необходимо проинтегрировать обе части уравнения, чтобы получить $p$ $$int frac{p}{1-p^2}dp = int frac{1}{y}dy.$$ В первом интеграле заносим под знак дифференциала $1-p^2$, чтобы получился натуральный логарифм, а во втором, используя таблицу интегрирования можно сразу записать ответ: $$-frac{1}{2} int frac{d(1-p^2)}{1-p^2} = ln|y| + C $$ $$-frac{1}{2} ln|1-p^2| = ln|y| + C.$$ Необходимо избавиться от логарифмов. Умножим обе части равенства на $(-2)$, а затем занесем эту двойку над икреком: $$ln|1-p^2| = -2ln|y|+C$$ $$ln|1-p^2| = ln frac{1}{y^2} + C.$$ Итак, теперь убирая логарифмы получаем: $$1-p^2 = C frac{1}{y^2}$$ $$p^2 = 1 – Cfrac{1}{y^2}$$ $$(y’)^2 = 1 – Cfrac{1}{y^2}.$$ Теперь найдем значение константы $C$ благодаря дополнительным условиям задачи $y = 1$ и $y’ = 1$. Подставляем их в последнее уравнение $$1^2 = 1 – Cfrac{1}{1^2} Rightarrow C = 0.$$ Зная теперь, что $C=0$ подставляем его в уравнение $(y’)^2 = 1 – Cfrac{1}{y^2}$: $$(y’)^2 = 1$$ $$y’ = pm 1.$$ Из условия помним, что $y’ = 1 > 0$, значит, берем только решение $y’ = 1$ и продолжаем его решать интегрированием $$y = int 1 dx = x + C.$$ Осталось найти снова постоянную $C$ теперь уже из условия $y(0) = 1$ $$y(0) = 0 + C = 1 Rightarrow C = 1.$$ Вот теперь можно записать ответ в виде частного решения, которое требовалось найти по условию данной задачи $$y = x + 1.$$ |
| Ответ |
| $$y = x + 1$$ |
Линейные однородные ДУ с постоянными коэффицентами
Линейность дифференциального уравнения заключается в том, что в уравнение входит неизвестная функция $y(x)$ и её производные только в первой степени, между собой не перемножаясь. Однородность определяется тем, что уравнение не содержит свободного члена. То есть он равен нулю.
Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами выглядит следующим образом $$y”+py’+qy = 0.$$ Чтобы его решить необходимо составить характиристический многочлен и найти его корни. Для этого нужно заменить $y$ на $lambda$, степень которых будет соответствовать порядку производной $$y” Rightarrow lambda^2, qquad y’ Rightarrow lambda, qquad y Rightarrow 1.$$
В зависимости от получившихся корней имеем общее решение в различных видах:
- Действительные корни $lambda_1 neq lambda_2$, тогда $y = C_1e^{lambda_1 x}+C_2e^{lambda_2 x}$
- Действительные корни $lambda_1 = lambda_2$, тогда $y = C_1e^{lambda_1 x}+C_2xe^{lambda_1 x}$
- Комплексные корни $lambda_{1,2} = alphapmbeta i$, тогда $y = C_1e^{alpha x}cos beta x + C_2e^{alpha x}sin beta x$.
| Пример 12 |
| Найти общее решение дифференциального уравнения второго порядка $y”+y’-2y = 0$. |
| Решение |
|
Первым делом составляем характеристический многочлен. Заменяем $y$ на $lambda$ со степенями соответствующими порядку производной $y$ $$lambda^2 + lambda -2 = 0.$$ Обратите внимание, что $y$ имеет производную нулевого порядка, поэтому он заменяется на $lambda^0 = 1$. Итак, перед нами квадратное уравнение, начинаем решать: $$lambda_{1,2} = frac{-1pm sqrt{1^2-4cdot 1 cdot (-2)}}{2cdot 1} = frac{-1pm 3}{2}$$ $$lambda_1 = -2, qquad lambda_2 = 1.$$ Так как получили отличающиеся действительные корни, то общее решение записывается следующим образом $$y = C_1 e^{-2x} + C_2 e^{x}.$$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$y = C_1 e^{-2x} + C_2 e^{x}$$ |
Линейные неоднородные ДУ с постоянными коэффициентами
Линейное неоднородное ДУ с постоянными коэффициентами отличается от предыдущего типа уравнений наличием правой части от знака равенства $$y”+py’+q = f(x).$$
Общее решение такого диффура складывается из двух частей: общего решения однородного уравнения и частного решения неоднородного уравнения $$y_text{о.н.} = y_text{о.о.} + y_text{ч.н.}.$$
Частное решение неоднородного уравнения $y_text{ч.н.}$ подбирается исходя из вида правой части дифференциального уравнения. Затем в нём неизвестные постоянные находятся методом неопределенных коэффициентов.
| № | Правая часть | Корни характеристического многочлена | Вид частного решения |
| 1 | $$P_n (x)$$ | Число 0 не является корнем характеристического уравнения. | $$tilde{P_n}(x)$$ |
| Число 0 – корень характеристического уравнения кратности $S$. | $$x^s tilde{P_n}(x)$$ | ||
| 2 | $$P_n (x) e^{alpha x}$$ | Число $alpha$ не является корнем характеристического уравнения. | $$tilde{P_n} (x) e^{alpha x}$$ |
| Число $alpha$ является корнем характеристического уравнения кратности $S$. | $$x^s tilde{P_n} (x) e^{alpha x}$$ | ||
| 3 | $$P_n (x) cos beta x + Q_m (x) sin beta x$$ | Число $pm ibeta$ не является корнем характеристического уравнения. | $$tilde {P_n} cos beta x + tilde{Q_m} sin beta x$$ |
| Число $pm ibeta$ является корнем характеристического уравнения кратности $S$. | $$x^s (tilde {P_n} cos beta x + tilde{Q_m} sin beta x)$$ | ||
| 4 | $$e^{alpha x}[P_n (x) cos beta x + Q_m (x) sin beta x]$$ | Число $alpha pm ibeta$ не является корнем характеристического уравнения. | $$e^{alpha x}[P_n (x) cos beta x + Q_m (x) sin beta x]$$ |
| Число $alpha pm ibeta$ является корнем характеристического уравнения. | $$x^s e^{alpha x}[P_n (x) cos beta x + Q_m (x) sin beta x]$$ |
| Пример 13 |
| Найти общее решение дифференциального уравнения второго порядка $y”+y = 4xcos x$. |
| Решение |
|
Сначала находим общее решение однородного уравнения $$y” + y = 0.$$ Строим характеристический многочлен $$lambda^2 + 1 = 0,$$ и находим его корни $$lambda_{1,2}=pm i.$$ Записываем получившееся общее решение однородного уравнения $$y_text{о.о.} = C_1 cos x + C_2 sin x.$$ Теперь необходимо подобрать частное решение неоднородного уравнения. Для этого смотрим на правую часть исходного уравнения и видим, что здесь многочлен первой степени умножается на косинус. Значит, необходимо выбрать из таблицы 3й случай. Причем корень характеристического уравнения совпадает с аргументом косинуса. Это значит, что требуется домножение на $x$ $$y_text{ч.н.} = x[(Ax+B)cos x + (Cx+D)sin x].$$Упростим последнее равенство и найдем от него вторую производную: $$y_text{ч.н.} = (Ax^2+Bx)cos x + (Cx^2 + Dx) sin x$$ $$y’_text{ч.н.} = (2Ax+B)cos x-(Ax^2+Bx)sin x + (2Cx+D)sin x + (Cx^2 + Dx) cos x.$$ Упростим $y’_text{ч.н}$ для удобства нахождения второй производной $$y’_text{ч.н.} = (2Ax+B+Cx^2+Dx)cos x + (2Cx+D-Ax^2-Bx)sin x.$$ Теперь можно найти вторую производную $$y”_text{ч.н.} = (2A+2Cx+D)cos x-(2Ax+B+Cx^2+Dx)sin x + (2C-2Ax-B)sin x + (2Cx+D-Ax^2-Bx)cos x.$$ Упрощаем последнее выражение $$y”_text{ч.н.} = (2A+4Cx+2D-Ax^2-Bx)cos x + (2C-4Ax-2B-Cx^2-Dx)sin x.$$ Подставляем найденные $y_text{ч.н.}$ и $y”_text{ч.н.}$ в исходный диффур из “дано” задачи $$(2A+4Cx+2D-Ax^2-Bx)cos x + (2C-4Ax-2B-Cx^2-Dx)sin x + (Ax^2+Bx)cos x + (Cx^2 + Dx) sin x = 4xcos x.$$ Упрощаем его $$(2A+4Cx+2D)cos x + (2C-4Ax-2B)sin x = 4xcos x.$$ Теперь подгоняем левую часть под правую, так чтобы можно было применить метод неопределенных коэффициентов и найти неизвестные $A,B,C,D$ $$(2A+2D)cos x+4Cxcos x + (2C-2B)sin x+(-4Ax)sin x = 4xcos x.$$ Смотрим на левую и правую часть и составляем систему $$begin{cases} 2A+2D = 0 \ 4C=4 \ 2C-2B=0 \ -4A = 0 end{cases} Leftrightarrow begin{cases} D=0 \ C= 1 \ B=1 \ A = 0end{cases}.$$ Подставляем полученные коэффициенты в частное решение неоднородного уравнения $$y_text{ч.н.} = xcos x + x^2sin x.$$ Теперь вспоминая, что $y_text{о.н.} = y_text{о.о.} + y_text{ч.н.}$ можем записать окончательный ответ $$y_text{о.н.} = C_1 cos x + C_2 sin x + xcos x + x^2sin x.$$ |
| Ответ |
| $$y = C_1 cos x + C_2 sin x + xcos x + x^2sin x$$ |
| Пример 14 |
| Найти общее решение дифференциального уравнения второго порядка $y”+y’=5x+2e^x$. |
| Решение |
|
Сначала найдем общее решение однородного дифференциального уравнения $$y”+y’=5x+2e^x.$$ Составляем характеристический многочлен однородного уравнения и находим его корни: $$lambda^2 + lambda = 0$$ $$lambda(lambda + 1) = 0$$ $$lambda_1 = 0, qquad lambda_2=-1.$$ Теперь можно записать общее решение $$y_text{о.о.} = C_1 + C_2e^{-x}.$$ Далее необходимо по правой части исходного неоднородного уравнения найти его частное решение путем подбора, используя данные таблицы. Первое слагаемое есть многочлен первой степени. И так как один из корней характеристического уравнения является нулем кратности 1, то решение ищем в виде $y = (Ax+B)x$. Второе слагаемое представляет собой произведение многочлена нулевой степени на экспоненту. Так как аргумент экспоненты не совпадает с одним из корней характеристического многочлена, то подбор будем делать в виде $y = Ce^x$. В итоге правую часть будем искать в виде суммы $$y_text{ч.н.} = (Ax+B)x+Ce^x.$$ Находим первую и вторую производную последней функции: $$y’ = 2Ax+B+Ce^x$$ $$y”=2A+Ce^x.$$ Подставляем полученные производные $y’$ и $y”$ в исходное дифференциальное уравнение: $$2A+Ce^x+2Ax+B+Ce^x = 5x+2e^x$$ $$2Ax+B+2A+2Ce^x=5x+2e^x.$$ Далее необходимо, используя метод неопределенных коэффициентов, найти значения $A,B,C$ составив систему уравнений $$begin{cases} 2A=5 \ 2C=2 \ B+2A = 0 end{cases} Leftrightarrow begin{cases} A=frac{5}{2} \ C=1 \ B=-5 end{cases}.$$ Подставляем найденные коэффициенты и получаем частное решение неоднородного уравнения $$y_text{ч.н.} = (frac{5}{2}x-5)x + e^x = frac{5}{2}x^2 – 5x + e^x.$$ Таким образом теперь можно записать общее решение неоднородного диффура $$y_text{о.н.} = y_text{о.о.} + y_text{ч.н.}=C_1 + C_2e^{-x} + frac{5}{2}x^2 – 5x + e^x.$$ |
| Ответ |
| $$y = C_1 + C_2e^{-x} + frac{5}{2}x^2 – 5x + e^x$$ |
Метод Лагранжа
Данный метод позволяет решать линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами даже в тех, случаях, когда правая часть уравнения не подходит под табличный вид. В этом случае целесообразно применить данный метод решения.
- Находим общее решение однородного уравнения $y = C_1 y_1(x) + C_2 y_2(x)$
- Варьируем постоянные $C_1$ и $C_2$ на функции $C_1(x)$ и $C_2(x)$
- Решаем систему методом Крамера $begin{cases} C_1 ‘(x) y_1 (x) + C_2 ‘(x) y_2 (x) = 0 \ C_1 ‘(x) y_1 ‘(x) + C_2 ‘(x) y_2 ‘(x) = f(x) end{cases} $
- Получаем $C_1(x)$ и $C_2(x).$
| Пример 15 |
| Найти частное решение дифференциального уравнения $$y”-2y’+y=frac{e^x}{x}, text{ при } y(1)=e, y'(1)=3e.$$ |
| Решение |
|
Так как правая часть диффура не подходит под табличный формат, то не получится подбирать частное решение по правой части как делали это в предыдущем примере. Воспользуется методом Лагранжа или как его еще называют вариация произвольной постоянной. Для начала найдем общее решение однородного уравнения $$y”-2y’+y=0.$$ Составляем характеристический многочлен и находим его корни: $$lambda^2-2lambda+1=0$$ $$(lambda-1)^2 = 0 Rightarrow lambda = 1 text{ с кратностью 2}.$$ Так как корень кратный, то общее решение однородного уравнения записывается следующим образом $$y = C_1 e^x + C_2 xe^x.$$ Теперь необходимо варьировать постоянные $C_1$ и $C_2$ на соответствующие функции $C_1 (x)$ и $C_2 (x)$. Теперь получившееся решение следует записать в виде $y = C_1 (x) e^x + C_2 (x) xe^x$. Здесь заметим, что $y_1 = e^x$ и $y_2 = xe^x$. Это нужно для дальнейшего хода решения, а именно построения системы уравнений. Составляем систему уравнений и решаем её методом Крамера $$begin{cases} C_1 ‘(x) e^x+C_2 ‘(x) xe^x = 0 \C_1 ‘(x) e^x + C_2 ‘(x) (e^x+xe^x) = frac{e^x}{x} end{cases}.$$ Находим главный определитель системы $$Delta = begin{vmatrix} e^x & xe^x \ e^x & e^x+xe^x end{vmatrix} = e^x(e^x+xe^x)-xe^{2x} = e^{2x}.$$ Вычисляем дополнительные определители: $$Delta_1 = begin{vmatrix} 0 & xe^x \ frac{e^x}{x} & e^x + xe^x end{vmatrix} = -xe^x frac{e^x}{x} = e^{2x}$$ $$Delta_2 = begin{vmatrix} e^x & 0 \ e^x & frac{e^x}{x} end{vmatrix} = e^x frac{e^x}{x} = frac{e^{2x}}{x}.$$ Итак, получаем решение системы уравнений $$C_1 ‘(x) = frac{Delta_1}{Delta} = frac{e^{2x}}{e^{2x}} = 1, qquad C_2 ‘(x) = frac{Delta_2}{Delta} = frac{e^{2x}}{x} frac{1}{e^{2x}} = frac{1}{x}.$$ Далее интегрируем полученные решения, чтобы избавиться от производной: $$C_1(x) = int 1 dx = x+tilde{C_1}$$ $$C_2(x)=int frac{dx}{x}=ln|x|+tilde{C_2}.$$ Подставляем полученные $C_1(x)$ и $C_2(x)$ в общее решение однородного уравнения и записываем общее решение неоднородного дифференциального уравнения $$y = (x+tilde{C_1}) e^x + (ln|x|+tilde{C_2}) xe^x.$$ По условию нам требуется найти частное решение при условиях $y(1)=e$ и $y'(1)=3e$. Поэтому находим сначала производную $$y’=e^x+(x+tilde{C_1})e^x+e^x+(ln|x|+tilde{C_2})(e^x+xe^x), $$ раскрываем скобки $$y’ = 2e^x+xe^x+tilde{C_1}e^x+e^xln|x|+xe^xln|x|+tilde{C_2}e^x+tilde{C_2}xe^x,$$ а затем составляем систему уравнений $$begin{cases} y'(1)=3e+tilde{C_1}e+2tilde{C_2}e = 3e \ y(1) = e+tilde{C_1}e + tilde{C_2}e = e end{cases} Rightarrow begin{cases} tilde{C_1}+2tilde{C_2}=0 \ tilde{C_1}+tilde{C_2}=0 end{cases} Rightarrow begin{cases} tilde{C_2} = 0 \ tilde{C_1}=0 end{cases}.$$ Теперь можно записать частное решение к задаче $$y = xe^x + xln|x|e^x = xe^x(1+ln|x|).$$ |
| Ответ |
| $$y = xe^x(1+ln|x|)$$ |
Примеры решения дифференциальных уравнений с ответами
Простое объяснение принципов решения дифференциальных уравнений и 10 наглядных примеров. В каждом примере поэтапный ход решения и ответ.
Помощь в написании работы
Алгоритм решения дифференциальных уравнений
Дифференциальные уравнения не так сильно отличаются от привычных уравнений, где необходимо найти переменную x, как кажется на первый взгляд. Всё различие лишь в том, что в дифференциальных уравнениях мы ищем не переменную, а функцию у(х), с помощью которой можно обратить уравнение в равенство.
Дифференциальное уравнение – это уравнение, содержащее саму функцию (y=y(x)), производные функции или дифференциалы (y′, y″) и независимые переменные (наиболее распространённая – х). Обыкновенным дифференциальным уравнением называют уравнение, в котором содержится неизвестная функция под знаком производной или под знаком дифференциала.
Чтобы решить ДУ, необходимо найти множество всех функций, которые удовлетворяют данному уравнению. Это множество в большинстве случаев выглядит следующим образом:y=f(x; С), где С – произвольная постоянная.
Проверить решённое ДУ можно, подставив найденную функцию в изначальное уравнение и убедившись, что уравнение обращается в тождество (равенство).
Примеры решения дифференциальных уравнений
Задание
Решить дифференциальное уравнение xy’=y.
Решение
В первую очередь, необходимо переписать уравнение в другой вид. Пользуясь
переписываем дифференциальное уравнение, получаем
Дальше смотрим, насколько реально разделить переменные, то есть путем обычных манипуляций (перенос слагаемых из части в часть, вынесение за скобки и пр.) получить выражение, где «иксы» с одной стороны, а «игреки» с другой. В данном уравнении разделить переменные вполне реально, и после переноса множителей по правилу пропорции получаем
Далее интегрируем полученное уравнение:
В данном случае интегралы берём из таблицы:
После того, как взяты интегралы, дифференциальное уравнение считается решённым. Решение дифференциального уравнения в неявном виде называется общим интегралом дифференциального уравнения.
То есть,
– это общий интеграл. Также для удобства и красоты, его можно переписать в другом виде: y=Cx, где С=Const
Ответ
y=Cx, где С=Const.
Задание
Найти частное решение дифференциального уравнения
.
Решение
Действуем по тому же алгоритму, что и в предыдущем решении.
Переписываем производную в нужном виде, разделяем переменные и интегрируем полученное уравнение:
Получили общий интеграл.Далее, воспользуемся свойством степеней, выразим у в «общем» виде и перепишем функцию:
Если – это константа, то
– тоже некоторая константа, заменим её буквой С:
– убираем модуль и теперь константа может принимать и положительные, и отрицательные значения.
Получаем общее решение:
где С=const.
Ответ
где С=const.
Задание
Решить дифференциальное уравнение
Решение
В первую очередь необходимо переписать производную в необходимом виде:
Второй шаг – разделение переменных и перенос со сменой знака второго слагаемого в правую часть:
После разделения переменных, интегрируем уравнение, как в примерах выше.
Чтобы решить интегралы из левой части, применим метод подведения функции под знак дифференциала:
В ответе мы получили одни логарифмы и константу, их тоже определяем под логарифм.
Далее упрощаем общий интеграл:
Приводим полученный общий интеграл к виду: F(x,y)=C:
Чтобы ответ смотрелся красивее, обе части необходимо возвести в квадрат.
Ответ
Общий интеграл:
где С=const.
Задание
Найти частное решение дифференциального уравнения
удовлетворяющее начальному условию y(0)=ln2.
Решение
Первый шаг – нахождение общего решения. То, что в исходном уравнении уже находятся готовые дифференциалы dy и dx значительно упрощает нам решение.
Начинаем разделять переменные и интегрировать уравнение:
Мы получили общий интеграл и следующий шаг – выразить общее решение. Для этого необходимо прологарифмировать обе части. Знак модуля не ставим, т.к. обе части уравнения положительные.
Получаем общее решение:
где С=const
Далее необходимо найти частное решение, которое соответствует заданному начальному условию y(0)=ln2.
В общее решение вместо «икса» подставляем ноль, а вместо «игрека» логарифм двух:
Подставляем найденное значение константы C=1 в общее решение.
Ответ
Частное решение:
.
Задание
Решить дифференциальное уравнение
.
Решение
При внимательном разборе данного уравнения видно, что можно разделить переменные, что и делаем, после интегрируем:
В данном случае константу C считается не обязательным определять под логарифм.
Ответ
Общий интеграл:
Задание
Найти частное решение дифференциального уравнения
удовлетворяющее начальному условию y(1)=e. Выполнить проверку.
Решение
Как и в предыдущих примерах первым шагом будет нахождение общего решения. Для этого начинаем разделять переменные:
Интегрируем:
Общий интеграл получен, осталось упростить его. Упаковываем логарифмы и избавляемся от них:
Используя
можно выразить функцию в явном виде.
Общее решение:
где С=const.
Осталось найти частное решение, удовлетворяющее начальному условию y(1)=e.
Подставляем найденное значение константы C=1 в общее решение.
Ответ
Частное решение:
Проверка
Необходимо проверить, выполняется ли начальное условие:
Из равенства выше видно, что начальное условие y(1)=e выполнено.
Далее проводим следующую проверку: удовлетворяет ли вообще частное решение
дифференциальному уравнению. Для этого находим производную:
Подставим полученное частное решение
и найденную производную в исходное уравнение
0=0
Получено верное равенство, значит, решение найдено правильно.
Задание
Найти общий интеграл уравнения
Решение
Данное уравнение допускает разделение переменных. Разделяем переменные и интегрируем:
Ответ
Общий интеграл:
Задание
Найти частное решение ДУ.
Решение
Данное ДУ допускает разделение переменных. Разделяем переменные:
Интегрируем:
Общий интеграл:
Найдем частное решение (частный интеграл), соответствующий заданному начальному условию
Подставляем в общее решение
Ответ
Частный интеграл:
Задание
Решить дифференциальное уравнение
Решение
Данное уравнение допускает разделение переменных. Разделяем переменные и интегрируем:
Левую часть интегрируем по частям:
В интеграле правой части проведем замену:
Таким образом:
(здесь дробь раскладывается методом неопределенных коэффициентов)
Обратная замена:
Ответ
Общий интеграл:
где С=const.
Задание
Решить дифференциальное уравнение
Решение
Данное уравнение допускает разделение переменных.
Разделяем переменные и интегрируем:
Методом неопределенных коэффициентов разложим подынтегральную функцию в сумму элементарных дробей:
Ответ
Общее решение:
где С=const.
Задача №1.
Найти общий интеграл дифференциального
уравнения
![]()
Решение:Данное уравнение
перепишем в виде:
![]() ,
,
далее
![]() это дифференциальное уравнение ( в
это дифференциальное уравнение ( в
дальнейшем ДУ) первого порядка с
разделяющимися переменными, т.е.

![]() или
или
![]() .
.
Ответ:
![]() – общий интеграл данного
– общий интеграл данного
ДУ.
Задача №2.Найти общий интеграл
дифференциального уравнения
![]()
Решение:
Данное уравнение является ДУ первого
порядка, однородным, т.к. его можно
привести к виду и
![]() однородная функция нулевого измерения
однородная функция нулевого измерения![]() и, сделав замену переменных
и, сделав замену переменных![]() ,
,
привести к виду![]() ,
,
далее вычисляя интеграл в левой части,
найти ответ. У нас
![]() ;
;
![]() ;
;

![]() .Окончательно:
.Окончательно:
![]()
Ответ:
![]() – общий интеграл ДУ.
– общий интеграл ДУ.
Задача №3.Найти решение задачи Коши
![]() ,
,![]() .
.
Решение:
ДанноеДУ является линейным
неоднородным ДУпервого
порядка. Решим его методом вариации
произвольной постоянной. Сначала решим
ДУ однородное, т.е.
![]() .
.
Это всегда ДУ с разделяющимися переменными![]() – общие решение однородного линейного
– общие решение однородного линейного
ДУ
![]() в таком виде будем искать общее решение
в таком виде будем искать общее решение
неоднородного ДУ, где![]() –
–
неизвестная функция,![]() Подставляем
Подставляем![]() и
и
у в исходноеДУ, будем
иметь;
 общее
общее
решение данного ДУ Найдем частное
решение, используя начальные условия
![]() .
.
Итак, задача Коши решена :найдено
частное решение, ДУ, отвечающее начальному
условию
![]()
![]()
Ответ:
![]()
Задача №4.Найти решение задачи Коши
![]() ,
,![]()
Решение:
Перепишем данноеДУ в
виде
![]() это уравнение Бернулли. Решаем методом
это уравнение Бернулли. Решаем методом
Бернулли:
![]()

общее решение исходного ДУ.
Решим задачу Коши:

![]()
Ответ:
![]() –
–
частное решение исходного ДУ,
удовлетворяющего начальному условию![]()
Задача №5.
Найти общий итеграл
дифференциального уравнения
![]()
Решение:
Данное ДУ перепишем в
виде
![]()
Проверим, является ли это ДУ
в полных дифференциалах. У нас
![]() ;
;![]() ;
;![]() ;
;![]() ;
;
так как![]() данное ДУ является ДУпервого
данное ДУ является ДУпервого
порядка, в полных дифференциалах, т.е.
имеет вид
![]() ,откуда
,откуда![]() общий интеграл исходного ДУ. Остается
общий интеграл исходного ДУ. Остается
найти функцию![]() ,
,
чей полный дифференциал стоит в левой
части уравнения и![]() ,
,![]() ;
;![]()
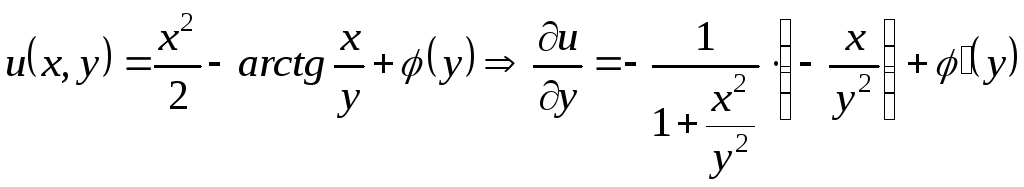 с другой стороны,
с другой стороны,
![]() значит ,
значит ,![]()
![]()
![]() .
.
Наконец,
![]() –
–![]()
![]() и общий интеграл имеет вид
и общий интеграл имеет вид![]() –
–![]()
![]() ,
,
окончательно![]() ,
,![]() .
.
Ответ: общий интеграл
![]()
Задача №6.Найти общее решение дифференциального
уравнения
![]()
Решение:
Данное ДУ второго порядка не содержит
искомой функций![]() ,
,
значит, замена переменных такова:
![]() ,
,
откуда уравнение принимает вид:![]() или
или
![]() ,
,
т.е. становится ДУ I порядка линейным
неоднородным, решаем его методом
вариации произвольной постоянной.
Сначала рассмотрим однородное уравнение:
![]() всегда с разделяющимися переменными:
всегда с разделяющимися переменными:
![]()
![]() ищемобщее решение неоднородного
ищемобщее решение неоднородного
ДУв таком же виде, только
![]() ,
,
т .е.
![]() подставляя в неоднородное ДУ, получаем
подставляя в неоднородное ДУ, получаем
 .
.
Найдем
![]() ,
,
выделив сначала целую часть дроби![]() =
=
![]()
 получим
получим![]()
![]() .Тогда
.Тогда
![]()
Ответ:![]() –
–
общее решение исходногоДУвторого порядка.
Задача №7.
Найти общее решение дифференциального
уравнения
![]()
Решение:Решаем данное дифференциальное уравнение
III порядка линейное неоднородное
с постоянными коэффициентами также,
как и предыдущее.
Сначала
![]() имеет характеристическое уравнение
имеет характеристическое уравнение![]() ,
,![]() ,
,![]()
![]() ,
,![]() ,
,
умножение наx вызвано
тем, что![]()
является простым корнем характеристического
уравнения, и число 2 стоит множетелем
при x в
степени показательной функции
![]() .
.
Значит![]()
![]()

![]()

![]() ;
;
![]()
Ответ:
![]()
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
1. Уравнения с разделяющимися переменными
Общий вид уравнений
 . (8.10)
. (8.10)
С учетом равенства
 (8.11)
(8.11)
уравнение (8.10) может быть записано в виде  .
.
Разделим обе части на произведение функций M(x)∙Q(y) (при условии  ) и после сокращения получим:
) и после сокращения получим:  . Так как переменные разделены, проинтегрируем уравнение
. Так как переменные разделены, проинтегрируем уравнение
почленно: . После нахождения интегралов получаем общий интеграл
. После нахождения интегралов получаем общий интеграл
исходного ДУ. Предполагая, что , мы могли потерять решения. Следовательно, необходимо
, мы могли потерять решения. Следовательно, необходимо
подстановкой M(x)=0, Q(y)=0 в исходное уравнение сделать проверку. В том
случае, когда данные функции удовлетворяют уравнению, они также являются его решениями.
Пример 8.2. Проинтегрировать уравнение  .
.
Решение. Представим уравнение в виде . Разделим переменные:
. Разделим переменные:  . Проинтегрируем уравнение:
. Проинтегрируем уравнение:
 .
.
После
применения теоремы о сумме логарифмов и потенцирования получаем
 – общий интеграл исходного уравнения
– общий интеграл исходного уравнения
2.
Однородные дифференциальные уравнения первого порядка
Общий вид уравнений
 , (8.12)
, (8.12)
где M(x;y) и N(x;y)– однородные функции аргументов x и y одного и
того же измерения m, то есть
имеют место равенства
 . (8.13)
. (8.13)
Метод решения уравнения (8.12) – деление на переменную
x в
степени измерения m:  . Далее уравнение преобразуются с помощью следующей замены:
. Далее уравнение преобразуются с помощью следующей замены:
 . (8.14)
. (8.14)
Однородное уравнение (8.12) принимает вид:  – уравнение с
– уравнение с
разделяющимися переменными. Следовательно, дальнейшее решение – по пункту 1.
Пример 8.3. Проинтегрировать уравнение  .
.
Решение. Поделим уравнение на x2, получим . После замены (8.14) заданное по условию уравнение принимает
. После замены (8.14) заданное по условию уравнение принимает
вид  ,
, . В результате интегрирования получим
. В результате интегрирования получим  . После обратной замены
. После обратной замены  – искомый общий
– искомый общий
интеграл 
Пример 8.4. Найти общее решение
(общий интеграл) дифференциального уравнения  .
.
Решение. Правая часть уравнения  обладает свойством
обладает свойством  . Поэтому заданное
. Поэтому заданное
уравнение является однородным дифференциальным уравнением первого порядка.
Совершим замену  , где u – некоторая
, где u – некоторая
функция от аргумента x. Отсюда . Исходное уравнение приобретает вид
. Исходное уравнение приобретает вид
 или
или  . Разделим переменные:
. Разделим переменные:  .
.
После
интегрирования обеих частей уравнения получаем
 . Таким образом,
. Таким образом,
 .
.
Потенцируя,
находим  .
.
Итак,
общий интеграл исходного уравнения приобретает вид cy=x2+y2, где c – произвольная
постоянная
3. Дифференциальные уравнения первого порядка, приводящиеся к однородным или к уравнениям с разделяющимися переменными
Общий вид уравнений
 , (8.15)
, (8.15)
где – числа.
– числа.
При c1=c2=0 уравнение
является однородным. Рассмотрим два случая при c1 и c2 не равных нулю одновременно.
1) Определитель . Вводят новые переменные u и v, положив x=u+x0, y=v+y0, где (x0;y0) – решение системы уравнений
. Вводят новые переменные u и v, положив x=u+x0, y=v+y0, где (x0;y0) – решение системы уравнений .
.
В результате данной подстановки уравнение (8.15)
становится однородным.
Пример 8.5. Найти общее решение
(общий интеграл) дифференциального уравнения  .
.
Решение. Определитель  , следовательно,
, следовательно,
решаем систему уравнений  . Получаем значения x0= –1; y0=2, с
. Получаем значения x0= –1; y0=2, с
использованием которых осуществляем
замену x=u–1;y=v+2, при этом  . Заданное по условию
. Заданное по условию
ДУ принимает вид:
 , (*) – однородное ДУ относительно функции v и переменной u.
, (*) – однородное ДУ относительно функции v и переменной u.
Обозначим  . Уравнение (*) принимает вид:
. Уравнение (*) принимает вид:  . Продолжим преобразования:
. Продолжим преобразования: . Проинтегрируем уравнение:
. Проинтегрируем уравнение:

С помощью формул
интегрирования (4.8) и (4.17) получаем:
 .
.
Осуществим обратную
подстановку :
:
 – общий интеграл исходного уравнения
– общий интеграл исходного уравнения
2) Определитель . Это означает пропорциональность коэффициентов
. Это означает пропорциональность коэффициентов  или
или
 . Уравнение (8.15) принимает вид:
. Уравнение (8.15) принимает вид:  . С помощью замены
. С помощью замены
 , оно приводится к
, оно приводится к
уравнению с разделяющимися переменными вида  .
.
Пример 8.6. Найти общее решение
(общий интеграл) дифференциального уравнения
 .
.
Решение. Определитель  , следовательно, осуществляем замену
, следовательно, осуществляем замену
 .
.
Исходное
уравнение принимает вид:
 или
или  .
.
Далее  . Разделим переменные:
. Разделим переменные:  или
или  . Проинтегрируем уравнение:
. Проинтегрируем уравнение:
 .
.
После обратной замены получим:  – общий интеграл
– общий интеграл
исходного уравнения
4.
Линейные дифференциальные уравнения первого порядка
Общий вид уравнений
 , (8.16)
, (8.16)
где
P(x) и Q(x) –
заданные функции (могут быть постоянными).
Уравнение (8.16) может быть решено двумя способами.
1) Метод Бернулли-Фурье состоит в том,
что решение ищется в виде произведения двух неизвестных функций y(x)=u(x)∙v(x) или коротко y=u∙v, при этом  . Одна из функций будет представлять общую часть решения и
. Одна из функций будет представлять общую часть решения и
содержать константу интегрирования c, другая функция может быть взята в частном виде при
конкретном значении константы (общее решение ДУ первого порядка должно содержать
одну константу интегрирования). Подставим выражения y и  в (8.16), после чего
в (8.16), после чего
оно принимает вид:
 . (8.17)
. (8.17)
Функцию v(x) подберем в частном виде так, чтобы выражение в
скобках обратилось в ноль. Для этого решим уравнение с разделяющимися
переменными  или
или  . Отсюда в результате интегрирования получим:
. Отсюда в результате интегрирования получим:  . Так функция v(x) выбиралась произвольно, то можно положить c = 1, тогда
. Так функция v(x) выбиралась произвольно, то можно положить c = 1, тогда  . Подставив найденную v(x) в (8.17), приходим к еще одному уравнению с
. Подставив найденную v(x) в (8.17), приходим к еще одному уравнению с
разделяющимися переменными  . Интегрируя его, получим функцию
. Интегрируя его, получим функцию  . Общее решение исходного ДУ (8.16) принимает вид
. Общее решение исходного ДУ (8.16) принимает вид
 . (8.18)
. (8.18)
Пример 8.7. Проинтегрировать уравнение  с помощью метода
с помощью метода
Бернулли.
Решение. Данное уравнение является линейным ДУ первого порядка с
функциями  . Применим подстановку
. Применим подстановку
y=u∙v, где u и v – некоторые функции аргумента x. Так
как y=u∙v,  то , и заданное уравнение принимает вид:
то , и заданное уравнение принимает вид:
 .
.
(**)
Выберем функцию u так, чтобы выражение, стоящее в скобках, обращалось в ноль, то есть  или
или
 .
.
Полагая c=1, получим
u=cos x.
При таком выборе функции u уравнение
(**) примет вид:
 . Отсюда v=tg x+c. Тогда
. Отсюда v=tg x+c. Тогда  – общее решение
– общее решение
заданного уравнения.
Общее решение заданного ДУ можно также получить,
пользуясь непосредственно формулой (8.18):
 .
.
По условию задачи имеем: P(x)=tg x,  . Следовательно,
. Следовательно,  . Так как
. Так как , то с использованием основного логарифмического тождества
, то с использованием основного логарифмического тождества
получаем:
 .
.
Таким образом,  – общее решение исходного дифференциального
– общее решение исходного дифференциального
уравнения
2) Метод Лагранжа иначе называют методом вариации произвольной постоянной.
Рассмотрим сначала соответствующее линейное однородное ДУ первого порядка, то есть
исходное уравнение без правой части  . Разделив переменные и проинтегрировав, в найденном решении
. Разделив переменные и проинтегрировав, в найденном решении
полагают постоянную c функцией c(x). После этого функцию y дифференцируют и вместе с  подставляют в исходное
подставляют в исходное
уравнение. При этом получают уравнение относительно неизвестной функции c(x), отыскав
которую, подставляют ее в y – общее решение заданного линейного неоднородного
уравнения (с правой частью).
Пример 8.8. Проинтегрировать уравнение  с помощью метода
с помощью метода
Лагранжа (сравни с примером 8.7).
Решение. Решим сначала соответствующее линейное однородное ДУ
первого порядка  или
или  . Разделим переменные:
. Разделим переменные:  . В результате интегрирования получаем:
. В результате интегрирования получаем:  – общее решение
– общее решение
соответствующего однородного уравнения. Применим метод варьирования константы,
то есть предположим c=c(x). Тогда общее решение исходного линейного
неоднородного уравнения будет иметь вид:  . Подставим y и
. Подставим y и  в исходное уравнение:
в исходное уравнение:
 . После сокращений получим:
. После сокращений получим:
 . Разделим переменные и проинтегрируем:
. Разделим переменные и проинтегрируем:  .
.
Подставляя найденное c(x) в y, имеем общее решение линейного неоднородного
уравнения:

5.
Уравнения Бернулли
Общий вид уравнений
 . (8.19)
. (8.19)
При n=1 (8.19)– уравнение с разделяющимися переменными. При n=0 (8.19)– линейное ДУ.
Рассмотрим  . Метод решения – деление уравнения на
. Метод решения – деление уравнения на  , после чего (8.19) принимает вид
, после чего (8.19) принимает вид  .
.
С помощью замены z=y–n+1
исходное уравнение становится линейным относительно функции z(x):
 , (8.20)
, (8.20)
то есть его решение находится аналогично пункту 4. На
практике искать решение уравнения (8.17) удобнее методом Бернулли в виде
произведения неизвестных функций y=u∙v. Заметим, что y=0 – всегда является решением исходного уравнения
(8.17).
Пример 8.9. Проинтегрировать уравнение  .
.
Решение. Заданное
уравнение является уравнением Бернулли. Положим y=u∙v, тогда  и уравнение примет
и уравнение примет
вид:
 .
.
Выберем функцию u так, чтобы выполнялось равенство: . Разделим переменные и
. Разделим переменные и
проинтегрируем:
 . При c=1 получим функцию
. При c=1 получим функцию .
.
Тогда заданное уравнение после сокращения на u примет
вид:  или
или  – уравнение
– уравнение
с разделяющимися переменными. Находим его общее решение: . Интегрируя последнее уравнение,
. Интегрируя последнее уравнение,
получим: . Следовательно, общее решение заданного уравнения имеет вид:
. Следовательно, общее решение заданного уравнения имеет вид:

6. Уравнения
в полных дифференциалах
6.1. Общий вид уравнений
 , (8.21)
, (8.21)
где
левая часть есть полный дифференциал некоторой функции F(x;y), то есть  . В этом случае ДУ (8.21) можно записать в виде
. В этом случае ДУ (8.21) можно записать в виде , а его общий интеграл будет F(x;y)=c.
, а его общий интеграл будет F(x;y)=c.
Условие, по которому можно судить, что выражение  является полным
является полным
дифференциалом, можно сформулировать в виде следующей теоремы.
Теорема 8.2.
Для того чтобы выражение  , где функции M(x;y) и N(x;y), их частные
, где функции M(x;y) и N(x;y), их частные
производные  и
и  непрерывны в некоторой
непрерывны в некоторой
области D плоскости x0y, было
полным дифференциалом, необходимо и
достаточно выполнение условия
 (8.22)
(8.22)
Таким образом, согласно определению полного
дифференциала (6.6) должны выполняться равенства:
 . (8.23)
. (8.23)
Формула (8.22) представляет собой теорему Шварца,
согласно которой смешанные производные второго порядка функции F(x;y) равны.
Зафиксируем переменную y и проинтегрируем первое уравнение из (8.23) по x, получим:
 . (8.24)
. (8.24)
Здесь
мы применили метод вариации произвольной постоянной, так как предположили, что
константа c зависит от y (либо
является числом). Продифференцировав (8.24) по переменной y
и приравняв производную к функции N(x;y), мы получим уравнение для нахождения неизвестной c(y).
Подставив c(y) в (8.24), находим функцию F(x;y) такую, что .
.
Пример 8.10. Решить
уравнение  .
.
Решение. Здесь функция  .
.
Проверим условие (8.22):  . Следовательно, левая часть заданного уравнения представляет собой полный дифференциал
. Следовательно, левая часть заданного уравнения представляет собой полный дифференциал
некоторой функции F(x;y). Для ее
отыскания проинтегрируем функцию M(x;y) по
переменной x, считая y=const:
 .
.
Пусть c=c(y),
тогда  . Продифференцируем данную функцию по y,
. Продифференцируем данную функцию по y,
получим  . Отсюда
. Отсюда  .
.
Найденное c(y) подставляем в функцию F(x;y), получаем
решение заданного ДУ:

Если условие (8.22) не выполняется, то ДУ (8.21) не
является уравнением в полных дифференциалах.
Однако это уравнение иногда можно привести к уравнению
в полных дифференциалах умножением его на некоторую функцию μ(x;y), называемую интегрирующим множителем.
Чтобы уравнение  было уравнение в полных
было уравнение в полных
дифференциалах, должно выполняться условие
 . (8.25)
. (8.25)
Выполнив дифференцирование  и приведя подобные
и приведя подобные
слагаемые, получим:  . Для нахождения μ(x;y) надо
. Для нахождения μ(x;y) надо
проинтегрировать полученное ДУ в частных производных. Решение этой задачи не
простое. Нахождение интегрирующего множителя может быть упрощено, если
допустить существование μ как функции только одного аргумента x либо
только y.
6.2. Пусть μ = μ(x). Тогда уравнение (8.25) принимает вид:
 (8.26)
(8.26)
При этом подынтегральное выражение должно зависеть только от x.
6.3. Пусть
μ = μ(y). Тогда
аналогично можно получить
 , (8.27)
, (8.27)
где подынтегральное выражение должно зависеть только
от y.
Пример 8.11. Решить
уравнение  .
.
Решение. Здесь  , то есть
, то есть  . Проверим существование интегрирующего множителя. По
. Проверим существование интегрирующего множителя. По
формуле (8.26) составляем подынтегральное выражение:
 , оно зависит только от
, оно зависит только от
переменной x. Следовательно, уравнение имеет интегрирующий
множитель μ(x). В нашем
случае он имеет вид  . Умножая исходное уравнение на
. Умножая исходное уравнение на
μ=x, получаем:  , то есть уравнение в полных дифференциалах. Действительно, для него
, то есть уравнение в полных дифференциалах. Действительно, для него . Решив его аналогично пункту 6.1, найдем, что общий
. Решив его аналогично пункту 6.1, найдем, что общий
интеграл исходного уравнения имеет вид 
7. Дифференциальные уравнения, неразрешенные относительно производной
К уравнениям данного вида относятся уравнения Лагранжа и Клеро, которые образуют достаточно большой класс ДУ, решаемых методом введения параметра  .
.
7.1.
Уравнение Лагранжа
Общий вид уравнений
 , (8.28)
, (8.28)
где
φ
и ψ– известные функции от  . После введения параметра
. После введения параметра  уравнение (8.28)
уравнение (8.28)
принимает вид
 . (8.29)
. (8.29)
Продифференцируем его по x:
 . (8.30)
. (8.30)
Полученное уравнение (8.30) является линейным уравнением относительно
неизвестной функции x = x(p). Решив
его, найдем:
x = λ(p;c). (8.31)
Исключая параметр p из уравнений
(8.29) и (8.31), получаем общий
интеграл уравнения (8.28) в
виде y = γ(x;c).
Примечание. При переходе к уравнению (8.30) мы делили на  . При этом могли быть потеряны решения, для которых
. При этом могли быть потеряны решения, для которых  или p = p0=const. Это
или p = p0=const. Это
означает, что p0 является
корнем уравнения p = φ(p)=0 (смотри уравнение (8.30)). Тогда
решение  для уравнения (8.28)
для уравнения (8.28)
является особым
7.2. Уравнение
Клеро представляет собой частный случай уравнения Лагранжа
при  , следовательно, его общий вид
, следовательно, его общий вид
 . (8.32)
. (8.32)
Вводим
параметр  , после чего уравнение (8.30) записывается так:
, после чего уравнение (8.30) записывается так:
 . (8.33)
. (8.33)
Продифференцируем уравнение (8.33) по переменной x:
 ,
,
то согласно (8.33), уравнение (8.32) имеет общее решение
 . (8.34)
. (8.34)
При  получаем частное решение уравнения
получаем частное решение уравнения
в параметрической форме:
 .
.
(8.35)
Это – особое решение уравнения Клеро, так как оно не
содержится в формуле общего решения уравнения.
Пример 8.12.
Решить уравнение Клеро  .
.
Решение. Согласно формуле (8.32) общее решение имеет вид y=cx+c2. Особое решение уравнения получим по (8.33) в виде . Отсюда следует:
. Отсюда следует:  , то есть
, то есть 
Вопросы для самопроверки
