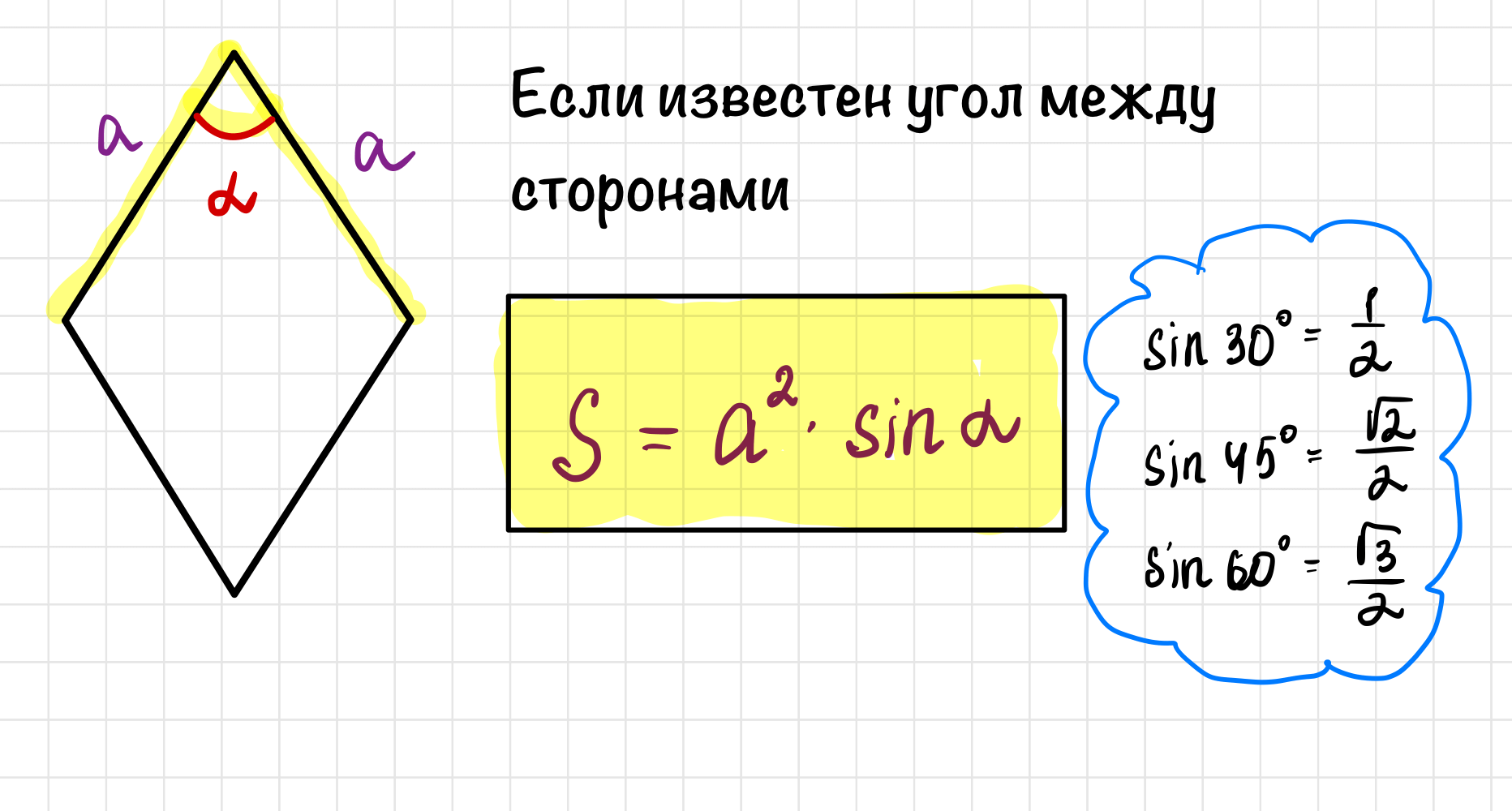
Ромб – это геометрическая фигура, у которой все стороны имеют одинаковую длину. В нашей статье подробно рассматривается задача нахождения площади ромба, сторона которого равна 20 сантиметрам, а диагонали находятся в отношении 3 к 4. Это интересная и полезная задача, которая поможет лучше понять принципы, лежащие в основе геометрии.
Перед тем, как перейти непосредственно к решению задачи, давайте ознакомимся с понятием диагонали и представленной формулой для нахождения площади ромба.
Диагонали в ромбе – это линии, соединяющие противоположные вершины этой фигуры. Входит в состав другого важного определения – формулы площади ромба, высчитываемой по рекомендованному алгоритму: берутся произведение диагоналей ромба (по памяти – это a*b, а не дважды a*b!), затем результат делится на высшую из двух функций – цена свечения квадратного корня (думаю, имеется в виду квадратный корень, но без сущ. ч. это ошибочно будет). Другими словами, площадь ромба будет равна квадратному корню от произведения длин его диагоналей через одну.
Таким образом, применим наставления выше для нашей текущей задачи, где диагонали ромба находятся в пропорции 3 к 4, а длина его стороны составляет 20 сантиметров. Не будем зря мараться пол-днем, погрузкой нас в мелочи: предлагаем, пожалуйста, приступить к кондратному и простому процессу вычислений и решения этой увлекательной задачи.
Площадь ромба через соотношение диагоналей
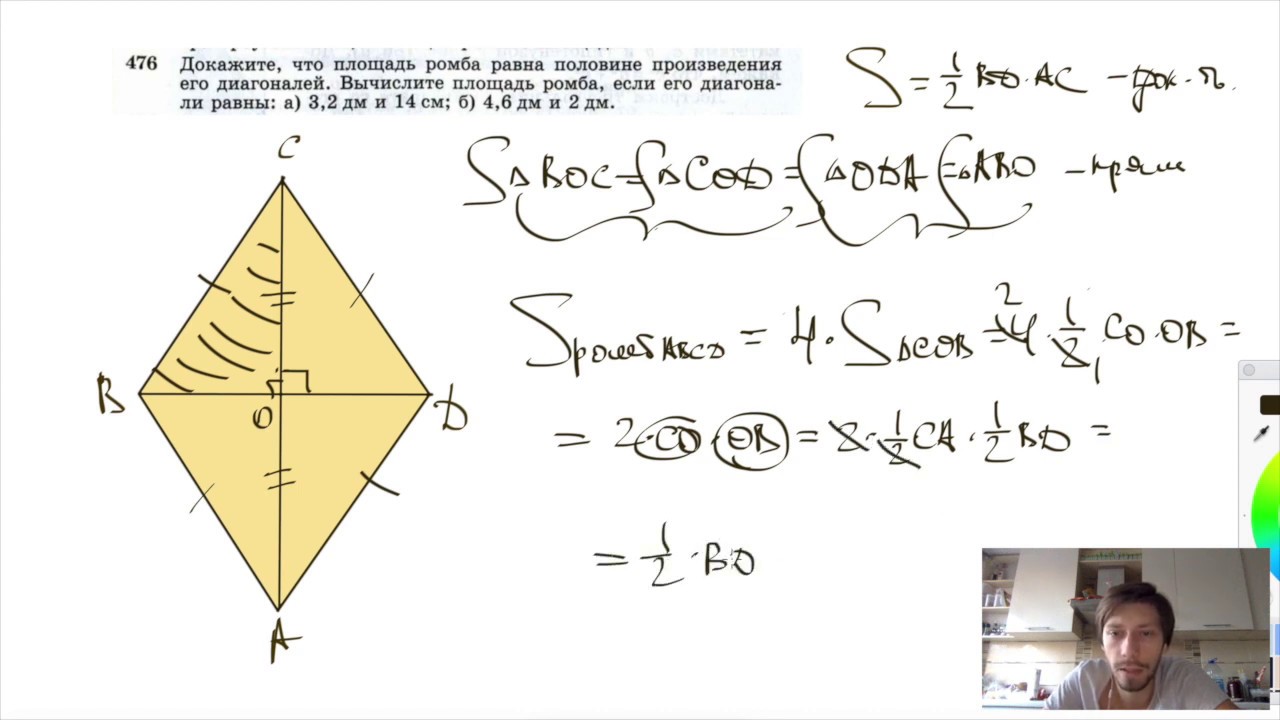
Понятие ромба и его диагоналей
Ромб – это четырехугольник, в котором все стороны равны. Диагонали ромба – это две линии, которые соединяют противоположные углы ромба. Диагонали ромба пересекаются внутри многоугольника и делят друг друга на равные части. Соотношение диагоналей ромба может быть полезным для определения площади этого многоугольника.
Формула площади ромба через соотношение диагоналей
Чтобы найти площадь ромба, используя соотношение его диагоналей, необходимо:
- Найти длину одной из диагоналей,
- Вычислить отношение противоположной диагонали,
- Перемножить получившиеся значения на квадратную глубину ромба.
Формула площади ромба через соотношение диагоналей выглядит следующим образом:
S = (d1 * d2) / 2
где S – площадь ромба, d1 и d2 – длины диагоналей ромба.
Пример расчета площади ромба
Предполагаем, что у нас есть ромб со стороной равной 20 см, и соотношение диагоналей 3 к 4. Для вычисления площади, необходимо найти длину одной из диагоналей:
d1 будет равно отношению диагоналей:
d1 = 3 / 4 * сторона ромба
Теперь вставляем масштабную сторону ромба:
d1 = 3 / 4 * 20 см = 15 см
Теперь из соотношения диагоналей разбиваем вторую диагональ:
d2 = 4 / 3 * сторона ромба
Теперь вставляйте масштабную сторону ромба:
d2 = 4 / 3 * 20 см = 26,67 см
Теперь найти площадь ромба:
S = (d1 * d2) / 2
Теперь перемножайте d1 на d2:
S = (15 см * 26,67 см) / 2
Теперь делайтеумножение:
S = 400 см² / 2
Теперь получите площадь ромба:
S = 200 см²
Таким образом, площадь ромба с стороной 20 см и диагоналями на пропорциях 3 к 4 составляет 200 квадратных сантиметров.
Алгебраическое выражение
В этом разделе статьи мы рассмотрим, как можно найти площадь ромба, если известен его сторона, равная 20 см, и если диагонали относятся как 3 4, используя алгебраическое выражение.
Алгебраическое выражение для площади ромба может быть записано следующим образом: S = 1/2 × d1 × d2, где S – это площадь ромба, а d1 и d2 – диагонали ромба.
Итак, давайте запишем алгебраическое выражение, исходя из условия:
d1 : d2 = 3 : 4, где d1 и d2 – диагонали ромба. Мы можем использовать дробь со знаменателем, равной 7, тогда всё станет ясно:
d1 = 3/7 × d и d2 = 4/7 × d, так как одна сторона ромба d = 20 см.
Теперь запишем алгебраическое выражение для площади ромба, поскольку алгебраическое выражение можно трансформировать:
S = 1/2 × (3/7) × d × 2d = 1/2 × 3 d^2 × 2
S = 3d
Теперь, когда имеется уже новое алгебраическое выражение для площади ромба, подставим d = 20 см.
S = 3 × 20 = 60 см².
Таким образом, при помощи алгебраического выражения мы вычислили площадь ромба, зная его сторону и соотношение диагоналей.
Пример решения
Чтобы найти площадь ромба, у которого сторона равна 20 см, а диагонали относятся как 3:4, необходимо использовать теорему Пифагора и формулу для расчета площади ромба.
Шаг 1. Вычисление длины диагоналей

У ромба диагонали равны и относятся как 3:4. Это означает, что где-то есть число a, такое, что одна диагональ = a*3 см, а другая диагональ = a*4 см.
Предположим, что сторона ромба образует угол Alpha между двумя диагоналями. Тогда по теореме Пифагора можно сказать, что сумма квадратов разности модул диагоналей одного ромба потомую и сходится у единицы:
(a*4)^2 + (a*3)^2 = 20^2
Проще говоря, 16a^2 + 9a^2 = 400:
25a^2 = 400
Вычислим a квадратным уравнением, разделив обе части на величину корня из 25:
a^2 = 400 : 25 = 16
a = sqrt(16) = 4 см
Шаг 2. Вычисление площади ромба
Теперь, когда мы знаем, какое значение имеет диагональ ромба, мы можем воспользоваться формулой для вычисления площади ромба:
Площадь ромба = (длина одной диагонали * длина другой диагонали) : 2
Площадь ромба = (4*3 см * 4*4 см) /2 см2
Площадь ромба = (12 см * 16 см) / 2 см2
Площадь ромба = 192 см2
Таким образом, площадь ромба, у которого сторона равна 20 см, а диагонали относятся как 3 4, равна 192 кв. см.
Исторические сведения
-
Происхождение арифметики и геометрии
Арифметика и геометрия имеют древнее происхождение, они были важными научными дисциплинами для различных культур. Например, геометрия была известна египетским жрецам ещё 5000 лет назад. Выполняя расчеты, связанные с строительством пирамид или размещением полей для посева, они научились рассчитывать такие величины, как площади, длины и углы. Арифметика также упоминается в древних математических текстах.
-
Ке mathematics plana debenudo Черезпиро по
Ке появлению квадратов, треугольников, ромбов и других фигур на фоне процветания математики на Ближнем Востоке за счет решения задач, связанных с хозяйственными проблемами, стали существовать фундаментальные труды, в которых рассматривалось и решение задач о площадях фигур.
-
Класичнии mathematicians
Могут быть упомянуты такие математики как Архимед, Еврикл, Эвклид и другие, что внесли значительный вклад в развитие геометрии и упрощение процесса вычисления площадей различных фигур.
-
Описание решения задачи
Касательно проекции задачи о вычислении площади ромба требуется обратить внимание на тот факт, что по правилу Пифагора площадь ромба равна отношению площади четырехугольника, состоящего из двух равных квадратов с стороной a, и получается сторона b ромба. Светогоче, площадь ромба со сторонами a и диагональю в соотношении 3:4 равна: S = 1/2*a*a = 1/2*20*20 cm² = 200 кв. см.
Все записанные факты свидетельствуют о том, что геометрия и арифметика постепенно развиваются под влиянием потребностей цивилизаций, которые имели некую взаимосвязь со своями окружением. Знания сначала коллектиивали знания и знания на край обыденнио романовым уже временем прослеживает //ад / в область требует коллектив. Это и наш:
Применение во время строительства
Поиск площади ромба
Чтобы вычислить площадь ромба, необходимо знать длину его стороны и пропорции диагоналей. В приведенном примере сторона ромба равна 20 см, а диагонали относятся как 3:4. Для нахождения площади следует использовать формулу:
S = (d1 * d2) / 2
Применение ромба на этапе проектирования
- Фасады: Ромбы могут вносить интересное разнообразие в архитектурный дизайн фасадов зданий, создавая более сложные и нетривиальные композиции.
- Окна: Площадь ромба может быть полезна при определении размера и расположения окон, чтобы оптимизировать количество света, проникающего внутрь помещения.
Применение ромба на этапе строительства

- Остекление: В производстве сложных оконных конструкций использование ромба может быть жизненно важным элементом, так как такие стёкла могут создавать эффект дизайнерского искусства и органично вписываться в пространство.
- Архитектурные детали: Конструктивные элементы, созданные по образу и подобию ромба, могут усиливать конструкцию здания и взвешивать его физические характеристики, такие как устойчивость и сопротивление ветру.
Таким образом, ромбы становятся не только красивым, но и практичным решением при создании архитектурных объектов. Применение площади ромба во время строительства позволяет достичь оптимального сочетания функциональности и эстетики.
Ромб и его связь с другими геометрическими фигурами
Ромб, как одна из основных геометрических фигур, имеет несколько связей с другими понятиями и фигурами в геометрии, которые можно рассмотреть более подробно.
Определение ромба
Ромб – это многоугольник с четырьмя сторонами, все из которых имеют одинаковую длину. Это значит, что все четыре угла ромба равны. В отличие от квадрата, диагонали ромба не обязаны быть равными, но ромб может быть образован прямыми, которые пересекаются под прямым углом и имеют равные длины.
Связь с другими геометрическими фигурами
- Квадрат – это ромб с четырьмя прямыми углами и равнобедренными диагональными углами. Дельтоиды также являются квадратами, но с другими углами и диагональными углами. Таким образом, квадрат является частным делом ромба.
- Трапеция – это многоугольник, у которого две пары противоположных сторон являются параллельными. Как и ромб, трапеция может иметь один или два равных угла. В случае, когда у ромба нет равных углов, его можно рассматривать как форму трапеции.
- Прямоугольник – это многоугольник с четырьмя углами, которые являются прямыми, и противоположными сторонами, которые имеют равные длины. Ромб можно рассматривать как частный случай прямоугольника, если все стороны ромба имеют одинаковую длину.
- Окружность – это простые замкнутые пространственные объекты, которые представляют собой ядро. В планарной геометрии, окружность имеет одни и те же характеристики, как и ромб, например: выравнивание осей, расположение, значение угла и так далее. Однако, окружность имеет выпуклую границу, а ромб является замкнутой рекуррентной геометрической фигурой.
- Наконец, теоремы Банаха-Фнеровича, которая определяет функции на разных многоугольниках, может быть обобщена на ромбы и на трапеции, ветви которых могут быть описано тремя и четырьмя условиями непрерывности.
Связанные темы

- Особые случаи ромбов, такие как квадраты и ромбы Соломона. Эти варианты имеют различные свойства и приложения.
- Металлические ромбы – это транскрипт сигналов, которые используются для идентификации радиопередатчиков транспортных средств и государственных кораблей по соглашению ITU O./ Region 1 (Europe), ITU O./ Region 2 (Americas) и ITU O./ Region 3 (Asia, Africa и остров Новая Гвинея).
- Прикрепление на ромбы на поверхность исключённой области на плоскости, две или более конечных величин, может быть только уникально решением геометрии.
Окончания в виде картинки обучения, в котором ромбы и практические применения могут быть представлены, продолжают выставляться лучший способы связи этой геометрической фигуры с другими фигурами и концепциями.
Вопрос-ответ:
Как найти площадь ромба, используя длину стороны и отношение его диагоналей?
Чтобы найти площадь ромба, используя длину стороны и отношение его диагоналей, нам нужно применить формулу площади ромба, которая выглядит следующим образом: площадь = (сторона × d1 × d2) / (2 × d1 + 2 × d2), где ‘d1’ и ‘d2’ – длины диагоналей и сторона равна 20 см. Так как мы имеем отношение диагоналей 3:4, можно сказать, что одна диагональ длина 3 × сторона и другая диагональ длины 4 × сторона. Таким образом, площадь ромба будет площадь = (20 × 60) / (2 × 60 + 2 × 80), что даст площадь ромба в 4800 квадратных сантиметров.
Могут ли диагонали ромба быть пропорциональны, если стороны ромба равны 20 см?
Да, диагонали ромба могут быть пропорциональны. В данном случае диагонали относятся как 3:4 к сторонам ромба. Это значит, что одна диагональ равна 3 раза стороне ромба (то есть 3 × 20 = 60 см) и другая диагональ равна 4 раза стороне ромба (то есть 4 × 20 = 80 см). Это показывает, что диагонали пропорциональны и можно найти площадь ромба, используя эти отношения.
Сколько будет площадь ромба, если стороны ромба равны 40 см и отношение диагоналей такое же – 3:4?
Если стороны ромба вместо 20 см будут равны 40 см, и отношение диагоналей останется таким же, как и раньше – 3:4, тогда для одной диагонали площадь будет 3 умножить на 40 (то есть 120 см) и для другой диагонали площадь будет 4 умножить на 40 (то есть 160 см). Используя формулу площади ромба, мы получим что площадь ромба будет равна 120 × 160 деленное на 2 × 120 + 2 × 160, что даст площадь ромба 9600 квадратных сантиметров.
Чему равна площадь ромба, если сторона равна 20 см, а диагонали обладают отношением 3:4?
Сначала мы должны найти длину диагоналей ромба. Поскольку отношение длин диагоналей равно 3:4, что даёт нам отношение 3/7. Зная сторону равную 20 см, мы можем воспользоваться этим соотношением для узнать длину диагоналей. Если первая диагональ стоит на месте 3 в этом отношении, а вторая на 4, это даст нам 3/7 * сторона = длина первой диагонали и 4/7 * сторона = длина второй диагонали. Умножая это на сторону 20 см для каждой диагонали, находим 3/7 * 20 = 8,57 см и 4/7 * 20 = 11,43 см. Теперь нам нужно найти площадь ромба используя формулу площади ромба = ½ * длина первой диагонали * длина второй диагонали = ½ * 8,57 см * 11,43 см = 48,62 кв. см.