Загрузить PDF
Загрузить PDF
В статистике абсолютная частота показывает, какое количество раз конкретное значение появляется в наборе данных. В отличие от нее, накопительная частота показывает сумму (или нарастающий итог) всех частот вплоть до текущей точки в наборе данных. Не беспокойтесь, если поначалу это кажется не совсем понятным: возьмите ручку и лист бумаги, и вы быстро во всем разберетесь!
-

1
Отсортируйте набор данных. «Набор данных» — это просто изучаемый вами список числовых значений. Отсортируйте его так, чтобы числа располагались по возрастанию.[1]
- Пример: предположим, список чисел представляет собой количество книг, которые каждый студент прочитал за последний месяц. После сортировки у вас получился следующий набор чисел: 3, 3, 5, 6, 6, 6, 8.
-

2
Посчитайте абсолютную частоту каждой величины. Частота значения показывает, сколько раз данное значение появляется в наборе данных. Это число можно называть абсолютной частотой, чтобы не путать его с накопительной частотой. Наиболее простой способ заключается в том, чтобы составить таблицу. Вверху левой колонки напишите «Значение» (или укажите, что измеряется данными числами). Вверху второй колонки напишите «Частота». Заполните таблицу для всех значений из списка.[2]
- Пример: вверху левой колонки напишите «Количество книг», а вверху правой колонки — «Частота».
- Во второй строке напишите первое количество прочитанных книг, то есть число 3.
- Посчитайте, сколько раз число 3 встречается в списке данных. В списке есть два числа 3, поэтому во второй строке колонки «Частота» запишите цифру 2.
- Повторите данную процедуру для всех значений списка, пока не заполните таблицу:
- 3 | Ч = 2
- 5 | Ч = 1
- 6 | Ч = 3
- 8 | Ч = 1
-

3
Найдите накопительную частоту для первого значения. Накопительная частота отвечает на вопрос «сколько раз встречается в списке данное значение или меньшая величина?». Всегда начинайте с наименьшего значения в наборе данных. Поскольку в нашем примере нет меньших значений, для данной величины накопительная частота равна абсолютной.[3]
-
Пример: наименьшее значение равно 3. Количество прочитавших 3 книги студентов составляет 2. Никто из студентов не прочитал меньшее число книг, поэтому накопительная частота равна 3. Впишите это значение в третью колонку таблицы:
- 3 | F = 2 | НЧ=2
-
Пример: наименьшее значение равно 3. Количество прочитавших 3 книги студентов составляет 2. Никто из студентов не прочитал меньшее число книг, поэтому накопительная частота равна 3. Впишите это значение в третью колонку таблицы:
-

4
Найдите накопительную частоту для следующей величины. Перейдите к следующему значению списка. Выше мы определили, сколько раз встречается в списке наименьшая величина. Чтобы определить накопительную частоту для второго значения списка, необходимо прибавить его абсолютную частоту к накопительной частоте предыдущего значения. Иными словами, следует взять последнюю накопительную частоту и прибавить к ней абсолютную частоту данной величины.[4]
-
Пример:
- 3 | Ч = 2 | НЧ = 2
- 5 | Ч = 1 | НЧ = 2+1 = 3
-
Пример:
-

5
Повторите процедуру для остальных значений. Постепенно продвигайтесь к более высоким числам. При этом каждый раз прибавляйте текущую абсолютную частоту к последней накопительной частоте.
-
Пример:
- 3 | Ч = 2 | НЧ = 2
- 5 | Ч = 1 | НЧ = 2 + 1 = 3
- 6 | Ч = 3 | НЧ = 3 + 3 = 6
- 8 | Ч = 1 | НЧ = 6 + 1 = 7
-
Пример:
-

6
Проверьте полученные результаты. В итоге вы сложите абсолютные частоты всех значений списка. Конечная накопительная частота должна соответствовать числу значений в списке. Есть два способа проверить, так ли это:
- Сложите абсолютные частоты всех значений: 2 + 1 + 3 + 1 = 7, в результате у вас получится накопительная частота.
- Посчитайте число значений в наборе данных. В нашем примере список имел следующий вид: 3, 3, 5, 6, 6, 6, 8. В этом списке семь величин, и итоговая накопительная частота также равна 7.
Реклама
-

1
Поймите разницу между дискретными и непрерывными данными. Дискретные данные можно посчитать, они не дробятся на более мелкие составляющие. Непрерывные данные часто не поддаются конечному счету, между двумя произвольными величинами обязательно найдутся другие возможные значения. Ниже приведена пара примеров:[5]
- Количество собак является дискретным множеством. Нет такого понятия, как половина собаки.
- Глубина снега представляет собой непрерывное множество. Она возрастает постепенно и непрерывно, а не на дискретные величины. Если вы измерите глубину снега в сантиметрах, то точное значение может оказаться, например, 20,6 сантиметра.
-

2
Разбейте непрерывные данные на интервалы. Наборы непрерывных данных часто имеют большое количество значений. Если попробовать представить такой набор описанным выше методом, таблица получится слишком длинной и малопонятной. В этом случае удобно разбить данные на отдельные интервалы. Эти интервалы должны быть одинаковой длины (например, 0—10, 11–20, 21–30 и так далее) независимо от того, сколько значений попадает в каждый интервал. Ниже приведена возможная таблица для непрерывного набора данных:[6]
- Набор данных: 233, 259, 277, 278, 289, 301, 303
- Таблица (в первой колонке интервал значений, во второй частота, в третьей накопительная частота):
- 200–250 | 1 | 1
- 251–300 | 4 | 1 + 4 = 5
- 301–350 | 2 | 5 + 2 = 7
-

3
Постройте линейный график. После того как вы рассчитаете накопительную частоту, возьмите лист миллиметровой бумаги. Отложите по горизонтальной оси (ось x) значения из набора данных, а по вертикальной (ось y) — накопительную частоту, и постройте график. Это значительно облегчит последующие вычисления.[7]
- Например, если набор данных включает числа от 1 до 8, отложите по горизонтальной оси 8 делений. Над каждым делением отметьте точкой соответствующее ему значение накопительной частоты. Соедините получившиеся точки линией.
- Если какое-либо значение не встречается, его абсолютная частота составляет 0. В этом случае прибавьте 0 к последней величине накопительной частоты и поставьте точку на том же уровне, что и в предыдущий раз.
- Поскольку накопительная частота всегда растет с продвижением к большим значениям, с перемещением вправо линия будет оставаться на той же самой высоте или подниматься. Если в какой-то точке линия опустилась вниз, значит, вы допустили ошибку (например, вместо накопительной частоты взяли абсолютную).
-

4
Найдите по графику медиану. Медиана — это значение, расположенное точно посередине набора данных. Половина значений находится выше медианы, а вторая половина расположена ниже нее. Медиану можно найти по графику следующим образом:
- Посмотрите на последнее значение в самом правом конце графика. Для него величина y соответствует суммарной накопительной частоте, которая равна общему числу точек в наборе данных. Предположим, эта величина равна 16.
- Умножьте эту величину на ½ и найдите соответствующее значение на оси y. В нашем примере получится 8. Найдите число 8 на оси y.
- Найдите точку на линии графика, значение y которой соответствует найденной величине. Проведите от цифры 8 на оси y горизонтальную прямую и определите точку ее пересечения с линией графика. Именно эта точка делит набор данных точно пополам.
- Найдите значение x в данной точке. Проведите из точки вертикальную прямую до пересечения с осью x. Точка пересечения определит медиану для изучаемого набора данных. Например, если получилось 65, значит половина данных расположена ниже 65, а вторая половина лежит выше этого значения.
-

5
Найдите по графику квартили. Квартили делят набор данных на четыре части. Эта процедура очень похожа на определение медианы. Единственное различие заключается в нахождении значений y:
- Чтобы определить величину y для нижнего квартиля, умножьте максимальное значение накопительной частоты на ¼. В результате вы получите значение x, ниже которого будет лежать ровно ¼ всех данных.
- Чтобы найти величину y для верхнего квартиля, умножьте максимальное значение накопительной частоты на ¾. В результате вы получите значение x, ниже которого будет лежать ¾, а выше — ¼ всех данных.
Реклама
Советы
- С помощью интервалов можно представлять любые большие, в том числе и дискретные наборы данных.
Реклама
Об этой статье
Эту страницу просматривали 72 751 раз.
Была ли эта статья полезной?
Раздел долгосрочного плана:
Элементы статистики
Школа:
Дата:
ФИО учителя:
Класс: 8
Количество присутствующих:
отсутствующих:
Тема урока
Накопленная частота
Тип урока
Урок изучения новой темы
Цели обучения, которые достигаются на данном уроке (ссылка
на учебную программу)
8.3.3.3
знать определение накопленной частоты;
Цели
урока
Учащиеся заполняют
таблицу накопленных частот и строят график накопленных частот.
Критерии оценивания
Учащийся
·
заполняет таблицу накопленных частот;
·
строит график накопленных частот;
·
находит медиану по графику накопленных частот.
Языковые
цели
Учащиеся объясняют
цель обработки данных, комментируют выполнение заданий на группировку данных, комментируют нахождение накопленных частот.
Лексика и терминология, специфичная для предмета:
Частота; интервальная
частотная таблица; длина интервала; модальный класс, накопленная частота.
Полезные выражения для диалогов и письма:
Для того,
чтобы найти накопленную частоту необходимо…
Представление данных
интервальной таблицы в виде накопленных частот используется для…
Привитие
ценностей
Привитие ценностей
осуществляется посредством работ, запланированных на данном уроке. Умение
учиться, анализировать ситуацию, адаптироваться к новым условиям, ставить
проблемы и принимать решения, работать в команде, отвечать за качество своей
работы, умение организовывать свое время.
Межпредметные связи
Примеры/задания, используемые
на уроке, рассматриваются из различных областей науки, например, из биологии,
экономики и т.д.
Предварительные знания
Учащиеся ранее изучили понятия
«гистограмма» и «интервальная таблица», научились строить гистограмму по
данным интервальной таблицы, и наоборот заполнять интервальную таблицу по
заданной гистограмме.
Ход урока
Запланированные
этапы урока
Запланированная
деятельность на уроке
Ресурсы
Начало урока
0-2 мин
2-7 мин
1. Организационный
момент. Целеполагание.
Учитель приветствует учащихся, проверяет готовность
учащихся к уроку. Учитель объявляет тему урока и цели
обучения. Совместно с учащимися формулируются цели
урока. Далее учитель озвучивает критерии оценивания, определяет «зону
ближайшего развития» учащихся, ожидания к концу урока.
2. Повторение.
Для актуализации знаний
учащихся, учитель задает следующие вопросы:
• Что называется частотой?
• Что называется плотностью частоты?
• Как построить гистограмму?
• Какие существуют виды величин?
• Как составить интервальную таблицу?
• Как вычислить среднее значение данных, представленных в виде
интервальной таблицы?
Презентация
Слайды 1-3
Презентация
Слайд 4
Середина урока
7-20 мин
20-38 мин
3.
Введение понятия накопленной частоты.
Учитель
рассматривает пример с учащимися с прошлого урока:
Среди учащихся 1
классов было проведено исследование, для выяснения того, сколько весит
портфель первоклассника. В результате исследования был получен следующий
числовой ряд (масса портфеля в кг):
2,1; 2,45; 1,9;
2,6; 3,1; 1,95; 3,4; 4,3; 1,15; 2,7; 2,2; 3,2; 2,4; 2,2; 1,8; 1,5; 2,4; 2,25;
2,6; 1,75.
Вопросы:
У скольки
учащихся масса портфеля меньше 3 кг? Меньше 4 кг? Больше 3 кг? Больше 4 кг?
У скольки
процентов учащихся масса портфеля меньше 3 кг? Меньше 4 кг? Больше 3 кг?
Больше 4 кг?
Для того, чтобы ответить на эти
вопросы и представить данные в наглядном виде применяется понятие накопленной
частоты.
Накопленная
частота показывает сколько чисел статистического
ряда не превышает заданного значения. Накопленные частоты образуются путем
сложения частот.
Пример:
В
интервальной таблице представлены следующие данные:
|
Длина |
|
|
|
|
|
|
Частота |
4 |
22 |
56 |
32 |
5 |
Накопленная
частота вычисляется следующим образом:
|
Длина |
<155 |
<160 |
<165 |
<170 |
<175 |
|
Накопленная частота |
4 |
4+22=26 |
26+56=82 |
82+32=114 |
114+5=119 |

Графиком
накопленных частот называется кумулята. С помощью этого графика очень удобно
представлять данные, а также находить медиану. В рассматриваемом примере
сумма всех частот равна 119, тогда медиане соответствует значение (119+1):2=60, следовательно, по графику найдем медиану 163 см.
4. Закрепление
изученного материала.
Учитель предлагает учащимся в
парах выполнить задания. Учитель при необходимости оказывает помощь учащимся,
обсуждает со всем классом типичные ошибки учащихся. При необходимости учитель
может организовать работу у доски, при этом уделяя внимание оформлению
решения.
Учитель оценивает работы
учащихся по установленным критериям, а также в ходе наблюдения за парной
работой определяет вклад каждого учащегося.
Критерии
оценивания к заданию №1:
Учащийся
–
верно вычисляет
среднее значение величин, представленных в виде интервального ряда;
–
верно находит
накопленные частоты;
–
правильно изображает
график накопленных частот.
Критерии оценивания к заданию №2:
Учащийся
–
верно заполняет
таблицу накопленных частот;
–
верно строит график
накопленных частот;
–
правильно отвечает на
поставленный вопрос, используя график накопленных частот.
Критерии оценивания к заданию №3:
Учащийся
–
верно заполняет
таблицу накопленных частот;
–
правильно строит
график накопленных частот;
–
верно находит
медиану, используя график накопленных частот.
Презентация
Слайд 5
Презентация
Слайд 6
Презентация
Слайд 7
Приложение 1
Презентация
Слайд 8
Презентация
Слайд 9
Презентация
Слайд 10
Конец урока
38-40 мин
5.
Подведение итогов урока. Рефлексия.
Учитель возвращается к целям
урока, обсуждая уровень их достижения.
Для дальнейшего планирования
уроков учащимся задаются вопросы:
• Сегодня я
узнал(а)…
• Было интересно…
• Было трудно…
• Я выполнял(а)
задания…
На вопросы учащиеся могут
ответить устно, либо письменно.
В качестве домашнего задания
учащимся можно предложить дополнительные разноуровневые задания, приведенные
в методических рекомендациях.
Презентация
Слайд 11
Стикеры
Методические рекомендации к проведению урока
Дифференциация –
каким образом Вы планируете оказать больше поддержки? Какие задачи Вы
планируете поставить перед более способными учащимися?
Оценивание – как
Вы планируете проверить уровень усвоения материала учащимися?
Здоровье и
соблюдение техники безопасности
Урок будет построен таким
образом, что ученики, не столь уверенные в своих силах, будут работать в
парах с более способными учениками и смогут узнать больше. Способные же
учащиеся могут проявить свои способности в качестве консультанта, а также
решая самостоятельно дополнительные задания повышенной сложности.
Во время индивидуальной работы
Вы можете помогать неуверенным ученикам, задавая наводящие вопросы.
Формативное оценивание
производится на каждом этапе урока (самооценивание, оценивание учителем по
критериям). Оценка путем наблюдения за вовлечением учеников при выполнении
заданий и за участием в диалогах, во всеобщих обсуждениях.
Прогресс, ответная реакция на
задания в парах будут тщательно рассмотрены для того, чтобы оценить вклад
каждого ученика и выявить наличие ошибок для их коррекции.
Все задания
подобраны с учетом возрастных особенностей учащихся. Смена видов
деятельности позволяет оптимально распределить силы и внимание учащихся для
наибольшего достижения результатов.

Содержание
- Формулы
- Прочие накопленные частоты
- Как получить накопленную частоту?
- Как заполнять частотную таблицу
- Таблица частотности
- Кумулятивное частотное распределение
- пример
- Предлагаемое упражнение
- Ответить
- Ссылки
В накопленная частота представляет собой сумму абсолютных частот f, от самой низкой до той, которая соответствует определенному значению переменной. В свою очередь, абсолютная частота – это количество раз, когда наблюдение появляется в наборе данных.
Очевидно, переменная исследования должна быть сортируемой. А поскольку накопленная частота получается сложением абсолютных частот, получается, что накопленная частота до последних данных должна совпадать с их суммой. В противном случае в расчетах будет ошибка.

Обычно накопленная частота обозначается как Fя (или иногда nя), чтобы отличить ее от абсолютной частоты fя и важно добавить для него столбец в таблице, с помощью которой организованы данные, известной как таблица частот.
Это упрощает, среди прочего, отслеживание того, сколько данных было подсчитано до определенного наблюдения.
А Фя он также известен как абсолютная совокупная частота. Если разделить на общие данные, мы получим относительная совокупная частота, окончательная сумма которых должна быть равна 1.
Формулы
Кумулятивная частота данного значения переменной Xя представляет собой сумму абсолютных частот f всех значений, меньших или равных ей:
Fя = f1 + f2 + f3 +… Fя
Путем сложения всех абсолютных частот получается общее количество данных N, то есть:
F1 + F2 + F3 +…. + Fп = N
Предыдущая операция кратко записывается с помощью символа суммирования ∑:
∑ Fя = N
Прочие накопленные частоты
Также могут накапливаться следующие частоты:
-Относительная частота: получается делением абсолютной частоты fя между общими данными N:
Fр = fя / N
Если относительные частоты сложить от самой низкой к той, которая соответствует определенному наблюдению, мы получим совокупная относительная частота. Последнее значение должно быть равно 1.
-Процент кумулятивной относительной частоты: накопленная относительная частота умножается на 100%.
F% = (fя / N) x 100%
Эти частоты полезны для описания поведения данных, например, при нахождении показателей центральной тенденции.
Как получить накопленную частоту?
Чтобы получить накопленную частоту, необходимо упорядочить данные и организовать их в таблице частот. Процедура иллюстрируется следующей практической ситуацией:
-В интернет-магазине, который продает сотовые телефоны, отчет о продажах определенного бренда за март месяц показал следующие значения за день:
1; 2; 1; 3; 0; 1; 0; 2; 4; 2; 1; 0; 3; 3; 0; 1; 2; 4; 1; 2; 3; 2; 3; 1; 2; 4; 2; 1; 5; 5; 3
Переменная – это количество телефонов, проданных за день и это количественно. Данные, представленные таким образом, не так легко интерпретировать, например, владельцы магазина могут быть заинтересованы в том, чтобы узнать, есть ли какая-либо тенденция, например, дни недели, когда продажи этого бренда выше.
Подобную информацию и многое другое можно получить, представив данные в упорядоченном виде и указав частоты.
Как заполнять частотную таблицу
Для расчета накопленной частоты данные сначала упорядочиваются:
0; 0; 0; 0; 1; 1; 1; 1; 1; 1; 1; 1; 2; 2; 2; 2; 2; 2; 2; 2; 3; 3; 3; 3; 3; 3; 4; 4; 4; 5; 5
Затем строится таблица со следующей информацией:
-Первый столбец слева с количеством проданных телефонов от 0 до 5 в порядке возрастания.
-Второй столбец: абсолютная частота, то есть количество дней, в течение которых было продано 0 телефонов, 1 телефон, 2 телефона и т. Д.
-Третий столбец: накопленная частота, состоящая из суммы предыдущей частоты и частоты данных, которые необходимо учитывать.
Этот столбец начинается с первых данных в столбце абсолютной частоты, в данном случае это 0. Для следующего значения сложите его с предыдущим. Это продолжается до тех пор, пока не будут достигнуты последние накопленные данные частоты, которые должны совпадать с общими данными.
Таблица частотности
В следующей таблице показаны переменная «количество телефонов, проданных за день», ее абсолютная частота и подробный расчет накопленной частоты.

На первый взгляд, можно сказать, что у рассматриваемого бренда один или два телефона почти всегда продаются в день, поскольку максимальная абсолютная частота составляет 8 дней, что соответствует этим значениям переменной. Только за 4 дня месяца они не продали ни одного телефона.
Как уже отмечалось, таблицу легче изучить, чем изначально собранные индивидуальные данные.
Кумулятивное частотное распределение
Кумулятивное распределение частот – это таблица, в которой показаны абсолютные частоты, совокупные частоты, совокупные относительные частоты и совокупные процентные частоты.
Хотя есть преимущество организации данных в таблице, подобной предыдущей, если количество данных очень велико, может оказаться недостаточно для их организации, как показано выше, потому что, если частот много, их все равно трудно интерпретировать.
Проблему можно решить, построив Распределение частоты по интервалам, полезная процедура, когда переменная принимает большое количество значений или если это непрерывная переменная.
Здесь значения сгруппированы в интервалы равной амплитуды, называемые класс. Классы характеризуются наличием:
-Предел класса: – крайние значения каждого интервала, их два, верхний предел и нижний предел. Как правило, верхняя граница относится не к интервалу, а к следующему, а нижняя – к.
-Классовый знак: является средней точкой каждого интервала и принимается в качестве его репрезентативного значения.
-Ширина класса: Он рассчитывается путем вычитания значения самого высокого и самого низкого данных (диапазона) и деления на количество классов:
Ширина класса = Диапазон / Количество классов
Подробное описание частотного распределения приведено ниже.
пример
Этот набор данных соответствует 40 баллам за тест по математике по шкале от 0 до 10:
0; 0;0; 1; 1; 1; 1; 2; 2; 2; 3; 3; 3; 3; 4; 4; 4; 4; 5; 5; 5; 5; 6; 6; 6; 6; 7; 7; 7; 7; 7; 7; 8; 8; 8; 9; 9; 9;10; 10.
Распределение частот может быть выполнено с определенным количеством классов, например 5 классами. Следует иметь в виду, что при использовании многих классов данные нелегко интерпретировать, и смысл группировки теряется.
А если, наоборот, они сгруппированы в очень немногие, то информация размывается и часть ее теряется. Все зависит от количества имеющихся у вас данных.
В этом примере рекомендуется иметь две оценки в каждом интервале, поскольку будет 10 оценок и будет создано 5 классов. Ранг – это вычитание между высшим и низшим классом, ширина класса составляет:
Ширина класса = (10-0) / 5 = 2
Слева интервалы закрыты, а справа открыты (кроме последнего), что обозначено скобками и круглыми скобками соответственно. Все они одинаковой ширины, но это не обязательно, хотя и является наиболее распространенным.
Каждый интервал содержит определенное количество элементов или абсолютную частоту, а в следующем столбце – накопленная частота, с которой переносится сумма. В таблице также указана относительная частота fр (абсолютная частота между общим количеством данных) и относительная частота в процентах fр ×100%.

Предлагаемое упражнение
Одна компания ежедневно звонила своим клиентам в течение первых двух месяцев года. Данные следующие:
6, 12, 7, 15, 13, 18, 20, 25, 12, 10, 8, 13, 15, 6, 9, 18, 20, 24, 12, 7, 10, 11, 13, 9, 12, 15, 18, 20, 13, 17, 23, 25, 14, 18, 6, 14, 16, 9, 6, 10, 12, 20, 13, 17, 14, 26, 7, 12, 24, 7
Сгруппируйте по 5 классам и составьте таблицу с частотным распределением.
Ответить
Ширина класса:
(26-6)/5 = 4
Пожалуйста, попытайтесь понять это, прежде чем увидите ответ.

Ссылки
- Беренсон, М. 1985. Статистика для управления и экономики. Interamericana S.A.
- Деворе, Дж. 2012. Вероятность и статистика для техники и науки. 8-е. Издание. Cengage.
- Левин, Р. 1988. Статистика для администраторов. 2-й. Издание. Прентис Холл.
- Вероятность и статистика. Ширина интервала классов. Получено с: pedroprobabilidadyestadistica.blogspot.com.
- Шпигель, М. 2009. Статистика. Серия Шаум. 4-й Издание. Макгроу Хилл.
- Уолпол, Р. 2007. Вероятность и статистика для инженерии и науки. Пирсон.
1. Накопленная частота и др.
2.
Предположим, есть список чисел,
представляющий собой количество книг,
которые каждый студент прочитал за
последний месяц.
После сортировки у нас получился следующий
набор чисел: 3, 3, 5, 6, 6, 6, 8.
3. 3, 3, 5, 6, 6, 6, 8
вверху левой колонки
пишем “Количество
книг”, а вверху
правой колонки —
“Частота”.
Во второй строке
пишем первое
количество
прочитанных книг,
то есть число 3, во
второй строке
колонки “Частота”
пишем цифру 2.
4.
Накопленная частота отвечает на
вопрос “сколько раз встречается в
списке данное значение или меньшая
величина?”.
Всегда начинайте с наименьшего
значения в наборе данных.
Поскольку в нашем примере нет
меньших значений, для данной
величины
5.
6.
Чтобы определить накопленную частоту для второго
значения списка, необходимо прибавить его абсолютную
частоту к накопительной частоте предыдущего значения.
Иными словами, следует взять последнюю накопленную
частоту и прибавить к ней абсолютную частоту данной
величины.
7.
8. Проверьте полученные результаты:
В итоге мы сложили абсолютные частоты всех значений
списка.
Конечная наколенная частота должна соответствовать
числу значений в списке.
Есть два способа проверить, так ли это:
Сложим абсолютные частоты всех значений:
2 + 1 + 3 + 1 = 7, в результате получится накопленная
частота.
Посчитаем число значений в наборе данных.
В нашем примере список имел следующий вид: 3, 3, 5,
6, 6, 6, 8.
В этом списке семь величин, и итоговая накопленная
частота также равна 7.
9.
10. Дискретные данные
можно посчитать,
они не дробятся на более мелкие
составляющие.
Количество собак является дискретным
множеством.
Нет такого понятия, как половина
собаки.
11. Непрерывные данные
часто не поддаются
конечному счету, между двумя произвольными
величинами обязательно найдутся другие
возможные значения.
Высота снега представляет собой непрерывное
множество.
Высота снега возрастает постепенно и
непрерывно, а не на дискретные величины.
Если вы измерите высоту снега в сантиметрах, то
точное значение может оказаться, например,
20,6 сантиметра.
12. Частости – это…
Существуют относительные показатели,
характеризующие долю частоты отдельных
вариантов в общей сумме частот.
Эти относительные показатели именуют
частостями и условно обозначают через ,
т.е. .
Сумма всех частостей равна единице.
Частости могут быть выражены и в
процентах, и тогда их сумма будет равна
100%.
13. Мода и медиана
Мода – это величина признака (варианта), которая
чаще всего встречается в данной совокупности, т.е.
имеет наибольшую частоту.
Мода имеет большое практическое применение и в
ряде случаев только мода может дать
характеристику общественных явлений.
Медиана – это варианта, которая находится в
середине упорядоченного (ранжированного)
вариационного ряда.
Рассмотрим расчет моды и медианы в дискретном
вариационном ряду:
14. Определить моду и медиану:
Стаж, лет, X
Число рабочих, чел, f
Накопленные частоты
1
2
2
3
4
6
4
5
(11)
8
4
15
10
1
16
ИТОГО:
16
Мода Мо = 4 года, так как этому значению
соответствует наибольшая частота f = 5.
Т.е. наибольшее число рабочих имеют стаж 4
года.
15. Медиана
Для того, чтобы вычислить медиану, найдем
предварительно половину суммы частот. Если сумма
частот является числом нечетным, то мы сначала
прибавляем к этой сумме единицу, а затем делим
пополам:
Ме=16/2=8
Медианой будет восьмая по счету варианта.
Для того, чтобы найти, какая варианта будет
восьмой по номеру, будем накапливать частоты до
тех пор, пока не получим сумму частот, равную или
превышающую половину суммы всех частот.
Соответствующая варианта и будет медианой.
16. Медиана
Ме = 4 года.
Т.е. половина рабочих имеет стаж меньше
четырех лет, половина больше.
Если сумма накопленных частот против
одной варианты равна половине сумме
частот, то медиана определяется как средняя
арифметическая этой варианты и
последующей.
17. Свойство медианы
Главное свойство Ме в том, что сумма абсолютных
отклонений значений признака от медианы
меньше, чем от любой
другой величины: .
Это свойство Ме может быть использовано,
например, при определении места строительства
общественных зданий, т.к. Ме определяет точку,
дающую наименьшее расстояние, допустим,
детских садов от местожительства родителей,
жителей населенного пункта от кинотеатра, при
проектировке трамвайных, троллейбусных
остановок и т.д.
18. Медиана. Пример 2:
Найти медиану дискретного ряда
16,13,15,10,19,22,25,12,18,14,19,14,16,10.
Решение. Ранжируем ряд:
10,10,12,13,14,14,15,16,16,18,19,19,22,25, выборка
содержит четное число элементов n=14, следовательно
медиана лежит между двумя средними элементами
выборки – между 7-элементом и 8-элементом:
10,10,12,13,14,14,15,16,16,18,19,19,22,25
и равна среднему арифметическому этих элементов:
Me=(15+16)/2=15,5
19.
20.
21.
Сначала выберем модальный интервал,
максимальная частота в нашем случае равна 10.
Таким образом, получаем:
Группы
предприятий по
стоимости ОПФ,
у.е.
Число
предприятий, f
Середина
интервалов,
х
Накопленная
частота, S
14-16
2
15
2
16-18
6
17
8
18-20
10
19
18
20-22
4
21
22
22-24
3
22
25
Итого:
25
22. Мода. Расчеты
1) По максимальной частоте найдем модальный
интервал: Fmax=10 → I = 18-20
2) По соответствующей формуле
Мода =18+2*(10-6)/(10-6)(10-4)=18,33 млн. руб.
– наиболее часто встречающаяся стоимость
ОПФ среди 25 предприятий.
23. Медиана. Расчеты:
Нам даны интервалы.
1) Найдем медианный интервал по накопленной
частоте. Нужная накопленная частота определяется
путем суммирования частот f до тех пор, пока
очередная накопленная частота впервые не
превысит половину совокупности n +1/2 или n/2.
Для нечетного ряда (25+1)/2= 13→S= 18 →18-20медианный интервал, так как в пределах этого
интервала расположена варианта, которая делит
совокупность на две равные части.
24. Медиана. Расчеты:
2) По соответствующей формуле
Медиана Ме =18+2[(25+1)/2 – 8/10]=18,9
млн.руб.
Из 25 малых предприятий региона 12 пр. имеют
стоимость ОПФ менее 18 млн.руб., а 12 пр.
более.
25. Медиана. Пример 3:
26. Решение:
Медианный интервал находится в
возрастной группе 25-30 лет, так как в
пределах этого интервала
расположена варианта,
которая делит совокупность
на две равные части
(Σfi/2 = 3462/2 = 1731).
27. Решение:
Далее подставляем в формулу необходимые
числовые данные и получаем значение медианы:
Это значит что одна половина студентов имеет
возраст до 27,4 года, а другая свыше 27,4 года.
Слайды и текст этой презентации
Слайд 1
Описание слайда:
Накопленная
частота
и др.
Расчеты,
Решение задач
Слайд 2
Описание слайда:
Предположим, есть список чисел, представляющий собой количество книг, которые каждый студент прочитал за последний месяц.
Предположим, есть список чисел, представляющий собой количество книг, которые каждый студент прочитал за последний месяц.
После сортировки у нас получился следующий набор чисел: 3, 3, 5, 6, 6, 6, 8.
Слайд 3
Описание слайда:
3, 3, 5, 6, 6, 6, 8
вверху левой колонки пишем “Количество книг”, а вверху правой колонки — “Частота”.
Во второй строке пишем первое количество прочитанных книг, то есть число 3, во второй строке колонки “Частота” пишем цифру 2.
Слайд 4
Описание слайда:
Накопленная частота отвечает на вопрос “сколько раз встречается в списке данное значение или меньшая величина?”.
Накопленная частота отвечает на вопрос “сколько раз встречается в списке данное значение или меньшая величина?”.
Всегда начинайте с наименьшего значения в наборе данных.
Поскольку в нашем примере нет меньших значений, для данной величины
накопленная частота
равна
абсолютной.
Слайд 5
Слайд 6
Описание слайда:
Чтобы определить накопленную частоту для второго значения списка, необходимо прибавить его абсолютную частоту к накопительной частоте предыдущего значения.
Чтобы определить накопленную частоту для второго значения списка, необходимо прибавить его абсолютную частоту к накопительной частоте предыдущего значения.
Иными словами, следует взять последнюю накопленную частоту и прибавить к ней абсолютную частоту данной величины.
Слайд 7
Слайд 8
Описание слайда:
Проверьте полученные результаты:
В итоге мы сложили абсолютные частоты всех значений списка.
Конечная наколенная частота должна соответствовать числу значений в списке.
Есть два способа проверить, так ли это:
Сложим абсолютные частоты всех значений:
2 + 1 + 3 + 1 = 7, в результате получится накопленная частота.
Посчитаем число значений в наборе данных.
В нашем примере список имел следующий вид: 3, 3, 5, 6, 6, 6, 8.
В этом списке семь величин, и итоговая накопленная частота также равна 7.
Слайд 9
Слайд 10
Описание слайда:
Дискретные данные
Дискретные данные можно посчитать, они не дробятся на более мелкие составляющие.
Количество собак является дискретным множеством.
Нет такого понятия, как половина собаки.
Слайд 11
Описание слайда:
Непрерывные данные
Непрерывные данные часто не поддаются конечному счету, между двумя произвольными величинами обязательно найдутся другие возможные значения.
Высота снега представляет собой непрерывное множество.
Высота снега возрастает постепенно и непрерывно, а не на дискретные величины.
Если вы измерите высоту снега в сантиметрах, то точное значение может оказаться, например, 20,6 сантиметра.
Слайд 12
Описание слайда:
Частости – это…
Существуют относительные показатели, характеризующие долю частоты отдельных вариантов в общей сумме частот.
Эти относительные показатели именуют частостями и условно обозначают через ,
т.е. .
Сумма всех частостей равна единице.
Частости могут быть выражены и в процентах, и тогда их сумма будет равна 100%.
Слайд 13
Описание слайда:
Мода и медиана
Мода – это величина признака (варианта), которая чаще всего встречается в данной совокупности, т.е. имеет наибольшую частоту.
Мода имеет большое практическое применение и в ряде случаев только мода может дать характеристику общественных явлений.
Медиана – это варианта, которая находится в середине упорядоченного (ранжированного) вариационного ряда.
Рассмотрим расчет моды и медианы в дискретном вариационном ряду:
Слайд 14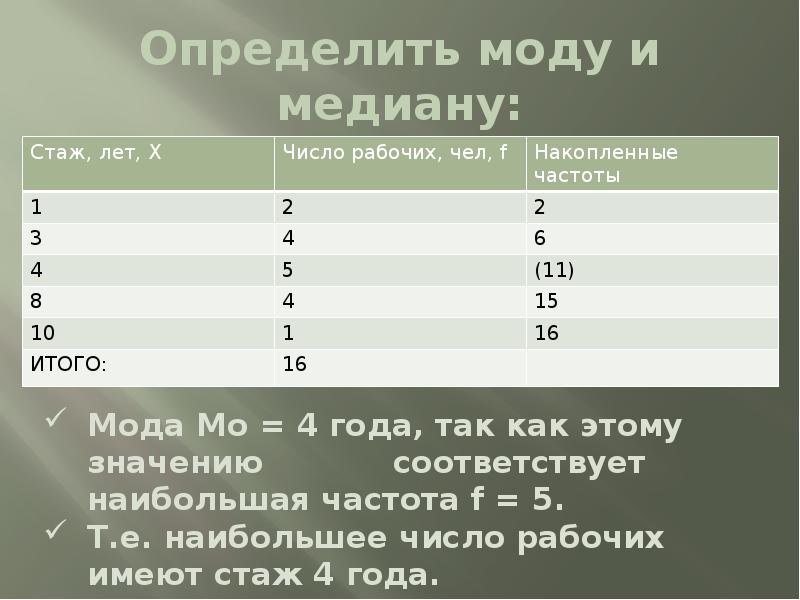
Описание слайда:
Определить моду и медиану:
Слайд 15
Описание слайда:
Медиана
Для того, чтобы вычислить медиану, найдем предварительно половину суммы частот. Если сумма частот является числом нечетным, то мы сначала прибавляем к этой сумме единицу, а затем делим пополам:
Ме=16/2=8
Медианой будет восьмая по счету варианта.
Для того, чтобы найти, какая варианта будет восьмой по номеру, будем накапливать частоты до тех пор, пока не получим сумму частот, равную или превышающую половину суммы всех частот. Соответствующая варианта и будет медианой.
Слайд 16
Описание слайда:
Медиана
Ме = 4 года.
Т.е. половина рабочих имеет стаж меньше четырех лет, половина больше.
Если сумма накопленных частот против одной варианты равна половине сумме частот, то медиана определяется как средняя арифметическая этой варианты и последующей.
Слайд 17
Описание слайда:
Свойство медианы
Главное свойство Ме в том, что сумма абсолютных отклонений значений признака от медианы меньше, чем от любой
другой величины: .
Это свойство Ме может быть использовано, например, при определении места строительства общественных зданий, т.к. Ме определяет точку, дающую наименьшее расстояние, допустим, детских садов от местожительства родителей, жителей населенного пункта от кинотеатра, при проектировке трамвайных, троллейбусных остановок и т.д.
Слайд 18
Описание слайда:
Медиана. Пример 2:
Найти медиану дискретного ряда
16,13,15,10,19,22,25,12,18,14,19,14,16,10.
Решение. Ранжируем ряд: 10,10,12,13,14,14,15,16,16,18,19,19,22,25, выборка содержит четное число элементов n=14, следовательно медиана лежит между двумя средними элементами выборки – между 7-элементом и 8-элементом:
10,10,12,13,14,14,15,16,16,18,19,19,22,25
и равна среднему арифметическому этих элементов:
Me=(15+16)/2=15,5
Слайд 19
Слайд 20
Слайд 21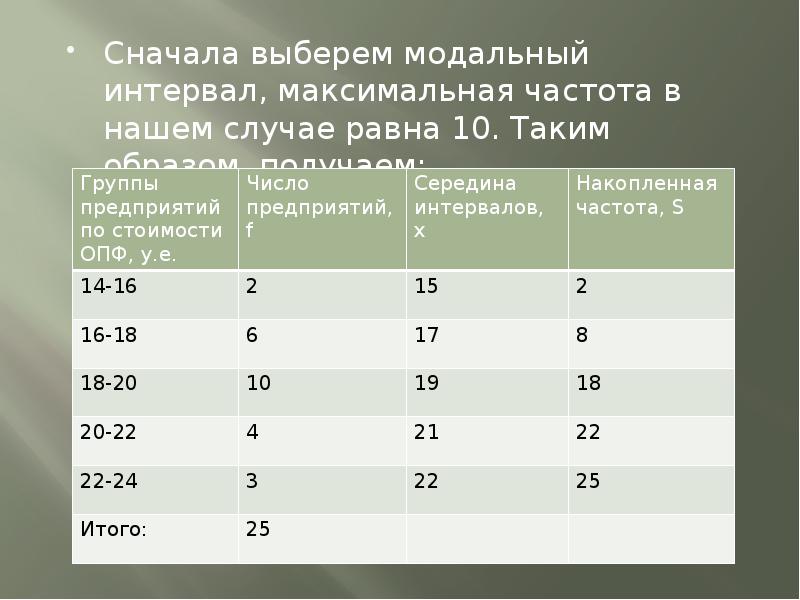
Описание слайда:
Сначала выберем модальный интервал, максимальная частота в нашем случае равна 10. Таким образом, получаем:
Сначала выберем модальный интервал, максимальная частота в нашем случае равна 10. Таким образом, получаем:
Слайд 22
Описание слайда:
Мода. Расчеты
1) По максимальной частоте найдем модальный интервал: Fmax=10 → I = 18-20
2) По соответствующей формуле
Мода =18+2*(10-6)/(10-6)(10-4)=18,33 млн. руб. – наиболее часто встречающаяся стоимость ОПФ среди 25 предприятий.
Слайд 23
Описание слайда:
Медиана. Расчеты:
Нам даны интервалы.
1) Найдем медианный интервал по накопленной частоте. Нужная накопленная частота определяется путем суммирования частот f до тех пор, пока очередная накопленная частота впервые не превысит половину совокупности n +1/2 или n/2.
Для нечетного ряда (25+1)/2= 13→S= 18 →18-20- медианный интервал, так как в пределах этого интервала расположена варианта, которая делит совокупность на две равные части.
Слайд 24![Медиана. Расчеты:
2) По соответствующей формуле
Медиана Ме =18+2[(25+1)/2 - 8/10]=18,9 млн.руб.
Из 25 малых предприятий региона 12 пр. имеют стоимость ОПФ менее 18 млн.руб., а 12 пр. более.](https://myslide.ru/documents_7/ab7f12bcab6db2fd60687dbfed8b42d0/img23.jpg)
Описание слайда:
Медиана. Расчеты:
2) По соответствующей формуле
Медиана Ме =18+2[(25+1)/2 – 8/10]=18,9 млн.руб.
Из 25 малых предприятий региона 12 пр. имеют стоимость ОПФ менее 18 млн.руб., а 12 пр. более.
Слайд 25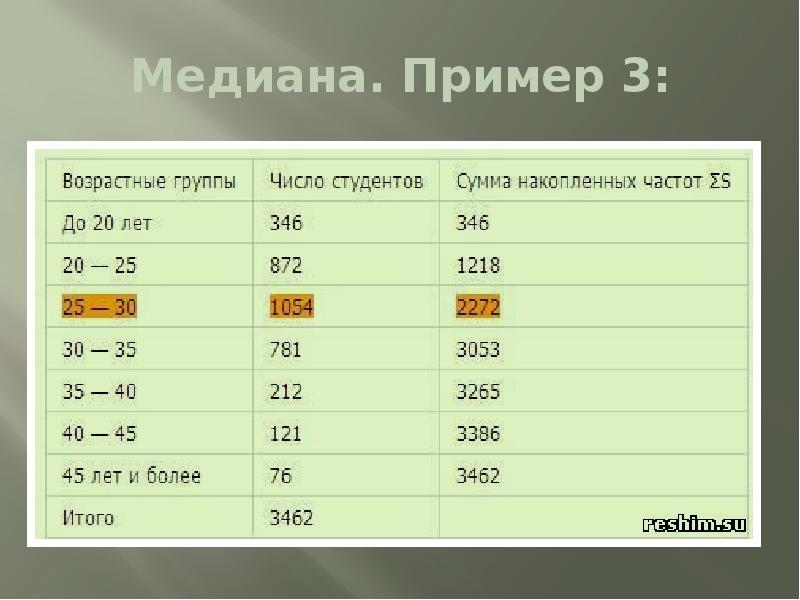
Описание слайда:
Медиана. Пример 3:
Слайд 26
Описание слайда:
Решение:
Медианный интервал находится в возрастной группе 25-30 лет, так как в пределах этого интервала расположена варианта,
которая делит совокупность
на две равные части
(Σfi/2 = 3462/2 = 1731).
Слайд 27
Описание слайда:
Решение:
Далее подставляем в формулу необходимые числовые данные и получаем значение медианы:
Слайд 28
Описание слайда:
Спасибо за внимание!
