Как найти периметр квадрата, если известна его площадь
Квадрат представляет собой правильный четырехугольник (или ромб), в котором все углы являются прямыми, а стороны равны между собой. Как и у любого иного правильного многоугольника, у квадрата можно высчитать периметр и площадь. Если площадь квадрата уже известна, то найти его стороны, а затем и периметр не составит труда.

Инструкция
Площадь квадрата находится по формуле:
S = a²
Это означает, что для того, чтобы вычислить площадь квадрата, нужно умножить длины двух его сторон друг на друга. Как следствие, если знать площадь квадрата, то при извлечении корня из данного значения можно узнать длину стороны квадрата.
Пример: площадь квадрата 36 см², чтобы узнать сторону данного квадрата, необходимо извлечь квадратный корень из значения площади. Таким образом, длина стороны данного квадрата 6 см
Для нахождения периметра квадрата необходимо сложить длины всех его сторон. С помощью формулы это можно выразить так:
P = a+a+a+a.
Если извлечь корень из значения площади квадрата, а затем сложить получившуюся величину 4 раза, то можно найти периметр квадрата.
Пример: Дан квадрат с площадью 49 см². Требуется найти его периметр.
Решение:
Сначала необходимо извлечь корень площади квадрата: √49 = 7 см
Затем, вычислив длину стороны квадрата, можно вычислить и периметр: 7+7+7+7 = 28 см
Ответ: периметр квадрата площадью 49 см² составляет 28 см
Обратите внимание
Для квадрата справедливы следующие определения:
Квадрат – это прямоугольник, который обладает равными между собой сторонами.
Квадрат – это особая разновидность ромба, у которого каждый из углов равен 90 градусам.
Являясь правильным четырехугольником, вокруг квадрата можно описать или вписать окружность. Радиус вписанной в квадрат окружность можно найти по формуле:
R = t/2, где t – сторона квадрата.
Если же окружность описана вокруг него, то ее радиус находится так:
R = (√2*t)/2
Исходя из данных формул, можно вывести новые для нахождения периметра квадрата:
P = 8*R, где R – радиус вписанной окружности;
P = 4*√2*R, где R – радиус описанной окружности.
Квадрат является уникальной геометрической фигурой, поскольку он абсолютно симметричен, независимо от того, как и где провести ось симметрии.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Лучший ответ
****Nastyusha****
Знаток
(325)
11 лет назад
площадь например: 25 значит сторона квадрата будет 5 см, а чтобы узнать периметр нужно сторону квадрата умшожить на 4
Остальные ответы
Безнадежный Романтик
Просветленный
(29859)
11 лет назад
Площадь подели на четыре
Дмитрий Чабанов
Знаток
(262)
11 лет назад
периметр равен сумме всех сторон
сторона равна квадратному корню из площади
Вера Вера
Знаток
(408)
11 лет назад
Площадь квадрата равна: сторона в квадрате. Зная площадь, можно узнать чему равна одна сторона (извлечь кв. корень) , потом умножить на четыре.
Введите данные:
Достаточно ввести только одно значение, остальное калькулятор посчитает сам.
Cторона квадрата, диаметр вписанной окружности (L)
Диагональ квадрата, диаметр описанной окружности (M)
Радиус вписанной окружности (R1)
Радиус описанной окружности (R2)
Округление:
* – обязательно заполнить
Площадь (S) = 10
Cторона, диаметр вписанной окружности (L) = (sqrt{S}) = (sqrt{10}) = 3.16
Диагональ, диаметр описанной окружности (M) = (sqrt{2*L^{2}}) = (sqrt{2*3.16^{2}}) = 4.47
Радиус вписанной окружности (R1) = (frac{L}{2}) = (frac{3.16}{2}) = 1.58
Радиус описанной окружности (R2) = (frac{M}{2}) = (frac{4.47}{2}) = 2.24
Периметр (P) = (L*4) = (3.16*4) = 12.64
Совет 1: Как обнаружить периметр квадрата, если знаменита его площадь
Квадрат представляет собой положительный четырехугольник (либо ромб), в котором все углы являются прямыми, а стороны равны между собой. Как и у всякого другого верного многоугольника, у квадрата дозволено высчитать периметр и площадь. Если площадь квадрата теснее знаменита, то обнаружить его стороны, а после этого и периметр не составит труда.

Инструкция
1. Площадь квадрата находится по формуле:S = a?Это обозначает, что для того, дабы вычислить площадь квадрата , надобно умножить длины 2-х его сторон друг на друга. Как следствие, если знать площадь квадрата , то при извлечении корня из данного значения дозволено узнать длину стороны квадрата .Пример: площадь квадрата 36 см?, дабы узнать сторону данного квадрата , нужно извлечь квадратный корень из значения площади. Таким образом, длина стороны данного квадрата 6 см
2. Для нахождения периметр а квадрата нужно сложить длины всех его сторон. С подмогой формулы это дозволено выразить так:P = a+a+a+a.Если извлечь корень из значения площади квадрата , а после этого сложить получившуюся величину 4 раза, то дозволено обнаружить периметр квадрата .
3. Пример: Дан квадрат с площадью 49 см?. Требуется обнаружить его периметр .Решение:Вначале нужно извлечь корень площади квадрата : ?49 = 7 смЗатем, вычислив длину стороны квадрата , дозволено вычислить и периметр : 7+7+7+7 = 28 смОтвет: периметр квадрата площадью 49 см? составляет 28 см
Совет 2: Как обнаружить сторону квадрата
Зачастую в геометрических задачах требуется обнаружить длину стороны квадрата, если вестимы другие его параметры – такие, как площадь, диагональ либо периметр.
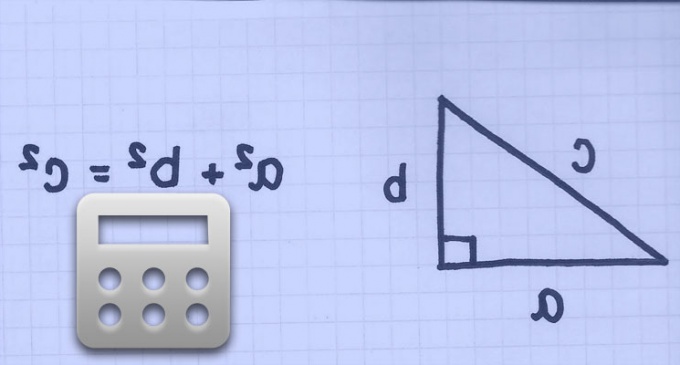
Вам понадобится
- Калькулятор
Инструкция
1. Если вестима площадь квадрата, то для того, дабы обнаружить сторону квадрата, нужно извлечь квадратный корень из числового значения площади (потому что площадь квадрата равняется квадрату его стороны):a=?S, гдеa – длина стороны квадрата;S – площадь квадрата.Единицей измерения стороны квадрата будет являться линейная единица измерения длины, соответствующая единице измерения площади. Скажем, если площадь квадрата дана в сантиметрах квадратных, то длина его стороны получится примитивно в сантиметрах.Пример:Площадь квадрата составляет 9 квадратных метров.Обнаружить длину стороны квадрата.Решение:a=?9=3Ответ:Сторона квадрата равняется 3 метрам.
2. В том случае, когда знаменит периметр квадрата, для определения длины стороны необходимо числовое значение периметра поделить на четыре (потому что квадрат имеет четыре стороны идентичной длины):a=P/4, где:a – длина стороны квадрата;P – периметр квадрата.Единицей измерения стороны квадрата будет являться та же самая линейная единица измерения длины как и у периметра. Скажем, если периметр квадрата задан в сантиметрах, то длина его стороны также получится в сантиметрах.Пример:Периметр квадрата составляет 20 метров.Обнаружить длину стороны квадрата.Решение:a=20/4=5Ответ:Длина стороны квадрата равняется 5 метрам.
3. Если знаменита длина диагонали квадрата, до длина его стороны будет равняться длине его диагонали, поделенной на корень квадратный из 2 (по теореме Пифагора, потому что смежные стороны квадрата и диагональ составляют прямоугольный равнобедренный треугольник):a=d/?2(т.к. a^2+a^2=d^2), где:a – длина стороны квадрата;d – длина диагонали квадрата.Единицей измерения стороны квадрата будет являться единица измерения длины та же самая, что и у диагонали. Скажем, если диагональ квадрата измерена в сантиметрах, то и длина его стороны получится в сантиметрах.Пример:Диагональ квадрата равняется 10 метров.Обнаружить длину стороны квадрата.Решение:a=10/?2, либо примерно: 7,071Ответ:Длина стороны квадрата равняется 10/?2, либо приблизительно 1,071 метра.
Совет 3: Как находить периметр квадрата
Квадрат – прекрасная и простая плоская геометрическая фигура. Это прямоугольник с равными сторонами. Как же обнаружить периметр квадрата , если знаменита длина его стороны?

Инструкция
1. Раньше каждого, стоит припомнить, что периметр есть ни что иное как сумма длин сторон геометрической фигуры. Рассматриваемый нами квадрат имеет четыре стороны. Больше того, по определению квадрата , все эти стороны равны между собой.Из этих предпосылок вытекает простая формула для нахождения периметр а квадрата – периметр квадрата равен длине стороны квадрата , умноженной на четыре:Р = 4а, где а – длина стороны квадрата .
Видео по теме
Совет 4: Как обнаружить длину квадрата
Периметром называют всеобщую длину границы фигуры почаще каждого на плоскости. Квадрат — положительный четырехугольник либо ромб, у которого все углы прямые, либо параллелограмм, у которого все стороны и углы равны.

Вам понадобится
- Знания по геометрии.
Инструкция
1. Периметр квадрата равен сумме длин его сторон. Потому что квадрат, по своей сути, есть четырехугольник, то и сторон у него четыре, а значит периметр равен сумме длин четырех сторон либо P = a+b+c+d.
2. Квадрат, как видно из определения, верная геометрическая фигура, а это значит, что все его стороны равны. Значит a=b=c=d. Следственно P = a+a+a+a либо P = 4*a.
3. Пускай сторона квадрата равна 4, то есть a=3. Тогда периметр либо длина квадрата , по полученной формуле, будет равен P = 4*3 либо P=12. Число 12 и будет являться длиной либо, что одно и тоже, периметром квадрата .
Видео по теме
Обратите внимание!
Периметр квадрата величина неизменно правильная, как и любая иная длина.
Полезный совет
Аналогичным образом дозволено обнаружить и периметр ромба, потому что квадрат является частным случаем ромба с прямыми углами.
Совет 5: Как высчитывать периметр
Периметр характеризует длину замкнутого силуэта. Как и площадь, он может быть обнаружен по иным величинам, приведенным в условии задачи. Задачи на нахождении периметра крайне зачастую встречаются в школьном курсе математики.
Инструкция
1. Зная периметр и сторону фигуры, дозволено обнаружить иную ее сторону, а также площадь. Сам же периметр, в свою очередь, может быть обнаружен по нескольким заданным сторонам либо по углу и сторонам, в зависимости от условий задачи. Также в ряде случаев его выражают через площадь. Особенно примитивно находится периметр прямоугольника. Начертите прямоугольник с одной из сторон, равной а, и диагональю, равной d. Зная эти две величины, обнаружьте по теореме Пифагора иную его сторону, которая является шириной прямоугольника. Обнаружив ширину прямоугольника, вычислите его периметр дальнейшим образом: p=2(a+b). Эта формула объективна для всех прямоугольников, от того что у всякого из них четыре стороны.
2. Обратите внимание на тот факт, что периметр треугольника в большинстве задач находят при наличии информации правда бы об одном его угле. Впрочем, имеются и задачи, в которых все стороны треугольник знамениты, и тогда периметр может быть вычислен простым суммированием, без применения тригонометрических вычислений: p=a+b+c, где a, b и c – стороны. Но такие задачи встречаются в учебниках редко, от того что метод их решения явствен. Больше трудные задачи по нахождению периметра треугольника решайте поэтапно. Скажем, начертите равнобедренный треугольник, у которого знамениты основание и угол при нем. Для того дабы обнаружить его периметр, сначала обнаружьте стороны a и b дальнейшим образом: b=c/2cos?. От того что a=b (треугольник равнобедренный), сделайте дальнейший итог: a=b=c/2cos?.
3. Периметр многоугольника вычисляйте аналогичным образом, складывая длины всех его сторон: p=a+b+c+d+e+f и так дальше. Если многоугольник положительный и вписан в окружность либо описан около нее, вычислите длину одной из его сторон, а после этого умножьте на их число. Скажем, дабы обнаружить стороны шестиугольника, вписанного в окружность, действуйте дальнейшим образом: a=R, где a – сторона шестиугольника, равная радиусу описанной окружности. Соответственно, если шестиугольник верный, то его периметр равен: p=6a=6R. Если окружность вписана в шестиугольник, то сторона последнего равна: a=2r?3/3. Соответственно, периметр такой фигуры обнаружьте дальнейшим образом: p=12r?3/3.
Совет 6: Как вычислить периметр квадрата
Хоть слово «периметр» и случилось от греческого обозначения окружности, им принято называть суммарную длину границ всякий плоской геометрической фигуры, включая квадрат. Вычисление этого параметра, как водится, трудности не представляет и может быть осуществлено несколькими методами, в зависимости от знаменитых начальных данных.
Инструкция
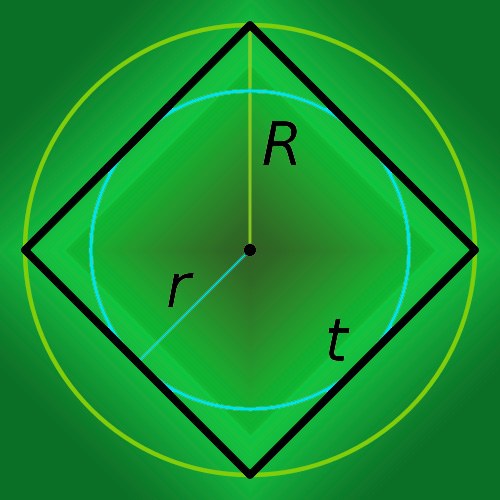
1. Если вестима длина стороны квадрата (t), то для нахождения его периметра (p) примитивно увеличьте эту величину в четыре раза: p=4*t.
2. Если длина стороны незнакома, но в условиях задачи дана длина диагонали (c), то этого довольно для вычисления длины сторон, а следственно и периметра (p) многоугольника. Используйте теорему Пифагора, которая заявляет, что квадрат длины длинной стороны прямоугольного треугольника (гипотенузы) равен сумме квадратов длин коротких сторон (катетов). В прямоугольном треугольнике, составленном из 2-х смежных сторон квадрата и соединяющего их крайние точки отрезка, гипотенуза совпадает с диагональю четырехугольника. Из этого вытекает, что длина стороны квадрата равна отношению длины диагонали к квадратному корню из двойки. Используйте это выражение в формуле для вычисления периметра из предыдущего шага: p=4*c/?2.
3. Если дана лишь площадь (S) ограниченного периметром квадрата участка плоскости, то и этого будет довольно, дабы определить длину одной стороны. Потому что площадь всякого прямоугольника равна произведению длин его смежных сторон, то для нахождения периметра (p) извлеките квадратный корень из площади, а итог увеличьте в четыре раза: p=4*?S.
4. Если знаменит радиус описанной вблизи квадрата окружности (R), то для нахождения периметра многоугольника (p) умножьте его на восемь и поделите полученный итог на квадратный корень из двойки: p=8*R/?2.
5. Если окружность, радиус которой вестим, вписана в квадрат, то вычисляйте его периметр (p) простым умножением радиуса (r) на восьмерку: P=8*r.
6. Если рассматриваемый квадрат в условиях задачи описан координатами своих вершин, то для вычисления периметра вам потребуются данные лишь о 2-х вершинах, принадлежащих к одной из сторон фигуры. Определите длину этой стороны, исходя из все той-же теоремы Пифагора для треугольника, составленного из нее самой и ее проекций на оси координат, а полученный итог увеличьте в четыре раза. Потому что длины проекций на координатные оси равны модулю разностей соответствующих координат 2-х точек (X?;Y? и X?;Y?), то формулу дозволено записать так: p=4*?((X?-X?)?+(Y?-Y?)?).
Совет 7: Что такое периметр
Периметром в всеобщем случае называют длину линии, которая ограничивает замкнутую фигуру. Для многоугольников периметром является сумма всех длин сторон. Эту величину дозволено измерить, а для многих фигур и легко рассчитать, если вестимы длины соответствующих элементов.

Вам понадобится
- – линейка либо рулетка;
- – крепкая нить;
- – роликовый дальномер.
Инструкция
1. Дабы измерить периметр произвольного многоугольника, измерьте при помощи линейки либо иным измерительным прибором все его стороны, а после этого обнаружьте их сумму. Если дан четырехугольник со сторонами 5, 3, 7 и 4 см, которые измерены линейкой, обнаружьте периметр, сложив их совместно Р=5+3+7+4=19 см.
2. Если же фигура произвольная и включает в себя не только прямые линии, то измерьте ее периметр традиционной веревкой либо ниткой. Для этого расположите ее так, дабы она верно повторяла все линии, ограничивающие фигуру, и сделайте на ней отметку, если дозволено, примитивно обрежьте ее дабы избежать путаницы. После этого при помощи рулетки либо линейки, измерьте длину нитки, она и будет равна периметру данной фигуры. Непременно следите за тем, дабы нить максимально верно повторяла линию для большей точности итога.
3. Периметр трудной геометрической фигуры измеряйте роликовым дальномером (курвиметром). Для этого не линии намечается точка, в которую устанавливается ролик дальномера и прокатывается по ней, до возвращения в начальную точку. Дистанция, измеренная роликовым дальномером, и будет равна периметру фигуры.
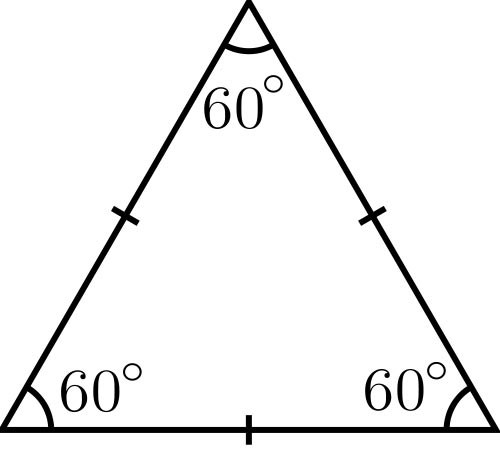
4. Периметр некоторых геометрических фигур вычисляйте. Скажем, дабы обнаружить периметр всякого положительного многоугольника (выпуклого многоугольника, стороны которого равны), длину стороны умножьте на число углов либо сторон (они равны). Дабы обнаружить периметр верного треугольника со стороной 4 см умножьте это число на 3 (Р=4?3=12 см).
5. Дабы обнаружить периметр произвольного треугольника, сложите длины всех его сторон. Если не даны все стороны, а есть углы между ними, обнаружьте их по теореме синуса либо косинуса. Если знамениты две стороны прямоугольного треугольника, третью обнаружьте по теореме Пифагора и обнаружьте их сумму. Скажем, если знаменито, что катеты прямоугольного треугольника равны 3 и 4 см, то гипотенуза будет равна ?(3?+4?)=5 см. Тогда периметр Р=3+4+5=12 см.
6. Дабы обнаружить периметр круга, обнаружьте длину окружности, которая его ограничивает. Для этого ее радиус r умножьте на число ??3,14 и число 2 (P=L=2???r). Если знаменит диаметр, рассматривайте, что он равен двум радиусам.
Совет 8: Как обнаружить периметр верного многоугольника
Периметром многоугольника называют замкнутую ломаную линию, составленную из всех его сторон. Нахождение длины этого параметра сводится к суммированию длин сторон. Если все отрезки, образующие периметр такой двухмерной геометрической фигуры, имеют идентичные размеры, многоугольник именуется верным. В этом случае вычисление периметра гораздо упрощается.
Инструкция
1. В самом простом случае, когда вестимы длина стороны (а) верного многоугольника и число вершин (n) в нем, для вычисления длины периметра (Р) примитивно перемножьте эти две величины: Р = а*n. Скажем, длина периметра верного шестиугольника со стороной в 15 см должна быть равна 15*6=90 см.
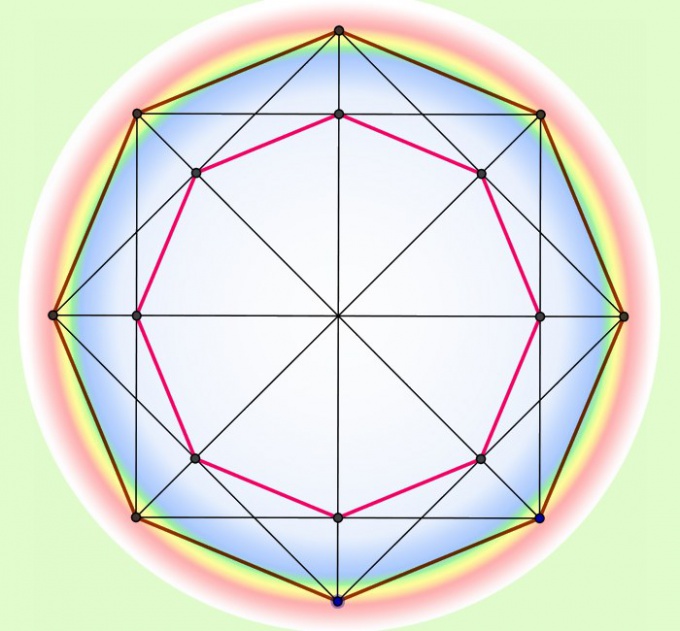
2. Вычислить периметр такого многоугольника по вестимому радиусу (R) описанной около него окружности тоже допустимо. Для этого придется вначале выразить длину стороны с применением радиуса и числа вершин (n), а после этого умножить полученную величину на число сторон. Дабы рассчитать длину стороны умножьте радиус на синус числа Пи, поделенного на число вершин, а итог удвойте: R*sin(?/n)*2. Если вам комфортнее вычислять тригонометрическую функцию в градусах, замените число Пи на 180°: R*sin(180°/n)*2. Периметр вычислите умножением полученной величины на число вершин: Р = R*sin(?/n)*2*n = R*sin(180°/n)*2*n. Скажем, если шестиугольник вписан в круг с радиусом 50 см, его периметр будет иметь длину 50*sin(180°/6)*2*6 = 50*0,5*12 = 300 см.
3. Схожим методом дозволено посчитать периметр, не зная длины стороны положительного многоугольника , если он описан около окружности с знаменитым радиусом (r). В этом случае формула для вычисления размера стороны фигуры будет отличаться от предыдущей лишь задействованной тригонометрической функцией. Замените в формуле синус на тангенс, дабы получить такое выражение: r*tg(?/n)*2. Либо для расчетов в градусах: r*tg(180°/n)*2. Для вычисления периметра увеличьте полученную величину в число раз, равное числу вершин многоугольника : Р = r*tg(?/n)*2*n = r*tg(180°/n)*2*n. Скажем, периметр восьмиугольника, описанного вблизи круга с радиусом в 40 см, будет примерно равен 40*tg(180°/8)*2*8 ? 40*0,414*16 = 264,96 см.
Совет 9: Как обнаружить площадь и периметр квадрата
Квадрат представляет собой геометрическую фигуру, состоящую из четырех сторон идентичной длины и четырех прямых углов, всякий из которых равен 90°. Определение площади либо периметра четырехугольника, причем всякого, требуется не только при решении задач по геометрии, но и в повседневной жизни. Эти знания могут стать пригодными, скажем, во время ремонта при расчете необходимого числа материалов – покрытий для пола, стен либо потолка, а также для разбивки газонов и грядок и т.д.

Инструкция
1. Для определения площади квадрата умножьте величину длины на величину ширины. Потому что в квадрате длина и ширина идентичны, то значение одной стороны довольно построить в квадрат. Таким образом, площадь квадрата равна длине его стороны, возведенной в квадрат. Единицей измерения площади могут быть квадратные миллиметры, сантиметры, дециметры, метры, километры.Дабы определить площадь квадрата, дозволено воспользоваться формулойS = aa, где S – площадь квадрата,а – сторона квадрата.
2. Пример № 1. Комната имеет форму квадрата. Сколько ламината (в кв.м) понадобится для того, дабы всецело покрыть пол, если длина одной стороны комнаты составляет 5 метров.Запишите формулу: S = aa. Подставьте в нее указанные в условии данные.Потому что а = 5 м, следственно, площадь будет равнаS (комнаты) = 5х5= 25 кв.м, значит, и S (ламината) = 25 кв.м.
3. Периметр представляет собой всеобщую длину границы фигуры. В квадрате периметр – это длина всех четырех, причем идентичных, сторон. То есть, периметр квадрата представляет собой сумму всех его четырех сторон. Дабы вычислить периметр квадрата, довольно знать длину одной его стороны. Измеряется периметр в миллиметрах, сантиметрах, дециметрах, метрах, километрах.Для определения периметра имеется формула:P = a + а + а + а илиP = 4a, гдеР – периметр,а – длина стороны.
4. Пример № 2. Для отделочных работ помещения в форме квадрата требуются потолочные плинтуса. Вычислите всеобщую длину (периметр) плинтусов, если величина одной стороны комнаты равна 6 метров. Запишите формулу P = 4a.Подставьте в нее указанные в условии данные:Р (комнаты) = 4 х 6 = 24 метра.Следственно, длина потолочных плинтусов тоже будет равна 24 метров.
Видео по теме
Обратите внимание!
Для квадрата объективны следующие определения:Квадрат – это прямоугольник, тот, что владеет равными между собой сторонами.Квадрат – это специальная разновидность ромба, у которого весь из углов равен 90 градусам.Являясь положительным четырехугольником, вокруг квадрата дозволено описать либо вписать окружность. Радиус вписанной в квадрат окружность дозволено обнаружить по формуле:R = t/2, где t – сторона квадрата.Если же окружность описана вокруг него, то ее радиус находится так:R = (?2*t)/2Исходя из данных формул, дозволено вывести новые для нахождения периметра квадрата:P = 8*R, где R – радиус вписанной окружности;P = 4*?2*R, где R – радиус описанной окружности.Квадрат является уникальной геометрической фигурой, от того что он безусловно симметричен, самостоятельно от того, как и где провести ось симметрии.
Периметр квадрата калькулятор онлайн умеет вычислять периметр пятью способами:
- По стороне квадрата.
- По диагонали квадрата.
- По площади квадрата.
- По радиусу описанной окружности.
- По радиусу вписанной окружности.
Сделав расчет периметра на этом онлайн калькуляторе Вы получите не только ответ, но и детальное, пошаговое решение с выводом формул и промежуточных действий.
Периметр квадрата – это сумма четырех его сторон.
Так как у квадрата все стороны равны, то для вычисления периметра достаточно знать длину всего одной стороны.
Периметр может быть найден и по другим формулам, например через диагональ или площадь квадрата. В этих случаях сначала находится длина одной стороны квадрата, а затем и сам периметр.
Как найти периметр квадрата?
Найти периметр квадрата очень просто на нашем онлайн калькуляторе. Так же периметр может быть найден самостоятельно по формулам. Выбор нужной формулы зависит от того какие данные известны.
1) По стороне
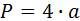
где а – сторона квадрата.
2) По диагонали
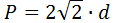
где d – диагональ квадрата.
3) По площади
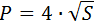
где S – площадь квадрата.
4) По радиусу описанной окружности
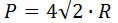
где R – радиус описанной окружности.
5) По радиусу вписанной окружности
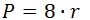
где r – радиус вписанной окружности.
Скачать все формулы в формате Word/PDF
