Натуральное уравнение кривой как найти - Сайт, где вы сможете решить свои вопросы

Содержание

Кривизна и кручение. Натуральные уравнения кривой

Краткие теоретические сведения

Кривизна кривой

Кривизной $k$ кривой в данной точке называют модуль скорости вращения касательной по отношению к длине дуги.

Регулярная дважды дифференцируемая без особых точек кривая $gamma$, заданная векторной функцией $vec{r}=vec{r}(t)$, имеет в каждой точке определенную кривизну, причем
$$
|k(t)|=frac{|vec{r’}(t)times vec{r”}(t)|}{|vec{r'(t)}|^3}.
$$

Для кривой, заданной параметрически
$$ x=x(t), ,, y=y(t), ,, z=z(t), $$
кривизна в точке $P(t=t_0)$ находится по формуле:
$$
k^2(t_0)=frac{left| begin{array}{cc}
y’ & z’ \
y”& z” \
end{array}
right|^2+left| begin{array}{cc}
z’ & x’ \
z”& x” \
end{array}
right|^2+left| begin{array}{cc}
x’ & y’ \
x” & y” \
end{array}
right|^2}{Bigl((x’)^2+(y’)^2+(z’)^2Bigr)^3},
$$
где все производные вычисляются при $t=t_0$.

Если кривая задана естественной параметризацией $vec{r}=vec{r}(s)$, то векторы $vec{r’}(s)$ и $vec{r”}(s)$ перпендикулярны, причем $|vec{r’}(s)|=1$. Тогда выражение для кривизны принимает вид:
$$
k(s)= |vec{r”}(s)|.
$$

Что вы скажете о кривой, которая в каждой свой точке имеет нулевую кривизну?

Для плоской кривой, лежащей в плоскости $(xy)$, кривизну можно найти по формулам:
$$
begin{array}{rl}
x=x(t), y=y(t):& k = displaystylefrac{|x’y”-x”y’|}{left((x’)^2+(y’)^2right)^{3/2}}, \
y=y(x):& k = displaystylefrac{|y”|}{left(1+(y’)^2right)^{3/2}}, \
rho=rho(varphi):& k = displaystylefrac{|rho^2+2(rho’)^2-rhorho”|}{left(rho^2+(rho’)^2right)^{3/2}}.\
end{array}
$$

Кручение

Абсолютным кручением $varkappa$ кривой называют скорость вращения соприкасающейся плоскости вокруг касательной.
$$
|varkappa (t)|=frac{|(vec{r’}(t), vec{r”}(t), vec{r”’}(t))|}{|vec{r’}(t)times vec{r”}(t)|^2}.
$$

В случае естественной параметризации
$$
|varkappa(s)|=frac{|(vec{r’}(s), vec{r”}(s), vec{r”’}(s))|}{k^2(s)}
$$

Для плоской кривой кручение равно нулю: $varkappa=0$!

Натуральные уравнения кривой

Если кривая задана естественной параметризацией $vec{r}=vec{r}(s)$, то кривизна и кручение будут являться функциями длины дуги
$$
k=k(s), quad varkappa=varkappa(s).
$$
Система этих двух соотношений называется натуральными уравнениями кривой.

Натуральные уравнения полностью определяют форму кривой, ибо связывают инварианты, которые не меняются при преобразовании координат (при изменении положения указанной кривой в пространстве относительно системы координат).

Решение задач

Задача 1 (Феденко №351)

Найдите кривизну кривой:
$$
x=a,mbox{cos}^3t,,,y=a,mbox{sin}^3t.
$$

Задача 2 (Феденко №380)

Найдите параболу $y=ax^2+bx+c$, имеющую с синусоидой $y=mbox{sin}x$ в точке $A(pi/2,1)$ общие касательную и кривизну.

Задача 3 (Феденко №405)

Составьте натуральные уравнения кривой:
$$
x=a(mbox{cos},t+t,mbox{sin},t), ,, y=a(mbox{sin},t-t,mbox{cos},t).
$$

Краткое решение задачи 3

$$
s=frac{at^2}{2}.
$$

$$
k=frac{1}{at}.
$$

$$
t=frac{1}{ak} Rightarrow s= frac{1}{2ak^2}.
$$

Натуральные уравнения:
$$
k=frac{1}{at},,,s=frac{at^2}{2}
$$
или
$$
k^2=frac{1}{2as}.
$$

Феденко записывает ответы через радиус кривизны:
$R=frac{1}{k}$.

Задача 4 (Феденко №486, №514)

Найдите кривизну и кручение, составьте натуральные уравнения кривой:
$$
x=a,mbox{ch}t, , y=a,mbox{sh}t, , z=a, t.
$$

Решение задачи 4

Задачу можно решать двумя способами:

1 способ. Найти $k(t), varkappa(t), s(t)$.

2 способ. Сначала найти выразить $t$ через $s$ и записать естественную параметризацию кривой $vec{r}=vec{r}(s)$. А далее найти $k(s)$ и $varkappa(s)$.

Воспользуемся первым способом.
begin{gather*}
vec{r}(t_0)={a,mbox{ch}t, , a,mbox{sh}t, , at},\
vec{r’}(t_0)={a,mbox{sh}t, , a,mbox{ch}t, , a},\
vec{r”}(t_0)={a,mbox{ch}t, , a,mbox{sh}t, , 0}\
vec{r”’}(t_0)={a,mbox{sh}t, , a,mbox{ch}t, , 0}.
end{gather*}

$$
Rightarrow quad k^2(t) = frac{1}{4a^2mbox{ch}^4t}.
$$
$$
Rightarrow quad k(t) = frac{1}{2a,mbox{ch}^2t}.
$$

begin{equation*}
varkappa(t) = frac{ left|
begin{array}{ccc}
a,mbox{sh}t & a,mbox{ch}t & a \
a,mbox{ch}t & a,mbox{sh}t & 0 \
a,mbox{sh}t & a,mbox{ch}t & 0 \
end{array}
right|}{a^4cdot 2mbox{ch}^2t} = frac{1}{2a,mbox{ch}^2t}.
end{equation*}

В задаче №473 была та же кривая и мы получили, что
$$s=asqrt{2},mbox{sh},t.$$
Используя тождества для гиперболических функций, выразим $t$ через $s$ и подставим их в выражения для кривизны и кручения:
begin{equation*}
s=asqrt{2},mbox{sh}t=asqrt{2},sqrt{mbox{ch}^2t-1} ,, Rightarrow ,, mbox{ch}^2t=frac{s^2}{2a^2}+1 ,, Rightarrow
end{equation*}
begin{equation*}
k(s)=varkappa(s)=frac{1}{2a,mbox{ch}^2t} = frac{a}{s^2+2a^2}.
end{equation*}

Вычисления сделаны для $a>0$.

Задача 5 (Феденко №496)

Найдите функцию $f(t)$, для которой данная кривая — плоская:
$$
vec{r}(t)={a,mbox{cos}t, , a,mbox{sin}t, , f(t)}
$$

Решение задачи 5

$$
begin{array}{lll}
x=a,mbox{cos}t,, &y=a,mbox{sin}t, , &z=f(t),\
x’=-a,mbox{sin}t, , &y’=a,mbox{cos}t, , &z’=f'(t),\
x”=-a,mbox{cos}t, , &y”=-a,mbox{sin}t, , &z”=f”(t),\
x”’=a,mbox{sin}t, , &y”’=-a,mbox{cos}t, , &z”’=f”'(t).
end{array}
$$

Для плоской кривой кручение равно нулю:
begin{equation*}
varkappa(t) = left|
begin{array}{rrr}
-a,mbox{sin}t & a,mbox{cos}t & f'(t) \
-a,mbox{cos}t & -a,mbox{sin}t & f”(t) \
a,mbox{sin}t & -a,mbox{cos}t & f”'(t) \
end{array}
right| = left( f'(t) + f”'(t) right)cdot2a^2=0.
end{equation*}
begin{equation*}
f'(t)=-f”'(t) quad Rightarrow quad f(t)=c_1+c_2,mbox{sin}t+c_3,mbox{cos}t.
end{equation*}

Как найти уравнение плоскости, в которой лежит кривая?

Известно, что плоская кривая лежит в своей соприкасающейся плоскости!
Второй способ — составить уравнение плоскости по трем точкам.

Источник

Натуральные уравнения — соотношения на кривизну и кручение бирегулярных кривых. Замечательное свойство натуральных уравнений в том, что по ним можно однозначно восстановить кривую.
Натуральные уравнения, уравнения, выражающие кривизну и кручение кривой как функции её дуги: , . Наименование «Натуральные уравнения» объясняется тем обстоятельством, что функции и не зависят от положения кривой в пространстве (от выбора системы координат), а зависят только от формы кривой. Две трижды непрерывно дифференцируемые кривые, имеющие одинаковые натуральные уравнения, могут отличаться друг от друга только положением в пространстве. Иначе говоря, форма кривой однозначно определяется её натуральными уравнениями. Если заданы две непрерывные функции и , из которых первая положительная, то всегда существует кривая, для которой данные функции являются соответственно кривизной и кручением.

Натуральные уравнения плоских кривых[править | править код]

Пусть f(s) — произвольная гладкая функция. В таком случае существует кривая gamma , единственная с точностью до сохраняющего ориентацию движения плоскости, параметризованная натуральным параметром и такая, что ${displaystyle f(s)=k_{o}(s)}$ во всех точках кривой. Здесь величина ${displaystyle k_{o}(s)}$ — ориентированная кривизна кривой gamma .

Натуральные уравнения в трехмерном пространстве[править | править код]

Пусть f(s) и g(s) — две произвольные гладкие функции, причём f(s) положительна. Тогда существует кривая gamma , параметризованная натуральным параметром , кривизна и кручение которой равны в каждой точке f(s) и g(s) соответственно. Такая кривая единственна с точностью до движения пространства, сохраняющего ориентацию.

Источник

Макеты страниц

Кривизна и кручение описывают кривую в определенном смысле единственным образом.

ТЕОРЕМА 8. Пусть функции имеют на сегменте непрерывные производные. Тогда существует единственная с точностью до положения в пространстве -регулярная кривая, кривизна и кручение которой в точке, отвечающей длине дуги равны соответственно

Будем рассматривать формулы Френе

как систему обыкновенных линейных дифференциальных уравнений относительно неизвестных функций

В качестве начальных данных для системы (7) выберем единичные попарно ортогональные векторы образующие правую тройку:

При сформулированных условиях согласно теореме существования и единственности решения задачи Коши для системы обыкновенных дифференциальных уравнений существует единственное решение системы (7) класса на сегменте удовлетворяющее начальным условиям

Рис. 24. Проекция кривой на спрямляющую плоскость близка к кубической параболе

Рис. 25. Винтовая линия

Докажем, что для любого векторы являются единичными, попарно ортогональными и образуют правую тройку.

Составим систему шести линейных дифференциальных уравнений относительно шести неизвестных скалярных функций следующим образом.

Умножим первое из уравнений (7) на вектор Получим или Это и есть первое из интересующих нас уравнений. Аналогично строятся уравнения

Чтобы построить четвертое уравнение, умножим первое из уравнений (7) скалярно на вектор второе — на вектор и сложим полученные результаты:

Аналогично строятся оставшиеся два уравнения

Полученная система шести уравнений является следствием системы (7). Поэтому набор функций

является ее решением и, кроме того, удовлетворяет условиям (11). Этой же системе и начальным условиям (11) удовлетворяет набор

Вследствие того что начальные условия однозначно определяют решение системы, получаем

Это означает, что векторы единичные и попарно ортогональные. Поэтому их смешанное произведение равно

Поскольку это произведение непрерывно и равно при то оно равно при любом Тем самым векторы образуют правую тройку.

Рассмотрим кривую L с радиус-вектором

Так как то длина дуги кривой

Найдем кривизну и кручение этой кривой. Используя первое из соотношений (7), по формуле (1) для кривизны имеем

Кручение вычислим по форглуле (3), используя соотношения (7) и только что полученную формулу

Итак, кривизна и кручение кривой L в точке, отвечающей ее длине дуги равны соответственно

Докажем теперь, что если кривизна и кручение некоторой другой кривой L равны то она отличается от кривой L только положением в пространстве.

Переместим кривую L в пространстве так, чтобы ее векторы при совпали с векторами кривой Убедимся, что перемещенная кривая L и кривая L совпадают.

Векторы кривой L являются решениями системы (7) (для кривой L это формулы Френе) с начальными данными По теореме единственности имеем

Поэтому а так как то

Замечание 1. Функции могут быть заданы и на другом множестве, например на полупрямой или на прямой

Замечание 2. Систему соотношений

называют натуральными уравнениями кривой. Согласно доказанной теореме кривая определяется натуральными уравнениями однозначно с точностью до положения в пространстве.

Пример. Найти кривизну и кручение винтовой линии

Так как

т. е. кривизна и кручение у винтовой линии постоянны.

Этим свойством обладают только винтовые линии.

Источник

Лекция 3

Формулы Френе.
Кривизна и кручение кривой в произвольной
параметризации. Винтовая линия.

Р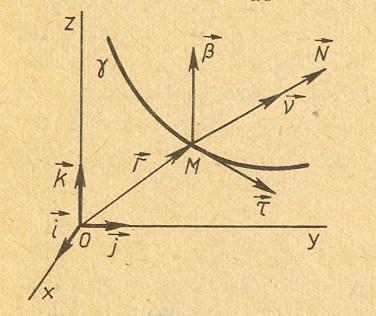ассмотрим
векторы

гладкой линии

заданной естественной параметризацией
.

1). Так как
то
(1)

2). Вектор

– единичный вектор гладкой нормали

параллелен
спрямляющей плоскости

3).
.
В (1) заменяем

и

по формулам (3) и (2). Получим

Подставим выражение

в (2).

4).
.
Дифференцируем по s:

=
.
Заменим

и

их выражениями по (3) и (4):

Формулы (3),(4),(5)
называются формулами Френе, которые
рассматривают связь между базисными
векторами сопровождающими треугольниками,
кручением и кривизной линии.

Определение 3.1.
Число

называется кручением линии

в точке М
на всей линии
.
Кручение есть функция параметра S.

Исходя из (5) и так
как
–
единичный вектор, то
.
Кручение больше 0 тогда и только тогда,
когда
и

противоположно направлены.

Геометрический
смысл кручения.

Модуль кручения
в данной точке кривой есть скорость
изменения направления функции b(S)
по отношению к естественному параметру
S.
Так как вектор b=b(S)
перпендикулярен соприкасающейся
плоскости, то абсолютная величина
кручения характеризует скорость
изменения положения соприкасающейся
плоскости по отношению к параметру S.

Если линия задана
в естественной параметризации, то
кривизна и кручение есть функция по
параметру S:

.Уравнения
такого вида называются натуральными
уравнениями кривой и характеризуют
кривую с точностью до движения, так как
если у двух кривых натуральные уравнение
совпадают, то кривые отличны только
положением в пространстве. Если у двух
кривых натуральные уравнения совпадают,
то на каждой из них существует естественная
параметризация, такая что в точках с
одинаковыми параметрами кривизна и
кручение одинаковы.

Вычислительная
формула для кручения линии заданной в
естественной параметризации.

–
продифференцируем
это равенство. Используем (5).

ыразим смешанное произведение
векторов производных:

формула
кручения (6)

Определение 3.2.
Линия называется плоской, если все её
точки принадлежат некоторой плоскости
.

Если во всех точках
гладкой плоской линии кручение равно
нулю.

Произвольная
параметризация.

Пусть кривая

задана произвольной параметризацией
своими параметрическими уравнениями:

Рассмотрим возможную
замену параметра t
на s,
причем функция s=h(t)
является допустимой заменой параметра
^-1
:
^-1

Найдем

Вектор
второй производной
параллелен
соприкасающейся плоскости, так как он
выражен через вектор

и
.

Рассмотрим векторное
произведение первой и второй производной.

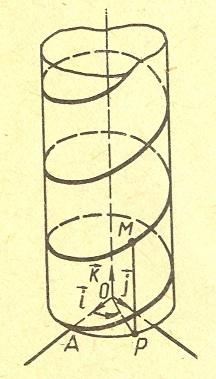
Винтовая линия

Винтовая
линия получена путем равномерного
вращения М
(х,у,z)

около оси Оz
и равномерного движения параллельно
оси Оz.
Является гладкой линией класса
.

Параметрические
уравнения винтовой линии:

Направляющая винтовой линии совпадает
с направляющей кругового цилиндра (ОХУ:
,
значит, винтовая линия лежит на прямом
круговом цилиндре с осью Оz.

Векторное уравнение
винтовой линии:
.

Используя формулу
,
имеем:
.
Таким образом,
.

Через М
проходит прямолинейная образующая МР
цилиндра, имеющая направляющий вектор

Так как
,
то винтовая линия пересекает все
образующие под постоянным углом (углом
между кривой и прямой называется угол
между касательной к этой кривой и данной
прямой).

Длина дуги винтовой
линии равна
.

Вектор главной
нормали:

Так как

(по формуле Френе), то

(k
– кривизна винтовой линии).

Главная нормаль
винтовой линии в точке М
есть
перпендикуляр к оси цилиндра, проведенный
через точку М,
т.к.

где Р
– проекция М
на ОХУ.
Вектор главной нормали направлен
противоположно вектору

Кручение винтовой
линии:
.
Знак кручения совпадает со знаком числа
b.

Винтовая линия
является частным случаем достаточно
широкого класса линий, называемых
кривыми Бертрана. Гладкая линия

называется кривой Бертрана, если для
нее существует другая гладкая линия

и такое отображение
,
что в каждой паре соответствующих точек
линии

и

имеют общую главную нормаль.