Нод это в математике как найти нод - Сайт, где вы сможете решить свои вопросы

Наибольшим общим делителем (НОД) двух целых чисел называется наибольший из их общих делителей. К примеру для чисел 12 и 8, наибольшим общим делителем будет 4.

Как найти НОД?

Способов найти НОД несколько. Мы рассмотрим один из часто используемых в математике — это нахождение НОД при помощи разложения чисел на простые множители. В общем случае алгоритм будет выглядеть следующим образом:

разложить оба числа на простые множители (подробнее о разложении чисел на простые множители смотрите тут);
выбрать одинаковые множители, входящие в оба разложения;
найти их произведение.

Примеры нахождения наибольшего общего делителя

Рассмотрим приведенный алгоритм на конкретных примерах:

Пример 1: найти НОД 12 и 8

1. Раскладываем 12 и 8 на простые множители:

2. Выбираем одинаковые множители, которые есть в обоих разложениях. Это: 2 и 2

3. Перемножаем эти множители и получаем: 2 · 2 = 4

Ответ: НОД (8; 12) = 2 · 2 = 4.

Пример 2: найти НОД 75 и 150

Этот пример, как и предыдущий с легкостью можно высчитать в уме и вывести ответ 75, но для лучшего понимания работы алгоритма, проделаем все шаги:

1. Раскладываем 75 и 150 на простые множители:

2. Выбираем одинаковые множители, которые есть в обоих разложениях. Это: 3, 5 и 5

3. Перемножаем эти множители и получаем: 3 · 5 · 5 = 75

Ответ: НОД (75; 150) = 3 · 5 · 5 = 75.

Частный случай или взаимно простые числа

Нередко встречаются ситуации, когда оба числа взаимно простые, т.е. общий делитель равен единице. В этом случае, алгоритм будет выглядеть следующим образом:

Пример 3: найти НОД 9 и 5

1. Раскладываем 5 и 9 на простые множители:

Видим, что одинаковых множителей нет, а значит, что это частный случай (взаимно простые числа). Общий делитель — единица.

Источник

Для этого термина существует аббревиатура «НОД», которая имеет и другие значения, см. Нод.

Наибольшим общим делителем (НОД) для двух целых чисел и называется наибольший из их общих делителей^[1]. Пример: для чисел 54 и 24 наибольший общий делитель равен 6.

Наибольший общий делитель существует и однозначно определён, если хотя бы одно из чисел или не равно нулю.

Возможные обозначения наибольшего общего делителя чисел и :

Понятие наибольшего общего делителя естественным образом обобщается на наборы из более чем двух целых чисел.

Связанные определения[править | править код]

Наименьшее общее кратное[править | править код]

Наименьшее общее кратное (НОК) двух целых чисел и — это наименьшее натуральное число, которое делится на и (без остатка). Обозначается НОК(m,n) или [m,n] , а в английской литературе .

НОК для ненулевых чисел и всегда существует и связан с НОД следующим соотношением:

Это частный случай более общей теоремы: если $a_{1},a_{2},dots ,a_{n}$ — ненулевые числа, — какое-либо их общее кратное, то имеет место формула:

$D=[a_{1},a_{2},dots ,a_{n}]cdot left({frac {D}{a_{1}}},{frac {D}{a_{2}}},dots ,{frac {D}{a_{n}}}right)$

Взаимно простые числа[править | править код]

Числа и называются взаимно простыми, если у них нет общих делителей, кроме pm 1 . Для таких чисел НОД. Обратно, если НОД то числа взаимно просты.

Аналогично, целые числа $a_{1},a_{2},dots a_{k}$ , где kgeq 2 , называются взаимно простыми, если их наибольший общий делитель равен единице.

Следует различать понятия взаимной простоты, когда НОД набора чисел равен 1, и попарной взаимной простоты, когда НОД равен 1 для каждой пары чисел из набора. Из попарной простоты вытекает взаимная простота, но не наоборот. Например, НОД(6,10,15) = 1, но любые пары из этого набора не взаимно просты.

Способы вычисления[править | править код]

Эффективными способами вычисления НОД двух чисел являются алгоритм Евклида и бинарный алгоритм.

Кроме того, значение НОД(m,n) можно легко вычислить, если известно каноническое разложение чисел и на простые множители:

$n=p_{1}^{{d_{1}}}cdot dots cdot p_{k}^{{d_{k}}},$

$m=p_{1}^{{e_{1}}}cdot dots cdot p_{k}^{{e_{k}}},$

где $p_{1},dots ,p_{k}$ — различные простые числа, а $d_{1},dots ,d_{k}$ и $e_{1},dots ,e_{k}$ — неотрицательные целые числа (они могут быть нулями, если соответствующее простое отсутствует в разложении). Тогда НОД(n,m) и НОК[n,m] выражаются формулами:

$(n,m)=p_{1}^{{min(d_{1},e_{1})}}cdot dots cdot p_{k}^{{min(d_{k},e_{k})}},$

$[n,m]=p_{1}^{{max(d_{1},e_{1})}}cdot dots cdot p_{k}^{{max(d_{k},e_{k})}}.$

Если чисел более двух: $a_{1},a_{2},dots a_{n}$ , их НОД находится по следующему алгоритму:

$d_{2}=(a_{1},a_{2})$

$d_{3}=(d_{2},a_{3})$

………

$d_{n}=(d_{{n-1}},a_{n})$

— это и есть искомый НОД.

Свойства[править | править код]

Основное свойство: наибольший общий делитель и делится на любой общий делитель этих чисел. Пример: для чисел 12 и 18 наибольший общий делитель равен 6; он делится на все общие делители этих чисел: 1, 2, 3, 6.
Если делится на , то НОД(m, n) = n. В частности, НОД(n, n) = n.
. В общем случае, если , где – целые числа, то .
— общий множитель можно выносить за знак НОД.
Если , то после деления на числа становятся взаимно простыми, то есть, $left({{frac {m}{D}},{frac {n}{D}}}right)=1$ . Это означает, в частности, что для приведения дроби к несократимому виду надо разделить её числитель и знаменатель на их НОД.
Мультипликативность: если $a_{1},a_{2}$ взаимно просты, то:

$(a_{1}cdot a_{2},b)=(a_{1},b)cdot (a_{2},b)$

left{acdot m+bcdot nmid a,bin mathbb{Z } right}

и поэтому

представим в виде линейной комбинации чисел

Это соотношение называется соотношением Безу, а коэффициенты

— коэффициентами Безу. Коэффициенты Безу эффективно вычисляются расширенным алгоритмом Евклида. Это утверждение обобщается на наборы натуральных чисел — его смысл в том, что подгруппа группы

, порождённая набором ${a_{1},a_{2},dots ,a_{n}}$

, — циклическая и порождается одним элементом: НОД(a₁, a₂, … , a_n).

Вариации и обобщения[править | править код]

Понятие делимости целых чисел естественно обобщается на произвольные коммутативные кольца, такие, как кольцо многочленов или гауссовы целые числа. Однако, определить НОД(a, b) как наибольший из общих делителей , нельзя, так как в таких кольцах, вообще говоря, не определено отношение порядка. Поэтому в качестве определения НОД берётся его основное свойство:

Наибольшим общим делителем НОД(a, b) называется тот общий делитель, который делится на все остальные общие делители

Для натуральных чисел новое определение эквивалентно старому. Для целых чисел НОД в новом смысле уже не однозначен: противоположное ему число тоже будет НОД. Для гауссовых чисел число различных НОД возрастает до 4.

НОД двух элементов коммутативного кольца, вообще говоря, не обязан существовать. Например, для нижеследующих элементов и кольца не существует наибольшего общего делителя:

a=4=2cdot 2=left(1+{sqrt {-3}}right)left(1-{sqrt {-3}}right),qquad b=left(1+{sqrt {-3}}right)cdot 2.

В евклидовых кольцах наибольший общий делитель всегда существует и определён с точностью до делителей единицы, то есть количество НОД равно числу делителей единицы в кольце.

См. также[править | править код]

Бинарный алгоритм вычисления НОД
Делимость
Алгоритм Евклида
Наименьшее общее кратное

Литература[править | править код]

Виноградов И. М. Основы теории чисел. М.-Л.: Гос. изд. технико-теоретической литературы, 1952, 180 с.

Примечания[править | править код]

↑ Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1982. — Т. 3. страница 857

Источник

Продолжаем изучать деление. В данном уроке мы рассмотрим такие понятия, как НОД и НОК.

НОД — это наибольший общий делитель.

НОК — это наименьшее общее кратное.

Тема довольно скучная, но разобраться в ней нужно обязательно. Не понимая этой темы, не получится эффективно работать с дробями, которые являются настоящей преградой в математике.

Наибольший общий делитель

Определение. Наибольшим общим делителем чисел a и b называется наибольшее число, на которое a и b делятся без остатка.

Чтобы хорошо понять это определение, подставим вместо переменных a и b любые два числа. Например, вместо переменной a подставим число 12, а вместо переменной b — число 9. Теперь попробуем прочитать это определение:

Наибольшим общим делителем чисел 12 и 9 называется наибольшее число, на которое 12 и 9 делятся без остатка.

Из определения понятно, что речь идёт об общем делителе чисел 12 и 9. Причем делитель является наибольшим из всех существующих делителей. Этот наибольший общий делитель (НОД) нужно найти.

Для нахождения наибольшего общего делителя двух чисел, используется три способа. Первый способ довольно трудоёмкий, но зато позволяет хорошо понять суть темы и прочувствовать весь ее смысл.

Второй и третий способы довольны просты и дают возможность быстро найти НОД. Рассмотрим все три способа. А какой применять на практике — выбирать вам.

Первый способ заключается в поиске всех возможных делителей двух чисел и в выборе наибольшего из них. Рассмотрим этот способ на следующем примере: найти наибольший общий делитель чисел 12 и 9.

Сначала найдём все возможные делители числа 12. Для этого разделим 12 на все делители в диапазоне от 1 до 12. Если делитель позволит разделить 12 без остатка, то мы будем выделять его синим цветом и в скобках делать соответствующее пояснение.

12 : 1 = 12
(12 разделилось на 1 без остатка, значит 1 является делителем числа 12)

12 : 2 = 6
(12 разделилось на 2 без остатка, значит 2 является делителем числа 12)

12 : 3 = 4
(12 разделилось на 3 без остатка, значит 3 является делителем числа 12)

12 : 4 = 3
(12 разделилось на 4 без остатка, значит 4 является делителем числа 12)

12 : 5 = 2 (2 в остатке)
(12 не разделилось на 5 без остатка, значит 5 не является делителем числа 12)

12 : 6 = 2
(12 разделилось на 6 без остатка, значит 6 является делителем числа 12)

12 : 7 = 1 (5 в остатке)
(12 не разделилось на 7 без остатка, значит 7 не является делителем числа 12)

12 : 8 = 1 (4 в остатке)
(12 не разделилось на 8 без остатка, значит 8 не является делителем числа 12)

12 : 9 = 1 (3 в остатке)
(12 не разделилось на 9 без остатка, значит 9 не является делителем числа 12)

12 : 10 = 1 (2 в остатке)
(12 не разделилось на 10 без остатка, значит 10 не является делителем числа 12)

12 : 11 = 1 (1 в остатке)
(12 не разделилось на 11 без остатка, значит 11 не является делителем числа 12)

12 : 12 = 1
(12 разделилось на 12 без остатка, значит 12 является делителем числа 12)

Теперь найдём делители числа 9. Для этого проверим все делители от 1 до 9

9 : 1 = 9
(9 разделилось на 1 без остатка, значит 1 является делителем числа 9)

9 : 2 = 4 (1 в остатке)
(9 не разделилось на 2 без остатка, значит 2 не является делителем числа 9)

9 : 3 = 3
(9 разделилось на 3 без остатка, значит 3 является делителем числа 9)

9 : 4 = 2 (1 в остатке)
(9 не разделилось на 4 без остатка, значит 4 не является делителем числа 9)

9 : 5 = 1 (4 в остатке)
(9 не разделилось на 5 без остатка, значит 5 не является делителем числа 9)

9 : 6 = 1 (3 в остатке)
(9 не разделилось на 6 без остатка, значит 6 не является делителем числа 9)

9 : 7 = 1 (2 в остатке)
(9 не разделилось на 7 без остатка, значит 7 не является делителем числа 9)

9 : 8 = 1 (1 в остатке)
(9 не разделилось на 8 без остатка, значит 8 не является делителем числа 9)

9 : 9 = 1
(9 разделилось на 9 без остатка, значит 9 является делителем числа 9)

Теперь выпишем делители обоих чисел. Числа выделенные синим цветом и являются делителями. Их и выпишем:

Выписав делители, можно сразу определить какой является наибольшим и общим.

Согласно определению, наибольшим общим делителем чисел 12 и 9, является число, на которое 12 и 9 делятся без остатка. Наибольшим и общим делителем чисел 12 и 9 является число 3

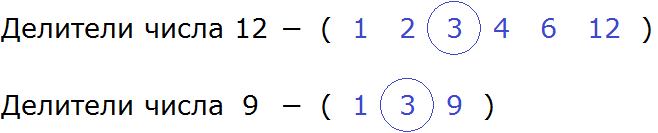
И число 12 и число 9 делятся на 3 без остатка:

12 : 3 = 4

9 : 3 = 3

Значит НОД (12 и 9) = 3

Второй способ нахождения НОД

Теперь рассмотрим второй способ нахождения наибольшего общего делителя. Суть данного способа заключается в том, чтобы разложить оба числа на простые множители и перемножить общие из них.

Пример 1. Найти НОД чисел 24 и 18

Сначала разложим оба числа на простые множители:

Теперь перемножим их общие множители. Чтобы не запутаться, общие множители можно подчеркнуть.

Смотрим на разложение числа 24. Первый его множитель это 2. Ищем такой же множитель в разложении числа 18 и видим, что он там тоже есть. Подчеркиваем обе двойки:

Снова смотрим на разложение числа 24. Второй его множитель тоже 2. Ищем такой же множитель в разложении числа 18 и видим, что его там второй раз уже нет. Тогда ничего не подчёркиваем.

Следующая двойка в разложении числа 24 также отсутствует в разложении числа 18.

Переходим к последнему множителю в разложении числа 24. Это множитель 3. Ищем такой же множитель в разложении числа 18 и видим, что там он тоже есть. Подчеркиваем обе тройки:

Итак, общими множителями чисел 24 и 18 являются множители 2 и 3. Чтобы получить НОД, эти множители необходимо перемножить:

2 × 3 = 6

Значит НОД (24 и 18) = 6

Третий способ нахождения НОД

Теперь рассмотрим третий способ нахождения наибольшего общего делителя. Суть данного способа заключается в том, что числа подлежащие поиску наибольшего общего делителя раскладывают на простые множители. Затем из разложения первого числа вычеркивают множители, которые не входят в разложение второго числа. Оставшиеся числа в первом разложении перемножают и получают НОД.

Пример 1. Найти НОД чисел 28 и 16.

В первую очередь, раскладываем числа 28 и 16 на простые множители:

Получили два разложения: и

Теперь из разложения первого числа вычеркнем множители, которые не входят в разложение второго числа. В разложение второго числа не входит семёрка. Её и вычеркнем из первого разложения:

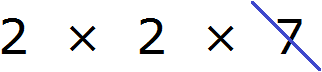
Теперь перемножаем оставшиеся множители и получаем НОД:

Число 4 является наибольшим общим делителем чисел 28 и 16. Оба этих числа делятся на 4 без остатка:

28 : 4 = 7

16 : 4 = 4

НОД (28 и 16) = 4

Пример 2. Найти НОД чисел 100 и 40

Раскладываем на множители число 100

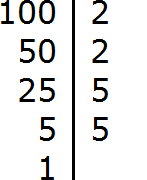
Раскладываем на множители число 40

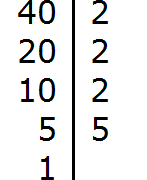
Получили два разложения: 2 × 2 × 5 × 5 и 2 × 2 × 2 × 5

Теперь из разложения первого числа вычеркнем множители, которые не входят в разложение второго числа. В разложение второго числа не входит одна пятерка (там только одна пятёрка). Её и вычеркнем из первого разложения

Перемножим оставшиеся числа:

Получили ответ 20. Значит число 20 является наибольшим общим делителем чисел 100 и 40. Эти два числа делятся на 20 без остатка:

100 : 20 = 5

40 : 20 = 2

НОД (100 и 40) = 20.

Пример 3. Найти НОД чисел 72 и 128

Раскладываем на множители число 72

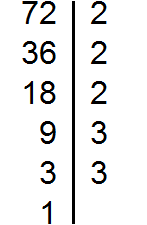
Раскладываем на множители число 128

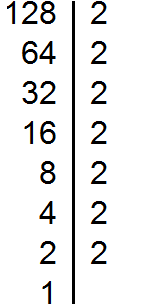Получили два разложения: 2 × 2 × 2 × 3 × 3 и 2 × 2 × 2 × 2 × 2 × 2 × 2.

Теперь из разложения первого числа вычеркнем множители, которые не входят в разложение второго числа. В разложение второго числа не входят две тройки (там их вообще нет). Их и вычеркнем из первого разложения:

Перемножим оставшиеся числа:

Получили ответ 8. Значит число 8 является наибольшим общим делителем чисел 72 и 128. Эти два числа делятся на 8 без остатка:

72 : 8 = 9

128 : 8 = 16

НОД (72 и 128) = 8

Нахождение НОД для нескольких чисел

Наибольший общий делитель можно находить и для нескольких чисел, а не только для двух. Для этого числа, подлежащие поиску наибольшего общего делителя, раскладывают на простые множители, затем находят произведение общих простых множителей этих чисел.

Например, найдём НОД для чисел 18, 24 и 36

Разложим на множители число 18

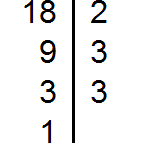
Разложим на множители число 24

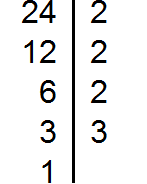
Разложим на множители число 36

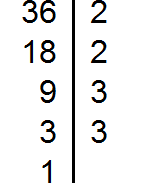
Получили три разложения:

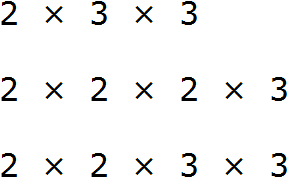
Теперь найдём и подчеркнём общие множители:

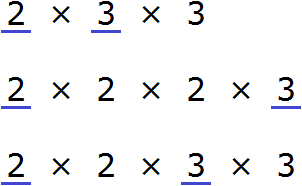
Мы видим, что общие множители для чисел 18, 24 и 36 это множители 2 и 3. Эти множители входят во все три разложения. Перемножив эти множители, мы получим НОД, который ищем:

2 × 3 = 6

Получили ответ 6. Значит число 6 является наибольшим общим делителем чисел 18, 24 и 36. Эти три числа делятся на 6 без остатка:

18 : 6 = 3

24 : 6 = 4

36 : 6 = 6

НОД (18, 24 и 36) = 6

Пример 2. Найти НОД для чисел 12, 24, 36 и 42

Разложим на простые множители каждое число. Затем найдём произведение общих простых множителей.

Разложим на множители число 12

Разложим на множители число 24

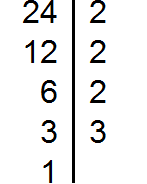
Разложим на множители число 36

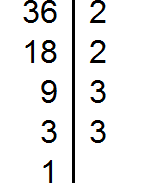
Разложим на множители число 42

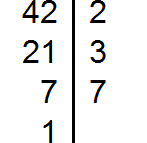
Получили четыре разложения:

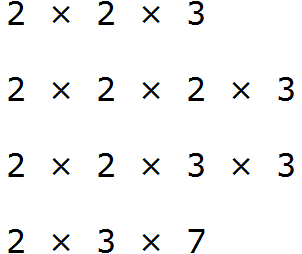
Теперь найдём и подчеркнём общие множители:

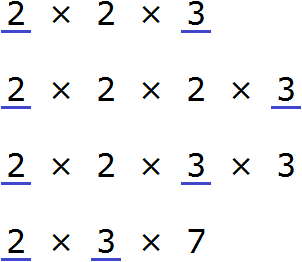
Мы видим, что общие множители для чисел 12, 24, 36, и 42 это множители 2 и 3. Перемножив эти множители, мы получим НОД, который ищем:

2 × 3 = 6

Получили ответ 6. Значит число 6 является наибольшим общим делителем чисел 12, 24, 36 и 42. Эти числа делятся на 6 без остатка:

12 : 6 = 2

24 : 6 = 4

36 : 6 = 6

42 : 6 = 7

НОД (12, 24 , 36 и 42) = 6

Наименьшее общее кратное

Из предыдущего урока мы знаем, что если какое-то число без остатка разделилось на другое, его называют кратным этого числа.

Оказывается, кратное может быть общим у нескольких чисел. И сейчас нас будет интересовать кратное двух чисел, причем оно должно быть максимально маленьким.

Определение. Наименьшее общее кратное (НОК) чисел a и b — это наименьшее число, которое кратно a и b. Другими словами, это такое маленькое число, которое делится без остатка на число a и число b.

Определение содержит две переменные a и b. Давайте подставим вместо этих переменных любые два числа. Например, вместо переменной a подставим число 9, а вместо переменной b подставим число 12. Теперь попробуем прочитать определение:

Наименьшее общее кратное (НОК) чисел 9 и 12 — это наименьшее число, которое кратно 9 и 12. Другими словами, это такое маленькое число, которое делится без остатка на число 9 и на число 12.

Из определения понятно, что наименьшее общее кратное это наименьшее число, которое делится без остатка на 9 и на 12. Это наименьшее общее кратное требуется найти.

Для нахождения наименьшего общего кратного (НОК) можно пользоваться тремя способами. Первый способ заключается в том, что можно выписать первые кратные двух чисел, а затем выбрать среди этих кратных такое число, которое будет общим для обоих чисел и маленьким. Давайте применим этот способ.

В первую очередь, найдем первые кратные для числа 9. Чтобы найти кратные для 9, нужно эту девятку поочерёдно умножить на числа от 1 до 9. Получаемые ответы будут кратными для числа 9.

Итак, начнём. Кратные будем выделять синим цветом:

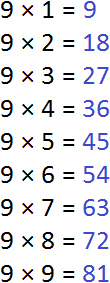
Теперь находим кратные для числа 12. Для этого поочерёдно умножим число 12 на все числа 1 до 12:

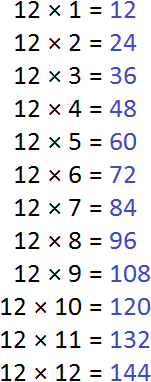
Теперь выпишем кратные обоих чисел:

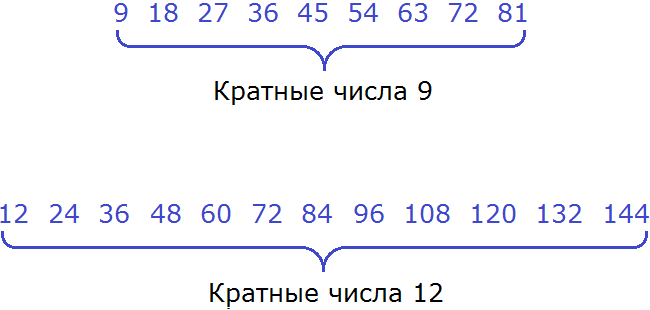
Теперь найдём общие кратные обоих чисел. Найдя, сразу подчеркнём их:

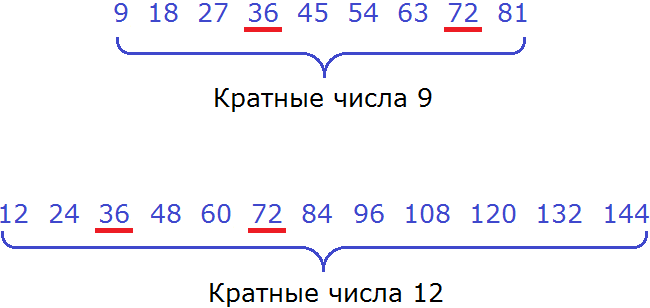
Общими кратными для чисел 9 и 12 являются кратные 36 и 72. Наименьшим же из них является 36.

Значит наименьшее общее кратное для чисел 9 и 12 это число 36. Данное число делится на 9 и 12 без остатка:

36 : 9 = 4

36 : 12 = 3

НОК (9 и 12) = 36

Второй способ нахождения НОК

Второй способ заключается в том, что числа для которых ищется наименьшее общее кратное раскладываются на простые множители. Затем выписываются множители, входящие в первое разложение, и добавляют недостающие множители из второго разложения. Полученные множители перемножают и получают НОК.

Применим данный способ для предыдущей задачи. Найдём НОК для чисел 9 и 12.

Разложим на множители число 9

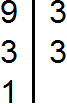
Разложим на множители число 12

Выпишем первое разложение:

Теперь допишем множители из второго разложения, которых нет в первом разложении. В первом разложении нет двух двоек. Их и допишем:

Теперь перемножаем эти множители:

Получили ответ 36. Значит наименьшее общее кратное чисел 9 и 12 это число 36. Данное число делится на 9 и 12 без остатка:

36 : 9 = 4

36 : 12 = 3

НОК (9 и 12) = 36

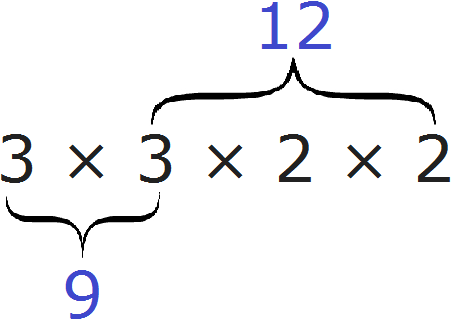
Говоря простым языком, всё сводится к тому, чтобы организовать новое разложение куда входят оба разложения сразу. Разложением первого числа 9 являлись множители 3 и 3, а разложением второго числа 12 являлись множители 2, 2 и 3.

Наша задача состояла в том, чтобы организовать новое разложение куда входило бы разложение числа 9 и разложение числа 12 одновременно. Для этого мы выписали разложение первого числа и дописали туда множители из второго разложения, которых не было в первом разложении. В результате получили новое разложение 3 × 3 × 2 × 2. Нетрудно увидеть воочию, что в него одновременно входят разложение числа 9 и разложение числа 12

Пример 2. Найти НОК чисел 50 и 180

Разложим на множители число 50

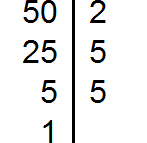
Разложим на множители число 180

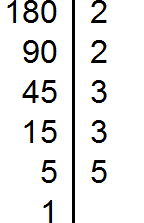
Выпишем первое разложение:

Теперь допишем множители из второго разложения, которых нет первом разложении. В первом разложении нет ещё одной двойки и двух троек. Их и допишем:

Теперь перемножаем эти множители:

Получили ответ 900. Значит наименьшее общее кратное чисел 50 и 180 это число 900. Данное число делится на 50 и 180 без остатка:

900 : 50 = 18

900 : 180 = 5

НОК (50 и 180) = 900

Пример 3. Найти НОК чисел 8, 15 и 33

Разложим на множители число 8

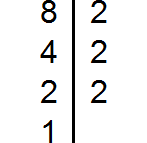
Разложим на множители число 15

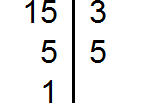
Разложим на множители число 33

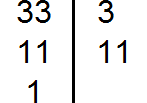
Выпишем первое разложение:

Теперь допишем множители из второго и третьего разложения, которых нет первом разложении. Допишем множители 3 и 5 из второго разложения, и множитель 11 из третьего разложения:

Теперь перемножаем эти множители:

Получили ответ 1320. Значит наименьшее общее кратное чисел 8, 15 и 33 это число 1320. Данное число делится на 8, 15 и 33 без остатка:

1320 : 8 = 165

1320 : 15 = 88

1320 : 33 = 40

НОК (8, 15 и 33) = 1320

Третий способ нахождения НОК

Есть и третий способ нахождения наименьшего общего кратного. Он работает при условии, что его ищут для двух чисел и при условии, что уже найден наибольший общий делитель этих чисел.

Данный способ разумнее использовать, когда одновременно нужно найти НОД и НОК двух чисел.

К примеру, пусть требуется найти НОД и НОК чисел 24 и 12. Сначала найдем НОД этих чисел:

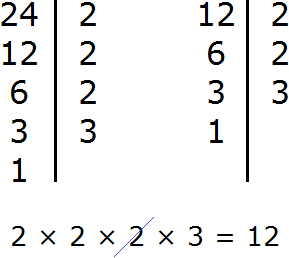
Теперь для нахождения наименьшего общего кратного чисел 24 и 12, нужно перемножить эти два числа и полученный результат разделить на их наибольший общий делитель.

Итак, перемножим числа 24 и 12

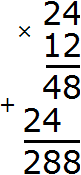
Разделим полученное число 288 на НОД чисел 24 и 12

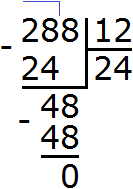
Получили ответ 24. Значит наименьшее общее кратное чисел 24 и 12 равно 24

НОК (24 и 12) = 24

Пример 2. Найти НОД и НОК чисел 36 и 48

Найдем НОД чисел 36 и 48

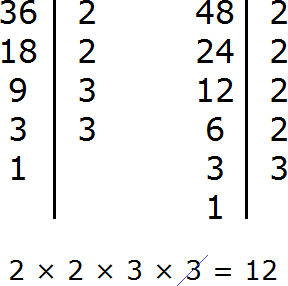
Перемножим числа 36 и 48

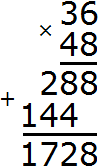
Разделим 1728 на НОД чисел 36 и 48

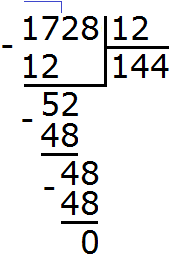
Получили 144. Значит наименьшее общее кратное чисел 36 и 48 равно 144

НОК (36 и 48) = 144

Для проверки можно найти НОК обычным вторым способом, которым мы пользовались ранее. Если мы всё сделали правильно, то должны получить 144

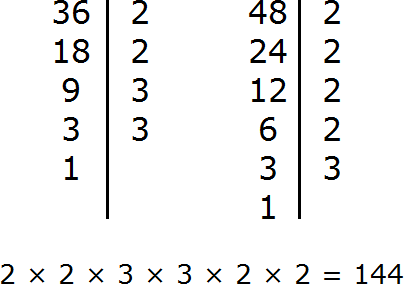
Не расстраивайтесь, если сразу не научитесь находить НОД и НОК. Главное понимать, что это такое и как оно работает. А ошибки вполне естественны на первых порах. Как говорят: «На ошибках учимся».

Задания для самостоятельного решения

Задание 1. Найдите НОД чисел 12 и 16

Решение:

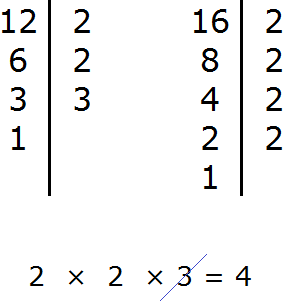
Задание 2. Найдите НОК чисел 12 и 16

Решение:

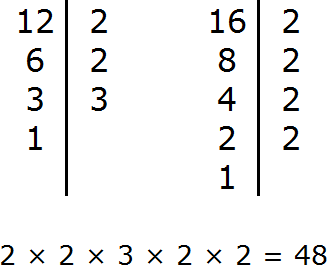
Задание 3. Найдите НОД чисел 40 и 32

Решение:

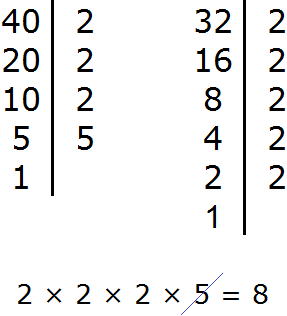
Задание 4. Найдите НОК чисел 40 и 32

Решение:

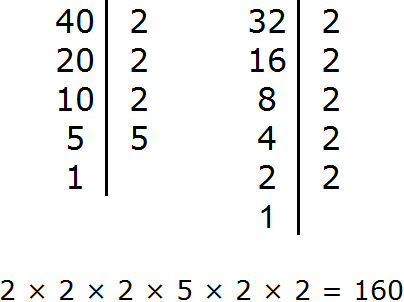
Задание 5. Найдите НОД чисел 54 и 86

Решение:

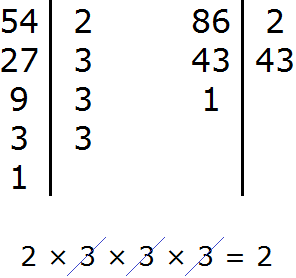
Задание 6. Найдите НОК чисел 54 и 86

Решение:

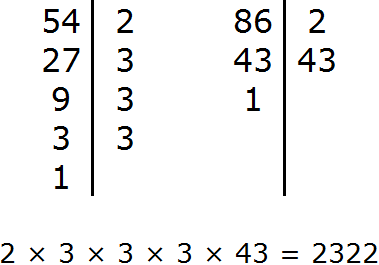
Задание 7. Найдите НОД чисел 98 и 35

Решение:

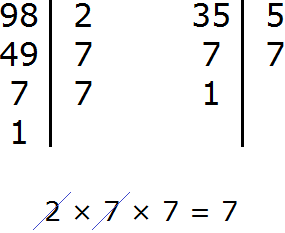
Задание 8. Найдите НОК чисел 98 и 35

Решение:

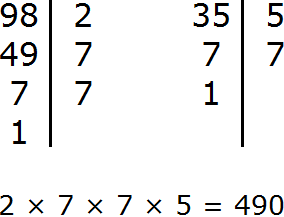
Задание 9. Найдите НОД чисел 112 и 82

Решение:

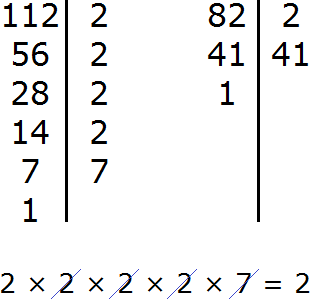
Задание 10. Найдите НОК чисел 112 и 82

Решение:

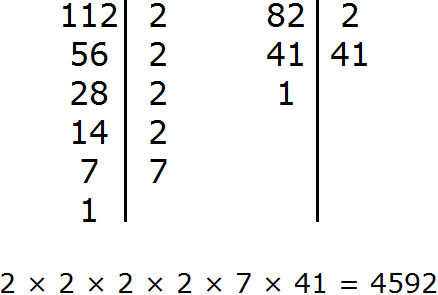
Задание 11. Найдите НОД чисел 24, 48, 64

Решение:

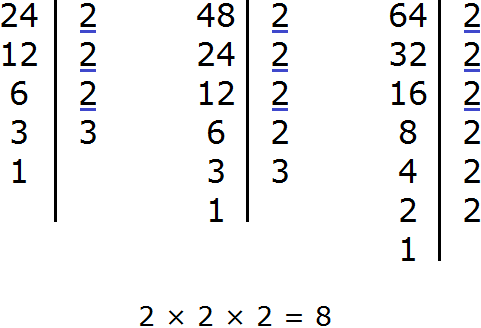
Задание 12. Найдите НОК чисел 24, 48, 64

Решение:

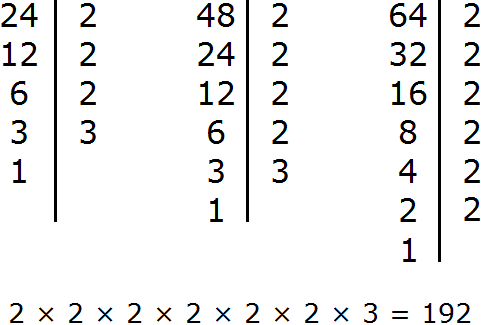
Задание 13. Найдите НОД чисел 18, 48, 96

Решение:

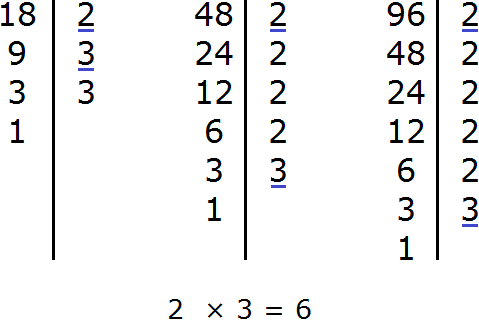
Задание 14. Найдите НОК чисел 18, 48, 96

Решение:

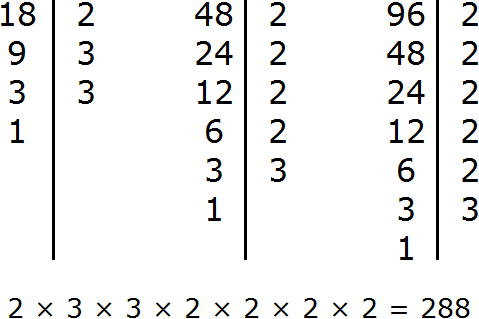
Задание 15. Найдите НОД чисел 28, 24, 76

Решение:

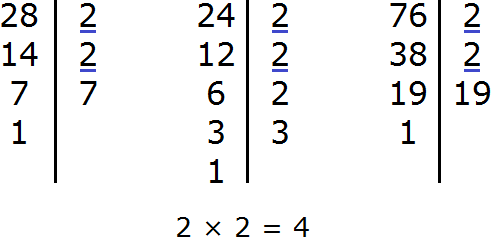
Задание 16. Найдите НОК чисел 28, 24, 76

Решение:

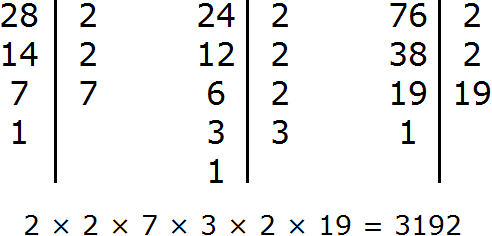
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Возникло желание поддержать проект?
Используй кнопку ниже

Источник

Делимость

До того как начать разбирать эти две аббревиатуры, рассмотрим сначала понятие делимости. Что значит фраза “число А делится на число Б”? Например, 24 делится на 6. И что значит “не делится”? Например, 27 не делится на 2.

Когда мы говорим о делимости, то речь идет о целочисленном делении целых чисел. И делимость означает, что число делится на делитель нацело, без остатка.

24 делится на 6, частное равно 4, а остаток нулю.

27 не делится на 2, частное равно 13, а остаток равен одному.

Апельсин делится по количеству его долек

Признаки делимости

Проверить, делится ли одно число на заданное, можно просто выполнив деление. Но если число большое, а результат самого деления нам не так чтобы нужен? Можно ли не находя частное, определить, делится ли число?

Существуют несколько признаков делимости, когда по внешнему вида числа мы можем определить, делится ли оно на заданное. Рассмотрим только некоторые из них, те, которые легко проверяются.

По последней цифре

Число делится на 2, если его последняя цифра – четная.

Число делится на 5, если его последняя цифра – 5 или 0.

Число делится на 10, если его последняя цифра – 0.

Например, 234 делится на 2, так как 4 – четная.

235 делится на 5, так как последняя цифра – 5.

190 делится на 10 и на 5, так как последняя цифра – 0.

По сумме цифр числа

Число делится на 3, если сумма цифр этого числа делится на 3.

Число делится на 9, если сумма цифр этого числа делится на 9.

Например, 393 делится на 3, так как сумма цифр этого числа 3+9+3=15 делится на 3.

180 делится на 9, так как сумма цифр этого числа 1+8+0=9 делится на 9.

Число делится на 6, если оно делится на 2 и на 3 одновременно.

Например, 36 делится на 2 (6 четная) и на 3 (3+6=9 – делится на 3), поэтому оно делится на 6.

Простые и составные числа

Среди натуральных чисел выделяют такие числа, которые делятся только на 1 и на самого себя. Такие числа называются простыми. Остальные числа, имеющие больше двух делителей, называют составными. Отдельно выделяют 1, у нее только один делитель.

Пример простого числа – 2, 3, 5, 7, 11, 13, 17, 19 и так далее. Существуют специальные таблицы простых чисел, но многие проблемы простых чисел до сих пор не решены.

Разложение на простые множители

Для составных чисел можно найти такие множители, которые будут только простыми числами, а произведение этих множителей будет равно исходному числу.

Например, 24=2*2*2*3.

Это произведение и называется разложением на простые множители. Если множители отсортированы по возрастанию, то для каждого конкретного числа это разложение будет единственным.

Для построения такого разложения существует четкий алгоритм.

Записываем в левый столбец исходное число, проводим вертикальную черту, отделяя правый столбец.
Проверяем, делится ли число на 2. Если да, то записываем 2 в правый столбец, в левый столбец в следующей строке записываем кратное исходного числа и 2.
Проверяем, делится ли полученное число на 2, если да, то действуем как в пункте 2.
Если нет, то проверяем, делится ли наше число на 3. Если да, то 3 записываем в правый столбец, а в левый столбец строчкой ниже пишем кратное от деления на 3 и переходим к пункту 3.
Если число не делится на 3, то переходим к следующему числу в списке простых чисел – 5.
Каждый раз начинаем проверку делимости с 2, постепенно переходя к все большим и большим простым числам, если это необходимо.
Так действуем до тех пор, пока число в левом столбце не станет равно 1. Тогда останавливаемся.
В правом столбце у нас записаны все простые множители числа.

Наибольший общий делитель

НОД или наибольший общий делитель для нескольких чисел – это такое наибольшее число, на которое делятся все эти числа.

Например, НОД(12, 18)=6.

Зная разложение чисел на простые множители, легко найти их НОД. Выписываем совпадающие множители, их произведение и даст нам НОД.

Наименьшее общее кратное

НОК или наименьшее общее кратное нескольких чисел – это такое наименьшее число, которое делится на все эти числа.

Например, НОК(4, 6)=12.

Зная разложение чисел на простые множители, легко найти их НОК. К множителям меньшего числа дописываем несовпадающие множители. Это произведение и даст нам НОК.

Найдем НОД и НОК для 60 и 75, зная их разложение на множители

Взаимно простые числа

Если у двух составных чисел нет общих простых множителей, то такие числа называются взаимно простыми. НОК таких чисел равен их произведению, а НОД равен 1.

Источник

Нахождение НОК и НОД двух натуральных чисел

Содержание:

Что такое НОК и НОД двух натуральных чисел
Особенности вычисления, алгоритм Евклида
Правило нахождения наибольшего общего делителя (НОД)
Правило нахождения наименьшего общего кратного (НОК)

Что такое НОК и НОД двух натуральных чисел

Натуральными числами называют числа, которые используются при счете – 1, 2, 3, 16, 25, 101, 2560 и далее до бесконечности. Ноль, отрицательные и дробные или нецелые числа не относятся к натуральным.

Наименьшее общее кратное (НОК) двух натуральных чисел a и b – это наименьшее число, которое делится без остатка на каждое из рассматриваемых чисел.

Наибольший общий делитель (НОД) двух натуральных чисел a и b – это наибольшее число, на которое делится без остатка каждое рассматриваемое число.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Свойства НОК и НОД для натуральных чисел a и b

(НОД (a, b) = НОД (b, a);)
(НОК (a, b) = НОК (b, a);)
(НОК;(a,b)=frac{a;times;b}{НОД;(a,b)}.)

Особенности вычисления, алгоритм Евклида

Рассмотрим два способа определения НОД и НОК с помощью алгоритма Евклида:

Способ деления.

При делении целых чисел с остатком, где a – делимое, b – делитель (b не равно 0) находят целые числа q и r согласно равенству (a=btimes) q+r, в котором q – неполное частное, r – остаток при делении (не отрицательное, по модулю меньше делителя).

Чтобы вычислить НОД, первоначально нужно выбрать наибольшее из двух чисел и поделить его на меньшее. Пока остаток не станет равным нулю, повторяется цикл деления делителя на остаток от деления в соответствии с формулой.

Пример №1

Вычислим НОД для чисел 12 и 20. Делим 20 на 12 и получаем 1 и 8 в остатке. Запишем иначе:

(20=12times1+8), так как остаток не равняется нулю, продолжаем деление. Делим 12 на 8 и получаем 1 и 4 в остатке. Записываем: (12=8times1+4) и по аналогии делим 8 на 4 и получаем 2 и 0 в остатке. НОД равен остатку, предшествующему нулю.

НОД (12;20) = 4

НОК получаем согласно свойству (НОК (a, b) = НОК;(a,b)=frac{a;times;b}{НОД;(a,b)}.) Подставляем числовые значения:

НОК (12; 20) = (12times20div4=60)

НОК (12;20) = 60

Способ вычитания.

Здесь повторяется цикл вычитания из наибольшего числа меньшего числа до момента, пока разность не станет равна нулю. НОД равен предшествующей нулю разности.

Пример №2

Вычислим НОД для тех же чисел, 12 и 20.

20 – 12 = 8 (разность не равна нулю, продолжаем)

12 – 8 = 4

8 – 4 = 4

4 – 4 = 0

НОД (12;20) = 4

НОК находим также, как и при методе деления.

Правило нахождения наибольшего общего делителя (НОД)

Для нахождения наибольшего общего делителя воспользуемся пошаговым алгоритмом:

Разложить числа на простые множители.
Найти общий множитель одного и другого числа.
Перемножить общие множители, если их несколько, и их произведение будет НОД.

Пример №3

Возьмем натуральные числа 24 и 36.

(24=2times2times2times3)

(36=2times2times3times3)

Правильно записать следующим образом:

(НОД (24;36)=2times3=6)

Примечание

В случае, когда одно или оба числа относятся к простым, т.е. делятся только на единицу и на само себя, то их НОД равняется 1.

Правило нахождения наименьшего общего кратного (НОК)

Для нахождения наименьшего общего кратного воспользуемся подробным алгоритмом:

Наибольшее из чисел, а затем остальные разложить на простые множители.
Выделить те множители, которые отсутствуют у наибольшего.
Перемножить множители п. 2 и множители наибольшего числа, получить НОК.

Пример №4

Возьмем натуральные числа 9 и 12.

(12=2times2times3)

(9=3times3) (видим, что у числа 12 отсутствует одна тройка)

Правильно записать следующим образом:

(НОК (9;12)=2times2times3times3=36)

Насколько полезной была для вас статья?

Рейтинг: 3.00 (Голосов: 4)

Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»

Текст с ошибкой:

Расскажите, что не так

Поиск по содержимому

Источник

Как найти НОД?

Примеры нахождения наибольшего общего делителя

Частный случай или взаимно простые числа

Связанные определения[править | править код]

Наименьшее общее кратное[править | править код]

Взаимно простые числа[править | править код]

Способы вычисления[править | править код]

Свойства[править | править код]

Вариации и обобщения[править | править код]

См. также[править | править код]

Литература[править | править код]

Примечания[править | править код]

Наибольший общий делитель

Второй способ нахождения НОД

Третий способ нахождения НОД

Нахождение НОД для нескольких чисел

Наименьшее общее кратное

Второй способ нахождения НОК

Третий способ нахождения НОК

Задания для самостоятельного решения

Делимость

Признаки делимости

Нахождение НОК и НОД двух натуральных чисел

Что такое НОК и НОД двух натуральных чисел

Особенности вычисления, алгоритм Евклида

Правило нахождения наибольшего общего делителя (НОД)

Правило нахождения наименьшего общего кратного (НОК)

Текст с ошибкой:

Поиск по содержимому

Вам также может понравиться

Как найти портативную колонку

Как найти бронь своих билетов

Как исправить реле холодильник

Добавить комментарий Отменить ответ