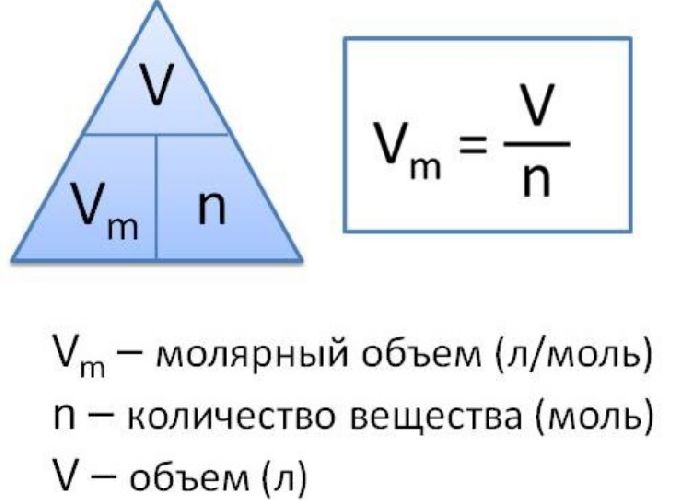
Один из основных понятий в математике и физике – это понятие объема. Объем это число, которое показывает, сколько места занимает вещество. Например, если нужно узнать, как много воды нужно налить в чашку, нужно использовать информацию об объеме чашки.
Существует несколько формул и методов вычисления объема, и каждый из них используется в разных ситуациях и соответствующих контекстах. Именно поэтому хорошее понимание данного понятия является важным для рационального управления ресурсами и решения разных инженерных задач. В данной статье мы разберем основные формулы для вычисления объема объектов таких как тела геометрические и приведем примеры применения этих правил.
Для диагностики и коррекции различных технических проблем также помогает соответствующее знание формул вычисления объема. Знать формулы для вычисления объема – значит быть в курсе особенностей разных систем и иметь средства для их тщательного изучения. Запомните – понимание, как найти формулы для вычисления объема, будет полезно в разных областях знаний и областях деятельности, поэтому проанализируйте и примените перечисленные ниже примеры и уроки к реальным сущностям.
Основы определения объема
Объем – это трёхмерная характеристика физического объекта, которая определяет суммарное количество пространства, занимаемого этим объектом. Объем изучается в разных областях науки, включая математику, физику, химию и геологию. В этом разделе мы рассмотрим основы определения объема различных трёхмерных тел.
Используемые термины
- Объем (обозначается V) – характеристика физического объекта, связанная с его формой и размерами.
- Трёхмерное тело – физический объект, обладающий тремя разными измерениями (длиной, шириной и высотой).
- Формула объема – математическое выражение, позволяющее вычислить объем трёхмерного тела на основе размеров этого тела.
- Геометрия – математическая дисциплина, изучающая пространственные структуры и отношения между ними.
Математические основы определения объема

Уточнённому определению объема может способствовать изучение геометрического пространства и знакомство с различными трёхмерными телами.
- Задача на объем – уравнение или контекст, в котором просится найти объем объекта или системы объектов.
- Формулы объема – математические выражения, которые описывают объем различных трёхмерных тел. Эти формулы основаны на свойствах и форме тел и могут включать в себя переменные для характерных размерностей.
К примеру, объем куба можно найти по формуле:
- V = a3, где a – длина ребра куба.
также объем параллелепипеда можно найти по формуле:
- V = a ∗ b ∗ h, где a и b – коэффициенты симметрии вдоль оси, а h – высота.
Объемы других трёхмерных фигур также можно вычислять различными формулами.
Различия в любых объемах
Объем может различаться в разных обстоятельствах, завися от размера и формы тела или системы тел. Здесь перечислены основные аспекты, влияющие на объем:
- Изменение размеров – удлинение, утоньшение или укорочение объекта может содействовать его объему.
- Смена формы – превращение трёхмерного тела в более компактное или менее компактное может увеличить или уменьшить объем.
- Анализ вещества – состав тела может быть отражен в его объеме, например, в случае вязкости или растворимости.
Графический способ вычисления объема
Методика вычисления

Чтобы вычислить объем по графическому изображению, выполним следующие действия:
- Идентифицируйте фигуру: Первым шагом является определение формы тела. Это может быть параллелепипед, цилиндр, шар, конус или другая геометрическая фигура.
- Вычислите измерения: Получите необходимые измерения для вычисления объема. Для параллелепипеда, например, вам нужно знать длину, ширину и высоту. Для цилиндра – радиус и высоту. В определенных случаях реальные размеры тела могут быть слишком мелкими или сложными для точного измерения, в таком случае можно использовать эквивалентные параметры или соотношения между размерами.
- Вычислите объем: На основе знаний о выбранной фигуре и обмерах выполните вычисления по соответствующей формуле для вычисления объема. Например для параллелепипеда он равен произведению длины, ширины и высоты (V = lwh).
Преимущества
- Быстрота: Графический способ вычисления объема был разработан ради экономии времени на измерениях и вычислениях .
- Меньший риск ошибок: Этот метод основан на оценке ступенчатой структуры тела, что минимизирует возможность ошибок в проведении измерений.
- Практичность: Графический способ может быть лучшими для произвольных или прозрачных объектов, для которых традиционные измерения не всегда полезны.
Ограничения
Иногда графический способ вычисления объема может быть неточным из-за особенностей тел, состоящих из сливающихся геометрических фигур. Тем не менее, данный метод прекрасно работает для простых геометрических тел и послужит гораздо более чем удобным средством в случае, когда производить точные измерения невозможно.
Формулы для расчета объема сферы и цилиндра
Когда вы решаете задачи с математикой или житейскими расчетами, вам может потребоваться вычислить объем некоторых объектов. Два таких объектов, сферы и цилиндра, имеют простые формулы для вычисления их объема.
Объем сферы

Формула объема сферы выглядит следующим образом:
V = (4/3) * π * R3
где:
- V – объем сферы,
- π (пи) – постоянная, равная приблизительно 3,14159,
- R – радиус сферы.
Чтобы найти объем сферы, вы должны знать только радиус и использовать формулу выше. Пи, или число Пьера, равняется приблизительно 3,14159, но вы можете найти более точные значения в таблицах или с помощью калькуляторов.
Объем цилиндра
Формула для объема цилиндра имеет следующий вид:
V = π * R2 * H
где:
- V – объем (тил) цилиндра,
- π (пи) – математическая константа, приблизительно равная 3,14159,
- R – радиус (радиус равен полуоси),
- В – высота цилиндра.
Для расчета объема цилиндра вам необходим радиус и высота цилиндра и известное значение числа пи.
Параметры сферы и цилиндра
Ниже представлена таблица сравнительного анализа параметров сферы и цилиндра:
| Шар | Цилиндр |
|---|---|
| Формула объема: V = (4/3) * π * R3 | Формула объема: V = π * R2 * H |
| Параметры: εлуад, пи, R (радиус) | Параметры: εлуад, пи, R (радиус), H (высота) |
Используя эти простые формулы, вы сможете вычислить объем сложных форм обучающимся в гипотетическом мышлении или при решении реальных задач.
Применение объема в научных исследованиях
Объем как ключевой показатель используется во многих научных исследованиях для решения некоторых важных задач. В данном разделе мы рассмотрим некоторые наиболее значимые сферы применения ося вида.
В физике
В физике объем имеет важное значение для определения свойств сред, включая их плотность и давление. Например, при изучении сжатых газов можно использовать уравнение состояния идеального газа, в котором объем является прямой пропорцией к температуре газа и обратной пропорциональности к его давлению.
В химии
В химии объемы используются для определения количества веществ, участвующих в химических реакциях, а также для вычисления результатов изменения молярной массы при проведении экспериментов, таких как определение температуры кипения или плотности жидкости. В качестве примера можно привести использование объема для определения растворимости ионов.
Применение объема в научных исследованиях
Объем как важный показатель находит различное применение в научных исследованиях. Ниже приведены наиболее интересные области использования.
В физике
В физике объем является фундаментальным параметром, оказывающим значительное влияние на изучение ядерных и звездных процессов. В рамках именитой модели Большого Взрыва оболочки космических объектов меняют свою форму и размеры, влияя на характеристики предметных областей.
В химии
В химии объем дает возможность составить точный отчет о проведенных экспериментах. Так, в ходе опытов и анализа оценивалось количество веществ, участвующих в химических реакциях, изменения объема служили основой вычисления некоторых тепла и давления.
Многие процессы происходят в среде, и использование объема способствует точным измерениям как для прояснения механизмов химических превращений молекул, так и для документирования цели эксперимента. Согласно определению величины объема можно утверждать, что при увеличении размера средины уровень протекания химической реакции снижается.
Применение объема в научных исследованиях
Объем активно применяется в различных научных исследованиях. Вот некоторые области использования.
В геофизике
Например, при изучении земного ядра и его природного состояния нельзя обойтись без рассмотрения объема, связанного с исследованием свойств планеты Земля, их строению и четко выявленных параметров. Это возможно благодаря физическому значению этого показателя – удовлетворение земных процессов.
В биофизике
В области биофизики объем используется для рассмотрения свойств живых объектов и их функций, а также для анализа различных биохимических процессов, происходящих в организмах. Этот показатель помогает узнать о пространственных размерах и массе стяжки клеток.
Влияние геометрических форм на объем тел
1. Пластические объемы. Объем плоской поверхности

Пластические объемы характеризуют отклонениеми внутри полировщица размера объектов из различных материалов: пластические кубы с металлическими, стеклянными кубами и другими шарообразными формами связаны с монтажом кубов.
2. Конструктивные объемы. Объемы панельно-стенных конструкций
Конструктивные объемы тела появляются при расточке и изготовлении плоско-литной поверхности или большой стрелены с контурами равносторонних прямоугольных формы или если есть прямоугольное качество во анфас и на разных участках шаровой треугольной формы, качестве круговой цилиндрической, усеченной конусообразной формы с соответствием и отличием в плоскости и в пространстве.
Увеличение объема твердого тела: результаты давно были опубликованы в специализированных журналах и исследованиях круговых поверхностей с ограничением полной картезианской области и формулы укорочения длины прямоугольного строительного материала параллелепипеда.
Можно заключить, что геометрические формы определяют масштабные отношения объема твердого тела, влияя на его геометрические характеристики. В разных случаях могут возникнуть особенности объема и его возможности, связанные с поверхностями трёхмерных форм. Однако его параметры всегда олицетворяют основные свойства выбранных качеств материи, организовавшиеся во внутренней информации различных геометрических составляющих с минимальным числом простых уравнений.
Интегральные методы в расчете объема
Интеграл Лебега, например, использует не только конечные объемы, но и более сложные фигуры, чтобы вычислять объемы. Этот метод использует принцип ограниченных изменений величин (погружений объемов), но при этом он допускает некоторые особенности геометрических тел, такие как неопределенные покрытия границ фигур и их перемещение в пространстве.
Также существует интегральный метод Гаусса, который использует статистические законы распределения вероятностей, дает возможность находить вероятностные оценки различных характеристик пространственных объектов и систем. Исходя из этих вероятностных оценок, можно использовать соответствующие интегралы для вычисления объема геометрических тел. Эти больше подходят в ситуациях, в которых будут возникать неустойчивости структур в объеме, так как метод позволяет предсказывать и оценки вероятности их дальнейшего развития.
Еще одной областью, где интегральные методы находят применение, является современный ракетостроение и авиационная техника. Здесь они часто используются для анализа и исследования воздухопложных режимов движения, аэродинамики, для прогнозирования и расчета внутрикамерных процессов, как давления и температуры.
В контексте оценок геометрических масштабов микродеталей (наноразмерных структур, включая структурный анализ межфазных поверхностей), интегральные методы включают в себя описанные выше. Так, используя принципы Гаусса или интеграла Лебега, ученые и инженерами могут считать размеры и отношений этих столь маленьких объектов, а также оптимизировать их моделирования и способы изготовления.
Конечно, почти все интегральные методы используют те или иные формулы интегралов для оценки тензорных величин (например, объемного напряжения, деформации, сдвигов, и снаружи и внутри тел), что позволяет с достаточной точностью понимать механические свойства и характеристики материалов, используемых в инженерных системах.
Вопрос-ответ:
Как можно определить объем тела, используя формулу?
Объем тела, такого как куб или цилиндр, можно найти с использованием математических формул. Например, для куба объем будет равен a * a * a (где “a” – длина стороны), а для цилиндра объем можно найти следующим образом: π * r² * h (где “π” – число Пи, “r” – радиус основания цилиндра, а “h” – высота). Таким образом, матematische Formeln помогают нам быстро и точно получить значения объема различных тел.
Чем отличается формула для объема куба от формулы для объема многоугольника?
Формула для высчитывания объема куба использует среднюю измеренную сторону “a” и возводит ее в третью степень, т.е. “a³”. В то же время формула для вычисления объема многоугольного параллелепипеда использует произведение его трёх измеряемых размеров (l * w * h), где “l” – длина, “w” – ширина, а “h” – высота. Эти формулы работают для различных форм тел, учитывая их уникальные характеристики.
Есть ли формула для вычисления объема нормальных объектов, таких как ледяной скульптур или неправильный кулак?
Для вычисления объема угловых или неправильных объектов, таких как ледяная скульптура или неправильный кулак, есть формула усеченного конуса. Эта формула предполагает знание конкретных параметров, таких как высота и радиус основы конуса, хотя в некоторых случаях для неправильных форм может потребоваться использование компьютерного моделирования или физического разделения объектов на более простые формы для более точного расчета.