
В математике куб – это твердое тело, у которого все стороны равны между собой, и это одна из самых важных фигур в геометрии. Объем куба – один из ключевых аспектов его изучения, так как он дает нам представление о пространстве, которое куб занимает. В этой статье мы рассмотрим несколько способов расчета объема куба и разберем, как тебя могут помочь в решении данной задачи.
Существует множество примеров, когда можно столкнуться с необходимостью найти объем куба – это может быть решение задач в школе, проектирование изготавливаемой мебели или даже строительство, где размеры кубических блоков играют важную роль. Поэтому эта тема довольно изучается и востребована.
В этой статье мы рассмотрим разные способы нахождения объема куба. К слову скажем, что узнать объем куба могут практически любые школьники. Данные способы настолько просты, что получится и найти калькулятор для вычислений пользователю не потребуется. Нужно только следовать нашим пунктам, и все получится!
Теперь давайте приступим к непосредственно расчету объема куба. Мы рассмотрим несколько основных методов: использование формулы, решение практических задач, использование правил геометрии. В конце этой статьи мы объединим все методы и разберем, как можно найти объем куба наиболее быстрым и самым простым способом.
Понятие и свойства куба
Куб обладает 12 ребрами, равной длины. Смежные рёбра на кубе образуют прямой угол, а каждая грань имеет четыре ребра. Куб также имеет восемь вершин, или углов, по два на каждой грани. На кубе существует 4 пар противоположных граней, и каждая пара является конгруэнтной, так как обе соответствующие грани имеют ту же площадь. Куб отличается своей тенденцией образовывать наибольшую возможную вместимость при ограниченной площади своей поверхности, что делает его идеальным вариантом при строительстве помещений и других объектов.
Один из важных свойств куба является то, что все его грани являются квадратами. Это означает, что если мы возьмем длину любой стороны куба, мы сможем вычислить площадь его основания и общую площадь всех граней просто умножением длины стороны на себя.
| Свойство | Значение |
|---|---|
| Количество граней | 6 |
| Количество ребер | 12 |
| Количество вершин | 8 |
| Протяженность ребра | a |
| Площадь основания(каждая грань) | a² |
| Общая площадь граней | 6*a² |
Куб является одним из основных геометрических тел, и имеет множество приложений в различных областях жизни, от математики и физики до архитектуры и строительства.
Основные характеристики куба
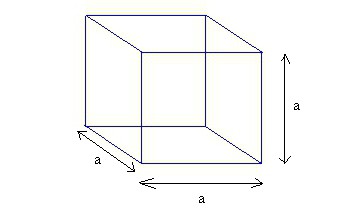
Однородность грани: Куб характеризуется тем, что все его грани и рёбра имеют одинаковую длину. Это означает, что он представляет собой образец симметрии и регулярности.
Точки связи ребра: У куба шесть квадратных граней, которые соединяются ребрами. Эти ребра образуются углами по 90 градусов, так что все грани ориентированы перпендикулярно друг другу.
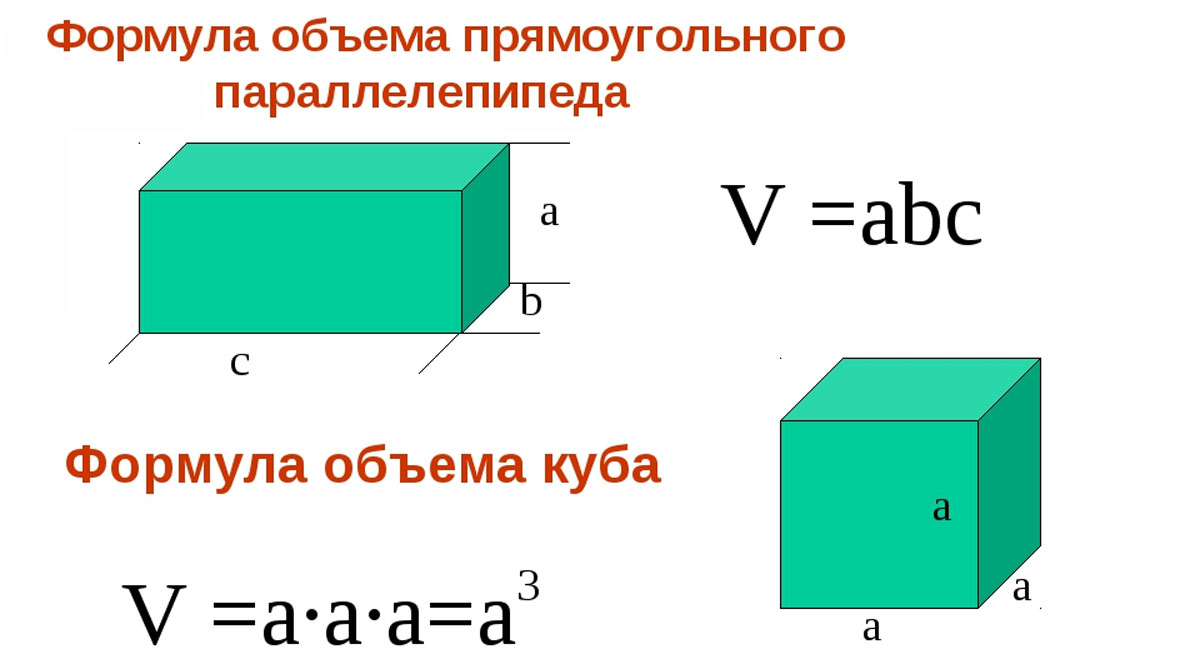
Формула объема куба: Примем за один из ребер a, тогда объём куба будет равен: V = a3. Это происходит потому, что высота, ширина и длина куба одинаковы, так что эти три измерения, умноженные друг на друга, дают объём.
Большое практическое применение: Куб часто используется в качестве основы для строительства различных конструкций, потому что он обладает стабильностью и равномерным распределением веса.
Куб в математике: Куб является важным понятием в геометрии и высшей математике, так как во всех его характеристиках есть равные единицы измерения, что полезно для математических вычислений и формул.
Типовые применения кубов

Наука и образовательные целей

Кубы играют важную роль в математике в качестве образца трёхмерной геометрии и их используют для иллюстрации и изучения различных математических принципов, таких как площадь, объём и теорию групп.
- Математика и геометрия: Кубы используются как образцы для изучения основ трёхмерной геометрии, объёмов и формы многогранников.
- Задачи на вычисление объёмов: Где участвует формула для нахождения объёма куба, считая сторону a, площадя поверхности и полная же площадь куба.
- Многоугольники и многогранники: Кубы используются как базовый шаблон для изучения многоугольников и многогранников, а также для иллюстрации возможных выбранных преобразований.
- Изучение тел с полостью: Основная идея подобного рассмотрения заключается в изучении тел с полостью, таких как шары, цилиндры, прямоугольные паралелепипеды и так далее, затрагивая самые разные области, от механики до химии.
Архитектура и строительство

Кубы применимы в архитектуре для создания эффективного использования пространства, которое считается удобным и простым в возведении, а также привлекательным для глаз.
- Промышленные здания и складские помещения: Подобное здание является типовым показателем для промышленных применений и складских помещений, когда главными требованиями к конструкции являются простота и эффективная организация площадей.
- Современная архитектура: От мегатонов любой степени сложности до подчеркнуто простых современных конструкций, куб считается одной из основных форм объёмов в самих современных зданий.
- Скульптуры и декоративное искусство: Кубы активно применяются в скульптуре и декоративном искусстве благодаря своей симметрии и простоте.
Технологии и промышленность
Кубы находят широкое применение в различных областях промышленности, где одинаковость формы становится главным критерием при производстве и сборочном процессе.
- Производство кубов из различных материалов: Кубы также практично производить и обрабатывать, поскольку это вызывает минимум сложностей при глубокой проработке формы и соединении других кубов при сборе.
- Структуры и здания: Возведение кубовидных структур и зданий хорошо подходит для отраслей, где преобладает технологичный дизайн и художественное развитие.
- Мультимедийные установки и технологические решения: Кубы работают как отличный инструмент для демонстрации технологий, в видео, монументальном искусстве, интерфейсах и т.д. Они обеспечивают определенный уровень визуальной гармония и прогрессивный дизайн.
История исследования кубов
Куб – один из самых изученных геометрических тел на протяжении всей истории. Его изучение началось еще в Древней Греции, где философы и математики пытались понять основы геометрии и ее применения.
Одним из самых известных математиков того периода был Евклид, который в своей знаменитой «Началах» описал куб как тело, ограниченное шести равными квадратами, то есть выпуклым шестьстенным телом, у которого все стороны и все углы равны. Он также дал способ нахождения объема куба, который заключается в умножении стороны куба на само себя два раза.
В последующие века ученые и математики продолжали исследовать свойства куба и других многогранников, работая над проблемами, возникающими в геометрии, физике и архитектуре.
Еще в Древнем Египте и Вавилоне кубы использовались в качестве основы строительства и создания опорных конструкций. В золотой век математики и архитекторы начали понимать, как использовать геометрию куба для создания стабильных и устойчивых построек.
В конце XIX и начале XX века развитие точных наук привело к серьезному вниманием исследованию конечных точек поверхности куба, а также его аналитической геометрии. Исследования Пьера Ферма и Габриэля Ламе помогли объяснить свойства куба и его взаимосвязь с другими геометрическими объектами.
Сегодня куб остается объектом изучения в различных областях, таких как теория чисел, физика, инженерия и кристаллография. Также куб часто символизирует начало, совершенство и симметрию. В артхаусной и модернистской архитектуре применение кубных форм до сих пор актуально.
Вопрос-ответ:
Как можно определить объем куба без доступа к математическим методам?
Объем куба можно определить, используя только знание того, что все его стороны являются одинаковой длины и все его углы являются прямыми углами. Поэтому объем куба вычисляется, умножая длину одной из сторон на себя три раза: V = a³, где a – длина стороны.
Может ли быть объем куба полученного из более крупного куба, вершина которого была выпилена на некоторой высоте?
Да, объем полученного куба равен разности объема исходного куба и объема выпиленной пирамиды: V = V_куБА – V_пирамиДА. Вычисление объема пирамиды осуществляется по той же формуле, что и объема куба (V = a³), но с учетом уменьшенных размеров.
Как проверить правильность вычисления объема куба, если известно, что он был срезан на некотором уровне?
Для проверки может использоваться метод малого блока, что означает погружение куба в воду. Вода впитывает вычегданный объем Куба. Затем можно измерить изменение уровня воды, и тем самым определить объем куба.
Какие физические свойства могут существенно влиять на измерение объема куба с точным обращением углов?
Иные физические свойства, которые могут существенно влиять на измерение объема куба, включают в себя температуру, внешнее давление и релаксация поверхности. Изменения этих параметров могут привести к изменению объема куба и затруднению получения точного измерения.
