Объем выборки как найти пример

Объем выборки как найти пример

Формула выборки — простаяПриведенная ниже формула для расчета объема выборки используется в тех случаях, когда опрашиваемым (респондентам) задается только один вопрос, на который существует только два варианта ответа. Например: «Да» и «Нет», «Покупаю» и «Не покупаю», «Пользуюсь» и «Не пользуюсь». Конечно, данную формулу можно применять только при проведении простейших исследований. Если Вам нужно определить объем выборочной совокупности при проведении более масштабных исследований, например анкетирования, то следует использовать другие формулы.

Содержание:

  • формула с пояснениями;
  • пример расчета объема выборки;
  • нормированное отклонение (таблица);
  • область применения;
  • особенности формулы.

Простая формула для расчета объема выборки

Ниже приведена простая формула для расчета объема выборки для тех случаев когда на заданный вопрос возможны лишь два варианта ответа:

Формула выборки — простая

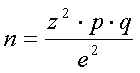
где: n – объем выборки;

z – нормированное отклонение, определяемое исходя из выбранного уровня доверительности (доверительного интервала, доверительной вероятности).

Этот показатель характеризует вероятность попадания ответов в специальный доверительный интервал — диапазон, границам которого соответствует определенный процент определенных ответов на некоторый вопрос.

Можно сказать, что уровень доверительности выражает вероятность того, что респонденты генеральной совокупности ответят так же, как и представители анализируемой выборки.

На практике доверительный интервал при проведении маркетинговых исследований часто принимают за 95% или 99%. Тогда значения z будут соответственно 1,96 и 2,58.

Также существует специальная таблица «Значение интеграла вероятностей», используя которую можно найти значение z для различных доверительных интервалов. Сокращенный вариант такой таблицы приведен ниже;

p – вариация для выборки, в долях.

Вариация характеризует величину схожести / несхожести ответов респондентов на вопрос. По сути, p — вероятность того, что респонденты выберут той или иной вариант ответа.

Допустим, если мы считаем, что четверть опрашиваемых выберут ответ «Да», то p будет равно 25%, то есть p = 0,25;

q = 1 – p.

Можно сказать, что q — это вероятность того, что респонденты не выберут анализируемый вариант ответа (в нашем примере ответят «Нет»). Например, если p = 0,25, то q = 1 – 0,25 = 0,75;

e – допустимая ошибка, в долях.

Значение допустимой ошибки заранее определяют исследователь и заказчик маркетингового исследования.

Пример расчета объема выборочной совокупности

Маркетинговая компания получила заказ на проведение социологического исследования с целью выявить долю курящих лиц в населении города. Для этого сотрудники компании будут задавать прохожим один вопрос: «Вы курите?». Возможных вариантов ответа, таким образом, только два: «Да» и «Нет».

Объем выборки в этом случае рассчитывается следующим образом. Уровень доверительности принимается за 95% (одно из стандартных значений для маркетинговых исследований), тогда нормированное отклонение z = 1,96. Проведя предварительный анализ населения города, вариацию принимаем за 50%, то есть условно считаем, что половина респондентов может ответить на вопрос о том, курят ли они — «Да». Тогда p = 0,5. Отсюда находим q = 1 – p = 1 – 0,5 = 0,5. исходя из требуемой заказчиком точности, допустимую ошибку выборки принимаем за 10%, то есть e = 0,1.

Подставляем эти данные в формулу и считаем:

Расчет выборки

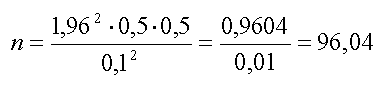
Округлив расчетное значение, получаем объем выборки n = 96 человек.

Следовательно, для проведения исследования с заданными параметрами (уровень доверительности, допустимая ошибка) компании необходимо опросить 96 человек.

Значение нормированного отклонения для различных доверительных интервалов

В таблице приведены некоторые значения нормированного отклонения (z) для важнейших уровней доверительности, или, иначе, доверительной вероятности (α):

α (%) 60 70 80 85 90 95 97 99 99,7
z 0,84 1,03 1,29 1,44 1,65 1,96 2,18 2,58 3,0

Конечно, в таблице приведены значения z только для основных уровней доверительности. Полную версию таблицы можно найти в интернете.

Область применения простой формулы выборки

При проведении простых исследований, когда нужно получить ответ всего на один простой вопрос. При этом шкала ответов, как правило, дихотомического характера. То есть предлагаются (или подразумеваются) варианты ответов по типу «Да» — «Нет», «Черное» — «Белое», «Куплю» — «Не куплю», и т. д. Иными словами возможны лишь два варианта ответа на заданный вопрос.

Особенности формулы расчета размера выборки

Для рассмотренной нами простой формулы определения объема выборки можно выделить несколько характерных особенностей:

  • перед тем, как рассчитывать объем выборки в данном случае желательно предварительно провести качественный анализ изучаемой генеральной совокупности. В частности установить степень схожести, близости изучаемых единиц совокупности в части их социальных, демографических, географических, иных характеристик. Также полезно провести пилотное (разведочное) исследование, чтобы установить приблизительную величину p;
  • нужно иметь в виду, что максимальная изменчивость (вариация ответов) соответствует значению p = 50%, так как тогда q = 50% и p × q = 0,5 × 0,5 = 0,25. Это наихудший случай, все другие значения p дадут изменчивость меньшего размера (например, при p = 80%, p × q = 0,8 × 0,2 = 0,16; а при p = 10%, p × q = 0,1 × 0,9 = 0,09). Впрочем, данный показатель влияет на объем выборки не очень сильно.

Также стоит отметить, что существует ряд иных формул для определения объема выборки в случаях с дихотомической шкалой ответов на единственный вопрос. Для более сложных маркетинговых исследований применяются другие формулы.

Источники

  1. Голубков Е. П. Маркетинговые исследования: теория, методология и практика. – М.: Издательство «Финпресс», 1998.

Статья дополнена и доработана автором 10 дек 2020 г.

© Копирование любых материалов статьи допустимо только при указании прямой индексируемой ссылки на источник: Галяутдинов Р.Р.

Нашли опечатку? Помогите сделать статью лучше! Выделите орфографическую ошибку мышью и нажмите Ctrl + Enter.

Библиографическая запись для цитирования статьи по ГОСТ Р 7.0.5-2008:
Галяутдинов Р.Р. Формула выборки – простая // Сайт преподавателя экономики. [2020]. URL: https://galyautdinov.ru/post/formula-vyborki-prostaya (дата обращения: 18.05.2023).

Источник

Запуск рекламной кампании в маркетинге предполагает А/В-тестирование, однако не каждый проведенный тест будет показательным, а его результаты – значимыми для статистики. Одна из распространенных ошибок при проведении исследований – неправильное определение нормального размера выборки. Как следствие – запуск рекламы, которая не даст результатов, и зря потраченные деньги.

Что такое объем выборки

Объем выборки – это количество людей из общего числа целевой аудитории (ЦА) продукта или бренда, участвовавших в исследовании, или количество заполненных анкет, которые были учтены при подсчете результатов.






















Что такое размер выборки


Выборка

Термин «выборка» говорит о том, что из всей совокупности участников опроса проводится оценка лишь части ответов.

В зависимости от параметров проекта, которые были указаны изначально, выборка может быть разной. Например, при случайной выборке респонденты выбираются из целевой совокупности случайным образом.

Зачем необходимо рассчитывать

Объем выборки определяют перед запуском количественных исследований в маркетинге (например, контент-анализа), чтобы узнать, какое число представителей ЦА должно поучаствовать в тестировании, и получить достоверные результаты. Если данных о объеме выборки нет, это может стать причиной того, что исследователь получит некорректные результаты.

Для качественных исследований объем выборки не определяют. Также он неактуален, если речь идет о проведении пилотных, т. е. предварительных исследований.

Основные понятия определения

В определении размера выборки участвуют различные параметры:

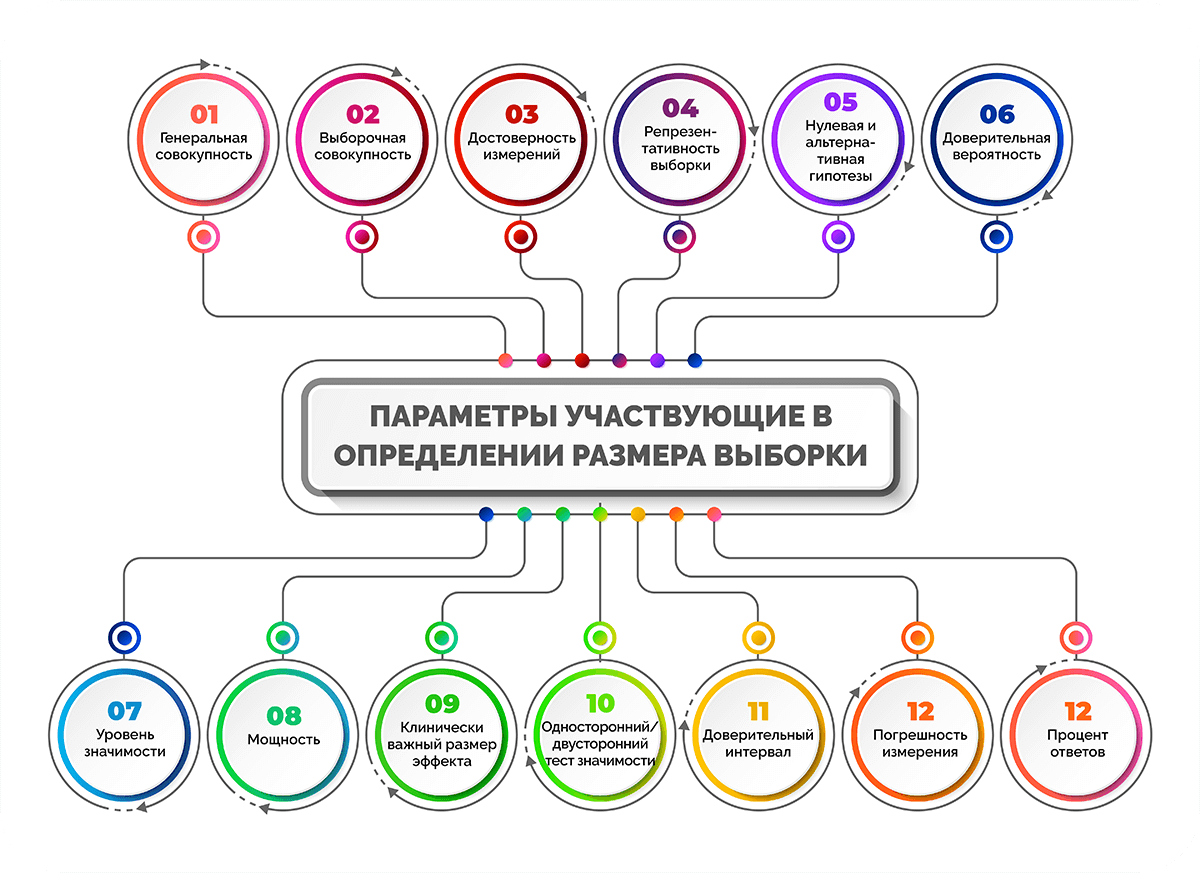
Параметры участвующие в определении размера выборки

Параметры
  • генеральная совокупность;
  • выборочная совокупность;
  • достоверность измерений;
  • репрезентативность выборки;
  • нулевая и альтернативная гипотезы;
  • доверительная вероятность;
  • уровень значимости;
  • мощность;
  • клинически важный размер эффекта;
  • односторонний / двусторонний тест значимости;
  • доверительный интервал;
  • погрешность измерения;
  • процент ответов.

Разберем, что означают основные из них.

Генеральная совокупность

Генеральной совокупностью называется общее количество объектов наблюдения, которые обладают определенными общими признаками (возраст, пол, оборот, численность, доход и пр.) и о которых будут сделаны заявления после обработки результатов исследования.

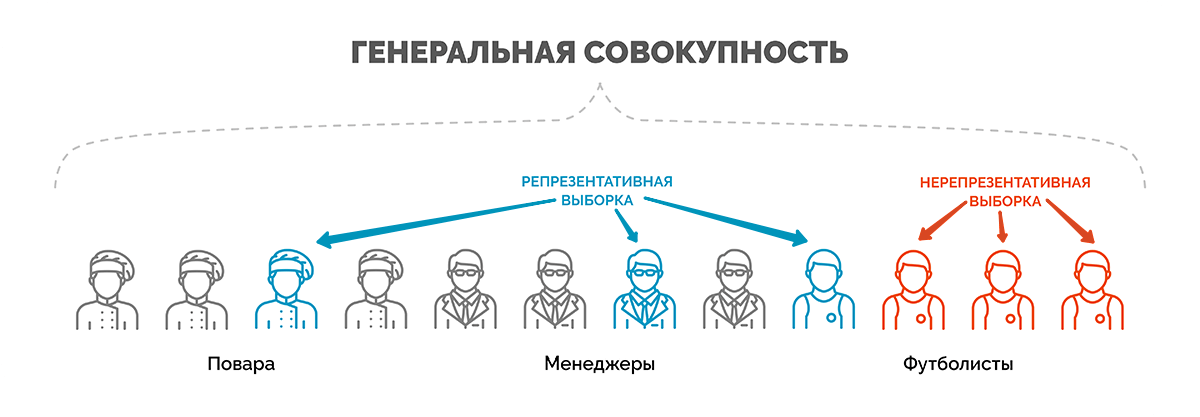
Генеральная совокупность


Пример

Объектами наблюдения могут быть люди, предприятия, домохозяйства, населенные пункты, отдельные малые социальные группы и т. д.

Если известно, что результаты опроса касаются всех жителей Москвы, то генеральная совокупность будет равна общей численности населения города, т. е. 13 млн человек (по данным 2021 года).

Оценивать свойства генеральный совокупностей, основываясь на выборочных методах, позволяет кривая нормального распределения.

Выборочная совокупность

Выборка или выборочная совокупность – это некоторая часть объектов из числа генеральной совокупности, отобранная для участия в исследовании с целью оценить распределение мнений и сделать итоговое заключение, которое будет распространяться на всю генеральную совокупность.

Характеристики выборочной совокупности должны корректно отражать параметры генеральной совокупности, т. е. обладать свойством репрезентативности. Только в данном случае заключение, сделанное исходя из результатов анализа выборки, будет с одинаковой вероятностью распространяться на представителей всей генеральной совокупности.

Выборка, состоящая из работников московских предприятий, не будет репрезентировать население города трудоспособного возраста и особенно все население столицы, т. к. не включает неработающих людей, женщин в декрете, удаленных сотрудников и т. д. Даже если мы будем увеличивать количество опрошенных работников столичных компаний, выборка все равно не сможет отразить характеристики генеральной совокупности, т. е. всего трудоспособного населения Москвы.

Погрешность измерений

Допустимая погрешность измерений – это процент возможной ошибки или отклонения результатов исследования, т. е. то значение, на которое истинный показатель может откланяться от значения, полученного в результате исследования.

Чем меньше погрешность, тем больше должна быть выборка.

Результаты опроса показали, что 60% опрощенных предпочитают делать покупки в сетевых магазинах. Предел погрешности 5% говорит о том, что в генеральной совокупности доля сторонников сетевых точек продаж может увеличиться или уменьшиться на 5% относительно уровня полученных 60%. Т. е. фактическое значение будет лежать в пределах значений от 55 до 65%.

Достоверность измерений

Уровень достоверности (надежности) измерений – это вероятность того, что полученные в результате исследования истинные результаты выбранного параметра генеральной совокупности находятся в пределах ее доверительного интервала (в примере выше это интервал 55-65%). Простыми словами, это степень уверенности в репрезентативности результатов.

Чем меньше доверительный интервал и выше заданный уровень достоверности, тем больше должна быть выборочная совокупность.

Если взять приведенный выше в статье пример с погрешностью в 5%, вы можете быть уверены в следующем: вероятность того факта, что от 55 до 65% людей предпочитают совершать покупки в сетевых магазинах, составляет не менее 95%.

Репрезентативность выборки

Под репрезентативностью понимают степень соответствия характеристик выборочной совокупности характеристикам генеральной совокупности, которые можно экстраполировать на всю популяцию.

  • выборка, состоящая на 100% из автомобилистов Санкт-Петербурга, не репрезентирует всех жителей Санкт-Петербурга;
  • выборка, состоящая только из российских фирм B2B с количеством сотрудников до 200 человек, не репрезентирует все компании страны, работающих в этом сегменте.

Исследование должно быть репрезентативным, если стоит задача по результатам количественного исследования сформировать представление о популяции в целом и правильно оценить ее. Если же исследование качественное или люди опрашиваются ради сбора мнений, предложений, идей, в этом случае репрезентативная выборка практически не играет роли.

Что влияет на результаты

Результаты тестирования могут изменяться под влиянием ряда факторов:

Факторы влияющие на результат

Факторы
  • количество вводных данных для анализа результатов;
  • правильность постановки гипотезы;
  • выбор той или иной метрики (показателя, переменных) для исследования;
  • количество тестируемых вариантов;
  • мощность исследования;
  • уровень статистической значимости;
  • стандартное отклонение (коэффициент) для количественных метрик;
  • клинически значимый эффект;
  • одно- / двусторонний тест значимости;
  • наличие парных данных в тестировании;
  • повторное измерение одних и тех же показателей;
  • равенство численности групп, участвующих в исследовании;
  • наличие иерархических данных.

Также расчет размера выборки может давать разные результаты, если анализ является:

  • рандомизированным и контролируемым;
  • рандомизированным и кластерным;
  • нерандомизированным экспериментом вмешательства;
  • исследованием эквивалентности;
  • исследованием распространенности;
  • обсервационным;
  • изучением специфичности и чувствительности теста.

Нерандомизированные тестирования взаимосвязей или различий предполагают задействования в маркетинговых исследованиях выборки гораздо большего размера, чтобы при анализе было не сложно учесть влияние третьих факторов.

Типы выборок

Различают два типа выборок: вероятностные и невероятностные или детерминированные. Каждая группа включает в себя виды. Разберем, какие из них входят в каждый тип.

Типы выборок

Типы

Вероятностные выборки:

  1. Случайная или простой случайный отбор – предполагает полный список элементов (отбираются при помощи таблицы случайных чисел), равную вероятность доступности всех из них и однородную генеральную совокупность;
  2. Механическая или систематическая – выступает в качестве разновидности случайной выборки, при этом упорядочивание происходит по тому или иному признаку, причем первый элемент отбирается случайно, затем с шагом n отбирается каждый последующий элемент;
  3. Стратифицированная или районированная – выборка используется при неоднородной генеральной совокупности, которая разделяется на страты (группы), в каждой из которых выполняется случайный отбор пропорционально их доле в генеральной совокупности;
  4. Серийная или кластерная, или гнездовая – единицами отбора выступают целые группы (гнезда или кластеры), которые могут попасть в выборку случайным образом, а все объекты внутри них подлежат сплошному исследованию.

Невероятностные (детерминированные) выборки:

  1. Квотная выборка – формируется несколько групп объектов, в каждой из которых зачастую пропорционально доле в генеральной совокупности задается определенное число объектов, которые нужно исследовать;
  2. Метод снежного кома – для формирования выборки каждый участник опроса предоставляет контакты своих знакомых; применяется для исследования труднодоступных групп респондентов;
  3. Стихийная выборка или выборка «первого встречного» – ее состав и размер заранее неизвестен и зависит от активности людей, опрос проводится среди самых доступных респондентов (интернет-опросы, опросы в журналах и газетах, анкеты на самозаполнение и т. д.);
  4. Выборка типичных случаев – для исследования отбираются отдельные представители генеральной совокупности, которым присуще среднее значение исследуемого признака.

Отбор в детерминированных выборках происходит не случайно, а по субъективным критериям: типичности, доступности, равного представительства каждой стороны и пр.

Расчет объема выборки

Расчет объема выборки – своего рода компромисс между требуемой мощностью исследования и возможностью реализовать его на практике с учетом имеющихся ресурсов и фокус-группы. При этом выбор метода расчета во многом определяется знаниями о параметрах и характеристиках изучаемых параметров.

Определить объем выборки можно двумя способами: по таблицам и с помощью формулы. Разберем эти методы.

По таблицам

Когда никаких данных о предстоящем исследовании нет, а сам эксперимент является инновационным, никто ранее ничего подобного не проводил и не предлагал решения, для определения объема выборки лучше выбрать табличный метод.

Ниже представлены различные методики. Выбор той или иной из них определяется имеющимися исходными данными или пожеланиями исследователя.

Таблица А. Определение объема выборки по методике К. А. Отдельновой

Уровень значимости

Уровень точности

Ориентировочное знакомство

Исследование средней точности

Исследование высокой точности

0,01

100

225

900

0,05

44

100

400

Объем выборки указан в абсолютных значениях.

Таблица Б. Методика определения размера выборки В. И. Паниотто

Размер генеральной совокупности

500

1000

2000

3000

4000

5000

10000

100000

∞

Объем выборки

222

286

333

350

360

370

385

398

400

Данные указаны в единицах.

Таблица В. Методика N. Fox для определения объема выборки

Процент допускаемой ошибки

Объем выборки в единицах

10

88

5

350

3

971

2

2188

1

8750

Таблица Г. Определение размера согласно способу K. Mitra, S. Das, M. Mandal

Величина различий между основной и контрольной группами

Уровень значимости

Мощность

Объем выборки

0,2

0,5

80

586

0,2

0,1

80

773

0,2

0,5

90

746

0,4

0,5

80

146

0,4

0,1

80

193

0,4

0,5

90

186

0,6

0,5

80

65

0,6

0,1

80

86

0,6

0,5

90

83

По формулам

Объем выборки, достаточный для проведения новых исследований, определяется следующими параметрами:

  • изменчивость признака;
  • уровень доверия;
  • размер эффекта.

Объем выборки всегда зависит от предполагаемой строгости эксперимента и изменчивости исследуемого признака.

Формула для оценки среднего значения размера выборки:

n = (z × σ / H)2, где:

n – размер выборки;

z – доверительный уровень (при р = 0,05 z = 1,96);

σ – стандартное отклонение;

Н – допустимая ошибка в натуральных величинах.

Формула для оценки доли выборки:

Формула для оценки доли выборки

Где:

n – размер выборки;

z – доверительный уровень (при р = 0,05 z = 1,96);

p – доля признака (наибольшее значение достигается при р = 0,5);

H – допустимая ошибка в процентах.

Еще одна формула расчета объема выборки (чаще всего калькулятор размера выборки использует именно ее):

формула расчета объема выборки

Где:

n – размер выборки;

z – нормированное отклонение;

p – вариация для выборки;

q = 1 – р;

е – допустимая ошибка.

Нормированное отклонение (z) определяется по таблице, зная основные значения доверительной вероятности (α).

α, %

60

70

80

85

90

95

97

99

99,7

z

0,84

1,03

1,29

1,44

1,65

1,96

2,18

2,58

3,0

Последняя формула расчета имеет особенности.

  • Начинать считать размер выборки следует с проведения качественного анализа генеральной совокупности, чтобы выяснить степень схожести и близости исследуемых единиц совокупности относительно их географических, демографических, социальных и других характеристик.
  • Рекомендуется предварительно выполнить пилотное исследование с целью определения приблизительного значения р.
  • Если максимальная вариация р = 50%, то и значение q = 50%, что является наиболее худшим вариантом.

Пример расчета размера выборки

Маркетолог проводит исследование с целью определить, нужны ли компании визитки. Для этого промоутеру предстоит опросить потенциальных клиентов и задавать только один вопрос: «Вы пользуетесь визитками?». На что человек должен будет ответить «Да» или «Нет».

В таком случае размер выборки будет рассчитываться так. Принимаем, что уровень доверительности равен 95% (стандартное значение). При этом нормированное отклонение z составит 1,96. После предварительного анализа предположим, что 80% представителей генеральной совокупности дадут положительный ответ, а значит, р = 0,8. Соответственно, q = 1 – 0,8 = 0,2. Вероятность допустимой ошибки примем за 10%, т. е. e = 0,1. Теперь можно выполнить расчет.

Расчета размера выборки

Округлив значение, получаем размер выборки n = 62 человека. Соответственно, в опросе с заданными параметрами нужно задействовать 62 человека из числа целевой аудитории компании.

Подходы к определению размера выборки

Выделяют несколько подходов, которые позволяют установить объем выборки для проведения статистического исследования.

Подходы к определению размера выборки

Подходы
  1. Арбитражный подход. Объем выборки составляет определенный процент от генеральной совокупности. Например, 10% от общего количество потребителей.
  2. Традиционный подход. Выборка составляется на основе определенных норм, которые были выработаны в процессе проведенных ранее исследований. Подход игнорирует обстоятельства и условия, строгая логика отсутствует.
  3. Затратный подход. Объем выборки определяется в зависимости от стоимости сбора информации и возможных затрат на материалы для проведения исследования.
  4. Подход на основе использования доверительных интервалов. Размер выборки в этом случае рассчитывается по формуле, что обеспечивает высокую точность результата:

    n = (p × q) / s2, где:

    n – размер выборки;
    p – вероятность того, что нужное событие наступит, %;
    q = 100% – p;
    s – стандартное отклонение, которое соответствует доверительному уровню.

Ошибки выборки

Объем выборки при массовом исследовании определяется двумя факторами:

  1. Точностью полученных данных или статистической погрешностью.
  2. Размером и количеством подгрупп, на которые будет разбита выборка при проведении анализа.

При любом исследовании, которое предполагает выборочный опрос респондентов из генеральной совокупности, может присутствовать погрешность данных или ошибка выборки. Выделяют два ее типа:

  • случайная – обусловлена действием статистических законов, поэтому очень легко рассчитывается по формулам теории вероятности и математической статистики;
  • систематическая – является следствием неточностей при проектировании выборки, определить ее степень смещения, направление и размер практически невозможно.

При расчете размера выборки важно так собрать данные, чтобы вероятность систематической ошибки в результате работы была минимальной.

Расчет случайной ошибки выборки зависит от объема последней, а также от степени однородности данных (дисперсии). Принцип такой: чем меньше дисперсия, тем меньше ошибка. Для расчета чаще всего используют онлайн калькуляторы.

Также выделяют:

  • Ошибки первого рода – альфа-ошибка, при которой делается вывод о достоверности гипотезы, которая на самом деле неверна. Величина выбирается произвольно в диапазоне от 0 до 1, чаще всего это значение 0,05 или 0,01.
  • Ошибки второго рода – бета-ошибка, при которой тот факт, что гипотеза неверна, остается не выявленным. Значение, как правило, устанавливается на уровне 0,2.

Расчет доверительного интервала

Для расчета доверительного интервала применяются достаточно простые формулы, выбор которых зависит от доли выборки в составе генеральной совокупности.

Если выборка значительно меньше генеральной совокупности:

Если выборка меньше генеральной совокупности

Если выборка и генеральная совокупность сопоставимы:

выборка и генеральная совокупность сопоставимы

В обеих формулах:

Δ – предельная ошибка выборки в процентах;

z – нормированное отклонение или z-фактор;

p – доля респондентов с наличием признака, который исследуется;

q – доля респондентов без исследуемого признака;

n – размер выборки;

N – объем генеральной совокупности (сколько всего респондентов).

Доверительный интервал удобно рассчитывать с помощью онлайн-калькулятора, который использует те же формулы, что мы привели выше. Просто введите необходимые переменные, и система рассчитает результат.

Расчет статистической значимости

Определить этот показатель проще всего с помощью онлайн-сервиса. Калькулятор позволяет проверить, существует ли статистически значимая разница между долями признака, которые были получены из независимых выборок.

Расчет статистической значимости

Рассчитывать статистическую значимость можно только в том случае, если произведения (n × p) и (n × (1 – р)) превышают значение 5. При этом n – объем выборки, р – доля признака.

Часто задаваемые вопросы

Обычно размер выборки и ее статистическая значимость прямо пропорциональны, т. е. с ростом выборки получение случайных результатов сводится к минимуму. Важность статистической значимости зависит от определенной ситуации. Вот некоторые из них.

Ситуация

Важность статистической значимости

Опросы сотрудников

Важна, т. к. повышает всесторонность выводов по итогам опроса.

Опросы клиентов об уровне их удовлетворенности

Не имеет значения, т. к. важен каждый ответ независимо от того, положительный он или отрицательный.

Исследование рынка

Имеет решающее значение, т. к. помогает сделать вывод о целевом рынке.

Опросы об образовании

Важна, если нужно использовать результаты исследования при внесении изменений в учебном заведении.
Не важна, если единственная цель применения – просто собрать обратную связь.

Здравоохранение

Помогает выявлять серьезные проблемы, делать выводы в исследованиях. Если же опрос проводится ради оценки удовлетворенности пациентов, то не имеет значения.

Опросы для развлечения

Не важна.

Заданный размер выборки нужен для получения оценок с желаемым уровнем точности, если речь идет об исследовании распространенности в популяции конкретной характеристики.

  • Мало просмотров.
  • Узкая тематика.
  • Низкий бюджет.
  • Высокий бюджет.

Чтобы правильно рассчитать размер выборки и провести показательное исследование с учетом выдвинутых требований:

  • наберитесь терпения и дождитесь, пока соберется требуемое количество респондентов;
  • будьте последовательны и показывайте рекламу только ЦА в определенное время;
  • устанавливайте высокий уровень достоверности при расчете выборки.

При определении объема выборки основную роль играет переменная исхода конкретного исследования. Если в расчет добавляются дополнительные важные переменные, то размер выборки должен позволять адекватно проанализировать их.

Это такое количество объектов исследования, которое позволит получить максимально точный и достоверный результат с предельно небольшой погрешностью. При этом его можно репрезентовать на более широкую аудиторию, в т. ч. по отношению к генеральной совокупности.

Заключение

Объем выборки – важный показатель, без которого невозможно провести адекватное исследование и сделать объективные выводы. Он отражает количество представителей целевой аудитории, которое будет принимать непосредственное участие в эксперименте, и требуется во всех случаях, когда стоит задача сделать определенные заключения по результатам опроса.

Нашли ошибку в тексте? Выделите нужный фрагмент и нажмите
ctrl
+
enter

Источник


Download Article


Download Article

Scientific studies often rely on surveys distributed among a sample of some total population. Your sample will need to include a certain number of people, however, if you want it to accurately reflect the conditions of the overall population it’s meant to represent. To calculate your necessary sample size, you’ll need to determine several set values and plug them into an appropriate formula.

  1. Image titled Calculate Sample Size Step 1

    1

    Know your population size. Population size refers to the total number of people within your demographic. For larger studies, you can use an approximated value instead of the precise number.

    • Precision has a greater statistical impact when you work with a smaller group. For instance, if you wish to perform a survey among members of a local organization or employees of a small business, the population size should be accurate within a dozen or so people.[1]
    • Larger surveys allow for a greater deviance in the actual population. For example, if your demographic includes everyone living in the United States, you could estimate the size to roughly 320 million people, even though the actual value may vary by hundreds of thousands.

  2. Image titled Calculate Sample Size Step 2

    2

    Determine your margin of error. Margin of error, also referred to as “confidence interval,” refers to the amount of error you wish to allow in your results.[2]

    • The margin of error is a percentage the indicates how close your sample results will be to the true value of the overall population discussed in your study.
    • Smaller margin of errors will result in more accurate answers, but choosing a smaller margin of error will also require a larger sample.
    • When the results of a survey are presented, the margin of error usually appears as a plus or minus percentage. For example: “35% of people agree with option A, with a margin of error of +/- 5%”
      • In this example, the margin of error essentially indicates that, if the entire population were asked the same poll question, you are “confident” that somewhere between 30% (35 – 5) and 40% (35 + 5) would agree with option A.

    Advertisement

  3. Image titled Calculate Sample Size Step 3

    3

    Set your confidence level. Confidence level is closely related to confidence interval (margin of error). This value measures your degree of certainty regarding how well a sample represents the overall population within your chosen margin of error.[3]

    • In other words, choosing a confidence level of 95% allows you to claim that you 95% certain that your results accurately fall within your chosen margin of error.
    • A larger confidence level indicates a greater degree of accuracy, but it will also require a larger sample. The most common confidence levels are 90% confident, 95% confident, and 99% confident.
    • Setting a confidence level of 95% for the example stated in the margin of error step would mean that you are 95% certain that 30% to 40% of the total concerned population would agree with option A of your survey.

  4. Image titled Calculate Sample Size Step 4

    4

    Specify your standard of deviation. The standard of deviation indicates how much variation you expect among your responses.

    • Extreme answers are more likely to be accurate than moderate results.
      • Plainly stated, if 99% of your survey responses answer “Yes” and only 1% answer “No,” the sample probably represents the overall population very accurately.
      • On the other hand, if 45% answer “Yes” and 55% answer “No,” there is a greater chance of error.
    • Since this value is difficult to determine you give the actual survey, most researchers set this value at 0.5 (50%). This is the worst case scenario percentage, so sticking with this value will guarantee that your calculated sample size is large enough to accurately represent the overall population within your confidence interval and confidence level.

  5. Image titled Calculate Sample Size Step 5

    5

    Find your Z-score. The Z-score is a constant value automatically set based on your confidence level. It indicates the “standard normal score,” or the number of standard deviations between any selected value and the average/mean of the population.

    • You can calculate z-scores by hand, look for an online calculator, or find your z-score on a z-score table. Each of these methods can be fairly complex, however.
    • Since confidence levels are fairly standardized, most researchers simply memorize the necessary z-score for the most common confidence levels:
      • 80% confidence => 1.28 z-score
      • 85% confidence => 1.44 z-score
      • 90% confidence => 1.65 z-score
      • 95% confidence => 1.96 z-score
      • 99% confidence => 2.58 z-score

    6. Advertisement

  1. Image titled Calculate Sample Size Step 6

    1

    Look at the equation.[4]
     If you have a small to moderate population and know all of the key values, you should use the standard formula. The standard formula for sample size is:

    • Sample Size = [z2 * p(1-p)] / e2 / 1 + [z2 * p(1-p)] / e2 * N]

      • N = population size
      • z = z-score
      • e = margin of error
      • p = standard of deviation

  2. Image titled Calculate Sample Size Step 7

    2

    Plug in your values. Replace the variable placeholders with the numerical values that actually apply to your specific survey.

    • Example: Determine the ideal survey size for a population size of 425 people. Use a 99% confidence level, a 50% standard of deviation, and a 5% margin of error.
    • For 99% confidence, you would have a z-score of 2.58.
    • This means that:
      • N = 425
      • z = 2.58
      • e = 0.05
      • p = 0.5

  3. Image titled Calculate Sample Size Step 8

    3

    Do the math. Solve the equation using the newly inserted numerical values. The solution represents your necessary sample size.

    • Example: Sample Size = [z2 * p(1-p)] / e2 / 1 + [z2 * p(1-p)] / e2 * N]

      • = [2.582 * 0.5(1-0.5)] / 0.052 / 1 + [2.582 * 0.5(1-0.5)] / 0.052 * 425]
      • = [6.6564 * 0.25] / 0.0025 / 1 + [6.6564 * 0.25] / 1.0625]
      • = 665 / 2.5663
      • = 259.39(final answer)

    4. Advertisement

  1. Image titled Calculate Sample Size Step 9

    1

    Examine the formula.[5]
     If you have a very large population or an unknown one, you’ll need to use a secondary formula. If you still have values for the remainder of the variables, use the equation:

    • Sample Size = [z2 * p(1-p)] / e2

      • z = z-score
      • e = margin of error
      • p = standard of deviation
    • Note that this equation is merely the top half of the full formula.

  2. Image titled Calculate Sample Size Step 10

    2

    Plug your values into the equation. Replace each variable placeholder with the numerical values chosen for your survey.

    • Example: Determine the necessary survey size for an unknown population with a 90% confidence level, 50% standard of deviation, a 3% margin of error.
    • For 90% confidence, use the z-score would be 1.65.
    • This means that:
      • z = 1.65
      • e = 0.03
      • p = 0.5

  3. Image titled Calculate Sample Size Step 11

    3

    Do the math. After plugging you numbers into the formula, solve the equation. Your answer will indicate your necessary sample size.

    • Example: Sample Size = [z2 * p(1-p)] / e2

      • = [1.652 * 0.5(1-0.5)] / 0.032
      • = [2.7225 * 0.25] / 0.0009
      • = 0.6806 / 0.0009
      • = 756.22 (final answer)

    4. Advertisement

  1. Image titled Calculate Sample Size Step 12

    1

    Look at the formula.[6]
     Slovin’s formula is a very general equation used when you can estimate the population but have no idea about how a certain population behaves. The formula is described as:

    • Sample Size = N / (1 + N*e2)

      • N = population size
      • e = margin of error
    • Note that this is the least accurate formula and, as such, the least ideal. You should only use this if circumstances prevent you from determining an appropriate standard of deviation and/or confidence level (thereby preventing you from determining your z-score, as well).

  2. Image titled Calculate Sample Size Step 13

    2

    Plug in the numbers. Replace each variable placeholder with the numerical values that apply specifically to your survey.

    • Example: Calculate the necessary survey size for a population of 240, allowing for a 4% margin of error.
    • This means that:
      • N = 240
      • e = 0.04

  3. Image titled Calculate Sample Size Step 14

    3

    Do the math. Solve the equation using your survey-specific numbers. The answer you arrive at should be your necessary survey size.[7]

    • Example: Sample Size = N / (1 + N*e2)

      • = 240 / (1 + 240 * 0.042)
      • = 240 / (1 + 240 * 0.0016)
      • = 240 / (1 + 0.384}
      • = 240 / (1.384)
      • = 173.41 (final answer)

    4. Advertisement

Calculator, Practice Problems, and Answers

Add New Question

  • Question

    If the total population size is not given in the problem, what formula will apply?

    Community Answer

    If the population size is not given, then a t-distribution formula is applicable.

Ask a Question

200 characters left

Include your email address to get a message when this question is answered.

Submit

Advertisement

Thanks for submitting a tip for review!

References

About This Article

Article SummaryX

To calculate sample size, first find the population size, or number of people taking your study, and margin of error, which is the amount of error you’ll allow in your results. Then, calculate your confidence level, which is how confident you are in percentage terms that your results will fall within your margin of error, and z-score, a constant value linked to your confidence level. Next, specify your standard of deviation, which is the amount of variation you expect in your results. Finally, plug your variables into the standard formula to figure out the sample size. To learn how to create a formula for unknown populations, read on!

Did this summary help you?

Thanks to all authors for creating a page that has been read 299,284 times.

Reader Success Stories

  • Orshio F

    “I recommend this to everyone who is on the same page I was until I found this article!”

Did this article help you?

Источник

Поскольку
массовый опрос, анкетирование, как
количественный метод, основан на
применении теории вероятности, мы имеем
возможность в математических терминах
оценить достоверность и допустимые
погрешности каждого добросовестно
проведенного исследования.

Под
доверительным интервалом понимают
диапазон, в который попадет истинное
значение изучаемого параметра генеральной
совокупности при данном уровне
достоверности. Чем он меньше, тем больше
должна быть выборка.

Под,
уровнем достоверности понимают
вероятность того, что истинное значение
изучаемого параметра генеральной
совокупности попадет в доверительный
интервал. Чем выше задаваемый уровень
достоверности, тем больше должна быть
выборка.

Важная
задача маркетингового исследования –
вычисление таких статистик, как выборочное
среднее и выборочная доля, и применение
их для оценки соответствующих истинных
значений генеральной совокупности.
Процесс распространения результатов
оценки выборки на оценку генеральной
совокупности называется статистическим
заключением (statistical
inference).

На
практике создается одна выборка заданного
объема и по ней вычисляются выборочные
статистики (а именно, среднее и доля).
Теоретически, для того чтобы оценить
параметр изучаемой совокупности исходя
из статистики выборки, нужно изучить
каждую возможную выборку. Если бы все
возможные выборки создавались в
действительности, распределение
статистики являлось бы выборочным
распределением. Несмотря на то, что на
практике создается только одна выборка,
понятие выборочного распределения
очень важно. Это дает возможность
использовать теорию вероятности для
того, чтобы делать выводы относительно
значений совокупности.

Статистика
(statistic) – описание характеристики
выборки. Статистика выборки используется
для оценки параметров генеральной
совокупности.

Выборочное
распределение
(sampling distribution) – это распределение
значений выборочных статистик,
рассчитанных для каждой возможной
выборки, которая формируется из изучаемой
совокупности при определенном плане
выборочного наблюдения.

Важные
характеристики выборочного распределения
среднего и соответствующие характеристики
доли для больших выборок (30 и больше)
следующие.

  1. Выборочное
    распределение среднего для больших
    выборок (n
    = 30
    и больше) можно свести к нормальному
    распределению.

  2. Среднее
    значение по совокупности μ = сумма
    элементов совокупности/количество
    элементов

  1. Стандартная
    ошибка (standard
    error) среднего или доли относится к
    выборочному распределению среднего
    или доли, а не к выборке или всей
    совокупности. В случае, если генеральная
    дисперсия (сумма квадратов отклонений
    каждого элемента выборки от генерального
    среднего / количество элементов
    совокупности) известна, используются
    следующие формулы для определения
    стандартной (среднеквадратической)
    ошибки:

Среднего: Доли:


  1. Часто
    среднеквадратичное отклонение изучаемой
    совокупности неизвестно. Тогда
    стандартная ошибка среднего может
    только оцениваться.


,
тогда

  1. Если
    объем выборки составляет 10% или больше
    от объема исследуемой совокупности,
    применение формул стандартной ошибки
    приведет к переоценке среднеквадратичного
    отклонения среднего или доли совокупности,
    Значит, его следует откорректировать,
    применив коэффициент окончательной
    коррекции совокупности. Тогда формула
    стандартной ошибки будет выглядеть
    следующим образом:

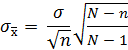
N
– объем генеральной совокупности, n
– объем выборки

Статистические
методы определения объема выборки

При
определении объема выборки следует
принимать во внимание многие качественные
факторы:

  • важность принимаемого
    решения,

  • характер
    исследования,

  • количество
    переменных,

  • характер анализа,

  • объемы выборки,
    которые использовались в подобных
    исследованиях,

  • ограниченность
    ресурсов.

Статистически
определенный объем выборки – это чистый
или конечный объем выборки, т.е. элементы
выборки, остающиеся после исключения
потенциальных респондентов, которые
не отвечают заданным критериям или не
закончили интервью. В зависимости от
коэффициентов охвата и завершенности
может потребоваться намного больший
объем исходной выборки. В коммерческих
маркетинговых исследованиях недостаток
времени, денег и хороших специалистов
может иметь решающее значение при
определении объема выборки.

Однако
профессиональный маркетолог должен
понимать статистические методы
определения объема выборки, основанные
на традиционном статистическом
заключении.

Этот
метод основан на создании доверительных
интервалов вокруг средних или долей
выборки.

Рассмотрим
понятие доверительного интервала. В
качестве примера предположим, что
исследователь провел простую случайную
выборку из 300 семей, чтобы оценить
ежемесячные расходы семьи на покупку
продуктов питания, и определил, что
средний ежемесячный расход семьи в
выборке равен 15000 рублей. Предыдущие
исследования показали, что стандартное
отклонение расходов в исследуемой
совокупности равно 9000 рублей.

Необходимо
найти интервал, в который попадал бы
определенный процент выборочных средних.
Предположим, необходимо определить
интервал вокруг среднего значения
совокупности, который включал бы 95%
выборочных средних, опираясь на выборку
из 300 семей. При нормальном распределении
95% наблюдений укладываются в ±1,96
среднеквадратических отклонений
среднего.

Для
того, чтобы вычислить доверительный
интервал, необходимо определить величину
Z,
в зависимости от выбранного уровня
достоверности. При уровне достоверности
95%, величина Z
составляет 1,96. Нет необходимости
пользоваться формулами, для вычисления
этой величины, т.к. существуют таблицы,
по которым легко вычислить Z
для любого уровня достоверности.

Следующий
шаг – вычисление доверительного
интервала, который устанавливается как

Для
начала вычислим стандартную ошибку
среднего. В нашем примере

Доверительный
интервал .= 15000±1.96*551 = 15000±1020

Таким
образом, 95%-ный доверительный интервал
находится в пределах от 16020 до 13980 рублей.
Другими словами, вероятность нахождения
истинного среднего значения наблюдаемой
совокупности в пределах от 16020 до 13980
рублей составляет 95%.

Метод,
использованный для создания доверительного
интервала, можно модифицировать так,
чтобы определить объем выборки с учетом
желательного доверительного интервала.

Предположим,
что необходимо рассчитать ежемесячные
расходы семьи на покупку продуктов
питания более точно, так, чтобы полученный
результат находился в пределах ±500
рублей от истинного среднего значения
исследуемой совокупности. Каким должен
быть объем выборки?

Ниже
приведен необходимый перечень действий,
которые необходимо выполнить.

  1. Определите
    степень точности. Это максимально
    допустимое различие (D)
    между выборочным средним и генеральным
    средним. В нашем примере D
    = ±500
    рублей.

  2. Укажите уровень
    достоверности. Предположим, что
    желательный уровень достоверности
    95%.

  3. Определите
    значение z,
    связанное
    с данным уровнем достоверности,
    воспользовавшись соответствующей
    таблицей (см. табл. 2 в Приложении). При
    95%-ном уровне достоверности вероятность
    того, что среднее значение генеральной
    совокупности выйдет за пределы
    одностороннего интервала, равна 0,025
    (0,05/2). Соответствующее значение z
    составляет
    1,96.

  4. Определите
    стандартное отклонение среднего
    генеральной совокупности. Его можно
    получить из вторичных источников или
    рассчитать, проведя разведочное
    исследование. Кроме того, стандартное
    отклонение можно установить на основе
    мнения исследователя. Например, диапазон
    нормально распределенной переменной
    примерно укладывается в шесть стандартных
    отклонений (по три слева и справа от
    среднего значения). Таким образом, можно
    рассчитать среднеквадратичное
    отклонение, разделив величину всего
    диапазона на 6. Исследователь часто
    может определить размеры диапазон,
    исходя из собственного понимания
    анализируемых явлений.

  5. Определите объем
    выборки, воспользовавшись формулой
    стандартной ошибки среднего:

;
или

В
нашем примере
1245

Из
формулы объема выборки видно, что она
растет с ростом изменчивости генеральной
совокупности, а также с увеличением
уровня достоверности и степени точности,
с которой должны проводиться расчеты.
Объем выборки прямо пропорционален

,
поэтому, чем больше показатель изменчивости
генеральной совокупности, тем больше
объем выборки.

Аналогично,
более высокий уровень достоверности
предполагает большее значение z
и, следовательно, больший объем выборки.
Переменные и z
находятся
в числителе. Увеличение степени точности
достигается уменьшением значения D
и,
следовательно, увеличивает объем
выборки, поскольку D
находится
в знаменателе.

  1. Если
    объем выборки составляет 10% и больше
    от объема генеральной совокупности,
    то применяется окончательная коррекция
    совокупности. Необходимый объем выборки
    рассчитывается по формуле:

где n
–
объем выборки до применения окончательной
коррекции;

– объем выборки
после применения окончательной коррекции,

N
– объем генеральной совокупности.

После
всего выше сказанного, следует добавить,
что объем генеральной совокупности N
не
влияет на объем выборки напрямую, за
исключением случаев, когда применяется
коэффициент окончательной коррекции
совокупности. Например, если исследуемые
характеристики всех элементов совокупности
идентичны, то выборки, состоящей из
одного элемента, вполне достаточно,
чтобы рассчитать среднее. Это также
правильно, если совокупность состоит
из 50, 500, 5000 или 50000 элементов. В то же
время изменчивость характеристик
совокупности напрямую влияет на объем
выборки. Эта изменчивость учитывается
при вычислении объема выборки с помощью
дисперсии совокупности или дисперсии
выборки

Определение
объема выборки: доля

Если
изучаемая статистика является не
средним, а долей, то маркетолог определяет
объем выборки аналогичным образом.
Предположим, что исследователя интересует
установление доли семей, владеющих
дисконтной карточкой универмага. Порядок
действий будет следующим.

  1. Укажите
    степень точности. Предположим, желательная
    степень точности такова, что допустимый
    интервал установлен на уровне

  2. Укажите
    уровень достоверности. Предположим,
    что желателен 95%-ный уровень достоверности.

  3. Определите
    значение z,
    связанное
    с данным уровнем достоверности. Как
    объяснялось при расчете среднего, оно
    составит z
    = 1,96.

  4. Определите
    генеральную долю

    .
    Ее можно получить из вторичных источников,
    в ходе экспериментального исследования
    или на основе мнения исследователя.
    Предположим, что на основе вторичных
    данных исследователь делает предположение,
    что 64% семей из изучаемой генеральной
    совокупности обладают дисконтной
    карточкой универмага. Следовательно,

    = 0,64.

  5. Определите
    объем выборки с помощью формулы
    стандартной ошибки доли:

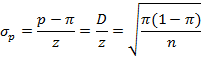
Следовательно,

В
нашем примере


355

  1. Если
    расчет

    был неверным, то доверительный интервал
    будет более или менее точным, чем
    необходимо. Предположим, что по окончании
    выборки рассчитывается значение доли
    р,
    равное
    0,55. Затем повторно вычисляется
    доверительный интервал, при этом

    используется
    для расчета неизвестного
    ,
    а именно ,

где

В нашем
примере

Доверительный
интервал тогда равен 0,55±1,96 (0,0264) = 0,55
±0,052, что означает, что он шире, чем было
задано. Это объясняется тем, что
среднеквадратичное отклонение выборки
при
р
= 0,55
оказалось большим, чем предположительное
значение среднеквадратичного отклонения
совокупности, при

= 0,64.

В
приведенных выше примерах мы рассмотрели
оценку одного параметра. На практике,
как правило, маркетолог определяет не
один, а сразу несколько параметров
целевой совокупности. В таких случаях
расчет объема выборки должен проводиться
с учетом всех оцениваемых параметров.

Корректировка
статистически определенного объема
выборки

Статистически
определенный объем выборки представляет
собой конечный, или чистый объем выборки,
который необходимо получить, чтобы
обеспечить расчет параметров с желательной
степенью точности и заданным уровнем
достоверности. При проведении опросов
он выражается в количестве завершенных
интервью. Для получения конечного объема
выборки необходимо связаться с гораздо
большим количеством потенциальных
респондентов. Другими словами, начальный
объем выборки должен намного превышать
конечный, поскольку коэффициенты охвата
и завершенности обычно составляют
меньше 100%.

Коэффициентом
охвата (incidence rate) называется степень
наличия или процент людей, подходящих
для участия в исследовании. Коэффициент
охвата определяет, какое количество
контактов с людьми необходимо осуществить,
чтобы в итоге получить объем выборки,
соответствующий заданным критериям.
Предположим, что для исследования
характеристик моющих средств необходимо
создать выборку из женщин-глав семьи в
возрасте от 25 до 55 лет. Приблизительно
75% женщин в возрасте от 20 до 60 лет, к
которым можно обратиться – это
женщины-главы семьи в возрасте от 25 до
55 лет. Это означает, что, в среднем,
необходимо обратиться к 1,33 женщин, чтобы
получить одного подходящего респондента.
Дополнительные критерии для отбора
респондентов (например, каким образом
использовался продукт) увеличивают
необходимое количество контактов.
Предположим, что дополнительным критерием
является использование женщиной моющего
средства для пола в течение последних
двух месяцев.

Предполагается,
что 60% женщин, к которым обратятся
исследователи, будут соответствовать
этому критерию. Тогда коэффициент охвата
составит 0,75 х 0,60 = 0,45. Таким образом,
конечный объем выборки следует увеличить
на 2,22 (1/0,45).

Точно
так же при определении объема выборки
необходимо учитывать ожидаемые отказы
людей, соответствующих критериям
исследования. Коэффициент завершенности
(completion rate) указывает процент респондентов,
соответствующих критериям отбора,
которые полностью прошли интервью.
Например, если исследователь предполагает,
что коэффициент завершенности интервью
составит 80% от числа подходящих
респондентов, необходимое количество
контактов следует умножить на коэффициент
1,25. Применение коэффициентов охвата и
завершенности означает, что число
контактов с потенциальными респондентами,
т.е. начальный
объем
выборки, должно быть в 2,22 х 1,25 (или 2,77)
раз больше необходимого объема выборки.
В целом, при наличии с
отборочных
критериев со степенью охвата Q1,
Q2,
Q3,… Qc каждый,
коэффициент охвата = Ql
x
Q2
x
Q3
х
… Qc.

Т.о.,

На
величину коэффициента завершенности
влияет отсутствие ответов (ненаблюдение).
Две главные проблемы, которые необходимо
решать в связи с отсутствием ответов
(ненаблюдением) при проведении выборки
– это увеличение коэффициентов отклика
и корректировка на неполучение данных.

Ошибка
неполучения данных или ненаблюдения
возникает, когда некоторые потенциальные
респонденты, включенные в выборку, не
отвечают на вопросы исследования.
Неответившие респонденты отличаются
от ответивших по демографическим,
психологическим, поведенческим и
личностным параметрам, а также имеют
другую социальную установку и мотивацию.
Если неответившие респонденты отличаются
от ответивших по характеристикам,
которые исследуются в данном случае,
результаты выборки будут опасно смещены.
Высокий коэффициент отклика обычно
означает низкий коэффициент ошибки
ненаблюдения, но при этом не будет его
адекватным показателем. Коэффициенты
отклика сами по себе не указывают,
являются ли респонденты представителями
начальной выборки. Увеличение коэффициента
отклика может не привести к уменьшению
ошибки ненаблюдения, если дополнительные
респонденты не отличаются от тех, кто
уже ответил, но отличаются от тех, кто
еще не ответил.

Контрольные
вопросы и вопросы для самостоятельного
изучения

  1. Приведите
    характеристики выборочного распределения.

  2. Что такое стандартная
    ошибка среднего и доли?

  3. Какие качественные
    факторы необходимо учитывать при
    определении объема выборки?

  4. Что показывает
    доверительный интервал?

  5. В чем различие
    между уровнем достоверности и степенью
    точности?

  6. Что такое коэффициент
    охвата и коэффициент завершенности?
    Каким образом определяется конечный
    объем выборки?

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
Источник

Объем выборки и репрезентативность

Планируем исследования и эксперименты

Если суп хорошо перемешать, то достаточно одной ложки, чтобы сделать вывод о вкусе всей кастрюли — Д.Гэллоп.

Для того, чтобы оценить любое явление, не обязательно изучать все объекты (генеральную совокупность). Для оценки здоровья человека не нужно анализировать всю кровь, достаточно небольшой пробирки. Чтобы понять настроения россиян можно не опрашивать 146 миллионов, а ограничиться несколькими тысячами. Оценка не сильно потеряет в точности.

По части судить о целом

О возможности судить о целом по части миру рассказал российский математик П.Л. Чебышев. «Закон больших чисел» простым языком можно сформулировать так: количественные закономерности массовых явлений проявляются только при

достаточном числе наблюдений

. Чем больше выборка, тем лучше случайные отклонения компенсируют друг друга и проявляется общая тенденция.

А.М. Ляпунов чуть позже сформулировал центральную предельную теорему. Она стала фундаментом для создания формул, которые позволяют рассчитать вероятность ошибки (при оценке среднего по выборке) и размер выборки, необходимый для достижения заданной точности.

Строгие формулировки:

Еще раз: чтобы корректно оценивать популяцию по выборке, нам нужна не обычная выборка, а репрезентативная выборка достаточного размера. Начнем с определения этого самого размера.

Как рассчитать объем выборки

Достаточный размер выборки зависит от следующих составляющих:

  • изменчивость признака (чем разнообразней показания, тем больше наблюдений нужно, чтобы это уловить);
  • размер эффекта (чем меньшие эффекты мы стремимся зафиксировать, тем больше наблюдений необходимо);
  • уровень доверия (уровень вероятности при который мы готовы отвергнуть нулевую гипотезу)

ЗАПОМНИТЕ
Объем выборки зависит от изменчивости признака и планируемой строгости эксперимента

Формулы для расчета объема выборки:

Формулы для определения достаточного объема выборки

Формулы расчета объема выборки

Ошибка выборки значительно возрастает, когда наблюдений меньше ста. Для исследований в которых используется 30-100 объектов применяется особая статистическая методология: критерии, основанные на распределении Стьюдента или бутстрэп-анализ. И наконец, статистика совсем слаба, когда наблюдений меньше 30.

Предельная ошибка выборки

График зависимости ошибки выборки от ее объема при оценке доли признака в г.с.

Чем больше неопределенность, тем больше ошибка. Максимальная неопределенность при оценке доли — 50% (например, 50% респондентов считают концепцию хорошей, а другие 50% плохой). Если 90% опрошенных концепция понравится — это, наоборот, пример согласованности. В таких случаях оценить долю признака по выборке проще.

Репрезентативность

Репрезентативность — это степень соответствия характеристик выборки характеристикам генеральной совокупности. Только данные по репрезентативным выборкам можно экстраполировать на всю популяцию.

Репрезентативность достигается за счет случайного отбора. Случайный отбор — хорошо. Детерминированный отбор — плохо. Он искажает структуру выборки и как следствие результат измерений. Нельзя судить о среднем росте россиян по росту ста баскетболистов, которые тренируются во дворе вашего дома, просто потому что вам так удобно.

Репрезентативность

Идеальная выборка — это когда каждый человек имеет равную вероятность попасть в число опрошенных. Полностью случайный отбор трудно достижим (это очень дорого), но к нему нужно стремиться. Сам метод сбора данных может деформировать выборку (онлайн опросы отсекают пенсионеров, опрос по стационарным телефонам — экономических активных мужчин). Представьте, как будут различаться рейтинги, если провести электоральный опрос в «Вконтакте» и в бумажной газете «Лечебные письма».

Типы выборок

Существует методология, которая позволяет сократить детерминированность при формировании выборки и приблизиться к случайному отбору.

Стратифицированная выборка. Выделяются объективно существующие страты и из каждой страты отбираются единицы пропорционально их доле в генеральной совокупности. Например для опроса россиян страты могут быть определены пропорцией населения в регионах. После чего респонденты внутри каждого региона отбираются случайным образом.

Механический отбор. Все объекты сортируются по порядковым номерам, после чего осуществляется отбор с шагом n. Например, можно отсортировать телефонные номера потенциальных участников исследования и звонить каждому 100-му.

Серийная выборка (гнездовая, кластерная). Объективно существующие группы отбираются случайным образом. Объекты внутри групп обследуются полностью. Например вскрывается один контейнер продукции и каждый товар проверяется на брак.

Метод снежного кома. У каждого респондента запрашиваются контакты его знакомых, которые подходят под условия отбора. Условия случайности отбора грубо нарушается, но это один из способов провести исследование среди труднодостижимых групп. Как быть иначе, если ваша цель — опросить любителей стальных гоночных велосипедов выпущенных не позже 1987 года.

Стихийная выборка (выборка по удобству). Применяется, когда низкая цена получения данных — это главный приоритет. Для повышения качества стихийной выборки на неё накладываются квоты. Заранее рассчитываются пропорции признаков в выборке так, чтобы они соответствовали структуре генеральной совокупности. В социологии такими признаками служат пол, возраст, профессия, семейный статус, регион проживания…

Хотите систематизировать свои знания по аналитике?

Встречайте «Анализ данных для хулиганов»


Онлайн пособие о том, как создавать великолепные продукты и эффективно управлять маркетингом на основе данных⚡

Методики / Фреймворки / Шаблоны для скачивания

Источник

Добавить комментарий