Обхват графа как найти

Обхват графа — длина наименьшего цикла, содержащегося в данном графе^[1]. Если граф не содержит циклов (то есть является ациклическим графом), его обхват по определению равен бесконечности^[2].
Например, 4-цикл (квадрат) имеет обхват 4. Квадратная решётка имеет также обхват 4, а треугольная сетка имеет обхват 3. Граф с обхватом четыре и более не имеет треугольников.

Клетки[править | править код]

Кубические графы (все вершины имеют степень три) с как можно меньшим обхватом известны как -клетки (или как (3,)-клетки). Граф Петерсена — это единственная 5-клетка (наименьший кубический граф с обхватом 5), граф Хивуда — это единственная 6-клетка, граф Макги — это единственная 7-клетка, а граф Татта — Коксетера — это единственная 8-клетка^[3]. Может существовать несколько (графов-)клеток для данного обхвата. Например, существует три неизоморфных 10-клетки, каждая с 70 вершинами — 10-клетка Балабана, граф Харриса и граф Харриса — Вонга.

Обхват и раскраска графа[править | править код]

Для любого положительного целого существует граф с обхватом и хроматическим числом . Например, граф Грёча является графом без треугольников и имеет хроматическое число 4, а многократное повторение конструкции Мыцельскиана, используемой для создания графа Грёча, образует графы без треугольников со сколь угодно большим хроматическим числом.
Пал Эрдёш доказал эту теорему используя вероятностный метод^[4].

План доказательства. Назовём циклы длиной не более короткими, а множества с и более вершин — большими. Для доказательства теоремы достаточно найти граф без коротких циклов и больших независимых множеств вершин. Тогда множества цветов в раскраске не будут большими, и, как следствие, для раскраски потребуется цветов.

Чтобы найти такой граф, будем фиксировать вероятность выбора равной . При малых в возникает лишь малое число коротких циклов. Если теперь удалить по вершине из каждого такого цикла, полученный граф не будет иметь коротких циклов, а его число независимости будет не меньше, чем у графа ^[1].

Близкие концепции[править | править код]

Нечётный обхват и чётный обхват графа — это длины наименьшего нечётного цикла и чётного цикла соответственно.

Окружность графа — это длина наибольшего по длине цикла, а не наименьшего.

Размышления о длине наименьшего нетривиального цикла можно рассматривать как обобщение 1-систолы или большей систолы в систолической геометрии.

Примечания[править | править код]

From Wikipedia, the free encyclopedia

In graph theory, the girth of an undirected graph is the length of a shortest cycle contained in the graph.^[1] If the graph does not contain any cycles (that is, it is a forest), its girth is defined to be infinity.^[2]
For example, a 4-cycle (square) has girth 4. A grid has girth 4 as well, and a triangular mesh has girth 3. A graph with girth four or more is triangle-free.

Cages[edit]

A cubic graph (all vertices have degree three) of girth g that is as small as possible is known as a g-cage (or as a (3,g)-cage). The Petersen graph is the unique 5-cage (it is the smallest cubic graph of girth 5), the Heawood graph is the unique 6-cage, the McGee graph is the unique 7-cage and the Tutte eight cage is the unique 8-cage.^[3] There may exist multiple cages for a given girth. For instance there are three nonisomorphic 10-cages, each with 70 vertices: the Balaban 10-cage, the Harries graph and the Harries–Wong graph.

Girth and graph coloring[edit]

For any positive integers g and χ, there exists a graph with girth at least g and chromatic number at least χ; for instance, the Grötzsch graph is triangle-free and has chromatic number 4, and repeating the Mycielskian construction used to form the Grötzsch graph produces triangle-free graphs of arbitrarily large chromatic number. Paul Erdős was the first to prove the general result, using the probabilistic method.^[4] More precisely, he showed that a random graph on n vertices, formed by choosing independently whether to include each edge with probability n^(1–g)/g, has, with probability tending to 1 as n goes to infinity, at most n⁄2 cycles of length g or less, but has no independent set of size n⁄2k . Therefore, removing one vertex from each short cycle leaves a smaller graph with girth greater than g, in which each color class of a coloring must be small and which therefore requires at least k colors in any coloring.

Explicit, though large, graphs with high girth and chromatic number can be constructed as certain Cayley graphs of linear groups over finite fields.^[5] These remarkable Ramanujan graphs also have large expansion coefficient.

[edit]

The odd girth and even girth of a graph are the lengths of a shortest odd cycle and shortest even cycle respectively.

The circumference of a graph is the length of the longest (simple) cycle, rather than the shortest.

Thought of as the least length of a non-trivial cycle, the girth admits natural generalisations as the 1-systole or higher systoles in systolic geometry.

Girth is the dual concept to edge connectivity, in the sense that the girth of a planar graph is the edge connectivity of its dual graph, and vice versa. These concepts are unified in matroid theory by the girth of a matroid, the size of the smallest dependent set in the matroid. For a graphic matroid, the matroid girth equals the girth of the underlying graph, while for a co-graphic matroid it equals the edge connectivity.^[6]

Computation[edit]

The girth of an undirected graph can be computed by running a breadth-first search from each node, with complexity where is the number of vertices of the graph and is the number of edges.^[7] A practical optimization is to limit the depth of the BFS to a depth that depends on the length of the smallest cycle discovered so far.^[8] Better algorithms are known in the case where the girth is even^[9] and when the graph is planar.^[10] In terms of lower bounds, computing the girth of a graph is at least as hard as solving the triangle finding problem on the graph.

References[edit]

Графы имеют различные свойства, которые используются для характеристики графов в зависимости от их структуры. Эти свойства определены в конкретных терминах, относящихся к области теории графов. В этой главе мы обсудим несколько основных свойств, которые являются общими для всех графиков.

Расстояние между двумя вершинами

Это число ребер в кратчайшем пути между вершиной U и вершиной V. Если существует несколько путей, соединяющих две вершины, то кратчайший путь рассматривается как расстояние между двумя вершинами.

Обозначение – d (U, V)

Может быть любое количество путей из одной вершины в другую. Среди них вам нужно выбрать только самый короткий.

пример

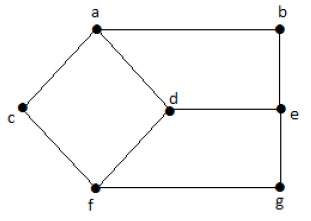
Посмотрите на следующий график –

Здесь расстояние от вершины ‘d’ до вершины ‘e’ или просто ‘de’ равно 1, поскольку между ними есть одно ребро. Существует много путей от вершины ‘d’ до вершины ‘e’ –

• да, а, бе
• дф, фг, гэ
• де (считается для расстояния между вершинами)
• дф, фц, ca, ab, be
• да, ac, cf, fg, ge

Эксцентриситет вершины

Максимальное расстояние между вершиной и всеми остальными вершинами рассматривается как эксцентриситет вершины.

Обозначение – e (V)

Расстояние от конкретной вершины до всех других вершин графа берется, и среди этих расстояний эксцентриситет является наибольшим из расстояний.

пример

На приведенном выше графике эксцентриситет «а» равен 3.

Расстояние от «a» до «b» равно 1 («ab»),

от ‘a’ до ‘c’ равно 1 (‘ac’),

от «а» до «d» равно 1 («объявление»),

от ‘a’ до ‘e’ равно 2 (‘ab’ – ‘be’) или (‘ad’ – ‘de’),

от ‘a’ до ‘f’ равно 2 (‘ac’ – ‘cf’) или (‘ad’ – ‘df’),

от ‘a’ до ‘g’ равно 3 (‘ac’ – ‘cf’ – ‘fg’) или (‘ad’ – ‘df’ – ‘fg’).

Таким образом, эксцентриситет равен 3, что является максимумом от вершины «а» от расстояния между «ag», которое является максимальным.

Другими словами,

е (б) = 3

е (с) = 3

е (д) = 2

е (е) = 3

е (е) = 3

е (г) = 3

Радиус связного графа

Минимальный эксцентриситет от всех вершин рассматривается как радиус графа G. Минимальный среди всех максимальных расстояний между вершиной до всех остальных вершин рассматривается как радиус графа G.

Обозначение – r (G)

Из всех эксцентриситетов вершин графа радиус связного графа является минимумом всех этих эксцентриситетов.

Пример – На приведенном выше графике r (G) = 2, что является минимальным эксцентриситетом для «d».

Диаметр графика

Максимальный эксцентриситет от всех вершин рассматривается как диаметр графа G. Максимальный из всех расстояний между вершиной до всех других вершин рассматривается как диаметр графа G.

Обозначение – d (G)

Из всех эксцентриситетов вершин графа диаметр связного графа является максимальным из всех этих эксцентриситетов.

Пример. На приведенном выше графике d (G) = 3; что является максимальным эксцентриситетом.

Центральная точка

Если эксцентриситет графа равен его радиусу, то он называется центральной точкой графа. Если

e (V) = r (V),

тогда «V» является центральной точкой графа «G».

Пример – в примере графика ‘d’ является центральной точкой графика.

e (d) = r (d) = 2

Центр

Множество всех центральных точек «G» называется центром графа.

Пример. В примере графика {‘d’} является центром графика.

Длина окружности

Число ребер в самом длинном цикле «G» называется окружностью «G».

Пример. На графике примера длина окружности равна 6, что мы получили из самого длинного цикла acfgeba или acfdeba.

обхват

Число ребер в кратчайшем цикле G называется его обхват.

Обозначения – g (G).

Пример – в примере графика обхват графа равен 4, который мы получили из кратчайшего цикла acfda или dfged или abeda.

Теорема о сумме степеней вершин

Если G = (V, E) ненаправленный граф с вершинами V = {V ₁ , V ₂ ,… V _n }, то

n ∑ i = 1 градус (V _i ) = 2 | E |

Следствие 1

Если G = (V, E) ориентированный граф с вершинами V = {V ₁ , V ₂ ,… V _n }, то

n ∑ i = 1 градус ⁺ (V _i ) = | E | = n ∑ i = 1 град ^– (V _i )

Следствие 2

В любом неориентированном графе число вершин с нечетной степенью является четным.

Следствие 3

В неориентированном графе, если степень каждой вершины равна k, то

к | V | = 2 | E |

Следствие 4

В неориентированном графе, если степень каждой вершины не меньше k, то

к | V | ≤ 2 | E |

Следствие 5

В неориентированном графе, если степень каждой вершины не более k, то

к | V | ≥ 2 | E |

Вершины периферийные – те, у которых e(x_i) = D(G).

Множество центральных вершин – центр, множество периферийных вершин – окраина.

Следовательно, вершина х₅ – центр графа, так как e(x₅) = r(G) = 1. Вершины x₁, x₂, x₃, x₄ – окраина.

Под средним диаметром графа понимают величину

D_ср= ,

где С – сумма кратчайших расстояний между всеми парами вершин графа, n – число вершин графа.

Для каждой пары вершин учитываем кратчайшие расстояния как d(a,b), так и d(b,a).

Найдем кратчайшие расстояния между всеми парами вершин графа G(6, 7) рис. 1.27:

d(a, b) = d(a, c) = d(b, a) = d(b, c) = d(c, a) =

= d(c, b) = d(c, d) = d(d, c) = d(d, e) = d(d, f) =

= d(e, d) = d(e, f) = d(f, d) = d(f, e) = 1,

d(a, d) = d(b, d) = d(c, e) = d(c, f) = d(d, a) = d(d, b) = d(e, c) = d(f, c)=

= d(a, e)= d(a, f) = d(b, e) = d(b, f) = d(e, a) = d(e, b) = d(f, a) = d(f, b) = 2.

Найдем сумму С всех этих расстояний: С = 1∙14 + 2∙8 + 3∙8 = 54.

Число вершин графа G(6, 7) n = 6.

Р
исунок 1.27

Найдем средний диаметр D_ср= = =1,8.

1.8. Обхват и окружение графа

Обхватом графа называют длину кратчайшего цикла (контура).

Для графа, показанного на рис. 1.28, кратчайший цикл:

a–e₇–e–e₈–d–e₃–a.

Длина этого цикла 3. Следовательно, обхват данного графа равен 3.

Окружением графа называют длину самого длинного простого цикла.

Для графа, показанного на рис. 1.28, окружение равно 5 – это длина цикла a, b, c, d, e, a.

Р
исунок 1.28

1.9. Граф – дерево

Дерево – это связный граф без циклов.

Число ребер у дерева m = n – 1 (минимальное число ребер у связного графа с n вершинами).

Следующие утверждения равносильны:

1. G – дерево.

2. G – связный граф без циклов.

3. G – связный граф с n – 1 ребром.

4. G – граф, в котором любые две вершины соединены простой цепью.

5. G – граф, у которого каждое ребро (дуга) является мостом.

У
далив, например, в графе рис. 1.29 ребро a получим граф, состоящий из двух компонент связности. Число компонент связности увеличилось до 2, следовательно, ребро a — мост. Аналогично, для других ребер.

Рисунок 1.29

Несколько деревьев образуют лес.

1.10. Обходы графа

Обходы графа совершаются с целью поиска вершины или ребра (дуги), обладающей тем или иным признаком. По организации обхода вершин (ребер) различают

• поиск в ширину,

• поиск в глубину.

Для пояснения различий этих поисков по исходному графу построим дерево рис. 1.30 с корнем в вершине – начале обхода (это этаж 1), от этой вершины проводим ребра, инцидентные ей, получаем этаж 2. Затем аналогично строим следующий этаж и т.д.

Р
исунок 1.30

Обход в ширину идет просмотром вершин этажа и далее по этажам. Это обслуживание очереди.

Обход в глубину – идем по ветви до конца, если нужная вершина не найдена, то возвращаемся до первого разветвления и далее по новой веточке вниз – обслуживание стека.

1.11. гамильтоновы и эйлеровы графы

Предположим, что имеем объект, функционирование которого описывается орграфом.

Предположим также, что неисправности объекта можно разделить на два типа:

• неисправность типа 1: приводит к потере вершины,

• неисправность типа 2: приводит к потере дуги.

При контроле работоспособности объекта с неисправностями типа 1 необходимо обойти все вершины.

При контроле работоспособности объекта с неисправностями типа 2 необходимо обойти все дуги (при этом будут пройдены и все вершины).

Очевидно, что время на проверку объекта в обоих случаях минимально, если вершины или дуги будут пройдены по одному разу.

Таким образом, задача построения проверок работоспособности объектов, функционирование которых может быть описано ориентированным графом, сводится к построению контуров или путей, включающих все вершины или все дуги по одному разу. Такие контуры или пути, а также графы, в которых их можно построить, называются гамильтоновыми (все вершины по одному разу) или эйлеровыми (все дуги по одному разу).

Граф, в котором можно обойти все вершины, побывав в них по одному разу, называется гамильтоновым. Если обход графа заканчивается в той же вершине, в которой начинался, то в результате получится гамильтонов цикл. Если обход графа закончится в другой вершине, то получится гамильтонова цепь.

Для неорграфа существует признак наличия гамильтонова цикла:

Если сумма степеней двух любых вершин графа больше или равна n , т.е. deg a + deg b  n , то в графе можно построить гамильтонов цикл.

Следствие: Если у любой вершины графа deg v_i  n/2, то в таком графе можно построить гамильтонов цикл.

Цикл (контур) и цепь (путь) называются эйлеровыми, если они содержат все ребра (дуги) графа по одному разу.

Признаком возможности построения такого цикла в неорграфе является четность степеней вершин графа. В орграфе полустепени захода и исхода должны быть равны в каждой вершине.

Признаком возможности построения эйлеровой цепи в неорграфе является наличие только двух вершин с нечетными степенями, а в орграфе наличие только двух вершин с разницей входящих и выходящих дуг, равной 1, причем в одной вершине должно быть больше выходящих дуг, а в другой входящих. Одна – будет началом, другая – концом цепи (пути).

Граф, который удовлетворяет условиям Эйлера, называется эйлеровым графом. Пример такого графа показан на рис. 1.31. У этого графа каждая вершина имеет четную степень, равную 2.

Цикл в этом графе a–e₁–b–e₃–c–e₂–a называется эйлеровым, так как он проходит через все ребра по одному разу.

Р
исунок 1.31

Примечание. Другие понятия и определения теории графов будут даны в последующих разделах при рассмотрении соответствующих тем, а также в указателе терминов и определений теории графов (См. Приложение).

1.12. Контрольные вопросы

1. Что называется графом? Какие графы вы знаете? Приведите примеры.

2. Что такое смежность вершин и смежность ребер (дуг)?

3. Какие вершина и ребро (дуга) инцидентны?

4. Что такое маршрут, цепь, путь, цикл, контур?

5. Что такое подграф и часть графа? Чем они отличаются?

6. Поясните понятия гомоморфизм и изоморфизм графов.

7. Что называется степенью вершины неорграфа? Орграфа? Чему равна сумма степеней вершин неорграфа? Орграфа?

8. Поясните понятия связность и достижимость. Что такое сильная связность, слабая связность, просто связность, вершинная связность, реберная связность?

9. Чем отличается компонента связности от компоненты сильной связности?

10. Какая вершина называется точкой сочленения?

11. Какое ребро (дуга) называется мостом (перешейком)?

12. Поясните понятия теории графов: расстояние, эксцентриситет, радиус, диаметр, средний диаметр.

13. Что такое центр и окраина графа? Приведите примеры графов с двумя и тремя центральными вершинами.

14. Что такое обхват графа? Что такое окружение графа?

15. Как организуется поиск в графах?

16. Какой граф называется гамильтоновым? Какому условию отвечает гамильтонов граф?

17. Какой граф называется эйлеровым? Каким условиям отвечает эйлеров граф?

2. Представление графов в ЭВМ

2.1. Матричная форма представления графов

2.1.1. Матрица смежности

Матрица смежности – это квадратная матрица А = , число строк и столбцов в которой равно числу вершин графа n, а элементы определяются по правилу

а_ij =

где e_ij – ребро (дуга), соединяющее вершины i и j.

Матрица А задает граф с точностью до изоморфизма (по графическому представлению графа однозначно строится матрица, а по матрице – графическое представление графа).

Два графа эквивалентны, если равны их матрицы смежности.

Два графа эквивалентны, если их матрицы смежности можно сделать одинаковыми путем одновременной перестановки строк и столбцов в одной из них.

Вот пример матрицы смежности

A_{6 6} = .

Задание. Нарисуйте граф.

Для неорграфа матрица смежности симметрична относительно главной диагонали. Для орграфа матрица смежности не симметрична.

Для мультиграфа и псевдографа:

a_ij=

m(x_i, x_j) –число ребер между вершинами х_i и х_j.

Если на вершинах графа заданы веса, то вводится дополнительный массив W длины n, в котором элемент w(i) задает значение веса вершины графа.

Если на ребрах (дугах) заданы веса, то для их задания применяется матрица смежности, но значения элементов равны весам связей.

Для мультиграфа, псевдографа с весами на ребрах и дугах используется трехмерная матрица, где третья размерность используется для записи веса ребра, дуги, петли.

2.1.2. Матрица инцидентности

Матрица инцидентности S = , имеет n строк и m столбцов, где n – число вершин в графе, m – число ребер (дуг) в графе. Элементы этой матрицы определяются по следующим правилам.

Для неорграфа

s_ij =

Вот пример матрицы инцидентности неорграфа.

S_{6 7} = .

Задание. Нарисуйте граф.

Для орграфа учитывается ориентация:

s_ij =

Здесь каждый столбец содержит один элемент, равный +1, и один элемент, равный –1, либо константу.

Два графа эквивалентны, если равны их матрицы инцидентности.

Для псевдографа показанного на рис. 2.1, получим такую матрицу (номера строк и столбцов соответствуют индексам вершин, ребер и дуг):

S_{6 9} = .

Матрица S задает граф с точностью до изоморфизма.

основное преимущество матрицы А перед матрицей S в том, что за один шаг алгоритма можно получить ответ на вопрос: есть ли ребро из вершины х_i в х_j?

Основной недостаток матрицы А – большой объем памяти независимо от числа ребер: n².

Е
сли заданы веса, то используются дополнительные векторы весов вершин и ребер (дуг).

Обхват графа — длина наименьшего цикла, содержащегося в данном графе^[1]. Если граф не содержит циклов (то есть является ациклическим графом), его обхват по определению равен бесконечности^[2].
Например, 4-цикл (квадрат) имеет обхват 4. Квадратная решётка имеет также обхват 4, а треугольная сетка имеет обхват 3. Граф с обхватом четыре и более не имеет треугольников.

Клетки

Кубические графы (все вершины имеют степень три) с как можно меньшим обхватом [math]displaystyle{ g }[/math] известны как [math]displaystyle{ g }[/math]-клетки (или как (3,[math]displaystyle{ g }[/math])-клетки). Граф Петерсена — это единственная 5-клетка (наименьший кубический граф с обхватом 5), граф Хивуда — это единственная 6-клетка, граф Макги — это единственная 7-клетка, а граф Татта — Коксетера — это единственная 8-клетка^[3]. Может существовать несколько (графов-)клеток для данного обхвата. Например, существует три неизоморфных 10-клетки, каждая с 70 вершинами — 10-клетка Балабана, граф Харриса и граф Харриса — Вонга.

Обхват и раскраска графа

Для любого положительного целого [math]displaystyle{ k }[/math] существует граф [math]displaystyle{ G }[/math] с обхватом [math]displaystyle{ g(G) ge k }[/math] и хроматическим числом [math]displaystyle{ chi(G) ge k }[/math]. Например, граф Грёча является графом без треугольников и имеет хроматическое число 4, а многократное повторение конструкции Мыцельскиана, используемой для создания графа Грёча, образует графы без треугольников со сколь угодно большим хроматическим числом.
Пал Эрдёш доказал эту теорему используя вероятностный метод^[4].

План доказательства. Назовём циклы длиной не более [math]displaystyle{ k }[/math] короткими, а множества с [math]displaystyle{ |G|/k }[/math] и более вершин — большими. Для доказательства теоремы достаточно найти граф [math]displaystyle{ G }[/math] без коротких циклов и больших независимых множеств вершин. Тогда множества цветов в раскраске не будут большими, и, как следствие, для раскраски потребуется [math]displaystyle{ k }[/math] цветов.

Чтобы найти такой граф, будем фиксировать вероятность выбора [math]displaystyle{ p }[/math] равной [math]displaystyle{ n^{epsilon – 1} }[/math]. При малых [math]displaystyle{ epsilon }[/math] в [math]displaystyle{ G }[/math] возникает лишь малое число коротких циклов. Если теперь удалить по вершине из каждого такого цикла, полученный граф [math]displaystyle{ H }[/math] не будет иметь коротких циклов, а его число независимости будет не меньше, чем у графа [math]displaystyle{ G }[/math]^[1].

Близкие концепции

Нечётный обхват и чётный обхват графа — это длины наименьшего нечётного цикла и чётного цикла соответственно.

Окружность графа — это длина наибольшего по длине цикла, а не наименьшего.

Размышления о длине наименьшего нетривиального цикла можно рассматривать как обобщение 1-систолы или большей систолы в систолической геометрии.

Примечания