Найти область аналитичности функции.
Пример 1:
Определить, является ли функция аналитической:

Решение от преподавателя:
Для данной функции находим:

Проверим выполнение условий Коши-Римана для данной функции:
– для первого условия находим:

– первое условие Коши-Римана выполнено на всей комплексной плоскости;

– второе условие Коши-Римана выполнено на всей комплексной плоскости.
Таким образом, оба условия Коши-Римана выполнены на всей комплексной плоскости. Следовательно, данная функция является аналитической на всей комплексной плоскости
Ответ: функция является аналитической на всей комплексной плоскости.
Пример 2:
Найти область аналитичности функции:
Решение от преподавателя:

Работа вам нужна срочно. Не волнуйтесь, уложимся!
Заполните, пожалуйста, данные для автора:
- 22423 авторов готовы помочь тебе.
- 2402 онлайн
Аналитические функции и их свойства
Определение аналитической функции
В теории и практике применения функций комплексного переменного интерес представляют дифференцируемые функции, причем имеющие производные не в отдельных точках, а на множествах — в областях. Такие функции называют аналитическими.
Имеют место следующие определения.
1. Функция, дифференцируемая в каждой точке области, называется аналитической в области.
2. Функция, аналитическая в окрестности некоторой точки, называется аналитической в этой точке.
3. Функция называется аналитической на замкнутом множестве , если она является аналитической в некоторой области
, содержащей это множество
.
4. Точки, в которых нарушается аналитичность функции, называются её особыми точками.
Дифференцируемость функции в точке, согласно утверждению 2.6, проверяется по правилу 2.1. Но аналитичность функции по определению связана с дифференцируемостью в области, в частности, в окрестности точки. Для исследования дифференцируемости в области (аналитичности) используется следующее обобщенное утверждение.
Утверждение 2.8. Если функция непрерывна в области и в каждой точке области выполняются условия Коши-Римана, то функция является аналитически в области.
Правило 2.2. Для исследования функции на аналитичность требуется выполнить следующие операции.
1. Найти действительную и мнимую части функции .
2. Найти частные производные функций и
или функций
и
в полярных координатах.
3. Если условия Коши-Римана (2.19) или (2.21) выполняются в каждой точке непрерывности функции, то функция в этой области аналитическая.
Производная аналитической функции может быть найдена с помощью определения, т.е. по формуле (2.1) или по формулам (2.20) или (2.22).
▼ Примеры 2.41-2.43
Пример 2.41. Исследовать на аналитичность функции:
a) ;
б) ;
в) в плоскости с разрезом по
.
Решение
Пример 2.42. Является ли функция двух действительных переменных аналитической?
Решение
Функция как функция комплексного переменного имеет вид
и является дифференцируемой на линиях или в точках — решениях системы
не образующих область. Поэтому она не является аналитической.
Пример 2.43. Доказать аналитичность функции во всей комплексной плоскости. Найти производную.
Решение
Запишем решение по правилу 2.2.
1. Действительную и мнимую части функции находим, используя формулу
Получаем .
2. Находим частные производные:
3. Условия (2.19) выполняются для любой точки , поэтому функция
дифференцируема при любом
. Кроме того, по формуле (2.20) получаем производную
, то есть
.
Здесь использованы формулы .
Свойства аналитических функций
Результаты примеров 2.41 и 2.43 не являются случайными. Более того, поскольку понятие аналитичности функции определяется через понятие дифференцируемости, то, учитывая утверждение 2.5 о свойствах функций, дифференцируемых в точке, убеждаемся в справедливости следующего утверждения.
Утверждение 2.9
1. Сумма, произведение функций, аналитических в точке, есть функция, аналитическая в этой точке. Поэтому, в силу аналитичности функции (см.пример 2.41), линейная комбинация функций, аналитических в точке, является аналитической функцией.
2. Частное функций, аналитических в точке, есть функция, аналитическая в этой точке, если знаменатель в ней отличен от нуля.
3. Суперпозиция аналитических функций — функция аналитическая.
4. Если — аналитическая в точке
и
, то обратная функция
является аналитической в
.
Эти свойства используются в большинстве случаев при исследовании функции на аналитичность. При этом отпадает необходимость проверять условия Коши-Римана. Правила нахождения производной такие же, как в действительном анализе (см. утверждение 2.5). Очевидно, совпадают и табличные производные и нет необходимости использовать формулу (2.20).
▼ Примеры 2.44-2.46
Пример 2.44. Доказать аналитичность во всей комплексной плоскости функций .
Решение
Аналитичность функций и
всюду в
следует из аналитичности функции
(пример 2.41) и п. 1 утверждения 2.9. Аналитичность многочлена
всюду в
является следствием аналитичности функции
(пример 2.41) и п. 1 утверждения 2.9.
Пример 2.45. Исследовать на аналитичность функции — рациональная функция.
Решение
Пример 2.46. Найти особые точки функций комплексного переменного:
а) ;
б) .
Решение
а) Особыми точками этих рациональных функций являются только нули знаменателей. Для это, очевидно, точки
; для
— корни уравнения
, то есть
, и точка
.
б) Особыми точками функции являются нули знаменателя, это точки
, и особая точка числителя
.
Для функции особые точки — нули знаменателя и
— особая точка знаменателя. Найдем нули знаменателя, как решения уравнений
и
. Получаем в результате
или
, и
.
Особыми точками функции являются только нули знаменателя, т.е.
, и точки, для которых
, то есть
, или
.
Бесконечная дифференцируемость аналитической функции
Отметим одно важное обстоятельство, связанное с определением производной функции комплексного переменного. В определении производной содержится требование, чтобы предел не зависел от способа стремления
к
, т.е. если существует производная
, то отношение
имеет один и тот же предел (при
) по любому пути и, в частности, по любому из бесконечного множества различных лучей, выходящих из точки
. Заметим, что для функции действительной переменной таких направлений только два — производная в точке слева и справа.
Указанное обстоятельство накладывает на дифференцируемую функцию комплексной переменной (а следовательно, и на аналитическую) более сильные ограничения, чем на дифференцируемую функцию действительной переменной, и является причиной появления некоторых дополнительных свойств этих функций.
Важным отличительным свойством аналитической функции комплексного переменного является следующее. Кроме того, что функция, согласно определению, имеет производную первого порядка в точке, она имеет в этой точке и производную любого порядка. А из существования производных любого порядка следует их непрерывность, так как непрерывность функции в точке является необходимым условием дифференцируемости. Так, из существования в точке производной второго порядка от некоторой функции следует непрерывность первой производной от этой функции в указанной точке и так далее.
Утверждение 2.10 (о бесконечной дифференцируемости аналитической функции). Функция, аналитическая в точке, имеет в этой точке производные любого порядка, которые являются непрерывными в этой точке.
Связь аналитических функций с гармоническими
Другая отличительная особенность аналитической функции связана с дифференцируемостью ее действительной и мнимой частей как функций двух действительных переменных. Во-первых, из формулы (2.19) и утверждения 2.10 следует, что эти функции имеют непрерывные частные производные любого порядка в области, где функция является аналитической. Во-вторых, нетрудно убедиться, что функции и
являются гармоническими в области аналитичности
.
Напомним, что гармонической в области называется функция
двух действительных переменных, которая имеет в
непрерывные частные производные до второго порядка включительно и удовлетворяет в
уравнению
(2.23)
Для доказательства справедливости равенства (2.23) для функций и
достаточно продифференцировать одно из равенств (2.19) (условия Коши-Римана) по
, другое — по
и воспользоваться равенством смешанных производных, которое имеет место в силу непрерывности этих производных.
Уравнение (2.23) называется уравнением Лапласа, его можно записать в виде , где
— оператор Лапласа. Уравнение имеет важное значение при решении плоских задач математической физики.
Сопряжённые гармонические функции
Две гармонические функции, связанные между собой условиями Коши-Римана, называются сопряженными гармоническими функциями. Полученное свойство аналитических функций запишем в виде утверждения.
Утверждение 2.11. Действительная и мнимая части любой аналитической в области функции являются в
сопряженными гармоническими функциями.
Учитывая, что действительная и мнимая части аналитической функции не являются независимыми друг от друга, а связаны условиями Коши-Римана, следует ожидать, что, используя эти условия, можно, зная одну из них, найти другую, а тем самым и аналитическую функцию, т.е. восстановить аналитическую функцию по заданной ее действительной или мнимой части.
Для функции, заданной в односвязной области, эта задача сводится к интегрированию полного дифференциала. Действительно, если — гармоническая в односвязной области
, то условие
(см. (2.23)) будет являться условием полного дифференциала для выражения
, т.е. существует однозначная в области
функция
, такая, что имеет место равенство
, и, следовательно,
(2.24)
С помощью (2.24) определяется функция по заданной гармонической функции
. Кроме того, сравнивая подынтегральное выражение и (2.24) с формулой полного дифференциала
для функции
, то есть
, получаем, что для частных производных функций
и
выполняются условия Коши-Римана, т.е. функция
является сопряженной с
. Из этого следует, что
— мнимая часть
и
— аналитическая функция. Полученный результат запишем в виде утверждения.
Утверждение 2.12. Для любой гармонической в односвязной области функции можно найти с точностью до постоянного слагаемого сопряженную с ней гармоническую функцию; задача решается интегрированием полного дифференциала по формуле (2.24). Постоянная определяется из дополнительного условия — задания искомой функции в некоторой точке.
Замечания 2.8
1. Если область многосвязная, то функция
, определяемая интегралом (2.24), а также функция
могут оказаться многозначными.
2. Интеграл в (2.24) не зависит от вида кривой. Если выбрать в качестве пути интегрирования ломаную, звенья которой параллельны координатным осям, то задачу можно свести к вычислению двух определенных интегралов:
(2.25)
Точка может быть выбрана любой из области определения функции. Заметим также, что в первом подынтегральном выражении значение переменной у при вычислении интеграла заменяется на
.
▼ Примеры 2.47-2.49
Пример 2.47. Проверить, что функция является гармонической. Найти сопряженную с ней функцию:
а) в области с разрезом по лучу ;
б) в плоскости с выколотой точкой .
Решение
Находим частные производные второго порядка от функции и проверяем равенство (2.23):
поэтому для любой точки плоскости, исключая точку
.
а) В односвязной области — плоскости с разрезом по действительной отрицательной полуоси в соответствии с утверждением 2.12 существует однозначная сопряженная с данной гармоническая функция. Определим ее по формуле (2.25):
Точку можно выбрать произвольной в указанной области, например
. Поэтому получаем
Нетрудно проверить, что полученная функция — гармоническая. В частности, при задании дополнительного условия
, находим значение
, то есть
и, следовательно, определенную гармоническую функцию
. Запишем функцию
, для которой заданная функция
является действительной частью, а найденная
— мнимой частью:
или — функция, аналитическая в плоскости с разрезом по лучу.
б) Область здесь не является односвязной (двусвязная). Находим функцию
по ее полному дифференциалу:
Если путь интегрирования — произвольная кривая, соединяющая точки и
, не проходящая через начало координат и не совершающая обхода вокруг
, в частности ломаная
(рис. 2.16), то результат получен в предыдущем пункте
.
Выберем теперь в качестве пути интегрирования кривую , которая, выходя из точки
, совершает один раз обход вокруг начала координат по произвольной замкнутой кривой, например по окружности радиуса
, и заканчивается в точке
(рис. 2.16). Интеграл можно представить в виде двух слагаемых:
Второе слагаемое вычислено выше. Найдем интеграл по контуру — по окружности радиуса , для которой запишем параметрические уравнения
Вычисляем криволинейный интеграл второго рода через определенный для случая параметрического задания кривой:
Таким образом, получаем результат .
Если совершает обход
раз вокруг начала координат по часовой стрелке или против часовой стрелки, то результат, очевидно, принимает вид
При задании дополнительного условия находим значение , например, при условии
имеем
. Получена многозначная функция (см. замечание 2.8)
, при этом
, очевидно, также многозначная,
или
.
Пример 2.48. Найти аналитическую функцию по заданной ее действительной части
.
Решение
Находим частные производные данной функции:
Так как равенство выполняется для любой точки
, то
— гармоническая в любой области
. Находим сопряженную с ней функцию по формуле (2.25):
Этот же результат можно получить, взяв при интегрировании , т.е.
Записываем функцию . В правой части равенства нужно заменить
и
их выражениями через переменную
; для удобства можно использовать равенство
, которое, очевидно, присутствует в выражении для
. Получаем
или , где
— комплексная константа.
Задачу можно решить иначе, используя непосредственно условия Коши-Римана. А именно из равенства находим
Заметим, что здесь интегрируется по одной из переменных (по ) функция двух переменных
, поэтому постоянная интегрирования, не зависящая от переменной интегрирования, является функцией параметра, т.е.
.
Далее, для нахождения функции используем другое условие Коши-Римана —
. Находим производную
от полученного выше выражения для
и приравниваем известной производной
. Из полученного равенства
определяем
Таким образом, найдена функция .
Пример 2.49. Пусть — гармоническая в области
функция. Найти сопряженную с ней функцию
, такую, что
, где
— аналитическая в области
функция.
Решение
Поставленную задачу можно сформулировать, как задачу восстановления аналитической функции по заданной ее мнимой части. Будем рассматривать случай односвязной области .
Функцию , согласно утверждению 2.12, находим интегрированием полного дифференциала:
или, используя условия Коши-Римана для пары сопряженных гармонических функций:
(2.26)
Если, как и выше, в качестве пути интегрирования, соединяющего точки и
, выбрать ломаную, звенья которой параллельны координатным осям, то из (2.26) получим два определенных интеграла:
(2.27)
Восстановление аналитической функции по действительной или мнимой части
Обобщая изложенный материал и рассмотренные примеры, можно сформулировать следующее правило нахождения аналитической функции по заданной ее действительной или мнимой части.
Правило 2.3. Для нахождения аналитической функции по заданной ее действительной или мнимой части необходимо выполнить следующие операции.
1. Найти частные производные до второго порядка заданной функции двух переменных или
. Проверить, если требуется, что заданная функция гармоническая, т.е. выполняется в некоторой области
равенство
или
.
2. Найти по заданной гармонической функции сопряженную с ней функцию, используя формулы (2.24) или (2.25) для нахождения или (2.26), (2.27) для нахождения
. Можно воспользоваться непосредственно условиями Коши-Римана (см. пример 2.48).
3. Записать функцию , где одна из функций (
или
) — заданная гармоническая, другая — гармоническая, сопряженная с ней. В односвязной области функция
— аналитическая (однозначная) и определена с точностью до постоянного слагаемого.
4. Если задано дополнительное условие — значение искомой функции в некоторой точке из области аналитичности функции, то следует использовать его для определения постоянной
, получившейся при нахождении сопряженной функции.
▼ Примеры 2.50-2.53
Пример 2.50. Найти аналитическую функцию , если
Решение
Запишем решение по правилу 2.3.
1. Находим частные производные функции
2. Находим функцию по формуле (2.27):
Можно проверить, что полученная функция является гармонической. Заметим, что при интегрировании можно взять
. Можно, как записано в правиле 2.3, при нахождении функции
использовать условия Коши-Римана непосредственно:
где — определенная, полученная при интегрировании функция, а функцию
требуется определить. Она находится из равенства, получаемого при сравнении выражения для
( известного из условия
, где
— заданная функция) с выражением для
, получаемым при дифференцировании по
функции
.
3. Записываем функцию
Преобразуем полученное выражение к функции переменной , используя формулы Эйлера
и тригонометрическую формулу для
. Получаем
или окончательно: , где
— действительная постоянная.
Пример 2.51. Показать, что функция является гармонической в области определения. Найти аналитическую функцию
, для которой
и
.
Решение
1. Находим частные производные функции
при
.
Далее находим производные второго порядка:
При и
частные производные
и
равны нулю, так как при этом
. Тем самым убеждаемся, что функция
удовлетворяет уравнению Лапласа
для любых
, за исключением точки
, т.е. всюду в области определения.
Согласно утверждению 2.12, в комплексной плоскости с выколотой точкой , то есть в
, существует функция
, для которой данная функция является действительной, как в данном случае, или мнимой частью. При этом в любой односвязной области
, в частности в плоскости с разрезом по лучу
(см. рис. 2.5), определяется однозначная аналитическая функция.
2. Находим функцию , сопряженную с функцией
. Используем условие Коши-Римана. Получаем:
Отсюда находим производную и приравниваем ее к
. Получаем равенство
, из которого определяем
.
В результате с точностью до произвольной постоянной с найдена функция , сопряженная с данной функцией
, причем
является мнимой частью аналитической в указанной области функции
, для которой
.
3. Записываем аналитическую функцию
или, переходя к переменной . Можно записать иначе:
или окончательно
, где
— комплексная константа.
4. Используем условие для нахождения
, или, вычисляя значение
, имеем
. Получаем
и
.
Пример 2.52. Существует ли аналитическая функция , для которой
а) ; б)
; в)
?
В случае положительного ответа найти .
Решение
а) Ответ на поставленный вопрос сводится к выяснению, является ли гармонической заданная функция двух переменных. Для гармонической функции или
находим решение по правилу 2.3.
1. Находим частные производные до второго порядка заданной функции двух переменных
Условие выполняется всюду, кроме точки
. Следовательно, функция
— гармоническая в области определения.
2. Находим сопряженную с функцию:
Полагаем , тогда остается одно слагаемое
, которое преобразуем следующим образом:
Для полученных интегралов применяем рекуррентную формулу:
при
и
.
В данном случае удобнее переписать выражение, применив эту формулу сначала для второго слагаемого
Таким образом, получена функция .
3. Записываем , преобразуя выражение к переменной
Окончательный ответ: — функция аналитическая всюду кроме
(при любом
).
б) Находим производные при
Условие выполняется на отдельных линиях вида
, следовательно,
не является гармонической. Поэтому не существует аналитической функции
, для которой
является действительной (и мнимой тоже) частью.
в) Находим производные второго порядка: . Условие
выполняется на прямых
. Функция
не является гармонической. Поэтому не существует аналитической функции
, для которой
является мнимой (и действительной тоже) частью.
Пример 2.53. Найти все аналитические функции, для которых действительная часть имеет вид .
Решение
Задача нахождения аналитической функции по ее действительной части решается, если является функцией гармонической. Здесь функция
задана, как сложная функция переменных
и
. Для решения задачи сначала определим вид гармонической функции
из условия
. Найдем частные производные второго порядка. По правилу дифференцирования сложной функции получаем:
, то есть
или
. Далее дифференцируем это произведение по переменной
, учитывая, что
— сложная функция переменной
В силу симметрии переменных вторая производная по имеет вид
Записываем уравнение Лапласа: . Обозначив
, получим для функции
дифференциальное уравнение второго порядка
, которое допускает понижение порядка с помощью замены
. Для нахождения вспомогательной функции
получаем простейшее дифференциальное уравнение
; разделяя переменные, находим
. Далее, интегрируя равенство
, получаем функцию
. Гармонические функции вида
записываются в форме
Далее, обычным образом находим сопряженную с функцию. Можно использовать результат примера 2.47. Получим
. В односвязной области — плоскости с разрезом
соответствующая аналитическая функция записывается в виде
Вводя новые обозначения для постоянных, окончательно получаем .
Приложения аналитических функций
Аналитические функции в задачах теории поля
Известные из интегрального исчисления функции многих переменных задачи векторного анализа — вычисления работы, потока векторного поля, нахождения потенциальной функции и потенциала, с физической точки зрения являются важнейшими задачами электростатики и гидродинамики, так называемыми задачами теории потенциала — исследования стационарных полей.
При исследовании плоских векторных полей в таких задачах применяются методы теории аналитических функций, так как задание функции в плоской области есть задание функции комплексного переменного.
Задание векторного поля (например, поля скоростей течения жидкости, газа) означает, что в некоторой плоской области
каждой точке
соответствует вектор
или пара
, т.е. каждому комплексному числу
соответствует число
.
Следовательно, задание векторного поля эквивалентно заданию функции комплексного переменного
.
При исследовании установившихся стационарных течений идеальной жидкости (газа) рассматриваются поля, безвихревые и без источников и стоков. Если поле или
— потенциальное (безвихревое), то по свойству таких полей выполняется условие
(2.28)
которое является условием потенциальности поля . При выполнении условия (2.28) существует функция
— потенциальная функция, для которой
и выражение
или
является полным дифференциалом, т.е.
(2.29)
Если поле к тому же соленоидально (без источников и стоков), то по определению таких полей дивергенция поля равна нулю,
, то есть
(2.30)
Условие (2.30) — является условием полного дифференциала некоторой функции , для которой справедливо равенство
(2.31)
Равенства (2.29) и (2.31) определяют для заданного поля или
две функции
и
.
Из этих условий следуют равенства и
, а также
, и поэтому
и
. Эти равенства, полученные для функций
, являются не чем иным, как условиями Коши-Римана некоторой аналитической функции
, для которой
.
Рассмотрим физический смысл функций и
как характеристик поля
.
Функция — потенциальная функция поля
; линии уровня
представляют собой семейство линий равного потенциала или семейство эквипотенциальных линий.
Линии уровня образуют семейство линий, ортогональных линиям семейства
, т.е. любая пара пересекающихся линий этих семейств образует в точке пересечения прямой угол, иначе линии уровня функций
— два семейства
и
образуют в плоскости
ортогональную сетку. Это связано с тем, что образами этих линий в плоскости
являются два ортогональных семейства
и
прямых, параллельных координатным осям
и
, а отображение с помощью аналитической функции
является конформным отображением, так как при таком отображении сохраняются углы (см. утверждение 2.7).
Вектор поля как градиент скалярного поля
, по свойству градиента направлен по нормали к линии уровня
и, следовательно, по касательной к линии
. Поэтому линии уровня
являются векторными линиями поля
, и если вектор
с физической точки зрения определяет скорость течения жидкости, то
— траектории жидких частиц. Поэтому линии
называются линиями тока поля
.
Сформулируем результат приведенных рассуждений в виде утверждения.
Утверждение 2.13
1. Исследование потенциального и соленоидального поля или
связано с исследованием функций
, которые определяются для заданного поля
по формулам (2.29) и (2.31).
2. Линии — эквипотенциальные линии, линии
-линии тока поля
. Они образуют два ортогональных друг другу семейства.
3. Функции и
являются сопряженными гармоническими функциями и определяют некоторую аналитическую функцию
. Тем самым подтверждается, что исследование поля
связано с исследованием функции
. Функция
, построенная таким образом, называется комплексным потенциалом поля
.
4. Для исследования потенциально-соленоидальных полей может быть успешно использован хорошо разработанный аппарат аналитических функций, в частности теория конформных отображений.
Аналитические функции в приложениях
Остановимся подробнее на свойстве конформности как геометрическом свойстве отображения.
Учитывая определение аналитической функции, утверждение 2.7 можно сформулировать следующим образом.
Утверждение 2.14 (о геометрическом свойстве конформного отображения). Отображение с помощью аналитической функции является конформным всюду в области аналитичности, где производная функции отлична от нуля, т.е. если , то отображение
обладает свойствами постоянства растяжения и сохранения углов (по величине и направлению отсчета) в бесконечно малой окрестности точки
аналитичности функции. Это означает, в частности, что оно сохраняет бесконечно малые окружности, т.е. окружность
, имеющая уравнение
, где
достаточно мало, при отображении
переходит в кривую
, которая с точностью до бесконечно малых величин может быть заменена окружностью
, где
(рис. 2.17).
Отображение с помощью аналитической функции можно рассматривать как преобразование подобия в бесконечно малом, так как сохраняется пропорциональность линейных размеров сходственных линий, в частности границ фигур, и имеет место равенство соответствующих углов. Так, треугольник плоскости переходит в подобный ему криволинейный треугольник плоскости
.
Теория и практика конформных отображений имеет широкое применение в различных областях: в теории потенциала, при решении краевых задач уравнений математической физики, прежде всего первой краевой задачи для уравнений Лапласа и Пуассона — задачи Дирихле и Неймана, в задачах гидродинамики и электростатики, теории упругости.
Во многих случаях возникает проблема сведения задачи, решаемой в некоторой заданной области, к решению ее в другой области, в частности в простейшей канонической области. Это — проблема нахождения отображения областей.
Для плоских областей такое отображение может определяться в виде
, т.е. сводится к нахождению соответствующей аналитической функции.
Каноническими областями при этом являются верхняя полуплоскость и круг единичного радиуса с центром в начале координат
. Принципиальным становится вопрос о самой возможности конформного отображения произвольных областей, а также о практическом осуществлении такого отображения, причем по возможности с помощью сравнительно простых функций.
Хорошо разработанная геометрическая теория функций комплексного переменного — теория конформных отображений дает ответы на эти вопросы. Первый вопрос решает теорема Римана, согласно которой для любой односвязной области, за исключением двух тривиальных случаев — всей плоскости и плоскости с одной удаленной точкой, существует конформное отображение ее на единичный круг.
Кроме того, простое дробно-линейное отображение переводит круг в себя, т.е. отображает круг
на круг
, так, что заданная точка круга
переходит в центр круга
. Это позволяет утверждать, что для любых двух односвязных областей (за исключением двух упомянутых случаев) существует конформное отображение, переводящее одну область в другую.
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Аналитическая функция. Дифференциал
Фундаментальным понятием в теории функций комплексного переменного является понятие аналитической функции.
Однозначная функция  называется аналитической (голоморфной) в точке
называется аналитической (голоморфной) в точке  , если она дифференцируема (выполнены условия Эйлера-Даламбера) в некоторой окрестности этой точки. Функция
, если она дифференцируема (выполнены условия Эйлера-Даламбера) в некоторой окрестности этой точки. Функция  называется аналитической в области
называется аналитической в области 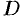 , если она дифференцируема в каждой точке
, если она дифференцируема в каждой точке 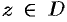 .
.
Как видно из этого определения, условие аналитичности в точке не совпадает с условием дифференцируемости функции в этой же точке (первое условие — более сильное).
Точки плоскости  , в которых однозначная функция
, в которых однозначная функция  аналитична, называются правильными точками
аналитична, называются правильными точками  . Точки, в которых функция
. Точки, в которых функция  не является аналитической, называются особыми точками этой функции.
не является аналитической, называются особыми точками этой функции.
Пусть функция 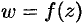 аналитична в точке
аналитична в точке  . Тогда
. Тогда 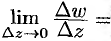
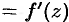 . Отсюда следует, что
. Отсюда следует, что 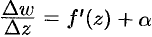 , где
, где 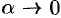 при
при 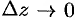 . Тогда приращение функции можно записать так:
. Тогда приращение функции можно записать так: 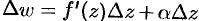 . Если
. Если 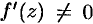 , то первое слагаемое
, то первое слагаемое 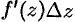 является при
является при 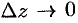 бесконечно малой того же порядка, что и
бесконечно малой того же порядка, что и 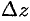 ; второе слагаемое
; второе слагаемое 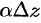 ; есть бесконечно малая более высокого порядка, чем
; есть бесконечно малая более высокого порядка, чем 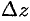 . Следовательно, первое слагаемое составляет главную часть приращения функции
. Следовательно, первое слагаемое составляет главную часть приращения функции 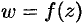 .
.
Дифференциалом 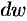 аналитической функции
аналитической функции 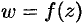 в точке
в точке  называется главная часть ее приращения, т. е.
называется главная часть ее приращения, т. е. 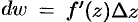 , или
, или 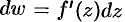 (так как при
(так как при 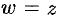 будет
будет 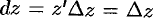 ). Отсюда следует, что
). Отсюда следует, что 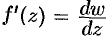 , т. е. производная функции равна отношению дифференциала функции к дифференциалу независимого переменного.
, т. е. производная функции равна отношению дифференциала функции к дифференциалу независимого переменного.
Замечание. Если функция 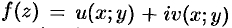 аналитична в некоторой области
аналитична в некоторой области 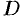 , то функции
, то функции 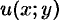 и
и 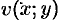 удовлетворяют дифференциальному уравнению Лапласа (
удовлетворяют дифференциальному уравнению Лапласа (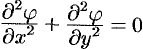 , см. п. 72.2).
, см. п. 72.2).
Действительно, дифференцируя первое из равенств Эйлера-Даламбера по 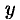 , а второе по
, а второе по 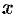 , получаем:
, получаем:
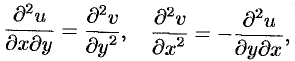
откуда 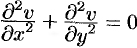 .
.
Функции 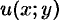 и
и 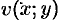 являются гармоническими функциями.
являются гармоническими функциями.
Пример №74.3.
Проверить, является ли функция 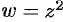 аналитической. Найти ее производную.
аналитической. Найти ее производную.
Решение:
Находим действительную 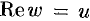 и мнимую
и мнимую 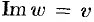 части функции:
части функции:
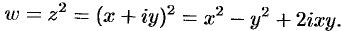
Таким образом, 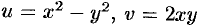 . Проверяем условия Эйлера-Даламбера (74.5):
. Проверяем условия Эйлера-Даламбера (74.5):
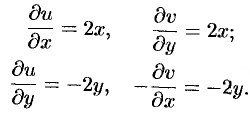
Условия (74.5) выполняются во всех точках комплексной плоскости  . Функция
. Функция 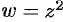 дифференцируема, следовательно, аналитична во всех точках этой плоскости. Ее производную найдем по одной из формул (74.6), например по первой:
дифференцируема, следовательно, аналитична во всех точках этой плоскости. Ее производную найдем по одной из формул (74.6), например по первой:
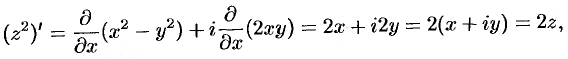
т. е. 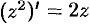 .
.
Заметим, что производную функции 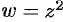 можно найти, воспользовавшись определением производной (74.4):
можно найти, воспользовавшись определением производной (74.4):
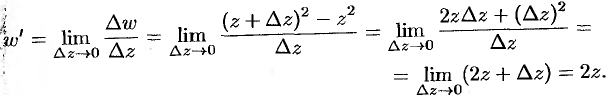
Пример №74.4.
Найти аналитическую функцию 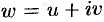 по ее заданной действительной части
по ее заданной действительной части 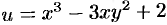 .
.
Решение:
Отметим, что функция и является гармонической функцией (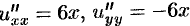 , следовательно,
, следовательно, 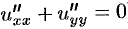 ).
).
Для определения мнимой части 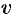 воспользуемся условиями Эйлера-Даламбера (74.5). Так как
воспользуемся условиями Эйлера-Даламбера (74.5). Так как 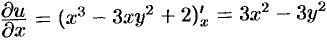 ,
,
то, согласно первому условию, 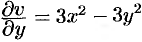 . Отсюда, интегрируя по
. Отсюда, интегрируя по 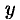 , находим:
, находим:
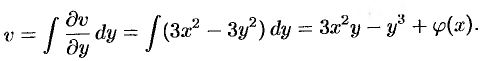
Для определения функции 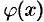 воспользуемся вторым условием Эйлера Даламбера. Так как
воспользуемся вторым условием Эйлера Даламбера. Так как
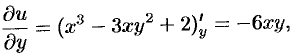
а
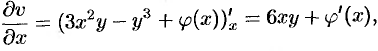
то 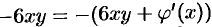 . Отсюда
. Отсюда  и
и 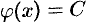 , где
, где 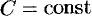 . Поэтому
. Поэтому 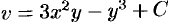 . Находим функцию
. Находим функцию 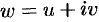 :
:
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
- Решение задач по высшей математике
Другие темы по высшей математике возможно вам они будут полезны:

Вот мы и добрались до очень интересной темы связанной напрямую с комплексными числами. Сегодня узнаем что же такое аналитическая функция и правила проверки.
Нужно дать определение. Но перед этим распишем комплексную функцию через действительную и мнимую части.
Функция комплексной переменной является аналитической и дифференцируемой, если для неё выполняются условия аналитичности:
1. Условия Коши-Римана:
2. Частная производная по “z сопряженному”:
3. Свойства аналитических функций: а) Сумма аналитических функций есть функция аналитическая. б) Произведение аналитических функций есть функция аналитическая.
Стоит отметить примеры не аналитических функций:
Держа всё это в голове или на бумаге, можно решить приличное количество задачек. Мы разберём пожалуй наиболее примитивные из них.
Задание №1:
Приступим к решению. Желательно использовать все свойства записанные ранее. Иначе могут возникнуть не состыковки.
Задание №2
Попробуем теперь условием Коши-Римана воспользоваться.
Главное в таких примерах не запутаться когда берёшь частные производные. Иногда могут попасться совсем уж навороченные.
Информации получили сегодня достаточно ещё и разобрали парочку примерчиков. По этому нужно пойти отдохнуть. Оставляйте в комментариях свои примеры. Спасибо за внимание.
Другие темы:
3.1 Дифференцирование функции комплексного переменного. Аналитичность функции
Определение
1. Функция
![]()
называется дифференцируемой
в точке
![]()
,
если существует предел
![]()
![]()
. (44)
Этот
предел называется производной
функции
в точке
.
Для
производной функции комплексного
переменного вводятся обозначения
![]()
,
![]()
.
Определение
2. Функция,
имеющая производную в некоторой точке,
называется дифференцируемой
в этой точке.
Теорема
1. Если функция
дифференцируема в точке, то она в этой
точке непрерывна.
Теорема,
обратная данной, неверна, так как можно
привести примеры функций, непрерывных
в точке, но не являющихся в ней
дифференцируемыми.
Теорема
2. Для того,
чтобы функция
была дифференцируемой в точке
![]()
,
необходимо и достаточно, чтобы приращение
функции
![]()
можно было представить в виде:
![]()
,
где
![]()
.
Теорема
3. Для того,
чтобы функция
![]()
была
дифференцируемой в точке
,
необходимо
и достаточно, чтобы функции
![]()
,
![]()
были дифференцируемы в этой точке
и выполнялись условия Коши-Римана
(иногда их называют условиями
Даламбера-Эйлера):
![]()
. (45)
Определение
3. Функция
![]()
называется аналитической
(регулярной)
в данной точке
,
если она
дифференцируема как в самой точке
,
так и в
некоторой ее окрестности.
Определение
4. Функция
называется аналитической
в области
,
если она
аналитична в каждой точке этой области.
Очевидно,
что функция, аналитическая в точке,
будет и дифференцируема в ней. Обратное
может не иметь места.
Из
определения следует, что функция
аналитична в области
,
если она дифференцируема в этой области.
Замечание.
Так как все определения аналогичны
определениям в случае функции
действительной переменной, значит для
функции комплексной переменной
справедливы обычные правила
дифференцирования и теоремы о производной
сложной и обратной функций.
Для
любой аналитической функции
имеем
![]()
. (46)
Пример
1. Показать,
что функция
![]()
аналитична, и найти
.
Получаем
![]()
,
т.е.
![]()
,
![]()
.
Поэтому
![]()
,
![]()
,
![]()
,
![]()
и, следовательно, условия (45) выполняются
во всей плоскости; по первой из формул
(46) имеем
![]()
.
Пример
2. Является
ли функция
![]()
аналитической хотя бы
в одной точке?
Получаем
![]()
,
так что
![]()
,
![]()
.
Условия Коши–Римана имеют вид:
![]()
,
![]()
и выполняются только в точке
![]()
.
Следовательно, функция
дифференцируема только в точке
и нигде не аналитична. По определению
(44) запишем:
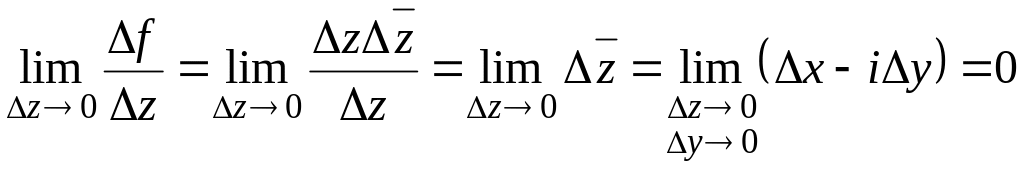
.
Таким образом, производная
![]()
существует и равна нулю.
3.2 Гармонические функции. Сопряженно-гармонические функции. Восстановление аналитической функции
Определение
1. Функция
называется гармонической
в области
,
если она имеет
в этой области непрерывные частные
производные до второго порядка
включительно и в этой области
лапласиан
![]()
,
т.е.
![]()
.
Определение
2. Две
гармонические функции
,
,
удовлетворяющие
условию (45), называются сопряженно-гармоническими
функциями.
Теорема.
Для того
чтобы функции
,
были
соответственно действительной и мнимой
частями аналитической
функции
![]()
,
необходимо
и достаточно, чтобы они были
сопряженно-гармоническими функциями.
Пользуясь
условиями
Коши-Римана, аналитическую функцию
можно
восстановить, если известна ее
действительная
или мнимая
часть
.
Пример
1. При каких
условиях трехчлен
![]()
является
гармонической функцией?
Находим:
![]()
,
![]()
.
Лапласиан
![]()
(т.е.
![]()
),
если
![]()
при любом
.
Пример
2. Найти
аналитическую функцию, если известна
ее мнимая часть
![]()
при
дополнительном условии
![]()
.
Так
как
![]()
,
то из условий Коши-Римана (45) находим
производные
![]()
(1);
![]()
(2). Решив первое из этих уравнений,
находим:
![]()
,
где
![]()
– произвольная функция переменной
.
Для определения
дифференцируем
![]()
по
и подставляем
в (2):
![]()
,
откуда
![]()
и
![]()
.
Следовательно,
![]()
и окончательно
получим:
![]()
![]()
.
Определим
![]()
:
![]()
и
![]()
;
таким образом,
![]()
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
