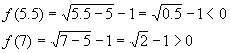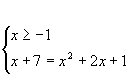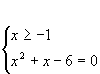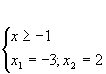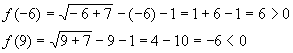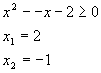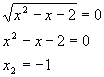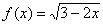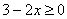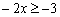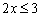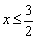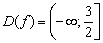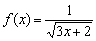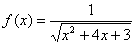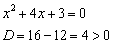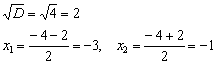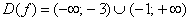Область определения иррациональной функции как найти

Учащиеся сельских школ не имеют возможности
обучаться в специализированных классах или в
классах с углубленным изучением математики,
поэтому с детьми, которым нравится математика, мы
более глубоко изучаем темы, не вошедшие в
обязательную программу, но знания которых
позволяют им успешно справиться с заданиями ЕГЭ
и тем самым без проблем поступить в ВУЗы и
продолжить образование. Одной из таких тем
является “Решение иррациональных уравнений и
неравенств”. Если решение иррациональных
уравнений в некоторых школьных учебниках
рассматривается, то решение иррациональных
неравенств нет. Я хочу предложить вам разработку
урока по теме “Решение иррациональных
неравенств методом интервалов”, который я
проводила для учащихся 9–10-х классов.

Для изучения выбрала этот метод, т.к. при его
использовании повторяется решение
иррациональных уравнений.

ХОД УРОКА

I. Приветствие учителя, обоснование темы и
цели урока.

Тема, с которой я вас хочу познакомить, поможет
при сдаче ЕГЭ и непременно понадобится вам для
продолжения образования. А в том, что вы захотите
его продолжить, я ничуть не сомневаюсь. Надеюсь,
что наше сотрудничество будет полезным и для вас
и для меня.

Я желаю вам успехов в сегодняшней работе и хочу
привести вам слова великого Микеланджело: “Если
бы люди знали, как много я тружусь, чтобы добиться
мастерства, они перестали бы считать меня таким
уж талантливым”. Слайд  1.

Действительно, только упорный труд приводит
нас к успеху. Мне бы очень хотелось, чтобы на
сегодняшнем уроке вы это почувствовали. Кто из
вас сейчас может с уверенностью сказать: “Я знаю
все досконально и могу без труда решать
иррациональные неравенства методом
интервалов?” Пожалуй, никто. Я, например,
готовясь к сегодняшнему уроку, еще много нового
открыла для себя, и хочу этим поделиться с вами.

Открываем тетради, записываем дату и тему
урока. Слайд  2.

Тема: Решение иррациональных
неравенств методом интервалов

Цель урока:

1. Усвоить алгоритм решения иррациональных
   неравенств методом интервалов.
2. Научиться решать иррациональные
   неравенства с применением алгоритма. Слайд  3

II. Итак, перейдем к реализации нашей цели:

Вспомним определение иррационального
неравенства: Слайд  4.

Иррациональным называют неравенства, в
которых переменные входят под знак корня.

Совместная работа учителя и учащихся при
разборе решения иррациональных неравенств
методом интервалов.

Решим неравенства: Слайд  5

1)

2)

3)

Разберем решение неравенств: Слайды 6–9.

1. равносильно

Шаг 1. Рассмотрим иррациональную
функцию и
найдем область определения

– область
определения

Шаг 2. Вычислим нули функции

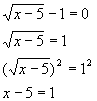
– нуль
функции

Шаг 3. На координатной прямой отмечаем
нуль функции принадлежащий области определения.
Получается два промежутка: [5;6) и (6;+). Определяем знак функции
на каждом промежутке. Выписываем промежуток, на
котором

Ответ:

2.
равносильно

Шаг 1. Рассмотрим иррациональную
функцию ,
найдем область определения

– область определения

Шаг 2. Вычислим нули функции

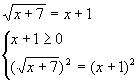
– нуль
функции

Шаг 3. На координатной прямой отмечаем
нуль функции, принадлежащий области определения.
Получаем два промежутка [-7;2) и (2;+). Определяем знак функции на
каждом промежутке. Выписываем промежуток на
котором .

Ответ:

3.

Шаг 1. Рассмотрим иррациональную
функцию ,
найдем область определения

и область
определения.

Шаг 2. Вычислим нули функции

-1; 1; 2 – нули функции

Шаг 3. На координатной прямой отмечаем
нули функции, принадлежащие области определения,
получается два промежутка (-;-1] и [2;+). Определяем знак функции на каждом
промежутке и выписываем промежуток на котором

Ответ: и

III. Итак, мы рассмотрели с вами решение трех
неравенств. Вы проследили порядок
выполнения заданий. Какие вопросы появились по
ходу объяснения? Если нет вопросов, то попробуйте
сами сформулировать алгоритм решения
иррационального неравенства методом интервала. (учащиеся
сами формулируют этапы решения иррационального
неравенства). Затем на экран проецируется
алгоритм, и, учащиеся проговаривают этапы
решения, особое внимание уделяется третьему
этапу.

Алгоритм решения иррациональных неравенств. Слайд
10

1. Рассмотрим иррациональную функцию; найдем
   область определения функции.
2. Вычислим нули функции.
3. На координатной прямой:

• отметим нули функции, принадлежащие области
  определения;
• определим знак функции на каждом промежутке;
• с учетом знака неравенства выпишем ответ.

Сейчас мы перейдем к очень ответственному
моменту, вы будете самостоятельно решать задания
с применением приведенного алгоритма. Я
предлагаю вам двигаться в своем собственном
темпе.

(Во время самостоятельной работы проходит по
рядам и смотрит, как ребята справляются с
заданиями, выделяет для себя группу контроля.
Если возникает необходимость дает
незначительные консультации на местах)

IV. Задания для самостоятельной работы:
Слайд 11

1.

2.

3.

V. Затем на экран проецируется пошаговая
проверка. За каждый правильный шаг, учащиеся
ставят себе плюс. Каждое задание оценивается
отдельно.

Проверяем: Слайд 12

1 неравенство:

1 шаг

2 шаг

3 шаг

2 неравенство

1 шаг и

2 шаг

3 шаг

3 неравенство

1 шаг

2 шаг и

3 шаг

На экран проецируем критерии оценки. Слайд 13

• 5 баллов – задание выполнено полностью и
  верно.




• 4 балла – задание верно выполнено на первом и
  втором шаге. Допущена ошибка в вычислениях на
  третьем шаге.




• 3 балла – задание верно выполнено на первом
  шаге, вычислительная ошибка на втором шаге.
• В остальных случаях – 2 балла.

VI. Затем каждый ученик получает лист
самоконтроля, на котором дано полное
решение всех трех неравенств, и с его помощью,
устраняет ошибки, допущенные в своей работе.

VII. Подводятся итоги урока и дается
задание на дом с ответами. Cлайд 14

1. Ответ

2. Ответ

3. Ответ

Нахождение области определения иррациональной функции

p -рациональное число, вида m/n

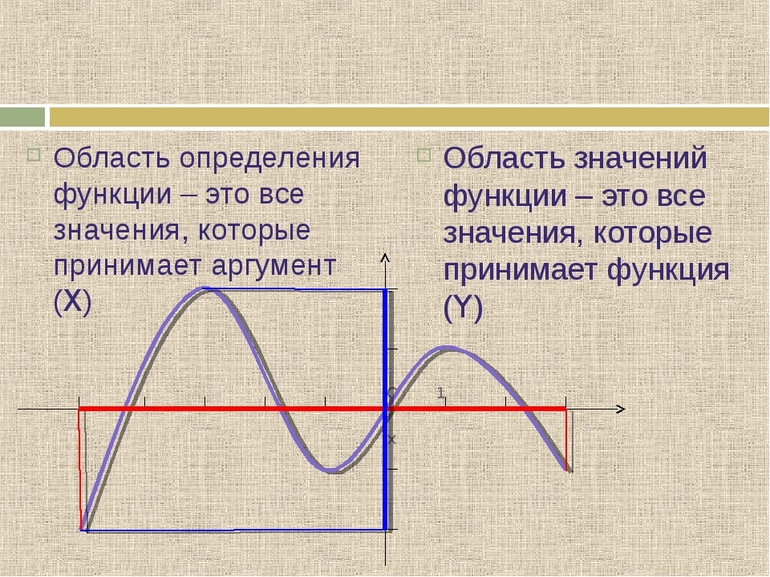
Областью определения функции называется множество всех значений аргумента x при которых функция имеет смысл

Если извлекается корень четной степени , то подкоренное выражение должно быть больше или равно нулю

Иррациональные уравнения. Можно ли писать ОДЗ?

Иррациональными называются уравнения, содержащие знак корня – квадратного, кубического или n-ной степени.

Мы помним из школьной программы: как только в уравнении или неравенстве встретились корни, дроби или логарифмы – пора вспомнить про область допустимых значений (ОДЗ) уравнения или неравенства.

По определению, ОДЗ уравнения (или неравенства) – это пересечение областей определения всех функций, входящих в уравнение или неравенство,

Например, в уравнении присутствует арифметический квадратный корень . Он определен
при .

В 2018-2019 году среди учителей появилось такое мнение, что писать слова «область допустимых значений» уже не модно. И что за это даже могут снизить оценку на экзамене.

Нет, оценку не снизят. И основных понятий школьной математики никто не отменял. Однако есть еще лучший способ оформления решения – в виде цепочки равносильных переходов. Смотрите, как решать и оформлять иррациональные уравнения:

1.Решите уравнение . Если уравнение имеет более одного корня, в ответе запишите меньший из корней.

Выражение под корнем должно быть неотрицательно. И сам корень – величина неотрицательная. Значит, и правая часть должна быть больше или равна нуля. Следовательно, уравнение равносильно системе:

Повторим, что решение таких уравнений лучше всего записывать в виде цепочки равносильных переходов. Если вы не очень хорошо понимаете, что такое система уравнений и совокупность уравнений, – повторите эту тему.

В ответ запишем меньший из корней: – 9.

Теперь уравнение, в котором есть ловушка.

2.Решите уравнение . Если уравнение имеет более одного корня, в ответе запишите меньший из корней.

Что получилось у вас? Правильный ответ: . Если у вас получилось – это был посторонний корень. Запишите решение в виде цепочки равносильных переходов, как в задаче 1, и вы поймете, что
не может быть корнем этого уравнения.

Запишем решение как цепочку равносильных преобразований. Учитесь читать такую запись и применять ее.

Произведение двух (или нескольких) множителей равно нулю тогда и только тогда, когда хотя бы один из них равен нулю, а другие при этом не теряют смысла.

А теперь сложное уравнение. Как это часто бывает, нас выручит замена переменной.

Причем новая переменная будет не одна, а целых две.

Мы можем, как в задаче 10, возвести обе части уравнения в квадрат. Но после этого придется еще раз возводить в квадрат, а это долгий способ.

Есть короткий путь!

Выразим через и :

и . Это выражения можно приравнять друг к другу.

Решим одно из уравнений. Все равно, какое, – ведь нам надо найти .

Ответ: . Заметим, что является также и корнем уравнения

Алгебра

План урока:

Иррациональные уравнения

Ранее мы рассматривали целые и дробно-рациональные уравнения. В них выражение с переменной НЕ могло находиться под знаком радикала, а также возводиться в дробную степень. Если же переменная оказывается под радикалом, то получается иррациональное уравнение.

Приведем примеры иррациональных ур-ний:

Заметим, что не всякое уравнение, содержащее радикалы, является иррациональным. В качестве примера можно привести

Это не иррациональное, а всего лишь квадратное ур-ние. Дело в том, что под знаком радикала стоит только число 5, а переменных там нет.

Простейшие иррациональные уравнения

Начнем рассматривать способы решения иррациональных уравнений. В простейшем случае в нем справа записано число, а вся левая часть находится под знаком радикала. Выглядит подобное ур-ние так:

где а – некоторое число (константа), f(x) – рациональное выражение.

Для его решения необходимо обе части возвести в степень n, тогда корень исчезнет:

Получаем рациональное ур-ние, решать которые мы уже умеем. Однако есть важное ограничение. Мы помним, что корень четной степени всегда равен положительному числу, и его нельзя извлекать из отрицательного числа. Поэтому, если в ур-нии

n – четное число, то необходимо, чтобы а было положительным. Если же оно отрицательное, то ур-ние не имеет корней. Но на нечетные n такое ограничение не распространяется.

Пример. Решите ур-ние

Решение. Справа стоит отрицательное число (– 6), но квадратный корень (если быть точными, то арифметический квадратный корень) не может быть отрицательным. Поэтому ур-ние корней не имеет.

Ответ: корней нет.

Пример. Решите ур-ние

Решение. Теперь справа стоит положительное число, значит, мы имеем право возвести обе части в квадрат. При этом корень слева исчезнет:

Пример. Решите ур-ние

Решение. Справа стоит отрицательное число, но это не является проблемой, ведь кубический корень может быть отрицательным. Возведем обе части в куб:

Конечно, под знаком корня может стоять и более сложное выражение, чем (х – 5).

Пример. Найдите решение ур-ния

Решение. Возведем обе части в пятую степень:

х 2 – 14х – 32 = 0

Получили квадратное ур-ние, которое можно решить с помощью дискриминанта:

D = b 2 – 4ac = (– 14) 2 – 4•1•(– 32) = 196 + 128 = 324

Итак, нашли два корня: (– 2) и 16.

Несколько более сложным является случай, когда справа стоит не постоянное число, а какое-то выражение с переменной g(x). Алгоритм решения тот же самый – необходимо возвести в степень ур-ние, чтобы избавиться от корня. Но, если степень корня четная, то необходимо проверить, что полученные корни ур-ния не обращают правую часть, то есть g(x), в отрицательное число. В противном случае их надо отбросить как посторонние корни.

Пример. Решите ур-ние

Решение. Возводим обе части во вторую степень:

х – 2 = х 2 – 8х + 16

D = b 2 – 4ac = (– 9) 2 – 4•1•18 = 81 – 72 = 9

Получили два корня, 3 и 6. Теперь проверим, во что они обращают правую часть исходного ур-ния (х – 4):

при х = 3 х – 4 = 3 – 4 = – 1

при х = 6 6 – 4 = 6 – 4 = 2

Корень х = 3 придется отбросить, так как он обратил правую часть в отрицательное число. В результате остается только х = 6.

Пример. Решите ур-ние

Решение. Здесь используется кубический корень, а потому возведем обе части в куб:

3х 2 + 6х – 25 = (1 – х) 3

3х 2 + 6х – 25 = 1 – 3х + 3х 2 – х 3

Получили кубическое ур-ние. Решить его можно методом подбора корня. Из всех делителей свободного коэффициента (– 26) только двойка обращает ур-ние в верное равенство:

Других корней нет. Это следует из того факта, что функция у = х 3 + 9х – 26 является монотонной.

Заметим, что если подставить х = 2 в левую часть исходного ур-ния 1 – х, то получится отрицательное число:

при х = 2 1 – х = 1 – 2 = – 1

Но означает ли это, что число 2 НЕ является корнем? Нет, ведь кубический корень вполне может быть и отрицательным (в отличие от квадратного). На всякий случай убедимся, что двойка – это действительно корень исходного уравнения:

Уравнения с двумя квадратными корнями

Ситуация осложняется, если в ур-нии есть сразу два квадратных корня. В этом случае их приходится убирать последовательно. Сначала мы переносим слагаемые через знак «=» таким образом, чтобы слева остался один из радикалов и ничего, кроме него. Возводя в квадрат такое ур-ние, мы избавимся от одного радикала, после чего мы получим более простое ур-ние. После получения всех корней надо проверить, какие из них являются посторонними. Для этого их надо просто подставить в исходное ур-ние.

Пример. Решите ур-ние

Решение. Перенесем вправо один из корней:

Возведем обе части в квадрат. Обратите внимание, что левый корень при этом исчезнет, а правый – сохранится:

Теперь снова перемещаем слагаемые так, чтобы в одной из частей не осталось ничего, кроме корня:

Снова возведем ур-ние в квадрат, чтобы избавиться и от второго корня:

(2х – 4) 2 = 13 – 3х

4х 2 – 16х + 16 = 13 – 3х

4х 2 – 13х + 3 = 0

D = b 2 – 4ac = (– 13) 2 – 4•4•3 = 169 –48 = 121

Имеем два корня: 3 и 0,25. Но вдруг среди них есть посторонние? Для проверки подставим их в исходное ур-ние. При х = 0,25 имеем:

Получилось ошибочное равенство, а это значит, что 0,25 не является корнем ур-ния. Далее проверим х = 3

На этот раз получилось справедливое равенство. Значит, тройка является корнем ур-ния.

Введение новых переменных

Предложенный метод последовательного исключения радикалов плохо работает в том случае, если корни не квадратные, а имеют другую степень. Рассмотрим ур-ние

Последовательно исключить корни, как в предыдущем примере, здесь не получится (попробуйте это сделать самостоятельно). Однако помочь может замена переменной.

Для начала перепишем ур-ние в более удобной форме, когда вместо корней используются степени:

х 1/2 – 10х 1/4 + 9 = 0

Теперь введем переменную t = x 1/4 . Тогда х 1/2 = (х 1/4 ) 2 = t 2 . Исходное ур-ние примет вид

Это квадратное ур-ние. Найдем его корни:

D = b 2 – 4ac = (– 10) 2 – 4•1•9 = 100 – 36 = 64

Получили два значения t. Произведем обратную замену:

х 1/4 = 1 или х 1/4 = 9

Возведем оба ур-ния в четвертую степень:

(х 1/4 ) 4 = 1 4 или (х 1/4 ) 4 = 3 4

х = 1 или х = 6561

Полученные числа необходимо подставить в исходное ур-ние и убедиться, что они не являются посторонними корнями:

В обоих случаях мы получили верное равенство 0 = 0, а потому оба числа, 1 и 6561, являются корнями ур-ния.

Пример. Решите ур-ние

х 1/3 + 5х 1/6 – 24 = 0

Решение. Произведем замену t = x 1/6 , тогда х 1/3 = (х 1/6 ) 2 = t 2 . Исходное ур-ние примет вид:

Его корни вычислим через дискриминант:

D = b 2 – 4ac = 5 2 – 4•1•(– 24) = 25 + 96 = 121

Далее проводим обратную заменуx 1/6 = t:

х 1/6 = – 8 или х 1/6 = 3

Первое ур-ние решений не имеет, а единственным решением второго ур-ния является х = 3 6 = 729. Если подставить это число в исходное ур-ние, то можно убедиться, что это не посторонний корень.

Замена иррационального уравнения системой

Иногда для избавления от радикалов можно вместо них ввести дополнительные переменные и вместо одного иррационального ур-ния получить сразу несколько целых, которые образуют систему. Это один из самых эффективных методов решения иррациональных уравнений.

Пример. Решите ур-ние

Решение. Заменим первый корень буквой u, а второй – буквой v:

Исходное ур-ние примет вид

Если возвести (1) и (2) в куб и квадрат соответственно (чтобы избавиться от корней), то получим:

Ур-ния (3), (4) и (5) образуют систему с тремя неизвестными, в которой уже нет радикалов:

Попытаемся ее решить. Сначала сложим (4) и (5), ведь это позволит избавиться от переменной х:

(х + 6) + (11 – х) = u 3 + v 2

из (3) можно получить, что v = 5 – u. Подставим это в (6) вместо v:

17 = u 3 + (5 – u) 2

17 = u 3 + u 2 – 10u + 25

u 3 + u 2 – 10u + 8 = 0

Получили кубическое ур-ние. Мы уже умеем решать их, подбирая корни. Не вдаваясь в подробности решения, укажем, что корнями этого ур-ния являются числа

подставим полученные значения в (4):

x + 6 = 1 3 или х + 6 = 2 3 или х + 6 = (– 4) 3

x + 6 = 1 или х + 6 = 8 или х + 6 = – 64

х = – 5 или х = 2 или х = – 70

Итак, нашли три возможных значения х. Но, конечно же, среди них могут оказаться посторонние корни. Поэтому нужна проверка – подставим полученные результаты в исходное ур-ние. При х = – 5 получим

Корень подошел. Проверяем следующее число, х = 2:

Корень снова оказался верным. Осталась последняя проверка, для х = – 70:

Итак, все три числа прошли проверку.

Уравнения с «вложенными» радикалами

Порою в ур-нии под знаком радикала стоит ещё один радикал. В качестве примера приведем такую задачу:

При их решении следует сначала избавиться от «внешнего радикала», после чего можно будет заняться и внутренним. То есть в данном случае надо сначала возвести обе части равенства в квадрат:

Внешний радикал исчез. Теперь будем переносить слагаемые, чтобы в одной из частей остался только радикал:

Хочется поделить полученное ур-ние (1) на х, однако важно помнить, что деление на ноль запрещено. То есть, если мы делим на х, то мы должны наложить дополнительное ограничение х ≠ 0. Случай же, когда х всё же равен нулю, мы рассматриваем отдельно. Для этого подставим х = 0 сразу в исходное ур-ние:

Получили верное рав-во, значит, 0 является корнем. Теперь возвращаемся к (1) и делим его на х:

Возводим в квадрат и получаем:

х 2 + 40 = (х + 4) 2

х 2 + 40 = х 2 + 8х + 16

И снова нелишней будет проверка полученного корня:

Иррациональные неравенства

По аналогии с иррациональными ур-ниями иррациональными неравенствами называют такие нер-ва, в которых выражение с переменной находится под знаком радикала или возводится в дробную степень. Приведем примеры иррациональных нер-в:

Нет смысла решать иррациональные нер-ва, если есть проблемы с более простыми, то есть рациональными нер-вами, а также с их системами. Поэтому на всякий случай ещё раз просмотрите этот и ещё вот этот уроки.

Начнем с решения иррациональных неравенств простейшего вида, у которых в одной из частей стоит выражение под корнем, а в другой – постоянное число. Достаточно очевидно, что нер-во вида

Может быть справедливым только тогда, когда

То есть, грубо говоря, нер-ва можно возводить в степень. Однако при этом могут возникнуть посторонние решения. Дело в том, что нужно учитывать и тот факт, что подкоренное выражение должно быть неотрицательным в том случае, если степень корня является четной. Таким образом, нер-во

при четном n можно заменить системой нер-в

Пример. При каких значениях x справедливо нер-во

Решение. С одной стороны, при возведении нер-ва в квадрат мы получим такое нер-во:

х ⩽ – 5 (знак нер-ва изменился из-за того, что мы поделили его на отрицательное число)

Получили промежуток х∈(– ∞; – 5). Казалось бы, надо записать ещё одно нер-во

чтобы подкоренное выражение было неотрицательным. Однако сравните (1) и (2). Ясно, что если (1) выполняется, то справедливым будет и (2), ведь если какое-то выражение больше или равно двум, то оно автоматически будет и больше нуля! Поэтому (2) можно и не решать.

Теперь посмотрим на простейшие нер-ва с корнем нечетной степени.

Пример. Найдите решение нер-ва

Решение. Всё очень просто – надо всего лишь возвести обе части в куб:

x 2 – 7x– 8 2 – 7x– 8 = 0

D = b 2 – 4ac = (– 7) 2 – 4•1•(– 8) = 49 + 32 = 81

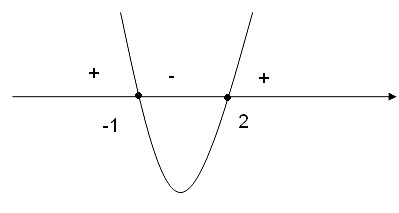
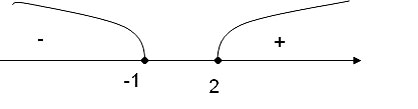
Далее полученные точки отмечаются на координатной прямой. Они разобьют ее на несколько промежутков, на каждом из которых функция у =x 2 – 7x– 8 сохраняет свой знак. Определить же этот самый знак можно по направлению ветвей параболы, которую рисует схематично:

Видно, что парабола располагается ниже оси Ох на промежутке (– 1; 8). Поэтому именно этот промежуток и является ответом. Нер-во строгое, поэтому сами числа (– 1) и 8 НЕ входят в ответ, то есть для записи промежутка используются круглые скобки.

Обратите внимание: так как в исходном нер-ве используется корень нечетной (третьей) степени, то нам НЕ надо требовать, чтобы он был неотрицательным. Он может быть меньше нуля.

Теперь рассмотрим более сложный случай, когда в правой части нер-ва стоит не постоянное число, а некоторое выражение с переменной, то есть оно имеет вид

Случаи, когда n является нечетным числом, значительно более простые. В таких ситуациях достаточно возвести нер-во в нужную степень.

Пример. Решите нер-во

Решение.Слева стоит кубический корень, а возведем нер-во в третью степень (при этом мы используем формулу сокращенного умножения):

И снова квадратное нер-во. Найдем нули функции записанной слева, и отметим их на координатной прямой:

D = b 2 – 4ac = (– 1) 2 – 4•1•(– 2) = 1 + 8 = 9

Нер-во выполняется при х∈(– ∞; – 1)⋃(2; + ∞). Так как мы возводили нер-во в нечетную степень, то больше никаких действий выполнять не надо.

стоит корень четной степени, то ситуация резко осложняется. Его недостаточно просто возвести его в n-ую степень. Необходимо выполнение ещё двух условий:

f(x) > 0 (подкоренное выражение не может быть отрицательным);

g(x) > 0 (ведь сам корень должен быть неотрицательным, поэтому если g(x)будет меньше нуля, то решений не будет).

Вообще говоря, в таких случаях аналитическое решение найти возможно, но это тяжело. Поэтому есть смысл решить нер-во графически – такое решение будет более простым и наглядным.

Пример. Решите нер-во

Решение. Сначала решим его аналитически, без построения графиков. Возведя нер-во в квадрат, мы получим

х 2 – 10х + 21 > 0(1)

Решением этого квадратного нер-ва будет промежуток (– ∞;3)⋃(7; + ∞). Но надо учесть ещё два условия. Во-первых, подкоренное выражение должно быть не меньше нуля:

Во-вторых, выражение 4 – х не может быть отрицательным:

Получили ограничение 2,5 ⩽ х ⩽ 4, то есть х∈[2,5; 4]. С учетом того, что при решении нер-ва(1) мы получили х∈(– ∞;3)⋃(7; + ∞), общее решение иррационального нер-ва будет их пересечением, то есть промежутком [2,5; 3):

Скажем честно, что описанное здесь решение достаточно сложное для понимания большинства школьников, поэтому предложим альтернативное решение, основанное на использовании графиков. Построим отдельно графики левой и правой части нер-ва:

Видно, что график корня находится ниже прямой на промежутке [2,5; 3). Возникает вопрос – точно ли мы построили график? На самом деле с его помощью мы лишь определили, что искомый промежуток находится между двумя точками. В первой график корня касается оси Ох, а во второй точке он пересекается с прямой у = 4 – х. Найти координаты этих точек можно точно, если решить ур-ния. Начнем с первой точки:

Итак, координата х первой точки в точности равна 2,5. Для нахождения второй точки составим другое ур-ние:

Это квадратное ур-ние имеет корни 3 и 7 (убедитесь в этом самостоятельно). Число 7 является посторонним корнем:

Подходит только число 3, значит, вторая точка имеет координату х = 3, а искомый промежуток – это [2,5; 3).

Ещё тяжелее случаи, когда в нер-ве с корнем четной степени стоит знак «>», а не « 1/2 = х – 3

Методы решения иррациональных уравнений

Методы решения иррациональных уравнений.

Цели:

Образовательная –познакомить учащихся с нестандартными методами решения иррациональных уравнений; систематизировать знания учащихся о методах решения иррациональных уравнений, способствовать формированию умений классифицировать иррациональные уравнения по методам решений, научить применять эти методы, выбирать рациональный путь решения. Развивающая –способствовать развитию математического кругозора, логического мышления. Воспитательная – содействовать воспитанию интереса к иррациональным уравнениям, воспитывать чувство коллективизма, самоконтроля, ответственности.

1. Повторить определение и основные методы решения иррациональных уравнений;

2. Продемонстрировать нестандартные методы решения иррациональных уравнений; формировать умение выбирать рациональные пути решения;

3. Освоение всеми учащимися алгоритмов решения иррациональных уравнений, закрепление теоретических знаний при решении конкретных примеров;

4. Развитие у учащихся логического мышления в процессе поиска рациональных методов и алгоритмов решения;

5. Развитие культуры научных и учебных взаимоотношений между учениками и между учениками и учителем; воспитание навыков совместного решения задач.

Тип урока: комбинированный

Методы обучения:

Информационно- иллюстративный; репродуктивный; проблемный диалог; частично-поисковый; системные обобщения.

Формы организации учебной деятельности:

Фронтальная, групповая, самопроверка, взаимопроверка, коллективные способы обучения.

Оборудование урока: компьютер, проектор, карточки с заданием, лист учета знаний.

Продолжительность занятия: 2 урока по 45 минут.

План урока:

I. Организационный момент. Постановка цели, мотивация.

II. Актуализация опорных знаний, проверка домашней работы.

III. Изучение нового материала.

IV. Закрепление изученного материала на данном уроке и ранее пройденного, связанного с новым.

V. Подведение итогов и результатов урока. Рефлексия.

VI. Задание на дом.

I Организационный момент. Постановка цели, мотивация.

II Актуализация опорных знаний проводится в форме беседы по лекционному материалу по данной теме с использованием компьютерной презентации. Проверка домашнего задания.

· Определение иррационального уравнения.

Уравнение, содержащее переменные под знаком корня или дробной степени, называется иррациональным.

Назовите иррациональные уравнения:

· Что значит решить иррациональное уравнение?

Это значит найти все такие значения переменной, при которых уравнение превращается в верное равенство, либо доказать, что таких значений не существует.

· Основные методы решения иррациональных уравнений.

1. Уединение радикала. Возведение в степень.

a) При решении иррационального уравнения с радикалом четной степени возможны два пути:

1) использование равносильных преобразований

для уравнения вида

для уравнения вида

2) после возведения в степень выполнение проверки, так как возможно появление посторонних корней

b) При решении иррационального уравнения с радикалом нечетной степени возведение в нечетную степень правой и левой части уравнения всегда приводит к равносильному уравнению и потеря корней или их приобретения происходить не может.

Пример 1:

Пример 2:

Пример 3:

Проверка: x=2 x=5

– посторонний корень

Если радикалов несколько, то уравнение возводить в степень приходится возводить неоднократно.

Пример 4:

Проверка показывает, что оба корня подходят.

Ответ:

2. Метод введения вспомогательного неизвестного или “метод замены

Пример 5:

Сделаем замену причём тогда

не удовлетворяет условию

Возвращаемся к замене:

Проверка показывает, что оба корня подходят.

Иногда удобно ввести не одну, а несколько переменных.

Пример 6: .

Заметим, что знаки х под радикалом различные. Введем обозначение

, .

Тогда,

Выполним почленное сложение обеих частей уравнения .

Имеем систему уравнений

Т. к. а + в = 4, то

Значит: 9 – x = 8 , х = 1.

3. Метод разложения на множители или расщепления.

· Произведение равно нулю тогда и только тогда, когда хотя бы один из входящих в него сомножителей равен нулю, а остальные при этом имеют смысл.

Пример 7:

III Изучение нового материала.

Нестандартные методы решения иррациональных уравнений.

4. Умножение на сопряжённое выражение.

5. Переход к модулю.

6. Использование свойств функции:

§ Область определения функции (ОДЗ)

§ Область значения функции

§ Свойство ограниченности функции (метод оценок)

§ Использование суперпозиций функций

· Умножение на сопряжённое выражение.

Воспользуемся формулой

Пример 8:

Умножим обе части уравнения на сопряжённое выражение:

Проверка показывает, что число является корнем.

Ответ:

· Переход к модулю.

Для этого метода воспользуемся тождеством:

Пример 9:

§ Если , то , тогда

тогда

§ Если , тогда ,а

§ Если , тогда , а

· Использование свойств функции:

§ Область определения функции (ОДЗ)

Иногда нахождение области определения функций, входящих в уравнение, существенно облегчает его решение.

Пример 10:

ОДЗ: ОДЗ: x=0 и x=1

Проверка показывает, что только x=1 является корнем.

Ответ:

Пример 11:

, тогда

Тогда невозможно.

Ответ: корней нет.

§ Область значений функции

Пример 12:

Данное уравнение не имеет решений, так как его левая часть – функция может принимать только неотрицательные значения.

Ответ: корней нет

Пример 13:

Учитывая то, что левая часть уравнения – функция может принимать только неотрицательные значения, решим неравенство:

неравенство решений не имеет, тогда и исходное уравнение тоже.

Ответ: корней нет

§ Свойство ограниченности функции (метод оценок)

· Если и , то

Пример 14:

Заметим, что , т. е. , а

Проверка показывает, что это значение является и корнем второго уравнения.

Ответ:

· Пусть – функция, возрастающая (убывающая) на некотором промежутке I. Тогда уравнение имеет на промежутке I не более одного корня.

· Пусть – функция, возрастающая на некотором промежутке I , а функция – убывающая на этом промежутке. Тогда уравнение имеет на промежутке I. не более одного корня

Пример 15: .

Рассмотрим функции и .

монотонно возрастает, а – убывает, следовательно, уравнение имеет не более одного корня.

Значение корня легко найти подбором:

Ответ:

Пример 16:

Функция возрастает на своей области определения, как сумма двух возрастающих функций, следовательно, уравнение имеет не более одного корня. Так как , то – единственный корень .

Ответ:

§ Использование суперпозиций функций

· Если – монотонно возрастающая функция, то уравнения и равносильны.

Пример 17:

Запишем уравнение в виде

Рассмотрим функцию – монотонно возрастающую, тогда уравнение имеет вид . Оно равносильно уравнению

Сделаем замену

не удовлетворяет условию

Ответ:

IV. Закрепление изученного материала на данном уроке и ранее пройденного, связанного с новым.

Решение уравнений в группах по 6 человек.

Ребята получают карточку с заданием. Решение уравнений обсуждают вместе, записывают его.

После выполнения группами заданий проводится взаимопроверка. Группы меняются заданиями с решениями по кругу:

2 3 4

Учащиеся групп обсуждают решение, исправляют ошибки и выставляют оценки.

Потом работы с выставленными оценками возвращаются в группы для обсуждения вклада каждого в решение проблемы.

Выставляются каждому оценки с занесением в оценочную таблицу. Учитель контролирует и вносит, если нужно, свои коррективы.

V. Подведение итогов и результатов урока. Рефлексия.

1)

2)

3)

4)

5)

6)

7)

8) *

Используемая литература.

1. Чулков курса «Уравнения и неравенства в школьном курсе математики»: Лекции 1-8. – М.: Педагогический университет «Первое сентября», 2006.

2. , , Морозова государственный экзамен. Математика. – Челябинск: Взгляд, 2006 –Ч.1,2

3. Шарыгин курс по математике: Решение задач. – М.: Просвещение, 1989

4. , Якушев : интенсивный курс подготовки к экзамену. – М.: Айрис-пресс, 2004.

5. , Голобородько и контрольные работы по алгебре и началам анализа для 10-11 классов. – М.: Илекса, 2006.

Задания для работы в группах:

1. Возведи обе части в квадрат:

2. Выполни замену:

4. Умножай на сопряжённое выражение:

5. Переходи к модулю:

6. Используй свойства функций:

7. Реши любым способом:

1. Возведи обе части в квадрат:

2. Выполни замену:

4. Умножай на сопряжённое выражение:

5. Переходи к модулю:

6. Используй свойства функций:

7. Реши любым способом:

Проверочная работа по теме: «Методы

[spoiler title=”источники:”]

http://100urokov.ru/predmety/urok-11-uravneniya-irracionalnye

http://pandia.ru/text/77/339/91706.php

[/spoiler]

В этом вопросе следует разбираться, поскольку понятие не только встречается в школьной и университетской программах, но и широко применяется в науке и программировании (разработке программного обеспечения и прошивки контроллеров).

Общие сведения

Областью определения произвольной функции является множество значений переменных, от которых она зависит и принимает определенное значение. Встречаются функции с одной или несколькими переменными. Для простоты исследования нужно рассмотреть первый тип. Для того чтобы найти область определения и множество значений функции, необходимо использовать простые примеры. Специалисты рекомендуют применять метод изучения «от простого к сложному».

Первый раз этот термин упоминается в школьной программе. Книга «Алгебра и начало анализа» дает базовые знания в этой области. Однако она написана не для всех понятным языком.

Обучаемый часто ищет информацию в интернете. В некоторых случаях ученики занимаются поиском готовых решений, а это не совсем правильно, поскольку математические дисциплины пригодятся при поступлении в высшие учебные заведения. Исследование функции — естественный процесс, который встречается в различных дисциплинах.

Программирование на разных языках пользуется огромной популярностью. В нем нужны математические знания для написания некоторых программ и игр. В последних следует производить точные расчеты и описывать некоторые функции героя. Например, удар мечом подчиняется определенному математическому закону или функции. Для корректной ее работы и тестирования следует находить грамотно ее область определения.

Основные понятия

Область определения функции обозначается буквой «D». Кроме того, указывается ее имя D (f). Допускается также следующее обозначение «D (y)». Если необходимо ее найти для нескольких функций, можно изменить обозначение. Для сложного типа функций z = f (a, b, x, y) эта величина обозначается таким образом: D (z). Аргумент — независимая переменная, принимающая определенные значения.

Существуют также сложные функции, которые включают в число своих переменных и другие функции. Пример, z = f (x, k, l, w, y). В нем величины x, k, l являются переменными, а w и y — следующими функциями: w = 2 * x1 + 5 и y = 2 / (x2 — 6). Для каждого типа функции существует определенный алгоритм, по которому следует находить D (f). Он основывается на многолетнем опыте специалистов и придуман для оптимизации вычислений.

Важно уметь правильно определять тип функции, поскольку от этого зависит процесс выбора алгоритма. Для одних можно сразу определить D (f), для других — решить уравнение или неравенство, для третьих следует решить систему уравнений и т. д.

Можно воспользоваться специальными программными модулями. Простым примером программы является онлайн-калькулятор, позволяющий не только вычислить D (f), но и начертить ее график. Кроме того, D (f) записывается в виде множества значений.

Например, D (y) = [0, 157). Это значит следующее: областью определения функции вида y = 3*x / sqrt (156 — |x|) является множество чисел, которые находятся в интервале от 0 включительно (скобка «[“) до 157 не включительно.

Типы функций

Функций существует огромное разнообразие. Они бывают простыми и сложными. Первые в математических дисциплинах классифицируются на несколько типов: алгебраические, тригонометрические и трансцендентные. Алгебраические классифицируются на рациональные и иррациональные. Рациональные бывают целыми и дробными. Тригонометрические включают в свой состав все функции с sin, cos, tg, ctg и т. д. Трансцендентные делятся на степенные, показательные и логарифмические.

Рациональные целые — выражения полиномиального типа (линейные). Они без корней и степеней, дробей и логарифмов, а также без тригонометрических функций. Областью их определения является множество всех действительных чисел (Z) от бесконечно малого до бесконечно большого числа.

Дробный тип — функции, в числителе и знаменателе которых находится переменная. Для нахождения D (f) нужно исключить все значения переменных в нем, приводящие к 0. Если встречается тригонометрические функции, то нужно вычислить все значения, приводящие к отсутствию D (f) на определенном интервале. Этот тип функций может быть иррациональным, дробным, линейным, а также использоваться вместе со степенью и логарифмом.

К иррациональным функциям относят выражения, которые содержат переменную величину под корнем. Значение D (f) — все Z, кроме переменных, приводящих к отрицательным значениям выражений с четными степенями корней. D (f) степенной функции являются все действительные числа. Однако если степень представлена дробным выражением, то значения переменных не должны приводить к неопределенности (например, 4/0, т. к. на 0 делить нельзя). Для функций с натуральным логарифмом выражение, находящееся под ним, должно быть больше 0.

Правильное обозначение

Очень важно правильно обозначать D (f), поскольку это существенно влияет на результат. Это позволит избежать многих ошибок в любой сфере.

Следует руководствоваться такими правилами:

1. Использовать скобку «[” и/или «]”, когда нужно указать принадлежность к множеству.
2. Круглые скобки используются в двух случаях: указывание границы бесконечности и значения, которое не входит в интервал.
3. Для объединения нескольких множеств нужно применять специальный символ «U».
4. Допускается использование круглых и квадратных скобок в одном множестве.

Примером в первом случае является множество [0, 100]: от 0 включительно и до 100 не включительно. Во втором случае — (8, 10): значение, равное 9, поскольку 8 и 10 — нижняя и верхняя границы, не принадлежащие множеству.

Два предыдущих множества можно объединить: [0, 100] U (8, 10). Пример записи последнего случая следующий: (20, 50].

Алгоритмы определения

Для удобства определения D (f) необходимо применять специальные алгоритмы, которые упрощают операцию. Целая рациональная функция, как уже было описано ранее, имеет D (f), принадлежащую множеству Z (весь ряд действительных чисел). Кроме того, степенная функция также имеет D (f), которая соответствует Z.

Если функция является дробной, то следует использовать следующий алгоритм:

1. Обратить внимание на знаменатель, который не должен быть равен 0.
2. Выписать выражение знаменателя и решить его, приравнивая к 0.
3. Записать интервал.

Если она представлена в виде четного корня, следует решить неравенство. Значение подкоренного выражения должно быть больше 0. В противном случае область определения под корнем не будет существовать (неопределенность).

Однако если корень нечетный, то D (f) — множество действительных чисел. Для функций с натуральным логарифмом (ln) значение выражения, которое находится под логарифмом, должно быть всегда больше 0. При отрицательных значениях ln «превращается» в неопределенность. Необходимо составить неравенство. Оно должно быть больше 0.

Для тригонометрических выражений синуса sin (x) и косинуса cos (x) множество всех Z является D (f). Однако для тангенса tg (x) и котангенса ctg (x) необходимо исключить значения переменной x = (Pi / 2) + Pi * k и x = Pi * k соответственно. В этих выражениях k является множеством действительных чисел.

Другие методы

Существуют также и другие методы определения D (f). Ее можно выяснить при помощи следующих инструментов: онлайн-калькулятора, специальных программ и построения графика. Первый способ позволяет довольно быстро найти необходимую величину. Но это не все его возможности. Можно с его помощью строить графики и находить все свойства функции.

Однако первый метод уступает второму, суть которого сводится к использованию специализированного программного обеспечения. В этом случае можно легко изобразить графики заданной функции, исследовать и найти ее основные свойства, а также D (f), представленных в виде функций. Например, зависимость амплитудных значений переменного электрического тока от времени.

В некоторых случаях можно найти D (f), построив ее график. Для этого следует подставить значение аргумента функции и получить ее значение. Построение таблицы зависимости значения функции от ее аргумента позволяет правильно построить графическое представление. Чтобы быстро строить графики, нужно знать их базовые виды: линейный, степенной (квадратичный, кубический и т. д. ), а также другие. Чем точнее графическая иллюстрация, тем легче определить D (f).

После заполнения таблицы значений следует приступать к построению графика. Для этого берутся точки с координатами из таблицы (x, y), и отмечаются на декартовой системе координат.

Затем их следует соединить. Получится график заданной функции, по которому не составит труда сделать определенные выводы.

Примеры решения

Теоретические знания необходимы, но некоторые люди делают огромную ошибку. Они не закрепляют их при помощи практики. Необходимо регулярно решать задачи на нахождения D (f), поскольку в этом случае набирается опыт. Наиболее простыми задачами считаются следующие: нахождения D (f) линейной, степенной, показательной и тригонометрической функций. Важным аспектом считается упрощение выражения. Для этого следует вспомнить также и формулы сокращенного умножения.

С дробными и иррациональными функциями могут возникнуть некоторые сложности, поскольку нужно решить уравнение или неравенство. Однако в последнем случае нельзя путать знак неравенства.

Для линейного вида

Нужно найти D (f) для y = 2*x — 3 * (x — 5). Для решения следует применить такой алгоритм:

1. Упростить выражение.
2. Определить D (f).

Для упрощения выражения следует раскрыть скобки. Конечно, это делать необязательно, поскольку ответ очевиден D (y) = (-бесконечность, +бесконечность). Но по правилам «хорошего тона» любое математическое выражение следует упрощать: y = 2 * x — 3 * x + 15 = – x + 15 = 15 — x. При решении следует правильно раскрывать скобки, а также следить за знаками. Малейшая ошибка может привести к значительному искажению графика.

В некоторых задачах следует также построить график функции. Для конкретного случая создается таблица зависимости значения «y» от аргумента. Не имеет смысла брать много значений «х», поскольку графиком является прямая. Известно, что необходимы только две точки для ее проведения. Подстановка количества значений «х», превышающих двух, является грубой и распространенной ошибкой.

Дробные и иррациональные

Пусть существует выражение вида y = 1 / [(x — 4) * (x + 4)]. Нужно определить D (f).

Решается задача таким способом:

1. Приравнивается знаменатель к 0.
2. Решается уравнение.
3. Определяется интервал допустимых значений.

Нужно решить уравнение (x — 4) * (x + 4) = 0. Из него видно, что x1 = 4 и x2 = -4, поскольку эти значения «превращают» знаменатель в неопределенность. Следовательно, D (y) = (-бесконечность, -4) U (4, +бесконечность).

В случае с иррациональным выражением: y = sqrt[4 * sqr (x) — 12 * x + 9], нужно решить уравнение подкоренного выражения.

Для решения квадратного уравнения следует применить такой алгоритм:

1. Записать неравенство: 4 * sqr (x) — 12 * x + 9 >= 0.
2. Дискриминант: D = [(- b)^2] – (4 * a * c) = [(-12)^2] – (4 * 4 * 9) = 144 — 144 = 0.
3. D = 0 — только одно решение.
4. x = (-b) / (2 * a) >= 12 / (2 * 4) >= 12 / 8 >= 6 / 4 >= 1,5.

Множество чисел D (y) ограничивается следующим интервалом (-бесконечность, 1.5) U (1.5, +бесконечность).

Таким образом, для нахождения множества значений D (f) для конкретного выражения следует воспользоваться специальными алгоритмами. На первоначальном этапе исследования функции следует определить ее тип, поскольку это поможет избежать многих сложностей в процессе решения.

Комментарии преподавателя

Область определения функции с корнем

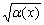
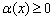
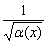
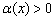
Функция с квадратным корнем  определена только при тех значениях «икс», когдаподкоренное выражение неотрицательно: . Если корень расположился в знаменателе , то условие очевидным образом ужесточается: . 

Пример 5

Найти область определения функции 

Решение: подкоренное выражение должно быть неотрицательным:

Прежде чем продолжить решение, напомню основные правила работы с  неравенствами, известные ещё со школы.

 Итак, для неравенства равносильны следующие преобразования:

1) Слагаемые можно переносить из части в часть со сменой знака.

2) Обе части неравенства можно умножить на положительное число.

3) Если обе части неравенства умножить на отрицательное число, то необходимо сменитьзнак самого неравенства. Например, если было «больше», то станет «меньше»; если было «меньше либо равно», то станет «больше либо равно».

В неравенстве 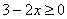 перенесём «тройку» в правую часть со сменой знака (правило №1):

Умножим обе части неравенства на –1 (правило №3):

Умножим обе части неравенства на 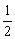 (правило №2):

Ответ: область определения: 

Ответ также можно записать эквивалентной фразой: «функция определена при ».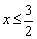
Геометрически область определения изображается штриховкой соответствующих интервалов на оси абсцисс. В данном случае:

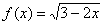
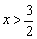
Ещё раз напоминаю геометрический смысл области определения – график функции  существует только на заштрихованном участке и отсутствует при .

В большинстве случаев годится чисто аналитическое нахождение области определения, но когда функция сложная, следует чертить ось 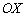 и делать пометки.

Пример 6

Найти область определения функции 

Это пример для самостоятельного решения.

Когда под квадратным корнем находится квадратный двучлен или трёхчлен, ситуация немного усложняется, и сейчас мы подробно разберём технику решения:

Пример 7

Найти область определения функции 

Решение: подкоренное выражение должно быть строго положительным, то есть нам необходимо решить неравенство 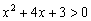. На первом шаге пытаемся разложить квадратный трёхчлен на множители:

Дискриминант положителен, ищем корни:

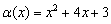
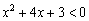
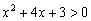
Таким образом, парабола  пересекает ось абсцисс в двух точках, а это значит, что часть параболы расположена ниже оси (неравенство ), а часть параболы – выше оси (нужное нам неравенство ).

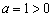
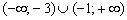
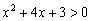
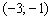
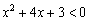
Поскольку коэффициент , то ветви параболы смотрят вверх. Из вышесказанного следует, что на интервалах  выполнено неравенство  (ветки параболы уходят вверх на бесконечность), а вершина параболы расположена на промежутке  ниже оси абсцисс, что соответствует неравенству :

 

Обратите внимание, что сами точки 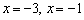 выколоты (не входят в решение), поскольку неравенство у нас строгое.

Ответ: область определения: 

Вообще, многие неравенства (в том числе рассмотренное) решаются универсальнымметодом интервалов, известным опять же из школьной программы. Но в случаях квадратных дву- и трёхчленов, на мой взгляд, гораздо удобнее и быстрее проанализировать расположение параболы относительно оси .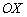 

Источник конспекта: http://www.mathprofi.ru/oblast_opredeleniya.html

Источник видео: http://www.youtube.com/watch?v=6aqZHIHeMeQ

Файлы

Нет дополнительных материалов для этого занятия.