Теорема Пифагора
- Обратная теорема Пифагора
Теорема Пифагора:
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Если ∠A = 90°, то a2 + b2 = c2.
Доказательство:
Возьмём прямоугольный треугольник с катетами a, b и гипотенузой c:
Достроим этот треугольник до квадрата со стороной a + b:
Площадь данного квадрата S будет равна (a + b)2:
S = (a + b)2.
С другой стороны, площадь этого квадрата состоит из четырёх одинаковых треугольник, площадь каждого из которых равна половине произведения их катетов (ab : 2), и квадрата со стороной c, поэтому:
S = (a + b)2
или
| S = 4 · ( | ab | ) + c2 = 2ab + c2 |
| 2 |
Таким образом:
(a + b)2 = 2ab + c2.
Так квадрат суммы двух чисел равен сумме квадрата первого числа, удвоенного произведения первого числа на второе и квадрата второго числа:
(a + b)2 = a2 + 2ab + b2,
то для того, чтобы наше равенство было верным c2 должен быть равен a2 + b2. Таким образом,
(a + b)2 = 2ab + c2, где c2 = a2 + b2.
Теорема доказана.
Обратная теорема Пифагора
Обратная теорема Пифагора:
Если в треугольнике квадрат длины одной стороны равен сумме квадратов длин других сторон, то этот треугольник – прямоугольный.
Если a2 + b2 = c2, то треугольник ABC — прямоугольный.
Доказательство:
Возьмём треугольник ABC со сторонами a, b и c, у которого c2 = a2 + b2. Докажем, что ∠A = 90°:
Рассмотрим прямоугольный треугольник A1B1C1 с прямым углом A1, у которого A1B1 = a и A1C1 = b:
По теореме Пифагора:
B1C12 = A1B12 + A1C12.
Значит B1C12 = a2 + b2. Но a2 + b2 = c2 по условию теоремы. Следовательно B1C12 = c2, откуда можно сделать вывод B1C1 = c.
Треугольники ABC и A1B1C1 равны по трём сторонам, поэтому ∠A = ∠A1 = 90°, то есть треугольник ABC является прямоугольным. Теорема доказана.
Теорема Пифагора
О важности теоремы Пифагора высказался Иоганн Кеплер: «Геометрия обладает двумя великими сокровищами: теоремой Пифагора и делением отрезка в крайнем и среднем отношении; первое можно сравнить с мерой золота, второе назвать драгоценным камнем»
Теорема Пифагора актуальна в заданиях как базового, так и профильного ЕГЭ по математике. За верное решение задач базового уровня дается 1 балл, за задания повышенного уровня начисляется 3 балла. В статье мы рассмотрим доказательство теоремы и решим пару задач по теме. Благодаря качественному изучению этого материала экзаменуемый справится с рядом заданий и получит за них наивысший балл.
Что такое теорема Пифагора
В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.
Важно!
Сторону прямоугольного треугольника, противолежащую прямому углу, называют гипотенузой, а стороны, прилежащие к прямому углу, — катетами. Гипотенуза больше любого из катетов («Геометрия. 8 класс. Учебник», А. Г. Мерзляк).
Формула теоремы Пифагора
c² = a² + b²
Из этой формулы выводятся следующие:
с = √a² + b²
a = √c² — b²
b = √c² — a²
Доказательство теоремы Пифагора
Дано:
△АВС — прямоугольный;
＜АСВ = 90⁰.
Доказать:
АВ² = АС² + ВС².
Доказательство:
Проведем высоту СН.
АН, НВ — проекции катетов АС и ВС на гипотенузу. По теореме о метрических соотношениях в прямоугольном треугольнике, квадрат катета равен произведению гипотенузы и проекции этого катета на гипотенузу. Значит,
АС² = АВ × АН; ВС² = АВ × НВ.
Сложим почленно эти равенства:
АС² + ВС² = АВ × АН + АВ × НВ = АВ × (АН + НВ) = АВ ×АВ = АВ².
Что и требовалось доказать.
Задачи на теорему Пифагора
Переходим к решению задач с помощью теоремы Пифагора.
Задача №1
Центр окружности, описанной около треугольника КРH, лежит на стороне КН. Радиус окружности равен 10. Найдите КР, если РН равен 12
Дано:
Описанная окружность с центром в точке О.
О ∈ КН;
R = 10;
РН = 12.
Найти: КР.
Решение:
Так как окружность описанная, то все вершины треугольника лежат на ней. Следовательно, угол ＜КРН — вписанный.
По условию задачи центр окружности О ∈ КН, значит, хорда КН является диаметром.
КН = 2R = 2 ✕ 10 = 20.
Вписанный угол ＜КРН, опирающийся на диаметр, — прямой, значит, треугольник КРН — прямоугольный.
По теореме Пифагора:
КР = √КН² — РН²,
КР = √400-144 = √256 = 16
Ответ: КР = 16
Теорема о трех перпендикулярах
Доказательство и формулировка теоремы о трех перпендикулярах
подробнее
Задача №2
Дано:
Пирамида МАВС с высотой МА. Известно, что в основании лежит прямоугольный треугольник с прямым углом С.
Найти:
1) Угол между ребрами МС и ВС. Ответ дайте в градусах.
2) МВ, если МС = 12, ВС = 5.
Решение:
1) Так как по условию задачи МА — высота пирамиды, то МА ⟂ (АВС). АС — проекция наклонной МС на плоскость АВС. Так как АС ⟂ ВС, то, по теореме о трех перпендикулярах, МС ⟂ ВС, следовательно, угол между МС и ВС равен 90° (градусов).
Ответ: 90°.
2) Так как из пункта 1 МС ⟂ ВС ⇒ треугольник МСВ — прямоугольный ⇒ по теореме Пифагора: МВ = √МС² + ВС² ⇒ МВ = √144 + 25 = √169 = 13.
Ответ: МВ = 13.
Популярные вопросы и ответы
Почему теорему Пифагора изучают на геометрии в 8 классе?
Потому что это необходимый теоретический материал для решения задач с помощью данной теоремы: квадратные уравнения, арифметический квадратный корень, подобие треугольников и другие. Эти темы изучаются именно в 8 классе.
Где и когда возникла теорема Пифагора?
Согласно сирийскому историку Ямвлиху, Пифагора познакомили с учителем математики Фалесом Милетским и его учеником Анаксимандром. После известно, что Пифагор отправился в Египет для продолжения своих исследований, был захвачен во время вторжения Камбиса II из Персии в 525 году до н. э. и доставлен в Вавилон. Пифагор вскоре поселился в Кротоне (ныне Кротон, Италия) и основал школу или, говоря современным языком, монастырь, где все члены дали строгий обет хранить тайну, а все новые математические результаты на протяжении нескольких столетий приписывались его имени. Таким образом, до конца неизвестно первое доказательство теоремы, а также есть некоторые сомнения в том, что сам Пифагор действительно ее доказал. Она была одной из первых теорем, пришедших из древних цивилизаций.
Теорема Пифагора — самый известный математический вклад ученого. Согласно одной из легенд, он был так счастлив, когда решил доказательство, что принес в жертву 100 быков.
Также при изучении вавилонских клинописных табличек и древнекитайских рукописей было установлено, что знаменитая теорема была известна задолго до Пифагора, возможно несколько тысячелетий до него. Так, немецкий математик Кантор выяснил, что равенство 32 + 42 = 52 было известно египтянам около 2300 лет до н. э., еще во времена царя Аменехмета (согласно папирусу 6 619 Берлинского музея). Такой треугольник со сторонами 3, 4, 5 получил название «египетский треугольник». Одни предполагают, что Пифагор дал теореме полноценное доказательство, а другие считают по-другому. Например, доказательство в «Началах Евклида» (Предложение 47), по утверждению Прокла, принадлежит самому Евклиду, а не Пифагору.
Где в жизни можно применить теорему Пифагора?
Широкое применение имеет теорема при решении геометрических задач: нахождении длин, расстояний в прямоугольном треугольнике. Большой спектр применения есть у этой великой теоремы в физике, астрономии, строительстве, архитектуре, литературе.
Как звучит обратная теорема Пифагора?
Если квадрат длины одной стороны треугольника равен сумме квадратов длин двух других сторон, то треугольник является прямоугольным.
Изображения на странице: wikipedia.org, Наталия Юмагулова.
На предыдущем уроке мы с вами познакомились с теоремой
Пифагора, которая звучит следующим образом: в прямоугольном треугольнике
квадрат гипотенузы равен сумме квадратов катетов.
На этом уроке мы сформулируем и докажем теорему,
обратную теореме Пифагора.
Теорема. Если квадрат
одной стороны треугольника равен сумме квадратов двух других сторон, то этот
треугольник – прямоугольный.
Доказательство.
Пусть ABC
– треугольник, для которого справедливо равенство: .
,
Докажем, что –
прямой.
–
прямоугольный.
–
прямой, ,
.
,
.
Следовательно, ,то
есть,.
по
третьему признаку.
Тогда .
Значит, –
прямоугольный.
Что и требовалось доказать.
Прямоугольные треугольники, у которых длины сторон
выражаются целыми числами, называются пифагоровыми треугольниками. Так
каждый из приведённых треугольников является пифагоровым.
В Древнем Египте для построения прямого угла строили
прямоугольный треугольник при помощи кольев и натянутых на них верёвок длиной
три, четыре и пять единиц.
Тогда угол между сторонами, равными трём и четырём,
получался прямым.
Задача. Выясните,
является ли треугольник прямоугольным, если его стороны выражаются числами: а) ,
,
;
б) ,
,
;
в) ,
,
.
Решение.
Задача. Найдите площадь
треугольника, если его стороны равны см,
см
и см.
Решение.
,
тогда –
прямоугольный, .
,
(см2).
Ответ: см2.
Задача. В равнобедренном
треугольнике длина
боковой стороны равна
см,
а основание –
см.
Найдите .
Решение.
см.
,следовательно,
–
прямоугольный, .
Так как –
равнобедренный, то .
,тогда
.
Ответ: .
Итак, на этом уроке мы вспомнили теорему Пифагора и
познакомились с обратной ей: если квадрат одной стороны треугольника равен
сумме квадратов двух других сторон, то этот треугольник – прямоугольный.
Отметили, что прямоугольные треугольники, у которых
длины сторон выражаются целыми числами, называются пифагоровыми треугольниками.
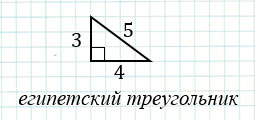
А также мы поговорили о египетском треугольнике,
который представляет собой треугольник со сторонами три, четыре, пять. При этом
если пропорционально увеличивать стороны такого треугольника, то полученные
треугольники, например, со сторонами шесть, восемь, десять; девять, двенадцать,
пятнадцать и так далее также будут прямоугольными.
- Главная
- Справочники
- Справочник по геометрии 7-9 класс
- Площадь
- Теорема, обратная теореме Пифагора
Теорема
Если квадрат одной стороны треугольника равен сумме квадратов двух других сторон, то треугольник прямоугольный.
Доказательство
Дано: 
АВС, АВ2 = АС2 + ВС2.
Доказать: АВС – прямоугольный.
Доказательство:
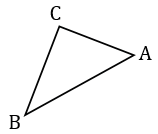
Рассмотрим прямоугольный А1В1С1, в котором 
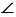С1 – прямой, А1С1 = АС и В1С1 = ВС.
По теореме Пифагора А1В12 = А1С12 + В1С12, учитывая то, что А1С1 = АС и В1С1 = ВС, получим, А1В12 = АС2 + ВС2, при этом по условию АВ2 = АС2 + ВС2, значит, А1В12 = АВ2, откуда А1В1 = АВ. Следовательно, 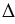АВС и 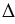А1В1С1 (по трем сторонам), поэтому 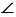С = 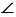С1, т.е. 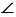С – прямой, тогда 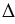АВС – прямоугольный. Теорема доказана.
Пифагоровы треугольники (пифагоровы тройки) – прямоугольные треугольники, у которых длины сторон выражаются целыми числами, которые называют пифагоровы числа. Пифагорова тройка – это три таких натуральных числа (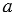
, 
, 
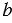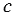), для которых справедливо квадратное уравнение: 
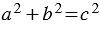. Так, например, если катеты треугольника равны 6 и 8, а гипотенуза равна 10, то такой треугольник будет пифагоровым, т.к. 62 + 82 = 36 + 64 = 100 = 102, т.е. пифагорова тройка будет: (6, 8, 10).
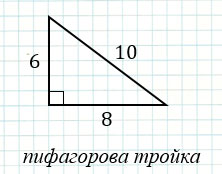
Также, к пифагоровым треугольникам относится треугольник со сторонами 3, 4, 5, который часто называют египетским треугольником, так как он был известен еще древним египтянам.
Советуем посмотреть:
Понятие площади многоугольника
Площадь квадрата
Площадь прямоугольника
Площадь параллелограмма
Площадь треугольника
Площадь трапеции
Теорема Пифагора
Формула Герона
Площадь
Правило встречается в следующих упражнениях:
7 класс
Задание 498,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 499,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 10,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 11,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 517,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 524,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 577,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1145,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1241,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1268,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Перейти к содержанию
Обратная теорема Пифагора
На чтение 1 мин
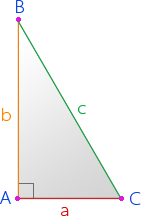
Рассмотрим прямоугольный треугольник АВС.
a, b – катеты прямоугольного треугольника
c – гипотенуза прямоугольного треугольника
A, B, C – вершины треугольника
Обратная теорема Пифагора формулируется следующим образом: если для положительных чисел a, b, c соблюдается уравнение,
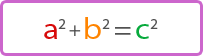
то существует прямоугольный треугольник АВС с катетами a, b и гипотенузой c.
Вам также может понравиться
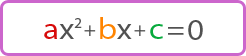
Рассмотрим квадратное уравнение где a – коэффициент
02.1к.
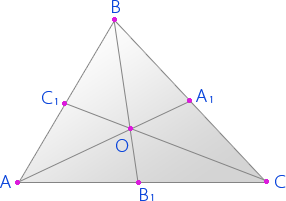
Рассмотрим произвольный треугольник АВС. A, B, C –
02.1к.
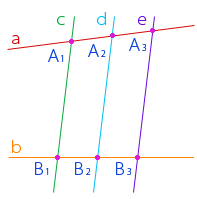
Рассмотрим параллельные прямые c, d, e и произвольные
01.9к.
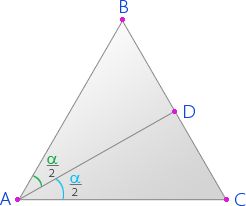
Рассмотрим произвольный треугольник АВС. α – угол треугольника
01.6к.
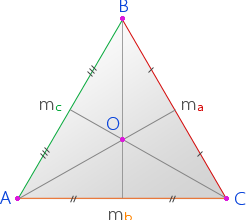
Рассмотрим произвольный треугольник АВС. ma – медиана
02.8к.
Рассмотрим произвольный многоугольник АВСDEF.
01.6к.
Рассмотрим произвольный треугольник АВС. α, β, γ –
01.5к.
Рассмотрим прямоугольный треугольник АВС.
01.5к.
