Соединение катушек
Соединение катушек индуктивности при отсутствии взаимного влияния магнитных полей катушек.
Последовательное соединение катушек индуктивности.
Суммарная индуктивность двух или нескольких катушек, соединенных последовательно и расположенных на таком расстоянии друг от друга, что магнитное поле одной катушки не пересекает витков другой (рисунок 1), равна сумме их индуктивностей.
Рисунок 1. Последовательное соединение катушект индуктивности.
Цепь, изображенная на рисунке 1, обладает общей индуктивностью L, которая выражается так:
где L1, L2 и L3 — индуктивности отдельных катушек.
Параллельное соединение катушек индуктивности.
Индуктивность цепи, составленной из тех же катушек при параллельном их соединении (рисунок 2) и при соблюдении того же условия относительно их расположения (отсутствие магнитного взаимодействия), подсчитывается по следующей формуле:
Рисунок 2. Параллельное соединение катушек индуктивности.
Индуктивность двух катушек, соединенных параллельно, определяется по следующей формуле:
Как видим, формулы для подсчета результирующих индуктивностей катушек, соединенных последовательно или параллельно и не взаимодействующих между собой, совершенно тождественны с формулами для подсчета омического сопротивления цепи при последовательном и параллельном соединении резисторов.
Соединение катушек при наличии взаимного влияния их магнитных полей.
Если катушки, включенные в цепь последовательно, расположены близко друг к другу, т. е. так, что часть магнитного потока одной катушки пронизывает витки другой, т. е. между катушками существует индуктивная связь (рисунок 3а), то для определения их общей индуктивности приведенная выше формула будет уже непригодна. При таком расположении катушек могут быть два случая, а именно:
- Магнитные потоки обеих катушек имеют одинаковые направления
- Магнитные потоки обеих катушек направлены навстречу друг другу
Тот или другой случай будет иметь место в зависимости от направления витков обмотки катушек и от направлений токов в них.
Рисунок 3. Соединение катушек индуктивности: а)суммарная индуктивность увеличивается за счет взаимной индукции б)суммарная индуктивность уменьшается за счет взаимной индукции.
Если обе катушки намотаны в одну сторону и токи в них текут в одном направлении, то это будет соответствовать первому случаю; если же токи текут в противоположных направлениях (рисунок 3б), то будет иметь место второй случай.
Разберем первый случай, когда магнитные потоки направлены в одну сторону. Очевидно, при этих условиях витки каждой катушки будут пронизываться своим потоком и частью потока другой катушки, т. е. магнитные потоки в той и в другой катушке будут больше по сравнению с тем случаем, когда между катушками нет индуктивной связи. Увеличение магнитного потока, пронизывающего витки той или иной катушки, равносильно увеличению ее индуктивности. Поэтому общая индуктивность цепи в рассматриваемом случае будет больше суммы индуктивностей отдельных катушек, из которых составлена цепь.
Рассуждая таким же образом, мы придем к выводу, что для второго случая, когда потоки направлены навстречу друг другу, общая индуктивность цепи будет меньше суммы индуктивностей отдельных катушек.
Подсчет величины индуктивности цепи, составленной из двух соединенных последовательно катушек индуктивности L1 и L2 при наличии между ними индуктивной связи, производится по формуле:
В первом случае ставится знак + (плюс), а во втором случае знак — (минус).
Величина М, называемая коэффициентом взаимной индукции, представляет собой добавочную индуктивность, обусловленную частью магнитного потока, общей для обеих катушек.
На явлении взаимоиндукции основано устройство вариометров. Вариометр состоит из двух катушек, общая индуктивность которых может, по желанию, плавно изменяться в некоторых пределах. В радиотехнике вариометры применяются для настройки колебательных контуров приемников и передатчиков.
ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!
Похожие материалы:
Добавить комментарий
Калькулятор параллельных индуктивностей
Параллельные и последовательные схемы соединения катушек индуктивности часто используются для получения
требуемой индуктивности. Для этого используются стандартные катушки с фиксированным значением индуктивности.
Если параллельно соединены только две катушки индуктивности, имеем:
Leq
Общая индуктивность соединенных параллельно катушек индуктивности,
не имеющих общего магнитного поля равна величине, обратной сумме величин, обратных их индуктивностям.
1Leq
=
N
∑
n=1
1L1
+
1L2
+
…
+
1Ln
Эквивалентная индуктивность всегда будет меньше самой малой индуктивности в группе катушек индуктивностей,
а добавление еще одной катушки всегда будет уменьшать эквивалентную индуктивность.
Расчет индуктивности
Расчет эквивалентной индуктивности
Расчет при известном эквивалентном значении
Для расчета введите значения индуктивности катушек и добавьте необходимое количество (max 8 шт.).
Для расчета введите значение эквивалентной индуктивности одной из катушек
Подбор катушки индуктивности на сайте
Внимание! Производители объединяют катушки индуктивности в серии или ряды: E6, E12, E24…
Для подбора компонента будет использована серия E12.
Обнаружили ошибку или неточность в работе калькулятора? Сообщите нам об этом.
Соблюдайте технику безопасности во время работы с электронными компонентами!
Индуктивность характеризует свойства элементов электрической цепи накапливать энергию магнитного поля. Также это мера связи между током и магнитным полем. Ещё её сравнивают с инерцией электричества – также, как массу с мерой инерции механических тел.
Содержание
- 1 Явление самоиндукции
- 2 Последовательное и параллельное соединение индуктивностей
- 2.1 Параллельное соединение
- 2.2 Последовательное соединение
- 3 Некоторые практические вопросы и конструкции катушек индуктивности
- 3.1 Добротность катушки индуктивности
- 3.2 Экранный эффект
- 3.3 Подстроечная индуктивность
- 3.4 Переменная индуктивность (вариометр)
- 3.5 Индуктивность в виде печатной спирали
- 3.6 Катушка с секционной намоткой
- 3.7 Катушка индуктивности на тороидальном сердечнике
Явление самоиндукции
Если ток, идущий через проводящий контур, изменяется по величине, то возникает явление самоиндукции. В этом случае изменяется магнитный поток через контур, и на выводах рамки с током возникает ЭДС, называемая ЭДС самоиндукции. Эта ЭДС противоположна направлению тока и равна:
ε=-∆Ф/∆t=-L*(∆I/∆t)
Очевидно, что ЭДС самоиндукции равна скорости изменения магнитного потока, вызванного изменением протекающего по контуру тока, а также пропорциональна скорости изменения тока. Коэффициент пропорциональности между ЭДС самоиндукции и скоростью изменения тока называется индуктивностью и обозначается L. Эта величина всегда положительна, и имеет единицу измерения в СИ 1 Генри (1 Гн). Также используются дробные доли – миллигенри и микрогенри. Об индуктивности в 1 Генри можно говорить, если изменение тока на 1 ампер вызывает ЭДС самоиндукции в 1 Вольт. Индуктивностью обладает не только контур, но и отдельный проводник, а также катушка, которую можно представить как множество последовательно включенных контуров.
В индуктивности запасается энергия, которую можно вычислить, как W=L*I2/2, где:
- W – энергия, Дж;
- L – индуктивность, Гн;
- I – ток в катушке, А.
И здесь энергия прямо пропорциональна индуктивности катушки.
Важно! В технике индуктивностью также называется устройство, в котором происходит запасание электрического поля. Реальный элемент, наиболее близкий к такому определению – катушка индуктивности.
Общая формула для расчета индуктивности физической катушки имеет сложный вид и для практических вычислений неудобна. Полезно запомнить, что индуктивность пропорциональна количеству витков, диаметру катушки и зависит от геометрической формы. Также на индуктивность влияет магнитная проницаемость сердечника, на котором расположена обмотка, но не влияет ток, протекающий по виткам. Для вычисления индуктивности каждый раз надо обращаться к приведенным формулам для конкретной конструкции. Так, для цилиндрической катушки её основная характеристика вычисляется по формуле:
L=μ*μ0*(N2*S/l),
где:
- μ – относительная магнитная проницаемость сердечника катушки;
- μ0 – магнитная постоянная, 1,26*10-6 Гн/м;
- N – количество витков;
- S – площадь витка;
- l – геометрическая длина катушки.
Для вычисления индуктивности для цилиндрической катушки и катушек других форм лучше воспользоваться программами-калькуляторами, в том числе онлайн-калькуляторами.
Последовательное и параллельное соединение индуктивностей
Индуктивности можно соединять последовательно или параллельно, получая набор с новыми характеристиками.
Параллельное соединение
При параллельном соединении катушек напряжение на всех элементах равны, а токи (переменные) распределяются обратно пропорционально индуктивностям элементов.
- U=U1=U2=U3;
- I=I1+I2+I3.
Общая индуктивность цепи определяется, как 1/L=1/L1+1/L2+1/L3. Формула справедлива для любого количества элементов, а для двух катушек упрощается до вида L=L1*L2/(L1+L2). Очевидно, что итоговая индуктивность меньше индуктивности элемента с наименьшим значен
Последовательное соединение
При таком виде соединения через цепь, составленную из катушек, течёт один и тот же ток, а напряжение (переменное!) на каждом компоненте цепи распределяется пропорционально индуктивности каждого элемента:
- U=U1+U2+U3;
- I=I1=I2=I3.
Суммарная индуктивность равна сумме всех индуктивностей, и будет больше индуктивности элемента с наибольшим значением. Поэтому такое соединение используют при необходимости получить увеличение индуктивности.
Важно! При соединении катушек в последовательную или параллельную батарею формулы расчёта верны только для случаев, когда исключено взаимное влияние магнитных полей элементов друг на друга (экранировкой, большим расстоянием и т.д.). Если влияние существует, то общее значение индуктивности будет зависеть от взаимного расположения катушек.
Некоторые практические вопросы и конструкции катушек индуктивности
На практике применяют различные конструкции катушек индуктивности. В зависимости от назначения и области применения устройства можно выполнить различным способом, но надо учитывать эффекты, возникающие в реальных катушках.
Добротность катушки индуктивности
У реальной катушки, кроме индуктивности, есть ещё несколько параметров, и один из самых важных – добротность. Эта величина определяет потери в катушке и зависит от:
- омических потерь в проводе обмотки (чем больше сопротивление, тем ниже добротность);
- диэлектрических потерь в изоляции провода и каркасе обмотки;
- потерь в экране;
- потерь в сердечнике.
Все эти величины определяют сопротивление потерь, а добротностью называют безразмерную величину, равную Q=ωL/Rпотерь, где:
- ω = 2*π*F – круговая частота;
- L – индуктивность;
- ωL – реактивное сопротивление катушки.
Можно приближённо говорить о том, что добротность равна отношению реактивного (индуктивного) сопротивления к активному. С одной стороны, с ростом частоты растёт числитель, но в то же время за счет скин-эффекта растёт и сопротивление потерь за счет уменьшения полезного сечения провода.
Экранный эффект
Для уменьшения влияния посторонних предметов, а также электрических и магнитных полей и взаимного влияния элементов посредством этих полей, катушки (особенно высокочастотные) часто помещают в экран. Кроме полезного эффекта, экранирование вызывает снижение добротности катушки, снижение её индуктивности и повышение паразитной ёмкости. Причём чем ближе стенки экрана к виткам катушки, тем выше вредное влияние. Поэтому экранированные катушки практически всегда выполняют с возможностью подстройки параметров.
Подстроечная индуктивность
В некоторых случаях требуется точно установить значение индуктивности на месте после подключения катушки к другим элементам цепи, компенсируя отклонение параметров при настройке. Для этого применяются разные способы (переключения отводов витков и т.п.), но наиболее точный и плавный метод – подстройка с помощью сердечника. Он выполняется в виде стержня с резьбой, который можно вворачивать и выворачивать внутри каркаса, настраивая индуктивность катушки.
Переменная индуктивность (вариометр)
Там, где требуется оперативная регулировка индуктивности или индуктивной связи, применяются катушки другой конструкции. Они содержат две обмотки – подвижную и неподвижную. Общая индуктивность равна сумме индуктивностей двух катушек и взаимной индуктивности между ними.
Изменением относительного положения одной катушки к другой, регулируется общее значение индуктивности. Такое устройство называется вариометром и часто применяется в связной аппаратуре для настройки резонансных контуров в тех случаях, когда применение конденсаторов переменной ёмкости по каким-то причинам невозможно. Конструкция вариометра довольно громоздкая, что ограничивает область его применения.
Шаровой вариометр
Индуктивность в виде печатной спирали
Катушки с небольшой индуктивностью можно выполнять в виде спирали из печатных проводников. Достоинством такой конструкции являются:
- технологичность производства;
- высокая повторяемость параметров.
К недостаткам относят невозможность точной подстройки при регулировке и сложность получения больших значений индуктивности – чем выше индуктивность, тем больше катушка занимает места на плате.
Катушка с секционной намоткой
Индуктивность без ёмкости бывает только на бумаге. При любой физической реализации катушки сразу же возникает паразитная межвитковая ёмкость. Это во многих случаях вредное явление. Паразитная ёмкость складывается с ёмкостью LC-контура, снижая резонансную частоту и добротность колебательной системы. Также у катушки возникает собственная резонансная частота, которая провоцирует нежелательные явления.
Для снижения паразитной ёмкости применяют различные способы, самый простой из которых – намотка индуктивности в виде нескольких последовательно включенных секций. При таком включении индуктивности складываются, а суммарная ёмкость снижается.
Катушка индуктивности на тороидальном сердечнике
Линии магнитного поля цилиндрической катушки
Линии магнитного поля цилиндрической катушки индуктивности проводят через внутреннюю часть обмотки (если там сердечник – то через него) и замыкаются снаружи через воздух. Этот факт влечёт за собой несколько недостатков:
- снижается индуктивность;
- характеристики катушки меньше поддаются расчёту;
- любой предмет, внесенный во внешнее магнитное поле, меняет параметры катушки (индуктивность, паразитная ёмкость, потери и т.п.), поэтому во многих случаях требуется экранировка.
От этих недостатков во многом свободны катушки, намотанные на тороидальных сердечниках (в виде кольца или «бублика»). Магнитные линии проходят внутри сердечника в виде замкнутых петель. Это означает, что внешние предметы практически не оказывают влияние на параметры намотанной на таком сердечнике катушки, и экранировка для такой конструкции не нужна. Также увеличивается индуктивность при прочих равных параметрах, а характеристики проще рассчитать.
Линии магнитного поля тороидальной катушки
К недостаткам катушек, намотанных на торах, относят невозможность плавной подстройки индуктивности на месте. Другая проблема – высокая трудоёмкость и низкая технологичность намотки. Впрочем, это относится ко всем индуктивным элементам в целом, в большей или меньшей степени.
Также общим недостатком физической реализации индуктивности являются высокие массогабаритные показатели, относительно невысокая надежность и низкая ремонтопригодность.
Поэтому в технике от индуктивных компонентов стараются избавляться. Но это возможно далеко не всегда, поэтому намоточные компоненты будут использоваться как в обозримом будущем, так и в среднесрочной перспективе.
Продолжаем обсуждение катушек индуктивности, в первой части (ссылка) мы обсудили все основные аспекты, а именно устройство катушек, принцип работы и их поведение при использовании в цепях постоянного и переменного тока. Но некоторые моменты остались незатронутыми, собственно, их мы и обсудим в этой статье. И начнем с очень важной характеристики, а именно добротности катушки индуктивности.
Активное сопротивление и добротность катушки индуктивности.
Итак, начнем мы с того, что обсудим некоторые характеристики катушек индуктивности, с которыми мы не успели познакомиться в предыдущей статье. И для начала рассмотрим активное сопротивление катушки.
Разбирая примеры включения катушек в различные цепи, мы считали их активное сопротивление равным 0 (такие катушки называют идеальными). Но на практике любая катушка обладает ненулевым активным сопротивлением. Таким образом реальную катушку индуктивности можно представить как идеальную катушку и последовательно включенный резистор:
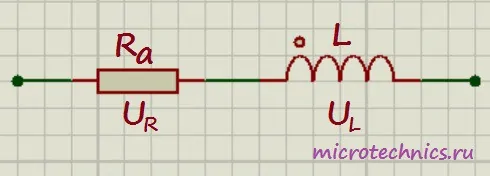
Идеальная катушка, как вы помните, не оказывает никакого сопротивления постоянному току, и напряжение на ней равно 0. В случае с реальной катушкой ситуация несколько меняется. При протекании по цепи постоянного тока напряжение на катушке будет равно:
Ну а поскольку частота тока равна 0 (постоянный ток), то реактивное сопротивление:
А что же будет происходить при включении реальной катушки индуктивности в цепь переменного тока? Давайте разбираться. Представим, что по данной цепи течет переменный ток i, тогда общее напряжение на цепи будет складываться из следующих компонент:
Напряжение на идеальной катушке, как вы помните, выражается через ЭДС самоиндукции:
u_L = -varepsilon_L = Lfrac{di}{dt}
И мы получаем для напряжения на реальной катушке индуктивности:
Отношение реактивного (индуктивного) сопротивления к активному называется добротностью и обозначается буквой Q:
Раз активное сопротивление R идеальной катушки равно 0, то значит ее добротность Q будет бесконечно большой. Соответственно, чем выше добротность катушки индуктивности, тем она ближе к идеальной. Таким образом активное сопротивление катушки мы рассмотрели, перейдем к следующему вопросу.
Энергия катушки индуктивности.
Электрический ток, протекающий через катушку способствует накоплению энергии в магнитном поле катушки. При пропадании/отключении тока эта энергия будет возвращена в электрическую цепь. С этим мы и столкнулись при рассмотрении катушек индуктивности в цепях постоянного тока. Больше тут добавить особо нечего, просто приведу формулу, по которой можно определить величину этой накопленной энергии:
Планомерно переходим к вариантам соединения катушек между собой. Все расчеты будем производить для идеальных катушек индуктивности, то есть их активные сопротивления равны 0. К слову, в большинстве теоретических задач и примеров, рассматриваются именно идеальные катушки. Но не стоит забывать о том, что в реальных цепях активное сопротивление не равно 0, и его необходимо учитывать при проведении любых расчетов.
Последовательное соединение катушек индуктивности.
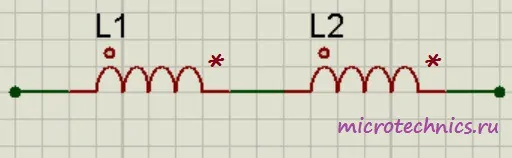
При последовательном соединении катушек индуктивности их можно заменить одной катушкой с величиной индуктивности, равной:
Вроде все просто, но тут есть один немаловажный нюанс. Данная формула справедлива только в том случае, если катушки расположены на таком расстоянии друг от друга, что магнитное поле одной катушки не пересекает витков другой:
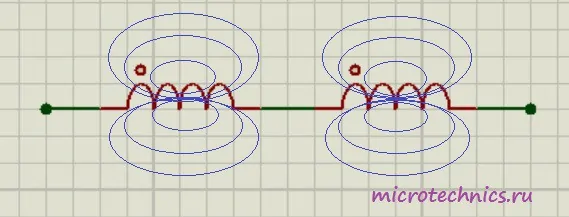
Если же катушки расположены близко друг к другу и часть магнитного поля одной катушки пронизывает вторую, то тут ситуация несколько другая. Возможны два варианта:
- магнитные потоки катушек имеют одинаковое направление
- магнитные потоки направлены навстречу друг другу
Первый случай называется согласным включением катушек – начало второй катушки подключается к концу первой. А второй вариант называют встречным включением – конец второй катушки подключается к началу первой. На схемах начало катушки обозначают символом “*“. Таким образом, на схеме, которая представлена на рисунке мы имеем согласное включение катушек индуктивности. Для этого случая общая индуктивность определяется так:
Где M – взаимная индуктивность катушек. При встречном включении последовательно соединенных катушек индуктивности:
L = L_1 + L_2medspace-medspace 2M
Можно заметить, что если потоки имеют одинаковое направление (согласное включение), то общая индуктивность увеличивается на двойную величину взаимной индуктивности. А если потоки направлены навстречу друг другу – уменьшается на ту же самую величину.
Параллельное соединение катушек индуктивности.
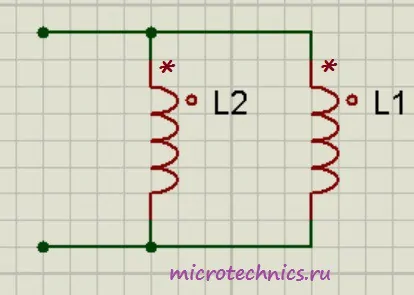
При параллельном соединении катушек индуктивности также возможны три варианта:
- Магнитное поле одной катушки не пересекает витков второй катушки, тогда: frac{1}{L_0} = frac{1}{L_1} +frac{1}{L_2} или L_0 = frac{L_1L_2}{L_1 + L_2}
- Часть магнитного потока одной катушки пронизывает витки второй и катушки включены согласно (как изображено на рисунке – то есть начала обеих катушек подключены к одному узлу). В этом случае: L_0 = frac{L_1L_2medspace-medspace M^2}{L_1 + L_2medspace-medspace 2M}
- Часть магнитного потока одной катушки пронизывает витки второй и катушки включены встречно. В этом случае: L_0 = frac{L_1L_2medspace-medspace M^2}{L_1 + L_2 + 2M}
Также как и в случае с последовательным соединением, при согласном включении общая индуктивность будет больше, чем при встречном включении, поскольку знаменатель дроби будет меньше.
Собственно, на этом заканчиваем разбор катушек индуктивности. Ранее мы изучили конденсаторы и резисторы, а в будущих статьях нам предстоит работать с цепями, включающими все эти элементы. Так что подписывайтесь на обновления и не пропускайте новые статьи 🤝
Теория индуктивностей
Характеристики магнитного поля
Магнитное поле создается постоянными магнитами и проводниками, по которым протекает электрический ток. Для характеристики магнитного поля вводятся такие величины:
Напряженность магнитного поля, характеризующая интенсивностъ магнитного поля в данной точке пространства. Напряженность магнитного поля, создаваемого током, определяется его величиной и формой проводника. Напряженность магнитного поля, в а/м внутри катушки. у которой длина намного больше диаметра, может быть определена по формуле
где I – ток (в а); w– число витков, l – длина катушки (в м).
Магнитный поток – общее количество магнитных силовых линий, пронизывающих контур. Для вакуума и практически для воздуха магнитный поток в веберах – вб, определяется по формуле
где S — площадь контура в квадратных метрах.
Магнитная индукция – интенсивность результирующего магнитного поля в данном веществе измеряется в веберах на метр квадратный (вб/м2)
Магнитная проницаемость – величина, показывающая, во сколько раз магнитная индукция в данном веществе больше или меньше на пряжеиности внешнего магнитного поля (ом*сек)/м
Магнитная проницаемость вакуума (магнитная постоянная) равна единице. Для воздуха μ приблизительно равна 1. У парамагнитных веществ (алюминий, платина) μ > 1, у диамагнитных (медь, висмут и др.) μ < 1, а у ферро магнитных (железо, никель, кобальт и некоторые сплавы) μ >>> 1. В соответствии с приведенными выше формулами для любого вещества можем написать:
Кроме практической системы единиц, пользуются абсолютной электромагнитной системой единиц. Соотношение между единицами этих систем следующее:
1 = 12,56*10-3 Э (эрстед);
1 вб = 108 мкс (максвелл);
1 вб/м2 = 104 гс (гаусс).
Индуктивность и взаимоиндуктивность
Индуктивность (коэффициент самоиндукции) численно равна э. д. с. самоиндукции (eL), возникающей в проводнике (контуре) при равномерном изменении тока в нем на 1 а в 1 сек.
Индуктивность, измеряется в следующих единицах:
1 гн = 1000 мгн;
1 мгн = 1000 мкгн;
1 мкгн = 1000 см.
Рис. 1 Схема взаимосвязанных индуктивностей.
Коэффициент взаимоиндукции М численно равен э. д. с. взаимоиндукции, возникающей в одном контуре при равномерном изменении тока на 1 а в 1 сек. в другом контуре (рис. 1).
Коэффициент взаимоиндукции измеряется в тех же единицах, что и индуктивность. Связь через общий магнитный поток двух катушек индуктивностью L1 и L2 называется индуктивной связью, характеризуемой коэффициентом связи
Зная коэффициент связи, можно определить коэффициент рассеяния
Если катушки находятся на общем замкнутом ферромагнитном сердечнике достаточно большого сечения, то k приблизительно равно 1, а ϭ приблизительно равна 0.
Соединение индуктивностей
Общая индуктивность L нескольких последовательно или параллельно соединенных индуктивностей при отсутствии, а также при наличии индуктивной связи между ними определяется по формулам, приведенным в таблице №1.
Таблица № 1
| Схема соединения | Общая индуктивность |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В формулах отмеченных значком * верхний знак алгебраического сложения, используется при согласованном включении индуктивностей, а нижний знак алгебраического сложения, используется при встречном включении индуктивностей.
Катушки с малой индуктивностью
Однослойные катушки
применяются на частотах выше 1500 кГц. Намотка может быть сплошная и с принудительным шагом. Однослойные катушки с принудительным шагом отличаются высокой добротностью (Q = 150 – 400) и стабильностью. Они применяются в основном в контурах КВ и УКВ. Высокостабильные катушки, применяемые в контурах гетеродинов на КВ и УКВ, наматываются при незначительном натяжении проводом, нагретым до 80—120°.
Для катушек с индуктивностью выше 15 – 20 мкГн применяется сплошная однослойная намотка. Целесообразность перехода на сплошную намотку определяется диаметром катушки. В таблице № 2, приведены ориентировочные значения индуктивности, при которых целесообразен переход на сплошную намотку:
Таблица № 2
| Диаметр каркаса (в мм.) |
6 |
10 |
15 |
20 |
25 |
|
Предельная индуктивность (в мкГн) |
1,8 |
4 |
10 |
20 |
30 |
Катушки со сплошной намоткой также отличаются высокой добротностью и широко используются в контурах на коротких, промежуточных и средних волнах, если требуется индуктивность не выше 200—500 мкГн. Целесообразность перехода на многослойную намотку определяется диаметром катушки. В таблице № 3, приведены ориентировочные значения индуктивности при заданных диаметрах, при которых целесообразен переход на многослойную намотку:
Таблица № 3
| Диаметр каркаса (в мм.) |
10 |
15 |
20 |
25 |
30 |
|
Предельная индуктивность (в мкГн) |
30 |
50 |
100 |
200 |
500 |
Индуктивность простой однослойной катушки может быть рассчитана по формуле (1):
где L – индуктивность (в мкГн), D – диаметр катушки (в см), I – длина намотки (в см), w – число витков.
При намотке однослойной катушки индуктивности с принудительным шагом, общая индуктивность (в мкГн), рассчитывается по формуле (2):
где L – индуктивность катушки, найденная по формуле (1) т. е. без поправки на шаг намотки;
А и В – поправочные коэффициенты, определяемые по графикам рис. 2а и 2б;
D – диаметр (в см);
w — число витков катушки.

Рис. 2 Графики поправочных коэффициентов для расчета индуктивности однослойных катушек с принудительным шагом намотки
d – диаметр провода;
t – шаг намотки;
Многослойные катушки могут быть разделены на простые и сложные. Примерами простых намоток являются рядовая многослойная намотка и намотка внавал.
Несекцнонированные многослойные катушки с простыми намотками отличаются пониженной добротностью и стабильностью, большой собственной емкостью, требуют применения каркасов со щечками.
Широкое применение имеют сложные универсальные намотки. В радиолюбительской практике находит применение также сотовая намотка. Индуктивность многослойной катушки может быть рассчитана по формуле:
где L – индуктивность катушки (в мкГн), D – средний диаметр намотки (в см), l – длина намотки (в см), t – толщина катушки (в см), w – число витков.
Если задана индуктивность и нужно рассчитать число витков, то следует задаться величинами D, l и t и подсчитать необходимое число витков. После этого следует произвести проверку толщины катушки по формуле:
где t – толщина катушки (в см), l – длина намотки (в мм), w – число витков. d0 – диаметр провода с изоляцией (в мм), α – коэффициент неплотности намотки. Значения коэффициента неплотности α, для многослойной намотки, могут быть взяты из таблицы 4.
Таблица 4
|
Диаметр провода без изоляции в (мм) |
Коэффициент неплотности α |
|
0,08 – 0,11 |
1,3 |
|
0,15 – 0,25 |
1,25 |
|
0,35 – 0,41 |
1,2 |
|
0,51 – 0,93 |
1,1 |
|
Более 1,0 |
1,05 |
Для намотки «внавал» α надо увеличить на 10% – 15%. Если фактическая толщина катушки отличается от принятой в начале расчета более чем на 10%, то следует задаться другими размерами катушки и повторить расчет.
Секционированные катушки индуктивности – рисунок 3, характеризуются достаточно высокой добротностью, пониженной собственной емкостью, меньшим наружным диаметром и допускают в небольших пределах регулировку индуктивности путем смещения секций.
Рис. 3 Секционированная катушка индуктивности.
Они применяются как в качестве контурных в контурах длинных и средних волн, так и в качестве дросселей высокой частоты.
Каждая секция представляет собой обычную многослойную катушку с небольшим числом витков. Число секций n может быть от двух до восьми, иногда даже больше. Расчет секционированных катушек сводится к расчету индуктивности одной секции. Индуктивность секционированной катушки, состоящей из n секций,
где Lc – индуктивность секции, k – коэффициент связи между смежными секциями.
Коэффициент связи зависит от размеров секций и расстояния между ними. Эта зависимость изображена на графике – рисунок 4.
Рис. 4 График зависимости коэффициента связи от размеров секций и расстояния между ними.
Отношение b/Dср выбирается так, чтобы величина коэффициента связи была в пределах 0,25 – 0,4. Это получается при расстояниях b = 2l. Расчет каждой секции производится обычным способом.
Корзиночная катушка, изображена на рисунке 5. Это плоскоспиральная намотка на основание в виде круга с нечетным числом радиальных прорезей. Через каждый разрез провод переходит с одной стороны круглого основания на другую.
Рис. 5 Корзиночная катушка индуктивности.
Индуктивность такой катушки в мкГн определяется по формуле:
где w – число витков, D2 – внешний диаметр намотки (в см), D1 – внутренний диаметр намотки (в см), k – поправочный коэффициент для корзиночных катушек, определяемый из таблицы 5.
Таблица 5. Поправочный коэффициент k для корзиночных катушек.
|
|
k |
|
1,2 |
3,3 |
|
1,5 |
3,0 |
|
1,8 |
2,7 |
|
2,0 |
2,6 |
|
3,0 |
2,1 |
|
5,0 |
1,6 |
|
8,0 |
1,2 |
|
10,0 |
1,0 |
Наилучшим соотношением для корзиночных катушек является D2 = 2D1
Торроидальные катушки индуктивности на немагнитном сердечнике – выполняются сплошной намоткой на кольцевом немагнитном сердечнике, со средним диаметром D, как правило, поперечное сечение кольца имеет форму окружности с диаметром d. Эскиз торроидальной катушки индуктивности на немагнитном сердечнике изображен на рисунке 6.
Рис. 6 Торроидальная катушка индуктивности на немагнитном сердечнике.
Индуктивность такой катушки в мкГн определяется по следующей формуле:
где D – средний диаметр торроидального сердечника (в см.), w – количество витков катушки, d – диаметр витка (в см.)
Собственная емкость катушек индуктивности
Собственная емкость изменяет параметры катушки, понижает добротность и стабильность настройки контуров. В диапазонных контурах эта емкость уменьшает коэффициент перекрытия диапазона.
Величина собственной емкости определяется типом намотки и размерами катушки. Наименьшая собственная емкость (несколько пф) у однослойных катушек, намотанных с принудительным шагом. Многослойные катушки обладают большей емкостью, величина которой зависит от способа намотки. Так, емкость катушек с универсальной намоткой составляет 5—25 пф, а с рядовой многослойной намоткой может быть выше 50 пф.
Катушки с большой индуктивностью
В катушках с большой индуктивностью применяются сердечники из ферромагнитных материалов. Индуктивность катушки с замкнутым стальным сердечником, измеряется в генри (гн) и рассчитывается по формуле:
Где μ – магнитная проницаемость материала, Sc – сечение сердечника в квадратных сантиметрах см2, ω – число витков катушки, lc– средняя длина магнитного пути в см. Схематическое изображение Ш – образного магнитного сердечника, приведено на рисунке 7.
Рис. 7 Ш – образный магнитный сердечник
Следует помнить, что магнитная проницаемость материала зависит от переменной составляющей индукции в сердечнике и от величины постоянного подмагничивания, а также от частоты. Ниже приводится методика расчета катушек индуктивности, работающих при малых значениях переменной составляющей индукции, например, дросселей сглаживающих фильтров для выпрямителей. Для катушек индуктивности, работающих без постоянного подмагничивания, число витков определяется по формуле:
Где L – индуктивность катушки в гн, lc – средняя длина магнитного пути в см, μн – начальная проницаемость магнитного материала, Sc – сечение сердечника в квадратных сантиметрах см2.
Для катушек индуктивности с постоянным подмагничиванием предварительно определяем ориентировочное значение действующей магнитной проницаемости, с учетом подмагничивания, по графикам для разных электротехнических сталей, приведенным на рис. 8, где I0 – ток подмагничивания, L – индуктивность.
Рис. 8 Графики для ориентировочного определения
действующей магнитной проницаемости при
постоянном подмагничивании
Ориентировочное число витков для катушек индуктивности с постоянным подмагничиванием определяем по формуле (*) :
Где μд – истинное значение магнитной проницаемости материала ферромагнитного сердечника. Истинное значение действующей магнитной проницаемости μд определяется по кривым рисунка 9.
Рис. 9 Графики для определения истинного значения
действующей магнитной проницаемости при
постоянном подмагничивании
Постоянное подмагничивание awo на 1 см длины магнитного пути для работы с графиками рисунка 4, можно определить по формуле:
где Io – ток подмагничивания в ма, lс – длина магнитного пути в см.
Далее определяется точное число витков катушки по приведенной выше формуле (*). Диаметр провода катушки в мм :
Где Io – ток подмагничивания в а.
Величина немагнитного зазора в сердечнике, изображенного на рисунке 1 высчитывается по формуле:
причем Z% определяется по кривым рисунка 10. Толщина немагнитной прокладки выбирается равной 0,5δз. Прокладки можно делать из любого листового изоляционного материала.
Рис. 10 Кривые для определения величины z%




























































