Общее среднее как его найти - Сайт, где вы сможете решить свои вопросы

Допустим, что все значения
количественного признака X
совокупности,
безразлично-генеральной или выборочной,
разбиты на несколько групп. Рассматривая
каждую группу как самостоятельную
совокупность, можно найти ее среднюю
арифметическую.

Групповой средней называют среднее
арифметическое значений признака,
принадлежащих группе.

Теперь целесообразно ввести специальный
термин для средней всей совокупности.

Общей средней
называют среднее
арифметическое значений признака,
принадлежащих всей совокупности.

Зная групповые средние и
объемы групп, можно найти общую среднюю:
общая средняя равна
средней арифметической групповых
средних, взвешенной по объемам групп,

Опуская доказательство, приведем
иллюстрирующий пример.

Пример.
Найти
общую среднюю совокупности, состоящей
из
следующих
двух групп:

Группа……………………….	первая	вторая
Значение признака…………	1	6	1	5
Частота………………………	10	15	20	30
Объем……………………….	10+15 = 25	20 + 30 = 50

Решение.
Найдем групповые средние:

=(10*1+15*6)/25=4;

=
(20*1+30*5)/50
= 3,4.

Найдем общую
среднюю по групповым средним:

=(25*
4 + 50*3,4)/(25 + 50) = 3,6.

Замечание.
Для упрощения расчета общей средней
совокупности большого объема целесообразно
разбить ее на несколько групп, найти
групповые
средние и по ним общую среднюю.

§ 7. Отклонение от общей средней и его свойство

Рассмотрим совокупность,
безразлично-генеральную или выборочную,
значений количественного признака X
объема n:

значения признака .…… x₁
x₂…
x_k

частоты………………………
n₁
n₂
… n_k

При
этом
.
Далее
для удобства записи знак суммы
заменен знаком.

Найдем общую среднюю:

Отсюда

.
(*)

Заметим, что поскольку x
– постоянная величина,
то

.
(**)

Отклонением называют
разность
между значением
признака и общей средней.

Теорема. Сумма
произведений отклонений на соответствующие
частоты равна нулю:

Доказательство. Учитывая (*) и (**), получим

Следствие. Среднее
значение отклонения равно нулю.

Пример.
Дано
распределение количественного признака
X:

x_i
1
2 3

n_i
10
4 6

Убедиться,
что сумма произведений отклонений на
соответствующие
частоты равна нулю.

Решение.
Найдем общую среднюю:

=
(10*1+4*2+6*3)/20
=1,8

Найдем
сумму произведений отклонений на
соответствующие
частоты:

§ 8. Генеральная дисперсия

Для того чтобы охарактеризовать
рассеяние значений количественного
признака X
генеральной совокупности
вокруг своего среднего значения, вводят
сводную характеристику – генеральную
дисперсию.

Генеральной дисперсией
D_г
называют среднее арифметическое
квадратов отклонений значений признака
генеральной совокупности от их среднего
значения .

Если все значения x₁,
х₂,
…, x_Nпризнака генеральной
совокупности объема N
различны, то

Если же значения признака
x₁,
х₂,
…, x_kимеют соответственно
частоты N₁,
N₂,…,
N_k,
причем N₁
+N₂+…+N_k=N,
то

т.е. генеральная дисперсия есть средняя
взвешенная квадратов отклонений с
весами, равными соответствующим частотам.

Пример.
Генеральная
совокупность задана таблицей распределения

x_i

2

4
5 6

N_i
8
9 10 3

Найти генеральную
дисперсию.

Решение.
Найдем генеральную среднюю (см. § 3):

Найдем генеральную
дисперсию;

Кроме дисперсии для характеристики
рассеяния значений признака генеральной
совокупности вокруг своего среднего
значения пользуются сводной характеристикой
– средним квадратическим отклонением.

Генеральным средним
квадратическим отклонением (стандартом)
называют квадратный
корень из
генеральной дисперсии:

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Среднее арифметическое

Онлайн калькулятор поможет найти среднее арифметическое чисел. Среднее арифметическое множества чисел (ряда чисел) — число, равное сумме всех чисел множества, делённой на их количество.

Программа вычисляет среднее арифметическое элементов массива, среднее арифметическое натуральных чисел, целых чисел, набора дробных чисел.

Формула которая используется для расчета среднего арифметического значения:

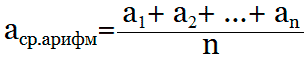
Приведём примеры нахождения среднего арифметического ряда чисел:
Среднее арифметическое двух чисел: (2+5)/2=3.5;
Среднее арифметическое трёх чисел: (2+5+7)/3=4.66667;
Среднее арифметическое 4 чисел: (2+5+7+2)/4=4;

Найти выборочное среднее (математические ожидание):
Среднее арифметическое 5 чисел: (2+5+7+2+3)/5=3.8;
Среднее арифметическое 6 чисел: (2+5+7+2+3+4)/6=3.833;
Среднее арифметическое 7 чисел: (2+5+7+2+3+4+8)/7=4.42857;
Среднее арифметическое 8 чисел: (2+5+7+2+3+4+8+5)/8=4.5;
Среднее арифметическое 10 чисел: (2+5+7+2+3+4+8+5+9+1)/10=4.6;

Пожалуйста напишите с чем связна такая низкая оценка:

Для установки калькулятора на iPhone – просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android – просто добавьте страницу
«На главный экран»

Смотрите также

Источник

Загрузить PDF

Чтобы вычислить среднее арифметическое в группе чисел, необходимо их сложить и разделить на количество чисел. В повседневной жизни среднее арифметическое может пригодиться, когда необходимо оценить ежемесячные расходы, узнать, сколько времени уходит на выполнение той или иной задачи, или определить количество людей на основе предыдущего посещения.

1

Найдите сумму чисел в данном ряду. Первым делом сложите все числа в числовом ряду. Предположим, вам дан ряд 1, 2, 3, and 6. В этом случае сумма будет составлять .^[1]
2

Разделите результат на количество чисел в ряду. Наш ряд состоит из четырех чисел, поэтому следует взять сумму, 12, и разделить ее на четыре.^[2]. Среднее арифметическое в этом ряду равняется 3.^[3]

Реклама

1
Запишите среднее арифметическое в каждой категории. Прежде всего найдите среднее арифметическое каждой категории, сложив все числа в ряду и разделив на количество чисел. Например, вам требуется найти средневзвешенное значение для класса и даны следующие числа:^[4]
- Среднее арифметическое домашней работы = 93 %
- Среднее арифметическое экзамена = 88 %
- Среднее арифметическое проверочной работы = 91 %
2
Запишите весовую категорию каждого среднего арифметического. Помните, что весовые категории должны в сумме составлять 100 %. Предположим, вам даны следующие весовые категории:
- Среднее арифметическое домашней работы = 30 % итоговой оценки
- Среднее арифметическое экзамена = 50 % итоговой оценки
- Среднее арифметическое проверочной работы = 20 % итоговой оценки
3
4

Сложите полученные результаты. Чтобы найти средневзвешенное значение, сложите все три результата: . Средневзвешенное значение для этого ряда равняется .

Реклама