
Любой физический объект в окружающем нас мире состоит из огромного количества элементарных частиц, обладающих зарядами. Элементарная частица протон имеет элементарный электрический заряд, которому приписывают (условно) положительный знак, элементарная частица электрон имеет элементарный отрицательный заряд.
Содержание:
-
- Электрический заряд
- Напряженность
- Потенциал, напряжение
-
Электрический заряд
Под электрическим зарядом понимают физическую величину, которая характеризует способность тел (объектов) вступать в электрическое взаимодействие. Электрический заряд обозначается через q (иногда для обозначения используют заглавную букву Q) и в Международной системе единиц (СИ) измеряется в Кулонах, [Кл].
Электрический заряд – дискретная величина, кратная элементарному электрическому заряду одного электрона (по модулю) e = 1,60217*10-9 Кл.
![]()
где N – целое число.
С физической точки зрения 1 кулон [Кл] соответствует электрическому заряду, проходящему через поперечное сечение проводника при силе тока 1 Ампер за 1 секунду.
Заряды существуют в двух видах: положительные (+) и отрицательные (-). Одноименные заряды отталкиваются, а разноименные – притягиваются.
Сила взаимодействия зарядов направлена вдоль прямой, соединяющей их, пропорциональна величине зарядов и обратно пропорциональна квадрату расстояния между ними (рисунок 1).
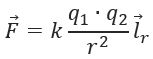
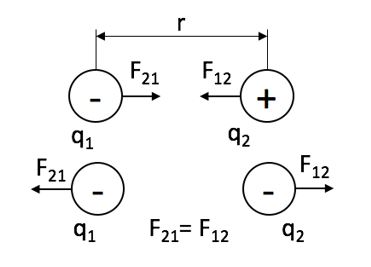
где k – коэффициент пропорциональности, зависящий от выбора системы единиц;
![]() – единичный вектор, направленный вдоль прямой, соединяющей заряды q1 и q2.
– единичный вектор, направленный вдоль прямой, соединяющей заряды q1 и q2.
Силу взаимодействия двух зарядов ![]() принято называть кулоновской силой в честь ученого-физика Шарля Кулона, обнаружевшего ее существование.
принято называть кулоновской силой в честь ученого-физика Шарля Кулона, обнаружевшего ее существование.
Если объект (система) не обменивается зарядами с окружающей средой, его называют электрически изолированным. В такой системе сумма электрических зарядов (положительных и отрицательных) не меняется со временем, то есть наблюдается закон сохранения заряда.
Большинство тел в природе электрически нейтральны, так как содержат заряды обоих типов в одинаковом количестве. Положительные и отрицательные заряды попарно нейтрализуют действие друг друга. Для перехода тела в заряженное состояние необходимо пространственно перераспределить в нем заряды, сконцентрировав одноименные заряды в одной области тела. Это возможно сделать, например, при помощи трения или взаимодействия с другим заряженным объектом (рисунок 2).

Электрический заряд порождает в окружающем его пространстве непрерывную материю, называемую электрическим полем. Благодаря электрическому полю заряды имеют возможность взаимодействовать между собой. В электротехнике электрическое поле характеризуется двумя величинами: напряженностью (силовая характеристика) и потенциалом (энергетическая характеристика).
Напряженность электрического поля
Напряженность электрического поля – это векторная физическая количественная характеристика электрического поля. Ее величина показывает силу, которая действует на пробный точечный единичный положительный заряд, помещенный в некоторую точку электрического поля.
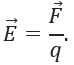
Под точечным зарядом понимают упрощенную модель положительного заряда, в которой его формой и размером можно пренебречь.
Вектор напряженности ![]() по направлению совпадает с вектором силы
по направлению совпадает с вектором силы ![]() , с которой электрическое поле действует на положительный точечный заряд, помещенный в заданную точку поля (рисунок 3).
, с которой электрическое поле действует на положительный точечный заряд, помещенный в заданную точку поля (рисунок 3).

Величина напряженности поля в точке А определяется согласно формуле

где r – расстояние от заряда q до точки А, k – коэффициент пропорциональности, зависящий от выбора системы единиц.
Электрическое поле графически изображается линиями напряженности электрического поля, которые условно принято обозначать исходящими из положительно заряженных элементов и входящими в отрицательно заряженные заряды (рисунок 4).
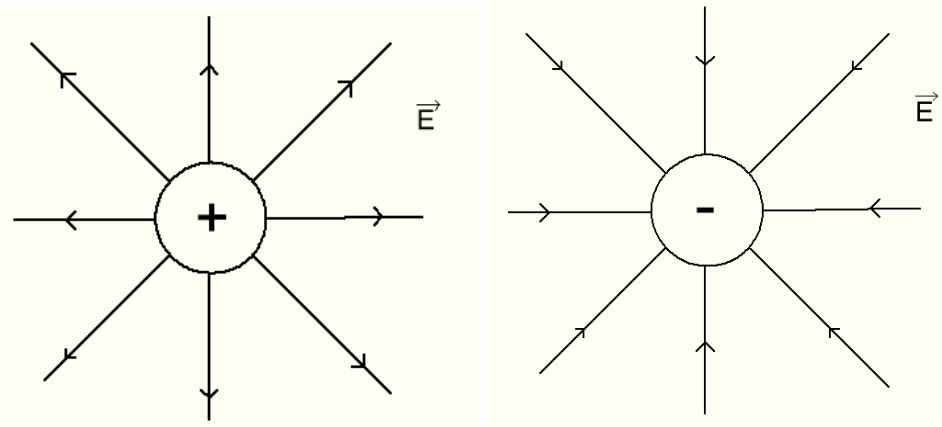

Рис. 4. Распределение линий напряженности для изолированных (а) и взаимодействующих (б) зарядов
Потенциал, напряжение
Физическую величину, равную отношению потенциальной энергии W электрического заряда в электростатическом поле к величине самого заряда q, называют потенциалом φ электрического поля

Потенциал – это скалярная величина, которая показывает, какую работу способно затратить поле, чтобы переместить единичный пробный положительный заряд в бесконечно удалённую точку. Единицей измерения электрического потенциала является вольт, [В].
При этом важно отметить, что работа сил электростатического поля при перемещении заряда из одной точки электрического поля в другую не зависит от формы траектории перемещения, а зависит только от начального и конечного положения заряда, а также от его величины.
Если имеется некоторая система, состоящая из N точечных зарядов, то потенциал ее электрического поля φ будет равен алгебраической сумме потенциалов полей каждого входящего в него заряда, то есть
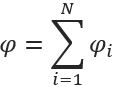
Напряжение электрического поля – это разность потенциалов между двумя точками этого поля (рисунок 5).
Напряжение (U) — это работа (А) совершаемая силой поля по перемещению заряженных частиц между двумя точками поля.
U = A/q [Дж/Кл] или [В]

Напряжение является относительной величиной, то есть всегда определяется относительно некоторого уровня. Нулевой уровень выбирается произвольно и не влияет на итоговое значение напряжения, так как соответствует разности потенциалов в двух точках (то есть изменению потенциальной энергии). Для простоты расчетов в качестве нулевого уровня в большинстве случаев принимают потенциал заземленного проводника или земли.
Как уже было отмечено ранее электрическое напряжение – это разность потенциалов двух точек, следовательно его значение определяется по формуле
![]()
В системе СИ за единицу измерения напряжения принимается вольт, [В]. Физически величина напряжения, равная 1 вольту, соответствует работе 1 джоуль при перемещении заряда в 1 кулон.
#1. Физическая величина измеряемая в кулонах?
Потенциал
Напряжение
Электрический заряд
Электрический заряд обозначается через q и в Международной системе единиц (СИ) измеряется в Кулонах, [Кл].
#2. Какие пары электрических зарядов будут притягиваться к друг другу?
Два положительных заряда
Два отрицательных заряда
Один отрицательный заряд, а другой положительный
Одноименные заряды отталкиваются, а разноименные – притягиваются.
#3. … – это работа совершаемая силой поля по перемещению заряженных частиц между двумя точками поля.
Напряжение
Сопротивление
Потенциал
Результат
Отлично!
Попытайтесь снова(
Главная
→
Примеры решения задач ТОЭ
→
Расчет электрической цепи постоянного тока с конденсаторами
Расчет электрической цепи постоянного тока с конденсаторами
Расчет электрической цепи постоянного тока с конденсаторами
Основные положения и соотношения
1. Общее выражение емкости конденсатора
C= Q U .
2. Емкость плоского конденсатора
C= ε a ⋅S d = ε r ⋅ ε 0 ⋅S d ,
здесь
S — поверхность каждой пластины конденсатора;
d — расстояние между ними;
εa = εr·ε0 — абсолютная диэлектрическая проницаемость среды;
εr — диэлектрическая проницаемость среды (относительная диэлектрическая проницаемость);
ε 0 = 1 4π⋅ с 2 ⋅ 10 −7 ≈8,85418782⋅ 10 −12 Ф м – электрическая постоянная.
3. При параллельном соединении конденсаторов С1, С2, …, Сn эквивалентная емкость равна
C= C 1 + C 2 +…+ C n = ∑ k=1 n C k .
4. При последовательном соединении конденсаторов эквивалентная емкость определяется из формулы
1 C = 1 C 1 + 1 C 2 +…+ 1 C n = ∑ k=1 n 1 C k .
Для двух последовательно соединенных конденсаторов эквивалентная емкость составляет:
C= C 1 ⋅ C 2 C 1 + C 2 ,
а напряжения между отдельными конденсаторами распределяются обратно пропорционально их емкостям:
U 1 =U⋅ C 2 C 1 + C 2 ; U 2 =U⋅ C 1 C 1 + C 2 .
5. Преобразование звезды емкостей в эквивалентный треугольник емкостей или обратно (рис. а и б)
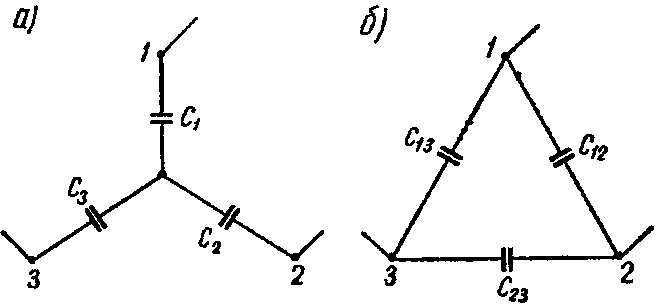
Рис. 0
осуществляется по формулам:
Y→Δ { C 12 = C 1 ⋅ C 2 ΣC ; C 13 = C 1 ⋅ C 3 ΣC ; C 23 = C 2 ⋅ C 3 ΣC , где ΣC= C 1 + C 2 + C 3 , Δ→Y { C 1 = C 12 + C 13 + C 12 ⋅ C 13 C 23 ; C 2 = C 12 + C 23 + C 12 ⋅ C 23 C 13 ; C 3 = C 13 + C 23 + C 13 ⋅ C 23 C 12 .
6. Энергия электростатического поля конденсатора:
W= C⋅ U 2 2 = Q⋅U 2 = Q 2 2C .
7. Расчет распределения зарядов в сложных цепях, содержащих источники э.д.с. и конденсаторы, производится путем составления уравнений по двум законам:
1) По закону сохранения электричества (закон сохранения электрического заряда): алгебраическая сумма зарядов на обкладках конденсаторов, соединенных в узел и не подключенных к источнику энергии, равна алгебраической сумме зарядов, имевшихся на этих обкладках до их соединения:
ΣQ=Σ Q ′ .
2) По второму закону Кирхгофа: алгебраическая сумма э. д. с. в замкнутом контуре равна алгебраической сумме напряжений на участках контура, в том числе на входящих в него конденсаторах:
∑ k=1 n E k = ∑ k=1 n U C k = ∑ k=1 n Q k C k .
Приступая к решению задачи, надо задаться полярностью зарядов на обкладках конденсаторов.
Решение задач на расчет электрической цепи постоянного тока с конденсаторами
Задача. Доказать формулу эквивалентной емкости при последовательном соединении конденсаторов (рис. 1).
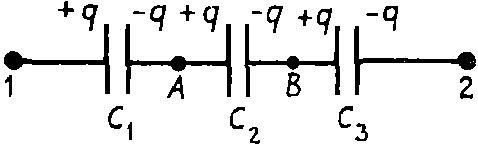
Рис. 1
Решение
На рис. 1 представлено последовательное соединение трех конденсаторов. Если батарею конденсаторов подключить к источнику напряжения U12, то на левую пластину конденсатора С1 перейдет заряд +q, на правую пластину конденсатора С3 заряд –q.
Вследствие электризации через влияние правая пластина конденсатора С1 будет иметь заряд –q, а так как пластины конденсаторов С1 и С2 соединены и были электронейтральны, то вследствие закона сохранения заряда заряд левой пластины конденсатора C2 будет равен +q, и т. д. На всех пластинах конденсаторов при таком соединении будет одинаковый по величине заряд.
Найти эквивалентную емкость — это значит найти конденсатор такой емкости, который при той же разности потенциалов будет накапливать тот же заряд q, что и батарея конденсаторов.
Разность потенциалов U12 = φ1 — φ2 складывается из суммы разностей потенциалов между пластинами каждого из конденсаторов
U 12 = φ 1 − φ 2 =( φ 1 − φ A )+( φ A − φ B )+( φ B − φ 2 )= U 1A + U AB + U B2 .
Воспользовавшись формулой напряжения на конденсаторе
U= q C ,
запишем
q C = q C 1 + q C 2 + q C 3 .
Откуда эквивалентная емкость батареи из трех последовательно включенных конденсаторов
1 C = 1 C 1 + 1 C 2 + 1 C 3 .
В общем случае эквивалентная емкость при последовательном соединении конденсаторов
1 C = 1 C 1 + 1 C 2 +…+ 1 C n = ∑ k=1 n 1 C k .
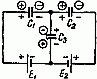
Задача 1. Определить заряд и энергию каждого конденсатора на рис. 2, если система подключена в сеть с напряжением U = 240 В.
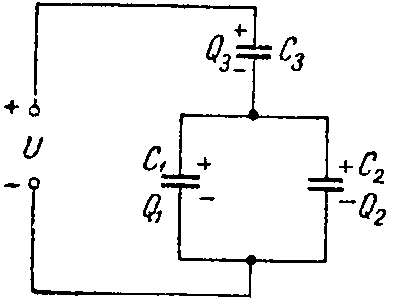
Рис. 2
Емкости конденсаторов: C1 =50 мкФ; C2 =150 мкФ; C3 =300 мкФ.
Решение
Эквивалентная емкость конденсаторов C1 и C2, соединенных параллельно
C12 = C1 + C2 = 200 мкФ,
эквивалентная емкость всей цепи равна
C= C 12 ⋅ C 3 C 12 + C 3 = 200⋅300 500 =120 мкФ.
Заряд на эквивалентной емкости
Q = C·U = 120·10–6·240 = 288·10–4 Кл.
Той же величине равен заряд Q3 на конденсаторе C3, т.е. Q3 = Q = 288·10–4 Кл; напряжение на этом конденсаторе
U 3 = Q 3 C 3 = 288⋅ 10 −4 300⋅ 10 −6 =96 В.
Напряжение на конденсаторах C1 и C2 равно
U1 = U2 = U — U3 = 240 — 96 = 144 В.
их заряды имеют следующие значения
Q1 = C1·U1 = 50·10–6·144 = 72·10–4 Кл;
Q2 = C2·U2 = 150·10–6·144 = 216·10–4 Кл.
Энергии электростатического поля конденсаторов равны
W 1 = Q 1 ⋅ U 1 2 = 72⋅ 10 −4 ⋅144 2 ≈0,52 Дж; W 2 = Q 2 ⋅ U 2 2 = 216⋅ 10 −4 ⋅144 2 ≈1,56 Дж; W 3 = Q 3 ⋅ U 3 2 = 288⋅ 10 −4 ⋅96 2 ≈1,38 Дж.
Задача 2. Плоский слоистый конденсатор (рис. 3), поверхность каждой пластины которого S = 12 см2, имеет диэлектрик, состоящий из слюды (εr1 = 6) толщиною d1 = 0,3 мм и стекла (εr2 = 7) толщиною d2 =0,4 мм.
Пробивные напряженности слюды и стекла соответственно равны E1 = 77 кВ/мм, E2 = 36 кВ/мм.
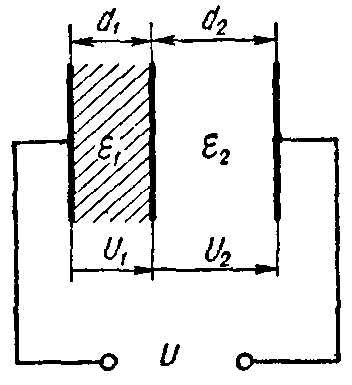
Рис. 3
Вычислить емкость конденсатора и предельное напряжение, на которое его можно включать, принимая для более слабого слоя двойной запас электрической прочности.
Решение
Эквивалентная емкость слоистого конденсатора определится как емкость двух последовательно соединенных конденсаторов
C= C 1 ⋅ C 2 C 1 + C 2 = ε a1 ⋅S d 1 ⋅ ε a2 ⋅S d 2 ε a1 ⋅S d 1 + ε a2 ⋅S d 2 = ε a1 ⋅ ε a2 ⋅S ε a1 ⋅ d 2 + ε a2 ⋅ d 1 .
Подставляя сюда числовые значения, предварительно заменив εa1 = εr1·ε0 и εa2 = εr2·ε0, получим
C= ε 0 ⋅ ε r1 ⋅ ε r2 ⋅S ε r1 ⋅ d 2 + ε r2 ⋅ d 1 =8,85⋅ 10 −12 ⋅ 6⋅7⋅12⋅ 10 −4 6⋅0,4⋅ 10 −3 +7⋅0,3⋅ 10 −3 =99⋅ 10 −12 Ф.
Обозначим общее напряжение, подключаемое к слоистому конденсатору, через Uпр, при этом заряд конденсатора будет равен
Q = C·Uпр.
Напряжения на каждом слое будут равны
U 1 = Q C 1 = C⋅ U пр ε a1 ⋅S d 1 = ε a2 ⋅ d 1 ε a1 ⋅ d 2 + ε a2 ⋅ d 1 ⋅ U пр ; U 2 = Q C 2 = C⋅ U пр ε a2 ⋅S d 2 = ε a1 ⋅ d 2 ε a1 ⋅ d 2 + ε a2 ⋅ d 1 ⋅ U пр .
Напряженности электростатического поля в каждом слое
E 1 = U 1 d 1 = ε a2 ε a1 ⋅ d 2 + ε a2 ⋅ d 1 ⋅ U ′ пр ; E 2 = U 2 d 2 = ε a1 ε a1 ⋅ d 2 + ε a2 ⋅ d 1 ⋅ U ″ пр .
Здесь U’np — общее напряжение, подключаемое к конденсатору, при котором пробивается первый слой, a U”np — общее напряжение, при котором происходит пробой второго слоя.
Из последнего выражения находим
U ′ пр = E 1 ⋅ ε a1 ⋅ d 2 + ε a2 ⋅ d 1 ε a2 =49,5 кВ; U ″ пр = E 2 ⋅ ε a1 ⋅ d 2 + ε a2 ⋅ d 1 ε a1 =27,0 кВ.
Таким образом, более слабым слоем является второй; согласно условию, принимая для него двойной запас прочности, находим, что конденсатор может быть включен на напряжение, равное
27,0 кВ / 2 = 13,5 кВ.
Задача 3. Обкладки плоского конденсатора с воздушным диэлектриком расположены на расстоянии d1 = 1 см друг от друга. Площадь обкладок S = 50 см2. Конденсатор заряжается до напряжения U = 120 В и затем отсоединяется от источника электрической энергии.
Определить, какую надо совершить работу, если увеличить расстояние между пластинами до d2 = 10 см. Краевым эффектом можно пренебречь; другими словами, емкость конденсатора можно считать обратно пропорциональной расстоянию между обкладками.
Решение
Энергия заряженного плоского конденсатора равна
W 1 = C 1 ⋅ U 2 2 = ε 0 ⋅S d 1 ⋅ U 2 2 ,
где С1 — емкость до раздвижения обкладок.
Так как конденсатор отключен от источника, то при изменении расстояния между обкладками его заряд остается постоянным. Поэтому из~ соотношения
Q = C2·U2,
где C2 — емкость конденсатора после раздвижения обкладок, следует, что, так как C2 = ε0·S/d2 стало меньше в 10 раз (d2 увеличилось в 10 раз), то напряжение на конденсаторе U2 увеличилось в 10 раз, т. е. U2 = 10U.
Таким образом, энергия конденсатора после отключения и раздвижения обкладок на расстояние d2 будет больше первоначальной
W 2 = ε 0 ⋅S d 2 ⋅ U 2 2 2 = ε 0 ⋅S 10 d 1 ⋅ ( 10U ) 2 2 =10⋅ ε 0 ⋅S d 1 ⋅ U 2 2 =10⋅ W 1 .
Увеличение энергии произошло за счет работы внешних сил, затраченной на раздвижение обкладок.
Таким образом, надо совершить работу, равную
W 2 − W 1 =9⋅ W 1 =9⋅ ε 0 ⋅S d 1 ⋅ U 2 2 =2,86⋅ 10 −7 Дж.
Задача 4. Для схемы (рис. 4) определить напряжение каждого конденсатора в двух случаях: при замкнутом и разомкнутом ключе К.
Даны: C1 = 30 мкФ; C2 = 20 мкФ; r1 = 100 Ом. r2 = 400 Ом. r3 = 600 Ом, U = 20 В.
Решение
Ключ К разомкнут. Конденсаторы соединены между собой последовательно; их ветвь находится под полным напряжением источника; напряжение распределяется между ними обратно пропорционально емкостям
U 1 = C 2 C 1 + C 2 ⋅U= 20⋅ 10 −6 30⋅ 10 −6 +20⋅ 10 −6 ⋅20=8 В; U 2 =U− U 1 =20−8=12 В.
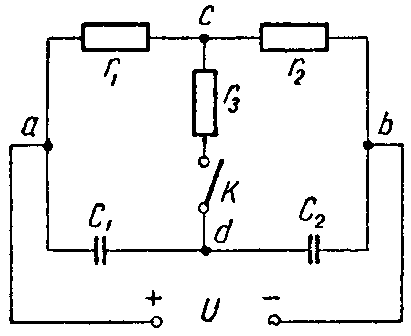
Рис. 4
Ключ К замкнут. Через сопротивления r1 и r2 протекает ток
I= U r 1 + r 2 = 20 500 =0,04 А,
а через сопротивление r3 ток не протекает.
Поэтому точки c и d равнопотенциальны (φc = φd). Следовательно, напряжение между точками a и c (Uac = φa — φc) равно напряжению между точками a и d (Uad = φa — φd).
Таким образом, напряжение на первом конденсаторе равно падению напряжения на сопротивлении r1
UC1 = I·r1 = 0,04·100 = 4 В.
Аналогично напряжение на втором конденсаторе равно
UC2 = I·r2 = 0,04·400 = 16 В.
Задача 5. Определить напряжение на зажимах конденсаторов и их энергию после перевода рубильника из положения 1 в положение 2, показанное пунктиром на рис. 5, если U = 25 В; C1 = 5 мкФ; C2 = 120 мкФ. Конденсатор C2 предварительно не был заряжен.
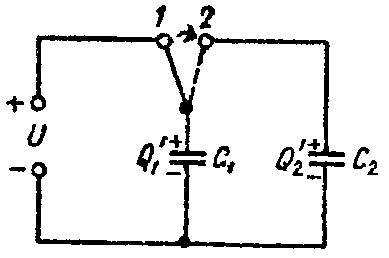
Рис. 5
Решение
Когда рубильник находится в положении 1, то конденсатор C1 заряжен до напряжения U и его заряд равен
Q = C1·U = 5·10–6·25 = 125·10–6 Кл.
После перевода рубильника в положение 2, заряд Q распределяется между конденсаторами C1 и C2 (рис. 5). Обозначим эти заряды через Q’1 и Q’2.
На основании закона сохранения электричества имеем
Q = Q’1 + Q’2 = 125 10–6 Кл. (1)
По второму закону Кирхгофа имеем
0= U C1 − U C2 = Q ′ 1 C 1 − Q ′ 2 C 2 ,
или
Q ′ 1 5⋅ 10 −6 − Q ′ 2 120⋅ 10 −6 =0. (2)
Решая уравнения (1) и (2), найдем
Q’1 = 5 10–6 Кл; Q’2 = 120 10–6 Кл.
Доставка свежих и аппетитных японских суши в Новороссийске – ям ям..
Напряжение на зажимах конденсаторов станет равным
U C1 = Q ′ 1 C 1 = U C2 = Q ′ 2 C 2 = 5⋅ 10 −6 5⋅ 10 −6 =1 В.
Энергия обоих конденсаторов будет равна
W= C 1 ⋅ U C1 2 2 + C 2 ⋅ U C2 2 2 =62,5⋅ 10 −6 Дж.
Подсчитаем энергию, которая была запасена в конденсаторе С1, при его подключении к источнику электрической энергии
W нач = C 1 ⋅U 2 = 5⋅ 10 −6 ⋅ 25 2 2 =1562,5⋅ 10 −6 Дж.
Как видим, имеет место большая разница в запасе энергии до и после переключения. Энергия, равная 1562,5·10–6 — 62,5·10–6 = 1500·10–6 Дж, израсходовалась на искру при переключении рубильника из положения 1 в положение 2 и на нагревание соединительных проводов при перетекании зарядов из конденсатора C1 в конденсатор C2 после перевода рубильника в положение 2.
Задача 6. Вычислить напряжение, которое окажется на каждом из конденсаторов схемы (рис. 6) после перевода рубильника К из положения 1 в положение 2.
Емкости конденсаторов равны: C1 = 10 мкФ; C2 = 30 мкФ; C3 = 60 мкФ; напряжение U = 30 В, а э. д. с. E = 50 В.
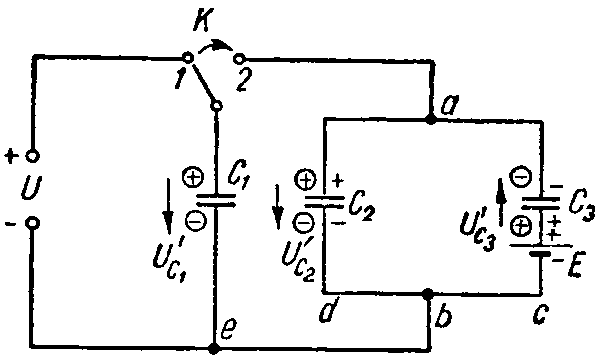
Рис. 6
Решение
Рубильник находится в положении 1. Заряд конденсатора C1 равен
Q1 = C1·U = 10·10–6·30 = 0,3·10–3 Кл.
В указанном положении рубильника конденсаторы C2 и C3 соединены последовательно друг с другом, поэтому их заряды равны: Q2 = Q3. Знаки зарядов показаны на рис. 6 отметками без кружков. По второму закону Кирхгофа имеем
E= U C2 + U C3 = Q 2 C 2 + Q 3 C 3 = Q 2 ⋅ C 2 + C 3 C 2 ⋅ C 3 ,
откуда
Q 2 = Q 3 = C 2 ⋅ C 3 C 2 + C 3 ⋅E= 30⋅ 10 −6 ⋅60⋅ 10 −6 90⋅ 10 −6 ⋅50=1⋅ 10 −3 Кл.
При переводе рубильника в положение 2 произойдет перераспределение зарядов. Произвольно задаемся новой полярностью зарядов на электродах (показана в кружках; предположена совпадающей с ранее имевшей место полярностью); соответствующие положительные направления напряжений на конденсаторах обозначены стрелками. Обозначим эти заряды через Q’1, Q’2 и Q’3. Для их определения составим уравнения на основании закона сохранения электрических зарядов и второго закона Кирхгофа.
Для узла a
Q’1 + Q’2 — Q’3 = Q1 + Q2 — Q3. (1)
Для контура 2ebda2
0= U ′ C1 − U ′ C2 = Q ′ 1 C 1 − Q ′ 2 C 1 .
Для контура bcadb
E= U ′ C2 − U ′ C3 = Q ′ 2 C 2 + Q ′ 3 C 3 .
Уравнения (1) — (3), после подстановки числовых значений величин, примут вид
Q’1 + Q’2 — Q’3 = 0,3·10–3; (4)
3Q’1 — Q’2 = 0; (5)
2Q’2 + Q’3 = 3·10–3. (6)
Решая совместно уравнения (4) — (6), получим
Q’1 = 0,33·10–3 Кл; Q’2 = 0,99·10–3 Кл; Q’3 = 1,02·10–3 Кл.
Так как знаки всех зарядов оказались положительными, то фактическая полярность обкладок соответствует предварительно выбранной.
Напряжения на конденсаторах после перевода рубильника будут равны
U C1 = Q ′ 1 C 1 = 0,33⋅ 10 −3 10⋅ 10 6 =33 В; U C2 = Q ′ 2 C 2 = 0,99⋅ 10 −3 30⋅ 10 6 =33 В; U C3 = Q ′ 3 C 3 = 1,02⋅ 10 −3 60⋅ 10 6 =17 В.
Задача 7. Определить заряд и напряжение конденсаторов, соединенных по схеме рис. 7, если C1 = 5 мкФ; C2 = 4 мкФ; C3 = 3 мкФ; э. д. с. источников E1 = 20 В и E2 = 5 В.
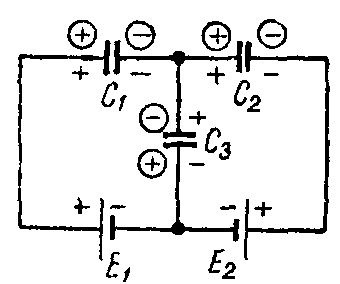
Рис. 7
Решение
Составим систему уравнений на основании закона сохранения электричества и второго закона Кирхгофа, предварительно задавшись полярностью обкладок конденсаторов, показанной в кружках
− Q 1 + Q 2 − Q 3 =0; E 1 = U C1 − U C3 = Q 1 C 1 − Q 3 C 3 ; E 2 =− U C2 − U C3 =− Q 2 C 2 − Q 3 C 3 .
Подставляя сюда числовые значения и решая эту систему уравнений, получим, что Q1 = 50 мкКл; Q2 = 20 мкКл; Q3 = –30 мкКл.
Таким образом, истинная полярность зарядов на обкладках конденсаторов C1 и C2 соответствует выбранной, а у конденсатора C3 — противоположна выбранной.
Задача 8. Пять конденсаторов соединены по схеме рис. 3-22, а, емкости которых C1 = 2 мкФ; C2 = 3 мкФ; C3 = 5 мкФ; C4 = 1 мкФ; C5 = 2,4 мкФ.
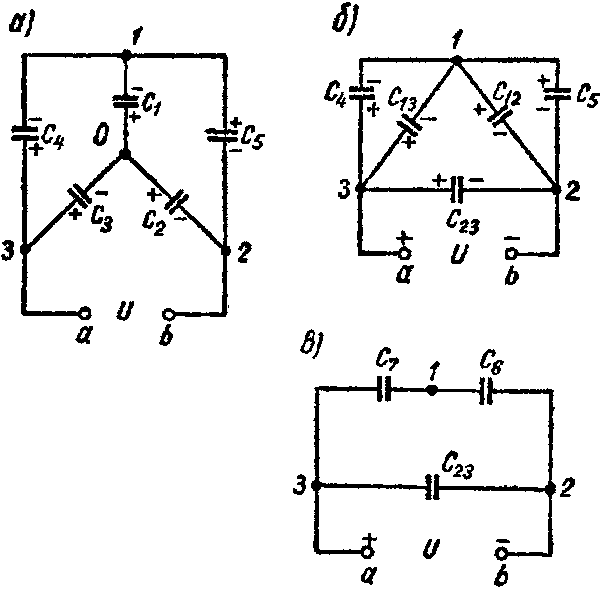
Рис. 8
Индивидуалка Дана (34 лет) т.8 926 650-82-63 Москва, метро Сокол.
Определить эквивалентную емкость системы и напряжение на каждом из конденсаторов, если приложенное напряжение U = 10 В.
Решение
1-й способ. Звезду емкостей C1, C2 и C3 (рис. 8, а) преобразуем в эквивалентный треугольник емкостей (рис. 8, б)
C 12 = C 1 ⋅ C 2 C 1 + C 2 + C 3 =0,6 мкФ; C 13 = C 1 ⋅ C 3 C 1 + C 2 + C 3 =1,0 мкФ; C 23 = C 2 ⋅ C 3 C 1 + C 2 + C 3 =1,5 мкФ.
Емкости C12 и C5 оказываются соединенными параллельно друг другу и подключенными к точкам 1 и 2; их эквивалентная емкость
C6 = C12 + C5 = 3 мкФ.
Аналогично
C7 = C13 + C4 = 2 мкФ.
Схема принимает вид изображенный на рис. 8, в. Емкость схемы между точками а и b равняется
C ab = C 23 + C 6 ⋅ C 7 C 6 + C 7 =2,7 мкФ.
Вычислим напряжение на каждом из конденсаторов.
На конденсаторе C7 напряжение равно
U 7 = C 6 C 6 + C 7 ⋅U=6 В.
Таково же напряжение и на конденсаторах C4 и C13
U4 = U31 = 6 В.
Напряжение на конденсаторе C6 равно
U6 = U — U7 = 4 В;
U5 = U12 = 4 В.
Вычислим заряды
Q4 = C4·U4 = 6·10–6 Кл;
Q5 = C5·U5 = 9,6·10–6 Кл;
Q12 = C12·U12 = 6·10–6 Кл;
Q13 = C13·U31 = 2,4·10–6 Кл.
По закону сохранения электричества для узла 1 схем 8, а и б имеем
–Q4 — Q1 + Q5 = –Q4 — Q13 + Q12 + Q5,
отсюда
Q1 = Q13 — Q12 = 3,6·10–6 Кл,
а напряжение на конденсаторе, емкостью C1 составляет
U 1 = Q 1 C 1 =1,8 В.
Далее находим напряжения и заряды на остальных конденсаторах
U31 = U1 + U3,
отсюда
U3 = U31 — U1 = 4,2 В;
Q3 = C3·U3 = 21·10–6 Кл,
также
U12 = U2 — U1 = 4,2 В,
откуда
U2 = U12 + U1 = 5,8 В;
Q2 = C2·U2 = 17,4·10–6 Кл.
Так как знаки всех зарядов оказались положительными, то фактическая полярность зарядов на обкладках совпадает с предварительно выбранной.
2-й способ. Выбрав положительные направления напряжений на конденсаторах (а тем самым и знаки зарядов на каждом из них) по формуле закона сохранения электричества (закона сохранения заряда) составляем два уравнения и по второму закону Кирхгофа три уравнения (рис. 8, а)
для узла 1
Q5 — Q1 — Q4 = 0; (1)
для узла О
Q1 + Q2 — Q3 = 0; (2)
для контура О13О
Q 1 C 1 − Q 4 C 4 + Q 3 C 3 =0; (3)
для контура О12О
Q 1 C 1 + Q 5 C 5 − Q 2 C 2 =0; (4)
для контура a3О2b
Q 3 C 3 + Q 2 C 2 =U. (5)
Система уравнений (1) — (5) — содержит пять неизвестных: Q1, Q2, Q3, Q4 и Q5. Решив уравнения, найдем искомые заряды, а затем и напряжения на конденсаторах. При втором способе решения эквивалентную емкость схемы Сab можно найти из отношения
C ab = Q U ,
где Q = Q3 + Q4, или Q = Q2 + Q5.
Задача 9. В схеме рис. 9 найти распределение зарядов, если E1 = 20 В; E2 = 7 В; C1 = 7 мкФ; C2 = 1 мкФ; C3 = 3 мкФ; C4 = 4 мкФ; C5 = C6 = 5 мкФ.
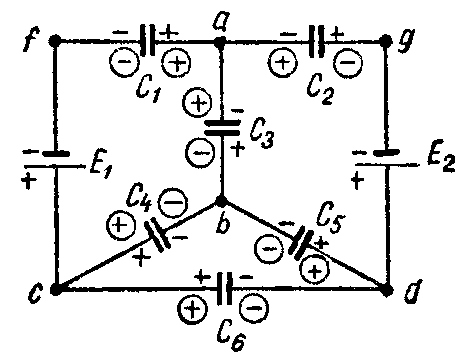
Рис. 9
Решение
При выбранном распределении зарядов (в кружках), как показано на схеме, система уравнений будет иметь вид:
для узла а
Q1 + Q2 + Q3 = 0;
для узла b
–Q3 — Q4 — Q5 = 0;
для узла c
–Q1 + Q4 + Q6 = 0;
для контура afcba
E 1 = U C1 + U C4 − U C3 = Q 1 C 1 + Q 4 C 4 − Q 3 C 3 ;
ля контура gdbag
E 2 = U C5 − U C3 + U C2 = Q 5 C 5 − Q 3 C 3 + Q 2 C 2 ;
для контура cbdc
0= U C4 − U C5 − U C6 = Q 4 C 4 − Q 5 C 5 − Q 6 C 6 .
Подставляя сюда числовые значения и решая полученную систему шести уравнений, найдем искомые заряды
Q1 = 35 мкКл; Q2 = –5 мкКл; Q3 = –30 мкКл;
Q4 = 20 мкКл; Q5 = 10 мкКл; Q6 = 15 мкКл.
Таким образом, истинные знаки зарядов Q1, Q4, Q5 и Q6 соответствуют выбранным, а знаки Q2 и Q3 противоположны выбранным.
Фактическое расположение знаков зарядов на конденсаторах дано не в кружках.
Задача 10. Определить заряд и энергию каждого конденсатора в схеме (рис. 10). Данные схемы: C1 = 6 мкФ; C2 = 2 мкФ; C3 = 3 мкФ; r1 = 500 Ом; r2 = 400 Ом; U = 45 В.
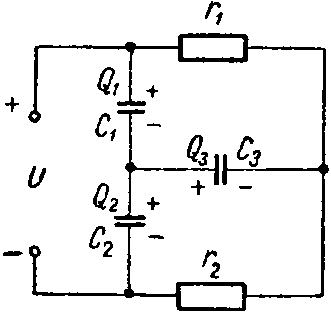
Рис. 10
Решение
Через сопротивления протекает ток
I= U r 1 + r 2 =0,05 А.
Задавшись полярностью зарядов на обкладках конденсаторов, составим систему уравнений:
− Q 1 + Q 2 + Q 3 =0; U= U C1 + U C2 = Q 1 C 1 + Q 2 C 2 ; I⋅ r 1 = U C1 + U C3 = Q 1 C 1 + Q 3 C 3 ,
или
Q 1 = Q 2 + Q 3 ; 45= Q 1 6⋅ 10 −6 + Q 2 2⋅ 10 −6 ; 25= Q 1 6⋅ 10 −6 + Q 3 3⋅ 10 −6 .
Решив эту систему уравнений, найдем, что
Q1 = 90 мкКл; Q2 = 60 мкКл; Q3 = 30 мкКл.
 последовательное соединение конденсаторов,
последовательное соединение конденсаторов,
параллельное соединение конденсаторов,
Расчет цепи конденсаторов,
Конденсатор в цепи постоянного тока,
Цепи с конденсаторами
Комментарии
Что такое электрическое поле
Долгое время ученые не могли толком объяснить, как именно заряженные тела взаимодействуют друг с другом, не соприкасаясь. Майкл Фарадей первым выяснил, что между ними есть некое промежуточное звено. Его выводы подтвердил Джеймс Максвелл, который установил, что для воздействия одного такого объекта на другой нужно время, а значит, они взаимодействуют через «посредника».
В современной физике электрическое поле — это некая материя, которая возникает вокруг заряженных тел и обусловливает их взаимодействие. Если речь идет о неподвижных объектах, поле называют электростатическим.
Тела, имеющие одноименные заряды, будут отталкиваться, а разноименные — притягиваться.

Получай лайфхаки, статьи, видео и чек-листы по обучению на почту
Узнай, какие профессии будущего тебе подойдут
Пройди тест — и мы покажем, кем ты можешь стать, а ещё пришлём подробный гайд, как реализовать себя уже сейчас

Определение напряженности электрического поля
Для исследования электрического поля используются точечные заряды. Давайте выясним, что это такое.
Точечным зарядом называют такой наэлектризованный объект, размерами которого можно пренебречь, поскольку он слишком мал в сравнении с расстоянием, отделяющим этот объект от других заряженных тел.
Теперь поговорим непосредственно о напряженности, которая является одной из главных характеристик электрического поля. Это векторная физическая величина. В отличие от скалярных она имеет не только значение, но и направление.
Для того, чтобы исследовать электрическую напряженность, нужно в поле заряженного тела q1 поместить еще один точечный заряд q2 (допустим, они оба будут положительными). Со стороны q1 на q2 будет действовать некая сила. Очевидно, что для расчетов нужно иметь в виду как значение данной силы, так и ее направление.
Напряженность электрического поля — это показатель, равный отношению силы, действующей на заряд в электрическом поле, к величине этого заряда.
Напряженность является силовой характеристикой поля. Она говорит о том, как сильно влияние поля в данной точке не только на другой заряд, но также на живые и неживые заряженные объекты.
Важно!
Иногда можно услышать оборот «напряжение электрического поля», но это ошибка — правильно говорить «напряженность».
Единицы измерения и формулы
Из указанного выше определения понятно, как найти напряженность электрического поля в некой точке:
E = F / q, где F — действующая на заряд сила, а q — величина заряда, расположенного в данной точке.
Если нужно выразить силу через напряженность, мы получим следующую формулу:
Направление напряженности электрического поля всегда совпадает с направлением действующей силы. Если взять отрицательный точечный заряд, формулы будут работать аналогично.
Поскольку сила измеряется в ньютонах, а величина заряда — в кулонах, единицей измерения напряженности электрического поля является Н/Кл (ньютон на кулон).
Принцип суперпозиции
Допустим, у нас есть несколько зарядов, которые взаимодействуют. Вокруг каждого существует свое электрическое поле. Тогда существует некая точка или область, в которой одновременно существует электрическое поле нескольких зарядов. Чему равна общая напряженность электрического поля, создаваемого этими зарядами?
Было установлено, что общая сила воздействия на конкретный заряд, расположенный в поле, является суммой сил, действующих на данный заряд со стороны каждого тела. Из этого следует, что и напряженность поля в любой взятой точке можно вычислить, просуммировав векторно напряженности, создаваемые каждым зарядом в отдельности в той же точке. Это и есть принцип суперпозиции.
Это правило корректно для любых полей, за некоторыми исключениями. Принцип суперпозиции не соблюдается в следующих случаях:
-
расстояние между зарядами очень мало — порядка 10-15м;
-
речь идет о сверхсильных полях с напряженностью более 1020в/м.
Но задачи с такими данными выходят за пределы школьного курса физики.
Напряженность поля точечного заряда
У электрического поля, создаваемого точечным зарядом, есть одна особенность — ввиду малой величины самого заряда оно очень слабо влияет на другие наэлектризованные тела. Именно поэтому такие «точки» используют для исследований.
Но прежде чем рассказать, от чего зависит напряженность электрического поля точечного заряда, рассмотрим подробнее, как взаимодействуют эти заряды.
Закон Кулона
Предположим, в вакууме есть два точечных заряда, которые статично расположены на некотором расстоянии друг от друга. В зависимости от одноименности или разноименности они могут притягиваться либо отталкиваться. В любом случае на них действуют силы, направленные вдоль соединяющей их прямой.
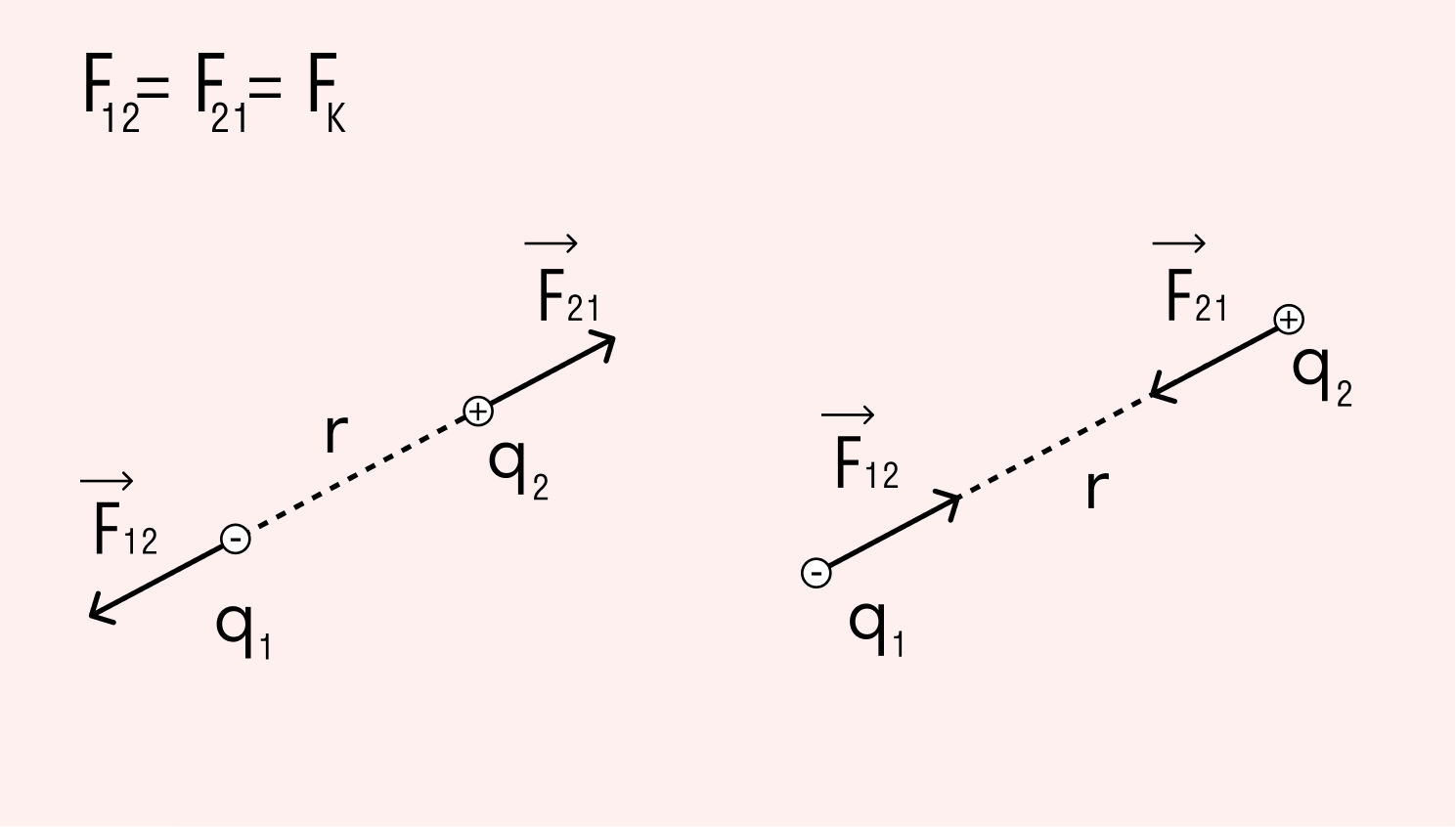
Закон Кулона
Модули сил, действующих на точечные заряды в вакууме, пропорциональны произведению данных зарядов и обратно пропорциональны квадрату расстояния между ними.
Силу электрического поля в конкретной точке можно найти по формуле: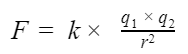 где q1 и q2 — модули точечных зарядов, r — расстояние между ними.
где q1 и q2 — модули точечных зарядов, r — расстояние между ними.
В формуле участвует коэффициент пропорциональности k, который был определен опытным путем и представляет собой постоянную величину. Он обозначает, с какой силой взаимодействуют два тела с зарядом 1 Кл, расположенные на расстоянии 1 м.
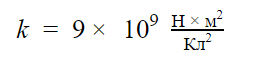
Важно!
Сила взаимодействия двух точечных зарядов остается прежней при появлении сколь угодно большого количества других зарядов в данном поле.
Учитывая все вышесказанное, напряжение электрического поля точечного заряда в некой точке, удаленной от заряда на расстояние r, можно вычислить по формуле:
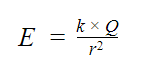
Итак, мы выяснили, что называется напряженностью электрического поля и от чего зависит эта величина. Теперь посмотрим, как она изображается графическим способом.
Онлайн-подготовка к ОГЭ по физике поможет снять стресс перед экзаменом и получить высокий балл.
Линии напряженности
Электрическое поле нельзя увидеть невооруженным глазом, но можно изобразить с помощью линий напряженности. Графически это будут непрерывные прямые, которые связывают заряженные объекты. Условная точка начала такой прямой — на положительном заряде, а конечная точка — на отрицательном.
Линии напряженности — это прямые, которые совпадают с силовыми линиями в системе из положительного и отрицательного зарядов. Касательные к ним в каждой точке электрического поля имеют то же направление, что и напряженность этого поля.
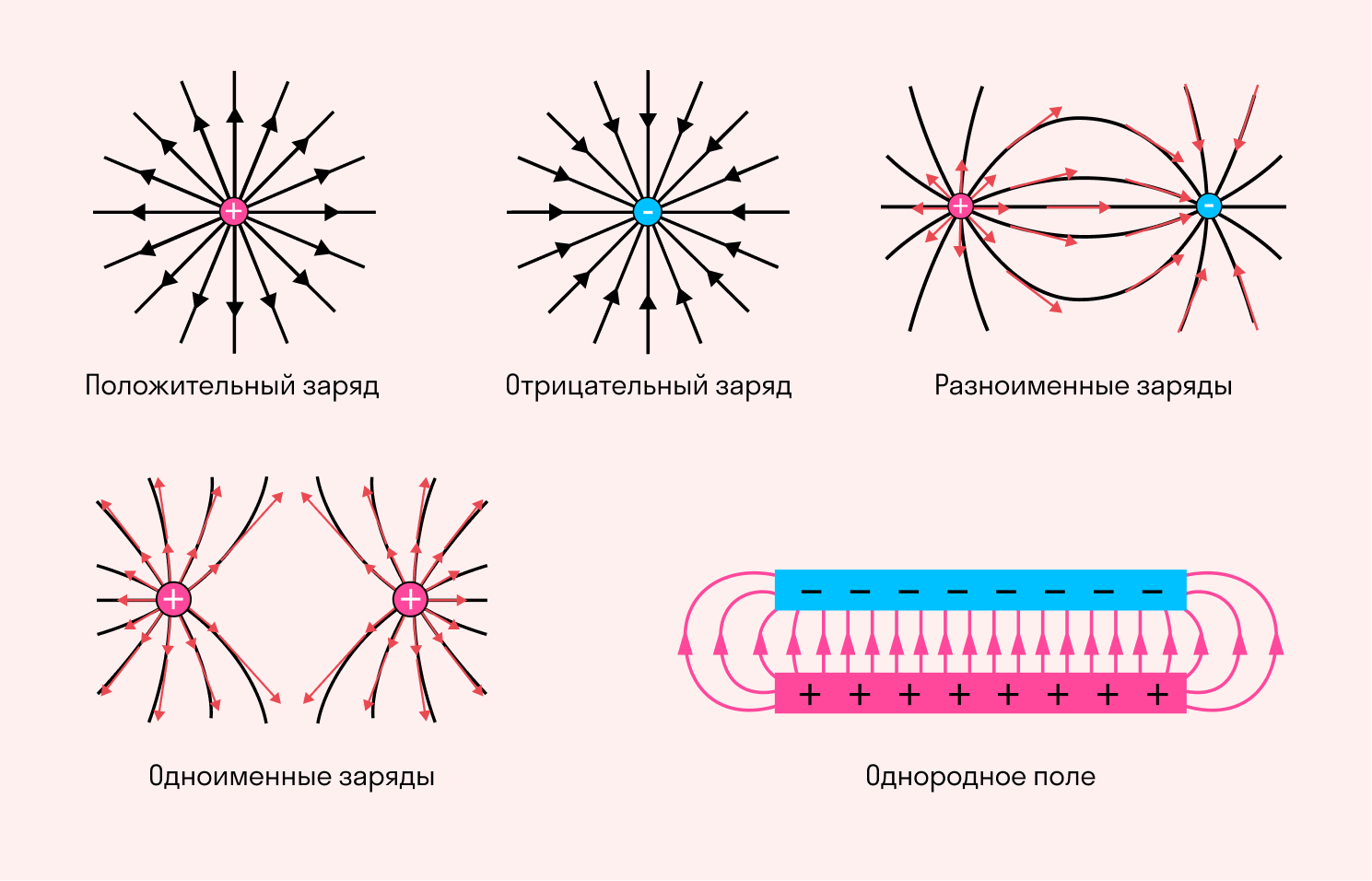
При графическом изображении силовых линий можно передать не только направление, но и величину напряженности электрического поля (разумеется, условно). В местах, где модуль напряженности выше, принято делать более густой рисунок линий. Есть и случаи, когда густота линий не меняется — это бывает при изображении однородного поля.
Однородное электрическое поле создается разноименными зарядами с одинаковым модулем, расположенными на двух металлических пластинах. Линии напряженности между этими зарядами представляют собой параллельные прямые всюду, за исключением краев пластин и пространства за ними.
-
Электростатика.
3.1. ОСНОВЕЫК ФОРМУЛЫ
Закон Кулона
![]()
,
где
F
– сила взаимодействия точечных зарядов
q1
и q2;
r
– расстояние между зарядами;
– диэлектрическая проницаемость; 0
– электрическая постоянная.
Напряженность электрического поля и потенциал
![]()
,
![]()
,
где
Wp
– потенциальная энергия точечного
положительного заряда q,
находящегося в данной точке поля (при
условии, что потенциальная энергия
заряда, удаленного в бесконечность,
равна нулю).
Принцип суперпозиции
полей
![]()
,
![]()
,
где
![]()
,
![]()
– напряженность и потенциал в данной
точке поля, создаваемого i–м
зарядом.
Напряженность и потенциал поля, создаваемого точечным зарядом,
![]()
,
![]()
,
где
r
– расстояние
от заряда q
до точки, в которой определяются
напряженность и потенциал.
Линейная плотность
заряда

.
Поверхностная
плотность заряда
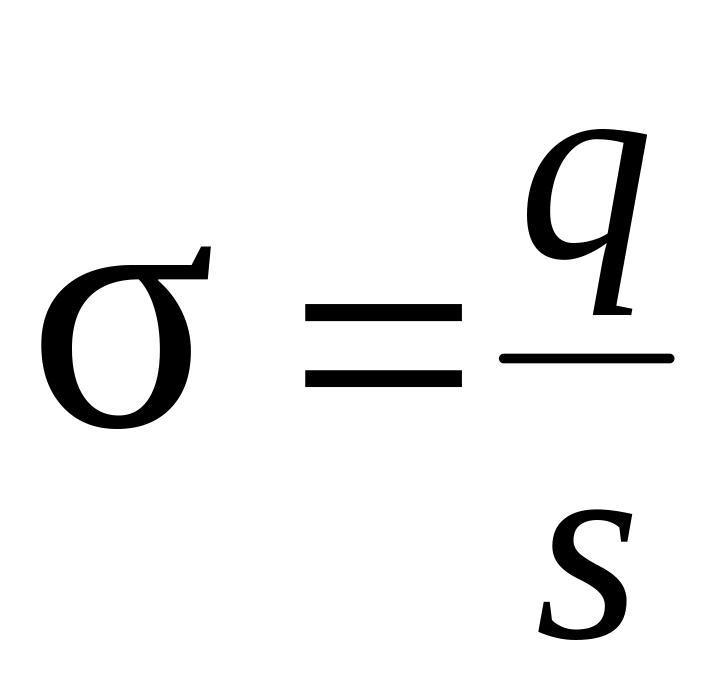
.
Напряженность
поля, создаваемого бесконечной прямой
равномерно заряженной нитью или
бесконечно длинным цилиндром,
![]()
,
где
r
– расстояние от нити или от цилиндра
до точки, в которой определяется
напряженность.
Напряженность
поля, создаваемого бесконечной равномерно
заряженной плоскостью,

.
Связь напряженности
с потенциалом:
а)
![]()
в случае однородного поля;
б)
![]()
в случае поля, обладающего центральной
или осевой симметрией.
Работа сил поля
по перемещению заряда q
из точки с потенциалом
![]()
в точку с потенциалом
![]()
,
![]()
.
Электроемкость
![]()
или
![]()
,
где
![]()
– потенциал проводника (при условии,
что в бесконечности потенциал проводника
принимается равным нулю); U
– разность потенциалов пластин
конденсатора.
Электроемкость
плоского конденсатора
![]()
,
где
S
– площадь пластины (одной) конденсатора,
d
– расстояние между пластинами.
Электроемкость
батареи конденсаторов:
а)
![]()
при последовательном соединении;
б)
![]()
при параллельном соединении,
где
N
– число
конденсаторов в батарее.
Энергия электрического
поля заряженного конденсатора:
![]()
,
![]()
,
![]()
.
4.2. Примеры решения задач.
Пример 1. Два точечных заряда
![]()
=
1 нКл и
![]()
=
– 2 нКл находятся на расстоянии d = 10 см
друг от друга. Определить напряженность
![]()
и потенциал φ поля, создаваемого этими
зарядами в точке А, удаленной от заряда
на расстояние
![]()
=
9 см и от заряда
на расстояние
![]()
=
7 см.
Дано:
=
1 нКл =![]()
Кл
=
– 2 нКл = ![]()
Кл
d = 10 см = 0,1 м
=
9 см = 0,09 м
=
7 см = 0,07 м
Е = ?, φ = ?
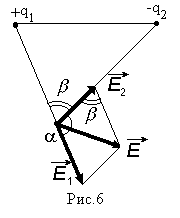
Решение:
По принципу суперпозиции напряженность
электрического поля в искомой точке
равна векторной сумме напряженностей
![]()
и
![]()
полей, создаваемых каждым зарядом в
отдельности:
![]()
.
Вектор
направлен по силовой линии от заряда
,
так как заряд
положителен; вектор
направлен по силовой линии к заряду
,
так как заряду
отрицателен. Абсолютное значение вектора
найдем по теореме косинусов:
![]()
,
где: α – угол между векторами
![]()
и
,
β = π – α.
Напряженность электрического поля в
воздухе (ε = 1), создаваемого точечными
зарядами
и
равна:
![]()
,
![]()
,
где:
![]()
.
Из треугольника со сторонами
,
,
d:
![]()
,
![]()
.
Подставив, находим:
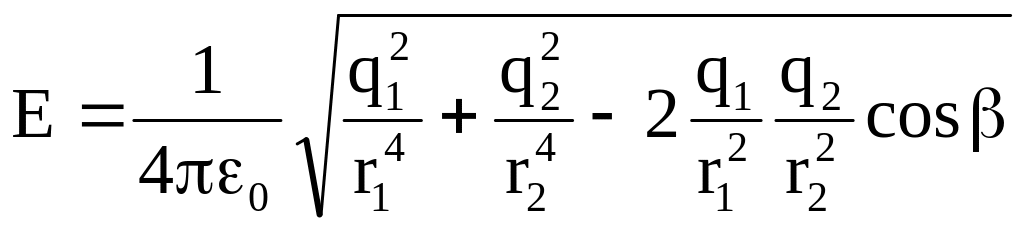
.
Размерность:
![]()
.
Вычисления:

,
![]()
.
По принципу суперпозиции потенциал
электрического поля, созданного двумя
зарядами
и
равен алгебраической сумме потенциалов
полей, созданных каждым зарядом в
отдельности:
![]()
.
Потенциалы электрических полей, созданных
в воздухе точечными зарядами
и
:
![]()
,
![]()
.
Подставим, получим:
![]()
.
Размерность:
![]()
.
При вычислении φ следует учитывать знак
заряда:
![]()
.
Ответ: Е = 3,58 кВ/м, φ = – 157 В.
Пример 2. Ромб (рис.7) составлен из
двух равносторонних треугольников со
сторонами а = 0,25 м. В вершинах при острых
углах ромба помещены заряды
=
=![]()
Кл.
В вершине при одном из тупых углов ромба
помещен заряд
![]()
=![]()
Кл.
Определить напряженность электрического
поля в четвертой вершине ромба. Какая
сила будет действовать на заряд
![]()
=![]()
Кл,
помещенный в эту вершину.
Дано:
=
=
Кл
а = 0,25 м
=
Кл
=
Кл
Е = ?, F = ?
Решение:
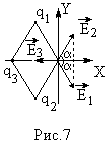
По принципу суперпозиции напряженность
электрического поля в искомой точке
равна векторной сумме напряженностей
,
,
полей, создаваемых каждым зарядом в
отдельности:
17
![]()
.
Модуль вектора![]()
:
![]()
,
где:![]()
и
![]()
проекции вектора
на координатные оси.
При выбранном направлении осей:
![]()
Напряженности полей, создаваемых
зарядами
,
,
соответственно равны:
![]()
,
![]()
,
![]()
.
Учитывая, что
=
,
получим:
![]()
,
![]()
.
Следовательно:
![]()
.
Размерность:
.
Вычисления:
![]()
.
Знак минус указывает на то, что проекция
,
а следовательно и вектор
направлены противоположно оси Х.
Сила, действующая на заряд
,
равна:
![]()
.
Ответ: Е = 360 В/м, F = 0,72 мкН.
Пример 3. Тонкий стержень длинной L
= 20 см несет равномерно распределенный
заряд. На продолжении оси стержня на
расстоянии а = 10 см от ближайшего конца
находится точечный заряд q1 = 40
нКл, на который со стороны стержня
действует сила F = 6 мкН. Определить
линейную плотность τ заряда на стержне.
Дано:
L = 20 см = 0,2 м
а = 10 см = 0,1 м
q1 = 40 нКл = 40·10–9 Кл
F = 6 мкН = 6·10–6 Н
τ = ?
Решение: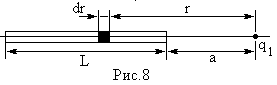
Сила взаимодействия F заряженного
стержня с точечным зарядом q1
зависит от линейной плотности τ заряда
на стержне. При вычислении силы F следует
иметь ввиду, что заряд на стержне не
является точечным, поэтому закон Кулона
непосредственно применить нельзя. В
этом случае можно поступить следующим
образом. Выделим на стержне (рис.8) малый
участок dr с зарядом dq = τ·dr. Этот заряд
можно рассматривать как точечный. Тогда,
согласно закону Кулона:
![]()
.
Интегрируя это выражение в пределах от
а до а + L получим:
![]()
.
Отсюда линейная плотность заряда:
![]()
,
где:![]()
.
Размерность:
![]()
.
Вычисления:![]()
.
Ответ: τ = 2,5 нКл/м.
Пример 4.
Электрическое поле образованно
положительно заряженной бесконечной
нитью с линейной плотностью заряда τ =
2·10-9 Кл/см. Какую скорость получит
электрон, приблизившись к нити с
расстояния r1 = 1 см до расстояния
r2 = 0,5 см от нити.
Дано:
τ = 2·10–9
Кл/см = 2·10–7 Кл/м
r1 = 1 см
= 10–2 м
r2 = 0,5
см = 0,5·10–2 м
е = – 1,6·10–19
Кл
v2 = ?
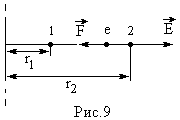
Решение.
Систему заряженная нить-электрон можно
рассматривать как замкнутую. Полная
энергия электрона, движущегося в
потенциальном поле заряженной нити,
будет постоянной:
![]()
,
где:![]()
–
кинетическая энергия электрона,
![]()
–
потенциальная энергия электрона.
На основании
закона сохранения энергии:
![]()
.
Учитывая, что v1 = 0, получим:
![]()
.
Для определения разности потенциалов
используем связь между напряженностью
поля и изменением потенциала:
![]()
.
Для поля с осевой симметрией, каким
является поле заряженной бесконечной
нити, это соотношение можно записать в
виде:
![]()
,
откуда
![]()
.
Интегрируя это выражение, найдем разность
потенциалов, двух точек отстоящих на
расстояния r1 и r2 от нити:

.
Напряженность поля, создаваемого
бесконечно длинной нитью:
![]()
,

,

.
Размерность:
![]()
.
Вычисления:
![]()
.
Ответ: v2 = 29,6 Мм/с.
Пример 5. Расстояние между пластинами
плоского конденсатора d = 4 см. Электрон
начинает двигаться от отрицательной
пластины в тот момент, когда от
положительной пластины начинает
двигаться протон. На каком расстоянии
от положительной пластины они встретятся?
Дано:
d = 4 см
qe = qp = 1,6·10–19 Кл
me
= 9,11·10–31
кг
mp
= 1,67·10–27
кг
х = ?
Решение.
На заряженную частицу в электрическом
поле действует сила Кулона: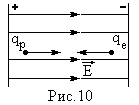
![]()
.
Силой тяжести пренебрегаем, т.к.
![]()
,
![]()
.
По второму закону Ньютона, т.к. силы не
зависят от времени, движение электрона
и протона равноускоренное. Начальная
скорость обеих частиц равна нулю.
Обозначим путь, пройденный протоном
через х, тогда электрон до встречи
пройдет путь d – x:
![]()
,
![]()
,
где: t- время движения частиц.
Найдем ускорение частиц:![]()
,
следовательно
![]()
,
![]()
.
Тогда:
![]()
,
![]()
.
Составим соотношение:
![]()
,
откуда:
![]()
,
![]()
.
Проверка размерности:
![]()
.
Подставим числовые значения и произведем
вычисления:
![]()
.
Ответ: х = 2,2 мкм.
П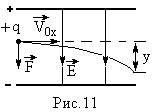
ример
6. Протон и α – частица, двигаясь с
одинаковой скоростью, влетают в плоский
конденсатор параллельно его пластинам.
Во сколько раз отклонение протона полем
конденсатора будет больше отклонения
α – частицы.
Дано:
v0α = v0p
mα = 4mp
qα = 2qp
![]()
Решение.
Заряженная частица, влетев в конденсатор
параллельно пластинам (вдоль оси Х) со
скоростью
![]()
,
испытывает со стороны поля конденсатора
действие кулоновской силы
![]()
,
направленной перпендикулярно пластинам
конденсатора (вдоль оси Y). Согласно 2-му
закону Ньютона движение частицы вдоль
оси Y будет равноускоренным:
![]()
.
Отклонение
частицы перпендикулярно пластинам
(вдоль оси Y):
![]()
.
Так как
![]()
,
то:
![]()
.
Движение частицы параллельно пластинам
равномерное (вдоль оси Х), поэтому время
движения частицы в конденсаторе:
![]()
,
где: L – длина
пластины конденсатора,
![]()
–
скорость движения частицы параллельно
пластинам.
Тогда отклонение
частицы полем конденсатора примет вид:
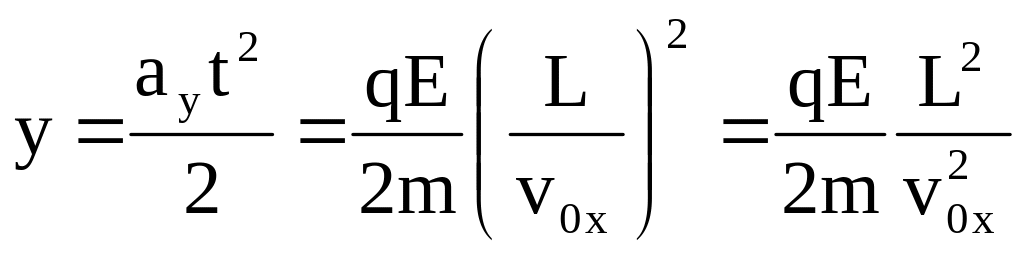
,
23
![]()
,
![]()
,

.
Отклонение протона полем конденсатора
в два раза больше отклонения α – частицы,
при условии, что обе частицы влетели в
конденсатор параллельно пластинам с
одинаковой скоростью.
Пример 7.
Электрон влетает в плоский горизонтальный
конденсатор параллельно его пластинам
со скоростью v0x = 107 м/с.
Напряженность поля в конденсаторе Е =
100 В/см, длина конденсатора L = 5 см. Найти
величину и направление скорости электрона
при вылете его из конденсатора.
Дано:
q = 1,6·10–19 Кл
m = 9,11·10–31 кг
v0x = 107 м/с
Е = 100 В/см =
=10000 В/м
L = 5 см = 5·10–2 м
v = ?, α = ?
Р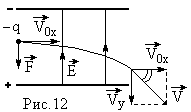
ешение
Пусть напряженность электрического
поля в конденсаторе направлена снизу
вверх. Тогда на электрон, влетевший в
конденсатор параллельно его пластинам
со скоростью
,
будет действовать кулоновская сила
.
В результате движение электрона по
вертикали будет равноускоренным, а по
горизонтали – по-прежнему равномерным.
При вылете из конденсатора скорость
электрона:
![]()
,
где:![]()
–
скорость движения параллельно пластинам,
![]()
–
скорость перпендикулярно пластинам.
Ускорение
электрона:
.
Время движения
электрона в конденсаторе:
.
Тогда:
![]()
.
Скорость
электрона при вылете:

.
Проверим
размерность:

.
Вычисления:

.
Угловое
отклонение электрона от горизонтального
направления:
![]()
,
![]()
.
Ответ: vy = 1,33·107 м/с, α = 410
.
Пример 8.
Конденсаторы с емкостями C1 = C2
=C4 =2 мкФ, С3 = 3 мкФ соединены
так, как показано на рисунке (рис.13а).
Напряжение на обкладках 4-го конденсатора
U4 = 50 В. Найти заряды и разности
потенциалов на обкладках каждого
конденсатора, а также общий заряд и
разность потенциалов батареи.
Дано:
C1 = C2
=C4 =2 мкФ
С3 = 3
мкФ
U4 = 50 В
C
= ?, q = ?, U = ?
q1,
q2,
q3,
q4 =
?
U1,
U2,
U3 =
?
Р
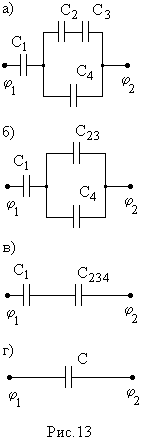
ешение.
Вычислим электроемкость батареи.
Преобразуем исходную схему (рис. 13 а) в
ряд эквивалентных схем (рис. 13 б, в, г).
Конденсаторы С2 и СЗ соединены
последовательно:
![]()
,
![]()
.
Эквивалентный
конденсатор С2З соединен с
конденсатором С4 параллельно,
поэтому:
![]()
.
Эквивалентный
конденсатор С234 соединен
последовательно с конденсатором С1:
![]()
.
Заряд на конденсаторе связан с разностью
потенциалов (напряжением) между его
обкладками, поэтому:
![]()
.
При параллельном соединение напряжения
на конденсаторах одинаковые, поэтому:
![]()
.
При последовательном
соединении заряд на каждом из конденсаторов
одинаковый, то есть:
![]()
.
Зная заряды,
найдем напряжения:
![]()
,
![]()
.
Общий заряд q
равен заряду первого конденсатора q1,
который равен заряду эквивалентного
конденсатора С2З4, который в свою
очередь равен сумме зарядов конденсаторов
С2З и С4:
![]()
Напряжение на
первом конденсаторе:
![]()
.
Общее напряжение или разность потенциалов
батареи:
![]()
.
Ответ: С = 1,23 мкФ, q = 160 мкКл, U = 130 В,
q1 = 160 мкКл, q2 = q3 = 60
мкКл, q4 = 100 мкКл,
U1 = 80 В, U2 = 30В, U3 = 20 В.
Пример 9.
Плоский конденсатор, площадь каждой
пластины которого S = 400 см2, заполнен
двумя слоями диэлектрика. Граница между
ними параллельна обкладкам. Первый слой
– парафин (1 =
2) толщины d1 = 0,2 см, второй слой
стекло (2 = 7)
толщины d2 = 0,3 см. Конденсатор
заряжен до разности потенциалов U = 600
B. Найти ёмкость конденсатора, напряженность
электрического поля и падение потенциала
в каждом слое, энергию конденсатора.
Дано:
S = 4·10-2
м2
d1 = 2·10-3
м
1 = 2
d2 = 3·10-3
м
2
= 7
U = 600 B
C – ?
Е1,
Е2 –
?
U1,
U2 –
?
W – ?
Решение.
Ёмкость конденсатора: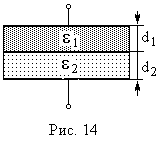
![]()
.
В плоском
конденсаторе в пределах каждого
диэлектрика электрическое поле однородно,
поэтому:
![]()
2
.
Напряженность
поля в каждом слое:
![]()
,
![]()
,
где:![]()
– поверхностная плотность заряда на
обкладках конденсатора.
Следовательно:
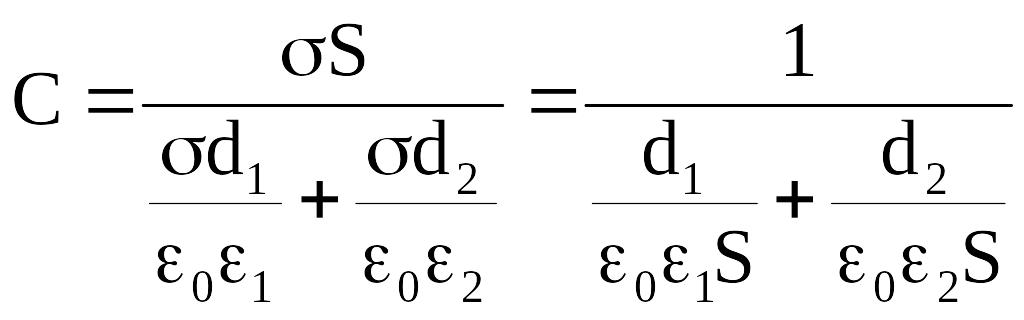
.
Из полученного
выражения следует, что данный конденсатор
с двумя слоями диэлектрика можно
рассматривать как 2 последовательно
соединенных конденсатора, ёмкости
которых:
![]()
,
![]()
.
Подставив числовые данные, получим C =
0,25·10-9 Ф. Граница раздела диэлектрика
параллельна обкладкам и, следовательно,
перпендикулярна силовым линиям поля.
Поэтому электрическое смещение D1 =
D2, то есть
![]()
,
![]()
.
Поэтому:
![]()
,
![]()
;
![]()
,
![]()
.
Произведя
вычисления, получим:
E1 = 2,1·105
В/м; Е2 = 0,6·105 В/м, U1 =
420 B, U2 = 180 B.
Энергия
заряженного конденсатора:
![]()
,
![]()
Энергию
конденсатора можно найти и по общей
формуле для энергии электрического
поля
![]()
,
где:![]()
– плотность энергии электрического
поля,
V – объём, в котором существует
электрическое поле.
В данном случае поле однородное, поэтому:
![]()
.
Ответ: C = 0,25·нФ,
E1 = 210·кВ/м; Е2 = 60·кВ/м,
U1
= 420 B, U2
= 180 B, W = 45·мкДж.
Пример 10.
Коаксиальный электрический кабель
состоит из центральной жилы и
концентрической по отношению к ней
цилиндрической оболочки, между которыми
находится изоляция
= 3,2. Найти ёмкость единицы длины такого
кабеля, если радиус жилы 1,3 см, радиус
оболочки 3,0 см.
Р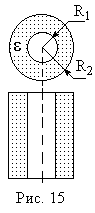
ешение:
Дано:
R1 =
1,3·10-2 м
R1 =
3,0·10-2 м
= 3,2
C1 – ?
Кабель можно
рассматривать как цилиндрический
конденсатор. Ёмкость конденсатора:
![]()
,
где: q – заряд на жиле, (1
– 2) – разность
потенциалов между жилой и оболочкой.
Ёмкость единицы
длины кабеля:
![]()
,
где:
– линейная плотность заряда. Разность
потенциалов связана с напряженностью
![]()
электрического поля, направленного
вдоль радиальных прямых от жилы к
оболочке:

.
Напряженность
поля заряженной жилы (нити):
![]()
.
Тогда:
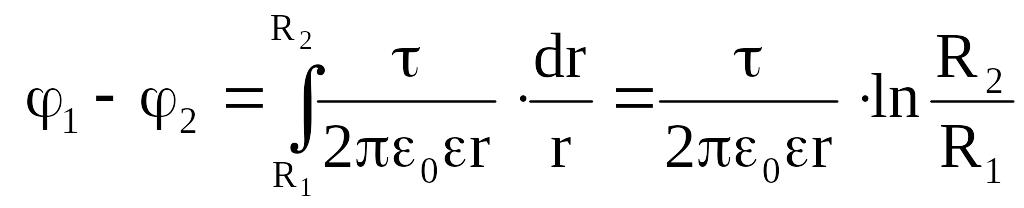
.![]()
Следовательно: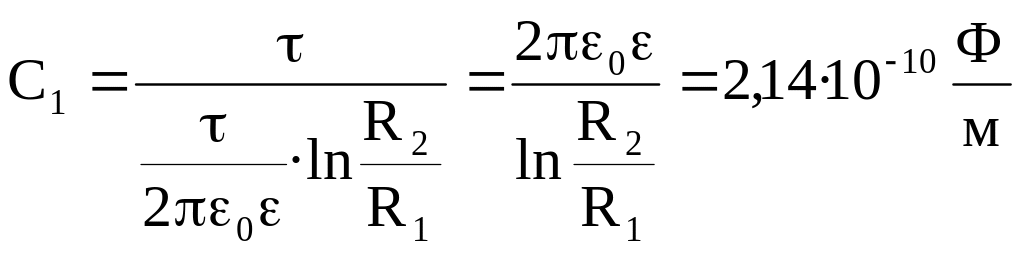
.
Ответ: С1
= 214 пФ/м.
Пример 11.
Как изменится энергия заряженного
плоского конденсатора (
= 1) при уменьшении расстояния между его
пластинами, если 1) конденсатор заряжен
и отключен 2) конденсатор подключен
к источнику постоянного напряжения.
Как зависит сила притяжения F между
пластинами от расстояния между ними?
Р
ешение:
-
Если конденсатор отключен
от источника напряжения, то заряд на
его обкладках не будет изменяться при
сближении пластин, то есть q = const, а
ёмкость увеличится, так как:
![]()
.
Энергия конденсатора выражается через
его заряд и ёмкость:
![]()
.
Видим, что при
сближении пластин отключенного
конденсатора его энергия уменьшается.
За счет убыли энергии конденсатора
совершается работа сил притяжения
обкладок при их сближении:
![]()
.
Сила притяжения:
![]()
или
![]()
.
Знак минус
указывает на то, что сила направлена в
сторону уменьшения х, то есть является
силой притяжения.
-
Согласно
условию, U = const. Поэтому воспользуемся
формулой, в которой энергия конденсатора
выражается через напряжение и ёмкость:
![]()
.
Следовательно, при сближении пластин
конденсатора, подключенного к источнику
напряжения, энергия конденсатора
увеличится на
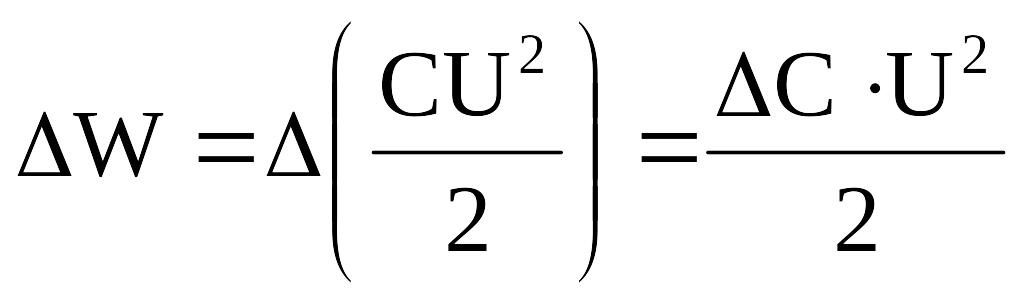
.
Возрастание ёмкости конденсатора при
постоянном напряжении означает увеличение
заряда на его пластинах. Значит, при
сближении пластин на них дополнительно
перейдут от источника напряжения заряды
q. Сообщение одной
пластине положительного заряда q,
а другой отрицательного заряда -q
эквивалентно перемещению заряда q
с одной обкладки на другую, то есть
источник напряжения совершает работу:
![]()
.
Видим, что
работа, совершаемая при сближении
пластин источником напряжения, в 2 раза
больше прироста энергии конденсатора.
Таким образом, теперь за счет энергии
источника напряжения увеличивается
энергия конденсатора W,
а также совершается работа А сил
напряжения пластин. По закону сохранения
энергии:
![]()
.
Отсюда:
![]()
.
Сила притяжения:
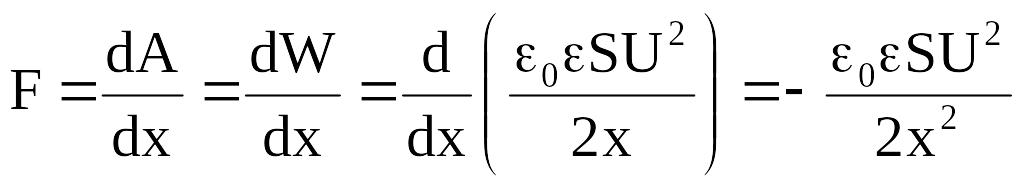
.
Видим, что сила
притяжения пластин обратно пропорциональна
квадрату расстояния между пластинами.
Ответ:
При уменьшении расстояния между
пластинами конденсатора: 1) при отключенном
источнике напряжения энергия конденсатора
уменьшается, сила притяжения между
пластинами постоянна; 2) при подключенном
источнике напряжения энергия конденсатора
увеличивается, сила притяжения между
пластинами увеличивается.
Пример 12.
Объёмная плотность энергии электрического
поля внутри заряженного плоского
конденсатора с твердым диэлектриком
( = 6,0) равна 2,5 Дж/м3.
Найти давление, производимое пластинами
площадью S = 20 см2 на диэлектрик, а
также силу, которую необходимо приложить
к пластинам для их отрыва от диэлектрика.
Дано:
w = 2,5 Дж/м3
=
6,0
S =
2·10-3
м2
p
– ?
Fотр – ?
Решение.
Притягиваясь друг к другу с силой F,
пластины конденсатора сжимают диэлектрик,
заключенный между ними. Давление:
![]()
,
где
![]()
,
так как q = const.
Изменение
энергии dW при перемещении пластин
конденсатора на расстояние dx равно:
![]()
.
Следовательно,
сила притяжения:
![]()
,
давление:
![]()
.
Знак минус
означает, что величины F и p направлены
в сторону уменьшения расстояния х.
Убедимся в
правильности размерности искомой
величины:
[р] = Дж/м3 =Н/ м2
= Па.
Под действием
внешней силы Fотр, направленной
наружу, пластина, отрываясь от диэлектрика,
переместится на расстояние dx, образуя
зазор. Работа силы Fотр пойдет на
увеличение энергии:
![]()
,
следовательно
![]()
.
Прирост энергии
конденсатора, связанный с увеличением
его объёма, равен
dW = w0Sdx,
где: w0 –
объёмная плотность энергии поля в
зазоре.
Следовательно:
![]()
.
Так как индукция
D0 в зазоре (
= 1) равна индукции D в диэлектрике, то:
![]()
,
![]()
,
следовательно
![]()
.
Тогда получим:
Fотр =
wS.
Сделаем проверку
размерности:
![]()
.
Подставим
числовые значения и произведем вычисления:
![]()
Ответ: р =
-2,5·Па, Fотр = 3 мН.

Закон Кулона
Закон сохранения электрического заряда
Напряженность
Принцип суперпозиции
Электрическое поле
Потенциал электростатического поля
Разность потенциалов
Теория
Совсем чуть−чуть.
Закон Кулона — сила, с которой два точечных заряда действуют друг на друга. Она обратно пропорциональна квадрату расстояния между ними и прямо пропорциональна произведению их зарядов.
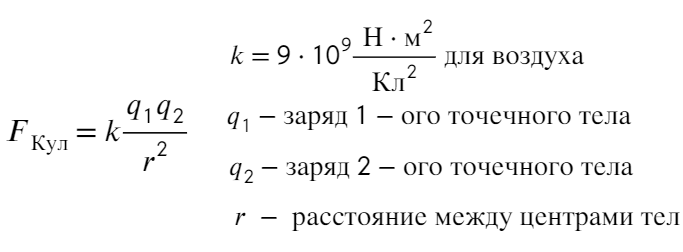
Заряды с одинаковым знаком отталкиваются, с разными — притягиваются. По III з. Ньютона сила действия одного заряда равна силе действия другого:
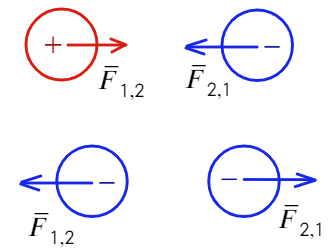
Наглядно рассказывается об этом в видео.
А напряженность — силовая характеристика электрического поля. По-простому: электрическое поле действует на заряд, и вот сила, с которой поле действует на заряд, и есть напряженность.
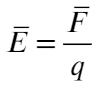
Напряженность НЕ зависит от величины заряда, помещенного в поле!
Задачи
Задача 1 Два одинаковых маленьких положительно заряженных металлических шарика находятся в вакууме на достаточно большом расстоянии друг от друга. Модуль силы их кулоновского взаимодействия равен F₁. Модули зарядов шариков отличаются в 5 раз. Если эти шарики привести в соприкосновение, а затем расположить на прежнем расстоянии друг от друга, то модуль силы их кулоновского взаимодействия станет равным F₂. Определите отношение F₂ к F₁.
Скажем, что заряд одного шарика q, другого 5q. Тогда сила Кулона между ними:
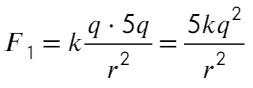
А если теперь соединить два шарика, то общий заряд разделится пополам (на каждый шарик). Общий заряд 5q + q = 6q, тогда на каждом шарике окажется по 3q. Тогда сила Кулона:
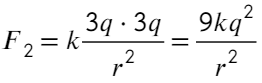
Отношение получится таким:
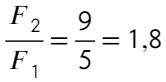
Ответ: 1,8
Задача 2 Два одинаковых маленьких разноименно заряженных металлических шарика находятся в вакууме на достаточно большом расстоянии друг от друга. Модуль силы их кулоновского взаимодействия равен F₁. Модули зарядов шариков отличаются в 4 раза. Если эти шарики привести в соприкосновение, а затем расположить на прежнем расстоянии друг от друга, то модуль силы их кулоновского взаимодействия станет равным F₂. Определите отношение F₁ к F₂.
Та же самая задача? А вот и нет, одно слово другое: разноименно вместо положительных. Это значит, что один шарик будет заряжен положительно, другой отрицательно. По сравнению с первым случаем сила Кулона никак не изменится по модулю (только по нарпавлению).
А вот после соприкосновения изменится. Общий заряд: 5q − q = 4q или q − 5q = − 4q, тогда на каждый шар пойдет по 2q:
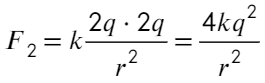
Отношение:
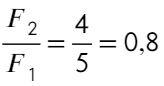
Ответ: 0,8
Задача 3 На нерастяжимой нити висит шарик массой 100 г, имеющий заряд 20 мкКл. Как необходимо зарядить второй шарик, который подносят снизу к первому шарику на расстояние 30 см, чтобы сила натяжения: а) увеличилась в 4 раза; б) рассмотреть случай невесомости?
В начальный момент времени на шарик действуют две силы:
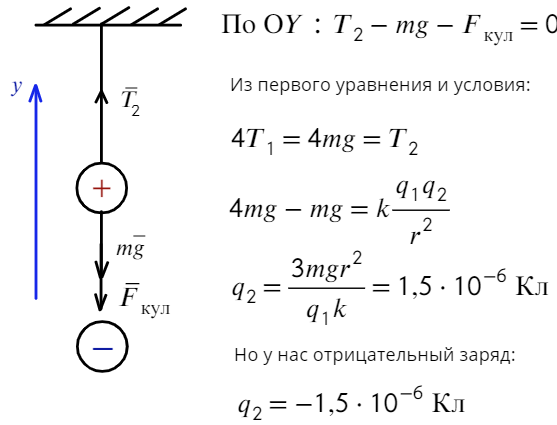
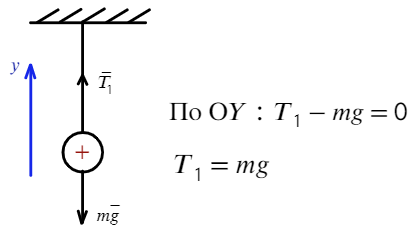 а) Чтобы сила натяжения увеличилась в 4 раза, сила Кулона должна быть направлена вниз, значит, нужно поднести отрицательно заряженный шарик. Запишем также уравнение на ось Y:
а) Чтобы сила натяжения увеличилась в 4 раза, сила Кулона должна быть направлена вниз, значит, нужно поднести отрицательно заряженный шарик. Запишем также уравнение на ось Y:
 б) Невесомость возникает, когда сила натяжения равна нулю. Для этого нужно, чтобы сила Кулона была направлена вверх, значит, подносим положительный заряд:
б) Невесомость возникает, когда сила натяжения равна нулю. Для этого нужно, чтобы сила Кулона была направлена вверх, значит, подносим положительный заряд:
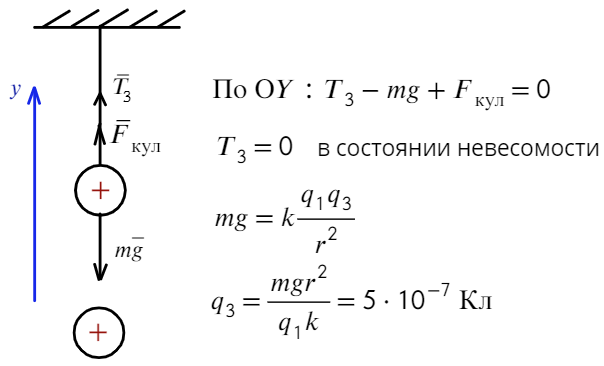 Ответ: −1,5 мкКл, 500 нКл.
Ответ: −1,5 мкКл, 500 нКл.
Задача 3 Фотон с длиной волны, соответствующей красной границе фотоэффекта, выбивает с поверхности пластинки электрон, который попадает в электрическое поле с напряженностью 125 В/м. Найти расстояние, которое он пролетит прежде, чем разгонится до скорости, равной 1% от скорости света.
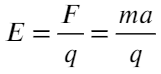
В задаче говорится про электрон, значит, его массу m = 9,1×10⁻³¹ кг и заряд q = 1,6 × 10⁻¹⁹ Кл можно посмотреть в справочных данных.
Найдем ускорение электрона в электрическом поле:
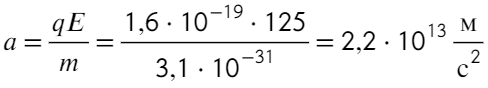
Остается найти пройденный путь в равноускоренном движении при нулевой начальной скорости:
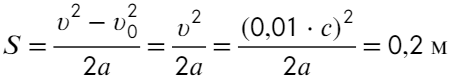
Ответ: 0,2 м
Задача 4 Полый заряженный шарик массой m = 0,4 г. движется в однородном горизонтальном электрическом поле из состояния покоя. Модуль напряженности электрического поля E = 500 кВ/м. Траектория шарика образует с вертикалью угол α = 45°. Чему равен заряд шарика?
Для начала разберемся, какие силы действуют на заряд:
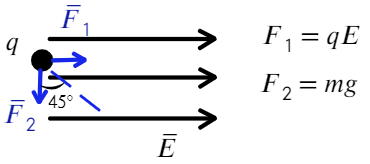
Заряд движется под углом 45 градусов, значит, отношением сил будет тангенс 45°:
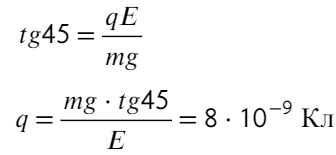
Ответ: 8×10⁻⁹ Кл
Задача 5 При нормальных условиях электрический «пробой» сухого воздуха наступает при напряжённости электрического поля 30 кВ/см. В результате «пробоя» молекулы газа, входящие в состав воздуха, ионизируются и появляются свободные электроны. Какую кинетическую энергию приобретёт такой электрон, пройдя в электрическом поле расстояние 10⁻⁵ см? Ответ выразите в электронвольтах. (ЕГЭ)
Задача кажется весьма тяжелой, но это обманчиво. Воспользуемся знакомой формулой напряженности:
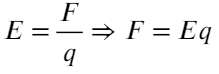
Домножим на длину обе части, тогда слева получится работа, а работа — это изменение энергии:
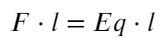
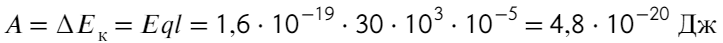
Переводить сантиметры не обязательно, они сократятся. Чтобы перевести джоули в электронвольты, нужно разделить на 1,6 × 10⁻¹⁹
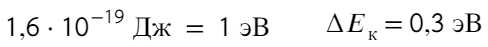
Ответ: 0,3 эВ
Задача 6 В вершинах равностороннего треугольника со стороной «а» находятся заряды +q, +q и -q. Найти напряженность поля Е в центре треугольника.
Покажем, как направлена напряженность: для двух положительных зарядов — от них (красные стрелочки), для отрицательного заряда — к нему (синяя стрелочка).
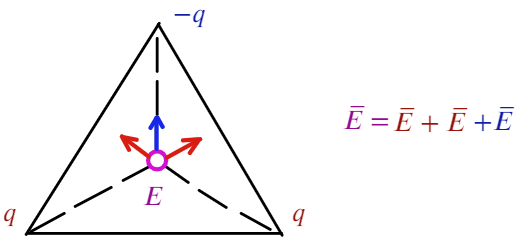
Угол между синим вектором и красным составляет 60°. Если продлить красный вектор до стороны, получится прямоугольный треугольник. Тогда, чтобы посчитать результирующую напряженность, спроецируем красные векторы на синий:
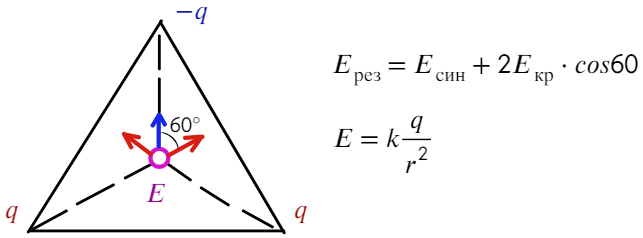
Остается разобрать на каком расстоянии находятся заряды от центра треугольника. Высоту треугольника можно найти по т. Пифагора, равна она а√3/2. А расстояние тогда составит 2/3 от высоты:
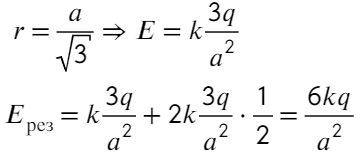
Ответ: 6kq/a²
Задача 6 Два шарика с зарядами Q = –1 нКл и q = 5 нКл соответственно, находятся в однородном электрическом поле с напряженностью Е = 18 В/м, на расстоянии r = 1 м друг от друга. Масса первого шарика равна M = 5 г. Определите, какую массу должен иметь второй шарик, чтобы они двигались с прежним между ними расстоянием и с постоянным по модулю ускорением. (ЕГЭ – 2016)
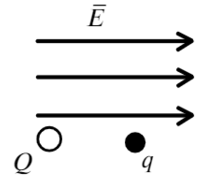
Направим ось X вправо и покажем, какие силы действуют на каждый заряд.
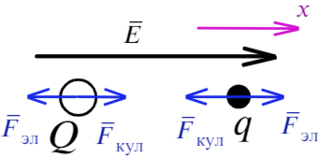
На положительный заряд электрическая сила действует по линиям напряженности, для отрицательного заряда все наоборот. Силы кулона направлены к зарядам, они разноименные. Составим уравнение для каждого заряда:
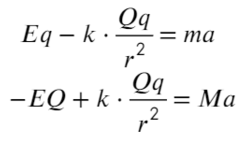
Сумма всех сила равна ma, потому что в условии сказано, что шарики двигаются с постоянным ускорением, а чтобы расстояние не менялось, двигаться они должны в одном направлении.
Разделим одно уравнение на другое и выразим массу:
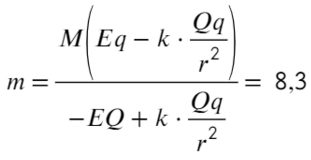
Ответ: 8,3 гр.
Задача 7 Четыре маленьких одинаковых шарика, связанных нерастяжимыми нитями одинаковой длины, заряженызарядами q, q, q и 2q. Сила натяжения нити, связывающей первый и второй шарики, равна T. Найти силу натяжения нити, связывающейвторой и третий шарики. (Росатом)
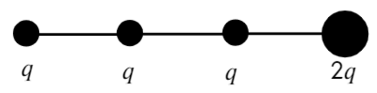
Покажем, каким силам противодействует сила натяжения Т. Воспользуемся принципом суперпозиции и законом Кулона:
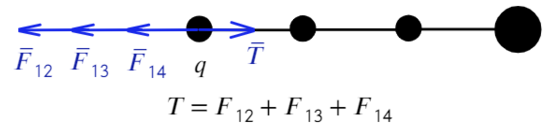
Сила натяжения Т удерживает первый шарик, других сил для него нет, значит, больше ничего для первого случая не требуется.
Как проще это запомнить: проводим линию перпендикулярно той нити, о которой говорим (красная черточка), после записываем только те силы между шариками, которые появляются по разные стороны от проведенной линии:
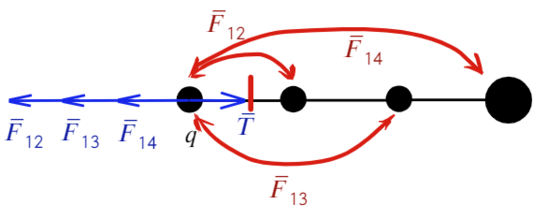
Теперь также составим уравнения для силы натяжения между вторым и третьим шариком:
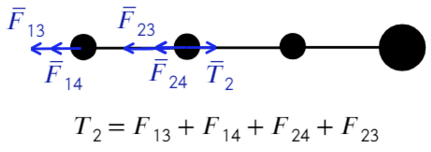
Распишим каждое уравнение по закону кулона, скажем, что расстояние между соседними шариками равно «а»:
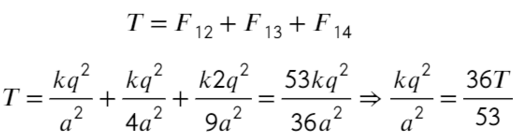
Второе уравнение с подстановкой выражения из первого:
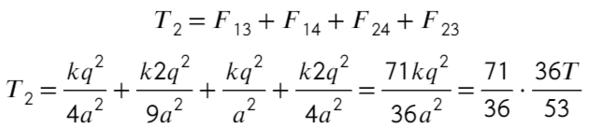
Ответ: 71T/53
Задача 8 Точечный заряд, расположенный в точке C, создаёт в точках A и B поле с напряжённостью Ea и Eb соответственно (см. рисунок; угол ACB — прямой). Найти напряжённость электрическогополя, создаваемого этим зарядом в точке M, являющейся основанием перпендикуляра, опущенного из точки C на прямую AB. (Росатом)
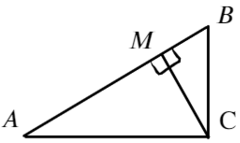
Запишем, чему равна напряженность в каждой из этих точек, взяв длины отрезков за a; b; h:
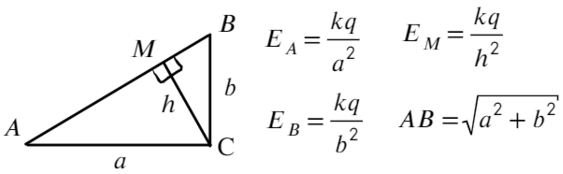
Площадь прямоугольного треугольника можно найти как полупроизведение катетов или как полупроизведение высоты и основания:
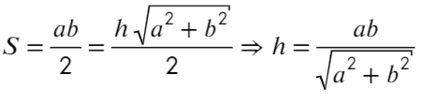
Возведем в квадрат получившиеся уравнение, а дальше смертельный номер: возводим в −1 степень и домножаем обе части на kq:
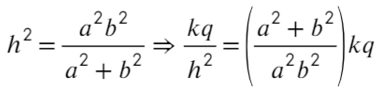
Выразим a² и b² через напряженность:
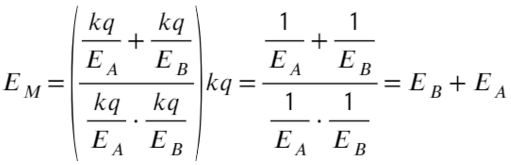
Ответ: Ea+Eb
Задача 9 Частицы с массами M и m, и зарядами q и −q соответственно вращаются с угловой скоростью ω по окружностям вокруг оси, направленной по внешнемуоднородному электрическому полю с напряжённостью E (рис.). Найдите расстояние L между частицами и расстояние H между плоскостями их орбит. (Всеросс. 2008)
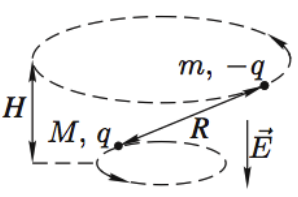 Накрест лежащие углы при параллельных прямых (движения частиц) и секущей силы Кулона равны α. Покажем какие силы действуют на каждую частицу:
Накрест лежащие углы при параллельных прямых (движения частиц) и секущей силы Кулона равны α. Покажем какие силы действуют на каждую частицу:
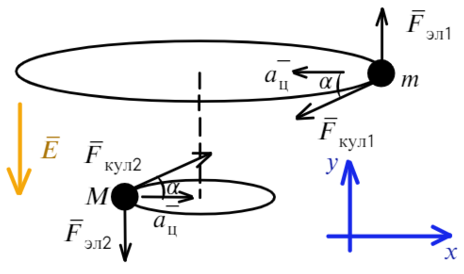
Запишем уравнения по осям на верхнюю частицу:
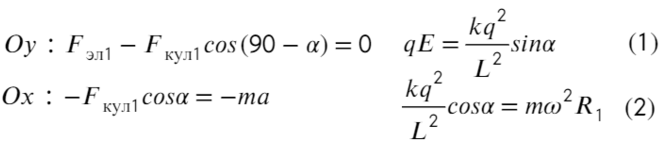
На нижнюю частицу:
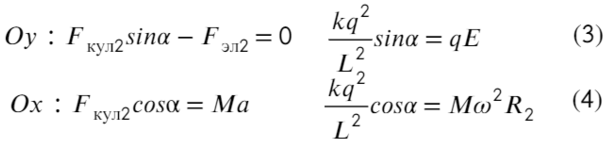
Построим два треугольника, которые показывают расстояние между частицами и высоту между ними.
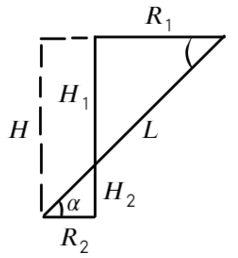
Разделим уравнения друг на друга, а также выразим тангенс угла из этих треугольников:
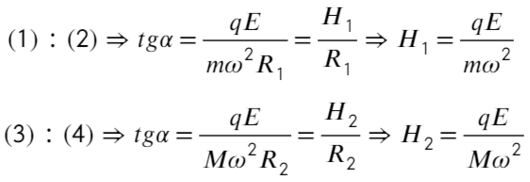
Сложим два уравнения, чтобы найти расстояние между плоскостями:
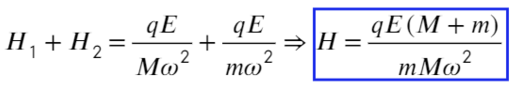
Пункт «а» решили, теперь с расстоянием разберемся: выразим из ур-ия (1) длину, а дальше из треугольника выразим синус угла альфа:
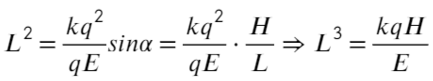
Вместо Н подставим то, что мы нашли:
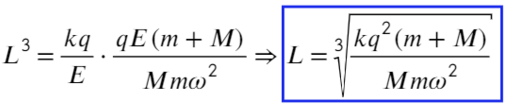
Задача 10 В точке O к стержню привязана непроводящая нить длиной R c зарядом q на конце. Известный эталонный заряд Q₂ и измеряемый заряд Q₁ установлены на расстояниях L₂ и L₁ от точки O. Все заряды одногознака и могут считаться точечными. Найдите величину заряда Q₁, если в состоянии равновесия нить отклонена на угол β от отрезка, соединяющегозаряды Q₂ и Q₁. (Всеросс. 2018)
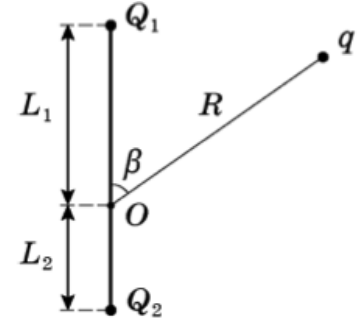
Проведем оси, подпишем расстояние от Q₁ до q и от Q₂ до q. Запишем ур-ия сил на каждую ось:
 Не хочется мучиться с силой натяжения нити, поэтому займемся ур-ем на ось Y:
Не хочется мучиться с силой натяжения нити, поэтому займемся ур-ем на ось Y:
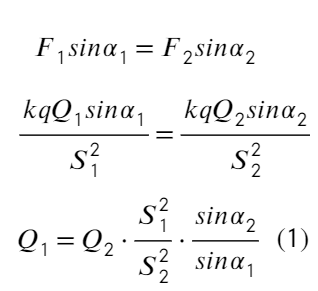
Из прямоугольных треугольников можно получить такие соотношения, а также из теоремы косинусов выразить S₁ и S₂:
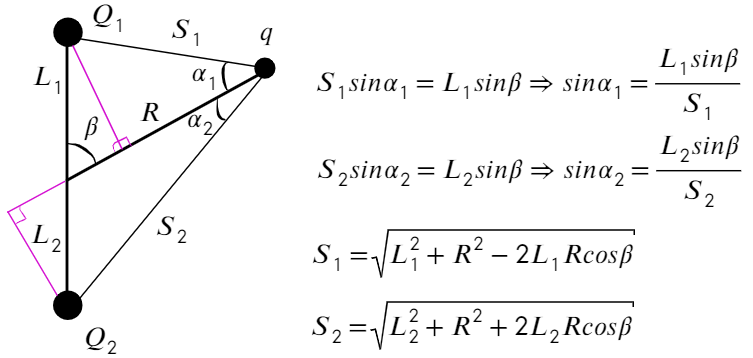
Подставим в ур-ие (1):
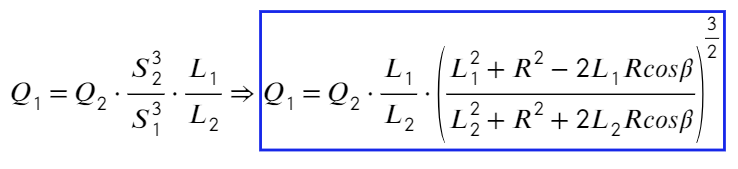
В качестве закрепления материала решите несколько похожих задач с ответами.
Будь в курсе новых статеек, видео и легкого технического юмора.
