Выбирайте формулу, ориентируясь на известные величины.
1. Если известны две соседние стороны
Просто перемножьте две стороны прямоугольника.
- S — искомая площадь прямоугольника;
- a и b — соседние стороны.
2. Если известны любая сторона и диагональ
Найдите квадраты диагонали и любой стороны прямоугольника.
От первого числа отнимите второе и найдите корень из результата.
Умножьте длину известной стороны на полученное число.
- S — искомая площадь прямоугольника;
- a — известная сторона;
- d — любая диагональ (напомним: обе диагонали прямоугольника имеют одинаковую длину).
3. Если известны любая сторона и диаметр описанной окружности
Найдите квадраты диаметра и любой стороны прямоугольника.
От первого числа отнимите второе и найдите корень из результата.
Умножьте известную сторону на полученное число.
- S — искомая площадь прямоугольника;
- a — известная сторона;
- D — диаметр описанной окружности.
4. Если известны любая сторона и радиус описанной окружности
Найдите квадрат радиуса и умножьте результат на 4.
Отнимите от полученного числа квадрат известной стороны.
Найдите корень из результата и умножьте на него длину известной стороны.
- S — искомая площадь прямоугольника;
- a — известная сторона;
- R — радиус описанной окружности.
5. Если известны любая сторона и периметр
Умножьте периметр на длину известной стороны.
Найдите квадрат известной стороны и умножьте полученное число на 2.
От первого произведения отнимите второе и разделите результат на 2.
- S — искомая площадь прямоугольника;
- a — известная сторона;
- P — периметр прямоугольника (равен сумме всех сторон).
6. Если известны диагональ и угол между диагоналями
Найдите квадрат диагонали.
Разделите полученное число на 2.
Умножьте результат на синус угла между диагоналями.
- S — искомая площадь прямоугольника;
- d — любая диагональ прямоугольника;
- α — любой угол между диагоналями прямоугольника.
7. Если известны радиус описанной окружности и угол между диагоналями
Найдите квадрат радиуса окружности, описанной вокруг прямоугольника.
Умножьте полученное число на 2, а потом на синус угла между диагоналями.
- S — искомая площадь прямоугольника;
- R — радиус описанной окружности;
- α — любой угол между диагоналями прямоугольника.
Читайте также 🎓❓📐
- ТЕСТ: Умеете ли вы считать в уме?
- Как легко и быстро считать проценты в уме
- Как найти площадь любого треугольника
- ТЕСТ: Сколько центнеров в тонне? А сантиметров в дециметре? Проверьте, умеете ли вы переводить единицы измерения
- Как освоить устный счёт школьникам и взрослым
Как найти площадь прямоугольника?
Анонимный вопрос
18 августа 2019 · 203,9 K
Редактор, автор и переводчик книг по математике · 18 авг 2019 ·
Чтобы найти площадь прямоугольника, надо его длину умножить на ширину
Обрати внимание, что длина и ширина должны быть выражены в одних единицах. Если длина и ширина в сантиметрах, то площадь получится в сантиметрах квадратных; если длина и ширина в километрах, то площадь получится в квадратных километрах. Если длина и ширина выражены в разных единицах, сначала приведи к одинаковым, а потом уж умножай.
Очень полезно познакомиться с площадями прямоугольников на практике. Давай я попробую угадать: площадь твоего стола меньше одного квадратного метра. Площадь твоей кровати больше одного квадратного метра, но меньше двух. Площадь твоей комнаты больше 10 квадратных метров и меньше 20 квадратных метров. Мне не видно, и я могла ошибиться. Так что измерь, посчитай и проверь, правильно ли я угадала.
120,8 K
площадь- это длина умноженая на ширину
Комментировать ответ…Комментировать…
7,2 K
Комментировать ответ…Комментировать…
Существует несколько способов найти площадь прямоугольника. Самый простой способ, если известны стороны прямоугольника, то достаточно их перемножить. Если стороны не известны, а имеется величины диагоналей прямоугольника и угла между ними, то нужно воспользоваться формулой, приведенной ниже:
1) через две стороны
S=a*b
2) через диагонали и угол
S=1/2*d(в квадрате)*sin(α)… Читать далее
7,7 K
Комментировать ответ…Комментировать…
Надо длину умножить на ширину
Пример : 3*2 = 6 квадратных сантиметров ( квадратные сантиметры пишутся так : см и мелкая 2 на верху) так же есть и другие квадратные
5,6 K
Комментировать ответ…Комментировать…
Пример:
У прямоугольника есть 4 стороны. Первые 2 стороны равны друг другу, как и вторые 2 стороны.
Значит, прямоугольник делится на a и b. Представим, что сторона a – 3 сантиметра, а b – 2 сантиметра. Площадь будет буквой S. Чтобы вычислить площадь прямоугольника, нужно сторону a умножить на b. S=a*b. S=3*2. 3*2 это шесть. Площадь обозначается квадратными сантиметрами. S=6 см2
5,1 K
-Как найти площадь Ленина?
-Надо длину Ленина, умножить на ширину Ленина!
Комментировать ответ…Комментировать…
Геймер, програмер, учу английский, чуть-чуть ютубер · 4 мая 2021
У прямоугольника есть длина и ширина.
Длину и ширину надо перемножить.
Ответ надо записывать в квадратной величине (результат и маленькая двойка сверху)
Пример:
Ширина = 3 см
Длина = 7 см
7*3 = 21(см2)
Ответ: 21 см2. Читать далее
2,6 K
Возьмите 2 игральных кубика. Бросьте оба. Первый показывает вам ширину прямоугольника, второй – длину. А площадь -… Читать дальше
Комментировать ответ…Комментировать…
Чтобы найти площадь прямоугольника, нужно умножить две его неравные стороны друг на друга. Также это выражается формулой S = a * b, где S – площадь, a и b – две неравные стороны прямоугольника.
В общей сложности, площадь прямоугольника, можно найти с помощью пяти разных формул.
1. Через две смежные стороны
2. Через любую сторону и периметр
3. Через любую сторону и… Читать далее
9,4 K
Комментировать ответ…Комментировать…
Что бы найти площадь треугольника, нужно воспольщоваться формулой:
S= a•b
Например:
Длина прямоугольника равна 8 см
Ширина прямоугольника равна 4см
Площадь прямоугольника равна 8•4=32 Читать далее
1,5 K
Комментировать ответ…Комментировать…
Чтобы найти площадь прямоугольника надо умножить длину на ширину пример:
a-9 см
b-3 см
s-? см
s=a*b
9*3=27(см)
Ответ:27 сантиметров площадь прямоугольника. Читать далее
2,5 K
Комментировать ответ…Комментировать…
Я работаю сама на себя – плету из бисера украшения и продаю. · 25 окт 2022
Для того чтобы найти площадь прямоугольника надо одну сторону прямоугольника (ширину) умножить на вторую сторону (длина).
Ширина – а
Длина – б
площадь – S
S = а умножить на б
360
Комментировать ответ…Комментировать…
Две фигуры называют равными, если одну их них можно так наложить на другую,
что эти фигуры совпадут.
Площади равных фигур равны. Их периметры тоже равны.
Площадь квадрата
Запомните!
Для вычисления площади квадрата нужно умножить его длину на саму себя.
S = a · a
Пример:
SEKFM = EK · EK
SEKFM = 3 · 3 = 9 см2
Формулу площади квадрата, зная
определение степени,
можно записать следующим образом:
S = a2
Площадь прямоугольника
Запомните!
Для вычисления площади прямоугольника нужно умножить его длину на ширину.
S = a · b
Пример:
SABCD = AB · BC
SABCD = 3 · 7 = 21 см2
Запомните!
Нельзя вычислять периметр или площадь, если длина и ширина выражены в разных единицах длины.
Обязательно проверяйте, чтобы и длина, и ширина были выражены в одинаковых единицах, то есть обе в см, м и т.д.
Площадь сложных фигур
Запомните!
Площадь всей фигуры равна сумме площадей её частей.
Задача: найти площадь огородного участка.
Так как фигура на рисунке не является ни квадратом, ни прямоугольником, рассчитать её площадь можно используя
правило выше.
Разделим фигуру на два прямоугольника, чьи площади мы можем легко рассчитать по известной формуле.
SABCE = AB · BC
SEFKL = 10 · 3 = 30 м2
SCDEF = FC · CD
SCDEF = 7 · 5 = 35 м2
Чтобы найти площадь всей фигуры, сложим площади найденных прямоугольников.
S = SABCE + SEFKL
S = 30 + 35 = 65 м2
Ответ: S = 65 м2 — площадь огородного участка.
Свойство ниже может вам пригодиться при решении задач на площадь.
Запомните!
Диагональ прямоугольника делит прямоугольник на два равных треугольника.
Площадь любого из этих треугольников равна половине площади прямоугольника.
Рассмотрим прямоугольник:
АС — диагональ прямоугольника
ABCD. Найдём площадь треугольников
ABC и

Вначале найдём площадь прямоугольника по формуле.
SABCD = AB · BC
SABCD = 5 · 4 = 20 см2
S
ABC = SABCD : 2
S
ABC = 20 : 2 = 10 см2
S
ABC =
S
ACD = 10 см2
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
3 декабря 2015 в 22:54
Ирина Петренко
Профиль
Благодарили: 0
Сообщений: 1
Ирина Петренко
Профиль
Благодарили: 0
Сообщений: 1
как написать правильно площадь треугольника?
0
Спасибо
Ответить
9 декабря 2015 в 19:41
Ответ для Ирина Петренко
Тима Клюев
Профиль
Благодарили: 0
Сообщений: 8
Тима Клюев
Профиль
Благодарили: 0
Сообщений: 8
S(рисуешь мини треугольник) = ,,,,,
0
Спасибо
Ответить
- Главная
- Справочник
- Как найти площадь прямоугольника
Поможем решить контрольную, написать реферат, курсовую и диплом от 800р
Узнать стоимость
Как найти площадь прямоугольника
Содержание:
- Формула
- Примеры вычисления площади прямоугольника
Формула
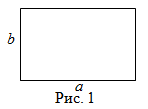
Чтобы найти площадь прямоугольника (рис. 1), надо его длину умножить на ширину, то есть
Прямоугольником называется четырехугольник, у которого все углы равны. Все углы в прямоугольнике прямые, то есть равны $90^{circ}$.
Примеры вычисления площади прямоугольника
Пример
Задание. Найти площадь прямоугольника, если одна его сторона равна 3 см, а вторая, смежная с ней – 5 см.
Решение. Искомая площадь прямоугольника равна произведению двух заданных сторон:
$S=3 cdot 5=15$ (см2)
Ответ. $S=15$ (см2)

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
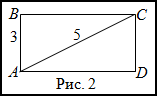
Задание. Найти площадь прямоугольника, если одна его сторона равна 3 м, а диагональ – 5 м.
Решение. Сделаем чертеж (рис. 2).
Рассмотрим прямоугольный треугольник $ABC$, из которого по
теореме Пифагора найдем длину катета $BC$ :
$B C=sqrt{A C^{2}-A B^{2}}=sqrt{5^{2}-3^{2}}=sqrt{25-9}=sqrt{16}=4$ (м)
Тогда искомая площадь равна
$S=3 cdot 4=12$ (м2)
Ответ. $S=12$ (м2)
Читать дальше: как найти площадь параллелограмма.
Статьи по теме
- Как найти площадь
- Как найти площадь треугольника
- Как найти площадь ромба
- Как найти площадь эллипса
- Как найти площадь прямоугольного треугольника
- Все темы раздела “Как найти площадь”

Разделы
- Формулы сокращенного умножения
- Формулы по физике
- Логарифмы
- Векторы
- Матрицы
- Комплексные числа
- Пределы
- Производные
- Интегралы
- СЛАУ
- Числа
- Дроби
Все еще сложно?
Не получается написать работу самому?
Доверь это кандидату наук!
Ищещь ответ на вопрос с которым нужна помощь?
80% ответов приходят в течение 10 минут
250 ответов по вашей теме сегодня
2 специалиста свободны онлайн
Ответы приходят уже через 10 минут
90% ответов положительные
Математика, 3 класс
Урок №22. Площадь прямоугольника
Перечень вопросов, рассматриваемых в теме:
- Как вычислить площадь прямоугольника?
- В каких единицах измеряется площадь?
- Какими способами можно сравнить геометрические фигуры?
Глоссарий по теме:
Площадь – внутренняя часть любой плоской геометрической фигуры.
Квадрат – это прямоугольник, у которого все стороны равны.
Прямоугольник – это четырёхугольник, у которого все углы прямые.
Квадратный сантиметр – квадрат со стороной 1 сантиметр.
Основная и дополнительная литература по теме урока:
1. Моро М. И., Бантова М. А. и др. Математика 3 класс. Учебник для общеобразовательных организаций М.; Просвещение, 2017. – с. 60-61.
2. Рудницкая В. Н. Тесты по математике:3 класс. М.: Издательство «Экзамен», 2016 с. 38-43.
3. Волкова Е. В. ВПР. Математика 3 класс Практикум по выполнению типовых заданий. ФГОС .М.: Издательство «Экзамен», 2018, с. 36-53.
Теоретический материал для самостоятельного изучения
Упоминание о первых геометрических фигурах встречается еще у древних египтян и древних шумеров. Учёными-археологами (они ищут разные исторические древности) был найден папирусный свиток (бумага древних египтян, изготавливаемая из растения папирус) с геометрическими задачами, в которых упоминались геометрические фигуры. И каждая из них называлась каким-то определенным словом. Одним определенным словом называлась фигура прямоугольник независимо от того какие стороны были у этого прямоугольника. А если у прямоугольника все стороны были одинаковые, то такой прямоугольник имел специальное название – квадрат. Таким образом, значит, что уже в те далекие времена люди имели представление о геометрии и знали изучаемые этой наукой фигуры. Название «геометрическая фигура» придумали древние греки. И названия всем геометрическим фигурам дали тоже древнегреческие учёные.
Найдём площадь геометрической фигуры.
Чтобы найти площадь фигуры, надо узнать сколько раз в фигуре поместится квадрат со стороной 1 см. Площадь этой геометрической фигуры составляет 18 квадратов. Для удобства подсчёта количество квадратов можно воспользоваться знаниями таблицы умножения. По 6 взять 3 раза получится 18 квадратов.
Найдём площадь прямоугольника со сторонами 6 см и 3 см.
Для этого достаточно умножить длину на ширину. 6 ∙ 3 = 18 см2
Таким образом, формулируем вывод: чтобы найти площадь прямоугольника, надо длину умножить на ширину.
S = a ∙ b
S – площадь
a – длина
b – ширина
Задания тренировочного модуля:
1. Заполните пропуски в таблице.
|
а |
5 |
6 |
3 |
|
|
b |
8 |
9 |
||
|
S |
15 |
56 |
24 |
Правильный ответ:
|
а |
5 |
7 |
6 |
3 |
|
b |
3 |
8 |
9 |
8 |
|
S |
15 |
56 |
54 |
24 |
2. Длина прямоугольника 8см, ширина 4 см. Чему равна площадь прямоугольника? Выделите правильный ответ.
12 см; 32 см; 24 см2; 32 см2; 24; 12 см2.
Правильный ответ: 32см2.