Расчет сетевого графика
Расчетные
параметры СГ:
i–j
–
код
данной работы;
i
–
код
начального события данной работы;
j
–
код
конечного события данной работы;
h
–
i
– код работ, предшествующих данной
работе;
h
–
код событий, предшествующих начальному
событию данной работы;
j–k
–
код
работ, последующих за конечным событием
данной работы;
k
–
код
событий, последующих конечному событию
данной работы;
L
–
путь;
L
кр –
критический
путь;
t
L
–
продолжительность пути;
T
L
кр
–
продолжительность критического пути
и критический срок;
ti–j
–
продолжительность работы;
Tр.н
i–j
–раннее
начало работы;
Tр.о
i–j
–раннее
окончание работы;
Tip–
ранний
срок свершения события I;
Tп.н
i–j
–
позднее начало работы i–j;
Tп.о
i–j
–
позднее
окончание работы i–j;
Tnj
–
поздний
срок свершения события j;
R
i–j
–
общий
(полный) резерв времени работы i–j;
r
i–j
–
частный (свободный) резерв времени
работы i–j;
Общая схема
кодирования работ и события показана
на рис.3.18.

Рис. 3.18. Общая
схема кодирования работ и событий
Расчет
сетевого графика аналитическим путем.
Расчет
временных
параметров СГ может выполняться по
работам или по событиям, как это
будет показано ниже.
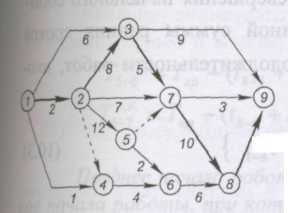
Рис. 3.19. Сетевой
график
Расчет
ранних сроков. Ранние
сроки
начала и окончания работ и свершения
событий
СГ рассчитывают, начиная от исходного
события последовательно по всем путям
СГ прямым ходом расчета. В результате
этого расчета кроме ранних сроков
устанавливают
также общую продолжительность
работы по графику в целом и по отдельным
его участкам (рис. 3.19).
Расчет
по работам. Раннее
начало работы Tр.н
i–j
–
самое
раннее из возможных время
начала работы – определяют продолжительностью
самого длинного пути от
исходного события до начального события
данной работы:
Tр.н
i-j
=max
th-i
(3.1)
Например, для
работы 6-8 (рис. 3.19) раннее начало:

Так
как продолжительность наибольшего пути
1-2, 2-5, 5-6 составляет
16, то работу 6-8 можно начать на 17-й день.
Раннее
окончание работы Tр.о
i–j
–
время окончания работы (она начата
в самый ранний из возможных сроков) –
определяют суммой раннего начала
и продолжительности данной работы:
Tр.о
i-j=
Tр.н
i-j+
th-i.
(3.2)
Например,
для работы 6-8 раннее окончание:
Tр.о6-8
=
Tр.н6-8+t6-8=16+6=22.
Расчет
по событиям. Ранний
срок свершения начального события
Тpi
определяют
максимальной величиной суммы ранних
сроков свершения предшествующих событий
и продолжительности работ, входящих
в данное событие:
Tpi=max{Tph+th-1}.
(3.3)
Например,

Естественно,
что расчет раннего срока свершения
конечного события
работы выполняют по той же формуле.
Расчет
поздних сроков. Расчет
поздних сроков окончания и начала работ
сетевого графика и свершения событий
производят после того, как определены
все ранние сроки и общая продолжительность.
Расчет ведут обратным ходом от завершающего
события к исходному последовательно
по
всем путям СГ.
Расчет
по работам. Позднее
окончание работы –
самый поздний из допустимых
сроков окончания работы, при котором
не увеличивается общая
продолжительность работ сетевого
графика.
Позднее
окончание рассматриваемой работы равно
минимальному из сроков поздних начал
последующих работ:
Tп.о
i- j=
minTп.н.j-k
(3.4)
Определение
позднего начала через позднее окончание
основано на том,
что расчет ведут от завершающего события,
у которого ранние и поздние сроки
совпадают, т. е. Tрk
= Tnk.,
поэтому,
рассчитав ранние сроки работ, мы
установили тем самым и поздний срок
завершающего события:
Tп.о
j–k
=Tкр=max
Tp.оj–k
.
(3.5)
Например, для
работы 2-5 позднее окончание:

Позднее
начало работы Tп.н
i–j
–
самый поздний из допустимых сроков
начала работы, при котором не увеличивается
общая продолжительность
работ. Позднее
начало работы равно разности между
величинами ее позднего
окончания и продолжительности:
Tп.н2-5
=
Tп.oi–j
–
ti–j
. (3.6)
Например, для
работы 2-5 позднее начало:
Tп.н2-5
=T2-5
– t2-5
=15
– 12 = 3.
Расчет
по событиям. Поздний
срок Тnj
свершения события j
определяется
минимальной величиной из значений
разности поздних сроков свершения
конечных событий k и продолжительности
работ, выходящих из данного
события j:
Tni
= min {Tnk
– tj-k}.
(3.7)
Например, для
события 5:

Сопоставление
ранних и поздних сроков работ и событий
позволяет
рассчитать резерв времени, критический
путь и провести анализ параметров
графика.
Если
ранние и поздние характеристики работ
совпадают, то работы
лежат на критическом пути. Критическими
являются те события, на
которых совпадают ранние и поздние
сроки свершений.
Для
критических работ
соблюдаются
следующие условия:
-
ранние
и поздние сроки начала работы и
соответственно их окончания
равны, т. е.
Tр.нi–j
= Tп.н.i–j
= Tнi–j;
Tр.о.i–j
= Tп.о.i–j
=Toi–j
(3.8)
или
при расчете по событиям
ранние
и поздние сроки свершения событий,
ограничивающих данную работу,
соответственно равны, т. е.
Tрi
= Tпi;
Tрj
=Tпj;
(3.9)
2)
разность между возможными сроками
окончания и начала работы
равна
ее продолжительности, т. е.
Toi-j
– THi-j=
ti-j
, (3.10)
или
разность между сроками свершения
конечного и начального
событий
равна
продолжительности данной работы, т. е.
Tj
–Ti
= Ti–j
(3.11)
Например,
для критической работы 3-7 первое
условие Tp.н3-7
=
Tп.н3-7
=10,
а также Tp.о3-7
=
Tп.о3-7
=15
соблюдено. Второе условие:
![]()
Общий
(полный) и частный резервы времени для
работ критического
пути равны нулю. Для
остальных работ определяют различные
виды
резервов времени.
Общий
(полный) резерв времени работы –
это
максимальное время,
за которое можно задержать начало работы
или увеличить ее продолжительность
без изменения общего срока строительства.
Величина
Ri–j
определяется
разностью поздних и ранних сроков начала
или окончания
работы:
Ri–j
= Tп.нi–j
– Tp.нi–j
=
Tп.оi–j
– Tp.оi–j
,
(3.12)
или
Ri–j
= Tп.оi–j
–
Tp.нi–j
–
ti–j
. (3.13)
Например,
общий резерв времени для работы
4-6
составляет
![]() ,
,
или
![]() ,
,
![]() ,
,
или
![]() ,
,
или
то же самое по
событиям:
Ri-j
= Tnj
– Tрi
– ti-j
,
R4-6
= Tn6
– Tp4
– t4-6
= 19 – 2 – 4 = 13 (3.14)
Частный
(свободный) резерв времени работы ri–j
–
максимальное
количество времени, на которое можно
перенести начало работы или
увеличить ее продолжительность без
изменения раннего начала последующих
работ. Оно имеет место, когда в событие
входят две работы и больше, и определяется
разностью значений раннего начала
последующей
работы и раннего окончания данной
работы.
Например,
для
работы 4-6
частный резерв
ri–j
= Tp.нj–k
– Tp.oi–j
,
r4-6
= Tp.н6-8
– Tp.o4-6
= 16 – 6 = 10 , (3.15)
или
в терминах
событий
ri-j
=Tpj
–
Tpi
– ti-j
(3.16)
Например, частный
резерв времени для той же работы 4-6
составляет
R4-6
= Tp6
– Tp6
– t4-6
= 16 – 2 – 4 = 10.
Расчет
сети непосредственно на графике. Расчет
непосредственно
на графике является самым простым и
быстрым из ручных способов. При
этом способе расчета строгое соблюдение
правила кодирования событий
не обязательно. Для записи результатов
расчета принимают одну из форм,
показанных на рис. 3.20.

Рис.
3.20. Варианты
формы записи результатов расчета: а –
по секторам; б
–
в виде дроби; 1 –
раннее начало работы Б; 2 –
позднее окончание работы А
Расчет
на сети требует проведения только чисто
механических операций
без обращения к формулам (рис. 3.21). Порядок
расчета:
1.
У исходного события под чертой (в
знаменателе) ставят нуль.
2.
Для каждого следующего события в
знаменателе записывают
число, равное сумме значения раннего
срока свершения предыдущего события и
продолжительности работы. Так, для
события 2 записывают 2 (0+2=2), для события
4 –
8
(2+6=8) и т. д.
3.
Если в событие входит две работы или
больше, то рассчитывают
значение каждой из них, записывая над
стрелкой, но в знаменатель
переносят только максимальное значение
из всех
полученных. Например, в событие 5 входят
работы 2-5 и 2-3
(через зависимость). Первый путь дает
значение 2+3=5, второй
–
2 + 5=7. Принимают максимальное 7 и записывают
в знаменатель.
В событие 11 входит четыре работы, из них
записывают
максимальное значение 39.
4.
В завершающем событии значение, записанное
в знаменатель,
определяющее длину критического пути,
переносят над чертой
(в числитель) (рис. 3.22).
5.
Значение числителей определяют, ведя
расчет от завершающего
события к исходному, вычитая из значения
поздних сроков
свершения конечного события
продолжительность предшествующих
им работ. В отличие от расчета ранних
сроков
(знаменатель), если из события выходят
две работы или
более, принимают не максимальное, а
минимальное значение. Например, из
события 7 выходят две работы со значениями
17 и 32; принимают минимальное 17.
6.
Критический путь проходит через события,
в которых значения
в числителе и знаменателе совпадают.
Полный и частный резерв
времени для работ критического пути
равен нулю. На рис.
3.23 дан сетевой график с расчетными
параметрами и показан
критический путь.
7.
Общий резерв времени для любой работы
определяют вычитанием
из значения числителя (конечного события
данной работы)
суммы значений знаменателя (начального
события данной
работы) и ее продолжительности. Так, для
работы 9-10 полный резерв равен 34 (числитель
конечного события) – 21
(знаменатель начального события) – 4
(продолжительность работы)
= 9. Резерв времени события равен разности
значений числителя и знаменателя.
Соответственно для события 10
полный резерв равен 34 (числитель) – 25
(знаменатель) =9.
8.
Частный резерв для любой работы определяют
вычитанием из
значения знаменателя конечного события
данной работы суммы
значений знаменателя начального события
и продолжительности данной работы.
Для работы 4-8 частный резерв равен
17- (8+8) = 1.

Рис.
3.21. Расчет
ранних начал работ сетевого графика

Рис.
3.22. Расчет
поздних окончаний работ сетевого графика

Рис. 3.23. Сетевой
график
Расчет
сетевого графика табличным методом.
При
расчете СГ события
кодируются в порядке возрастания (табл.
3). Сверху вниз заполняют три первые
колонки. По порядку номеров рассматривают
каждое событие.
Из первого события выходит работа 1-2,
записывают ее код в гр. 2,
продолжительность, равную 2, –
в гр. 3, а так как предшествующих ей работ
нет, в гр. 1 ставим прочерк.
Из
события 2 выходят три работы: 2-3 с
продолжительностью 5 дн; 2-4
с продолжительностью 6 дн; 2-5 с
продолжительностью 3 дн. Записывают
коды работ и их продолжительность в гр.
2 и 3, затем рассматривают работы, входящие
в событие 2. Такой оказывается работа
1-2, так как только эта работа в гр. 2
оканчивается цифрой 2. Начальным событием
этой работы является
событие 1. Номер 1 записывают в гр. 1 для
всех трех работ и т. д. Зависимость вносят
в таблицу с нулевой продолжительностью
(3-5, 7-8).
Если
работа имеет несколько предшествующих
событий, то записывают
все их коды. Работе 5-7 предшествуют
работы 2-5 и 3-5, имеющие
начальные события 2 и 3, их коды 2 и 3
записывают в гр. 1.
В
гр. 4, 5 записывают расчет ранних параметров
работы
–
раннее
начало и раннее окончание. Расчет ведут
от исходного события до завершающего.
Для простых событий, в которые входит
только одна работа, раннее начало этой
работы равно раннему окончанию
предшествующей работы.
Раннее окончание работы равно сумме ее
раннего начала плюс продолжительность
данной работы, т. е. данные гр. 4 плюс
данные гр. 3 заносят
в гр. 5.
Раннее
начало исходной работы 1 -2 равно 0 (гр.
4); раннее окончание
работы 1-2 равно 2(0+2). Работе 2-3 предшествует
работа 1-2, для которой
раннее окончание равно 2 (гр. 5). А так как
раннее окончание предшествующей
работы равно раннему началу последующей,
число 2 записывают в гр. 4 рассматриваемой
работы 2-3. Прибавив к 2 продолжительность
работы 5 записывают в гр. 5 число 7.
Таблица
3.
Расчет параметров
сетевого графика
|
Сроки оки ооки |
работы |
Резервы работ |
||||||||||
|
и |
ранние |
поздние |
частные |
5 |
||||||||
|
Код |
Код i-j |
Прдолжительность |
начало |
окончание (гр. 3 + гр. 4) |
окончания |
общие
(гр. |
частные |
Отметка |
||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|||
|
1-2 |
2 |
0 |
2 |
0 |
2 |
0 |
0 |
+ |
||||
|
1 |
2-3 |
5 |
2 |
7 |
2 |
7 |
0 |
0 |
+ |
|||
|
1 |
2-4 |
6 |
2 |
8 |
3 |
9 |
1 |
0 |
– |
|||
|
1 |
2-5 |
3 |
2 |
5 |
9 |
12 |
7 |
2 |
– |
|||
|
2 |
3-5 |
0 |
7 |
7 |
12 |
12 |
5 |
0 |
– |
|||
|
2 |
3-6 |
7 |
7 |
14 |
7 |
14 |
0 |
0 |
+ |
|||
|
2 |
4-8 |
8 |
8 |
16 |
9 |
17 |
1 |
1 |
– |
|||
|
2;3 |
5-7 |
5 |
7 |
12 |
12 |
17 |
5 |
5 |
– |
|||
|
3 |
6-7 |
3 |
14 |
17 |
14 |
17 |
0 |
0 |
+ |
|||
|
3 |
6-11 |
8 |
14 |
22 |
31 |
39 |
17 |
17 |
– |
|||
|
5; 6 |
7-8 |
0 |
17 |
17 |
17 |
19 |
0 |
0 |
+ |
|||
|
5; 6 |
7-11 |
7 |
17 |
24 |
32 |
39 |
15 |
15 |
– |
|||
|
4; 7 |
8-9 |
4 |
17 |
21 |
17 |
21 |
0 |
0 |
+ |
|||
|
8 |
9-10 |
4 |
21 |
25 |
30 |
34 |
0 |
0 |
– |
|||
|
8 |
9-11 |
18 |
21 |
39 |
21 |
39 |
0 |
0 |
+ |
|||
|
9 |
10-11 |
5 |
25 |
30 |
34 |
39 |
9 |
9 |
– |
Ранние
начала работ 2-4 и 2-5 также
равны 2, так как им предшествует то же
самое событие 2. В гр. 4 против кода этих
работ записывают 2, а в гр. 5 заносят
соответственно 8(2+6)
и 5(2+3). Работам 3-5 и 3-6 также предшествует
только одна работа 2
-3 с цифрой 7 в гр. 5. Переносят 7 в гр.4 и т.
д.
При
рассмотрении сложного события, т. е.
когда ему предшествуют
две работы и более, раннее начало
последующей работы будет равно наибольшему
значению их ранних окончаний предшествующих
работ. В настоящей
таблице работы 5-7, 7-8, 7-11 и 8-9 имеют по две
предшествующие работы (см. гр. 1).
Например, работе 5-7 предшествуют работы
2-5
и 3-5 с начальными событиями 2 и 3.
Так
как ранние характеристики работ, в том
числе и работ 2-5 и 3-5,
рассчитаны, остается только сравнить
их величины. Раннее окончание работы
2-5 равно 5, а работы 3-5 равно 7. Большее из
этих чисел 7 переносим
в гр. 4 строки работы 5-7, после чего
определяют раннее окончание этой работы:
7+5=12.
В
гр. 6, 7 записывают расчеты поздних
параметров работ
–
позднее начало и позднее окончание.
Расчет ведут в обратном порядке, т. е.
от завершающих работ до исходной снизу
вверх. Для простого события, из которого
выходит только одна работа, позднее
окончание предшествующей работы равно
позднему началу рассматриваемой работы.
Позднее начало данной
работы равно разности между ее поздним
окончанием и продолжительностью.
Для
сложного события, из которого выходит
несколько работ, позднее
окончание предшествующих работ равно
меньшему из поздних начал
рассматриваемых работ. Так, для завершающей
работы 10-11, как и для
других работ, оканчивающихся завершающим
событием сети (событие
11), позднее окончание работ равно
наибольшей величине из всех ранних
окончаний работ, т. е. работе 9-11 (гр. 5).
Это число записывают в гр. 7
работ 10-11 и 9-11. Из гр. 7 вычитают
продолжительность работы (гр. 3) и
получают позднее начало для работы (гр.
6) 10-11, равное 39-5=34, и для работы
9-11, равное 39-18=21.
Работа
9-10 кончается событием 10; таким событием
начинается работа
10-11, ее значение 34 из гр. 5 переносят в
гр. 7 нашей работы. Вычтя
из гр. 7 значение гр. 3, записывают в гр.
6 число 30. В этом же порядке продолжают
расчет снизу вверх. При расчете сложных
событий отличие заключается в необходимости
выбора минимального значения из
нескольких
возможных. Позднее начало исходной
работы должно быть равно нулю.
Гр.
8
–
общий резерв времени определяют как
разность между значениями
гр. 6 и 4 или гр. 7 и 5. Так, для работы 1-2
полный резерв R|1-2=0(0-0=0)
или 2-2=0; для работы 2-4 R2–4=
1(3-2=1) или 9-8=1 и т. д. до конца.
В
гр. 9 записывают частный резерв времени,
который определяют как
разность между ранним началом последующей
работы по гр. 4 и ранним
окончанием данной работы по гр. 5.
Работы,
не имеющие общего резерва, естественно,
не имеют и частного
резерва, поэтому в гр. 9 ставят 0 всюду,
где 0 имеется в гр. 8. Первой
работой, имеющей резерв, будет работа
2-4. Для определения раннего начала
последующей работы надо найти в гр. 2
любую работу, начинающуюся
с последней цифры кода нашей работы, т.
е. с цифры 4. Такой будет
работа 4-8, имеющая по гр. 4 раннее начало
8. Раннее окончание нашей
работы по гр. 5 тоже равно 8, значит,
частный резерв равен
r2-4
= tp.н4-8
–
tp.o2-4
=
8-8=0.
Последующей
по отношению к работе 2-5 будет работа
5-7 со значением
раннего начала 7. Раннее окончание работы
2-5 равно 5. Отсюда частный
резерв r2-5
= 7-5 = 2.
Гр.
10
–
критический путь при табличном методе
расчета лежит на работах,
общий резерв времени которых равен 0.
Отмечаем знаком “+” работы,
лежащие на критическом пути. К таким
работам относятся все, имеющие 0 в гр.
8. На графике критический путь должен
представлять собой
непрерывную последовательность работ
от начального события до конечного.
Анализируя
таблицу, мы получаем сведения о длине
критического пути,
ранних и поздних началах и окончаниях
каждой из работ, общих и частных
резервах времени.
Степень детализации работ в сетевом графике может быть различной и зависит от назначения модели. Для бригадиров, мастеров и производителей работ разрабатываются более подробные модели. Руководители монтажных управлений и трестов пользуются сетевой моделью, выполненной в укрупненном виде.
Расчет сетевого графика заключается в нахождении критического пути и определении резервов времени для работ, которые не располагаются на этом пути.
При производстве расчетов сетевых моделей применяют следующие обозначения его параметров.
Продолжительность работы Ti-j) (здесь i и j— номера соответственно начального и конечного событий, т. е. i -j — код рассматриваемой работы).
Раннее начало работы Ti-j) — характеризуется выполнением всех предшествующих работ и определяется продолжительностью максимального пути от исходного события всей модели до начального события рассматриваемой работы.
Раннее окончание работы Ti-j — определяется суммой раннего начала и продолжительности рассматриваемой работы.
Позднее окончание работы Тi-j-, — определяется разностью продолжительности критического пути и максимальной продолжительности пути от завершающего события всей модели до конечного события рассматриваемой работы.
Позднее начало работы Ti-j — определяется разностью позднего окончания и продолжительности рассматриваемой работы.
Общий резерв времени работы Ri-j — характеризуется возможностью роста продолжительности работы без увеличения продолжительности критического пути и определяется как разность между поздним и ранним окончанием рассматриваемой работы.
Частный резерв времени работы ri-j — характеризуется возможностью увеличения продолжительности работы без изменения раннего начала последующей работы и определяется разностью между ранним началом последующей работы и ранним окончанием рассматриваемой работы. Частный резерв имеет место, когда одним событием заканчивается не менее двух работ. Полным резервом пути R называют разность между продолжительностью критического пути модели и продолжительностью рассматриваемого пути.
Проследим на фрагменте сетевой модели, изображенном на рис. 3.1, как определяются ее параметры. Из определения критического пути (путь максимальной продолжительности от события О до события 6) находим путь 0—2—4—5—6, равный 21. К работе 5—6 (начальное и конечное события) от исходного события О можно подойти следующими путями: 0—/—3—5; 0—2—3—5; О—2—4—5. Из определения раннего начала выбираем путь максимальной продолжительности 0—2—4—5, равный 13. Это и будет раннее начало работы 5—6. Раннее окончание этой же работы получаем, суммируя раннее начало и продолжительность работы: 13 + 8 = 21.
Найдем позднее окончание работы 0—2. Подойти к конечному событию 2 от завершающего события 6 можно по путям 6—5— 3—2; 6—5—4—2 и 6—4—2, максимальный из которых составит 14. Тогда позднее окончание работы 0—2 будет 21 — 14 = 7. Позднее начало этой же работы получим как разность позднего окончания и продолжительности работы 7 — 7 = 0.
Раннее окончание работы 3—5 составляет 12, а позднее окончание этой же работы — 13. Общий резерв работы 3—5 будет 1.
Чаще всего при составлении сетевых графиков расчет основных параметров выполняют в табличной форме и непосредственно на графике (табл. 3.1).
Таблица 3.1. Таблица расчетов параметров сетевого графика

Рассчитанный критический путь сетевого графика может оказаться больше нормативного или директивного сроков строительства. В этом случае производят корректировку сетевого графика за счет привлечения дополнительных ресурсов и совмещения отдельных работ.
При расчете параметров непосредственно на графике каждое событие разделяют на 4 сектора. В верхнем секторе записывается номер данного события, в нижнем — номер предшествующего события, через которое к данному идет максимальный путь. В левом секторе фиксируют рассчитанное максимальное раннее начало работ, выходящих из рассматриваемого события, в правом — рассчитанное минимальное позднее окончание работ, входящих в рассматриваемое событие. Резервы записываются под стрелками и обозначаются дробью, числителем которой является общий резерв работы, знаменателем — частный резерв.
Общий резерв работы принадлежит не только первой работе, но и всем последующим работам данного пути. В случае использования на одной из работ общего резерва критический путь не изменит своей продолжительности, но все последующие работы окажутся критическими и лишатся резерва. На практике общий резерв используется частично на различных работах в пределах их частных резервов. Следует отметить, что сумма частных резервов работ на определенном пути равна общему резерву на первой работе этого пути.
Отличие частного резерва от общего заключается в том, что частный резерв может быть использован только на рассматриваемой или предшествующих работах и не может быть использован на последующих.
Наличие резервов у некритических работ позволяет сдвигать эти работы во времени, что предопределяет значительное число вариантов организации работ. Выбор и сопоставление сетевых моделей могут обеспечить высокие технико-экономические показатели, избавить модель от элементов случайности. При значительных размерах моделей неизбежно применение ЭВМ для механизации выбора оптимального варианта.
Как отмечалось выше, между однородными и разнородными работами потока существуют связи, обозначаемые на сетевой модели пунктирными стрелками. Эти связи являются одним из важных факторов при формировании методов организации строительно-монтажных работ. Различают ресурсные, фронтальные и ранговые связи.
Связь, отражающая степень непрерывности выполнения смежных однородных работ (степень непрерывности использования ресурсов) внутри любого частного потока, называется ресурсной (организационной).
Связь между двумя смежными разнородными работами на любом фронте работ, отражающая непрерывность освоения частных фронтов, называется фронтальной (технологической).
Связь между несколькими работами, начинающимися одним событием (имеющим одно раннее начало), называется ранговой (работы одного ранга).
Приведенные выше способы расчета обеспечивают учет ресурсных и фронтальных связей, не учитывая ранговых связей.
Сетевой график – это динамическая модель проекта, которая отражает последовательность и зависимость работ, необходимых для успешного завершения проекта. Сетевой график отражает сроки выполнения запланированных работ и ресурсы, необходимые для их выполнения, а также прямые финансовые затраты, возникающие при реализации этих работ.
В английском языке для определения сетевого графика используется термин Project Network — is a graph depicting the sequence in which a project’s terminal elements are to be completed by showing terminal elements and their dependencies.
Основной целью использования сетевого графика является эффективное планирование и управление работами и ресурсами проекта. При этом, под ресурсами в данном контексте понимается как оборудование, производственные мощности или денежные средства, так и трудовые ресурсы, внутренние или внешние для организации, выполняющей проект.
Наибольшая эффективность применения сетевого графика достигается при его использовании для планирования проектов или отдельных взаимосвязанных работ. Сетевой график позволяет довольно точно определить плановые сроки завершения проекта и выявить возможные варианты их сокращения. И, что более важно, сетевой график позволяет на ранней стадии планирования проекта выявить критический путь. Кроме этого сетевой график позволяет осуществлять базовый контроль над ходом работ проекта, их сроками и исполнением бюджета.
Виды сетевых графиков
Сетевой график — это граф, на котором события (состояния работ или объектов в определенный момент времени) представлены в виде вершин, а работы проекта представлены в виде дуг, соединяющих вершины графа. Сетевой график, представленный в таком виде, изначально является частью метода PERT (Program Evaluation and Review Technique).
На практике же чаще используется другой вариант сетевого графика, когда вершинами графа являются работы, а дуги обозначают взаимосвязь между ними. Такой вид сетевого графика является частью метода критического пути (англ., CPM — Critical Path Method).
Рассмотрим второй вариант графика и алгоритм его построения подробнее.
Алгоритм построения сетевого графика
Алгоритм построения сетевого графика по методу критического пути состоит из 10 следующих шагов.
Шаг 1. Определить основную цель проекта
Определить основную цель проекта – результат, который должен быть получен после успешного завершения проекта. Это необходимо для определения границ проекта и первоначальной оценки его сроков.
Шаг 2. Выявить ограничения
Выявить ограничения, влияющие отдельные работы проекта или весь сетевой график. Типовыми ограничениями являются доступность ресурсов, сроки или стоимость. Кроме этого, ограничения могут быть заданы законодательными требованиям.
Шаг 3. Определить состав работ
Определить состав работ, необходимых для достижения цели, поставленной на шаге 1.
Шаг 4. Оценить длительность работ
Оценить длительность каждой из работ и определить ресурсы, необходимые для ее успешного выполнения. Команда управления проектом должна договориться о том, какие единицы измерения использовать для оценки длительности работ (часы, дни или, например, месяцы), а также выработать требования к максимальной длительности одной работы. Все работы, превышающую эту длительность, должны быть декомпозированы.
Шаг 5. Определить последовательность работ
Определить последовательность работ. Определить работу, которая должна быть выполнена в первую очередь. В некоторых случаю таких работ может быть несколько и они будут выполняться параллельно. Эта работа должна быть самой левой на графе.
Определить работу, которая должны быть выполнена сразу же после первой. Далее определяется работа, которая должна начинаться сразу же после второй, и так далее, пока все работы не будут рассмотрены. Если работа начинается до завершения предыдущей, то предыдущую работу необходимо разделить на составляющие. Работы могут выполняться параллельно, но при условии, что связь работ точно определена.
Начало выполнения параллельных работ должно быть строго привязано к завершению предыдущих работ.
Шаг 6. Указать связи между работами
Указать связи между работами, обычно в виде стрелок, которые показывают последовательность выполнения работ. Направление стрелок устанавливается слева направо.
Шаг 7. Определить раннее начало и раннее окончание
Определить раннее начало и раннее окончание для каждой из работ. Для этого сетевой график просматривают слева направо начиная с первой работы (крайней левой) и далее по очереди двигаются к последней. Последующая работа не может быть начата до тех пор, пока не завершены все предшествующие ей работы. Раннее начало последующей работы будет совпадать с ранним завершением предшествующей.
Если предшествующих работ несколько, то ранним началом последующей работы будет наибольшее из значений раннего окончания одной из предшествующих работ. Раннее окончание каждой из работ определяется как раннее начало плюс длительность работ, оцененная на шаге 4.
Шаг 8. Определить поздние начало и окончание
Определить поздние начало и окончание для каждой из работ. Для этого сетевой график просматривают в обратном направлении — начинают с последней работы (самой правой) и далее по очереди двигаются к первой. Предшествующая работа должна быть завершена до того, как начнется каждая из последующих работ. Позднее окончание работы будет совпадать с поздним началом последующей работы. Если последующих работ несколько, то поздним окончанием работы будет наименьшее из значений позднего начала последующих работ. Позднее начало каждой работы определяется как позднее окончание минус длительность работы.
Шаг 9. Определить временной резерв
Определить временной резерв для каждой из работ. Резерв времени вычисляется как разница между поздним и ранним началом или поздним и ранним окончанием работы.
Шаг 10. Выявить критический путь
Критический путь — это цепочка работ, у которых резерв времени равен нулю. При оптимизации сетевого графика в первую очередь проводится оптимизация работ, лежащих на критическом пути.
Пример построения сетевого графика
Несмотря на то, что описанный выше алгоритм может показаться сложным, на самом же деле построение сетевого графика задача несложная. Для того, чтобы убедиться в этом рассмотрим построение сетевого графика на простом примере ремонта детской комнаты.
Шаг 1. Определить основную цель проекта
Представьте, что сейчас лето, вашему сыну исполнилось 7 лет и в сентябре он идет в школу. Вы решил обновить его комнату к новому учебному году и сделать ее подходящей для школьника, т.е. должно появиться полноценной рабочее место, зонирование комнаты измениться, и т.д.
В этом случае целью нашего небольшого проекта будет — сделать комнату пригодной и приятной для проживания мальчика, который пойдет в начальную школу.
Шаг 2. Выявить ограничения
Бюджет не более 100,000 руб., ремонтные работы можно вести только в рабочие дни с 10:00 до 18:00 с обязательным перерывом с 12:00 до 14:00. Итого получается — 6 рабочих часов в день.
Шаг 3. Определить состав работ
Немного поразмыслив мы накидали основные работы, которые надо сделать, а именно:
- Нам нужен дизайн-проект новой комнаты;
- Нам надо закупить материалы для ремонта;
- Надо составить смету ремонта;
- Надо выполнить сам ремонт;
- И т.к. мы решили сделать небольшую перепланировку, то надо согласовать ее с ТСЖ.
Отобразим эти работы в виде блоков:
Рисунок 1. Состав работ
Шаг 4. Оценить длительность работ
Мы решили оценивать длительность работ в днях, т.к. до начала учебного года еще достаточно времени, то такая точность планирования нас вполне устраивает.

Рисунок 2. Длительность работ
Шаг 5. Определить последовательность работ
Теперь определим последовательность работ, мы будем использовать схему построения сетевого графика «сверху-вниз». Первая работа, которую необходимо выполнить — это работа «Разработать дизайн-проекта«. Затем мы оценим стоимость проекта, а параллельно начнем согласование с ТСЖ, т.к. эта задача занимает много времени. После того, как мы оценим проект и его согласуем, мы приступим к покупке всех необходимых материалов и уже затем начнем сам ремонт.

Рисунок 3. Последовательность работ
Шаг 6. Указать связи между работами
Укажем стрелками связи между работами.
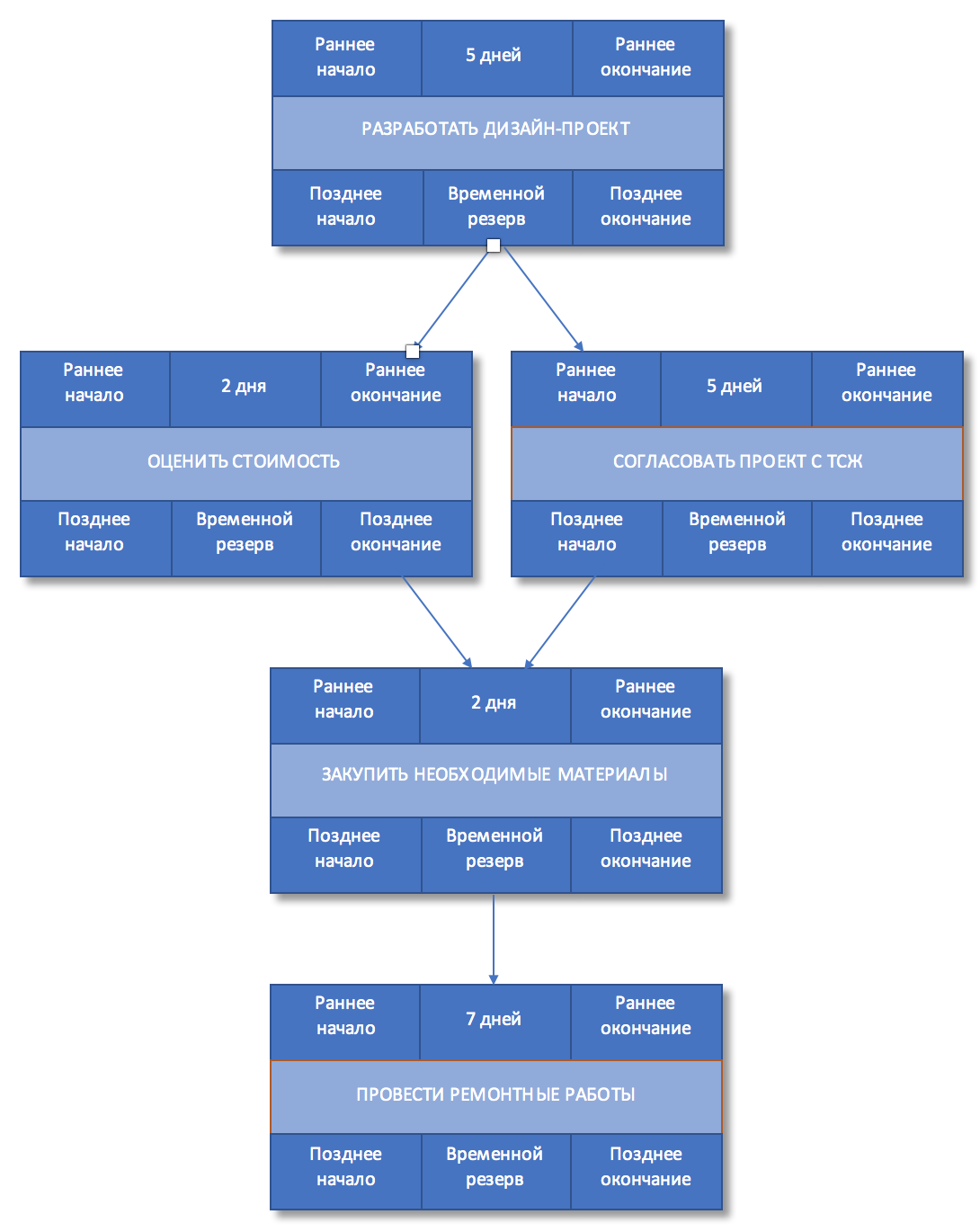
Рисунок 4. Связи между работами
Шаг 7. Определить раннее начало и раннее окончание
Т.к. мы выбрали модель сетевого график «сверху-вниз», то начинаем его и просматривать сверху вниз, начиная с самой верхней работы, и далее по очереди двигаемся к самой нижней работе.
Напомним, что раннее начало последующей работы будет совпадать с ранним завершением предшествующей, а раннее окончание каждой из работ определяется как раннее начало плюс длительность работ Если предшествующих работ несколько, то ранним началом последующей работы будет наибольшее из значений раннего окончания одной из предшествующих работ.
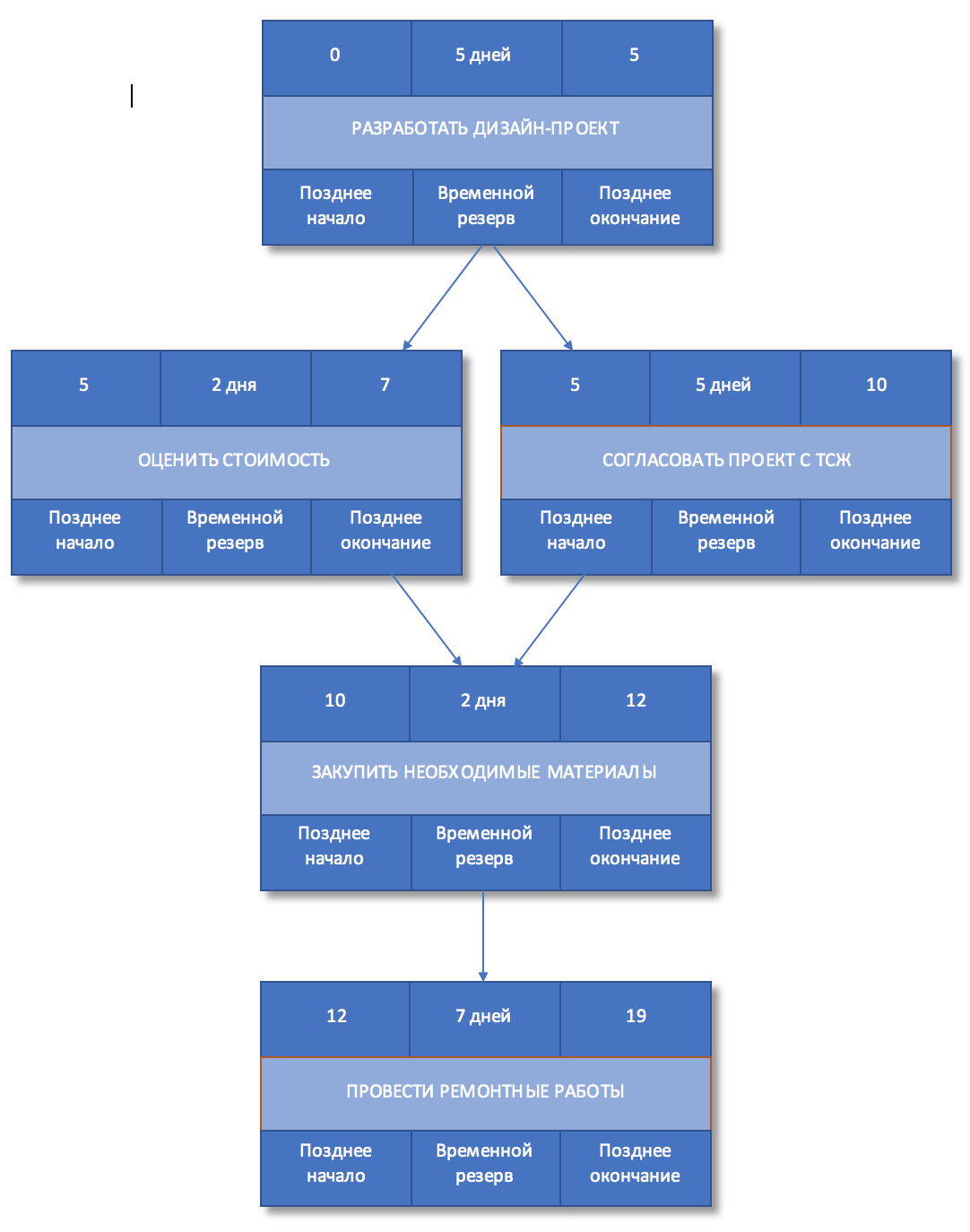
Рисунок 5. Раннее начало и окончание работ
Шаг 8. Определить поздние начало и окончание
Для того, чтобы определить поздние начало и окончание просмотрим сетевой график в обратном направлении — снизу вверх. Позднее окончание работы будет совпадать с поздним началом последующей работы. Если последующих работ несколько, то поздним окончанием работы будет наименьшее из значений позднего начала последующих работ. Позднее начало каждой работы определяется как позднее окончание минус длительность работы.
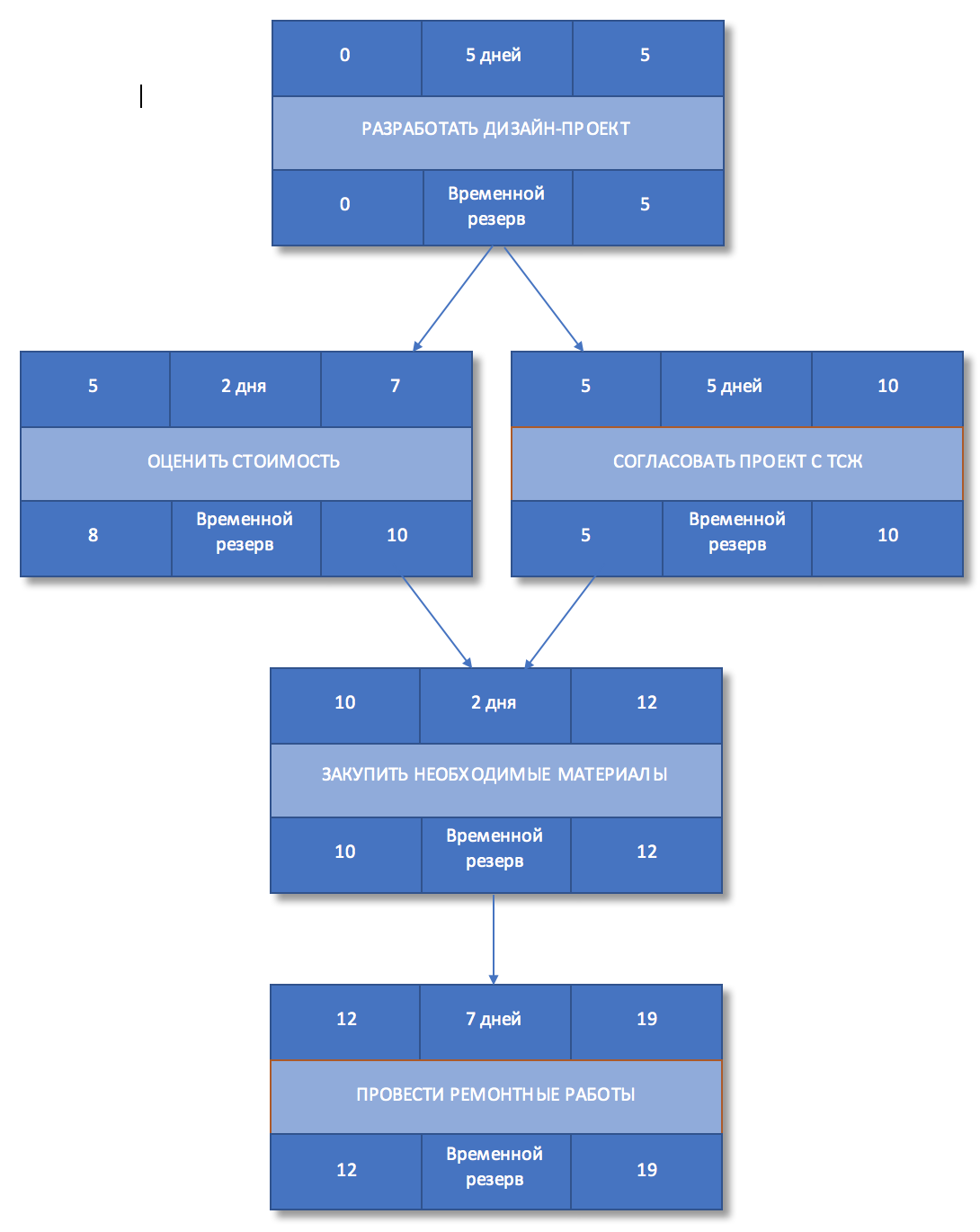
Рисунок 6. Позднее начало и окончание работ
Шаг 9. Определить временной резерв
Вычислим временной резерв для каждой из работ. Он вычисляется как разница между поздним и ранним началом или поздним и ранним окончанием работы.
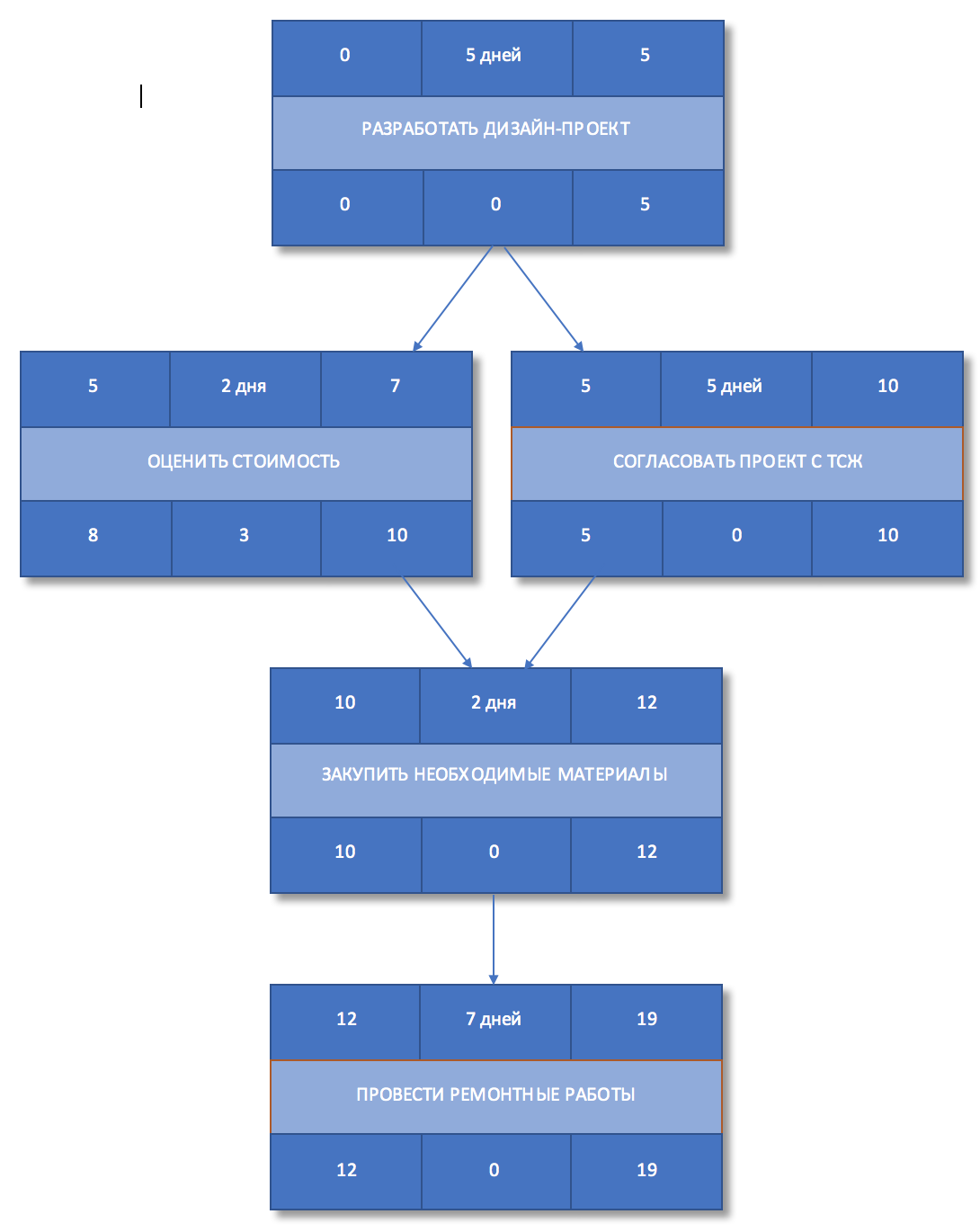
Рисунок 7. Временной резерв
Шаг 10. Выявить критический путь
Как мы уже знаем, критический путь — это цепочка работ, у которых резерв времени равен нулю. Выделим такие задачи на сетевом графике.
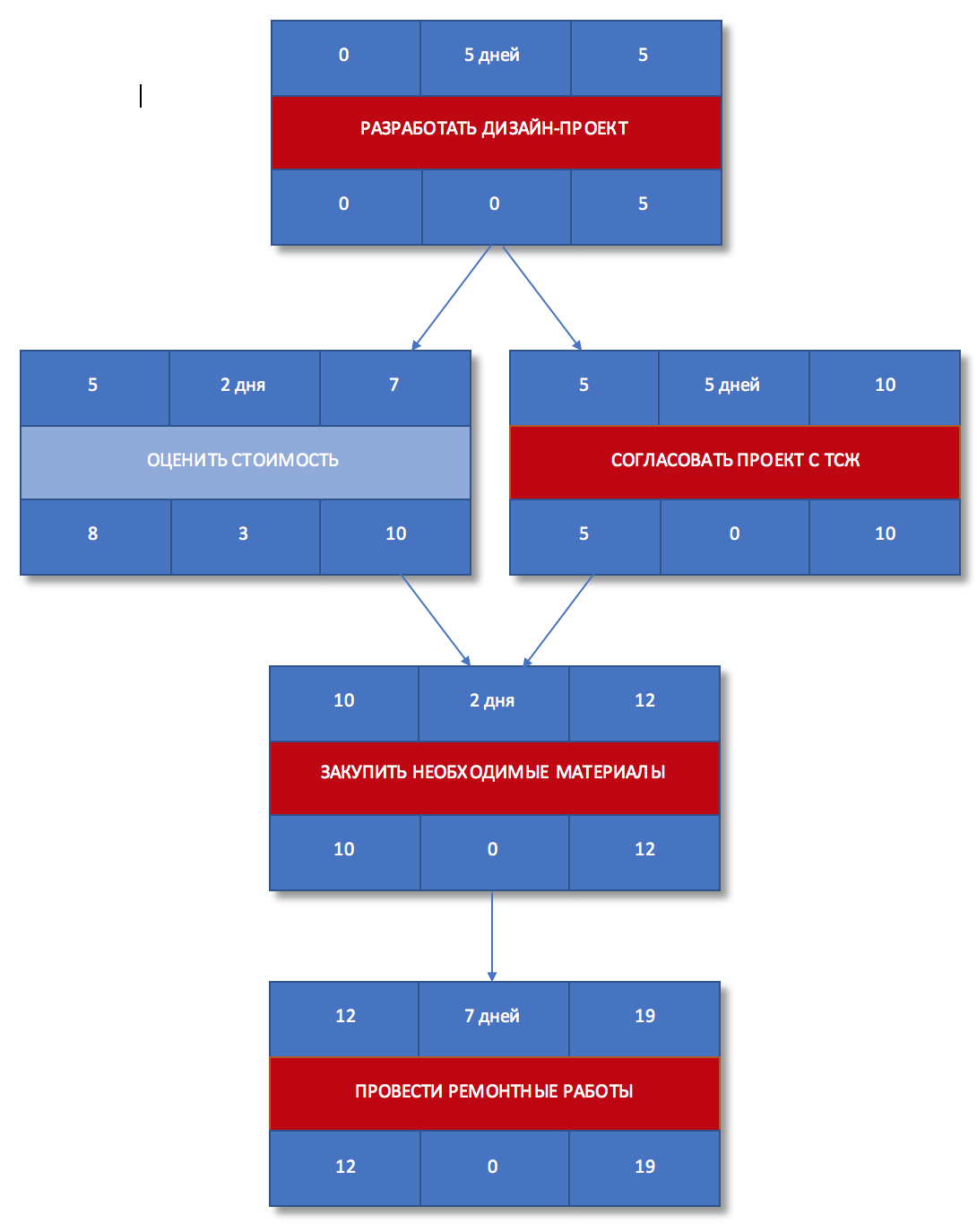
Рисунок 8. Критический путь
Задачи «Разработать дизайн-проект«, «Согласовать проект с ТСЖ» и «Закупить необходимые материалы«, «Провести ремонтные работы» составляю критический путь, а его длина составляет 19 дней. Это означает, что в текущем виде проект не может быть выполнен быстрее, чем за 19 дней. Если мы хотим сократить сроки проекта, то нам необходимо оптимизировать задачи, лежащие на критическом пути.
Например, мы можем начать ремонтные работы раньше получения согласования на перепланировку от ТСЖ, приняв на себя риски того, что согласование может быть не получено.
Просмотры: 137 129
