Определить взаимное расположение плоскостей как найти

Определить взаимное расположение плоскостей как найти

Взаимное расположение плоскостей

Параллельные плоскости

Получим условия параллельности или совпадения двух плоскостей rho_{1} и rho_{2} заданных общими уравнениями:

rho_{1}colon,A_{1}cdot x+B_{1}cdot y+C_{1}cdot z+D_{1}=0; quad rho_{2}colon,A_{2}cdot x+B_{2}cdot y+C_{2}cdot z+D_{2}=0,.

(4.23)

Необходимым и достаточным условием параллельности или совпадения плоскостей (4.23) является условие коллинеарности их нормалейvec{n}_{1}=A_{1}cdotvec{i}+B_{1}cdotvec{j}+C_{1}cdotvec{k}, vec{n}_{2}=A_{2}cdotvec{i}+B_{2}cdotvec{j}+C_{2}cdotvec{k}. Следовательно, если плоскости (4.23) параллельны или совпадают, то vec{n}_{1}parallelvec{n}_{2} т.е. существует такое число lambdane0 что

vec{n}_{1}=lambdacdotvec{n}_{2} quad Leftrightarrow quad begin{cases}A_{1}=lambdacdot A_{2},\ B_{1}=lambdacdot B_{2},\ C_{1}=lambdacdot C_{2}.end{cases} и наоборот.

Плоскости совпадают, если помимо этих условий справедливо D_{1}=lambda D_{2}. Тогда первое уравнение в (4.23) имеет вид lambda(A_{2}x+B_{2}y+C_{2}z+D_{2})=0 т.е. равносильно второму, поскольку lambdane0.

Таким образом, плоскости (4.23) параллельны тогда и только тогда, когда соответствующие коэффициенты при неизвестных в их уравнениях пропорциональны, т.е. существует такое число lambdane0, что A_{1}=lambda A_{2}, B_{1}=lambda B_{2}, C_{1}=lambda C_{2}, но D_{1}nelambda D_{2}. Плоскости (4.23) совпадают тогда и только тогда, когда все соответствующие коэффициенты в их уравнениях пропорциональны: A_{1}=lambda A_{2}, B_{1}=lambda B_{2}, C_{1}=lambda C_{2} и D_{1}=lambda D_{2}.

Условия параллельности и совпадения плоскостей (4.23) можно записать в виде

rho_{1}parallelrho_{2} quad Leftrightarrow quad frac{A_{1}}{A_{2}}= frac{B_{1}}{B_{2}}= frac{C_{1}}{C_{2}}nefrac{D_{1}}{D_{2}}; quad rho_{1}equivrho_{2} quad Leftrightarrow quad frac{A_{1}}{A_{2}}= frac{B_{1}}{B_{2}}= frac{C_{1}}{C_{2}}= frac{D_{1}}{D_{2}},.

Отсюда следует критерий параллельности или совпадения двух плоскостей (4.23):

rho_{1}parallelrho_{2} или rho_{1}equivrho_{2} quad Leftrightarrow quad operatorname{rang}! begin{pmatrix}A_{1}&B_{1}&C_{1}\A_{2}&B_{2}&C_{2}end{pmatrix}=1.

Поверхности уровня линейного четырехчлена

Семейство параллельных плоскостей

Поверхностью уровня функции f(x,y,z) трех переменных называется геометрическое место точек координатного пространства Oxyz, в которых функция принимает постоянное значение, т.е. f(x,y,z)=text{const}.

Для линейного четырехчлена p(x,y,z)=Ax+By+Cz+D уравнение поверхности уровня p(x,y,z)=text{const}. имеет вид

Acdot x+Bcdot y+Ccdot z+D=text{const}.

(4.24)

При любом фиксированном значении постоянной уравнение (4.24) описывает плоскость. Рассмотрим поведение семейства поверхностей уровня, отличающихся значением постоянной. Поскольку коэффициенты A,,B и C не изменяются, то у всех плоскостей (4.24) будет одна и та же нормаль vec{n}=Avec{i}+Bvec{j}+Cvec{k}. Следовательно, поверхности уровня линейного четырехчлена P(x,y,z)=Ax+By+Cz+DD представляют собой семейство параллельных плоскостей (рис.4.19). Поскольку нормаль совпадает с градиентом (см. пункт 3 замечаний 4.2), а градиент направлен в сторону наискорейшего возрастания функции, то при увеличении постоянной поверхности уровня (4.24) переносятся параллельно в направлении нормали.

Пересекающиеся плоскости

Необходимым и достаточным условием пересечения двух плоскостей (4.22) является условие неколлинеарности их нормалей, или, что то же самое, условие непропорциональности коэффициентов при неизвестных:

operatorname{rang}!begin{pmatrix}A_{1}&B_{1}&C_{1}\A_{2}&B_{2}&C_{2}end{pmatrix}=2.

(4.25)

При этом условии система уравнений

begin{cases}A_{1}cdot x+B_{1}cdot y+C_{1}cdot z+D_{1}=0,\ A_{2}cdot x+B_{2}cdot y+C_{2}cdot z+D_{2}=0end{cases}

имеет бесконечно много решений, которые определяют прямую пересечения плоскостей, заданных уравнениями (4.23).

Угол между плоскостями

Угол между двумя плоскостями можно определить как угол между их нормальными векторами. По этому определению получаются не один угол, а два смежных угла, дополняющих друг друга до pi. В элементарной геометрии из двух смежных углов, как правило, выбирается меньший, т.е. величина varphi угла между двумя плоскостями удовлетворяет условию 0leqslantvarphileqslantfrac{pi}{2}.

Если vec{n}_{1}= A_{1}vec{i}+B_{1}vec{j}+C_{1}vec{k},~ vec{n}_{2}= A_{2}vec{i}+B_{2}vec{j}+C_{2}vec{k} — нормали к плоскостям rho_{1} и rho_{2} соответственно (рис.4.20,а), то величина varphi угла между этими плоскостями вычисляется по формуле:

cosvarphi=frac{|,langle,vec{n}_{1},vec{n}_{2},rangle,|}{|vec{n}_{1}|cdot|vec{n}_{2}|}=frac{|A_{1}cdot A_{2}+B_{1}cdot B_{2}+C_{1}cdot C_{2}|}{sqrt{A_{1}^2+B_{1}^2+C_{1}^2}cdotsqrt{A_{2}^2+B_{2}^2+C_{2}^2}},.

Необходимым и достаточным условием перпендикулярности плоскостей (4.23) является условие ортогональности их нормалей, т.е. langle,vec{n}_{1},vec{n}_{2},rangle=0:

A_{1}cdot A_{2}+B_{1}cdot B_{2}+C_{1}cdot C_{2}=0,.

При пересечении двух плоскостей образуются четыре двугранных угла (рис.4.20). Величина varphi двугранного угла удовлетворяет условию 0<varphi<pi,.

Двугранные углы, образуемые пересечением двух плоскостей

По формуле

cosvarphi=frac{langle,vec{n}_{1},vec{n}_{2},rangle}{|vec{n}_{1}|cdot|vec{n}_{2}|}=frac{A_{1}cdot A_{2}+B_{1}cdot B_{2}+C_{1}cdot C_{2}}{sqrt{A_{1}^2+B_{1}^2+C_{1}^2}cdotsqrt{A_{2}^2+B_{2}^2+C_{2}^2}}

(4.26)

получаем острый двугранный угол varphi, образованный плоскостями (4.23), если A_{1}A_{2}+B_{1}B_{2}+C_{1}C_{2}>0 (рис.4.20,а), и тупой в противном случае: A_{1}A_{2}+B_{1}B_{2}+C_{1}C_{2}<0 (рис.4.20,б). Другими словами, по формуле (4.26) находится тот двугранный угол, образованный плоскостями, в котором лежат точки, принадлежащие разноименным полупространствам, определяемым данными плоскостями. На рис.4.20 изображены пересекающиеся плоскости, положительные и отрицательные полупространства отмечены знаками + или – соответственно.

Пример 4.10. Найти величину того угла, образованного плоскостями rho_{1}colon5x-3y+4z-3=0 и rho_{2}colon2x+y+2z+4=0, внутри которого лежит точка M(5;2;1).

Решение. По уравнениям плоскостей находим нормали vec{n}_{1}=5vec{i}-3vec{j}+4vec{k}, vec{n}_{2}=2vec{i}+vec{j}+2vec{k}, а также величину varphi угла между нормалями, используя (4.26):

cosvarphi=frac{5cdot2+(-3)cdot1+4cdot2}{sqrt{5^2+(-3)^2+4^2}cdotsqrt{2^2+1^2+2^2}}=frac{15}{3sqrt{50}}=frac{1}{sqrt{2}} quad Leftrightarrow quad varphi=frac{pi}{4},.

Подставляя координаты точки M(5;2;1) в левые части уравнений плоскостей, выясняем, каким полупространствам принадлежит эта точка. Для плоскости rho_{1} имеем 5cdot5-3cdot2+4cdot1-3>0 значит, точка M лежит в положительном полупространстве, определяемом плоскостью rho_{1}. Для плоскости rho_{2} имеем 2cdot5+2+2cdot1+4>0 значит, точка M лежит также в положительном полупространстве, определяемом плоскостью rho_{2}. Поскольку точка M принадлежит одноименным полупространствам (положительным), то искомый угол — это угол psi, смежный найденному углу varphi=frac{pi}{4}: psi=pi-varphi=pi-frac{pi}{4}=frac{3pi}{4},.

Пучки плоскостей

Собственные и несобственные пучки плоскостей

Собственным пучком плоскостей называется совокупность всех плоскостей, проходящих через фиксированную прямую (ось пучка).

Несобственным пучком плоскостей называется совокупность плоскостей, параллельных фиксированной плоскости (осью несобственного пучка плоскостей считается бесконечно удаленная прямая).

Любые две плоскости rho_{1} и rho_{2} определяют пучок плоскостей, содержащий заданные плоскости rho_{1} и rho_{2}. Если плоскости rho_{1} и rho_{2} пересекаются, то прямая m пересечения является осью собственного пучка (рис.4.21,а). Если плоскости rho_{1} и rho_{2} параллельны, то они определяют несобственный пучок параллельных плоскостей (рис.4.21,б).

Пусть заданы уравнения двух плоскостей (4.23):

rho_{1}colon~A_{1}cdot x+B_{1}cdot y+C_{1}cdot z+D_{1}=0; quad rho_{2}colon~A_{2}cdot x+B_{2}cdot y+C_{2}cdot z+D_{2}=0.

Линейной комбинацией этих уравнений называется уравнение

lambda_{1}cdot(A_{1}cdot x+B_{1}cdot y+C_{1}cdot z+D_{1})+lambda_{2}cdot(A_{2}cdot x+B_{2}cdot y+C_{2}cdot z+D_{2})=0,

(4.27)

где числа lambda_{1},,lambda_{2} — коэффициенты линейной комбинации. Его можно записать в форме

(lambda_{1}cdot A_{1}+lambda_{2}cdot A_{2})cdot x+ (lambda_{1}cdot B_{1}+lambda_{2}cdot B_{2})cdot y+ (lambda_{1}cdot C_{1}+lambda_{2}cdot C_{2})cdot x+ lambda_{1}cdot D_{1}+lambda_{2}cdot D_{2}=0.

Заметим, что линейная комбинация уравнений является уравнением первой степени для любых значений коэффициентов, кроме случая, когда все коэффициенты при неизвестных равны нулю, т.е. при одновременном выполнении условий

lambda_{1}cdot A_{1}+lambda_{2}cdot A_{2}=0, quad lambda_{1}cdot B_{1}+lambda_{2}cdot B_{2}=0, quad lambda_{1}cdot C_{1}+lambda_{2}cdot C_{2}=0.

Эти значения параметров lambda_{1},,lambda_{2} считаются недопустимыми.

Уравнение (4.27) называется уравнением пучка плоскостей, содержащего плоскости

A_{1}cdot x+B_{1}cdot y+C_{1}cdot z=0, quad A_{2}cdot x+B_{2}cdot y+C_{2}cdot z=0.

При любых допустимых значениях параметров lambda_{1},,lambda_{2} уравнение (4.27) задает плоскость, принадлежащую пучку, и наоборот, для любой плоскости пучка найдутся такие значения параметров lambda_{1},,lambda_{2}, что уравнение (4.27) будет задавать эту плоскость.

Доказательство утверждения аналогично доказательству свойства пучка прямых.

Пример 4.11. Составить уравнение плоскости, проходящей через прямую пересечения плоскостей 2x+2y-z+3=0, 6x-3y+2z+1=0 и через точку M^{ast}(2;3;1).

Решение. Искомая плоскость входит в пучок плоскостей, задаваемый уравнением (4.27)

lambda_{1}cdot(2cdot x+2cdot y-z+3)+lambda_{2}cdot(6cdot x-3cdot y+2cdot z+1)=0.

Подставляя координаты точки M^{ast}(2;3;1), получаем:

lambda_{1}cdot(2cdot2+2cdot3-1+3)+lambda_{2}cdot(6cdot2-3cdot3+2cdot1+1)=0 quad Leftrightarrow quad 12cdotlambda_{1}+6cdotlambda_{2}=0.

Возьмем, например, lambda_{1}=-1,~lambda_{2}=2 и подставим в уравнение пучка:

-1cdot(2x+2y-z+3)+2cdot(6x-3y+2z+1)=0 quad Leftrightarrow quad 10x-8y+5z-1=0.

Итак, искомое уравнение получено.

Связки плоскостей

Собственные и несобственные связки плоскостей

Собственной связкой плоскостей называется совокупность всех плоскостей, проходящих через фиксированную точку (центр связки).

Несобственной связкой плоскостей называется совокупность плоскостей, параллельных фиксированной прямой (центром несобственной связки плоскостей считается бесконечно удаленная точка).

Уравнение собственной связки плоскостей с центром M_{0}(x_{0},y_{0},z_{0}) имеет вид

Acdot(x-x_{0})+Bcdot(y-y_{0})+Ccdot(z-z_{0})=0,

где A,,B,,C — произвольные параметры, одновременно не равные нулю.

Уравнение связки плоскостей (собственной (рис.4.22,а) или несобственной (рис.4.22,6)) можно получить в виде линейной комбинации уравнений трех плоскостей:

lambda_{1}(A_{1}x+B_{1}y+C_{1}z+D_{1})+lambda_{2}(A_{2}x+B_{2}y+C_{2}z+D_{2})+lambda_{3}(A_{3}x+B_{3}y+C_{3}z+D_{3})=0,

(4.28)

где lambda_{1},,lambda_{2},,lambda_{3} — коэффициенты линейной комбинации. Заметим, что линейная комбинация уравнений является уравнением первой степени для любых значений коэффициентов, кроме случая, когда все коэффициенты при неизвестных равны нулю. Эти значения параметров lambda_{1},,lambda_{2},,lambda_{3} считаются недопустимыми.

Уравнение (4.28) называется уравнением связки плоскостей, содержащей три плоскости

A_{1}x+B_{1}y+C_{1}z+D_{1}=0, quad A_{2}x+B_{2}y+C_{2}z+D_{2}=0, quad A_{3}x+B_{3}y+C_{3}z+D_{3}=0.

При любых допустимых значениях параметров lambda_{1},,lambda_{2},,lambda_{3} уравнение (4.28) задает плоскость, принадлежащую связке, и наоборот, для любой плоскости связки найдутся такие значения параметров lambda_{1},,lambda_{2},,lambda_{3}, что уравнение (4.28) будет задавать эту плоскость.

Доказательство утверждения аналогично доказательству свойства пучка прямых.

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

Взаимное
расположение плоскостей будем исследовать
через взаимное расположение их нормальных
векторов.

Пусть
плоскости
изаданы своими общими уравнениями, из
которых сразу определяем нормальные
векторы этих плоскостей:

;

.

  • Пучок
    плоскостей
    это бесконечное множество плоскостей,
    которые проходят через прямую пересечения
    двух данных непараллельных плоскостей.
    Аналитически пучок плоскостей задается
    уравнением

,

где
коэффициент

это любое действительное число.

Пример
21.Составить уравнение плоскости,
проходящей через точкуи прямую

Решение.
Идея
решения 
найти искомую плоскость как отдельную
плоскость пучка плоскостей (Рис. 17).
Для этого от общих уравнений прямой
перейдем к уравнению пучка плоскостей,
проходящих через:

:.

Приведем
подобные относительно
,и:

.

Уравнение
искомой плоскости получается из этого
уравнения при каком-то конкретном
значении коэффициента .
Найдем это значение. Для этого координаты
точки
подставим в уравнение пучка:

.

Найденное
значение
подставим в общее уравнение пучка:

.

Для
упрощения умножим все уравнение на 7 :

.

  • Признак
    параллельности плоскостей:

.
(19)

Так
же как и у плоских прямых уравнения
параллельных плоскостей могут быть
приведены к такому виду, когда они
отличаются только свободными членами,
т. е.

;

,
где
.

  • Расстояние
    между параллельными плоскостями:

(20)

  • Признак
    перпендикулярности плоскостей:

(21)

По
этой формуле, например, можно проверить
правильно ли мы нашли проектирующую
плоскость в предыдущем примере.

Пример22.
Проверить перпендикулярна ли плоскость

плоскости.

Решение.
По уравнениям плоскостей строим их
нормальные векторы:
и.
Вычислим их скалярное произведение:.
Действительно, проектирующая плоскость
в примере 20 была найдена верно.

  • Угол
    между плоскостями:

(22)

  • Расстояние
    от точки
    до плоскостинаходится по формуле

(23)

Пример
23.
Найти расстояние от точки
до плоскости

.

Решение.

Для
решения достаточно подставить числовые
данные задачи в формулу (23).

.

Глава 3. Прямая в пространстве

§ 1 Вступление

В
аналитической геометрии пространственная
прямая
это геометрическое место точек в
пространстве, координаты которых
удовлетворяют одному из трех видов
уравнений.

канонические
уравнения пространственной

прямой;

параметрические
уравнения

пространственной
прямой;

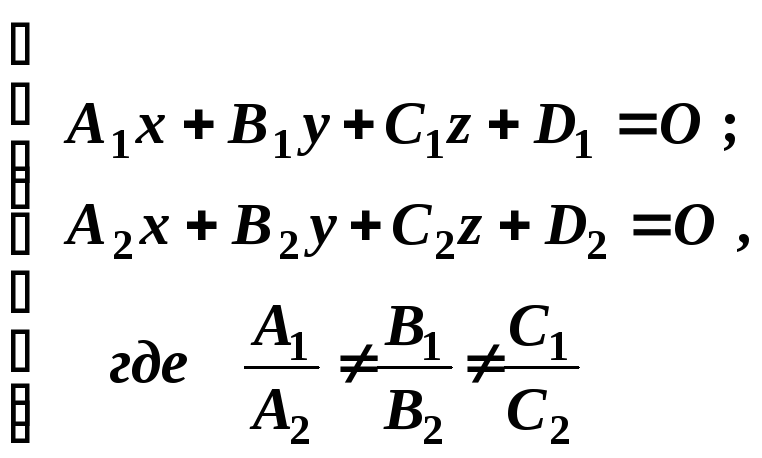общие уравнения
пространственной прямой.

§ 2 Вывод уравнения пространственной прямой при разных способах ее задания.

  • Канонические
    уравнения пространственной прямой,
    проходящей через данную точку
    параллельно заданному вектору.

(24)

Пример
24.
Даны вершины тетраэдра:
,,и.
Найти канонические уравнения высоты
тетраэдра, проведенной из вершинык основанию.

Решение.

Впримере16 уравнение плоскости основаниябыло
выведено:

.

По
этому уравнению сразу находим нормальный
вектор плоскости основания:

.

Высота
и векторперпендикулярны одной и той же плоскостиплоскости основания,
а значит они параллельны, и поэтому
векторможно взять в качестве направляющего
для высоты.

Точка,
заведомо лежащая на
,
естьэто точка.
Тогда по формуле (24 ) находим уравнение.

  • Параметрические
    уравнения пространственной прямой,
    проходящей через данную точку
    параллельно заданному вектору.

(
25)

Параметрические
уравнения пространственной прямой мы
будем выводить из канонических уравнений
этой прямой. Для этого пропорцию в
канонических уравнениях нужно приравнять
к параметру
,
затем «разорвать» эту пропорцию на три
уравнения и разрешить их относительно,и.

Пример
25.
Даны вершины тетраэдра:
,,и.
Найти параметрические уравнения высоты
тетраэдра, проведенной из вершинык основанию.

Решение.В примере 24 были выведены канонические
уравнения высоты.
Выполним над ними действия, указанные
выше.

параметрические
уравнения высоты
.

  • Канонические
    уравнения пространственной прямой,
    проходящей через две заданных точки
    и.

(26)

Замечания

  1. Для
    получения канонических уравнений
    прямой совершенно безразлично какую
    точку считать первой, а какую второй.

  2. Если
    в знаменателях пропорции получится
    много минусов, то все знаменатели можно
    умножить на ( 1 ).
    Новая пропорция задает ту же самую
    прямую.

  3. Если
    знаменатели содержат дробные числа,
    то для упрощения вычислений их можно
    умножить на одно и то же число, чтобы
    знаменатели стали целыми.

Пример
26.
Даны вершины тетраэдра:
,,и.
Найти канонические уравнения бокового
ребра.

Решение.Будем для определенности считать точкупервой, а точкувторой. Тогда

.

Можно
было в числителях пропорции вычитать
координаты точки
.
Тогда уравнениеимело бы вид:

.

  • Общие
    уравнения пространственной прямой.

(27)

Поскольку
большинство задач на пространственную
прямую используют канонические
уравнения, то рассмотрим переход от
общих уравнений пространственной
прямой к каноническим.

Пример
27.Составить канонические
уравнения прямой

Решение.Способ
1.Для канонических уравнений нужно
иметь одну точку (любую), лежащую на
этой прямой, и какой-нибудь вектор
ненулевой длины, параллельный этой
прямой. В качестве искомой точки можно
взять любую точку, координаты которой
совпадают с каким-либо частным решением
системы уравнений, задающих прямую.
Поскольку в ней два уравнения и три
неизвестных, то одна переменная является
свободной. Пусть это будет переменнаяи пусть для простоты вычислений.
Тогда система примет вид.
Искомая точка.

Теперь
найдем направляющий вектор. Нормальные
векторы данных плоскостей при совмещении
их начал в точке на прямойобразуют плоскость, перпендикулярную
этой прямой. Можно сказать и иначе:
прямаяперпендикулярна плоскости нормальных
векторов. Наряду с прямойесть
вектор, перпендикулярный этой же
плоскости. Это векторное произведение
нормальных векторов заданных плоскостей,
т.е..
Следовательно, векторпараллелен прямой,
а значит его можно взять в качестве
направляющего для.
Найдем его координаты.

.

Тогда
канонические уравнения прямой
примут
вид:

.
Можно для упрощения дальнейших
вычислений уменьшить знаменатели в
пропорции вдвое. Новое уравнение
задает ту же самую прямую.

Способ
2.Как известно, канонические уравнения
прямойможно построить, если известны координаты
двух точек, заведомо лежащих на этой
прямой. Одна уже найденаэто точка.
Вторую найдем тем же способом. Для этого
в системеположим теперь, например,.
Система примет видСложим (I) и (II):
.
Тогда.
Подставим координаты найденных точек
в формулу (26) :.
Умножим все знаменатели на (1)
:.
Как и следовало ожидать, получилось
то же самое уравнение , что и при первом
способе.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
Источник

Взаимное расположение плоскостей: параллельность, перпендикулярность, пересечение трёх плоскостей в одной точке

Угол между двумя плоскостями, условия параллельности и перпендикулярности плоскостей

Пусть две плоскости и заданы общими уравнениями и .

Вопрос об определении угла между ними сводится к определению угла между векторами нормалей к ним

и .

Из определения скалярного произведения и из выражения в координатах длин векторов и и их скалярного произведения получим

Условие параллельности плоскостей и эквивалентно условию коллинеарности векторов и и заключается в пропорциональности координат этих векторов:

.

Условие перпендикулярности плоскостей и может быть выражено равенством нулю скалярного произведения векторов нормалей к ним и :

.

Пример 1. Установить, параллельны ли две плоскости, одна из которых задана уравнением , а другая — уравнением .

Решение. Составим уравнения коэффициентов уравнений плоскостей:

Так как , то коэффициенты пропорциональны, следовательно данные две плоскости параллельны.

Пример 2. Установить, перпендикулярны ли плоскости, заданные уравнениями и .

Решение. Плоскости перпендикулярны в том случае, когда векторы и нормалей к ним перпендикулярны и удовлетворяют условию равенства нулю их скалярного произведения. Так как , то указанное условие выполнено и, значит, данные плоскости перпендикулярны.

Условие пересечения трёх плоскостей в одной точке, точка пересечения

Необходимым и достаточным условием того, что три плоскости имеют только одну общую точку (то есть, пересекаются в этой точке), является условие неравенства нулю определителя, составленного из коэффициентов уравнений:

Это условие совпадает с условием того, что система линейных уравнений имеет одно единственное решение (пройдя по ссылке можно увидеть иллюстрацию как раз на примере плоскостей).

Решение системы общих уравнений плоскостей (если оно существует и единственное) и даёт точку пересечения трёх плоскостей.

Пример 3. Установить, пересекаются ли три плоскости в одной точке, если пересекаются, найти точку пересечения. Плоскости заданы уравнениями:

Решение. Сначала проверим, выполняется ли условие пересечения плоскостей в одной точке. Для этого установим, отличен ли от нуля определитель системы:

Определитель отличен от нуля, следовательно система уравнений имеет единственное решение, а, значит, три плоскости пересекаются в одной точке.

Для нахождения этой точки продолжим решать систему уравнений методом Крамера. Перенесём свободные члены в правые части уравнений:

Найдём определители при неизвестных:

Нетрудно заметить, что по формулам Крамера (определитель при неизвестной делить на определитель системы) все неизвестные оказались равными единице. Таким образом, получили точку пересечения трёх плоскостей:

Для проверки решения подобных задач целесообразно воспользоваться калькулятором, решающим системы уравнений методом Крамера.

Пример 4. Установить, пересекаются ли три плоскости в одной точке, если пересекаются, найти точку пересечения. Плоскости заданы уравнениями:

Решение. Проверим, пересекаются ли плоскости в одной точке. Для этого вычислим определитель системы:

Определитель равен нулю, следовательно, данные три плоскости не пересекаются в одной точке.

Для проверки решения подобных задач целесообразно воспользоваться калькулятором, решающим системы уравнений методом Крамера.

Уравнение плоскости, проходящей через данную точку и параллельной данной плоскости

Пусть даны точка и плоскость . Тогда уравнение плоскости, проходящей через данную точку, и параллельной данной плоскости, имеет вид

.

Пример 5. Составить уравнение плоскости, проходящей через точку (3, -5, 1) , и параллельной плоскости .

Решение. Подставляем в формулу, данную в теоретической сравке к этой главе, данные точки и другой плоскости. Получаем:

Последнее и есть искомое уравнение плоскости, проходящей через данную точку, и параллельной данной плоскости.

Взаимное расположение плоскостей

Параллельные плоскости

Получим условия параллельности или совпадения двух плоскостей и заданных общими уравнениями:

Необходимым и достаточным условием параллельности или совпадения плоскостей (4.23) является условие коллинеарности их нормалей Следовательно, если плоскости (4.23) параллельны или совпадают, то т.е. существует такое число что

Плоскости совпадают, если помимо этих условий справедливо Тогда первое уравнение в (4.23) имеет вид т.е. равносильно второму, поскольку

Таким образом, плоскости (4.23) параллельны тогда и только тогда, когда соответствующие коэффициенты при неизвестных в их уравнениях пропорциональны, т.е. существует такое число что но Плоскости (4.23) совпадают тогда и только тогда, когда все соответствующие коэффициенты в их уравнениях пропорциональны: и

Условия параллельности и совпадения плоскостей (4.23) можно записать в виде

Отсюда следует критерий параллельности или совпадения двух плоскостей (4.23):

Поверхности уровня линейного четырехчлена

Поверхностью уровня функции трех переменных называется геометрическое место точек координатного пространства в которых функция принимает постоянное значение, т.е.

Для линейного четырехчлена уравнение поверхности уровня имеет вид

При любом фиксированном значении постоянной уравнение (4.24) описывает плоскость. Рассмотрим поведение семейства поверхностей уровня, отличающихся значением постоянной. Поскольку коэффициенты и не изменяются, то у всех плоскостей (4.24) будет одна и та же нормаль Следовательно, поверхности уровня линейного четырехчлена D представляют собой семейство параллельных плоскостей (рис.4.19). Поскольку нормаль совпадает с градиентом (см. пункт 3 замечаний 4.2), а градиент направлен в сторону наискорейшего возрастания функции, то при увеличении постоянной поверхности уровня (4.24) переносятся параллельно в направлении нормали.

Пересекающиеся плоскости

Необходимым и достаточным условием пересечения двух плоскостей (4.22) является условие неколлинеарности их нормалей, или, что то же самое, условие непропорциональности коэффициентов при неизвестных:

При этом условии система уравнений

имеет бесконечно много решений, которые определяют прямую пересечения плоскостей, заданных уравнениями (4.23).

Угол между плоскостями

Угол между двумя плоскостями можно определить как угол между их нормальными векторами. По этому определению получаются не один угол, а два смежных угла, дополняющих друг друга до В элементарной геометрии из двух смежных углов, как правило, выбирается меньший, т.е. величина угла между двумя плоскостями удовлетворяет условию

Если — нормали к плоскостям и соответственно (рис.4.20,а), то величина угла между этими плоскостями вычисляется по формуле:

Необходимым и достаточным условием перпендикулярности плоскостей (4.23) является условие ортогональности их нормалей, т.е.

При пересечении двух плоскостей образуются четыре двугранных угла (рис.4.20). Величина двугранного угла удовлетворяет условию

получаем острый двугранный угол , образованный плоскостями (4.23), если 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAAOQAAAAUCAMAAACqG2GmAAAAM1BMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAADbQS4qAAAAEHRSTlMA2+pwDT6+X6AdLK9Qy49/usJWAwAAA2ZJREFUWMPlV9mCpCAMlDPc8P9fuxwRBNF153GHF7ujhlSlkuBx/K7FzYNd/0cgrd/bpf/qgam6LFtoAbTH73QZ5RMJXMvZrKOk1JrDmo9u+PxfJLJ9zqXPIAXQxADAp7DYSbXLpD6KyiYlDg6S2Mkek3XZnbf0kxtHlZcTsT6l7X7kAXy+JVaLboRwmpZblOAesA1m4dsQ0t63Kc7Q2+ss2U+clyjUNXoWaOKbJ2Pcgy+Q1D3rEcG4ZbuAQbOdI6UXXimqkU1k9bfNzY1j/KH+xIVXTnLKNiWjSU6L/goytKB0onyRGWCGzQeQsmMQV1le8nd3AzKsUfJaHPxSIgGyb7HZ3x0kmafmsFp8FYP2ZPEkK0/cUrdveXqWQ6fIXNR6rYGdWp1fYJoGb1SbkUUN9xCEPPbg6011446GvPwqphxftUe+d+Sn6Oy+PbHH3jCCVWaqkQayq0GWEkWVXOYi96bYm9ac+RtIl6wQAjzuJcZ2stilqhYh+CtIupCtNWKfW7bbUC+sHVZAkGdLcVJrHWrXAEXhMviyvdU7sEi7eDSUFWW9uEtJQi9JE7wcScCSpPrggUlixnApi7B60SiHUR78Eo8f3SabRWDEboRhrDSd8imTnMi8SKVKawKj6zR7AZdzCn33B5Bn6yrNlee5PQSosTQhd/Gcq15TbguSX4pe8wRLx+ay9gqza9U6ELfIFVUeGIqthdpBKmitMZQsFK/wKleckmcTHSBxSh6ldUS/zK6bXEeja/LGXVXHxPIPWbgKm3OSu4TTuqvE2XtWzgxS+Ku2Cwv6FSRg1cTGVgeJlGbVypYjot5AhhMNNNIR5JmDrEiOIOAm1cni/ZiphsTpXHeCFIShd4x27ZorSFUFlWu7YekgW6nqmBCMI/wNZD4LiNYQ+BXkmUqHTB3BPjcdJD1LIlBd1ZFq0ZVrbS3kHNypeNXlSlkX9SNIWR/M66QTQSq0J3meV6R+7a4HV/lsrnpWesJioirIcw65CaObxwfSQKIi+/lHYP+JwQ4j3kfIciCU+3NSHv3wCjI/42B8PwxVcgd9/JTNhxsXtqcyA/AwmvcgQTKmxBLKD0ByHxksJxbG3/xsD/XGMxbjT78qwSai7puaVNY/fD6bLFO7YUEVP+q7n1jiuSux1MD+k+a3rj+cGyJvT1X7swAAAABJRU5ErkJggg==» style=»vertical-align: middle;» /> (рис.4.20,а), и тупой в противном случае: (рис.4.20,б). Другими словами, по формуле (4.26) находится тот двугранный угол, образованный плоскостями, в котором лежат точки, принадлежащие разноименным полупространствам, определяемым данными плоскостями. На рис.4.20 изображены пересекающиеся плоскости, положительные и отрицательные полупространства отмечены знаками + или – соответственно.

Пример 4.10. Найти величину того угла, образованного плоскостями и внутри которого лежит точка

Решение. По уравнениям плоскостей находим нормали а также величину угла между нормалями, используя (4.26):

Подставляя координаты точки в левые части уравнений плоскостей, выясняем, каким полупространствам принадлежит эта точка. Для плоскости имеем 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAAN8AAAARBAMAAACvNWTbAAAAMFBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAlTPQ5AAAAEHRSTlMAYP4P3segIFPuP7ONfi1w1Fgf5QAAAqVJREFUOMtjYKA7KAAjCDBGYkMA3wMEm/0BhmZhJFl0uXcYqu3AZOa2nQdgIk1hOwNQlDC6uS6AsblcZ15AM4FRHc60SkGTE02NQBPhcfMBUUlKjnChT0pzDFDUrHzAqgFjlxZw60DtgQlVwi3kmT0FLWjmMQShhchJg0qQ13KWI4R+r0O1j+HSBjYdGPtmA5cSRJoFJrQF4UMGF1Sd/NoMh0DG8zbARJjnMvAqA+l8JFXf0EP9dQPCh5cSGCYtQLGQMQ23hXw7GIJAMcB+FBbPjIoMjCDD8qsQ6eSbFUa6MHKGsewLGCYVoFhYaobbQqCPVMCqma9+hvB5tRg4dIF0aqw3PBxbYrag2VjojZRs+VQZUCzcxYbHQnaRcKjFXy9DohlooRqQTmOw3AASBoktNWCbjqqtZyvYBRAnsc5DsZDxAMRCA6wWMp6Gp1KR4yCSDWohmAXMEQkQZaA0wigIApDY5p4FsgnijJ8LIJKSgoISQJapAdhCqCkQC8E6JSD2JMHTS+thJAsfMLDpAykhkDcfgxIXqoWMKiAL9UBMDj8QaQi2UBDIyl21WgPoBA5tHBY2OcAsXL0dGqS6YPeBLeQDBaumAb82SrhcM+BSAkYiMzgilz7gf4AcpKmhkaoJYCdjCVLedIZFsBju3gXOKIqghAqylFsPlq5UGfh1UBKakgCjJjzJhDOwPkDNh6y4Ew2TIkOTArTMyYOkIl0GXqB6dj+GlxtgqnYwmDqjaAs1YNOFFytTXJwMiLaQNZjh0AVIIj0OKyYYTEA2LcmZBs8WpTmuqNmidE8SvKBNUlJCyxY8kzRhRS+jp9IUAZRcEX1MB5INL8OETONDQTaxdyDsYG5cjJa4F/ZhqWBYiKmFuCTA5vJ+Rgg1LiCzRuOnoDYEAJ1BjPvu16j0AAAAAElFTkSuQmCC» style=»vertical-align: middle;» /> значит, точка лежит в положительном полупространстве, определяемом плоскостью Для плоскости имеем 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAAMYAAAARBAMAAAB0js75AAAALVBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAACttl6nAAAADnRSTlMAYQ6sm+EgQMJ68VMw0spZRHUAAAJySURBVDjLvZXNa9RAGMafzWa/SJBOD3oQlhSsiMqyUAUtKBVq/QDFr9iDCKs9KIJSxc+DotVCW3sI0kK9iEqVirisgngQS0EQW6EsiBcV6bpL17aav8HMTCbZGbrrzRySd57MvL/MM+9MgP9yfQjDHGDJLzcqbVk4qebSmlSFdXn99WAg7Nw05Eg91hwv5yQh9WJiKmhMd6sZU3OKcGnbMJDo034UhLLfPeZH/vfcxWSRRxf4YwQzT0XvM/1VP9ogpBmFkVjCZgt6N9IHhLTjsoi4ZJYRK3Ghiz8mrFQlyBAVjB5hVT9jXAv81IuYbUJ0AZmfQtoFmZFYtPSKxMhPGX/qM1JjjBEZFAavzyKTRbwZmYcB41ROYuAN9AWJ8QlGuT7j4zrulXHHz3OuAytYqnRWDNq99bAlMYDW3xLDm36pPmM46a9Hoo1Xxg2foX2heTUq7aGTkxlpR2HMsh7WcoyUIxgw23rZaI9BJf07bbUzDUk67CUhjwhhpWU+o/fzhAwSspIt62d6jx0KGS2EjBGyyotOI2DA3EJnMukx6EqMMu+20wLu5U5wRjOVzzoKI8qm0fo4ZJxgjNVedOvK9arYPfF9hdArow/3vNZaWg8V6EuSV9o3TMtedUKnem45rwYGhn511CJoUWVuAletwPxICcl5iREt4L7E0B28r7/miM0Jp/gmTnr7w0HiiW0XxfyO0mKrZbTb9nOJ8cC2x//NMPiKe19dxd4ckq7rBrX7rnNcqt2I93K+lqF5QlC7sbx7RGZE84s0l3E7ONNGR9QzLf5W2YPh1dXo6O6RmxfDc9QkVt1Rjiq8asRoafjz+Avab6T1GhuezwAAAABJRU5ErkJggg==» style=»vertical-align: middle;» /> значит, точка лежит также в положительном полупространстве, определяемом плоскостью Поскольку точка принадлежит одноименным полупространствам (положительным), то искомый угол — это угол смежный найденному углу

Пучки плоскостей

Собственным пучком плоскостей называется совокупность всех плоскостей, проходящих через фиксированную прямую ( ось пучка ).

Несобственным пучком плоскостей называется совокупность плоскостей, параллельных фиксированной плоскости (осью несобственного пучка плоскостей считается бесконечно удаленная прямая).

Любые две плоскости и определяют пучок плоскостей, содержащий заданные плоскости и Если плоскости и пересекаются, то прямая пересечения является осью собственного пучка (рис.4.21,а). Если плоскости и параллельны, то они определяют несобственный пучок параллельных плоскостей (рис.4.21,б).

Пусть заданы уравнения двух плоскостей (4.23):

Линейной комбинацией этих уравнений называется уравнение

где числа — коэффициенты линейной комбинации. Его можно записать в форме

Заметим, что линейная комбинация уравнений является уравнением первой степени для любых значений коэффициентов, кроме случая, когда все коэффициенты при неизвестных равны нулю, т.е. при одновременном выполнении условий

Эти значения параметров считаются недопустимыми.

Уравнение (4.27) называется уравнением пучка плоскостей, содержащего плоскости

При любых допустимых значениях параметров уравнение (4.27) задает плоскость, принадлежащую пучку, и наоборот, для любой плоскости пучка найдутся такие значения параметров что уравнение (4.27) будет задавать эту плоскость.

Доказательство утверждения аналогично доказательству свойства пучка прямых.

Пример 4.11. Составить уравнение плоскости, проходящей через прямую пересечения плоскостей и через точку

Решение. Искомая плоскость входит в пучок плоскостей, задаваемый уравнением (4.27)

Подставляя координаты точки получаем:

Возьмем, например, и подставим в уравнение пучка:

Итак, искомое уравнение получено.

Связки плоскостей

Собственной связкой плоскостей называется совокупность всех плоскостей, проходящих через фиксированную точку ( центр связки ).

Несобственной связкой плоскостей называется совокупность плоскостей, параллельных фиксированной прямой (центром несобственной связки плоскостей считается бесконечно удаленная точка).

Уравнение собственной связки плоскостей с центром имеет вид

где — произвольные параметры, одновременно не равные нулю.

Уравнение связки плоскостей (собственной (рис.4.22,а) или несобственной (рис.4.22,6)) можно получить в виде линейной комбинации уравнений трех плоскостей:

где — коэффициенты линейной комбинации. Заметим, что линейная комбинация уравнений является уравнением первой степени для любых значений коэффициентов, кроме случая, когда все коэффициенты при неизвестных равны нулю. Эти значения параметров считаются недопустимыми.

Уравнение (4.28) называется уравнением связки плоскостей, содержащей три плоскости

При любых допустимых значениях параметров уравнение (4.28) задает плоскость, принадлежащую связке, и наоборот, для любой плоскости связки найдутся такие значения параметров что уравнение (4.28) будет задавать эту плоскость.

Доказательство утверждения аналогично доказательству свойства пучка прямых.

Математический портал

Nav view search

Navigation

Search

Взаимное расположение плоскостей, угол между плоскостями.

Литература: Сборник задач по математике. Часть 1. Под ред А. В. Ефимова, Б. П. Демидовича.

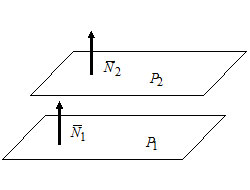
Условие параллельности двух плоскостей:

Пусть $P_1: A_1x+B_1y+C_1z+D_1=0,$ $overline_1=(A_1, B_1, C_1);$

$P_2: A_2x+B_2y+C_2z+D_2=0,$ $overline_2=(A_2, B_2, C_2).$

Плоскости $P_1$ и $P_2$ параллельны тогда и только тогда, когда $overline_1paralleloverline_2Leftrightarrow$ $frac=frac=frac.$

Условия перпендикулярности двух плоскостей:

Пусть $P_1: A_1x+B_1y+C_1z+D_1=0,$ $overline_1=(A_1, B_1, C_1);$

$P_2: A_2x+B_2y+C_2z+D_2=0,$ $overline_2=(A_2, B_2, C_2).$

$P_1perp P_2Leftrightarrow$ $overline_1perpoverline_2Leftrightarrow$ $cdot+cdot+C_1cdot C_2=0.$

Угол между плоскостями:

Пусть $P_1: A_1x+B_1y+C_1z+D_1=0,$ $overline_1=(A_1, B_1, C_1);$

$P_2: A_2x+B_2y+C_2z+D_2=0,$ $overline_2=(A_2, B_2, C_2).$

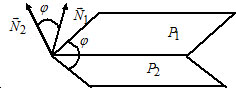
Примеры.

В задачах исследовать взаимное расположение заданных плоскостей. При этом, в случае $P_1parallel P_2$ то найти расстояние между плоскостями, а в случае — косинус угла между ними.

2.185. $P_1: -x+2y-z+1=0;$ $P_2: y+3z-1=0.$

Решение.

Вычислим угол между заданными плоскостями.

$P_1: -x+2y-z+1=0, Rightarrowoverline_1=(-1, 2, -1);$

$P_2: y+3z-1=0, Rightarrowoverline_2=(0, 1, 3).$

Соответственно, плоскости пересекаются и косинус кратчайшего угла между плоскостями

Ответ: Плоскости пересекаются. $coswidehat<(P_1, P_2)>=frac<1><2sqrt<15>>.$

Решение.

Вычислим угол между заданными плоскостями.

$P_1: x-y+1=0, Rightarrowoverline_1=(1, -1, 0);$

$P_2: y-z+1=0, Rightarrowoverline_2=(0, 1, -1).$

Соответственно, плоскости пересекаются и косинус кратчайшего угла между плоскостями

Ответ: Плоскости пересекаются. $coswidehat<(P_1, P_2)>=frac<1><2>.$

2.196. Составить уравнение плоскости $P,$ проходящей через точку $A(1, 1, -1)$ и перпендикулярной к плоскостям $P_1: 2x-y+5z+3=0$ и $P_2: x+3y-z-7=0.$

Решение.

Для того, чтобы плоскость $P$ была перпендикулярно плоскостям $P_1$ и $P_2,$ достаточно, чтобы она была параллельна их нормалям $N_1$ и $N_2.$ Или, что тоже самое, перпендикулярна векторному произведению $[N_1, N_2]$

$P_1: 2x-y+5z+3=0, Rightarrowoverline_1=(2, -1, 5);$

$P_2: x+3y-z-7=0, Rightarrowoverline_2=(1, 3, -1).$

Теперь выпишем уравнение плоскости, проходящей через заданную точку $A(1, 1, -1)$ и перпендикулярной вектору $[N_1, N_2]=(-14, 7, 7):$

Ответ: $-2x+y+z+2=0.$

Домашнее задание.

В задачах исследовать взаимное расположение заданных плоскостей. При этом, в случае $P_1parallel P_2$ то найти расстояние между плоскостями, а в случае — косинус угла между ними.

источники:

http://mathhelpplanet.com/static.php?p=vzaimnoe-raspolozhenie-ploskostyei

http://mathportal.net/index.php/analiticheskaya-geometriya/vzaimnoe-raspolozhenie-ploskostej-ugol-mezhdu-ploskostyami

Источник

Взаимное расположение плоскостей, угол между плоскостями.  

Литература: Сборник задач по математике. Часть 1. Под ред А. В. Ефимова, Б. П. Демидовича.

Условие параллельности двух плоскостей:

Пусть $P_1: A_1x+B_1y+C_1z+D_1=0,$ $overline{N}_1=(A_1, B_1, C_1);$    

          $P_2: A_2x+B_2y+C_2z+D_2=0,$ $overline{N}_2=(A_2, B_2, C_2).$

Плоскости $P_1$ и $P_2$ параллельны тогда и только тогда, когда $overline{N}_1paralleloverline{N}_2Leftrightarrow$ $frac{A_1}{A_2}=frac{B_1}{B_2}=frac{C_1}{C_2}.$

 ploskost-parallel   

Условия перпендикулярности двух плоскостей:  

Пусть $P_1: A_1x+B_1y+C_1z+D_1=0,$ $overline{N}_1=(A_1, B_1, C_1);$          

          $P_2: A_2x+B_2y+C_2z+D_2=0,$ $overline{N}_2=(A_2, B_2, C_2).$  

$P_1perp P_2Leftrightarrow$ $overline{N}_1perpoverline{N}_2Leftrightarrow$ ${A_1}cdot{A_2}+{B_1}cdot{B_2}+C_1cdot C_2=0.$      

ploskost-perpend

Угол между плоскостями:  

Пусть $P_1: A_1x+B_1y+C_1z+D_1=0,$ $overline{N}_1=(A_1, B_1, C_1);$            

          $P_2: A_2x+B_2y+C_2z+D_2=0,$ $overline{N}_2=(A_2, B_2, C_2).$

$coswidehat{(P_1, P_2)}=$ $frac{overline N_1cdot overline N_2}{|overline N_1||overline N_2|}=$ $frac{{A_1}cdot{A_2}+{B_1}cdot{B_2}+C_1cdot C_2}{sqrt{A_1^2+B_1^2+C_1^2}cdotsqrt{A_2^2+B_2^2+C_2^2}}.$    

ploskost-ugol

Примеры.

В задачах исследовать взаимное расположение заданных плоскостей. При этом, в случае $P_1parallel P_2$ то найти расстояние между плоскостями, а в случае – косинус угла между ними. 

2.185. $P_1: -x+2y-z+1=0;$ $P_2: y+3z-1=0.$

Решение.

Вычислим угол между заданными плоскостями.

$P_1: -x+2y-z+1=0, Rightarrowoverline{N}_1=(-1, 2, -1);$

$P_2: y+3z-1=0, Rightarrowoverline{N}_2=(0, 1, 3).$

Отсюда 

$coswidehat{(P_1, P_2)}=$ $frac{overline N_1cdot overline N_2}{|overline N_1||overline N_2|}=$ $frac{-1cdot 0+2cdot1-1cdot 3}{sqrt{(-1)^2+2^2+(-1)^2}cdotsqrt{0^2+1^2+3^2}}=frac{-1}{sqrt{60}}=frac{-1}{2sqrt{15}}.$

Соответственно, плоскости пересекаются и косинус кратчайшего угла между плоскостями

$coswidehat{(P_1, P_2)}=frac{1}{2sqrt{15}}.$

Ответ: Плоскости пересекаются. $coswidehat{(P_1, P_2)}=frac{1}{2sqrt{15}}.$

2.187. $P_1: x-y+1=0;$ $P_2: y-z+1=0.$

Решение.

Вычислим угол между заданными плоскостями.

$P_1: x-y+1=0, Rightarrowoverline{N}_1=(1, -1, 0);$

$P_2: y-z+1=0, Rightarrowoverline{N}_2=(0, 1, -1).$

Отсюда 

$coswidehat{(P_1, P_2)}=$ $frac{overline N_1cdot overline N_2}{|overline N_1||overline N_2|}=$ $frac{1cdot 0+(-1)cdot1+0cdot (-1)}{sqrt{(1)^2+(-1)^2+0^2}cdotsqrt{0^2+1^2+(-1)^2}}=frac{-1}{sqrt{4}}=frac{-1}{2}.$

Соответственно, плоскости пересекаются и косинус кратчайшего угла между плоскостями

$coswidehat{(P_1, P_2)}=frac{1}{2}.$

Ответ: Плоскости пересекаются. $coswidehat{(P_1, P_2)}=frac{1}{2}.$

2.196. Составить уравнение плоскости $P,$ проходящей через точку $A(1, 1, -1)$ и перпендикулярной к плоскостям $P_1: 2x-y+5z+3=0$ и $P_2: x+3y-z-7=0.$

Решение.

Для того, чтобы плоскость $P$ была перпендикулярно плоскостям $P_1$ и $P_2,$ достаточно, чтобы она была параллельна их нормалям $N_1$ и $N_2.$ Или, что тоже самое, перпендикулярна векторному произведению $[N_1, N_2]$

$P_1: 2x-y+5z+3=0, Rightarrowoverline{N}_1=(2, -1, 5);$

$P_2: x+3y-z-7=0, Rightarrowoverline{N}_2=(1, 3, -1).$

$[N_1, N_2]=begin{vmatrix}i&j&k\2&-1&5\1&3&-1end{vmatrix}=i(1-15)-j(-2-5)+k(6+1)=$ $=-14i+7j+7k.$

Теперь выпишем уравнение плоскости, проходящей через заданную точку $A(1, 1, -1)$  и перпендикулярной вектору $[N_1, N_2]=(-14, 7, 7):$

$-14(x-1)+7(y-1)+7(z+1)=0  |:7$

$-2(x-1)+y-1+z+1=0$

$-2x+y+z+2=0.$

Ответ: $-2x+y+z+2=0.$

Домашнее задание.

В задачах исследовать взаимное расположение заданных плоскостей. При этом, в случае $P_1parallel P_2$ то найти расстояние между плоскостями, а в случае – косинус угла между ними. 

2.186. $P_1: 2x-y+z-1=0;$ $P_2: -4x+2y-2z-1=0.$

2.188. $P_1: 2x-y-z+1=0;$ $P_2: -4x+2y+2z-2=0.$

Источник

Данный калькулятор предназначен для определения взаимного расположения двух плоскостей в пространстве онлайн.

Две плоскости могут иметь три варианта взаимного расположения относительно друг друга. Во-первых, плоскости могут быть параллельны. Во-вторых, они могут быть перпендикулярны. В таком случае угол между плоскостями равен 90 градусам. В-третьих, плоскости могут пересекаться, образовывая при этом два острых и два тупых угла.

Таким образом, с помощью данного калькулятора определяется следующее: пересекаются или нет плоскости, и, если они пересекаются, то перпендикулярны ли они.

Чтобы ответить на вопрос о взаимном расположении плоскостей, необходимо ввести уравнения заданных плоскостей в калькулятор и нажать кнопку «Вычислить».

×

Пожалуйста напишите с чем связна такая низкая оценка:

×

Для установки калькулятора на iPhone – просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android – просто добавьте страницу
«На главный экран»

Источник

Добавить комментарий