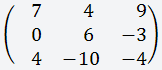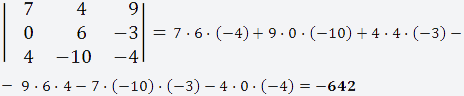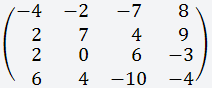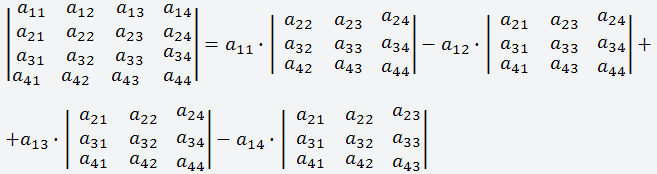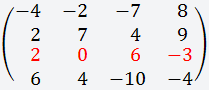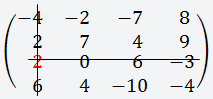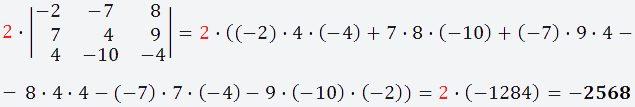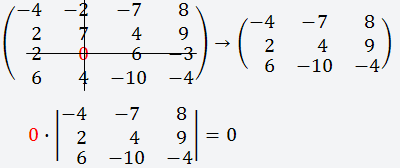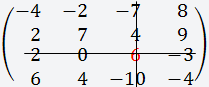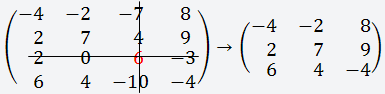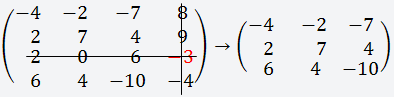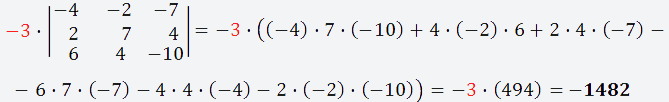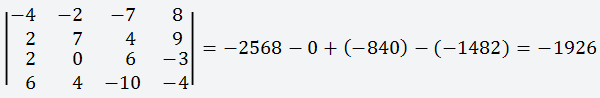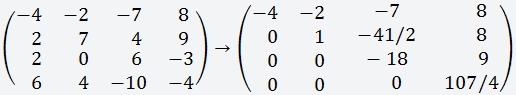Определитель матрицы 2х3 как найти - Сайт, где вы сможете решить свои вопросы

Уважаемые студенты!
Заказать решение задач можно у нас всего за 10 минут.

Определитель матрицы

Пусть задана матрица второго порядка $ A = begin{pmatrix} a_{11}&a_{12}\a_{21}&a_{22} end{pmatrix} $. Тогда её определитель находится по формуле:

$$ Delta = begin{vmatrix} a_{11}&a_{12}\a_{21}&a_{22} end{vmatrix} = a_{11}cdot a_{22} – a_{12}cdot a_{21} $$

Из произведения элементов, стоящих на главной диагонали $ a_{11}cdot a_{22} $, вычитается произведение элементов, расположенных на побочной диагонали $ a_{12}cdot a_{21} $. Это правило верно только (!) для определителя 2-го порядка.

Если дана матрица третьего порядка $ A = begin{pmatrix} a_{11}&a_{12}&a_{13}\a_{21}&a_{22}&a_{23}\a_{31}&a_{32}&a_{33} end{pmatrix} $, то вычислить её определитель следует по формуле:

$$ Delta = begin{vmatrix} a_{11}&a_{12}&a_{13}\a_{21}&a_{22}&a_{23}\a_{31}&a_{32}&a_{33} end{vmatrix} = $$

$$ = a_{11}a_{22}a_{33} + a_{12}a_{23}a_{31}+a_{21}a_{32}a_{13} – a_{13}a_{22}a_{31}-a_{23}a_{32}a_{11}-a_{12}a_{21}a_{33} $$

Пример 1

Найти определитель матрицы $ A = begin{pmatrix} 1&2\3&4 end{pmatrix} $

Решение

Обратим внимание на то что матрица квадратная второго порядка, то есть количество столбцов равно количеству строк и они содержат по 2 элемента. Поэтому применим первую формулу. Перемножим элементы, стоящие на главной диагонали и вычтем из них произведение элементов, стоящих на побочной диагонали:

$$ Delta = begin{vmatrix} 1&2\3&4 end{vmatrix} = 1 cdot 4 – 2 cdot 3 = 4-6 = -2 $$

Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!

Ответ

$$ Delta = -2 $$

Пример 2

Вычислить определитель $ A = begin{pmatrix} 2&2&1\1&-3&-1\3&4&-2 end{pmatrix} $

Решение

Так как в задаче квадратная матрица 3-го порядка, то найти определитель матрицы следует по второй формуле. Для простоты решения задачи достаточно подставить вместо $ a_{ij} $ переменных, стоящих в формуле значения из матрицы нашей задачи:

$$ Delta = begin{vmatrix} 2&2&1\1&-3&-1\3&4&-2 end{vmatrix} = $$

$$ = 2cdot (-3) cdot (-2) + 2cdot (-1) cdot 3 + 1cdot 4cdot 1 – $$ $$ – 1cdot (-3)cdot 3 – (-1)cdot 4cdot 2 – 2cdot 1cdot (-2) = $$

$$ = 12 – 6 + 4 + 9 + 8 + 4 = 31 $$

Стоит отметить когда мы находим произведения элементов на побочной диагонали и подобных её, то перед произведениями ставится знак минус.

Ответ

$$ Delta = 31 $$

Пример 3

Найти определитель матрицы $ A = begin{pmatrix} 1&3&-2\-2&4&1 end{pmatrix} $

Решение

Замечаем сразу, что количество строк не равно количеству столбцов, поэтому матрица не является квадратной. Так как определить существует только у квадратных матриц, то задача не имеет решения.

Ответ

Невозможно посчитать определитель

Источник

Содержание:

Вычисления определителей второго порядка
Методы вычисления определителей третьего порядка
Приведение определителя к треугольному виду
Правило треугольника
Правило Саррюса
Разложение определителя по строке или столбцу
Разложение определителя по элементам строки или столбца
Теорема Лапласа

В общем случае правило вычисления определителей
$n$-го порядка
является довольно громоздким. Для определителей второго и третьего порядка существуют рациональные способы их вычислений.

Вычисления определителей второго порядка

Чтобы вычислить определитель матрицы второго порядка, надо от произведения
элементов главной диагонали отнять произведение
элементов побочной диагонали:

$$left| begin{array}{ll}{a_{11}} & {a_{12}} \ {a_{21}} & {a_{22}}end{array}right|=a_{11} cdot a_{22}-a_{12} cdot a_{21}$$

Пример

Задание. Вычислить определитель второго порядка
$left| begin{array}{rr}{11} & {-2} \ {7} & {5}end{array}right|$

Решение. $left| begin{array}{rr}{11} & {-2} \ {7} & {5}end{array}right|=11 cdot 5-(-2) cdot 7=55+14=69$

Ответ. $left| begin{array}{rr}{11} & {-2} \ {7} & {5}end{array}right|=69$

Методы вычисления определителей третьего порядка

Для вычисления определителей третьего порядка существует такие правила.

Правило треугольника

Схематически это правило можно изобразить следующим образом:

Произведение элементов в первом определителе, которые соединены прямыми,
берется со знаком “плюс”; аналогично, для второго определителя – соответствующие произведения берутся со знаком “минус”, т.е.

$$left| begin{array}{ccc}{a_{11}} & {a_{12}} & {a_{13}} \ {a_{21}} & {a_{22}} & {a_{23}} \ {a_{31}} & {a_{32}} & {a_{33}}end{array}right|=a_{11} a_{22} a_{33}+a_{12} a_{23} a_{31}+a_{13} a_{21} a_{32}-$$

$$-a_{11} a_{23} a_{32}-a_{12} a_{21} a_{33}-a_{13} a_{22} a_{31}$$

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Пример

Задание. Вычислить определитель $left| begin{array}{rrr}{3} & {3} & {-1} \ {4} & {1} & {3} \ {1} & {-2} & {-2}end{array}right|$ методом треугольников.

Решение. $left| begin{array}{rrr}{3} & {3} & {-1} \ {4} & {1} & {3} \ {1} & {-2} & {-2}end{array}right|=3 cdot 1 cdot(-2)+4 cdot(-2) cdot(-1)+$

$$+3 cdot 3 cdot 1-(-1) cdot 1 cdot 1-3 cdot(-2) cdot 3-4 cdot 3 cdot(-2)=54$$

Ответ. $left| begin{array}{rrr}{3} & {3} & {-1} \ {4} & {1} & {3} \ {1} & {-2} & {-2}end{array}right|=54$

Правило Саррюса

Справа от определителя дописывают первых два столбца и произведения элементов на главной диагонали и на диагоналях, ей
параллельных, берут со знаком “плюс”; а произведения элементов побочной диагонали и диагоналей, ей параллельных,
со знаком “минус”:

$$-a_{13} a_{22} a_{31}-a_{11} a_{23} a_{32}-a_{12} a_{21} a_{33}$$

Пример

Задание. Вычислить определитель $left| begin{array}{rrr}{3} & {3} & {-1} \ {4} & {1} & {3} \ {1} & {-2} & {-2}end{array}right|$ с помощью правила Саррюса.

Решение.

$$+(-1) cdot 4 cdot(-2)-(-1) cdot 1 cdot 1-3 cdot 3 cdot(-2)-3 cdot 4 cdot(-2)=54$$

Ответ. $left| begin{array}{rrr}{3} & {3} & {-1} \ {4} & {1} & {3} \ {1} & {-2} & {-2}end{array}right|=54$

Разложение определителя по строке или столбцу

Определитель равен сумме произведений элементов строки определителя на их
алгебраические дополнения. Обычно выбирают
ту строку/столбец, в которой/ом есть нули. Строку или столбец, по которой/ому ведется разложение, будет обозначать стрелкой.

Пример

Задание. Разложив по первой строке, вычислить определитель $left| begin{array}{lll}{1} & {2} & {3} \ {4} & {5} & {6} \ {7} & {8} & {9}end{array}right|$

Решение. $left| begin{array}{lll}{1} & {2} & {3} \ {4} & {5} & {6} \ {7} & {8} & {9}end{array}right| leftarrow=a_{11} cdot A_{11}+a_{12} cdot A_{12}+a_{13} cdot A_{13}=$

$1 cdot(-1)^{1+1} cdot left| begin{array}{cc}{5} & {6} \ {8} & {9}end{array}right|+2 cdot(-1)^{1+2} cdot left| begin{array}{cc}{4} & {6} \ {7} & {9}end{array}right|+3 cdot(-1)^{1+3} cdot left| begin{array}{cc}{4} & {5} \ {7} & {8}end{array}right|=-3+12-9=0$

Ответ. $left| begin{array}{lll}{1} & {2} & {3} \ {4} & {5} & {6} \ {7} & {8} & {9}end{array}right|=0$

Этот метод позволяет вычисление определителя свести к вычислению определителя более низкого порядка.

Пример

Задание. Вычислить определитель $left| begin{array}{lll}{1} & {2} & {3} \ {4} & {5} & {6} \ {7} & {8} & {9}end{array}right|$

Решение. Выполним следующие
преобразования над строками определителя: из второй строки отнимем четыре
первых, а из третьей первую строку, умноженную на семь, в результате, согласно свойствам определителя, получим определитель,
равный данному.

$$left| begin{array}{ccc}{1} & {2} & {3} \ {4} & {5} & {6} \ {7} & {8} & {9}end{array}right|=left| begin{array}{ccc}{1} & {2} & {3} \ {4-4 cdot 1} & {5-4 cdot 2} & {6-4 cdot 3} \ {7-7 cdot 1} & {8-7 cdot 2} & {9-7 cdot 3}end{array}right|=$$

$$=left| begin{array}{rrr}{1} & {2} & {3} \ {0} & {-3} & {-6} \ {0} & {-6} & {-12}end{array}right|=left| begin{array}{ccc}{1} & {2} & {3} \ {0} & {-3} & {-6} \ {0} & {2 cdot(-3)} & {2 cdot(-6)}end{array}right|=0$$

Определитель равен нулю, так как вторая и третья строки являются пропорциональными.

Ответ. $left| begin{array}{lll}{1} & {2} & {3} \ {4} & {5} & {6} \ {7} & {8} & {9}end{array}right|=0$

Для вычисления определителей четвертого порядка и выше применяется либо разложение по строке/столбцу, либо приведение
к треугольному виду, либо с помощью теоремы Лапласа.

Разложение определителя по элементам строки или столбца

Пример

Задание. Вычислить определитель
$left| begin{array}{llll}{9} & {8} & {7} & {6} \ {5} & {4} & {3} & {2} \ {1} & {0} & {1} & {2} \ {3} & {4} & {5} & {6}end{array}right|$ , разложив его по элементам какой-то строки или какого-то столбца.

Решение. Предварительно выполним
элементарные преобразования над строками определителя, сделав
как можно больше нулей либо в строке, либо в столбце. Для этого вначале от первой строки отнимем девять третьих,
от второй – пять третьих и от четвертой – три третьих строки, получаем:

$$left| begin{array}{cccc}{9} & {8} & {7} & {6} \ {5} & {4} & {3} & {2} \ {1} & {0} & {1} & {2} \ {3} & {4} & {5} & {6}end{array}right|=left| begin{array}{cccc}{9-1} & {8-0} & {7-9} & {6-18} \ {5-5} & {4-0} & {3-5} & {2-10} \ {1} & {0} & {1} & {2} \ {0} & {4} & {2} & {0}end{array}right|=left| begin{array}{rrrr}{0} & {8} & {-2} & {-12} \ {0} & {4} & {-2} & {-8} \ {1} & {0} & {1} & {2} \ {0} & {4} & {2} & {0}end{array}right|$$

Полученный определитель разложим по элементам первого столбца:

$$left| begin{array}{rrrr}{0} & {8} & {-2} & {-12} \ {0} & {4} & {-2} & {-8} \ {1} & {0} & {1} & {2} \ {0} & {4} & {2} & {0}end{array}right|=0+0+1 cdot(-1)^{3+1} cdot left| begin{array}{rrr}{8} & {-2} & {-12} \ {4} & {-2} & {-8} \ {4} & {2} & {0}end{array}right|+0$$

Полученный определитель третьего порядка также разложим по элементам строки и столбца, предварительно получив нули,
например, в первом столбце. Для этого от первой строки отнимаем две вторые строки, а от третьей – вторую:

$$left| begin{array}{rrr}{8} & {-2} & {-12} \ {4} & {-2} & {-8} \ {4} & {2} & {0}end{array}right|=left| begin{array}{rrr}{0} & {2} & {4} \ {4} & {-2} & {-8} \ {0} & {4} & {8}end{array}right|=4 cdot(-1)^{2+2} cdot left| begin{array}{ll}{2} & {4} \ {4} & {8}end{array}right|=$$

$$=4 cdot(2 cdot 8-4 cdot 4)=0$$

Ответ. $left| begin{array}{cccc}{9} & {8} & {7} & {6} \ {5} & {4} & {3} & {2} \ {1} & {0} & {1} & {2} \ {3} & {4} & {5} & {6}end{array}right|=0$

Замечание

Последний и предпоследний определители можно было бы и не вычислять,
а сразу сделать вывод о том, что они равны нулю, так как содержат пропорциональные строки.

Приведение определителя к треугольному виду

С помощью элементарных преобразований над строками или столбцами определитель приводится к треугольному виду и тогда его
значение, согласно свойствам определителя, равно произведению
элементов стоящих на главной диагонали.

Пример

Задание. Вычислить определитель
$Delta=left| begin{array}{rrrr}{-2} & {1} & {3} & {2} \ {3} & {0} & {-1} & {2} \ {-5} & {2} & {3} & {0} \ {4} & {-1} & {2} & {-3}end{array}right|$ приведением его к треугольному виду.

Решение. Сначала делаем нули в первом столбце под главной диагональю. Все преобразования
будет выполнять проще, если элемент $a_{11}$ будет
равен 1. Для этого мы поменяем местами первый и второй столбцы определителя, что, согласно свойствам определителя,
приведет к тому, что он сменит знак на противоположный:

$$Delta=left| begin{array}{rrrr}{-2} & {1} & {3} & {2} \ {3} & {0} & {-1} & {2} \ {-5} & {2} & {3} & {0} \ {4} & {-1} & {2} & {-3}end{array}right|=-left| begin{array}{rrrr}{1} & {-2} & {3} & {2} \ {0} & {3} & {-1} & {2} \ {2} & {-5} & {3} & {0} \ {-1} & {4} & {2} & {-3}end{array}right|$$

Далее получим нули в первом столбце, кроме элемента $a_{11}$ ,
для этого из третьей строки вычтем две первых, а к четвертой строке прибавим первую, будем иметь:

$$Delta=-left| begin{array}{rrrr}{1} & {-2} & {3} & {2} \ {0} & {3} & {-1} & {2} \ {0} & {-1} & {-3} & {-4} \ {0} & {2} & {5} & {-1}end{array}right|$$

Далее получаем нули во втором столбце на месте элементов, стоящих под главной диагональю. И снова, если
диагональный элемент будет равен $pm 1$ , то
вычисления будут более простыми. Для этого меняем местами вторую и третью строки (и при этом меняется на
противоположный знак определителя):

$$Delta=left| begin{array}{rrrr}{1} & {-2} & {3} & {2} \ {0} & {-1} & {-3} & {-4} \ {0} & {3} & {-1} & {2} \ {0} & {2} & {5} & {-1}end{array}right|$$

Далее делаем нули во втором столбце под главной диагональю, для этого поступаем следующим образом:
к третьей строке прибавляем три вторых, а к четвертой – две вторых строки, получаем:

$$Delta=left| begin{array}{rrrr}{1} & {-2} & {3} & {2} \ {0} & {-1} & {-3} & {-4} \ {0} & {0} & {-10} & {-10} \ {0} & {0} & {-1} & {-9}end{array}right|$$

Далее из третьей строки выносим (-10) за определитель и делаем нули в третьем столбце под
главной диагональю, а для этого к последней строке прибавляем третью:

$$Delta=-10 left| begin{array}{rrrr}{1} & {-2} & {3} & {2} \ {0} & {-1} & {-3} & {-4} \ {0} & {0} & {1} & {1} \ {0} & {0} & {-1} & {-9}end{array}right|=$$

$$=-10 cdot left| begin{array}{cccc}{1} & {-2} & {3} & {2} \ {0} & {-1} & {-3} & {-4} \ {0} & {0} & {1} & {1} \ {0} & {0} & {0} & {-8}end{array}right|=(-10) cdot 1 cdot(-1) cdot 1 cdot(-8)=-80$$

Ответ. $Delta=-80$

Теорема Лапласа

Теорема

Пусть $Delta$ – определитель
$n$-го порядка. Выберем в нем произвольные
$k$ строк (или столбцов), причем
$k leq n-1$ . Тогда сумма произведений всех
миноров
$k$-го порядка, которые содержатся в выбранных
$k$ строках (столбцах), на их
алгебраические дополнения равна определителю.

Пример

Задание. Используя теорему Лапласа, вычислить определитель
$left| begin{array}{rrrrr}{2} & {3} & {0} & {4} & {5} \ {0} & {1} & {0} & {-1} & {2} \ {3} & {2} & {1} & {0} & {1} \ {0} & {4} & {0} & {-5} & {0} \ {1} & {1} & {2} & {-2} & {1}end{array}right|$

Решение. Выберем в данном определителе пятого порядка две строки –
вторую и третью, тогда получаем (слагаемые, которые равны нулю, опускаем):

$$left| begin{array}{rrrrr}{2} & {3} & {0} & {4} & {5} \ {0} & {1} & {0} & {-1} & {2} \ {3} & {2} & {1} & {0} & {1} \ {0} & {4} & {0} & {-5} & {0} \ {1} & {1} & {2} & {-2} & {1}end{array}right|=left| begin{array}{cc}{1} & {-1} \ {4} & {-5}end{array}right| cdot(-1)^{2+4+2+4} cdot left| begin{array}{ccc}{2} & {0} & {5} \ {3} & {1} & {1} \ {1} & {2} & {1}end{array}right|+$$

$$+left| begin{array}{ll}{1} & {2} \ {4} & {0}end{array}right| cdot(-1)^{2+4+2+5} cdot left| begin{array}{rrr}{2} & {0} & {4} \ {3} & {1} & {0} \ {1} & {2} & {-2}end{array}right|+left| begin{array}{cc}{-1} & {2} \ {-5} & {0}end{array}right| cdot(-1)^{2+4+5} cdot left| begin{array}{ccc}{2} & {3} & {0} \ {3} & {2} & {1} \ {1} & {1} & {2}end{array}right|=$$

$$=-23+128+90=195$$

Ответ. $left| begin{array}{rrrrr}{2} & {3} & {0} & {4} & {5} \ {0} & {1} & {0} & {-1} & {2} \ {3} & {2} & {1} & {0} & {1} \ {0} & {4} & {0} & {-5} & {0} \ {1} & {1} & {2} & {-2} & {1}end{array}right|=195$

Читать дальше: обратная матрица.

Источник

Пример вычисления
определителя (детерминанта) матрицы

Определитель матрицы — является
многочленом от элементов квадратной
матрицы (если элементы матрицы это
числа, тогда определитель матрицы тоже
будет числом).

Для нахождения определителя матрицы,
исходная матрица должна быть квадратной.

Пример №1

Дана матрица размером 2х2;

Что бы вычислить определитель матрицы
2х2 нужно из произведения элементов
главной диагонали, вычесть произведение
элементов побочной диагонали;

Ответ: -6

Пример №2

Дана матрица размером 3х3;

Что бы вычислить определитель матрицы
3х3 нужно воспользоваться формулой;

Подставляем наши значения в формулу;

Пример №3

Дана матрица размером 4х4;

Есть два способа вычисления определителя
матрицы:

По определению – через разложение
по строке или столбцу;
По методу Гаусса – приведение матрицы
к треугольному виду (этот способ лучше
использовать для решения матриц,
размером 4х4 и более).

Решим пример первым
способом (по определению – через
разложение по строке или столбцу)

Чтобы вычислить определитель матрицы,
нужно воспользоваться следующей
формулой, в ней рассмотрен пример
разложения матрицы по первой строке;

Итак, начнём

Выбираем строку или столбец (любую),
лучше всего выбирать строку или столбец,
где больше нулей, для удобства
вычисления;
В данном случае мы выбираем
третью строку, так как в ней присутствует
ноль;

Берём первый элемент этой строки
(2);
Теперь вычёркиваем
третью строку и первый столбец;

Получаем матрицу 3х3;

Согласно формуле, мы умножаем выбранный
нами элемент на определитель получившейся
матрицы;

Вычисление определителя матрицы 3х3,
мы рассматривали в примере №2

Далее делаем всё тоже самое, что и в
шаге два, только берём второй элемент
данной строки (0) и
вычёркиваем третью строку и второй
столбец;

Так как этот элемент равен нулю, то ни
чего не нужно считать и так всё ясно;

Теперь берём третий элемент строки (6)
и вычёркиваем третью строку и третий
столбец;

Получаем матрицу 3х3;

Вычисляем определитель этой матрицы и
умножаем на выбранный нами элемент (6)

Берём четвёртый элемент строки (-3)
и вычёркиваем третью строку и четвёртый
столбец;

Получаем матрицу 3х3;

Вычисляем определитель этой матрицы и
умножаем на выбранный нами элемент (-3)

Чтобы вычислить определитель исходной
матрицы, нужно сложить полученные
результаты;

Ответ: -1926

Опишем решение примера
вторым способом (по методу Гаусса
– приведение матрицы к треугольному
виду)

Суть способа заключается в том, чтобы
перед вычислением определителя, привести
матрицу к треугольному виду. Если в ходе
приведения матрицы к треугольному виду
вы умножаете (делите) строку на число,
то на это же число нужно будет умножить
(разделить) полученный в конце определитель;

Пример приведения матрицы к треугольному
виду мы уже рассматривали здесь

Итак, мы привили матрицу к треугольному
виду;

Теперь чтобы вычислить определитель
приведённой матрицы, нужно перемножить
все элементы, стоящие на главной
диагонали;

Ответ: -1926

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Найти определитель (детерминант) матрицы онлайн

На данной странице калькулятор поможет найти определитель матрицы онлайн с подробным решением. При решении можно выбрать правило треугольника, правило Саррюса. Разложение определителя по строке или столбцу. Приведение определителя к треугольному виду. Для расчета задайте целые или десятичные числа.

Определитель матрицы

Размерность матрицы:

Павило:

A

Другой материал по теме

Свойства определителя матрицы с примерами
Определитель матрицы второго порядка
Определитель матрицы методом треугольника
Определитеть матрицы методом Саррюса
Разложить определитель по строке или столбцу
Приведение определителя матрицы к треугольному виду

Источник

Найти определитель матрицы: онлайн калькулятор

Матрица представляет математический объект, который записан в виде таблицы элементов. Ее размер задается количеством столбцов и строк. В квадратной матрице число столбцов и строк одинаковое.

Чтобы найти определитель матрицы онлайн с помощью нашего сервиса, выберите необходимое число столбцов и строк. Затем введите значения в предназначенные для этого пустые поля и запустите расчет. Ответом будет найденный определитель (детерминант) – величина, которая может быть рассчитана и поставлена в однозначное соответствие квадратной матрице.

Определитель матрицы онлайн

Вычислить определитель матрицы онлайн понадобится студентам при решении задач по алгебре и высшей математике, научным сотрудникам для проверки правильности вычислений и сведения погрешностей к минимуму.

На нашем сайте вы можете посчитать определитель матрицы онлайн бесплатно. Выбор встроенного алгоритма вычислений связан с размером матрицы:

Для матриц порядка n=2 детерминант находится по формуле: Δ=a₁₁*a₂₂-a₁₂*a₂₁.
Для матриц порядка n=3 детерминант находится с помощью алгебраического дополнения или методом Саррюса.
При размерности матрицы больше трех она раскладывается на алгебраические дополнения, для которых рассчитываются свои детерминанты (миноры).

Вы сможете найти определитель матрицы с онлайн-калькулятором, что позволит проводить дальнейшие расчеты без ошибок и погрешностей. Это важно учитывать при разработке инструментов статистики в науке и технике, где точность вычислений имеет большое значение. Часто искомое значение определителя требуется как промежуточный результат для решения комплекса задач. В таком случае использование онлайн-калькулятора необходимо для экономии времени.

С помощью нашего сервиса легко осуществлять подготовку к занятиям. Самостоятельно искать решение и сверятся с полученным детерминантом матрицы онлайн.

Источник