Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 19 сентября 2015 года; проверки требуют 5 правок.
Оптическая длина пути между двумя точками среды — расстояние, на которое свет (оптическое излучение) распространился бы в вакууме за время его прохождения между этими точками[1].
Оптическая длина пути 
в однородной среде с показателем преломления 
равна произведению геометрической длины пути 
, пройденного светом, на показатель преломления :
В случае неоднородной среды путь, пройденный светом, необходимо предварительно разбить на столь малые элементарные промежутки 
, что показатель преломления на каждом из них можно считать постоянным. Тогда для оптической длины пути каждого из них можно записать
Соответственно, полная оптическая длина пути, пройденного светом между некоторыми точками А и В среды, будет результатом интегрирования по всей траектории луча света:
Оптическая разность хода[править | править код]
Если два световых луча имеют общие начальную и конечные точки, то разность оптических длин путей таких лучей называют оптической разностью хода[2][3].
Примечания[править | править код]
- ↑ Оптическая длина пути // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Большая Российская энциклопедия, 1992. — Т. 3. — С. 431. — 672 с. — 48 000 экз. — ISBN 5-85270-019-3.
- ↑ Сивухин Д. В. Общий курс физики. — 3-е изд., стереот. — М.: Физматлит, МФТИ, 2005. — Т. IV. Оптика. — С. 205. — 792 с. — ISBN 5-9221-0228-1.
- ↑ ГОСТ 7601-78. Физическая оптика. Термины, буквенные обозначения и определения основных величин. Дата обращения: 19 сентября 2015. Архивировано 30 ноября 2021 года.
Оптическая длина пути.
ОПТИЧЕСКАЯ ДЛИНАПУТИ -произведениедлины пути светового луча напоказатель
преломлениясреды (путь,
который прошел бысветза то жевремя,
распространяясь в вакууме).
Расчет интерференционной картины от двух источников.
Расчет интерференционной картины от
двух когерентных источников.
Рассмотрим две когерентные световые
волны, исходящие из источников
и
(рис.1.11.).
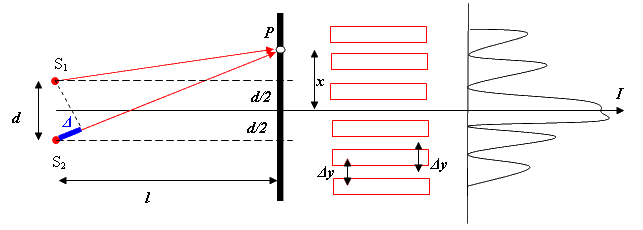
Рис. 1.11.
Экран для наблюдения интерференционной
картины (чередование светлых и темных
полос) поместим параллельно обеим щелям
на одинаковом расстоянии
.Обозначим
за x – расстояние от центра интерференционной
картины до исследуемой точки Р на
экране.
Расстояние между источниками
и
обозначим
какd. Источники
и
расположены
симметрично относительно центра
интерференционной картины. Из рисунка
видно, что
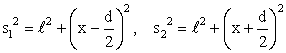
Следовательно
и оптическая разность хода равна
Разность хода
составляет
несколько длин волн и всегда значительно
меньше
и
,
поэтому можем считать, что
и
.
Тогда выражение для оптической разности
хода будет иметь следующий вид:
, (1.94)
Так как расстояние от источников до
экрана во много раз превосходит
расстояние от центра интерференционной
картины до точки наблюдения
,
то можно допустить, что
т.
е.
, (1.95)
Подставив значение
(1.95)
в условие (1.92) и выразив х, получим, что
максимумы интенсивности будут наблюдаться
при значениях
, (1.96)
где
–
длина волны в среде, аm– порядок
интерференции, ахmax –
координаты максимумов интенсивности.
Подставив (1.95) в условие (1.93), получим
координаты минимумов интенсивности
, (1.97)
На экране будет видна интерференционная
картина, которая имеет вид чередующихся
светлых и темных полос. Цвет светлых
полос определяется светофильтром,
используемым в установке.
Расстояние между соседними минимумами
(или максимумами) называется шириной
интерференционной полосы. Из (1.96) и
(1.97) следует, что эти расстояния имеют
одинаковое значение. Чтобы рассчитать
ширину интерференционной полосы, нужно
из значения координаты одного максимума
вычесть координату соседнего максимума
, (1.98)
Для этих целей можно использовать и
значения координат двух любых соседних
минимумов.
Координаты минимумов и максимумов интенсивности.
Оптическая длина путей лучей. Условия
получения интерференционных максимумов
и минимумов.
В вакууме скорость света равна
,
в среде с показателем преломления n
скорость света v становится меньше и
определяется соотношением (1.52)
Длина волны в вакууме
,
а в среде – в n раз меньше чем в вакууме
(1.54):
При переходе из одной среды в другую
частота света не изменяется, так как
вторичные электромагнитные волны,
излучаемые заряженными частицами в
среде, есть результат вынужденных
колебаний, совершающихся с частотой
падающей волны.
Пусть два точечных когерентных источника
света
и
излучают
монохроматический свет (рис.1.11). Для
них должны выполнятся условия
когерентности:
.
До точки P первый луч проходит в среде
с показателем преломления
путь
,
второй луч проходит в среде с показателем
преломления
–
путь
.
Расстояния
и
от
источников до наблюдаемой точки
называются геометрические длины путей
лучей. Произведение показателя
преломления среды на геометрическую
длину пути называется оптической длиной
пути L=ns. L1 = 
и
L1 = 
–
оптические длины первого и второго
путей, соответственно.
Пусть
и
–
фазовые скорости волн.
Первый луч возбудит в точке P колебание:
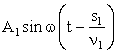, (1.87)
а второй луч – колебание
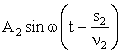, (1.88)
Разность фаз колебаний, возбуждаемых
лучами в точке P, будет равна:
, (1.89)
Множитель
равен
(
–
длина волны в вакууме), и выражению для
разности фаз можно придать вид
, (1.90)
где
, (1.91)
есть величина, называемая оптической
разностью хода. При расчете интерференционных
картин следует учитывать именно
оптическую разность хода лучей, т. е.
показатели преломления сред, в которых
лучи распространяются.
Из формулы (1.90) видно, что если оптическая
разность хода равна целому числу длин
волн в вакууме
, (1.92)
то разность фаз
и
колебания будут происходить с одинаковой
фазой. Числоmназывается порядком
интерференции. Следовательно, условие
(1.92) есть условие интерференционного
максимума.
Если
равна
полуцелому числу длин волн в вакууме,
, (1.93)
то
,
так что колебания в точке P находятся
в противофазе. Условие (1.93) – условие
интерференционного минимума.
Итак, если на длине равной оптической
разности хода лучей
,
укладывается четное число длин полуволн,
то в данной точке экрана наблюдается
максимум интенсивности. Если на длине
оптической разности хода лучей
укладывается
нечетное число длин полуволн, то в
данной точки экрана наблюдается минимум
освещенности.
Напомним, что если два пути лучей
оптически эквивалентны, они называются
таутохронными. Оптические системы –
линзы, зеркала – удовлетворяют условию
таутохронизма.
Соседние файлы в предмете Физика
- #
- #
- #
- #
- #
- #
- #
- #
- #
From Wikipedia, the free encyclopedia
The figure shows the optical path of a Mirau-objective respectively a Mirau-interferometer. Reference beam (4 to 6) and object beam (7) have identical optical path length and can thus cause white light interference.
Optical path (OP) is the trajectory that a light ray follows as it propagates through an optical medium.
The geometrical optical-path length or simply geometrical path length (GPD) is the length of a segment in a given OP, i.e., the Euclidean distance integrated along a ray between any two points.[1]
The mechanical length of an optical device can be reduced to less than the GPD by using folded optics.
The optical path length in a homogeneous medium is the GPD multiplied by the refractive index of the medium.
Factors affecting optical path[edit]
Path of light in medium, or between two media is affected by the following:
- Reflection
- Total internal reflection
- Refraction
- Dispersion of light
- Absorption
Simple materials used[edit]
- Lenses
- Prisms
- Mirrors
- Transparent materials (e.g. optical filters)
- Translucent materials (e.g. frosted glass)
- Opaque materials
References[edit]
- ^ Bass, M.; DeCusatis, C.; Enoch, J.M.; Lakshminarayanan, V.; Li, G.; MacDonald, C.; Mahajan, V.N.; Van Stryland, E. (2009). Handbook of Optics, Third Edition Volume I: Geometrical and Physical Optics, Polarized Light, Components and Instruments(set). Handbook of Optics. McGraw-Hill Education. ISBN 978-0-07-162925-6. Retrieved 2021-10-11.
