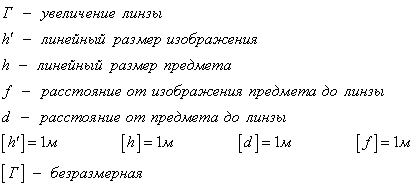Мы уже познакомились с явлением преломления света на границе двух плоских сред. Но на практике особый интерес представляет явление преломления света на сферических поверхностях линз.
Определение
Линза — прозрачное тело, ограниченное сферическими поверхностями.
Какими бывают линзы?
По форме различают следующие виды линз:
- Выпуклые — линзы, которые посередине толще, чем у краев.
- Вогнутые — линзы, которые посередине тоньше, чем у краев.
Выпуклые линзы тоже имеют разновидности:
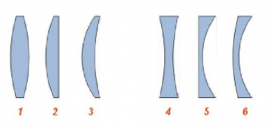
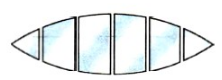
- Двояковыпуклая — линза, ограниченная с обеих сторон выпуклыми сферическими поверхностями (СП). Такая линза изображена ниже на рисунке 1.
- Плосковыпуклая — линза, ограниченная выпуклой СП с одной стороны и плоской поверхностью с другой (рис. 2)
- Вогнуто-выпуклая — линза, ограниченной с одной стороны вогнутой СП, а с другой — выпуклой СП (рис. 3).
Разновидности вогнутых линз:
- Двояковогнутая — линза, ограниченная с обеих сторон вогнутыми СП (рис. 4).
- Плосковогнутая — линза, ограниченная вогнутой СП с одной стороны и плоской поверхностью с другой (рис. 5)
- Выпукло-вогнутая — линза, ограниченной с одной стороны выпуклой СП, а с другой — вогнутой СП (рис. 6).
Тонкая линза
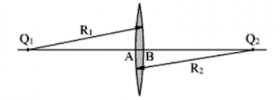
Мы будем говорить о линзах, у которых толщина l = AB намного меньше радиусов сферических поверхностей этой линзы R1 и R2. Такие линзы называют тонкими.
Определение
Тонкая линза — линза, толщина которой пренебрежимо мала по сравнению с радиусами сферических поверхностей, которыми она ограничена.
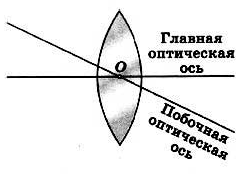
Главная оптическая ось тонкой — прямая, проходящая через центры сферических поверхностей линзы (на рисунке она соответствует прямой O1O2).
Оптический центр линзы – точка, расположенная в центре линзы на ее главной оптической оси (на рисунке ей соответствует точка О). При прохождении через оптический центр линзы лучи света не преломляются.
Побочная оптическая ось — любая другая прямая, проходящая через оптический центр линзы.
Изображение в линзе
Подобно плоскому зеркалу, линза создает изображения источников света. Это значит, что свет, исходящий из какой-либо точки предмета (источника), после преломления в линзе снова собирается в точку (изображение) независимо от того, какую часть линзы прошли лучи.
Определение
Оптическое изображение — картина, получаемая в результате действия оптической системы на лучи, испускаемые объектом, и воспроизводящая контуры и детали объекта.
Практическое использование изображений часто связано с изменением масштаба изображений предметов и их проектированием на поверхность (киноэкран, фотоплёнку, фотокатод и т. д.). Основой зрительного восприятия предмета является его изображение, спроектированное на сетчатку глаза.
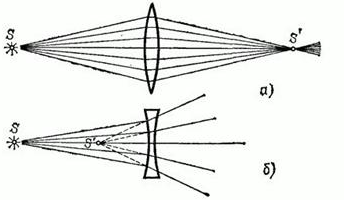
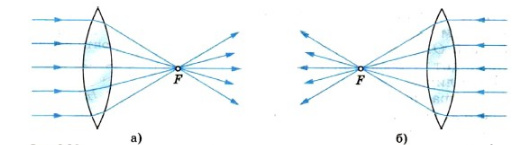
Изображения разделяют на действительные и мнимые. Действительные изображения создаются сходящимися пучками лучей в точках их пересечения (см. рисунок а). Поместив в плоскости пересечения лучей экран или фотоплёнку, можно наблюдать на них действительное изображение.
Если лучи, выходящие из оптической системы, расходятся, но если их мысленно продолжить в противоположную сторону, они пересекутся в одной точке (см. рисунок б). Эту точку называют мнимым изображением точки-объекта. Она не соответствует пересечению реальных лучей, поэтому мнимое изображение невозможно получить на экране или зафиксировать на фотоплёнке. Однако мнимое изображение способно играть роль объекта по отношению к другой оптической системе (например, глазу или собирающей линзе), которая преобразует его в действительное.
Собирающая линза
Обычно линзы изготавливают из стекла. Все выпуклые линзы являются собирающими, поскольку они собирают лучи в одной точке. Любую из таких линз условно можно принять за совокупность стеклянных призм. В воздухе каждая призма отклоняет лучи к основанию. Все лучи, идущие через линзу, отклоняются в сторону ее главной оптической оси.
Если на линзу падают световые лучи, параллельные главной оптической оси, то при прохождении через нее они собираются на одной точке, лежащей на оптической оси. Ее называют главным фокусом линзы. У выпуклой линзы их два — второй главный фокус находится с противоположной стороны линзы. В нем будут собираться лучи, которые будут падать с обратной стороны линзы.
Главный фокус линзы обозначают буквой F.
Определение
Фокусное расстояние — расстояние от главного фокуса линзы до их оптического центра. Оно обозначается такой же букой F и измеряется в метрах (м).
В однородных средах главные фокусы собирающих линз находятся на одинаковом расстоянии от оптического центра.
Пример №1. Что произойдет с фокусным расстоянием линзы, если ее поместить в воду?
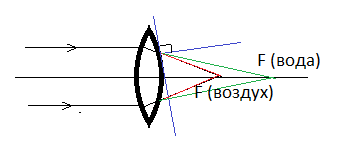
Вода — оптически более плотная среда, поэтому преломленные лучи будут располагаться ближе к перпендикуляру, восстановленному к разделу двух сред. Следовательно, фокусное расстояние увеличится. На рисунке лучам, выходящим из линзы в воздухе, соответствуют красные линии. Лучам, выходящим из линзы в воде — зеленые. Видно, что зеленые линии больше приближены к перпендикуляру, восстановленному к разделу двух сред, что соответствует закону преломления света.
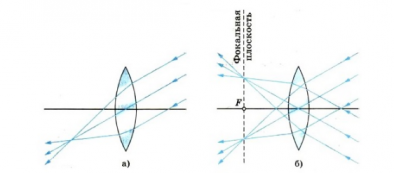
Направим три узких параллельных пучка лучей от осветителя под углом к главной оптической оси собирающей линзы. Мы увидим, что пересечение лучей произойдет не в главном фокусе, а в другой точке (рисунок а). Но точки пересечения независимо от углов, образуемых этими пучками с главной оптической осью, будут располагаются в плоскости, перпендикулярной главной оптической оси линзы и проходящей через главный фокус (рисунок б). Эту плоскость называют фокальной плоскостью.
Поместив светящуюся точку в фокусе линзы (или в любой точке ее фокальной плоскости), получим после преломления параллельные лучи.
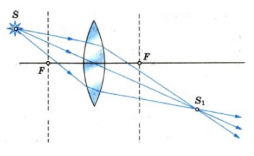
Если сместить источник дальше от фокуса линзы, лучи за линзой становятся сходящимися и дают действительное изображение.
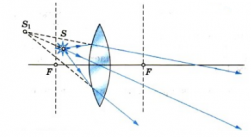
Когда же источник света находится ближе фокуса, преломленные лучи расходятся и изображение получается мнимым.
Рассеивающая линза
Вогнутые линзы обычно являются рассеивающими (лучи, выходя из них, не собираются, а рассеиваются). Это бывает если, поместить вогнутую линзу в оптически менее плотную среду по сравнению с материалом, из которого изготовлена линза. Так, стеклянная линза в воздухе является рассеивающей.
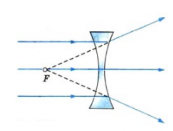
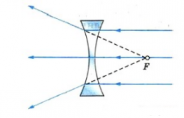
Если направить на вогнутую линзы световые лучи, являющиеся параллельными главной оптической оси, то образуется расходящийся пучок лучей. Если провести их продолжения, то они пересекутся в главном фокусе линзы. В этом случае фокус (и изображение в нем) является мнимым. Этот фокус располагается на фокусном расстоянии, равном F.
Другой мнимый фокус находится по другую сторону линзы на таком же расстоянии при условии, что среда по обе стороны линзы одинаковая.
Оптическая сила линзы
Оптическая сила линзы — величина, характеризующая преломляющую способность симметричных относительно оси линз и центрированных оптических систем, состоящих из таких линз.
Обозначается оптическая сила линзы буквой D. Единица измерения — диоптрий (дптр). Оптической силой в 1 дптр обладает линза с фокусным расстоянием 1 м.
Оптическая сила линзы равна величине, обратной ее фокусному расстоянию:
D=±1|F|
D > 0, если линза собирающая, D < 0, если линза рассеивающая. Чем ближе к линзе ее фокусы, тем сильнее линза преломляет лучи, собирая или рассеивая их, и тем больше оптическая сила линзы.
Пример №2. Найти фокусное расстояние линзы, если ее оптическая сила равна –5 дптр.
Так как оптическая силы линзы отрицательная, речь идет о рассеивающей линзе. Следовательно, будем использовать формулу:
D=−1|F|
Отсюда:
|F|=−1D=−1−5=0,2 (м)
Задание EF18041
Ответ:
а) 14 дптр
б) 20 дптр
в) 17 дптр
г) 33 дптр
Алгоритм решения
1.Записать формулу для нахождения оптической силы линзы.
3.Найти точку на главной оптической оси точку главного фокуса линзы.
4.Вычислить фокусное расстояние и перевести его в СИ.
5.Вычислить оптическую силу линзы.
Решение
Оптическая сила линзы определяется формулой:
D=1F
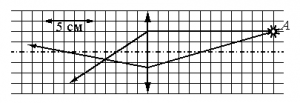
На рисунке видно, что 5 клеток = 5 см. Следовательно, 1 клетка = 1 см. После прохождения сквозь линзу лучи света, параллельные главной оптической оси, фокусируются в главном фокусе, который лежит на этой оси. Значит, фокус находится в точке пересечения этой оси и луча. От него до линзы 3 клетки. Следовательно, фокусное расстояние равно 3 см, или 0,03 м.
Отсюда:
D=10,03≈33 (дптр)
Ответ: г
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17706
Стеклянную линзу (показатель преломления стекла nстекла = 1,54), показанную на рисунке, перенесли из воздуха (nвоздуха = 1) в воду (nводы = 1,33). Как изменились при этом фокусное расстояние и оптическая сила линзы?
Ответ:
а) Фокусное расстояние уменьшилось, оптическая сила увеличилась.
б) Фокусное расстояние увеличилось, оптическая сила уменьшилась.
в) Фокусное расстояние и оптическая сила увеличились.
г) Фокусное расстояние и оптическая сила уменьшились.
Алгоритм решения
1.Установить характер преломления лучей линзой при ее перемещении из воздуха в воду.
2.Выяснить, как от этого зависят фокусное расстояние и оптическая сила линзы.
Решение
Чтобы узнать, что произойдет с лучами света при прохождении их сквозь линзу, погруженную воду, найдем относительные показатели преломления:
nвоздух−стекло=nстеклоnвоздух=1,541=1,54
nвода−стекло=nстеклоnвода=1,541,33≈1,16
Видно, что относительный показатель преломления уменьшился. Значит, преломленный линзой луч будет менее отклоняться от нормали, проведенной в точке падения на линзу. Следовательно, чтобы достигнуть главной оптической оси, ему придется пройти большее расстояние. Это говорит о том, что фокусное расстояние линзы увеличится.
Оптическая сила линзы — величина, обратная ее фокусному расстоянию. Если оно увеличится, то оптическая сила уменьшится.
Ответ: б
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18076
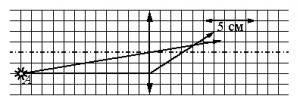
Какова приблизительно оптическая сила этой линзы?
Ответ:
а) –33,3 дптр
б) 7,7 дптр
в) 25,0 дптр
г) 33,3 дптр
Алгоритм решения
1.Записать формулу для нахождения оптической силы линзы.
2.Рассчитать длину 1 клетки.
3.Найти точку на главной оптической оси точку главного фокуса линзы.
4.Вычислить фокусное расстояние и перевести его в СИ.
5.Вычислить оптическую силу линзы.
Решение
Оптическая сила линзы находится по формуле:
D=1F
На рисунке видно, что 5 соответствуют 5 см. Следовательно, 1 клетка равна 1 см. После прохождения сквозь линзу лучи света, параллельные главной оптической оси, фокусируются в фокусе, который лежит на этой оси. Из рисунка видно, фокус находится в точке пересечения этой оси и луча, параллельного ей. Эту точку и линзу разделяют 3 клетки. Следовательно, фокусное расстояние равно 3 см, или 0,03 м.
Отсюда:
D=10,03≈33,3 (дптр)
Ответ: г
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 15.4k
Линза — деталь из прозрачного однородного материала, ограниченная криволинейными (чаще всего сферическими) или криволинейной и плоской поверхностями.
В зависимости от формы различают два типа линз:
- собирающие — линзы, у которых середина толще их краёв;
- рассеивающие — линзы, края которых толще середины.
Собирающие: (1) — двояковыпуклая; (2) — плоско-выпуклая; (3) — вогнуто-выпуклая.
Рассеивающие: (4) — двояковогнутая; (5) — плоско-вогнутая; (6) — выпукло-вогнутая.
Если через центры кривизны поверхностей линзы провести прямую (AB), то эта прямая будет называться главной оптической осью линзы.
Главная оптическая ось линзы — это прямая, проведённая через центры сферических поверхностей.
Если на собирающую линзу пустить пучок света параллельно главной оптической оси, то после прохождения лучей через линзу они пересекутся в одной точке (F), которая называется фокусом линзы.
Расстояние от оптического центра линзы до фокуса называется фокусным расстоянием.
Если пустить пучок света параллельно главной оптической оси на рассеивающую линзу, то после прохождения через линзу получится расходящийся пучок, как бы выходящий из фокуса линзы. Это мнимый фокус (лучи не проходят через него в действительности, нам это только кажется).
В рассеивающей линзе фокусное расстояние принято считать отрицательным.
(F<0).
Оптическая сила (D) линзы зависит как от радиусов кривизны (R_1) и (R_2) ее сферических поверхностей, так и от показателя преломления (n) материала, из которого изготовлена линза: (D=frac{1}{F}=(n-1)(frac{1}{R_1}+frac{1}{R_2})).
Обрати внимание!
Если поместить рассеивающую линзу в среду с показателем преломления большим, чем у вещества, из которого она сделана, то линза будет действовать как собирающая.
Аналогично, если поместить собирающую линзу в среду с большим показателем преломления, чем у вещества, из которого она сделана, то линза будет действовать как рассеивающая.
IV. Оптика
Тестирование онлайн
Характеристики изображения
1) Изображение может быть мнимое или действительное. Если изображение образовано самими лучами (т.е. в данную точку поступает световая энергия), то оно действительное, если же не самими лучами, а их продолжениями, то говорят, что изображение мнимое (световая энергия не поступает в данную точку).
2) Если верх и низ изображения ориентированы аналогично самому предмету, то изображение называется прямым. Если же изображение перевернуто, то его называют обратным (перевернутым).
3) Изображение характеризуется приобретаемыми размерами: увеличенное, уменьшенное, равное.
Изображение в плоском зеркале
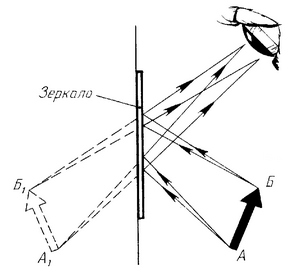
Изображение в плоском зеркале является мнимым, прямым, равным по размерам предмету, находится на таком же расстоянии за зеркалом, на каком предмет расположен перед зеркалом.
Линзы
Линза представляет собой прозрачное тело, ограниченное с двух сторон криволинейными поверхностями.
Различают шесть типов линз.
Собирающие: 1 – двояковыпуклая, 2 – плоско-выпуклая, 3 – выпукло-вогнутая. Рассеивающие: 4 – двояковогнутая; 5 – плосковогнутая; 6 – вогнуто-выпуклая.
Собирающая линза
Рассеивающая линза
Характеристики линз.
NN – главная оптическая ось – прямая линия, проходящая через центры сферических поверхностей, ограничивающих линзу;
O — оптический центр — точка, которая у двояковыпуклых или двояковогнутых (с одинаковыми радиусами поверхностей) линз находится на оптической оси внутри линзы (в её центре);
F – главный фокус линзы – точка, в которую собирается пучок света, распространяющийся параллельно главной оптической оси;
OF – фокусное расстояние;
N’N’ – побочная ось линзы;
F’ – побочный фокус;
Фокальная плоскость – плоскость, проходящая через главный фокус перпендикулярно главной оптической оси.
Ход лучей в линзе.
Луч, идущий через оптический центр линзы (О), не испытывает преломления.
Луч, параллельный главной оптической оси, после преломления проходит через главный фокус (F).
Луч, проходящий через главный фокус (F), после преломления идет параллельно главной оптической оси.
Луч, идущий параллельно побочной оптической оси (N’N’), проходит через побочный фокус (F’).
Формула линзы.
При использовании формулы линзы следует верно использовать правило знаков: +F – линза собирающая; -F – линза рассеивающая; +d – предмет действительный; -d – предмет мнимый; +f – изображение предмета действительное; -f – изображение предмета мнимое.
Величина, обратная фокусному расстоянию линзы, называется оптической силой.
Поперечное увеличение – отношение линейного размера изображения к линейному размеру предмета.
Современные оптические устройства используют системы линз для улучшения качества изображений. Оптическая сила системы линз, сложенных вместе, равна сумме их оптических сил.
Глаз
Для введённых нами линз существует два условно разных типа задач:
- задачи на построение в собирающей и рассеивающей линзах
- задачи на формулу для тонкой линзы
Первый тип задач основан на фактическом построении хода лучей от источника и поиска пересечения преломлённых в линзах лучей. Рассмотрим ряд изображений, полученных от точечного источника, который будем помещать на различных расстояниях от линз. Для собирающей и рассеивающей линзу существуют рассмотренные (не нами) траектории распространения луча (рис. 1) от источника .
Рис.1. Собирающая и рассеивающая линзы (ход лучей)
Для собирающей линзы (рис. 1.1) лучи:
- синий. Луч, идущий вдоль главной оптической оси, после преломления проходит через передний фокус.
- зелёный. Луч, проходящий через оптический центр линзы, не испытывает преломления (не отклоняется от первоначального направления).
- красный. Луч, идущий через передний фокус, после преломления распространяется параллельно главной оптической оси.
Пересечение любых из этих двух лучей (чаще всего выбирают лучи 1 и 2) дают изображение ().
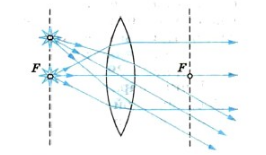
Для рассеивающей линзы (рис. 1.2) лучи:
- синий. Луч, идущий параллельно главной оптической оси, преломляется так, что продолжения луча проходит через задний фокус.
- зелёный. Луч, проходящий через оптический центр линзы, не испытывает преломления (не отклоняется от первоначального направления).
Пересечение продолжений рассмотренных лучей даёт изображение ().
Аналогично сферическому зеркалу, получим набор изображений от предмета, расположенного на различных расстояниях от зеркала. Введём те же обозначения: пусть — расстояние от предмета до линзы,
— расстояние от изображения до линзы,
— фокусное расстояние (расстояние от фокуса до линзы).
Для собирающей линзы:
(источник находится очень далеко от линзы). В этом случае мы можем считать, что все лучи от источника идут параллельно друг другу (рис. 2). Пустим два луча параллельно главной оптической оси линзы.
Рис. 2. Собирающая линза (источник в бесконечности)
Т.к. все лучи, идущие параллельно главной оптической оси линзы, после преломления в линзе проходят через фокус, то точка фокуса и является точкой пересечения преломлённых лучей, тогда она же и есть изображение источника (точечное, действительное).
(источник находится за двойным фокусным расстоянием) (рис. 3).
Рис. 3. Собирающая линза (источник за двойным фокусом)
Воспользуемся ходом луча, идущего параллельно главной оптической оси (отражается в фокус) и идущего через главный оптический центр линзы (не преломляется). Для визуализации изображения введём описание предмета через стрелку. Точка пересечения преломившихся лучей — изображение (уменьшенное, действительное, перевёрнутое). Положение — между фокусом и двойным фокусом.
(источник находится ровно в двойном фокусе) (рис. 4).
Рис. 4. Собирающая линза (источник в двойном фокусе)
Воспользуемся ходом луча, идущего параллельно главной оптической оси (отражается в фокус) и идущего через главный оптический центр линзы (не преломляется). Точка пересечения преломившихся лучей — изображение (того же размера, действительное, перевёрнутое). Положение — ровно в двойном фокусе.
(источник между фокусом и двойным фокусом) (рис. 5)
Рис. 5. Собирающая линза (источник между двойным фокусом и фокусом)
Воспользуемся ходом луча, идущего параллельно главной оптической оси (отражается в фокус) и идущего через главный оптический центр линзы (не преломляется). Точка пересечения преломившихся лучей — изображение (увеличенное, действительное, перевёрнутое). Положение — за двойным фокусом.
(источник находится ровно в фокусе собирающей линзы) (рис. 6)
Рис. 6. Собирающая линза (источник в фокусе)
Воспользуемся ходом луча, идущего параллельно главной оптической оси (отражается в фокус) и идущего через главный оптический центр линзы (не преломляется). В этом случае, оба преломлённых луча оказались параллельными друг другу, т.е. точка пересечения отражённых лучей отсутствует. Это говорит о том, что изображения нет.
(источник находится между фокусом и главным оптическим центром) (рис. 7)
Рис. 7. Собирающая линза (источник перед фокусом)
Воспользуемся ходом луча, идущего параллельно главной оптической оси (отражается в фокус) и идущего через главный оптический центр линзы (не преломляется). Однако преломлённые лучи расходятся, т.е. сами преломлённые лучи не пересекутся, зато могут пересечься продолжения этих лучей. Точка пересечения продолжений преломлённых лучей — изображение (увеличенное, мнимое, прямое). Положение — по ту же сторону, что и предмет.
Для рассеивающей линзы построение изображений предметов практически не зависит от положения предмета, так что ограничимся произвольным положением самого предмета и характеристикой изображения.
(источник находится очень далеко от линзы). В этом случае, мы можем считать, что все лучи от источника идут параллельно друг другу (рис. 8). Пустим два луча параллельно главной оптической оси линзы.
Рис. 8. Рассеивающая линза (источник в бесконечности)
Т.к. все лучи, идущие параллельно главной оптической оси линзы, после преломления в линзе должны проходить через фокус (свойство фокуса), однако после преломления в рассеивающей линзе лучи должны расходится. Тогда в фокусе сходятся продолжения преломившихся лучей. Тогда точка фокуса и является точкой пересечения продолжений преломлённых лучей, т.е. она же и есть изображение источника (точечное, мнимое).
- любое другое положение источника (рис. 9).
Рис. 9. Рассеивающая линза (произвольное положение источника)
Воспользуемся ходом луча, идущего параллельно главной оптической оси (продолжение отражённого луча проходит через передний фокус) и идущего через главный оптический центр линзы (не преломляется). Тогда изображением будет пересечение продолжений преломлённых лучей.
Второй тип задач связан с формулой тонкой линзы. Такие задачи основываются на числовых данных параметров, характеризующих положение источника, изображения или фокуса линзы. Рассмотрим произвольную систему (рис. 10). Пусть положение источника (), изображения (
) и фокуса системы (
) задано.
Рис. 10. Формула тонкой линзы
Тогда взаимосвязь между параметрами положения элементов можно описать формулой:
(1)
Важно: для использования формулы (1) необходимо помнить правило расстановки знаков. Если линза собирающая, то , если рассеивающая, то
. В случае действительных предметов и изображений:
,
, а в случае мнимых предметов и изображений:
и
.
И последним параметром, характеризующим линзы или систему линз, является оптическая сила линзы (). Её нахождение довольно простое:
(2)
Размерность оптической силы линзы: м
=дптр (диоптрии). Оптическая сила собирающей линзы положительна, рассеивающей — отрицательна.
Вывод: задачи с линзами, в целом, разделены на два класса. Задачи на построение основываются на рисунках 2-9. Достаточно проанализировать ход лучей и найти изображение (рис.1). Численные значения в дано указывают на задачи на формулу тонкой линзы (1).
В
данной теме будет рассмотрено решение задач на построение изображений в линзе.
Задача
1.
На рисунке изображен предмет АВ и собирающая линза. Постройте
изображение предмета если он находится а) за двойным фокусом б) между фокусом
и двойным фокусом.
РЕШЕНИЕ
Изобразим
на чертеже собирающую линзу, её главную оптическую ось, фокусы и двойные
фокусы.
Двойной
фокус – это точка, находящаяся на оптической оси на расстоянии от оптического
центра, вдвое большем, чем фокусное расстояние. Изобразим предмет АВ,
находящийся за двойным фокусом.
Точка
А находится на оптической оси линзы, поэтому её изображение тоже будет находится
на оптической оси. Чтобы получить изображение точки В, понадобится два
луча. Один направим параллельно оптической оси, а второй – через оптический
центр. Лучи, проходящие через оптический центр, не преломляются, поэтому легко
можем продолжить последний луч. Луч, параллельный оптической оси преломляется,
и после преломления проходит через фокус линзы. На пересечении этих лучей и
формируется изображение точки В, которое обозначим как B’.
Точка A’
будет
находится на главной оптической оси.
Во
втором случаи поступаем таким же образом используя два луча.
Таким
образом, получено действительное и перевёрнутое изображение. Только в этот раз
оно является увеличенным и находится за двойным фокусом.
Задача
2.
На рисунке указан источник света и его изображение в линзе. Также на рисунке
указана главная оптическая ось линзы. На основании этих данных, найдите
положение оптического центра линзы, её фокусов, а также определите тип линзы.
РЕШЕНИЕ
В
первую очередь, проведём прямую через источник света и его изображение (она называется
побочной оптической осью). Точка пересечения этой прямой с главной оптической
осью является оптическим центром линзы.
Обозначим
на нашем чертеже линзу. От источника света направим луч на линзу параллельно
главной оптической оси. Известно, что луч преломляясь идёт через фокус и через
изображение (или же, через изображение идёт продолжение луча). Проведём
пунктирную прямую через точку, в которой луч падает на линзу и через изображение
источника света. Точка, в которой данная прямая пересекает главную оптическую
ось и будет являться фокусом линзы.
Теперь,
с уверенностью можно сказать, что прямая, которую построили является
продолжением преломлённого луча. По характеру преломления луча или, исходя из
того, что изображение мнимое и находится ближе фокуса, можно заключить, что
линза является рассеивающей.
Задача
3.
На рисунке изображен луч АВ, прошедший через рассевающую линзу. Также,
на рисунке указаны положения фокусов линзы. Постройте ход падающего луча.
РЕШЕНИЕ
Отметим
на чертеже оптический центр линзы. Поскольку имеются положения фокусов линзы, можно
провести фокальную плоскость. Теперь проведём продолжение преломлённого луча до
пересечения с фокальной плоскостью. Точку пересечения обозначим за F’.
Через
эту точку и оптический центр линзы пройдёт побочная оптическая ось. Луч, идущий
вдоль этой оси пройдёт, не меняя своего направления (поскольку он пройдёт через
оптический центр). Луч, параллельный побочной оси, преломляется таким образом,
что продолжение преломлённого луча пройдёт через точку F’.
Таким образом, построен падающий луч.
Задача
4.
Постройте изображение предмета АВ в соответствии с указанным рисунком.
РЕШЕНИЕ
Здесь
сложность заключается в том, что предмет проходит через фокус, причём, таким
образом, что часть предмета находится на расстоянии, ближе фокусного, а часть –
между фокусом и двойным фокусом.
Можно
попытаться разбить предмет на два отрезка: AF
и FB. Очевидно, что
изображения и того, и другого отрезка будут уходить в бесконечность, поскольку,
точка F, естественно,
находится на фокусном расстоянии от линзы. А, как изветно, изображения
предметов, находящихся на фокусном расстоянии от линзы, не формируются (или
формируются в бесконечности).
Однако,
следует заметить, что луч, идущий в направлении от точки А к точке В
преломляется таким образом, что преломлённый луч параллелен главной оптической
оси. Можно построить продолжение этого луча.
Таким
образом, все точки изображения предмета АВ будут лежать на прямой,
проходящей через указанный луч и его продолжение. Проведём прямую через точку А
и оптический центр до пересечения с указанной ранее прямой. В точке пересечения
получится изображение точки А, которое обозначим как A’.
Аналогично,
проведём прямую через оптический центр и точку D
– таким образом, получим точку B’.
Если попытаться получить изображения других точек аналогичным способом, то можно
убедиться, что изображение данного предмета получается разрозненным (то есть,
делится на две части). Действительно, ведь изображение той части предмета,
которая находится перед фокусом, является мнимым, а изображение части,
находящейся между фокусом и двойным фокусом является действительным.
Задача
5.
На рисунке указан предмет, который находится на таком расстоянии от линзы, что
его изображение является действительным и увеличенным ровно в 2 раза. Постройте
это изображение и найдите длину отрезка A’C’,
если длина отрезка AB
равна 15 см, а длина
отрезка A’B’
равна 35 см. Угол BAC
прямой.
РЕШЕНИЕ
Отметим
на чертеже фокусы и двойные фокусы линзы. Отметим эти точки таким образом,
чтобы наш предмет находился между фокусом и двойным фокусом, поскольку именно в
этом случае получается действительное и увеличенное изображение (которое будет
находится за двойным фокусом). Итак, чтобы построить изображение, необходимо
получить изображения точек А, В и С. Построим эти точки
используя два луча.
Т.к.
изображение больше предмета в два раза, то
По
теореме Пифагора
Ответ: 18 см.